Модифицируемый метод Эйлера
реклама
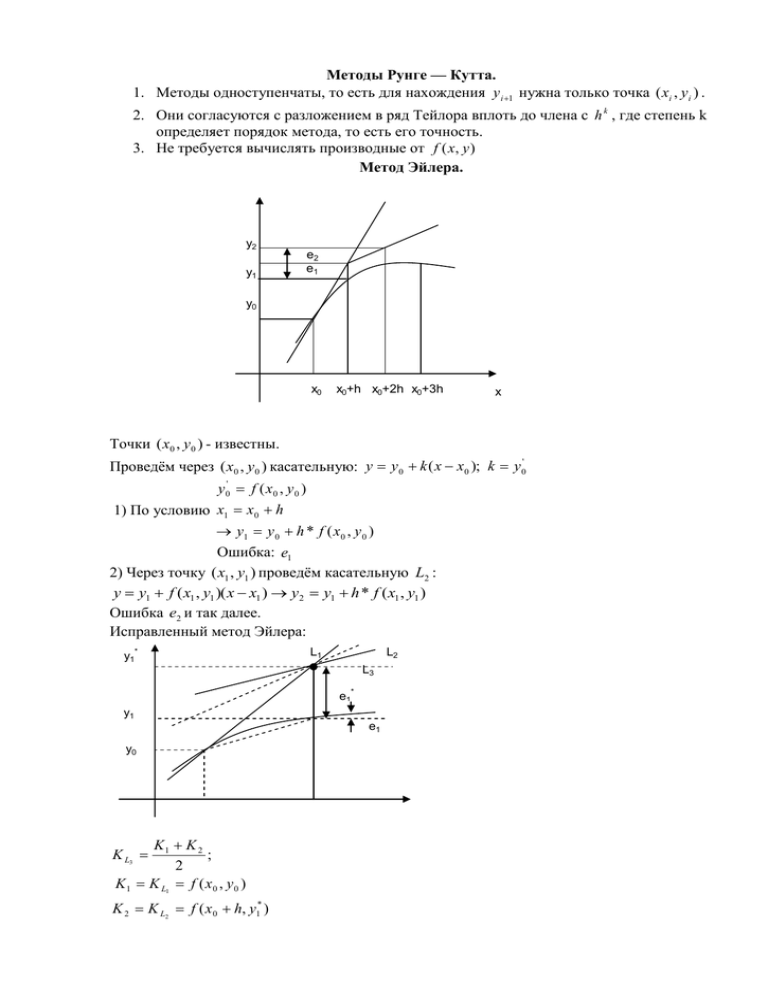
Методы Рунге — Кутта. 1. Методы одноступенчаты, то есть для нахождения y i 1 нужна только точка ( xi , yi ) . 2. Они согласуются с разложением в ряд Тейлора вплоть до члена с h k , где степень k определяет порядок метода, то есть его точность. 3. Не требуется вычислять производные от f ( x, y ) Метод Эйлера. y2 y1 e2 e1 y0 x0 x0+h x0+2h x0+3h x Точки ( x0 , y0 ) - известны. Проведём через ( x0 , y0 ) касательную: y y 0 k ( x x0 ); k y 0' y 0' f ( x0 , y 0 ) 1) По условию x1 x0 h y1 y 0 h * f ( x0 , y 0 ) Ошибка: e1 2) Через точку ( x1 , y1 ) проведём касательную L2 : y y1 f ( x1 , y1 )( x x1 ) y2 y1 h * f ( x1 , y1 ) Ошибка e2 и так далее. Исправленный метод Эйлера: y1* L1 L2 L3 e1* y1 y0 K1 K 2 ; 2 K 1 K L1 f ( x0 , y 0 ) K L3 K 2 K L2 f ( x0 h, y1* ) e1 где y1* y 0 h * f ( x0 , y 0 ) , то есть K 2 f ( x0 h, y0 h * f ( x0 , y0 )) K L3 K L4 f ( x0 , y 0 ) f ( x0 h, y 0 h * f ( x0 , y 0 )) 2 1 h [ f ( x0 , y 0 ) f ( x0 h, y 0 h * f ( x0 , y 0 ))] 2 1 y m h [ f ( x m , y m ) f ( x m h, y m h * f ( x m , y m ))] 2 y1 y 0 y m 1 f ( x, y) f ( xi , yi ) ( x xi ) f x' ( y yi ) f y' f ( x0 h, y0 h * f ( x0 , y0 )) f ( x0 , y0 ) h f x' h * f ( x0 , y0 ) f y' Модифицированный метод Эйлера. h y1* y 0 f ( x0 , y 0 ) 2 h h h K L3 K L3 f ( x0 , y1* ) f ( x 0 , y 0 f ( x0 , y 0 )) 2 2 2 h h y1 y 0 h * f ( x0 , y 0 f ( x0 , y 0 )) 2 2 h h y m 1 y m h f ( x m , y m f ( x m , y m )) 2 2 L1 y1* L2 L3//L2 y1 y0 x0 Метод Эйлера. y2 y1 e2 e1 y0 x0 x0+h x0+2h x0+3h x Точка ( x0 , y0 ) - известна. Проведём через ( x0 , y0 ) касательную y y 0 k ( x x0 ) , где k y 0' . Так как по условию: y 0' f ( x0 , y 0 ) x1 x0 h Откуда y1 y0 h * f ( x0 , y0 ) . Ошибка равна e1 , затем e2 , так как y2 y1 h * f ( x1 , y1 ) Исправленный метод Эйлера L2 y1* L1 L4 y1 L3 y0 x0 x0 +h Через ( x0 , y0 ) проведём L` : K1 K L1 f ( x0 , y 0 ) Через ( x1 , y1* ) проведём L2 : K 2 K L2 f ( x0 h, y1* ) K1 k 2 2 f ( x0 , y0 ) f ( x0 h, y0 h * f ( x0 , y0 )) K3 K 4 2 Затем K 3 K L3 1 h [ f ( x0 , y 0 ) f ( x0 h, y 0 h * f ( x0 , y 0 ))] 2 1 y m h [ f ( x m , y m ) f ( x m h, y m h * f ( x m , y m ))] 2 y1 y 0 y m 1 Метод Рунге – Кутта 4-го порядка. h y m 1 y m ( K 1 2 K 2 2 K 3 K 4 ) 6 K1 f ( xm , y m ) h h K 2 f ( xm , y m K1 * ) 2 2 h h K 3 f ( xm , y m K 2 * ) 2 2 K 4 f ( x m h, y m K 3 * h) Программы: h y m 1 y m [ f ( x m , y m ) f ( x m h, y m h f ( x m , y m ))] 2 Sub Euler () Dim x As Single ' начальное значение Dim x1 As Single ' конечное значение Dim N As Integer ' число шагов Dim Y As Single ' начальное значение функции Dim H As Single ' шаг интегрирования H = (x1 – x) / N: y1 = y For i = 1 to N Call funk (x, f): f1 = f x = x + h: y = y + f * h: call funk (x, f) y = y1 + h * (f1 + f) / 2: y1 = y next i sub funk (x, f) f = - exp (- x) end sub y’ = e x ; y(0) 1; x 2; n 20 y = e 2 0,13533528 - точное y (2) = 0,13461485 – метод Эйлера Модифицированный метод Эйлера. h h y m 1 y m h[ f ( x m , y m f ( x m , y m ))] 2 2 h = (x1 - x) / N/2: y1 = y for i = 1 to n call funk (x, f ) x = x + h: y = y + f * h: call funk (x, f) y1 Модифицируемый метод Эйлера h h ym+n = ym + h[f(xm+ , ym + f(xm, ym)] 2 2 h = (x1 – x)/N/2 : y1 = y for i = 1 to n call funk(x, f) x = x + h: y = y + f * h: call funk(x, f) y1 = y1 + f * 2 * h : x = x + h : y = y1 next i y(2) = ,135695455 Усовершенствованный метод последовательный приближений y=f(x) f(a) f(xn-1) 45° Q f(xn) (λ-1)∆x ∆x λ∆x xn xn+1 a f(xn-1) = xn; f(xn) = xn+1 ∆x = xn-1 – xn = f(xn) - xn xn+1 = xn + ∆x, лучше взять xn+1 = xn + λ *∆x, λ>1 ( 1)x 1 1 1 tg = x f (a) f ( xn) f ' ( ) , где xn a tg = a xn 1 1 f ' ( ) —известно, но можно принять f'( f ( xn) f ( xn 1) f ( xn) xn ) xn xn 1 xn xn 1 f'( ) = 1 1 Геометрический процесс отыскания следующего приближения xn-1 сводится к тому, что проводится хорда через точки (xn, f(xn)) и (xn-1, f(xn-1)) и определяется точка ее пересечения с прямой y = x. Сходимость: 1) 0<f'(x)<1 1< < поправки ∆x малы, но 1< < увеличит их и сходимость улучшиться 2) -1<f'(x)<0 1 1 2 1 1 их 2 уменьшит и метод сходится быстрее: поправки уменьшаются 1 на коэффициент между и 1. 2 поправки велики, а Расходится: 3) f'(x)>1 1 0 1 f ' ( ) Так как 0 , то в усовершенствованном методе знаки поправок изменяются нужным образом. axn 4) f'(x)<-1 xn+1 0< 1 — расходится, так как поправки велики 2 1 и процесс расходится. 2 Описанная модификация метода итераций принадлежит Векштейну (1958 г) Каждая поправка умножается на коэффициент между 0 и Пусть xn 1 a и xn 1 1 f ' ( xn ) Метод Ньютона – Рафсона f ( xn ) xn f ( xn ) xn f ' ( xn ) 1 f ' ( xn ) 1 f ' ( xn ) f ( x) x f ' ( x) g ( xn ), где g ( x) 1 f ' ( x) xn1 xn * x xn ( f ( xn ) xn ) xn (1) xn1 f ( xn ) xn f ' ( xn ) или xn1 1 f ' ( xn ) Если g ' ( x) 1 , то метод сходится: f ' ( x) f ' ( x) xf ' ' ( x)1 f ' ( x) f ( x) xf ' ( x)( f ' ' ( x)) 1 f ' ( x)2 xf ' ' ( x) xf ' ' ( x) f ' ( x) f ( x) f ' ' ( x) xf ' ( x) f ' ' ( x) f ' ' ( x) f ( x) x 1 f ' ( x)2 1 f ' ( x)2 g ' ( x) Так как f (x) = x, (F (x) = 0 = x – f (x)), то для x, близких к «a», (f (x) - x) – мало. Поэтому (1) сходится, если: 1) x 0 выбрано близко к решению x = f (x) 2) f ''(x) – не становится слишком большой. 3) f ' (x) не слишком близка к 1. Это и есть знаменитый метод Ньютона – Рафсона. f ( xn ) xn f ' ( x) xn F ( xn ) xn ( x' n F ' ( xn )) xn F ( xn ) xn xn F ' ( xn ) F ( xn ) xn1 xn 1 f ' ( xn ) F ' ( xn ) F ' ( xn ) F ' ( xn ) F (x) = x – f (x) = 0 Или: 1) x 0 близко к корню F (x) = 0 2) F ' ' ( x) 0 - не слишком большая 3) F ' ( x0 ) - не близка к нулю «3)» означает, что никакие два корня не находятся слишком близко один к другому. Геометрическое толкование. а) xn , то есть равен углу наклона касательной к y = f (x) в точке x xn y=f(x) xn б) a xn+2 xn+1 y=F(x) a xn+2 xn+1 xn x Уравнение касательной: y F ( x0 ) F ' ( x0 )( x x0 ) Пусть y 0 0 F ( x0 ) F ' ( x0 ) ( x1 x0 ) F ( x0 ) x1 x0 F ' ( x0 ) x 2 x1 F ( x1 ) F ' ( x1 ) x n x n 1 F ( x n 1 ) F ' ( x n 1 ) xn xn1 2m1 M2 m1 min F ' ( x) m[ , ] M 2 max F ' ' ( x) m[ , ] x 0 выбирать так, чтобы F ( x0 ) * F ' ' ( x0 ) 0 Пример: F (x) = sin x – x + 0.15 = 0 на отрезке [0.5; 1] с погрешностью 10 4 F ' ( x) cos x 1 sin x n 1 x n 1 0.15 x n x n 1 n 1, 2 , ... cos x n 1 1 F ( x0 ) * F ' ' ( x0 ) 0; F ' ' ( x) sin x 0 для 0.5 x 1 То необходимо найти x 0 , чтобы F ( x0 ) 0 Cos 0,5 Это верно при x 0 = 1 Sin 1 m1 min f ' ( x) на [0.5; 1] F ' ( x) cos x 1; m1 cos 0.5 1 0.88 1 0.12 m1 1 cos x 0.12 M 2 max F ' ' ( x) m[0.5;1] F ' ' ( x) sin x M 2 sin 1 0.84 Примечание: если 2m1 10 2 , то можно xn xn1 10 1 M2 1) x0 1; 10 3 , т.к. 1 10 1 10 4 10 3 ; n 0 sin xn xn 0.15 cos xn 1 3) Вычисляем xn1 xn 2) xn1 xn 4) Проверяем 1 и так далее. Случай почти равных корней x0=x1 a1 a2 x1 x Производная f ' ( x) близка к 1 при x a1 или x a2 f (a 2 ) f (a1 ) f ' ( x) 1 a 2 a1 На основании теоремы о среднем a a2 x 1 2 Итерационный процесс осциллирует между x 0 и x1 до бесконечности, не сходясь ни к одному значению корня. Другими словами – не удаётся отделить эти два корня, так как они расположены слишком близко один к другому. f ( xn ) xn f ( xn ) Трудности возникают, так как xn1 , где 1 f ' ( xn ) 0 1 f ' ( xn ) Мейкон (1963) предложил метод, согласно которому сначала находят значение x, где f ' ( x) 1 , то есть решается уравнение: x x f ' ( x) 1 Пусть x x - решение. Эта точка a1 x a 2 Положим для начального приближения x Пусть d a1 a2 2 a2 a1 , т.е. a1 x d и a2 x d 2 Разложим f (x) в ряд Тейлора в окрестности точки x : f ' ( x) 1 f ( x) f ( x) ( x x) f ' ' ( x)( x x) 2 ... 1! 2! 1 Так как f ' ( x) 1 то f ( x) f ( x) ( x x) f ' ' ( x)( x x) 2 2! Пусть x x d 1 f ' ' ( x)d 2 2 Но по условию f ( x d ) x d 1 x d f ( x) d f ' ' ( x)d 2 2 f ( x d ) f ( x) d d 2( x f ( x)) f ' ' ( x) Если F ( x) x f ( x) 0, то F ' ' ( x) f ' ' ( x) и d 2 F ( x) , так как надо решить F ' ' ( x) уравнение F ' ( x) 0 x-d x x-d Сначала решаем: x x f ' ( x) 1 Потом ищется: d 2( x f ( x)) f ' ' ( x) Затем начальные приближения для a1 и a2 Если f ' ' ( x) 0 , то это означает что f ' ( x) 1 имеет более чем один корень вблизи x , тогда сначала решается уравнение f ' ' ( x) 0 , то это означает, что f ' ( x) 1 имеет более чем один корень x . Метод хорд Каждое значение xn+1 находится как точка пересечения оси абсцисс с хордой, проведенной через точки F(a) и F(b) , причем одна из этих точек фиксируется — та, для которой F(x)·F''(x)>0. Если неподвижен конец хорды x = a, то F ( xn) xn+1 = xn ( xn a) F ( xn) F (a) Если неподвижен конец хорды x = b, то F ( xn) (b xn) F (b) F ( x) Если |xn+1 - xn|> ,то в первом случае считаем b = xn+1, во втором a = xn+1 и повторяем вычисление. При использовании метода хорд полагается, что корень x находится на отрезке [a,b]. xn+1 = xn - Метод секущих Реализуется алгоритмом, описанным выше, если абсцисса a и b взяты с одной стороны от корня. Необходимость вычисления F'(x) и выбора одной из двух формул затрудняют практическое применение методов хорд и секущих в отдельности. x2 a x0=b x x1 F(x) b0a1 b1a2 b2a3 x0 x1 x2 x3 x Полином Чебышева Применяется в уникальном процессе, называемом экономизацией, для преобразования разложения функции в быстросходящийся полином. Свойства полиномов Чебышева 1. Они являются ортогональными с соответствующей весовой функцией, определенной либо на непрерывном интервале, либо на ряде дискретных интервалов. 2. Они равно пульсирующие функции, то есть изменяются между равными максимальными и минимальными значениями. 3. Нули полиномов Чебышева чередуются один за другим. 4. Все полиномы Чебышева удовлетворяют трехчленным рекуррентным соотношением. 5. Они легко вычисляются и обращаются в форму степенного ряда на основании исходной формы. Все эти свойства образуют аппроксимирующую функцию минимакс (то есть в процессе аппроксимации минимизируется максимальная ошибка) В МНК минимизируется сумма квадратов ошибок. В МНК максимальная ошибка может принимать достаточно большое значение. В аппроксимации Чебышева средняя ошибка часто может принимать большое значение, а минимизируется максимальная ошибка. Определение полиномов Чебышева T0(x) = 1 Tn(x) = Cos(n ) Cos = x Полиномы Чебышева ортогональны, так как косинус является ортогональной функцией и Cos(n ) является полиномом в степени n величин . Cos(n+1) + Cos(n-1) = 2Cos Cosn Tn+1 + Tn-1 = 2xTn Tn+1 = 2xTn - Tn-1 Так как T0 = 1; T1= x, то T2 = 2xT1 – T0 = 2x2 – 1 T3 = 2xT2 - T1 = 2x(2x2 – 1) – x = 4x3 – 3x То есть T0 = 1 T1 = x T2 = 2x2 – 1 T3 = 4x3 – 3x T4 = 8x4 – 8x2 +1 T5 = 16x5 – 20x3 +5x T6 = 32x6 – 48x4 + 18x2 -1 T7 = 64x7 – 111x5 +56x3 -7x T8 = 128x8 – 256x6 +160x4 – 32x2 +1 Можно образовать таблицу степеней x в выражения полиномов Чебышева, проводя решение относительно степеней x из этой таблицы: 1 = T0 x = T1 x2 = (T0 + T2)/2 x3 = (3T1 + T3)/4 x4 = (3T0 + 4T2 + T4)/8 x5 = (10T1 + 5T3 + T5)/16 x6 = (10T0 + 15T2 + 6T4 + T6)/32 x7 = (35T1 + 21T3 + 7T5 + T7)/64 x8 = (35T0 + 56T2 + 28T4 + 8T6 + T8)/128 Важное свойство полиномов Чебышева заключается в том, что во всех полиномах степени n имеется коэффициент определение 1 и это полиномы Чебышева при делении на 2n-1 обладают наименьшим экстремальным значением в интервале -1 x +1 Не существует других полиномов степени n, эти коэффициенты равны 1 и которые обладают меньшим экстремальным значением, чем Tn ( x ) 1 max n 1 n 1 в интервале |x| 1 2 2 Это является важным положением, так как утверждает, что если аппроксимировать функцию на интервале |x| 1 при помощи полиномов Чебышева, ограниченных n членами, максимальной ошибкой приближения будет 1/2n-1 Разложим функцию f(x) в ряд с помощью полиномов Чебышева: n f(x) = a T ( x) n n n 0 Метод аппроксимации f(x) с помощью полиномов Чебышева является простым в употреблении и обладает умеренной сходимостью любого ограниченного разложения функции f(x) в ряд. m a x Так как f(x) = n n , то n 0 f(x) = a0 + x(a1 +x(a2 + … + x(am-1 + am x))) …) — этот ряд можно привести к ряду полиномов Чебышева, начиная от внутренних скобок, в виде am-1 + am x = am-1 T0 + am T1 Можно умножить n скобочное гнездо: a0T0 + a1T1 + … +anTn на x и добавить к нему следующий коэффициент степени nm-n-1, чтобы получить (n+1) гнездо. Тогда применяя xT0 = T1; xTn = (Tn+1 + Tn-1)/2 приводим степенной ряд в n скобках, осуществляя преобразование в (n+1) степенной ряд полиномов Чебышева следующим образом: anTn an 1Tn 1 a1 a 3 a2 a1 ... ( )T 2 (a 0 )T 1 (am n 1 )T 0 2 2 2 2 2 Например: N fN(x) = a x N n n 0 f0 = a0 f1 = a0 + a1 x a0 T0 a0 T0 + a1 T1 a2 a2 f2 = a0 + a1 x + a2 x2 (a0 + )T0 + a1 T1 + ( )T2 2 2 a2 3a 3 a2 a3 f3 = a0 + a1 x + a2 x2+a3 x3 (a0 + )T0 +( a1+ )T1 + ( )T2+( )T2 2 2 4 4 a 2 3a 3 3a 3 f4 = a0 + a1 x + a2 x2+a3 x3 + a4 x4 (a0 + + )T0 +(a1+ )T1a1+ 2 8 4 1 a3 a4 (a 2 a 4)T 2 ( )T 3 ( )T 4 2 4 8 a 2 3 a 3 3a 3 10a 5 f4 = a0 + a1 x + a2 x2+a3 x3 + a4 x4 +a5 x5 (a0 + + )T0 +( a1+ + )T1+ 2 16 8 4 a2 a4 a 3 5a 5 a4 a5 +( )T2+ ( )T3+( )T4+( )T5 2 4 16 8 16 и т.д. То есть можно вместо f(x) = a0 + a1 x + a2 x2 +…+am xm брать ряд f(x) = b0 + b1 T1 + b2 T2 +…+bm Tm Для того, чтобы этот процесс был точным, ряд должен быть записан в такой форме, где вычисляется f(x) при x (x) 1. Пример: x2 x3 y = ln(1+x) x (1) 2 3 T0 T2 3T 1 T 3 y T1 – ( )+( ) 4 12 T 0 15T 1 T 2 T 3 y(2) 4 12 4 12 Отбрасывая в (1) последний член, получаем погрешность ( ), равную 0,333 при x = 1. А в ряд (2) при отбрасывании последних двух членов: 1 1 = -00,1666… (так как Tn 1) 12 4 Таким образом, можно написать T 0 15T 1 T 2 , обеспечивающее лучшую точность, чем (1). y = ln(1+x) 4 12 4 Теперь, используя определение полиномов Чебышева можно написать: 1 15 2 x 2 1 y = ln(1+x) — это и есть экономизация. 4 12 4 4 Численная оценка полиномов Чебышева Tn(x) = 2xTn-1(x) – Tn-2(x) T0 = 1; T = x T 0 15 T2 T2 y = ln(1+x) - T 1 (3) 4 12 4 12 Можно оценить (3) первой оценкой численного значения для 4 полиномов Чебышева: (пусть x = 0.3) T0 = 1; T = 0.3 T2 = (2)(0.3)T1 – T0 = 2·0.3·0.3-1 = -0.82 T3 = (2)(0.3)T2 – T1 = -2·0.3·0.82 – 0.3 = 0.792 1 15 1 1 y = ln(1.3) ( )0.3 (0.82) (0.792) 0.2640 4 12 4 12 y = ln(1.3) = 0.26236426 Экономизируем разложение ряда Маклорена: x2 x3 x4 x5 x6 ex = 1 + x + ... 2 6 24 120 720 1 = T0 x = T1 1 x 2= (T 0 T 2) 2 1 x 3= (3T 1 T 3) 4 1 x 4= (3T 0 4T 2 T 4) 8 1 (10T 1 5T 3 T 5) x 5= 16 1 (10T 0 15T 2 6T 4 T 6) x 6= 32 1 1 1 1 (3T 0 4T 2 T 4) (10T 1 5T 3 ...) +… e x= T 0 T 1 (T 0 T 2) (3T 1 T 3) 4 24 192 1920 e x= 1.2661T0 + 1.1302T1 + 0.2715T2 + 0.0443T3 + … e x= 1.2661 + 1.1302x + 0.2715(2x2 - 1) + 0.0444(4x 3– 3x) + … e x 0.9946 + 0.9974x + 0.5430x2 + 0.1771x3 + … x3 x5 6 120 1 1 (3T 1 T 3) (10T 1 5T 3 T 5) Sin x = T1 24 1920 169 5 1 T1 T3 T5 Sin x = 192 128 1920 x5 изменяет коэффициент T1< на 1%, x7 - <0.01% 169 5 T1 T3 Sin x = 192 128 T1 = x; T3 = 4x3 – 3x; Sin x = 0.9974x – 0.1562x 3= x(0.9974 – 0.1562x2) Sin x = x - Маклор Ошибка 2·10-3 1·10-3 0 1·10-3 0,2 0,4 0,6 0,8 1
