Численные методы математического программирования

Муниципальное бюджетное общеобразовательное учреждение
«Лицей №39»
РАЗРАБОТКА УРОКА
по предмету
«ИНФОРМАТИКА И ИКТ»
Численные методы математического программирования.
Сравнение методов нахождение корней нелинейных уравнений
методом деления отрезка пополам
(метод бисекции) и методом хорд.
Интегрированный урок учителей математики и информатики
учитель информатики и ИКТ Мишина Ирина Николаевна
г. Озерск
2015 г.
1
Аннотация:
На
данном
уроке
учителем
математики
были
рассмотрены принципы нахождения корней алгебраического многочлена
двумя
численными методами: методом деления отрезка пополам (метод
бисекции) и методом хорд с учетом определяемой точности. Затем учителем
информатики вместе с учениками физико-математического профиля были
разработаны алгоритмы вычисления корней этими методами, а также в среде
Free Pascal
проверку.
были разработаны программы, реализующие этот поиск и
В этой работе
приводится описание как самих численных
методов, так и программ, включая примеры и «экранные копии».
Многие задачи математики сводятся к отысканию корней функций, т. е.
к решению уравнений вида F(x)=0. Однако лишь весьма редко существуют
формулы для «точного» решения таких уравнений.
Поэтому возникает
задача о приближенном решении уравнений.
Метод деления отрезка пополам (метод бисекции)
Допустим, что нам удалось найти отрезок [a,b], на котором
расположено искомое значение корня x=c (рис.1). В качестве начального
приближения корня c0 принимаем середину отрезка c0=(a+b)/2. Далее,
исследуем значения функции F(x) на концах отрезков [a,c0] и [с0,b], т.е. в
точках a, c0, b. Тот из отрезков, на концах которого F(x) принимает значения
разных знаков, содержит искомый корень, поэтому его принимаем в качестве
нового отрезка [a1,b1]. Вторую половину отрезка [a,b], на которой знак F(x)
не меняется, отбрасываем. В качестве первого приближения корня
принимаем середину нового отрезка c1=(a1+b1)/2 и т.д. Таким образом, k-е
приближение вычисляется как ck=(ak+bk)/2. После каждой итерации отрезок,
на котором расположен корень, уменьшается вдвое, а после k-той итерации
сокращается в 2k раз.
Пусть приближенное решение x требуется найти с точностью до
некоторого заданного малого числа  > 0. Взяв в качестве приближенного
решения k-е приближение корня ck, запишем это условие в виде:
2
c  ck   .
Итерационный метод можно завершить и тогда, когда значение
функции F(x) после k-той итерации станет меньшим по модулю заданного
малого числа :
F (ck )  
Y
F(b)
a
c0 c2
0
c c1
b
X
F(a)
Рис.1
Пусть для определенности F(a)<0, F(b)>0. В качестве начального
приближения корня примем c0=(a+b)/2. Поскольку в рассматриваемом случае
F(c0)<0, то c  [c0,b], и рассматриваем только отрезок [c0,b], т.е. a1=c0, b1=b.
Следующее приближение: c1=(c0+b)/2. При этом отрезок [c1,b] отбрасываем,
поскольку F(c1)>0 и F(b)>0. Таким образом, c  [c0,с1], a2=c0, b2=c1.
Аналогично находим другие приближения: c2=(c0+c1)/2 и т.д. до выполнения
условия F (ck )   .
В отличие от большинства других итерационных методов метод
деления отрезка пополам всегда сходится, причем можно гарантировать, что
полученное решение будет иметь любую наперед заданную точность
(разумеется, в рамках разрядности компьютера).
Однако, метод деления отрезка пополам довольно медленный и обычно
для этого метода N (число итераций) больше, чем для некоторых других
методов, что не является препятствием к применению этого метода, если
каждое вычисление значения функции F(x) несложно.
3
Алгоритм итерационного процесса нахождения корня уравнения
методом деления отрезка пополам:
Начало
a, b, 
C:= ( a + b )/2
Вычисление
F(a)
Вычисление F(a)
Вычисление F(b)
Вычисление F(c)
0
1
F(a)*F(c)< 0
B:=c
0
A:=c
F (c)  
1
C
Конец
Применение
вычислительной
техники
значительно
облегчит
и
убыстрит процесс нахождения корней нелинейных уравнений методом
бисекции.
4
Пример: Решить уравнение y = 2x - cos x с точностью 109 методом
бисекции.
Решение: Предварительно с помощью программы Advanced Grapher
(программа построения графиков функций) находим отрезок [0,1], на
котором расположено искомое значении корня.
Предлагаемая программа вычисления:
Program polovinnoe;
Var {раздел описания переменных}
a,b,c,f1,f2,f3:real;
Begin
{отрезок [0,1]}
A:=0;
B:=1;
Repeat
C:=(a+b)/2;
F1:=2*a-cos(a);
F2:=2*b-cos(b);
F3:=2*c-cos(c);
If f1*f3<0 then b:=c else a:=c;
Until abs(f3)<0.000000001;
Writeln(‘корень уравнения равен’,c);
5
Readln;
End.
В результате выполнения программы находим решение: x=0,450183611
Если корней на отрезке несколько, то необходимо дополнить
предложенную программу расчетом еще одного корня, определив с помощью
программы Advanced Grapher еще один отрезок, на котором расположено
искомое значение еще одного корня.
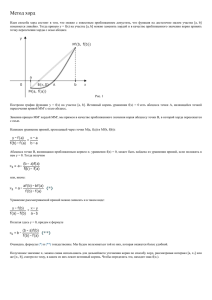
Метод хорд
Пусть функция F(x)=0 непрерывна и монотонна на отрезке [a,b]. Если
ее значения на концах этого отрезка имеют разные знаки, то на отрезке [a,b]
лежит только один корень уравнения F(x)=0. В данном методе процесс
итераций состоит в том, что в качестве приближений корню уравнения
принимаются значения точек пересечения хорды с осью абсцисс.
Допустим, что нам удалось найти отрезок [a,b], на котором
расположено искомое значение корня. Чтобы найти приближенное значение
корня, проведем хорду, соединяющую точки A(a,F(a)) и B(b,F(b)), и найдем
точку ее пересечения с осью абсцисс (рис.2).
y
B
F(b)
0
a
b
F(a)
A
Рис.2
Сначала находим уравнение хорды AB:
y  F (a)
xa

F (b)  F (a) b  a
6
x
Решая
получившееся
линейное
уравнение
для
y=0,
находим
приближенное значение корня:
x1  a 
ba
F (a)
F (b)  F (a)
(1)
Чтобы получить более точное значение корня уравнения F(x)=0, надо
вычислить значение F(x1) и в зависимости от его знака применит формулу
вида (1) или к отрезку [a1,x1], или к отрезку [x1,b]. Процесс приближенный и
ведется до тех пор, пока не получатся два значения абсциссы, совпадающие в
пределах заданной точности:
xk  xk 1  
Алгоритм итерационного процесса нахождения корня уравнения
методом хорд:
Начало
a, b, 
Вычисление F(a)
Вычисление
F(a)
Вычисление F(b)
X1  a 
ba
F (a)
F (b)  F (a)
Вычисление F(x1)
X 2  x1 
1
b  a  x1
F ( x1 )
F (b)  F ( x1 )
2
7
2
1
0
F(a)*F(x1)< 0
B:=x2
A:=x2
0
1
1
x1  x2  
X2
Конец
Применение
вычислительной
техники
значительно
облегчит
и
убыстрит процесс нахождения корней нелинейных уравнений методом хорд.
Пример: Решить уравнение y = 2x - cos x с точностью 109 методом
хорд.
Решение: Предварительно с помощью программы Advanced Grapher
(программа построения графиков функций) находим отрезок [0,1], на
котором расположено искомое значении корня.
8
Предлагаемая программа вычисления:
Program hord;
Var {раздел описания переменных}
A,b,f1,f2,f3:real;
Begin
{отрезок [0,1]}
A:=0;
B:=1;
Repeat
F1:=2*a-cos(a);
F2:=2*b-cos(b);
X1:=a-(b-a)/(f2-f1)*f1;
F3:=2*x1-cos(x1);
X2:=x1-(b-x1)/(f2-f3)*f3;
If f1*f3<0 then b:=x2 else a:=x2;
Until abs(x1-x2)<0.000000001;
Writeln(‘корень уравнения равен’,x2);
Readln;
End.
В результате выполнения программы находим решение: x=0,450183611
Если корней на отрезке несколько, то необходимо дополнить
предложенную программу расчетом еще одного корня, определив с помощью
программы Advanced Grapher еще один отрезок, на котором расположено
искомое значение еще одного корня.
Сравнение методов бисекции и хорд и анализ результатов
Метод деления отрезка пополам и метод хорд похожи, в частности,
процедурой проверки знаков функции на концах отрезка. При этом метод
хорд дает более быструю сходимость итерационного процесса. Кроме того,
оба рассмотренных метода не требуют знания дополнительной информации о
9
функции F(x). Непрерывность F(x) гарантирует успех применения этих
методов. В результате выполнения задания на были создана программы ,
находящие корни алгебраического многочлена с указываемой точностью
посредством следующих методов:
 метод деления отрезка пополам (метод бисекции);

метод хорд.
Фактические результаты совпали с формальными.
Задание для учащихся
№
Функция
Точность
1.
x 4  5x  7  0
10-5
2.
x 4  8x  1  0
10-5
3.
cos x  x 2
10-6
4.
x 4  3x  1  0
10-5
5.
x 2  20 sin x  0
10-7
6.
x4  x2  4  0
10-6
7.
tg (0,3x  0,4)  x 2
10-4
8.
5 x 6  5 x  47,071  0
10-6
9.
1,8x 2  sin 10 x  0
10-6
10.
x  1 0,5 arctan x
10-5
11.
x 3  x 2  11  0
10-4
12.
ctgx  0,25 x  0
10-6
13.
x 3  3x 2  12 x  12  0
10-5
14.
x  sin x  0,25
10-4
15.
x  ( x  1) 3
10-5
10
Метод
бисекции
Метод хорд
Вывод: Ученики 11 класса физико-математического профиля научились
находить корни алгебраического многочлена двумя численными методами:
методом деления отрезка пополам (метод бисекции) и методом хорд с учетом
определяемой точности.
11
Список литературы
1. Гутер Р.С. , Овчинский Б.В. «Элементы численного анализа и
математический обработки результатов опыта». Москва, «Наука», 1979
2. Калиткин Н.Н. «Численные методы». Москва, «Наука», 1978
3. Крылов В.И., БабковВ.В., Монастырский П.И. «Вычислительные
методы». Москва, «Наука», 1976
12