Применение исследовательского метода на уроках математики

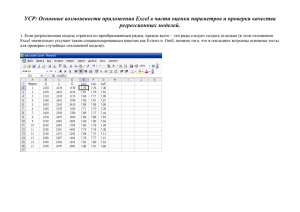
Применение исследовательского метода на уроках математики с
использованием компьютерных технологий при обобщении материала
по теме «Функции и их свойства»
И.Г. Коваленко,
учитель математики
МОУ СОШ № 14
"Человек, не знающий математики,
не способен ни к какой другой науке".
Ф. Бэкон
"Математику уж затем нужно учить,
что она мозги в порядок приводит".
М. Ломоносов
Чем стремительнее развивается прогресс, тем более зависимыми мы становимся от
точной науки. Математика повсюду. От кодирования данных для телефонных карт памяти,
до сложнейших расчетов при прогнозировании погоды. Роль математики в современном
мире бесценна. На современном уровне, математика становится языком общения человека с
природой, c социумом. Математика начинается, как только возникает закономерность и
возникает интерес ее моделирования. Она формирует определённый образ мышления,
умение абстрагировать, развивает логику, умение практически применять полученные
знания.
Иногда большая часть знаний на уроках математики преподносится в готовом виде и
не требует дополнительных поисковых усилий, и основной трудностью для учащихся
является самостоятельный поиск информации, добывание знаний. Поэтому одним из
важнейших условий повышения эффективности учебного процесса является организация
учебной исследовательской деятельности и развитие её основного компонента –
исследовательских умений, которые не только помогают школьникам лучше справляться с
требованиями программы, но и развивают у них логическое мышление, создают внутренний
мотив учебной деятельности в целом, демонстрируют практическую значимость изученного
материала, а применение компьютерных технологий позволит повысить качество
образования, соответствовать реалиям сегодняшнего дня, даст возможность эффективнее
распределять свое время, реализовывать творческий потенциал.
Стремительное развитие научно-технического прогресса требует от выпускников
школы, чтобы они не только квалифицированно разбирались в специальных и научных
областях знаний, но и умели формировать и защищать свои идеи и предложения. Для этого,
прежде всего, необходимо уметь самостоятельно анализировать и обобщать факты, явления
и информацию. Динамика преобразований окружающего мира такова, что человек все чаще
оказывается в новых для себя ситуациях, где готовые рецепты не работают. На ученика
сегодня обрушивается целая лавина многообразной, противоречивой информации.
Исследовательский навык, приобретенный в школе, поможет выпускнику:




расширить знания и представления об окружающем мире, увидеть бесконечность его
познания;
работать с различными источниками информации, осуществлять выбор наиболее
значимого содержания из имеющегося информационного массива;
сформировать научно-исследовательские навыки;
реализовать личный творческий потенциал, самоутвердиться.
Важной задачей изучения математики является получение школьниками знаний по
теме «Функции и их свойства», как важнейшей математической модели для описания и
исследования
разнообразных
процессов
(равномерных,
равноускоренных,
экспоненциальных, периодических и др.). Важность этой темы состоит еще и в том, что она
способствует формированию у учащихся представлений о роли математики в развитии
цивилизации и культуры, как средства моделирования явлений реального мира и процессов.
Но все это надо понять, осмыслить и осознать. Как это сделать понятным и самое главное
доступным для учащихся? Ведь порой на уроках
используется преимущественно
информационное изложение материала, организующее лишь репродуктивную деятельность
учащихся. Не секрет, что многие учащиеся не понимают смысл изучения темы «Функции и
их свойства», не видят практического применения знаний. И вообще мы часто слышим от
учеников вопрос: «А за чем мне нужна математика?». В своей работе я хотела бы показать
один из вариантов применения исследовательской деятельности, которая позволит оживить
уроки математики, внести разнообразие в учебный процесс, расширит кругозор учащихся и
позволит помочь в овладении системой математических знаний и умений, необходимых для
применения в практической деятельности, изучения смежных дисциплин, продолжения
образования.
На момент окончания изучения раздела «Функции и их свойства» (9 класс) учащийся
умеет:
 находить значения функций, заданных формулой, таблицей, графиком по ее
аргументу; решать обратную задачу;
 извлекать информацию, представленную в таблицах, на графиках;
 строить графики изученных функций, описывать их свойства, определять свойства
функции по ее графику.
Использование компьютерных технологий позволит учащимся применить
полученные знания для интерпретации графиков зависимостей между величинами, переводя
их на язык функций, и исследовать, анализировать реальные зависимости в практической
деятельности и повседневной жизни. А это увлекательно, полезно, информативно и
актуально.
Лекция и компьютерный практикум по теме
«Получение регрессионных моделей в MS Excel».
Цель: показать практическую значимость изученного материала по теме «Функции и их
свойства», расширить кругозор учащихся, совершенствовать
навыки работы с
информационными технологиями.
Мотивация.
Мы научились находить значения функций, заданных формулой, таблицей, графиком
по ее аргументу и решать обратную задачу; извлекать информацию, представленную в
таблицах, на графиках; строить графики изученных функций, описывать их свойства,
определять свойства функции по ее графику.
Вопрос к классу: как вы думаете, где могут пригодиться знания по этой теме?
Специалистам в области планирования и управления часто для принятия решений
приходится выполнять обработку данных: производить расчеты, выполнять логический
анализ данных и др.
Используя компьютерные программные средства, можно уже сейчас попробовать
решать некоторые задачи планирования и управления. Для этого нужно понимать суть
решаемой проблемы, использовать свои математические знания, подготовить и вводить в
компьютер исходные данные, интерпретировать готовые результаты.
При решении задач планирования и управления очень важна форма отображения
результатов. Человеком легче воспринимаются результаты, если они представлены в
наглядной форме в виде рисунков, графиков, диаграмм. Визуализация больших массивов
числовой информации позволяет человеку лучше понимать характер изменения величин,
легче производить сравнение.
Решение задач планирования и управления постоянно требует учета зависимостей
одних факторов от других. Вот некоторые примеры таких зависимостей:
 время падения тела на землю зависит от первоначальной высоты;
 частота заболевания жителей бронхиальной астмой зависит от качества
городского воздуха;
 температура воздуха в определенный сезон в различных районах зависит от
географических широт этих мест.
Приведите примеры других зависимостей.
Побуждение к деятельности, постановка учебной задачи.
Как решаются такие задачи? Как построить математическую модель – описать
зависимость между величинами?
Нужно получить формулу, отражающую зависимость одной величины от другой. На
математическом языке это называется функциональной зависимостью.
В практических исследованиях возникает необходимость описать приблизительно
(аппроксимировать) диаграмму рассеяния величин математическим уравнением. То есть
зависимость между переменными величинами Y и Х можно выразить аналитически с
помощью формул и уравнений и графически в виде геометрического места точек в системе
прямоугольных координат.
На начальном этапе вид такой функции неизвестен, ее ищут методом подбора по
экспериментальным данным. Требования к искомой функции: график функции должен
проходить вблизи экспериментальных точек так, чтобы отклонения этих точек от графика
были минимальны и равномерны. Полученную функцию в статистике называют
регрессионной моделью.
Регрессионный анализ – статистический метод, используемый для исследования
отношений между двумя величинами. Регрессионный анализ используется для определения
общего вида уравнения регрессии, оценки параметров этого уравнения, а также проверки
различных статистических гипотез.
Уравнение регрессии тем лучше описывает зависимость, чем меньше рассеяние диаграммы,
чем больше теснота взаимосвязи. Уравнение прямой линии пригодно для описания только
линейных зависимостей. В случае нелинейных зависимостей математическая запись может
отображаться уравнениями параболы, гиперболы и др. Необходимо также сделать одно
важное замечание о значении показателей, характеризующих взаимосвязь признаков. Все
они дают лишь количественную меру связи, но ничего не говорят о причинах зависимости.
Определить эти причины — дело самого исследователя.
Статистические данные всегда являются приближенными (усредненными), поэтому
они носят оценочный характер. Однако они верно отражают характер зависимости величин
(для достоверности результатов этих данных должно быть много).
Получение регрессионной модели происходит в два этапа:
1. подбор вида функции (для этого и пригодятся полученные знания по теме
«Функции и их свойства»).
2. вычисление параметров функции (для этого используется метод наименьших
квадратов, предложенный в XVIII веке немецким математиком К. Гауссом. Он
очень широко используется в статистической обработке данных и встроен во
многие математические пакеты программ, в том числе и в MS Excel).
График регрессионной модели называют трендом. Выбор типа регрессионной
модели пользователь производит сам. Вот тут и пригодятся знания о графиках изученных
функций. Характеристикой построенной модели является параметр R2 – коэффициент
детерминированности. Чем его значение ближе к 1, тем модель лучше.
Рассмотрим пример.
Некая фирма решила использовать модель линейной регрессии для определения
зависимости вида y = a + bx между годовым объемом продаж и годовыми расходами на
рекламу. За предшествующие годы были собраны следующие данные:
Объем продаж (млн. $) Расходы на рекламу (тыс. $)
26
69
12
30
20
51
23
62
16
35
Строим сначала точечную диаграмму, далее регрессионную модель, находим
уравнение прямой и исследуем, делая выводы.
Объем продаж (млн. $)
Зависимость годового объема продаж от
расходов на рекламу
30
y = 0,3261x + 3,2921
R2 = 0,9745
25
20
15
10
5
0
0
20
40
60
80
Расходы на рекламу (тыс. $)
Например, можно рассчитать ожидаемые продажи, используя уравнение y = 3,2921 +
0,3261x. Допустим, что расходы на рекламу на следующий год составят 45 000 $, то можно
ожидать, что тогда продажи составят 17 967 000 $. Это поможет спланировать работу фирмы
и достичь наилучших результатов.
Регрессия широко используется при решении различных бизнес-задач, таких как
прогнозирование продаж, курсов валют и акций, оценивания различных бизнес-показателей
по наблюдаемым значениям других показателей, выявление зависимостей между
показателями и т.д.
Компьютерный практикум «Получение регрессионных моделей в MS Excel».
Цель: научиться применять полученные математические знания по теме «Функции и их
свойства» используя компьютерные технологии при решении исследовательских задач.
Используемые программные средства: табличный процессор MS Excel.
Рассмотрим задачу, в которой находится зависимость заболевания раком легких от
количества выкуренных сигарет. Такая зависимость, к сожалению, существует. Ее можно
установить экспериментальным путем: путем сбора многочисленных данных, их анализа и
обобщения.
Информационная справка выводится на экран.
Важным этиологическим фактором в развитии рака лёгкого, влияющим на увеличение
его частоты, особенно среди мужчин, является курение. Среди больных раком лёгкого было
только 0,3% некурящих. Экспериментальные, клинические и статистические работы
последних лет убедительно доказали роль табачного дыма в развитии рака лёгкого. Наряду с
местным канцерогенным воздействием табачного дёгтя на слизистую оболочку дыхательных
путей здесь имеет значение общее воздействие этого яда на организм, которое снижает его
сопротивляемость по отношению к различным вредным агентам. Длительное и упорное
раздражение слизистой оболочки табачным дёгтем часто приводит к этому заболеванию.
За последние годы внимание исследователей всё больше привлекает вопрос о влиянии
курения табака на развитие рака лёгкого. Этому вопросу посвящено большое количество
экспериментальных, клинических и статистических работ. А мы попытаемся представить
эти результаты графически и сделать прогнозирование по регрессионной модели и провести
исследование.
Табличное представление статистических данных.
М
К
0
3,4
10
28,6
20
51,4
30
74,3
40
144
50
217
60
263
К – коэффициент летальности от рака легких на 100000 населения.
М – количество сигарет, выкуренных за день.
Надо получить формулу, отражающую зависимость увеличения коэффициента
летальности К от количества выкуренных сигарет в день М. Вид такой функции пока не
известен, вид регрессионной функции определяем путем подбора по экспериментальным
данным. Если мы это сделаем, то сможем прогнозировать процесс путем вычислений и даже
за пределами экспериментальных данных.
Этим мы и будем заниматься в ходе компьютерного практикума.
Практическая часть.
Учащиеся разбиваются на группы и вводят табличные данные и строят точечную диаграмму.
Графическое представление
статистических данных
Коэффициент
летальности
300
250
200
150
100
50
0
0
20
40
60
80
Кол-во сигарет в день
Каждой группе дается задание.
Задание: подберите вид функции наиболее описывающую зависимость между этими
количественными характеристиками. Ответ обоснуйте, используя знания по теме «Функции
и их свойства».
После обсуждения и высказывания предположений приступаем к реализации исследования.
Алгоритм получения с помощью MS Excel регрессионных моделей (функций) с построением
тренда (графика).
o Выделяем поле диаграммы и выполняем команду Диаграмма  Добавить
линию тренда  в открывшемся окне на закладке «Тип» выбрать один из
видов трендов;
o Перейти к закладке «Параметры»  установить галочки на флажках
«показать уравнения на диаграмме» и «поместить на диаграмму R2», щелкнуть
по кнопке «ОК».
Диаграмма готова. Аналогично получаются другие типы трендов. Квадратичный тренд
получают, выбрав полиноминальный тип функции степени 2 (квадратичную функцию еще
называют полиномом 2 степени). Иногда используют полиномы и более высоких степеней.
MS Excel дает возможность пользователю самому задавать тип регрессионной модели
(для этого и пригодятся полученные знания по теме «Функция и ее свойства») и не
ограничиваться предполагаемым меню из шести функций.
Для продолжения линии тренда за границы области данных, приведенных в исходной
таблице, надо сделать следующее:
 На вкладке «Параметры» в области «Прогноз» в строке «вперед» установить
число – единицу используемого масштаба по горизонтальной оси.
Полученная регрессионная модель может использоваться для предсказания,
прогнозирования значений параметров, в точках, не являющихся экспериментальными,
используя полученную формулу.
Мы получили две регрессионные модели: линейную и квадратичную (можно исследовать и
другие).
Заболеваемость
Заболеваемость
300
200
Коэффициент
летальности
Коэффициент
летальности
250
300
y = 4,4579x - 22,064
R2 = 0,948
150
100
50
0
-50 0
20
40
60
Кол-во сигарет в день
80
y = 0,0534x 2 + 1,2536x + 4,6381
R2 = 0,9889
250
200
150
100
50
0
0
20
40
60
80
Кол-во сигарет в день
Обсуждение и подведение итогов.
Из двух выбранных моделей значение R2 наибольшее у квадратичной функции у =
0,0534х2 +1,2536х + 4,6381. Она лучше отражает рост коэффициента летальности. Теперь
можно оценить уровень летального исхода не только для тех значений, которые были
получены путем сбора и анализа, но и для других значений. Это важно с практической точки
зрения и поможет многим сделать выводы о вреде курения.
Задание:
 произвести прогноз по регрессионной модели в пределах экспериментальных
значений и за пределами экспериментальных данных, сделать выводы.
 провести исследование самостоятельно (учащимся предлагаются карточки с
другими заданиями);
Рефлексия деятельности. Подведение итогов, оценка работы класса.
Домашнее задание.
Соберите информацию (используйте Интернет-ресурсы), установите зависимость между
величинами, проведите исследование, будьте готовы к представлению результатов
исследования.
Напоследок хочу отметить еще и профориентационную направленность этой работы.
Исследовательская деятельность, умение самостоятельно анализировать и обобщать факты,
явления и информацию, знания, полученные на уроках математики, являются неотъемлемой
частью работы аналитика – новой, высокооплачиваемой и востребованной профессии,
которая появилась у нас в России совсем недавно.
Полученные знания имеют практическое применение. Проводя исследования для
некой фирмы, аналитик осуществляет собор информации, затем синтезирует и обобщает
информацию, сопоставляет факты, цифры, события, формирует свое видение ситуации. На
основании сделанных заключений и выводов аналитик дает прогнозы и советы относительно
будущего развития компании. В своих исследованиях, как только определяется линия
регрессии, аналитик сразу же оказывается в состоянии построить график, например,
ожидаемой (предсказанной) оплаты труда и реальных обязательств компании по выплате
жалования. Таким образом, аналитик может определить, какие позиции недооценены (лежат
ниже линии регрессии), какие оплачиваются слишком высоко (лежат выше линии
регрессии), а какие оплачены адекватно.
Надеюсь, что предложенная работа повысит интерес учащихся к математике,
расширит их кругозор и, возможно, теперь будет реже звучать вопрос «А зачем мне нужна
математика?».