Б3.В.21 Теория чиселx
реклама
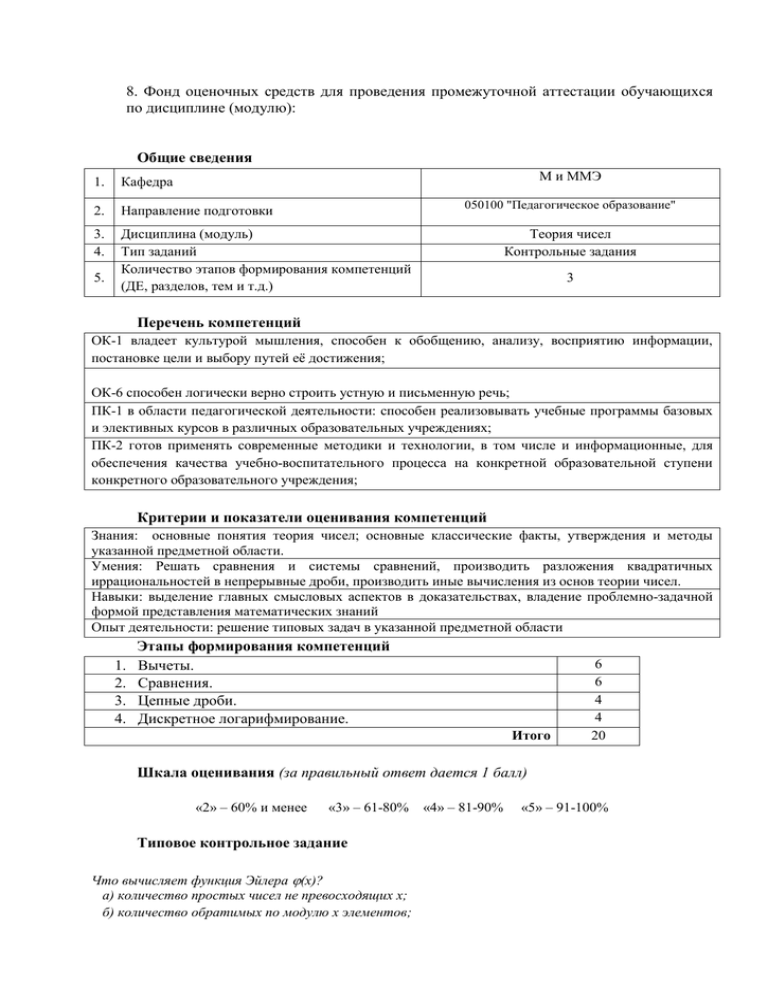
8. Фонд оценочных средств для проведения промежуточной аттестации обучающихся по дисциплине (модулю): Общие сведения М и ММЭ 1. Кафедра 2. Направление подготовки 3. 4. Дисциплина (модуль) Тип заданий Количество этапов формирования компетенций (ДЕ, разделов, тем и т.д.) 5. 050100 "Педагогическое образование" Теория чисел Контрольные задания 3 Перечень компетенций ОК-1 владеет культурой мышления, способен к обобщению, анализу, восприятию информации, постановке цели и выбору путей её достижения; ОК-6 способен логически верно строить устную и письменную речь; ПК-1 в области педагогической деятельности: способен реализовывать учебные программы базовых и элективных курсов в различных образовательных учреждениях; ПК-2 готов применять современные методики и технологии, в том числе и информационные, для обеспечения качества учебно-воспитательного процесса на конкретной образовательной ступени конкретного образовательного учреждения; Критерии и показатели оценивания компетенций Знания: основные понятия теория чисел; основные классические факты, утверждения и методы указанной предметной области. Умения: Решать сравнения и системы сравнений, производить разложения квадратичных иррациональностей в непрерывные дроби, производить иные вычисления из основ теории чисел. Навыки: выделение главных смысловых аспектов в доказательствах, владение проблемно-задачной формой представления математических знаний Опыт деятельности: решение типовых задач в указанной предметной области 1. 2. 3. 4. Этапы формирования компетенций Вычеты. Сравнения. Цепные дроби. Дискретное логарифмирование. Итого 6 6 4 4 20 Шкала оценивания (за правильный ответ дается 1 балл) «2» – 60% и менее «3» – 61-80% Типовое контрольное задание Что вычисляет функция Эйлера (x)? а) количество простых чисел не превосходящих x; б) количество обратимых по модулю х элементов; «4» – 81-90% «5» – 91-100% в) число единиц кольца Zx; г) количество множителей в разложении x на простые сомножители. Выберите правильные ответы. Методические материалы, определяющие процедуры оценивания знаний Примерный перечень вопросов к экзамену. 1. Натуральные, целые, рациональные, вещественные числа. Деление с остатком в натуральных числах. 2. НОД и алгоритм Евклида. Представимость НОД в виде d = xa + yb. 3. Понятие простого числа. Бесконечность множества простых чисел. Основная теорема арифметики. 4. Вычеты. Основные системы вычетов. 5. , Кольцо Zn. Условие, при котором это кольцо является полем. 6. Единицы кольца Zn. 7. Функция Эйлера. Ее мультипликативность и формулы для вычисления. 8. Понятие сравнения. Частное и общее решение. Число решений. Эквивалентные сравнения. 9. Понятие системы сравнений. Частное и общее решение. Число решений. Эквивалентные системы сравнений. 10. Сравнения первой степени. Алгоритм решения. 11. Системы сравнений первой степени. Алгоритм сведения к одному сравнению первой степени. 12. Квадратичные вычеты и невычеты по простому неченому модулю. Количество вычетов и невычетов. 13. Символ Лежандра и его свойства. 14. Символ Якоби и его свойства. 15. Квадратичный закон взаимности. 16. Понятие первообразного корня по модулю m. Примеры. 17. Теорема о модулях, по которым имеются первообразные корни. Примеры. 18. Теорема о первообразных корнях по простому модулю p. 19. Дискретное логарифмирование и его применение в кодировании секретной информации. 20. Цепные дроби и их свойства (подходящие дроби, их вычисление, их поведение, разность соседних дробей). 21. Разложение вещественных чисел в цепные дроби (алгоритм, характер сходимости, единственность, критерий рациональности). 22. Периодические цепные дроби. 23. Признаки делимости. Контрольные вопросы и задания для проведения текущего контроля. 1. 2. 3. 4. 5. Понятие простого числа. Полные системы вычетов. Единицы кольца вычетов. Функция Эйлера. Число решений сравнения. 2 6. Сравнения первой степени. 7. Квадратичные вычеты. 8. Квадратичный закон взаимности. 3








