3 - Московский государственный технический университет им.Н

Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального
образования
——————————————————————————————————————————————
«Московский государственный технический университет имени Н. Э. Баумана»
(МГТУ им. Н.Э.Баумана)
Утверждено
Первым проректором —
проректором по учебной работе
ПЛАНЫ УЧЕБНЫХ ЗАНЯТИЙ СТУДЕНТОВ
первого курса второго семестра 2012 /2013 учебного года
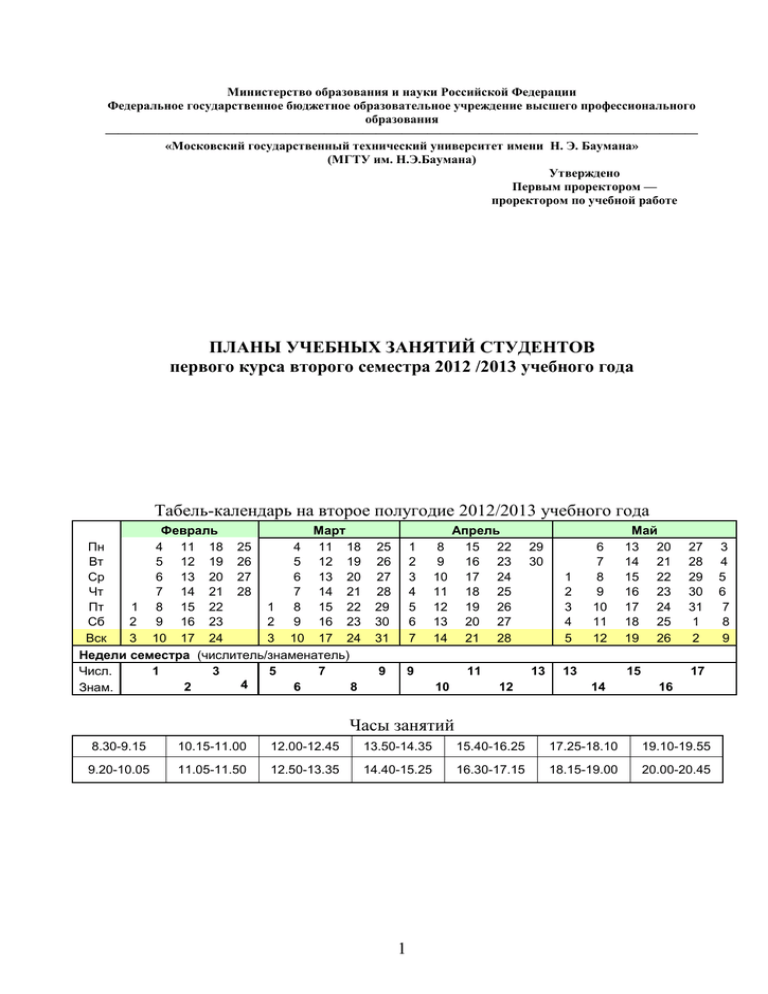
Табель-календарь на второе полугодие 2012/2013 учебного года
Февраль
Март
Пн
4 11 18 25
4 11 18
Вт
5 12 19 26
5 12 19
Ср
6 13 20 27
6 13 20
Чт
7 14 21 28
7 14 21
Пт
1 8 15 22
1 8 15 22
Сб
2 9 16 23
2 9 16 23
Вск
3 10 17 24
3 10 17 24
Недели семестра (числитель/знаменатель)
1
3
5
7
Числ.
4
2
6
8
Знам.
25
26
27
28
29
30
31
1
2
3
4
5
6
7
9
9
8
9
10
11
12
13
14
Апрель
15 22
16 23
17 24
18 25
19 26
20 27
21 28
11
10
29
30
1
2
3
4
5
13
12
6
7
8
9
10
11
12
13
14
Май
13 20
14 21
15 22
16 23
17 24
18 25
19 26
27
28
29
30
31
1
2
15
17
16
Часы занятий
8.30-9.15
10.15-11.00
12.00-12.45
13.50-14.35
15.40-16.25
17.25-18.10
19.10-19.55
9.20-10.05
11.05-11.50
12.50-13.35
14.40-15.25
16.30-17.15
18.15-19.00
20.00-20.45
1
3
4
5
6
7
8
9
Содержание
Стр.
АНГЛИЙСКИЙ ЯЗЫК для студентов факультетов РЛМ, ИУ, ФН, ИБМ………………………………….3
АНГЛИЙСКИЙ ЯЗЫК для студентов факультетов СМ, РК, МТ, Э………………………………………...5
НЕМЕЦКИЙ ЯЗЫК для студентов всех факультетов…………………………………………………………8
ФРАНЦУЗСКИЙ ЯЗЫК для студентов всех факультетов…………………………………………………….9
РУССКИЙ ЯЗЫК ДЕЛОВОГО ОБЩЕНИЯ………………………………..……………………….…………11
ФИЗИКА……………………………………………………………………..………………………..………….14
ИНТЕГРАЛЫ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ……………………………………….……….....17
ИНТЕГРАЛЫ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ для студентов ИБМ …………………………..22
ЛИНЕЙНАЯ АЛГЕБРА И ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ…………………………………..26
ЛИНЕЙНАЯ АЛГЕБРА И ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ для ИБМ…………….………….31
ЛИНЕЙНАЯ АЛГЕБРА………………………………………………………………………………………….35
МАТЕМАТИЧЕСКИЙ АНАЛИЗ……………………………………………………………………………….38
ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ для специальности ИУ9………………….43
МАТЕМАТИЧЕСКИЙ АНАЛИЗ для специальности ИУ9………………………..….……………………….51
МАТЕМАТИЧЕСКИЙ АНАЛИЗ для специальности УЦ……………………………………………………..61
СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ. ЛИНЕЙНАЯ АЛГЕБРА
для специальности УЦ…………………………………………………………………………….………………66
ВВЕДЕНИЕ В СПЕЦИАЛЬНОСТЬ для ФН2…………………………………………………….……………..73
ХИМИЯ для бакалавров………………………………………………………………………….……………….76
НЕОРГАНИЧЕСКАЯ ХИМИЯ для бакалавров Э9…………………………………………………….……….81
ХИМИЯ для специалистов факультета Э………………………………………………………….……………83
ХИМИЯ для специалистов факультета ПСО…………………………………………………….……………..87
ОБЩАЯ И НЕОРГАНИЧЕСКАЯ ХИМИЯ для бакалавров ИУ4………………………………………………90
ХИМИЯ для специальности ЮР………………………………………….……………………………………….93
ФИЗИЧЕСКАЯ ХИМИЯ для бакалавров ФН4…………………………………………………………………..96
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА для студентов ИУ2………………………………………………………….101
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА для студентов факультета ПС……………………………………...………107
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА для студентов кафедры СМ5……………………………………………….113
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА для студентов факультетов СМ (кроме СМ5), РК4, 5, 9, 10……..………121
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА для студентов факультетов МТ, Э…………………………...…………….129
ФИЗИЧЕСКАЯ КУЛЬТУРА……………………………………………………………………...……………….136
2
АНГЛИЙСКИЙ ЯЗЫК
для студентов факультетов РЛМ, ИУ, ФН, ИБМ.
Практические занятия
1.Письменная контрольная работа по модулю
4 (по пройденному материалу занятий 1- 4).
(40 мин.)
МОДУЛЬ 4
Аудиторное занятие 1. (ОЛ1)
1.Грамматика. Повторение времен упр.1
стр.62.Согласование времен упр. 2,3.стр.63
2.Ведение лексики ур.4 упр. 8,9,10 стр.66.
3.Работа с текстом 4 А 1 ч.- лексикограмматический разбор текста.
Домашнее задание
1.Текст 4 А 2 ч.- читать, отвечать на вопросы.
2.Упр.4, 5(письменно), 6 стр.64.
Аудиторное занятие 2. (ОЛ1)
1.Проверка д.з. Работа с текстом 4А.
Упр. 11, 12 стр. 69, упр.1, 2 стр.73.
2.Закрепление грамматики упр. 15. стр70.
3.Аудирование по теме урока.
Домашнее задание.
1.Упр.14 стр.69-70.
2.Упр.27 стр.73
Аудиторное занятие 3. (ОЛ1)
1.Проверка д.з.
2.Работа с лексикой урока 4.
3.Упр-я для самостоятельной работы по
выбору преподавателя.
Домашнее задание.
1.Подготовиться контролю лексики ур.4.
2.Текст 4 В. Знать содержание текста.
Составить и записать вопросы по
содержанию текста.
Аудиторное занятие 4. (ОЛ1)
1.Контроль лексики урока 4.
2.Проверка д.з. Работа с текстом 4В.
3.Работа с текстом 4С- прочитать и
выполнить задание.
Домашнее задание.
1.Подготовить сообщение
по темам: «Будущее ТВ.
История ТВ. Современные
средства связи»/по выбору/
2.Подготовиться к контрольному
мероприятию по модулю 4.
Аудиторное занятие 5. (ОЛ1)
Рубежный контроль 1
2.Мини-конференция
темам.
по
подготовленным
Домашнее задание.
1.Текст 5А 1 ч.- прочитать, знать содержание.
2.Упр.7- 9 стр.84-85.
МОДУЛЬ 5
Аудиторное занятие 6. (ОЛ1)
1.Грамматика. Определение.Упр.1, 2, 3стр.8283.
Бессоюзные
определительные
придаточные предложения. Упр.4, 5 стр. 8384.
2.Работа с лексикой урока 5. Упр.10,11 стр.86
3.Текст 5А - прослушивание, лексикограмматический разбор текста.
Домашнее задание.
1.Текст 5А 2 ч.- прочитать, знать содержание,
отвечать на вопросы.
2.Упр.6 стр.84.
Аудиторное занятие 7. (ОЛ1)
1.Проверка д.з.
2.Упр.1,2 стр.93.
3.Работа с текстом 5В (по заданию).
4.Аудирование по теме урока.
Домашнее задание.
1.Подготовиться к контролю лексики урока 5.
2.Упр.17 стр. 89
3.Текст 5С - знать содержание. Составить и
записать вопросы по содержанию текста.
Аудиторное занятие 8. (ОЛ1)
1.Контроль лексики урока 5.
2.Проверка д.з.
3.Работа с текстом 5 С- ответы на вопросы.
Беседа по тексту.
Домашнее задание.
Подготовить сообщение по устной теме урока
«Компьютеры». Упр.4, 5 стр. 94.
Аудиторное занятие 9. (ОЛ1)
3
1.Проверка д.з. Мини-конференция по
подготовленным сообщениям.
2.Письменный перевод упр.31 стр. 92.
Домашнее задание.
1. Подготовиться к контрольному
мероприятию по модулю 5.
2.Проработать тексты на стр. 261-263
(по выбору студента) - кратко передать
содержание выбранного текста.
Аудиторное занятие 10. (ОЛ1)
Рубежный контроль 2
1.Письменная контрольная работа по модулю
5 (по пройденному материалу занятий 6-9).
(40мин).
2.Беседа по выбранным текстам.
3.Грамматика. Модальные глаголы и их
эквиваленты упр.1, 2, 3 стр.102-103.
Домашнее задание.
1.Упр. 4, 5, 6, 8, 9 стр.103.
2.Письменный перевод упр.7 стр.104.
2.Текст 6В-знать содержание.
Составить и записать вопросы по
содержанию текста.
Аудиторное занятие 13. (ОЛ1)
1.Контроль лексики урока 6.
2.Проверка д.з.
3.Упражнения из раздела самостоятельной
работы (по выбору преподавателя).
Домашнее задание.
1.Текст 6 С- знать содержание.
Составить и записать вопросы по
содержанию текста.
2.Упр.31 стр.114.
3.Проработать тексты на стр.261-263
(по выбору студента) - кратко передать
содержание выбранного текста.
Аудиторное занятие 14. (ОЛ1)
1.Проверка д.з. Работа с лексическим
материалом.
2.Беседа по текстам
на стр.264-265. Задавать и отвечать на
вопросы.
Домашнее задание.
1.Подготовиться к контрольному
мероприятию по модулю 6.
2.Подготовиться к беседе по теме
«Материалы нового поколения».
Аудиторное занятие 15. (ОЛ1)
Рубежный контроль 3.
1.Письменная контрольная работа по модулю
6 (по пройденному материалу занятий 11-14)
(40 мин).
2.Мини-конференция по теме урока
“Материалы нового поколения”.
Домашнее задание.
1. Текст 6 D-прочитать, знать содержание.
Аудиторное занятие 16. (ОЛ1)
1.Проверка д.з. Беседа по тексту 6 D.
2.Просмотр и обсуждение видеоматериала.
Домашнее задание.
Упражнения и тексты по усмотрению
преподавателя.
Аудиторное занятие 17(ОЛ1)
Итоговое занятие.
МОДУЛЬ 6
Аудиторное занятие 11. (ОЛ1)
1.Проверка д.з.
2.Закрепление грамматики урока 6.
Упр. 21, 22 стр.111.
3.Введение лексики урока 6 упр.13,14,15,16
стр.106-107
4.Текст 6А 1ч. - прослушивание, лексикограмматический разбор текста.
Домашнее задание.
1.Работа с лексикой ур.6. Упр.10,11,12 стр.
106.
2. Ответы на вопросы к тексту 6А. Упр.17
стр.110, упр.1 стр.114
Аудиторное занятие 12. (ОЛ1)
1.Проверка д.з.
Беседа по тексту 6А.
2.Работа с дополнительным текстом 6Взадать вопросы, обсудить.
3. Работа с лексикой ур.6. Упр.10,11,12 стр.
106.
Домашнее задание.
1.Подготовиться к контролю
лексики урока 6.
Самостоятельная подготовка
1.Текущее домашнее задание включает в себя: выполнение грамматических упражнений к
каждому пройденному уроку, перевод предложений с иностранного языка на родной и наоборот,
прослушивание текстов А учебника в лабораториях устной речи или дома, переписав их на
4
электронные носители в специализированной лаборатории факультета «Лингвистика», ауд. 417л.,
работу с дополнительными текстами В и С в каждом уроке учебника.
2.Подготовка к тесту №1 по материалу модуля 4 (ОЛ1): дополнительные задания стр.79-81.
3.Подготовка к тесту №2 по материалу модуля 5 (ОЛ1): дополнительные задания стр.97-101.
4.Подготовка к тесту №3 по материалу модуля 6(ОЛ1): дополнительные задания стр.119-122.
▼ Вопросы для подготовки к рубежному контролю / зачёту
1.Условием получения отметки о сдаче 1, 2 и 3 рубежного контроля по модулям семестра является
сдача текущего материала на аудиторных занятиях путем устных ответов, выполнение поурочных
домашних заданий, участие в обсуждении устных тем уроков с получением баллов по балльнорейтинговой системе.
2.Условием получения зачёта является получение студентом от 20 до 33 баллов по 1-му, 2-ому и
3-ему модулям при сумме не ниже 60. При низкой посещаемости занятий студенту могут быть
предложены задания по материалам модулей, к которым относятся пропущенные занятия.
▼ Основная и дополнительная литература
Основная литература (ОЛ)
1. Орловская И.В., Самсонова Л.С., Скубриева А.И. Учебник английского языка для технических
вузов. М.: изд-во МГТУ им. Баумана, 2007 – 448 с.
Дополнительная литература (ДЛ))
1. R. Murphy. English Grammar in Use. Cambridge University Press, 2004 – 375 с.
2. Словари: - Lingvo 8.0- 12.0
- Longman WordWise Dictionary
Рекомендуемые Интернет-сайты:
1.
2.
3.
http://www.englishlearner.com
http://www.breakingnewsenglish.com
http:// www.bbc.com.uk
АНГЛИЙСКИЙ ЯЗЫК
для студентов факультетов СМ, РК, МТ, Э.
Практические занятия
1.Текст 4 А 2 ч.- читать, отвечать на вопросы.
2.Упр.4, 5(письменно), 6 стр.64.
Аудиторное занятие 2. (ОЛ1)
1.Проверка д.з. Работа с текстом 4А.
Упр. 11, 12 стр. 69, упр.1, 2 стр.73.
2.Закрепление грамматики упр. 15. стр70.
3.Аудирование по теме урока.
Домашнее задание.
1.Упр.14 стр.69-70.
МОДУЛЬ 4
Аудиторное занятие 1. (ОЛ1)
1.Грамматика. Повторение времен упр.1
стр.62.Согласование времен упр. 2,3.стр.63
2.Ведение лексики ур.4 упр. 8,9,10 стр.66.
3.Работа с текстом 4 А 1 ч.- лексикограмматический разбор текста.
Домашнее задание
5
2.Упр.27 стр.73
Аудиторное занятие 3. (ОЛ1)
1.Проверка д.з.
2.Работа с лексикой урока 4.
3.Упр-я для самостоятельной работы по
выбору преподавателя.
Домашнее задание.
1.Подготовиться контролю лексики ур.4.
2.Текст 4 В. Знать содержание текста.
Составить и записать вопросы по
содержанию текста.
Аудиторное занятие 4. (ОЛ1)
1.Контроль лексики урока 4.
2.Проверка д.з. Работа с текстом 4В.
3.Работа с текстом 4С- прочитать и
выполнить задание.
Домашнее задание.
1.Подготовить сообщение
по темам: «Будущее ТВ.
История ТВ. Современные
средства связи»/по выбору/
2.Подготовиться к контрольному
мероприятию по модулю 4.
Аудиторное занятие 5. (ОЛ1)
Рубежный контроль 1
1.Письменная контрольная работа по модулю
4 (по пройденному материалу занятий 1- 4).
(40 мин.)
2.Мини-конференция
темам.
по
3.Работа с текстом 5В (по заданию).
4.Аудирование по теме урока.
Домашнее задание.
1.Подготовиться к контролю лексики урока 5.
2.Упр.17 стр. 89
3.Текст 5С - знать содержание. Составить и
записать вопросы по содержанию текста.
Аудиторное занятие 8. (ОЛ1)
1.Контроль лексики урока 5.
2.Проверка д.з.
3.Работа с текстом 5 С- ответы на вопросы.
Беседа по тексту.
Домашнее задание.
Подготовить сообщение по устной теме урока
«Компьютеры». Упр.4, 5 стр. 94.
Аудиторное занятие 9. (ОЛ1)
1.Проверка д.з. Мини-конференция по
подготовленным сообщениям.
2.Письменный перевод упр.31 стр. 92.
Домашнее задание.
1. Подготовиться к контрольному
мероприятию по модулю 5.
2.Проработать тексты на стр. 261-263
(по выбору студента) - кратко передать
содержание выбранного текста.
Аудиторное занятие 10. (ОЛ1)
Рубежный контроль 2
1.Письменная контрольная работа по модулю
5 (по пройденному материалу занятий 6-9).
(40мин).
2.Беседа по выбранным текстам.
3.Грамматика. Модальные глаголы и их
эквиваленты упр.1, 2, 3 стр.102-103.
Домашнее задание.
1.Упр. 4, 5, 6, 8, 9 стр.103.
2.Письменный перевод упр.7стр.104.
подготовленным
Домашнее задание.
1.Текст 5А 1 ч.- прочитать, знать содержание.
2.Упр.7- 9 стр.84-85.
МОДУЛЬ 5
Аудиторное занятие 6. (ОЛ1)
1.Грамматика. Определение.Упр.1, 2, 3стр.8283.
Бессоюзные
определительные
придаточные предложения. Упр.4, 5 стр. 8384.
МОДУЛЬ 6
Аудиторное занятие 11. (ОЛ1)
1.Проверка д.з.
2.Закрепление грамматики урока 6.
Упр. 21, 22 стр.111.
3.Введение лексики урока 6 упр.13,14,15,16
стр.106-107
4.Текст 6А 1ч. - прослушивание, лексикограмматический разбор текста.
Домашнее задание.
1.Работа с лексикой ур.6. Упр.10,11,12 стр.
106.
2. Ответы на вопросы к тексту 6А. Упр.17
стр.110, упр.1 стр.114
Аудиторное занятие 12. (ОЛ1)
2.Работа с лексикой урока 5. Упр.10,11 стр.86
3.Текст 5А - прослушивание, лексикограмматический разбор текста.
Домашнее задание.
1.Текст 5А 2 ч.- прочитать, знать содержание,
отвечать на вопросы.
2.Упр.6 стр.84.
Аудиторное занятие 7. (ОЛ1)
1.Проверка д.з.
2.Упр.1,2 стр.93.
6
1.Проверка д.з.
Беседа по тексту 6А.
2.Работа с дополнительным текстом 6Взадать вопросы, обсудить.
3. Работа с лексикой ур.6. Упр.10,11,12 стр.
106.
Домашнее задание.
1.Подготовиться к контролю
лексики урока 6.
2.Текст 6В-знать содержание.
Составить и записать вопросы по
содержанию текста.
Аудиторное занятие 13. (ОЛ1)
1.Контроль лексики урока 6.
2.Проверка д.з.
3.Упражнения из раздела самостоятельной
работы (по выбору преподавателя).
Домашнее задание.
1.Текст 6 С- знать содержание.
Составить и записать вопросы по
содержанию текста.
2.Упр.31 стр.114.
3.Проработать тексты на стр.261-263
(по выбору студента) - кратко передать
содержание выбранного текста.
Аудиторное занятие 14. (ОЛ1)
1.Проверка д.з. Работа с лексическим
материалом.
2.Беседа по текстам
на стр.264-265. Задавать и отвечать на
вопросы.
Домашнее задание.
1.Подготовиться к контрольному
мероприятию по модулю 6.
2.Подготовиться к беседе по теме
«Материалы нового поколения».
Аудиторное занятие 15. (ОЛ1)
Рубежный контроль 3.
1.Письменная контрольная работа по модулю
6 (по пройденному материалу занятий 11-14)
(40 мин).
2.Мини-конференция по теме урока
“Материалы нового поколения”.
Домашнее задание.
1. Текст 6 D-прочитать, знать содержание.
Аудиторное занятие 16. (ОЛ1)
1.Проверка д.з. Беседа по тексту 6 D.
2.Просмотр и обсуждение видеоматериала.
Домашнее задание.
Упражнения и тексты по усмотрению
преподавателя.
Аудиторное занятие 17(ОЛ1)
Итоговое занятие.
Самостоятельная подготовка
1.Текущее домашнее задание включает в себя: выполнение грамматических упражнений к
каждому пройденному уроку, перевод предложений с иностранного языка на родной и
наоборот, прослушивание текстов А учебника в лабораториях устной речи или дома, переписав
их на электронные носители в специализированной лаборатории факультета «Лингвистика»,
ауд. 417л., работу с дополнительными текстами В и С в каждом уроке учебника.
2.Подготовка к тесту №1 по материалу модуля 4 (ОЛ1): дополнительные задания стр.79-81.
3.Подготовка к тесту №2 по материалу модуля 5 (ОЛ1): дополнительные задания стр.97-101.
4.Подготовка к тесту №3 по материалу модуля 6(ОЛ1): дополнительные задания стр.119-122.
▼ Вопросы для подготовки к рубежному контролю / зачёту
1.Условием получения отметки о сдаче 1, 2 и 3 рубежного контроля по модулям семестра
является сдача текущего материала на аудиторных занятиях путем устных ответов, выполнение
поурочных домашних заданий, участие в обсуждении устных тем уроков с получением баллов
по балльно-рейтинговой системе.
2.Условием получения зачёта является получение студентом от 20 до 33 баллов по 1-му, 2-ому
и 3-ему модулям при сумме не ниже 60. При низкой посещаемости занятий студенту могут
быть предложены задания по материалам модулей, к которым относятся пропущенные занятия.
▼ Основная и дополнительная литература
7
Основная литература (ОЛ)
2. Орловская И.В., Самсонова Л.С., Скубриева А.И. Учебник английского языка для
технических вузов. М.: изд-во МГТУ им. Баумана, 2007 – 448 с.
Дополнительная литература (ДЛ))
1. R. Murphy. English Grammar in Use. Cambridge University Press, 2004 – 375 с.
2. Словари: - Lingvo 8.0- 12.0
- Longman WordWise Dictionary
4.
5.
6.
Рекомендуемые Интернет-сайты:
http://www.englishlearner.com
http://www.breakingnewsenglish.com
http:// www.bbc.com.uk
НЕМЕЦКИЙ ЯЗЫК
для студентов всех факультетов
АУДИТОРНЫЕ ЗАНЯТИЯ
МОДУЛЬ 1: Великие учёные 20 века. (ОЛ-1)
Занятие 1. Текст 5А 1/2 «N.I. Shukowskij»; упр.1, 2 стр.76. Упр.3 стр.76; упр.7 (1-5) стр.77
Занятие 2. Текст 5А 2/2 «N.I. Shukowskij». Упр.5 стр. 77; упр.8, 9 стр. 72; задания к тексту
стр.75; упр. 10, 11 стр.78.
Занятие 3. Текст 5В «Geheimnisvolle Strahlen»; стр. 79 упр. 14; упр. 16 стр. 79; задания к тексту
1, 2 стр.82-83; упр.15 стр. 79.
Занятие 4. упр.3 стр.83; упр.18, 19 стр.80-81; подготовка к контрольной работе.
Занятие 5. Контрольная работа. (45-50 мин).Текст 6А 1/2 „А. Einstein“; упр.1 стр.89; упр. 4
стр. 90.
Требования к контрольной работе - знание активной лексики (около 40 лексических единиц)
текстов 5А; 5В; и грамматику.
Грамматические темы: придаточные дополнительные и определительные; местоименные
наречия; Futurum, Perfekt.
МОДУЛЬ 2: Германия, государственное устройство, экономика. (ОЛ-1)
Занятие 6. Текст 6А 2/2 „А. Einstein“. Упр.2 стр.89; упр.5 стр.90; стр. 90-91 упр. 7, 8; упр. 12
стр. 92.
Занятие 7. Текст 6В; упр.6 стр.90, упр. 9, 10 стр.91, упр.13 стр.92; текст 6С – задания к тексту
стр.96.
Занятие 8. Текст 8А (часть I). Упр. 1, 2½ стр.123, стр.124 упр.5, стр.126 упр.11.
Занятие 9. Текст 8А (часть II), упр.2 А,В стр.122; стр.123 упр.2 2/2, упр.3, 4, 6 ½, стр.124,
упр.12 стр.126, упр.16 стр.127.
Занятие 10. Контрольная работа. (45-50 мин); текст 8В.
Требования к контрольной работе - знание активной лексики (около 40 лексических единиц) и
грамматики текстов 6А; 6В; 8А.
Грамматические темы: Plusquamperfekt; инфинитивные группы и обороты; придаточные
предложения времени, причины; Passiv (все времена), Infinitiv Passiv, безличный пассив.
8
МОДУЛЬ 3: Немецкоговорящие страны. (ОЛ-1)
Занятие 11. Текст 8В пересказ, текст 9А ½ «Österreich». Упр. 1,2 стр.143; упр.8, 11 стр.145
Занятие 12. Текст 9А 2/2, текст 9В; упр.3, 4 стр.144, упр. 8, 11 стр.145.
Занятие 13. Тексты 9С стр.151-152, упр.5 стр. 144, упр.7 стр.145. Стр.156, упр.1,2,3,4.
Занятие 14. Текст 9Е стр.155, стр.156 упр.1-4. Подготовка к контрольной работе.
Занятие 15. Контрольная работа. (45-50 мин); текст 8С стр.134-135.
Требования к контрольной работе - знание грамматики текстов 8В, 9А, 9В, 9С, 9D и знание
активной лексики (около 40 лексических единиц).
Грамматические темы: результативный пассив; склонение прилагательных; повторение Perfekt,
Futurum, местоименные наречия, придаточные дополнительные, определительные, времени,
причины, Plusquamperfekt, инфинитивные группы, Passiv (все времена), Infinitiv Passiv,
безличный пассив.
Занятие 16-17. Проработка и устной темы “Bundesrepublik Deutschland“. (ОЛ-1)
САМОСТОЯТЕЛЬНАЯ ПОДГОТОВКА
МОДУЛЬ 1-3:
Текущее домашнее задание включает в себя: выполнение грамматических упражнений к
каждому пройденному уроку, перевод предложений с иностранного языка на родной и
наоборот, проработка текстов А учебника, работу с дополнительными текстами В и С в каждом
уроке учебника.
Подготовка к контрольной работе по материалу модуля (ОЛ-1).
ЗАЧЕТ
Условием получения отметки о сдаче 1, 2 и 3 модуля семестра является сдача текущего
материала на аудиторных занятиях путем устных ответов, выполнение поурочных домашних
заданий, участие в обсуждении устных тем уроков, положительным написанием контрольной
работы с получением баллов по балльно-рейтинговой системе.
ОСНОВНАЯ И ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
Основная литература (ОЛ)
1. Богданова Н.Н., Семёнова. Е.Л. Учебник немецкого языка для технических вузов и
университетов. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2009
2.
ФРАНЦУЗСКИЙ ЯЗЫК
для студентов всех факультетов
АУДИТОРНЫЕ ЗАНЯТИЯ
МОДУЛЬ 1: Факультеты МГТУ им. Н.Э.Баумана. (ОЛ-1)
Занятие 1. Текст 4А ½ “Comment a-t-on découvert l’électron? ”; упр.1,2,3 стр.4, упр.4,5,6 стр.5
Занятие 2. Текст 4А 2/2; упр.1,2,3,4,5 стр.7-8.
Занятие 3. 4В “Le role de l’électron dans l’électricité”; упр. 8 стр.9, упр.9,10,11 стр.10.
Занятие 4. Текст 4C “L’électron ou se trouve-t-il dans la matière?“; упр.12 стр.10; зад.3,4 стр.11
Занятие 5. Контрольная работа. (45-50 мин), тест, текст 4D.
9
Требования к контрольной работе - знание грамматики текстов 4А, 4В, 4С,4D и знание
активной лексики (около 40 лексических единиц).
Грамматические темы: повторение Passé composé, Imparfait, Passé simple.Давнопрошедшее
время(Plus-que parfait).Причастие прошедшего времени (Participe présent).Деепричастие
(Gérondif).
МОДУЛЬ 2: Франция, государственное устройство, экономика. (ОЛ-1)
Занятие 6. Текст 5A 1/2 “La Russie et la France: nouvelles formes de coopération“; упр.1,2,3
стр.14; упр.4,5 стр.15
Занятие 7. Текст 5A 2/2 ; упр.1,2,3,4 стр.18.
Занятие 8. Текст 5B “Lancement de la première sonde lunaire européenne”; упр.5,6,7 стр.20.
Занятие 9. Текст 5C “Les villes spatiales”; упр.8,9,10 стр.20-21
Занятие 10. Контрольная работа. (45-50 мин), тест, текст 5D
Требования к контрольной работе - знание грамматики текстов 5А, 5В, 5С, 5D и знание
активной лексики (около 60 лексических единиц).
Грамматические темы: простое будущее время, наречия, степени сравнения наречий.
МОДУЛЬ 3: Сотрудничество России и Франции в области науки и образования. (ОЛ-1)
Занятие 11. Текст 6А ½ “Des robots et des hommes”; упр.1,2 стр.25; упр.3,4 стр.26
Занятие 12. Текст 6А 2/2; упр.5,6 стр.26; упр.7,8 стр.27.
Занятие 13. Текст 6В “Un robot industriel”; упр.9,10,11 стр.30; упр.12,13,14 стр.32.
Занятие 14. Текст 6С “L’évolution du robot”; упр.15,16,17,18 стр.32-33
Занятие 15. Контрольная работа. (45-50 мин), тест, текст 6D
Требования к контрольной работе - знание грамматики текстов 6А, 6В, 6С,6D и знание
активной лексики (около 30 лексических единиц).
Грамматические темы: безличные конструкции, усилительный оборот c’est(ce sont) … qui(que),
meme,tout, on.
Занятие 16-17. Проверка домашнего чтения, сдача устных тем. (ОЛ-1)
САМОСТОЯТЕЛЬНАЯ ПОДГОТОВКА
МОДУЛЬ 1-3:
Текущее домашнее задание включает в себя: выполнение грамматических упражнений к
каждому пройденному уроку, перевод предложений с иностранного языка на родной и
наоборот, проработка текстов А учебника, работу с дополнительными текстами В и С в каждом
уроке учебника.
Подготовка к контрольной работе по материалу модуля (ОЛ-1).
ЗАЧЕТ
Условием получения отметки о сдаче 1, 2 и 3 модуля семестра является сдача текущего
материала на аудиторных занятиях путем устных ответов, выполнение поурочных домашних
заданий, участие в обсуждении устных тем уроков, положительным написанием контрольной
работы с получением баллов по балльно-рейтинговой системе.
ОСНОВНАЯ И ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
10
Основная литература (ОЛ)
3. Токарева С.А., Фомина М.А. Методические указания по чтению и переводу для студентов I
курса на французском языке. - М.: Изд-во МГТУ им. Н.Э.Баумана, 2007
РУССКИЙ ЯЗЫК ДЕЛОВОГО ОБЩЕНИЯ
Дисциплина состоит из 3-х учебных модулей.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Примечание
1.
Упражнения
1-4
4
2.
Домашние задания
текущие
1-4
3
3.
Аттестация по модулю
4
1
РК – 1 / 2-я
нед.
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
4.
Упражнения
5-12
8
5.
Домашние задания
текущие
5-12
7
6.
Аттестация по модулю
12
1
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
7.
Упражнения
13-17
5
8.
Домашние задания
текущие
13-16
4
9.
Аттестация по модулю
17
1
11
Примечание
Модуль 1. Речевая коммуникация и вербальная культура специалиста
Семинары
Занятие 1. Цели и задачи курса как базовой
дисциплины в подготовке специалистов инженерноэкономического профиля. Коммуникативно-речевая
компетенция специалиста. Природа и механизмы
речемыслительной деятельности. Функции языка,
формы и типы речевого общения, русский речевой и
невербальный этикет. Теория речевой коммуникации:
виды речевой деятельности, модели, задачи.
Диагностика стартового уровня культуры речи.
ОЛ-1, 4, 5; ДЛ-6; ЭР-9, 11.
Занятие 2. Культура речи: аспекты и критерии.
Нормативная
база
современного
русского
литературного
языка.
Орфоэпические,
морфологические, лексические, синтаксические и
стилистические нормы: анализ трудных случаев
произношения, формообразования, согласования.
Тренировочные упражнения по употреблению
языковых и речевых норм, закреплению навыков
нормативной устной и письменной коммуникации.
ОЛ-1, 4, 5; ДЛ-6; ЭР-9, 11.
Модуль 2. Официально-деловой стиль речи и культура делового общения
Семинары
Занятие 3. Национальный язык и его разновидности.
Функционально-стилевая дифференциация речи.
Стили речи: назначение, сфера употребления,
конструктивные
и
языковые
особенности.
Официально-деловой стиль: сфера функционирования,
подстили, жанры. Письменная деловая коммуникация
и основы документоведения.
ГОСТ на ведение
деловой
документации.
Логические
основы
содержания деловых бумаг. Общие правила
оформления документов, состав реквизитов.
Тренировочные упражнения по закреплению
навыков нормативной деловой коммуникации.
ОЛ-2, 4, 5; ДЛ-6, 7; МЛ-8; ЭР-9, 10, 11.
Занятие 4. Документы личного характера:
назначение, сфера употребления. Жанры частных
деловых бумаг: заявление, объяснительная записка,
автобиография, резюме, характеристика, доверенность,
расписка.
Содержательно-композиционные
и
языковые особенности личных документов.
Логико-смысловое редактирование текстов частных
деловых бумаг, их составление в разных жанрах.
ОЛ-2, 4, 5; ДЛ-6, 7; МЛ-8; ЭР-9, 10, 11.
Занятие 5. Документы служебного характера:
назначение, сфера употребления. Основные виды и
жанры служебных деловых бумаг: организационнораспорядительные (приказ, распоряжение, устав,
договор) и информационно-справочные (докладная и
служебная записки, акт, протокол, отчет, справка,
деловое письмо). Содержательно-композиционные и
языковые особенности служебных документов.
Логико-смысловое
редактирование
текстов
служебных документов, их составление.
ОЛ-2, 4, 5; ДЛ-6, 7; МЛ-8; ЭР-9, 10, 11.
Занятие 6. Устная деловая коммуникация: сферы,
ситуации,
жанры,
конструктивно-языковая
специфика. Деловая беседа, её структурные
особенности, правила подготовки и проведения.
Собеседование как вид деловой беседы. Телефонный
разговор.
Основные
стратегии
и
тактики,
риторические
приемы
гармонизации
устного
делового общения.
Презентации
и
ролевые
(деловые)
игры:
моделирование ситуаций делового общения.
ОЛ-2, 4, 5; ДЛ-6, 7; МЛ-8; ЭР-9, 10, 11.
Модуль 3. Культура научной и научно-деловой коммуникации
Семинары
Занятие 7. Научный стиль речи: назначение, сфера
функционирования, конструктивные и лингвистические
особенности, подстили, жанры. Научный текст и его
организация. Первичные и вторичные научные
тексты. Вторичные научные тексты как виды
аналитической обработки информации. План,
тезисы, конспект, аннотация, рецензия, реферат:
структурные и языковые особенности.
Логико-смысловое и языковое редактирование
научного текста, составление разножанровых
вторичных текстов.
ОЛ-3, 4, 5; ДЛ-6; ЭР-9, 11.
Занятие 8. Первичные научные тексты как виды
представления
результатов
исследовательской
деятельности. Структура и композиция научной
работы. Жанры первичных научных текстов. Приемы
цитирования.
Оформление
справочнобиблиографического аппарата научной работы.
Составление
первичных
научных
текстов.
Закрепление навыков оформления текстового
материала работы, ссылок и библиографического
описания информационных источников.
ОЛ-3, 4, 5; ДЛ-6; ЭР-9, 11.
Занятие 9. Зачет по курсу.
12
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала занятий, изучении литературных
(основных и дополнительных) и электронных источников, в выполнении домашних заданий, подготовке к текущим и
рубежным контрольным работам, к ответам на теоретические вопросы и к выполнению практических заданий
зачетной работы по курсу.
Контрольные мероприятия и сроки их проведения
1. РК «Диагностический тест по русскому языку и культуре речи».
Срок проведения – 1 / 2-я неделя.
2. Контроль по модулю «Речевая коммуникация и вербальная культура специалиста».
Срок проведения – 3 / 4-я неделя.
3. ДЗ №1 «Культура деловой речи».
Срок выдачи 9 / 10- неделя, срок сдачи – 11/ 12-я неделя.
4. Контроль по модулю «Официально-деловой стиль речи и культура делового общения».
Срок проведения – 12-я неделя.
5. ДЗ №2 «Культура научной речи».
Срок выдачи 13 / 14-я неделя, срок сдачи – 15 / 16-я неделя.
6. Контроль по модулю «Культура научной и научно-деловой коммуникации».
Срок проведения – 16-я неделя.
7. Зачет по курсу.
Срок проведения – 17-я неделя.
Зачет
Условием получения зачета является положительная аттестация по трем модулям курса, суммирующая
результаты текущей успеваемости на аудиторных занятиях, выполнения проверочных и рубежных работ, домашних
заданий, а также оценку личных качеств студента по балльно-рейтинговой системе контроля знаний.
Литература
Основная литература (ОЛ)
1. Жилина О.А., Романова Н.Н. Русский язык и культура речи. Ч. 1. Основы культуры речи: Учебное пособие. – М.:
Изд-во МГТУ им. Н.Э.Баумана, 2008. – 152 с.
2. Жилина О.А., Романова Н.Н. Русский язык и культура речи. Ч. 2. Культура деловой речи: Учебное пособие. – М.:
Изд-во МГТУ им. Н.Э.Баумана, 2007. – 108 с.
3. Жилина О.А., Романова Н.Н. Русский язык и культура речи. Ч. 3. Культура научной речи: Учебное пособие. – М.:
Изд-во МГТУ им. Н.Э.Баумана, 2009. – 75 с.
4. Скорикова Т.П. Практикум по «Русскому языку и культуре речи»: Учебное пособие. – М.: Изд-во МГТУ им.
Н.Э.Баумана, 2013.
5. Романова Н.Н., Скорикова Т.П. Рабочая тетрадь: Учебное пособие. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2013.
Дополнительная литература (ДЛ)
6. Боженкова Р.К. Русский язык и культура речи: Учебник. – М.: Флинта: Наука, 2011. – 608 с.
7. Хазагеров Г.Г., Корнилова Е.Е. Риторика для делового человека: Учебное пособие. – М.: Флинта: Московский
психолого-социальный институт, 2001. – 136 с.
Методические пособия (МЛ)
8. Романова Н.Н. Методические указания к изучению дисциплины «Русский язык и культура речи». Ч. 1. Культура
деловой речи. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2007. – 47 с.
Электронные ресурсы (ЭР)
9. Скорикова Т.П. Русский язык и культура речи: методические рекомендации к изучению курса лекций для студентов
МГТУ им. Н.Э. Баумана всех факультетов и специальностей. – ФГУП НТЦ «Информрегистр». Депозитарий
электронных изданий, рег. свид-во № 18802 от 22.03.2010 (электронное издание). – 74 с.
URL:http// fl.bmstu.ru/index.php/component/docman/doc_download/116----.html
10. Яковлева Е.А. Основы деловой коммуникации: Учебное пособие для студентов МГТУ им. Н.Э.Баумана по
дисциплине «Русский язык и культура речи». – ФГБОУ ВПО «Московский государственный технический
университет им. Н.Э.Баумана», 2010 (электронное издание). – 3 п.л.
11. Конспект лекций, справочные материалы // сайт каф. Л-1 факультета «Лингвистика».
13
ФИЗИКА
▼ Аудиторные занятия
1.
ОЛ-4 §1.1-1.7. ОЛ-6 §1.1-1.5. ДЛ-14 §81, 82,85. МП-7,
МП-8.
Лекция 8-9. «Элементы релятивистской механики».
Преобразования Галилея. Инвариантность уравнений
механики относительно преобразований Галилея.
Специальная теория относительности. Постулаты
Эйнштейна. Преобразования Лоренца. Кинематические
следствия из преобразований Лоренца. Релятивистский
закон сложения скоростей. Интервал событий.
Элементы релятивистской динамики. Взаимосвязь
массы и энергии. Связь между импульсом и энергией
релятивистской
частицы.
Основное
уравнение
релятивистской динамики.
ОЛ-2 §6.1-.6.8. ОЛ-5 §7.1-7.5, 8.1-8.4. ДЛ-12 §10-17,20.
Лекции
МОДУЛЬ 1:
Физические основы механики.
Лекция 1. Вводная. Предмет физики. Физический
объект, физическое явление, физический закон. Физика
и современное естествознание. Системы отсчёта.
Кинематика материальной точки. Угловые скорость и
ускорение твёрдого тела. Классический закон сложения
скоростей и ускорений при поступательном движении
подвижной системы отсчета.
ОЛ-2. Введение. §1.1-1.5. ОЛ-5. Введение, §1.1-1.3. ДЛ12 §1.- 4, 7-9. ДЛ-14 § 1- 4.
Лекция 2. «Закон сохранения импульса». Силы.
Инерциальная
система
отсчёта.
Динамика
материальной точки. Механическая система и её центр
масс. Уравнение изменения импульса механической
системы. Закон сохранения импульса.
ОЛ-2 §2.1-2.6, 2.8-2.11,3.1,3.10. ОЛ-5 §2.1-2.5, 3.13.4..ДЛ-12 §18,19,21,23.. ДЛ-14 §9—13, 18, !9..
Лекция 3. «Закон сохранения момента импульса».
Момент силы. Моменты импульса материальной точки
и механической системы. Уравнение моментов
механической системы. Закон сохранения момента
импульса механической системы.
ОЛ-2 §3.12, 5.1-5.4. ОЛ-5 §5.1-5.4. ДЛ-12 §21,24,31,32.
ДЛ-14 §30,32,33-36.
Лекция 4. «Закон сохранения энергии в механике».
Работа и кинетическая энергия. Консервативные силы.
Работа в потенциальном поле. Потенциальные энергии
тяготения и упругих деформаций. Связь между
потенциальной энергией и силой. Закон сохранения
энергии.
ОЛ-2 §3.2-3.8, 5.6-5.8.. ОЛ-5 §4.1-4.6. ДЛ-12 §25,33.ДЛ14 §22-29..
Лекция 5-6. «Колебания». Гармонические колебания.
Векторная диаграмма. Сложение гармонических
колебаний одного направления равных и близких
частот.
Сложение
взаимно
перпендикулярных
гармонических колебаний равных и кратных частот.
Свободные незатухающие колебания. Энергия и
импульс
гармонического
осциллятора.
Фазовая
траектория. Физический маятник. Квазиупругая сила.
Свободные затухающие колебания. Декремент и
логарифмический декремент колебаний. Вынужденные
колебания. Установившиеся вынужденные колебания.
Механический резонанс.
ОЛ-2 §8.1, 8.4-8.9, 8.11.. ОЛ-5 §6.1-6.4. ДЛ-12 §50-54.
ДЛ-14 §39-41,81,82,85.
Лекция 7. «Механические волны». Виды механических
волн. Упругие волны в стержнях. Волновое уравнение.
Плоская гармоническая волна, длина волны, фазовая
скорость. Сферические волны. Объёмная плотность
энергии волны. Вектор Умова-вектор плотности потока
энергии. Когерентные волны. Интерференция волн.
Стоячая волна.
МОДУЛЬ 2:
Физическая термодинамика.
Лекция 10. Статистический и термодинамический
методы
описания
макроскопических
тел.
Термодинамическая
система.
Термодинамические
состояния,
обратимые
и
необратимые
термодинамические процессы. Внутренняя энергия и
температура термодинамической системы. Теплота и
работа. Адиабатически изолированная система. Первое
начало термодинамики.
ОЛ-1 Введение, §1.1-1.5. ОЛ-3 §1.1-1.7. ОЛ-7 §1.1-1.2.
ДЛ-13 §1,14,16. ДЛ-15 §13,41,29.
Лекция 11. Уравнения состояния термодинамических
систем. Уравнение Клапейрона-Менделеева. Идеальногазовый термометр. Основное уравнение молекулярнокинетической теории. Равномерное распределение
энергии по степеням свободы молекул. Внутренняя
энергия идеального газа. Эффективный диаметр и
средняя длина свободного пробега молекул газа.
Экспериментальные подтверждения молекулярнокинетической теории.
ОЛ-1 §2.1-2.3. ОЛ-3 §1.8, 2.2-2.5, 7.2. ОЛ-7 § 1.5,1.6,2.3.
ДЛ-13 §8,10,11.ДЛ-15 §7,8,14,86,87.
Лекция 12. Теплоемкость идеального газа при
изопроцессах. Адиабатический процесс, уравнение
Пуассона. Политропический процесс. Теплоемкость и
работа в политропических процессах. Газ Ван-дерВаальса. Внутренняя энергия газа Ван-дер-Ваальса.
ОЛ-1 §2.4-2.7. ОЛ-3 §1.9-1.13. ОЛ-7 §1.3,1.4,1.7. ДЛ-13
§10,17,18,32. ДЛ-15 §18,21,98,103.
Лекция 13. Тепловые и холодильные машины. Второе
начало термодинамики. Цикл Карно. Теорема Карно.
Термодинамическая шкала температур. Неравенство
Клаузиуса. Термодинамическая энтропия. Закон
возрастания энтропии. Третье начало термодинамики.
ОЛ-1 §3.1,3.2,3.4-3.10. ОЛ-3 §2.11,3.1-3.5. ОЛ-7 §3.13.5. ДЛ-13 §19-22. ДЛ-15 §27-31, 37,40,41.
Лекция 14. Основное неравенство и основное
уравнение
термодинамики.
Понятие
о
14
термодинамических потенциалах. Эффект ДжоуляТомпсона. Принцип Ле-Шателье-Брауна. Введение в
термодинамику необратимых процессов.
ОЛ-1 §4.1-4.5.. ОЛ-3 §3.6. ОЛ-7 §3.5,3.6. ДЛ-13
§23,33,57. ДЛ-15 §29,45,46.
Лекция 15. Статистическое описание равновесных
состояний. Функция распределения. Барометрическая
формула.
Распределения
Больцмана.
Принцип
детального равновесия. Распределение Максвелла.
Экспериментальная
проверка
распределения
Максвелла. Фазовое пространство. Распределение
Максвелла-Больцмана.
Равновесные
флуктуации.
Статистическое
обоснование
второго
начала
термодинамики.
Формула
Больцмана
для
статистической энтропии.
ОЛ-1 §5.1-5.9. ОЛ-3 §1.14,2.1,2.6-2.8,2.10. ОЛ-7 §2.12.4. ДЛ-13 §8-10. ДЛ-15 §72,76,77.
Лекция 16. Термодинамические потоки. Явления
переноса в газах: диффузия, теплопроводность и
вязкость. Эффузия в разреженном газе. Физический
вакуум.
Броуновское
движение.
Производство
энтропии в необратимых процессах.
ОЛ-1 §6.1-6.5. ОЛ-3 §7.1,7.3-7.7. ОЛ-7 §6.2,6.3. ДЛ-13
§50-52,54.ДЛ-15 §86-89,93,95.
Лекция 17. Агрегатные состояния вещества. Условия
равновесия фаз. Явления на границе раздела газа,
жидкости и твердого тела. Капиллярные явления.
Фазовые переходы первого и второго рода. Диаграммы
состояния. Критические явления при фазовых
переходах.
ОЛ-1 §7.1-7.7. ОЛ-3 §5.1-5.5,6.1-6.5. ОЛ-7 §5.1-5.4. ДЛ13 §34,35,41. ДЛ-15 §111,112,116,120.
Лекция 18. Обзорная лекция.
2.
Занятие 4. Закон сохранения энергии в механике.
Ауд.: ОЛ-8 № 1.158, 1.180, 1.194, 1.211, 1.310(б) или
ОЛ-9 № 1.148, 1.164, 1.176, 1.191, 1.282(б), 1.292(б).
Дома: ОЛ-8 № 1.149, 1.169 или ОЛ-9 № 1.142, 1.157;
ОЛ-10 № 2.76, 2.87.
Занятие5. Колебания и волны.
Ауд.: ОЛ-8 № 3.27, 3.64, 3.85, 3.186 или ОЛ-9 № 4.25,
4.57, 4.79, 4.177.
Дома: ОЛ-8 № 3.12, 3.180 или ОЛ-9 № 4.12, 4.176; ОЛ10 № 6.45, 7.4.
МОДУЛЬ 2:
Занятие 6. Теория относительности.
Ауд.: ОЛ-8 № 1.398, 1.415, 1.428, 1.443 или ОЛ-9 №
1.365, 1.382, 1.395, 1.409.
Дома: ОЛ-8 № 1.396, 1.417 или ОЛ-9 № 1.363, 1.384;
ОЛ-10 № 5.9, 5.30.
Занятие 7. Термодинамика.
Ауд.: 0Л-8 № 6.3, 6.30, 6.47, 6.154 или ОЛ-9 № 2.3, 2.30,
2.47, 2.138.
Дома: ОЛ-8 № 6.32, 6.137; или ОЛ-9 № 2.32, 2.122; ОЛ10 № 11.6, 11.61.
Занятие
8.
Равновесные
статистические
распределения.
Ауд.: 0Л-8 № 6.84, 6.96, 6.124, 6.208 или ОЛ-9 № 2.81,
2.95, 2.119, 2.252.
Дома: ОЛ-8 № 6.68, 6.192 или ОЛ-9 № 2.68, 2.236; ОЛ10 № 10.16, 10.60.
3.
Занятия в физической лаборатории
МОДУЛЬ 1:
Занятие 1. Лабораторная работа по механике.
ОЛ-2, 5.
Занятие 2. Лабораторная работа по механике.
ОЛ-2, 5.
Занятие 3. Лабораторная работа по механике.
ОЛ-2, 5.
Занятие 4. Лабораторная работа по колебаниям
и волнам.
ОЛ-1, 2, 4, 6.
Семинары
МОДУЛЬ 1:
Занятие 1. Кинематика.
Ауд.: ОЛ-8 № 1.15, 1.25, 1.41, 1.45, 1.52 или ОЛ-9 №
1.15, 1.26, 1.41, 1.45, 1.52.
Дома: ОЛ-8 № 1.20, 1.47 или ОЛ-9 № 1.20, 1.46; ОЛ-10
№ 1.26, 1.54.
Занятие 2. Закон сохранения импульса.
Ауд.: ОЛ-8 № 1.88, 1.108, 1.125, 1.144 или ОЛ-9 № 1.85,
1.103, 1.120, 1.138.
Дома: ОЛ-8 № 1.87, 1.117 или ОЛ-9 № 1.84, 1.112; ОЛ10 № 2.34, 2.39.
Занятие 3. Закон сохранения момента импульса.
Ауд. ОЛ-8 № 1.228, 1.292, 1.310(а), 1.324 (а) или ОЛ-9
№ 1.207, 1.266, 1.282(а), 1.292(а).
Дома: ОЛ-8 № 1.229, 1.287 (а) или ОЛ-9 №1.208, 1.263
(а); ОЛ-10 № 3.25, 3.29.
Занятие 5. Рубежный контроль модуля 1.
МОДУЛЬ 2:
Занятие 6. Лабораторная работа по термодинамике.
ОЛ-1, 3, 7.
Занятие 7. Лабораторная работа по термодинамике.
ОЛ-1, 3, 7.
Занятие 8. Рубежный контроль модуля 2.
▼ Самостоятельная подготовка
МОДУЛЬ 1:
Проработка курса лекций, учебников проводится по темам лекций 1 - 7, семинаров 1 - 5 и занятий в физической
лаборатории 1 - 4.
Подготовка к рубежному контролю по темам лекций 1 - 7, материалам семинаров 1 - 5 и занятий в физической
лаборатории 1 - 4.
15
МОДУЛЬ 2:
Проработка курса лекций, учебников проводится по темам лекций 8-16, семинаров 6 - 8 и занятий в физической
лаборатории 6,7.
Подготовка к рубежному контролю по темам лекций 8 - 16, материалам семинаров 6- 8 и занятий в физической
лаборатории 6, 7.
▼ Основная и дополнительная литература
Основная литература (ОЛ)
Глаголев К.В., Морозов А.Н.. Физическая термодинамика. – М. : Изд-во МГТУ, 2004.
Савельев И.В. Курс общей физики. Механика.- М. : Наука. Физматлит, 2004, 1998.
Савельев И.В. Курс общей физики. Молекулярая физика и термодинамика. - М. : Наука. Физматлит, 2004,
1998.
4. Савельев И.В. Курс общей физики. Волны. Оптика - М. : Наука. Физматлит, 2004, 1998.
5. Иродов И.Е. Механика. Основные законы. - М.-С.-П.:Физматлит, 2006, 2000
6. Иродов И.Е. Волновые процессы. Основные законы. - М.-С.-П.:Физматлит, 2006, 1999.
7. Иродов И.Е. Физика макросистем. Основные законы. . М.-С.-П.:Физматлит, 2006, 2001.
8. Иродов И.Е. Задачи по общей физике.- М.: Бином, 19982001.
9. Иродов И.Е. Задачи по общей физике.- М.: Наука, 1988.
10. Чертов А.Г., Воробьев А.А. Задачник по физике.- М.: Высшая школа, 2003, 1988.
11. Гладков Н.А., Романов А.С. Методические указания к домашнему заданию по курсу общей физики по
теме «Законы сохранения. Колебания. Волны», 2012 г.
1.
2.
3.
Дополнительная литература (ДЛ)
12.
13.
14.
15.
16.
Матвеев А.Н. Механика и теория относительности. М.: Высшая школа, 1986.
Матвеев А.Н. Молекулярная физика. - М.: Высшая школа, 1987.
Сивухин Д.В. Курс общей физики. Том I. Механика. -М.: Наука,1989.
Сивухин Д.В. Общий курс физики. Том II. Термодинамика и молекулярная физика. -М.: Наука,1990.
Методические указания к решению задач по курсу общей физики. Раздел «Механика» под редакцией
Яковлева М.А. – М:Изд-во МГТУ, 2001,1983
Методические пособия, изданные в МГТУ (МП)
1.
2.
3.
4.
5.
Еркович О.С., Морозов А.Н. Методические указания к решению задач по курсу общей физики.
Статистическая физика.-М.: Изд-во МГТУ, 2007.-26с.
Еркович О.С., Морозов А.Н. Решение задач по курсу общей физики. Процессы переноса.- М. Изд-во
МГТУ, 2009.-24с.
Голубев В.Г., Яковлев М.А. Олимпиадные задачи по физике. Разделы: Механика, термодинамика. .М.:Изд-во МГТУ, 2006.-44с
Веретимус Д.К., Веретимус Н.К., Креопалов Д.В. Механические колебания.- .-М.:Изд-во МГТУ, 2008.-24с
Веретимус Д.К., Веретимус Н.К., Креопалов Д.В. Механические волны..-М.:Изд-во МГТУ, 2009.-29с
16
ИНТЕГРАЛЫ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Дисциплина состоит из 2-х учебных модулей и экзамена.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-8
16
Упражнения
1-9
28
Домашние задания
текущие
1-9
12
Контроль по модулю №1
10
6
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
9-17
18
Упражнения
10-17
23
Домашние задания
текущие
10-17
12
16
6
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Контроль по модулю №2
Примечание
Модуль 1:Интегралы
Лекции
Лекция
1.Первообразная
и
ее
свойства.
Неопределенный интеграл, его свойства, связь с
дифференциалом.
Таблица
основных
неопределенных
интегралов.
Интегрирование
подстановкой
и
заменой
переменного.
Интегрирование по частям.
Лекция 3.Определенный интеграл как предел
интегральных сумм. Теорема об интегрируемости
кусочно-непрерывных функций (без док-ва).
Геометрическая интерпретация определенного
интеграла. Основные свойства определенного
интеграла. Теоремы об оценке и о среднем значении.
ОЛ-1, § 1.1–1.4; ОЛ-3, гл. X, § 1–3, § 10–14; ОЛ-5, гл.
5, § 5.1–5.2.
ОЛ-1, § 6.1–6.2, 6.5–6.8; ОЛ-3, гл. XI, § 1–3; ОЛ-5,
гл.6, § 6.1–6.2.
Лекция 2.Рациональные дроби. Разложение
правильной рациональной дроби в сумму
простейших (без док-ва). Интегрирование основных
типов функций. Примеры интегралов, не
выражающихся через элементарные функции.
Лекция 4. Определенный интеграл с переменным
верхним пределом, теорема о его производной.
Формула Ньютона — Лейбница. Вычисление
определенных интегралов подстановкой и по частям.
Интегрирование периодических функций,
интегрирование четных и нечетных функций на
отрезке, симметричном относительно начала
координат.
ОЛ-1, § 1.1–1.6; § 3–4; ОЛ-1, § 2.1–2.4; ОЛ-3, гл. X, §
4–14, гл. VII § 1–2; ОЛ-5, гл. 5, § 3-5.
17
ОЛ-1, § 6.9–6.10; ОЛ-3, гл. XI, § 4–6; ОЛ-5, гл.6, §
6.3–6.4.
Лекции 7-8. Вычисление площадей плоских фигур,
ограниченных кривыми, заданными в декартовых
координатах, параметрически и в полярных
координатах. Вычисление объемов тел по площадям
поперечных сечений и объемов тел вращения.
Вычисление длины дуги кривой и площади
поверхности вращения.
Лекции5-6. Несобственные интегралы по
бесконечному промежутку (I-го рода).
Несобственные интегралы от неограниченных
функций на отрезке (II-го рода). Признаки
сходимости несобственных интегралов. Абсолютная
и условная сходимости. Несобственные интегралы с
несколькими особенностями.
ОЛ-1, § 9.1–9.5; ОЛ-3, гл. XII, § 1, 2, 4, 5; ОЛ-5, гл. 7,
§ 7.1–7.5.
ОЛ-1, § 7.1–7.6, 7.8; ОЛ-3, гл. XI, § 7; ОЛ-5, гл. 6, §
6.8–6.11.
Упражнения
Занятие 1.Непосредственное интегрирование по
таблице. Интегрирование методом подстановки.
Ауд.: ОЛ-8, гл.6, §1: 6.15, 6.23, 6.24, 6.27, 6.29, 6.35,
6.37, 6.40, 6.42, 6.43, 6.44, 6.48 6.52, 6.53, 6.56, 6.60,
6.62, 6.65, 6.74, 6.79, 6.83, 6.89, 6.95, 6.98, 6.100,
6.102, 6.107 или
ОЛ-9, гл.4, §1: 1032, 1040, 1044, 1046, 1050, 1062,
1063, 1065, 1066, 1073, 1075, 1080, 1093, 1082, 1086,
1095, 1104, 1119, 1133, 1137, 1145, 1149,1153, 1159,
1163, 1167, 1179, 1189.
Дома: ОЛ-8, гл.6, § 1: 6.20, 6.22, 6.25, 6.32, 6.38, 6.39,
6.41 6.45, 6.46, 6.47, 6.49, 6.54, 6.57, 6.61, 6.66, 6.68,
6.72, 6.76, 6.80, 6.85, 6.86, 6.92, 6.97, 6.101, 6.104,
6.106, 6.112 или
ОЛ-9, гл.4, § 1: 1037, 1041, 1057, 1069, 1070, 1074,
1077, 1083, 1085, 1094, 1108, 1096, 1101, 1114, 1120,
1130, 1146, 1152, 1154, 1162, 1172 1182, 1188.
Занятие 2.Интегрирование по частям.
Ауд.: ОЛ-8, гл. 6, § 1: 6.129, 6.130, 6.132, 6.135, 6.124,
6.128, 6.136, 6.143, 6.151, 6.157, 6.144, 6.146, 6.147,
6.155, 6.156 или
ОЛ-9, гл. 4, § 3: 1214, 1219, 1236, 1231, 1213, 1223,
1227, 1234, 1235, 1252, 1253, 1245, 1237, 1228, 1242,
1246.
Дома: ОЛ-8, гл. 6, § 1: 6.125, 6.131, 6.140, 6.142,
6.127, 6.138, 6.145, 6.152, 6.153, 6.154, 6.137, 6.141
или
ОЛ-9, гл. 4, § 3: 1215, 1217, 1229, 1232, 1244, 1237,
1241, 1254, 1239, 1249, 1222, 1226.
Занятие
3.
Интегрирование
выражений,
содержащих квадратный трехчлен.
Ауд.: ОЛ-8, гл. 6, § 2: 6.158, 6.161, 6.163, 6.165, 6.271,
6.250, 6.254, 6.255, 6.257, 6.259, 6.260, 6.264, 6.275
или
ОЛ-9, гл. 4, § 4: 1225, 1259, 1261, 1262, 1265, 1266,
1269, 1271, 1272, 1274, 1277, 1278, 1279.
Дома: ОЛ-8, гл. 6, § 2:, 6.159, 6.160, 6.162, 6.164,
6.251, 6.252, 6.253, 6.256, 6.258, 6.265, 6.280 6.276,
6.277 или
ОЛ-9, гл. 4, § 4: 1258, 1260, 1263, 1267, 1270, 1268,
1273, 1275, 1276.
Занятие 4.Интегрирование рациональных дробей.
Ауд.: ОЛ-8, гл. 6, § 2: 6.167, 6.168, 6.177, 6.171, 6.179,
6.178, 6.174, 6.185, 6.186, 6.188 или
ОЛ-9, гл. 4, § 5: 1282, 1284, 1286, 1289, 1290, 1298,
1308, 1313, 1314.
Дома: ОЛ-8, гл. 6, § 2: 6.129, 6.170, 6.173, 6.180,
6.181, 6.184, 6.187, 6.189 или
ОЛ-9, гл. 4, § 5: 1283, 1285, 1292, 1295, 1296, 1297,
1305, 1307, 1311.
Занятие 5.Интегрирование тригонометрических
функций.
Ауд.: ОЛ-8, гл. 6, § 2: 6.190, 6.191, 6.195, 6.197, 6.198,
6.201, 6.203, 6.206, 6.209, 6.212, 6.213, 6.216 или
ОЛ-9, гл. 4, § 7: 1338, 1341, 1345, 1347, 1350, 1351,
1355, 1359, 1365, 1366.
Дома: ОЛ-8, гл. 6, § 2: 6.192, 6.194, 6.196, 6.199,
6.202, 6.204, 6.208, 6.210, 6.211, 6.214, 6.215, 6.217
или
ОЛ-9, гл. 4, § 7: 1339, 1340, 1344, 1346, 1348, 1352,
1358, 1362, 1367, 1368, 1372.
Занятие 6.Интегрирование тригонометрических
функций.
Интегрирование
некоторых
иррациональных функций.
Ауд.: ОЛ-8, гл. 6, § 2: 6.219, 6.222, 6.225, 6.226, 6.238,
6.240, 6.242, 6.244, 6.261, 6.262, 6.264, 6.266, 6.267
или
ОЛ-9, гл. 4, § 6, 7: 1377, 1382, 1388, 1380, 1389, 1318,
1320, 1322, 1325, 1403, 1405, 1407, 1411, 1412.
Дома: ОЛ-8, гл. 6, § 2: 6.218, 6.223, 6.224, 6.227,
6.239, 6.241, 6.243, 6.245, 6.263, 6.256, 6.268, 6.269
или
ОЛ-9 гл. 4 § 6, 7: 1373, 1378, 1381, 1389, 1387, 1315,
1317, 1319, 1321, 1323, 1324, 1404, 1406, 1408, 1413.
Занятие
7.Контрольная
работа
«Техника
интегрирования».
Занятие 8. Вычисление определенного интеграла.
Его свойства и геометрическая интерпретация.
Ауд.: ОЛ-8, гл. 6, § 4: 6.326, 6.337, 6.340, 6.346, 6.350,
6.379, 6.387, 6.390, 6.395, 6.399, 6.406, 6.364(б, в),
6.365 (а, в), 6.366 (а, г), 6.369, 6.370, 6.378 (в задачах
6.326, 6.337, 6.340, 6.399, 6.406 дать геометрическую
интерпретацию) или
ОЛ-9, гл. 5, § 2, 4–6: 1521, 1529, 1534, 1536, 1538,
1576, 1587, 1590, 1592, 1598, 1592, 1598, 1599, 1600,
1610(а, б), 1611 (а, в), 1612, 1614, 1619, 1621 (в
задачах 1521, 1529, 1536, 1599, 1600 дать
геометрическую интерпретацию).
Дома: ОЛ-8, гл. 6, § 4: 6.328, 6.336, 6.341, 6.347,
6.386, 6.394, 6.400, 6.403, 6.464 (а), 6.365 (б), 6.366 (б,
в), 6.368, 6.371 (в задачах 6.336, 6.338, 6.341, 6.399,
6.347 дать геометрическую интерпретацию) или
18
ОЛ-9, гл.5, § 2, 4–6: 1522, 1527, 1537, 1539, 1541,
1589, 1591, 1593, 1601, 1602, 1610 (в), 1611 (б), 1613,
1618, 1620 (в задачах 1527, 1537, 1541, 1601 дать
геометрическую интерпретацию).
Занятие 9. Вычисление площади плоской фигуры в
декартовой и полярной системах координат.
Ауд.: ОЛ-8, гл. 6, § 6: 6.453, 6.456, 6.467, 6.478,
6.479, 6.483, 6.486, 6.488 или
ОЛ-9, гл. 5, § 7: 1623, 1624, 1633, 1638, 1650, 1655,
1658, 1663.
Дома: ОЛ-8, гл. 6, § 6: 6.457, 6.464, 6.468, 6.480,
6.481, 6.484, 6.487, 6.492 или
ОЛ-9, гл. 5, § 7: 1626, 1634, 1636, 1645, 1653, 1656,
1657, 1661.
Занятия
10-11.Несобственные
интегралы.
Исследование
несобственных
интегралов
на
сходимость. Вычисление объемов тел по площадям
поперечных сечений, вычисление объемов тел
вращения. Приложения определенного интеграла в
физике.
Ауд.: ОЛ-8, гл. 6, § 5, 6: 6.411, 6.417, 6.419, 6.424,
6.433, 6.435, 6.437, 6.441, 6.426, 6.428, 6.430, 6.432,
6.443, 6.445, 6.447, 6.449, 6.451, 6.533, 6.535, 6.536,
6.538, 6.540, 6.541, 6.543, 6.560, 6.573, 6.581 или
ОЛ-9, гл.5, § 3, 9: 1551, 1552, 1555, 1556, 1560, 1562,
1546, 1549, 1550, 1558, 1559, 1570, 1573, 1571, 1707,
1708, 1688, 1691, 1692, 1694, 1701 (в), 1702, 1703.
Дома: ОЛ-, гл. 6, § 5, 6: 6.412, 6.418, 6.420, 6.434,
6.436, 6.439, 6.429, 6.431, 6.442, 6.444 6.446, 6.448,
6.534, 6.537, 6.542, 6.544, 6.561, 6.574, 6.582 или
ОЛ-9, гл. 5, § 3, 9: 1554, 1559, 1563, 1565, 1547, 1557,
1566, 1567, 1572, 1646, 1683, 1691 (а), 1697, 1709,
1689, 1695, 1697, 1701 (б) 1704.
Занятия 12-13.Вычисление длины дуги и площади
поверхности вращения.
Ауд.: ОЛ-8, гл. 6, § 6: 6.494, 6.500, 6.506, 6.507, 6.509,
6.519 (а), 6.523 (б), 6.527, 6.530 или
ОЛ-9, гл.5, § 8, 10: 1665, 1667, 1669, 1676, 1680, 1715,
1722 (б), 1723 (в), 1725.
Дома: ОЛ-8, гл. 6, § 6: 6.499, 6.504, 6.511, 6.519 (б),
6.523 (а), 6.526, 6.529, 6.531 или
ОЛ-9 гл. 5 § 8, 10: 1666 1670, 1678, 1679, 1716,
1722(а), 1723(б), 1726.
Занятие 14.Контроль по модулю 1 (РК №1).
Модуль 2:Дифференциальные уравнения
Лекции
Лекция
1.Обыкновенное
дифференциальное
уравнение (ОДУ) первого порядка, его решения.
Частное и общее решения. Интегральные кривые.
Задача Коши дляОДУ первого порядка. Теорема
Коши о существовании и единственности решения
ОДУ (без вывода). Решение ОДУ первого порядка: с
разделяющимися переменными, однородные ОДУ,
линейные ОДУ (однородные и неоднородные),
уравнения Бернулли. Геометрическая интерпретация
ОДУ первого порядка. Изоклины. Геометрическое
решение ОДУ с помощью изоклин.
вронскиане системы линейно зависимых функций.
Теорема о вронскиане системы линейно независимых
решений однородного ЛДУ. Теорема о структуре
общего решения однородного ЛДУ. Размерность
пространства решений и фундаментальная система
решений
однородного
ЛДУ.
Формула
Остроградского — Лиувилля и ее следствия.
Понижение порядка однородного ЛДУ при
известном частном решении.
ОЛ-2, § 6.1–6.3; ОЛ-4, гл. XIII, § 20; ОЛ-6, гл.1, §
1.15.
ОЛ-2, § 1.1-1.3, 2.1, 2.2, 2.4, 3.1–3.4; ОЛ-4, гл. ХШ, §
1–5, 7–9, 3, 11, 12; ОЛ-6, гл. 1, § 1.1, 1.2, 1.3, 1.4.
Лекции 5-6. Однородные ЛДУ с постоянными
коэффициентами. Характеристическое уравнение
однородного ЛДУ. Построение общего решения по
корням характеристического уравнения (вывод для
n=2). Неоднородные ЛДУ, структура их общего
решения. Теорема о наложении частных решений.
Метод Лагранжа вариации постоянных (вывод для
n=2). Нахождение частного решения неоднородного
ЛДУ с постоянными коэффициентами и правой
частью специального вида.
Лекция 2.ОДУ n-го порядка. Частное и общее
решения. Задача Коши дляОДУ n-го порядка и ее
геометрическая интерпретация (при n=2). Теорема
Коши о существовании и единственности решения
ОДУ (без док-ва). Краевая задача. Понижение
порядка некоторых типов ОДУ n-го порядка.
ОЛ-2, § 4.4, 11.1, 11.2; ОЛ-4, гл. XIII, § 16–18; ОЛ-6
гл.1, § 1.11, 1.13, 1.14.
ОЛ-2, § 6.2, 6.4–6.6; ОЛ-4, гл. XIII, § 21–25; ОЛ-6,
гл.1, § 1.16–1.18.
Лекции 3-4.Линейные дифференциальные уравнения
(ЛДУ) n-го порядка, уравнения однородные и
неоднородные. Теорема о существовании и
единственности
решения.
Дифференциальный
оператор L[y], его свойства. Линейное пространство
решений однородного ЛДУ. Линейно зависимые и
независимые системы функций на отрезке.
Определитель Вронского (вронскиан). Теорема о
Лекция7. Нормальные системы ОДУ. Задача и
теорема Коши для системы ОДУ. Частное и общее
решения системы ОДУ. Сведение ОДУ высшего
порядка к нормальной системе ОДУ первого порядка
и сведение нормальной системы ОДУ первого
порядка к ОДУ высшего порядка (вывод для n=2).
19
Первые интегралы системы. Понижение порядка
системы ОДУ при помощи первых интегралов.
Интегрируемые комбинации. Симметрическая форма
записи нормальной автономной системы ОДУ.
Лиувилля. Теоремы о структуре общего решения
однородной и неоднородной систем линейных ОДУ
первого порядка. Метод вариации постоянных.
Однородные системы линейных ОДУ с постоянными
коэффициентами. Характеристическое уравнение
системы. Построение общего решения по корням
характеристического уравнения (вывод только для
случая действительных и различных корней).
ОЛ-2, § 4.1, 4.2, 6.1, 8.1–8.4; ОЛ-4, гл. XI, § 29, ОЛ-6,
гл.1, § 1.19, 1.22
Лекции 8-9. Системы линейных ОДУ первого
порядка. Определитель Вронского. Фундаментальная
система решений. Формула Остроградского —
ОЛ-2, § 5.1–5.7; 6.; ОЛ-4, гл. XIII, § 30, ОЛ-6, гл.1, §
1.20-22.
Упражнения
Занятие 1.ОДУ первого порядка, его решение.
Геометрическое решение ОДУ первого порядка
методом
изоклин.
Интегрирование
ОДУ
с
разделяющимися переменными и однородных ОДУ.
Ауд.: ОЛ-8, гл.9, §1: 9.1, 9.4, 9.9, 9.18, y '   y  x / 4 
Ауд.: ОЛ-8, гл. 9, §2: 9.286, 9.291, 9.293, 9.294, 9.324,
9.322, 9.337, 9.327, 9.333, 9.336, 9.339, 9.296, 9.300,
9.298 или
ОЛ-9, гл.9, § 11–13: 2968 (а, в, е, д), 2976, 2983, 2987,
3045, 3051, 3057, 3052, 2969 (а, в, г).
Дома: ОЛ-8, гл.9, § 2: 9.288, 9.289, 9.295, 9.325, 9.326,
9.328, 9.330, 9.332, 9.334, 9.338, 9.299, 9.301 или
ОЛ-9, гл.9, § 11–13: 2968 (б, г, д), 2981, 2982, 3055,
3056, 3048, 3049, 2969 (б).
Занятие 6.Интегрирование линейных неоднородных
ОДУ с постоянными коэффициентами и специальной
правой частью.
Ауд.: ОЛ-8, гл.9, § 2: 9.346, 9.349, 9.352, 9.354, 9.357,
9.360, 9.366, 9.373, 9.369, 9.371, 9.376 или
ОЛ-9 гл.9, § 12, 13: 2994 (а, в, д), 2999 3004, 3000,
3016, 3019, 3064, 3062, 3063, 3067.
Дома: ОЛ-8, гл.9, § 2: 9.347, 9.349, 9.350, 9.353, 9.355,
9.361, 9.362, 9.370, 9.372, 9.374 или
ОЛ-9, гл.9, § 12, 13: 2994 (б, г, е), 3003, 3002, 2995,
3018, 3012, 3060, 3061, 3065.
Занятие
7.
Интегрирование
линейных
неоднородных ОДУ высшего порядка методом
вариации произвольных постоянных.
Ауд.: ОЛ-8, гл. 9, § 2: 9.342, 9.344, 9.381, 9.383, 9.308,
9.310
проинтегрировать
уравнения( y1 -частное
решение соответствующего однородного уравнения):
2
(решить методом изоклин), 9.27, 9.30, 9.33, 9.35, 9.39,
9.44, 9.48, 9.49, 9.55, 9.64, 9.65 или
ОЛ-9 гл.9, §1,3,4,9: 2706, 2719, 2737, y '   y  x / 4 
2
(решить методом изоклин), 2742, 2744, 2746, 2748,
2750, 2770, 2772, 2775, 2848, 2852.
Дома:ОЛ-8, гл.9, §1:9.3, 9.6, 9.12, 9.20, y   y  2x
(решить методом изоклин), 9.22, 9.26, 9.28, 9.34, 9.36,
9.40, 9.45, 9.47, 9.51, 9.53, 9.66 или
ОЛ-9, гл.9, §1, 3, 4, 9: 2708, 2720, 2736, y   y  2x
(решить методом изоклин), 2743, 2745, 2747, 2769,
2771, 2773, 2873, 2834, 2840, 2857, 2874.
Занятие 2.Интегрирование линейных ОДУ первого
порядка и уравнений Бернулли.
Ауд.: ОЛ-8, гл.9, § 1: 9.67, 9.72, 9.74, 9.78, 9.83, 9.88,
9.91, 9.92, 9.95 или
ОЛ-9 гл.9 §5, 9: 2785, 2787, 2789, 2791, 2793, 2794,
2847, 2850, 2854, 2881.
Дома: ОЛ-8 гл. 9 § 1: 9.68, 9.69, 9.75, 9.79, 9.80, 9.84,
9.87, 9.93, 9.94 или
ОЛ-9 гл. 9 § 5, 9: 2786, 2790, 2792, 2795, 2844, 2856,
2858, 2866.
Занятие 3. ОДУ высших порядков, основные
понятия. Интегрирование уравнений, допускающих
понижение порядка.
Ауд.: ОЛ-8, гл. 9, § 2: 9.202, 9.210, 9.214, 9.215, 9.216,
9.229, 9.239, 9.247, 9.251, 9.273 или
ОЛ-9, гл. 9, § 10: 2910, 2926, 2935, 2921, 2938, 2943,
2945, 2950, 2951, 2966.
Дома: ОЛ-8 гл. 9 § 2: 9.203, 9.208, 9.213, 9.220, 9.223,
9.237, 9.238, 9.248, 9.249, 9.271 или
ОЛ-9, гл. 9, § 10: 2918, 2919, 2923, 2327, 2940, 2941,
2952, 2953, 2947, 2965.
Занятие 4.Контрольная работа «Дифференциальные
уравнения первого порядка».
Занятие 5.Интегрирование линейных однородных
ОДУ
высших
порядков
с
постоянными
коэффициентами.
Фундаментальная
система
решений, восстановление линейного однородного
ОДУ по фундаментальной системе решений.
а) x2 1  ln x  y  xy  y 
1ln x 2
x
, y1  x ;
б) y   y   e 2 x y  e3 x , y1  cos e x .
в) y   4 y   2
sin 2 x
cos2 2 x
или
ОЛ-9, гл. 9, § 11–13: 3033, 3035, 3038 (а), 3066, 2971,
2973, задачи а), б), в) (см. выше).
Дома: ОЛ-8, гл. 9, § 2: 9.343, 9.345, 9.385,
проинтегрировать уравнения ( y1 -частное решение
соответствующего однородного уравнения):
а) x 2 y   xy   3 y  5 x 4 , y1  1/ x ;
б) ( x  1) y   xy   y  ( x  1) 2 e x , y1  x ;
в) y   y   ( x  1) / x 2 или
ОЛ-9, гл. 9, § 11–13: 3032, 3034, 3037, 2972, 2974,
2975, задачи а), б), в) (см. выше).
20
Занятие 8. Интегрирование нормальных систем
ОДУ
первого
порядка
сведением
к
дифференциальному уравнению высшего порядка.
Ауд.: ОЛ-8, гл. 9, § 3: 9.402, 9.409, 9.412, 9.413, 9.417,
9.429 или
ОЛ-9 гл. 9 § 15:, 3079, 3080, 3087, 3088 (а, б), 3090.
Дома: ОЛ-8, гл.9, § 3: 9.403, 9.410, 9.414, 9.415, 9.419,
9.420, 9.428, 9.430 или
ОЛ-9, гл.9, § 15: 3078, 3083, 3085, 3088 (в), 3089.
Занятие 9. Интегрирование систем линейных
однородных ОДУ с постоянными коэффициентами.
Общее решение. Фундаментальная система решений.
Ауд.: ОЛ-8, гл. 9, § 3: 9.431, 9.433, 9.435.
Дома: ОЛ-8, гл.9, § 3: 9.432, 9.434, 9.436.
Занятие 10.Контроль по модулю 2 (РК №2).
Занятие 11. Интегрирование систем линейных
неоднородных ОДУ первого порядка методом
вариации постоянных.
Ауд.: ОЛ-8, гл. 9, § 3: 9.441, 9.443, 9.445.
Дома: ОЛ-8, гл.9, § 3: 9.442, 9.444, 9.448.
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, выполнении домашних заданий,
подготовке к контрольным работам и рубежным контролям.
Контрольные мероприятия и сроки их проведения
Модуль 1.
1. ДЗ №1 «Определенный интеграл и его приложения»
Срок выдачи 5 неделя, срок сдачи – 10 неделя
2. КР №1 «Техника интегрирования»
Срок проведения - 6 неделя
3. Контроль по модулю №1 (РК №1) «Определенный интеграл и его приложения».
Срок проведения – 10 неделя
Модуль 2.
1. ДЗ №2 «Дифференциальные уравнения»
Срок выдачи 12 неделя, срок сдачи – 15 неделя
2. КР №2 «Дифференциальные уравнения первого порядка»
Срок проведения - 13 неделя
3. Контроль по модулю №2 (РК №2) «Дифференциальные уравнения высших порядков».
Срок проведения – 16 неделя
Литература
1.
2.
3.
4.
5.
6.
7.
Основная литература (ОЛ)
Зарубин В.С., Иванова Е.Е., Кувыркин Г.Н. Интегральное исчисление функций одного переменного:
Учеб. для вузов / Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. –
528 с. (Сер. Математика в техническом университете, вып. VI).
Агафонов С.А., Герман А.Д., Муратова Т.В. Дифференциальные уравнения: Учеб. для вузов / Под ред.
В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2006. – 352 с. (Сер. Математика в
техническом университете, вып. VIII).
Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 1. – М.: Интеграл-Пресс,
2006. – 416 с.
Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 2. – М.: Интеграл-Пресс,
2006. – 544 с.
Бугров Я.С., Никольский С.М. Высшая математика. Т. 2. Дифференциальное и интегральное исчисление.
– М.: Дрофа, 2003. – 512 с.
Бугров Я.С., Никольский С.М. Высшая математика. Т. 3. Дифференциальные уравнения. Кратные
интегралы. Ряды. Функции комплексного переменного. – М.: Дрофа, 2003. – 512 с.
Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа:
Учеб. пособие для втузов / Под ред. А.В. Ефимова, Б.П. Демидовича. – М.: Наука, 1993. – 478 с.
21
Сборник задач по математике для втузов. Ч. 2. Специальные разделы математического анализа: Учеб.
пособие для втузов / Под ред. А.В. Ефимова и Б.П. Демидовича. – М.: Наука, 1986. – 368 с.
Задачи и упражнения по математическому анализу для втузов / Под ред. Б.П. Демидовича. – М.:
Интеграл-Пресс, 1997. – 416 с.
8.
9.
1.
2.
3.
4.
3.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
1.
2.
Дополнительная литература (ДЛ)
Вся высшая математика: Учебник для втузов: В 6 т. / Краснов М.Л., Киселев А.И., Макаренко и др. – Т.
2. – М.: Эдиториал УРСС, 2000. – 184 с.
Вся высшая математика: Учебник для втузов: В 6 т. / Краснов М.Л., Киселев А.И., Соболев С. К. и др. –
Т. 3. – М.: Эдиториал УРСС, 2001. – 237с.
Филиппов А.Ф. Введение в теорию дифференциальных уравнений. Учеб.для вузов. – М.: Эдиториал
УРСС, 2004. – 238 с.
Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. – 3-е изд. – М.: ЛИБРОКОМ: URSS,
2009. - 235 с. – ISBN 978-5-397-00658-3
2.
Методические пособия
Ахметова Ф.Б., Добрица Б.Т., Сырцов А.В. Неопределенный интеграл. – М.: МГТУ, 2008.
Галкин С.В. Интегральное исчисление и дифференциальные уравнения. – М.: Изд-во МГТУ, 2007. –
160 с.
Добрица Б.Т., Роткова О.В., Шахов Е.М. Неопределенный интеграл. – М.: МГТУ, 1988.
Копаев А.В., Маркелов Г.Е., Тесалина А.А. Определенный интеграл. Методические указания для
выполнения домашнего задания. – М.: Изд-во МГТУ, 2002. – 69 с.
Минеева О.М., Неклюдов А.В., Скуднева О.В. Несобственные интегралы. Методические указания для
выполнения домашнего задания. – М.: Изд-во МГТУ, 2003. – 41 с.
Богомолов В.Г., Кандаурова И.Е., Шишкина С.И. Дифференциальные уравнения первого порядка. – М.:
Изд-во МГТУ, 2001. – 37 с.
Пелевина И.Н., Раров Н.Н., Филиновский А.В. Дифференциальные уравнения высших порядков.
Методические указания для выполнения домашнего задания. – М.: Изд-во МГТУ, 2001. – 38 с.
Добрица Б.Т., Янов И.О. Системы дифференциальных уравнений. Методические указания к выполнению
типового расчета. – М.: Изд-во МГТУ, 2002. – 42 с.
Казанджан Г.П., Савин А.С., Филиновский А.В. Системы дифференциальных уравнений и элементы
теории устойчивости. Методические указания к выполнению домашнего задания. – М.: Изд-во МГТУ, 2002.
– 28 с.
Добрица Б.Т., Пелевина А.Ф., Янов И.О. Элементы теории устойчивости. Методические указания. - М.:
Изд-во МГТУ, 2001. – 45 с.
Ковалев Я.Г., Киреева Ю.Г., Лунева М.С., Тесалина А.А. Определенный интеграл. Методические
указания для выполнения домашнего задания. – М.: МВТУ, 1987.
Белова Т.И., Грешилов А.А., Пелевина А.Ф. Дифференциальные уравнения первого порядка.
Метод.указания по курсу «Высшая математика» – М.: Изд-во МГТУ, 1989. – 32 с.
Белова Т.И., Грешилов А.А., Пелевина А.Ф. Дифференциальные уравнения высших порядков.
Метод.указания по курсу «Высшая математика» – М.: Изд-во МГТУ, 1990. – 36 с.
Рекомендуемые Интернет-сайты:
Иванков П.Л. Конспект лекций по интегралам и дифференциальным уравнениям. http://mathmod.bmstu.ru
http://www.mathelp.spb.ru - лекции по высшей математике
ИНТЕГРАЛЫ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
для ИБМ
Дисциплина состоит из двух учебных модулей и экзамена
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-10
10
Упражнения
1-10
20
22
Примечание
Домашние задания текущие
1-10
10
11
2
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
11-17
7
Упражнения
11-17
14
Домашние задания текущие
11-17
6
17
2
Контроль по модулю №1
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Контроль по модулю №2
ЛЕКЦИИ
Примечание
Задача Коши и ее геометрическая интерпретация.
Теорема Коши о существовании и единственности
решения задач Коши.
Модуль 1. Интегральное исчисление
Лекция 1. Первообразная и ее свойства.
Неопределенный интеграл, его свойства, связь с
дифференциалом.
Таблица
интегралов.
Интегрирование подстановкой и по частям.
Лекция 6. ДУ второго порядка, допускающие
понижение порядка. Линейные дифференциальные
уравнения (ЛДУ) 2-го порядка, однородные и
неоднородные. Линейность пространства решений
однородного
ЛДУ.
Линейно
зависимые
и
независимые системы функций на промежутке.
Определитель Вронского, его свойства Структура
общего решения однородного ДУ 2-го порядка.
Лекции 2. Разложение правильной рациональной
дроби на простейшие. Интегрирование простейших
дробей.
Интегрирование
некоторых
тригонометрических
выражений.
Примеры
интегралов, не выражающихся через элементарные
функции.
Лекция 7. Формула Остроградского – Лиувилля и ее
следствия. Однородные ЛДУ 2-го порядка с
постоянными коэффициентами. Характеристическое
уравнение.
Построение
общего
решения
Однородного ЛДУ 2-го порядка по корням
характеристического уравнения. Неоднородные
ЛДУ 2-го порядка. Структура общего решения.
Теорема о наложении частных решений.
Лекция 3. Задачи, приводящие к понятию
определенного интеграла. Определенный интеграл
как предел интегральных сумм. Физическая и
экономическая
интерпретация
определённого
интеграла. Свойства определенного интеграла.
Формула
Ньютона—Лейбница.
Вычисление
определенных интегралов подстановкой и по
частям. Интегрирование четных и нечетных
функций по отрезку, симметричному относительно
начала координат.
Лекция 8. Решение неоднородного ЛДУ второго
порядка с правой частью специального вида.
Решение НЛДУ 2-го порядка методом Лагранжа
вариации постоянных.
Лекция 4. Вычисление площадей плоских фигур в
декартовых и полярных координатах. Вычисление
объемов тел по площадям поперечных сечений и
объемов тел вращения, вычисление длины дуги
кривой и площади поверхности вращения.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Модуль 1. Интегральное исчисление
Занятия 1. Непосредственное интегрирование.
Таблица интегралов. Интегрирование подстановкой
(подведением под знак дифференциала).
Ауд.: ОЛ-6, № 1040, 1047, 1048(а), 1077, 1081, 1083,
1095, 1096, 1098, 1102, 1119, 1129, 1134, 1164, 1184,
1192, 1198 , или
ОЛ-7, № 6.21, 6.25, 6.28, 6.48, 6.52, 6.56, 6.62,
6.64, 6.65, 6.74, 6.87, 6.95, 6.114;
Дома: ОЛ-6, № 1039, 1044, 1049(а), 1078, 1080, 1082,
1085, 1093, 1097, 1101, 1120, 1127 1135, 1166, 1176,
1191(в, г),
или
ОЛ-7, №
6.22, 6.26, 6.27, 6.51, 6.55, 6.57,
6.60, 6.66, 6.85, 6.116, 6.117.
Модуль 2. Дифференциальные уравнения
Лекция 5. Инженерные и экономические задачи,
приводящие к дифференциальным уравнениям.
Дифференциальные уравнения (ДУ) первого
порядка, его решения (частные и общие).
Интегральные кривые. Задача Коши для ДУ 1-го
порядка, Теорема Коши о существовании и
единственности решения ДУ (без вывода). Методы
решения ДУ 1-го порядка: с разделяющимися
переменными и линейные. Дифференциальные
уравнения 2-го порядка, частные и общие решения.
23
Занятие
2.
Нахождение
интегралов
вида
Ax  B dx и
Ax  B dx , где
2
Y  x   x   .
 Y
 Y
Интегрирование по частям.
Ауд.: ОЛ-6, № 1214, 1219, 1211, 1213, 1225, 1230,
1231, 1227, 1255, 1256, 1262, 1259, 1265, 1266, 1269,
1270, 1272, 1274, или
ОЛ-7, № 6.128, 6.130, 6.135, 6.147, 6.155*, 6.158,
6.161, 6.163, 6.165, 6.254, 6.256, 6.258;
Дома: ОЛ—6 № 1216, 1212, 1222, 1223, 1226, 1228,
1229, 1257, 1258, 1259, 1263, 1266, 1267, 1271, 1273,
1276
или
ОЛ—7 № 6.131, 6.140, 6.142, 6.138, 6.137, 6.159,
6.160, 6.162, 6.252, 6.253, 6.259, 6.277.
Занятие 3. Интегрирование рациональных дробей.
Ауд.: ОЛ–6, № 1283, 1281, 1289, 1294, 1293, 1297;
или ОЛ–7, № 6.166, 6.167, 6.168, 6.177, 6.179, 6.178,
6.174, 6.185.
Дома: ОЛ–6, № 1282, 1284, 1285, 1290, 1283, 1300;
или
ОЛ–7, 6. 69, 6.170, 6.172, 6.180, 6.181.
Занятие 4. Интегрирование тригонометрических
функций.
Ауд.: ОЛ–6, № 1339, 1342, 1345, 1349, 1348, 1352,
1359, 1365, 1382, 1373, 1391, 1394;
или ОЛ—7 № 6.190, 6.191, 6.206, 6.195, 6.197,
6.198, 6.196, 6.203, 6.212, 6.221, 6.219.
Дома: ОЛ—6 № 1338, 1340, 1343, 1347, 1350, 1351,
1358, 1372, 1376, 1383, 1392, 1393,
или ОЛ—7, № 6.192, 6.194, 6.199, 6.202, 6.204,
6.217, 6.218, 6.227.
Занятие 5. Интегрирование иррациональных
выражений.
Ауд.: ОЛ–6 № 1315, 1318, 1324, 1325, 1403, 1405,
1412,
ли ОЛ–7, № 6.238, 6.240, 6.242, 6.260, 6.262, 6.263;
Дома: ОЛ–6, № 1317, 1319, 1323, 1406, 1413, 1414,
или ОЛ–7, № 6.239, 6.243, 6.245, 6.248, 6.249,
6.268.
Занятие 6. Контрольная работа «Техника
интегрирования».
Дома: ОЛ—6 № 1634, 1636, 1639, 1651, 1658, 1661,
или ОЛ—7 № 6.457, 6.464, 6.468, 6.480, 6.488,
6.491.
Занятие 9. Вычисление объемов тел по площадям
поперечных сечений и объемов тел вращения.
Ауд.: ОЛ—6 №1695, 1691, 1692, 1701(а), 1709, 1711,
или ОЛ—7 № 6.536, 6.538, 6.541, 6.543, 6.533;
Дома: ОЛ—6 № 1689, 1690, 1693, 1701(б), 1708,
1712,
или ОЛ—7 № 6.535, 6.537, 6.544, 6.542, 6.533.
Занятие 10. Вычисление длины дуги и площади
поверхности вращения.
Ауд.: ОЛ—6 № 1671, 1680, 1677, 1718, 1723(а),
1725,
или ОЛ—7 № 6.493, 6.494, 6.505, 6.509, 6.511,
6.522, 6.530;
Дома: ОЛ—6 № 1670, 1675, 1679, 1715, 1719, 1726,
или ОЛ—7 № 6.499, 6.500, 6.502, 6.512, 6.520,
6.528, 6.529.
Занятие 11. Рубежный контроль по модулю 1.
Модуль 2. Дифференциальные уравнения
Занятие 12. Дифференциальное уравнение (ДУ)
первого порядка, его решение. Интегрирование ДУ
уравнений с разделяющимися переменными,
однородной правой частью, линейных и типа
Бернулли.
Ауд.: ОЛ—6 № 2742, 2744, 2748, 2750, 2770, 2775,
2848, 2852, 2785, 2789, 2791, 2793, 2794, 2850, 2854,
2881;
или ОЛ—8 № 9.27, 9.30, 9.35, 9.44, 9.48, 9.49,
9.64, 9.67, 9.72, 9.83, 9.88, 9.85;
Дома: ОЛ—6 № № 2743, 2745, 2747, 2769, 2771,
2773, 2834, 2840, 2857, 2786, 2790, 2792, 2795, 2844,
2856, 2866.
или ОЛ—8 № 9.26, 9.28, 9.34, 9.36, 9.40, 9.45,
9.47, 9.66, 9.68, 9.75, 9.84, 9.94.
Занятие 13. Интегрирование дифференциальных
уравнений
второго
порядка,
допускающих
понижение порядка.
Ауд.: ОЛ—8 гл.9: № 9. 215, 9.216, 9.219, 9.239,
9.247, 9.251, 9.252,
или ОЛ—6 №. 2911, 2926, 2935, 2921, 2938, 2943,
2945, 2950, 2951, 2966;
Дома: ОЛ—8 гл. 9: № 9.218, 9.220, 9.223, 9.238,
9.248, 9.249, 9.253.
или ОЛ—6, № 2918, 2919, 2923, 2927, 2940, 2941,
2952, 2953, 2947, 2965.
Занятие 7. Вычисление определенных интегралов.
Ауд.: ОЛ—6 № 1524, 1526, 1531, 1537, 1582, 1587,
1591, 1599, 1600,
или ОЛ—7 № 6.337, 6.340, 6.346, 6.387, 6.388,
6.395, 6.406, 6.407;
Дома: ОЛ—6 № 1525, 1527, 1530, 1538, 1540, 1583,
1601, 1603,
или ОЛ—7 № 6.328, 6.336, 6.338, 6.347, 6.386,
6.394, 6.400, 6.402.
Занятие 8. Вычисление площадей плоских фигур в
декартовых и полярных координатах.
Ауд.: ОЛ—6 № 1633, 1635, 1638, 1650, 1655, 1656,
1657,
или ОЛ—7 № 6.456 6.467 6.478 6.489 6.492;
Занятие 14. Решение однородных линейных ДУ 2го порядка с постоянными коэффициентами.
Решение неоднородных линейных ДУ 2-го порядка
методом Лагранжа (вариации произвольных
постоянных).
Ауд.: ОЛ—8 гл. 9 № 9.322, 323, 337, 342, 344, 308,
310, (а) найти общее решение ДУ, если известно y1
24
– частное решение соответствующего однородного
уравнения:
2
x 2 1  ln x  y   xy   y  1  ln x  / x; y1  x ;
Занятие 15. Решение неоднородных ЛДУ второго
порядка с постоянными коэффициентами и правой
частью специального вида.
Ауд.: ОЛ—8 гл. 9: 9.346, 9.350, 9.348, 9.352, 9.356,
9.364, 9.370,
или ОЛ—6 № 2994(а, в, е, д), 2995, 2999, 3001,
3005, 3008, 3012, 3018, 3028.
Дома: ОЛ—8 гл. 9: 9.347, 9.351, 9.353, 9.360, 9.363,
9.372,
или ОЛ—6 № 2994(6, г), 2997, 3000, 3002, 3009,
3010, 3021, 3029.
или ОЛ—6 № 2979, 2982, 2987, 3033, 3035,
3038(а), 3066, 2971, 2973 и задача (а) см. выше.
Дома: ОЛ—8 гл. 9: № 9.324, 325, 338, 343, 345, 311;
найти общее решение ДУ, где y1 – частное решение
соответствующего однородного уравнения:
(б) x2 y  xy  3 y  5x4 , y1  1 x ;
(в)  x  1 y   xy  y   x  1 e x , y1  x ;
2
Занятие 16. Рубежный контроль по модулю 2.
или ОЛ—6, № 2976, 2981, 2989, 3032, 3034, 3037,
2972, 2974, 2975 и задачи (б), (в) см. выше.
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, подготовке к выполнению
контрольных работ и Рубежных контролей, выполнении индивидуальных ДЗ.
Контрольные мероприятия:
Модуль 1. Интегральное исчисление
1. Контрольная работа № 1 по теме «техника интегрирования Срок проведения – 7 неделя
2. Домашнее задание № 1 «Приложения определенного интеграла» Сроки: выдача– 6 неделя, прием – 11 неделя.
3. Рубежный контроль № 1 по теме «интегральное исчисление», практика. Срок – 12 неделя
4. Рубежный контроль № 1 по теме «интегральное исчисление», теория. Срок – 13 неделя.
Модуль 2. Дифференциальные уравнения
5. Рубежный контроль № 2 «дифференциальные уравнения», практика. Срок: 16 неделя.
6. Рубежный контроль № 2 «дифференциальные уравнения», теория. Срок: 17 неделя.
Литература
1.
2.
3.
4.
5.
6.
7.
1.
2.
Основная литература (ОЛ).
Зарубин В.С., Иванова Е.Е., Кувыркин Г.Н. Интегральное исчисление функций одного переменного: Учеб. для
вузов / Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. – 506 с. (Сер.
Математика в техническом университете. Вып. VI).
Пискунов Н. С. Дифференциальное и интегральное исчисление для втузов. Т. 1. — М.: Интеграл-Пресс, 2010, –
416 с..
Бугров Я. С., Никольский С. М. Высшая математика. Том 2. Дифференциальное и интегральное исчисление.–
М.: Дрофа, 2007, – 512
Пискунов Н. С. Дифференциальное и интегральное исчисление для втузов. Т. 2. — М.: Интеграл-Пресс, 2010, –
544 с.
Бугров Я. С., Никольский С. М. Высшая математика. Том 3. Дифференциальные уравнения. Кратные интегралы.
Ряды. Функции комплексного переменного. – М.: Дрофа, 2005, – 288 с.
Задачи и упражнения по математическому анализу для втузов. Под ред. Б. П. Демидовича.—М.: Астрель, 2010. –
496 с..
Сборник задач по математике для втузов. Под ред. А.В.Ефимова и Б. П. Демидовича. Т. 1.—М.: Астрель, 2005.
Методические и учебные пособия (МП)
Ахметова Ф. Х., Добрица Б. Т., Сырцов А. В. Неопределенный интеграл: метод. указания к практическим
занятиям. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2008. – 48 с.
Копаев А.В., Маркелов Г.Е., Тесалина А.А. Определенный интеграл. Методические указания к выполнению
домашнего задания. – М.: Изд-во МГТУ, 2002.-69 с.
25
3.
4.
5.
6.
7.
1.
Белов В. Н., Косова А. В., Чуев В. Ю. Определенный интеграл: метод. указания к выполнению типового
расчета. – М.: Изд-во МГТУ им. Н. Э. Баумана, 2009. – 45 с.
Дуров В. В., Неклюдов А. В. Метод дифференциалов в приложениях определенного интеграла: метод.
указания к практическим занятиям. – М.: Изд-во МГТУ им. Н. Э. Баумана, 1993. – 50 с.
Галкин С.В. Интегральное исчисление и дифференциальные уравнения. – М.: Изд-во МГТУ, 2007. – 160 с.
Богомолов В.Г., Кандаурова И.Е., Шишкина С.И. Дифференциальные уравнения первого порядка. -М.: Издво МГТУ, 2001.-37 с
Пелевина И.Н. Раров Н.Н., Филиновский А.В. Дифференциальные уравнения высших порядков. Методические
.указания к выполнению домашнего задания. – М.: Изд-во МГТУ им.Н.Э.Баумана,2001. – 38с.
Электронные ресурсы (ЭР)
Соболев С.К. Дифференциальные уравнения. Методические указания к решению задач. – М.: МГТУ им. Н.Э.
Баумана, 2008 (Электронное издание).– 25 с. http://hoster.bmstu.ru/~fn1/?page_id=30.
ЛИНЕЙНАЯ АЛГЕБРА И ФУНКЦИИ НЕСКОЛЬКИХ
ПЕРЕМЕННЫХ
Дисциплина состоит из 2-х учебных модулей и экзамена.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-8
16
Упражнения
1-9
18
Домашние задания
текущие
1-9
12
9
4
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
9-17
18
Упражнения
10-17
16
Домашние задания
текущие
10-17
10
16
4
Контроль по модулю №1
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Контроль по модулю №2
Примечание
Модуль 1:Линейная алгебра
Лекции
Лекция
1.Аксиомы
и
примеры
линейных
пространств. Линейно зависимые и линейно
независимые
векторы.
Критерий
линейной
зависимости, его следствия. Определение базиса и
размерности линейного пространства. Теорема о
единственности разложения по базису. Координаты
26
вектора. Линейные операции над векторами в базисе.
Матрица перехода к новому базису. Преобразование
координат вектора при переходе к новому базису.
ОЛ-1,
гл. 1,
базиса из собственных векторов в случае
действительных
и
некратных
корней
характеристического уравнения. Матрица линейного
оператора в базисе, состоящем из его собственных
векторов.
ОЛ-Error!
Unknown switch argument., гл. 2, § 1, 2,
4.
§
1.1–1.8;
ОЛ-1, гл. 5 § 5.1–5.5, гл. 6, § 6.1, 6.2; ОЛ-3, гл. 5, § 3.
Лекция 2.Подпространства линейного пространства.
Ранг системы векторов, связь с рангом матрицы.
Линейная
оболочка.
Примеры.
Евклидово
пространство, аксиомы и примеры. Норма вектора.
Неравенство Коши-Буняковского и неравенство
треугольника. Ортогональность векторов. Линейная
независимость ортогональной системы ненулевых
векторов. Ортонормированный базис евклидова
пространства. Вычисление скалярного произведения
и нормы вектора в ортонормированном базисе.
Лекции5-6. Линейные операторы в евклидовых
пространствах. Сопряженный и самосопряженный
операторы, их матрицы в ортонормированном
базисе. Свойства корней характеристического
многочлена
самосопряженного
оператора:
вещественность и равенство алгебраических и
геометрических
кратностей
(без
док-ва).
Ортогональность
собственных
векторов
самосопряженного
оператора,
отвечающих
различным собственным значениям. Существование
ортонормированного
базиса
из
собственных
векторов самосопряженного оператора (док-во для
случая
различных
собственных
значений).
Ортогональные преобразования, ортогональные
матрицы
и
их
свойства.
Диагонализация
симметрической
матрицы
ортогональным
преобразованием.
ОЛ-1, гл. 2, § 2.1, 2.4–2.6, гл. 3, § 3.1–3.7; ОЛ-3, гл. 2,
§ 3, гл. 4, § 1, 2.
Лекция
3.Теорема
о
существовании
ортонормированного
базиса
и
процесс
ортогонализации Грама - Шмидта (без док-ва).
Линейные операторы и их матрицы (определение,
примеры). Преобразование матрицы линейного
оператора при переходе к новому базису,
инвариантность
ее
определителя.
Подобные
матрицы. Действия над линейными операторами и
соответствующие действия с их матрицами.
Собственные векторы и собственные значения
линейного оператора.
ОЛ-1, гл. 6, § 6.3; ОЛ-3, гл. 5.
Лекция 7. Квадратичные формы. Координатная и
матричная формы записи. Преобразование матрицы
квадратичной формы при переходе к новому базису.
Ранг квадратичной формы, его независимость от
выбора базиса. Знакоопределенные квадратичные
формы. Критерий Сильвестра (без док-ва).
Канонический вид квадратичной формы. Метод
Лагранжа. Закон инерции квадратичных форм (без
док-ва).
ОЛ-1, гл. 3, § 3.8, гл. 4 § 4.1–4.5; ОЛ-3, гл. 5, §1, 2.
Лекция 4. Характеристический многочлен линейного
оператора, его независимость от базиса. След
матрицы линейного оператора и его инвариантность.
Характеристический многочлен и собственные
значения матрицы. Свойство множества собственных
векторов, отвечающих одному и тому же
собственному
значению.
Алгебраическая
и
геометрическая кратности собственного значения,
связь между ними (без док-ва). Теорема о линейной
независимости собственных векторов, отвечающих
различным собственным значениям. Существование
ОЛ-1, гл. 8, § 8.1–8.3, 8.6; ОЛ-3, гл. 5, § 6.
Лекция 8. Приведение квадратичной формы к
каноническому
виду
ортогональным
преобразованием. Приведение уравнений кривых и
поверхностей второго порядка к каноническому виду
с помощью ортогонального преобразования.
ОЛ-1, гл. 8, § 8.4, 8.5; гл. 9, § 9.1–9.3; ОЛ-3, гл. 5, § 6.
Упражнения
Занятие 1.Линейное пространство. Линейная
зависимость. Базис и размерность пространства.
Переход к новому базису.
Ауд.: ОЛ-6, гл. 4: 4.1–4.9 (неч.), 4.15, 4.17, 4.21, 4.24,
4.28, 4.30, 4.37 или
ДЛ-3, гл. 3: 7–17 (неч.), 21–25 (неч.), 29–33 (неч.), 40,
53–57(неч.), 63.
Дома: ОЛ-6, гл. 4: 4.2–4.10 (четн.), 4.16, 4.18, 4.19,
4.25, 4.31 или
ДЛ-3, гл. 3: 8–14 (четн.), 22–26 (четн.), 30–34 (четн.),
42, 54–58 (четн.), 64.
Занятие 2.Ранг системы векторов. Линейная
оболочка системы векторов. Подпространство
линейного пространства.
Ауд.: ОЛ-6, гл. 4: 4.45–4.53 (неч.) или
ДЛ-3, гл. 3: 73–77 (неч.), 87–91 (неч.), 95–99 (неч.).
Дома: ОЛ-6, гл. 4: 4.46, 4.48, 4.52, 4.54 или
ДЛ-3, гл. 3: 74–78 (четн.), 88–92 (четн.), 96–100
(четн.), гл. 4: 6–12 (четн.), 32, 38.
Занятие 3. Евклидовы пространства. Процесс
ортогонализации Грама – Шмидта.
Ауд.: ОЛ-6, гл. 4: 4.63 (а), 4.64 (а), 4.65 (а,б), 4.67–
4.76 (неч.), или
27
ДЛ-3, гл. 4: 5–12 (неч.), 17– 24 (неч.), 31, 37, 39, 47,
49, 53, 57, 59.
Дома: ОЛ-6, гл. 4: 4.63 (б), 4.64 (б), 4.65 (в), 4.67–4.76
(четн.) или
ДЛ-3, гл. 4: 5–12 (четн.) 17–24 (четн.), 32, 38, 48, 50,
54, 58, 60.
Занятие 4.Линейные операторы и их матрицы.
Преобразование матрицы линейного оператора при
переходе к новому базису. Действия над линейными
операторами.
Ауд.: ОЛ-6, гл. 4: 4.83 – 4.99 (неч.), 4.103, 4.106 (б),
4.107, 4.110, 4.113 или
ДЛ-3, гл. 5: 1, 5, 7, 21, 23, 25, 32 (а), 33 (а), 44, 45 (а),
47, 49, 51 (а, б), 71.
Дома: ОЛ-6, гл. 4: 4.84, 4.86, 4.90 – 4.100 (четн.),
4.102, 4.104, 4.108, 4.110(б), 4.118 или
ДЛ-3, гл. 5: 6, 8, 22, 24, 32 (6), 33 (б), 43, 45 (б), 48, 51
(в, г), 72.
Занятие 5.Собственные векторы и собственные
значения линейного оператора. Диагонализация
симметричных
матриц
ортогональным
преобразованием.
Ауд.: ОЛ-6, гл. 4: 4.129, 4.131, 4.135–4.143 (неч.),
4.174, 4.183, 4.191 или
ДЛ-3, гл. 5: 75–80 (неч.). 89–100 (неч.), 155–162
(неч.).
Дома: ОЛ-6, гл. 4: 4.130, 4.132, 4.134–4.142 (четн.),
4.176, 4.184, 4.186 или
ДЛ-3, гл. 5: 75–80 (четн). 89–100 (четн.), 156–162
(четн.).
Занятие
6.Квадратичные
формы,
критерий
Сильвестра. Преобразование матрицы квадратичной
формы при переходе к новому базису.
Ауд.: ОЛ-6, гл. 4: 4.218–4.225 (четн.) или
ДЛ-3, гл. 6: 13, 15, 43, 45.
Дома: ОЛ-6, гл. 4: 4.218–4.233 (неч.) или
ДЛ-3, гл. 6: 14, 16, 44, 46.
Занятия 7-8.Приведение квадратичной формы к
каноническому
виду
методом
Лагранжа
и
ортогональным
преобразованием.
Приведение
кривых второго порядка к каноническому виду.
Ауд.: ОЛ-6, гл. 4: 4.210, 4.211, 4.213, 4.215, 4.226,
4.228, 4.231 или
ДЛ-3, гл. 6: 19, 21, 23 (б), 29, 31, 35, 47, 49, 55.
Дома: ОЛ-6, гл. 4: 4.212, 4.214, 4.216, 4.227, 4.229,
4.230 или
ДЛ-3, гл. 6: 20, 22, 23 (а), 30, 32, 36, 48, 50, 56.
Занятие 9.Контроль по модулю 1 (РК №1).
Модуль 2:Функции нескольких переменных
Лекции
доказательством). Восстановление функции по ее
полному
дифференциалу.
Применение
дифференциала
ФНП
к
приближенным
вычислениям. Производная сложной функции.
Частная
и
полная
производные
ФНП.
Инвариантность формы первого дифференциала.
Дифференциалы высших порядков.
n
Лекция 1. Метрика и окрестности в R . Открытые,
n
замкнутые, ограниченные и связные множества в R .
n
Граница множества. Понятие области в R .
Скалярная функция нескольких переменных (ФНП)
n
как отображение F : W R ( W R ). Линии и
поверхности уровня. Предел ФНП. Бесконечно
малые и бесконечно большие ФНП. Непрерывность
ФНП в точке, на множестве. Свойства ФНП,
непрерывных на множестве (без док-ва).
ОЛ-2, гл. 2, §2.7, ОЛ-4, гл. 8, §7–10; ОЛ-5, гл. 8, §6–9.
Лекция 4. Неявные функции. Теорема о
существовании (без док-ва) и дифференцируемости
неявной ФНП. Производная ФНП по направлению и
градиент, их свойства.
ОЛ-2, гл. 1, § 1.1–1.7; ОЛ-4, гл. 8, § 1–4; ОЛ-5, гл. 8, §
1–3, 11, 12.
ОЛ-2, гл. 2, § 2.7, гл. 3, § 3.5, гл. 4, § 4.1–4.3; ОЛ-4,
гл. 8, §10, 11; ОЛ-5, гл. 8, § 9, 15.
Лекция
2.Частные
производные
ФНП,
геометрическая интерпретация для п = 2. Частные
производные высших порядков. Теорема о
независимости смешанных частных производных от
порядка дифференцирования. Матрица Гессе.
Дифференцируемость ФНП. Необходимые условия и
достаточное условие дифференцируемости.
Лекция5. Касательная плоскость и нормаль к
поверхности, условия их существования и вывод
уравнений. Геометрический смысл дифференциала
функции двух переменных. Формула Тейлора для
ФНП (без док-ва).
ОЛ-2, гл. 2, § 2.1–2.6, гл. 3, § 3.1, 3.2; ОЛ-4, гл. 8, § 5,
6; ОЛ-5, гл. 8, § 4, 5.
ОЛ-2, гл. 5, § 5.1–5.4, гл. 3, § 3.4; ОЛ-4, гл. 8, §14, 15,
17; ОЛ-5, гл. 8, § 7, 8, 13–16.
Лекция
3.
Полный
дифференциал
ФНП.
Необходимые и достаточные условия того, что
Лекции6-7. Экстремум ФНП. Необходимое условие
существования экстремума. Достаточные условия
экстремума (формулировка с помощью матрицы
Гессе, без док-ва). Условный экстремум ФНП, его
выражение
полным
дифференциалом
является
(необходимость
с
28
геометрическая интерпретация (при n  2 ), функция
Лагранжа. Необходимое условие существования
условного
экстремума
(вывод
для n  2 ).
Достаточные условия (без док-ва). Нахождение
наибольшего
и
наименьшего
значений
дифференцируемой
ФНП
на
замкнутом
ограниченном множестве.
ВФНП. Геометрическая интерпретация для n, m = 2,
3. Предел ВФНП. Непрерывность ВФНП. Матрица
Якоби
ВФНП,
якобиан
(при m  n ).
Дифференцируемость ВФНП, ее дифференциал.
Производная сложной ВФНП в матричной форме.
ОЛ-2, гл. 6, § 6.1–6.4, гл. 7, § 7.1–7.4; ОЛ-4, гл. 8,
§ 18; ОЛ-5, гл. 8, § 19.
Лекция 9. Обзорная.
ОЛ-2, гл. 1, § 1.2–1.4, гл. 2, § 2.3, 2.6, 2.7; ДЛ -2, гл. 5,
§ 41, пп. 41.4–41.7.
Лекция 8. Векторная ФНП (ВФНП) как отображение
F : W R m ( W R n ). Координатные функции
Упражнения
Занятие 1.Область определения ФНП. Линии и
поверхности уровня. Предел и непрерывность ФНП.
Ауд.: ОЛ-8: 1792 (в), 1793 (г), 1794 (в), 1795 (а),
1796 (в), 1797 (б, в), 1788 (в), найти предел
lim ( x3  3 y 2 )  e( x
x 
y 
2
 y2 )
,
проверить
Дома: ОЛ-8: 1801–1825 (четн.), 1891, 1893, 1898,
1838, 1840, 1845, 1916, 1925 или
ОЛ-6, гл. 7: 7.56, 7.58, 7.59, 7.62, 7.64, 7.67, 7.88, 7.90,
7.92, 7.102, 7.107.
Занятия 3-4. Производная сложной и неявной ФНП.
Производная по направлению и градиент ФНП.
Касательная плоскость и нормаль к поверхности.
Ауд.: ОЛ-8: 1856, 1861, 1864, 1865, 1870, 1944, 1946,
1948, 1950, 1955, 1876, 1878, 1882 (а), 1886, 1889,
1981 (а), 1982, 1985, 1986 или
ОЛ-6, гл. 7: гл. 7: 7.114, 7.119, 7.122, 7.129, 7.135,
7.141, 7.145, 7.149, 7.152, 7.229 (а), 7.233 (а), 7.232,
7.234, 7.239 (а); ОЛ-7, гл. 10: 10.31–10.43 (неч.).
Дома: ОЛ-8: 1857, 1862, 1863, 1871, 1943, 1947, 1949,
1956, 1877, 1879, 1882 (6), 1883, 1888, 1981 (б), 1984,
1987, 1990 или
ОЛ-6, гл. 7: 7.116, 7.118, 7.123, 7.130, 7.136, 7.140,
7.146, 7.150, 7.151; 7.229 (б), 7.233 (б,в), 7.235, 7.239
(б); ОЛ-7, гл. 10: 10.32–10.44 (четн.).
Занятия 5-6.Безусловный и условный экстремум
ФНП.
Ауд.: ОЛ-8: 2008, 2010, 2012, 2016, 2016.1, 2021–
2024, 2031 или
ОЛ-6, гл. 7: 7.187–7.195 (неч.), 7.201, 7.205, 7.214.
Дома: ОЛ-8: 2009, 2011, 2014, 2016.2, 2023, 2024,
2033 или
ОЛ-6, гл. 7: 7.187–7.195 (четн.), 7.202–7.204, 7.210–
7.213.
Занятие 7.Контроль по модулю 2 (РК №2).
функцию
 x3 3 y 4
, x 2  y 2  0; на непрерывность в точке

f ( x, y )   x 2  y 2
0,
x 2  y 2  0,

(0; 0) или
ОЛ-6, гл. 7: 7.6, 7.8, 7.10, 7.19, 7.21 (построить линии
и поверхности уровня), 7.32, 7.35, 7.44, 7.46, 7.50,
7.55.
Дома: ОЛ-8 гл. 4: 1792 (е, и), 1793 (б, в), 1794(г, ж),
1796 (а, б), 1797 (г, е), 1799 (б) или
ОЛ-6, гл. 7: 7.7, 7.9, 7.13, 7.20 (построить линии и
поверхности уровня), 7.33, 7.34, 7.45, 7.47, 7.51.
Занятие 2.Частные производные 1-го порядка.
Частные
производные
высших
порядков.
Дифференциал первого и второго порядка ФНП.
Ауд.: ОЛ-8: 1801–1825 (неч), 1892, 1894, 1897, 1834,
1838, 1844, 1917, 1924 или
ОЛ-6, гл. 7: 7.57, 7.60, 7.61, 7.63, 7.66, 7.87, 7.89, 7.91,
7.103,
7.105,
проверить
функцию
4
2
4
2
2

 x  x  y ; x  y  0;
на
f ( x, y)  
2
2
0;
x

y

0.


дифференцируемость в точке (0,0).
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, выполнении домашних заданий,
подготовке к контрольным работам и рубежным контролям.
Контрольные мероприятия и сроки их проведения
Модуль 1.
1. ДЗ №1 «Линейная алгебра»
Срок выдачи 1 неделя, срок сдачи – 8 неделя
2. Контроль по модулю №1 (РК №1) «Линейная алгебра».
Срок проведения – 9 неделя
29
Модуль 2.
1. ДЗ №2 «Функции нескольких переменных»
Срок выдачи 9 неделя, срок сдачи – 16 неделя
Примечание. Домашнее задание №2 по усмотрению кафедры может быть заменено контрольной работой.
2. Контроль по модулю №2 (РК №2) «Дифференциальные уравнения высших порядков».
Срок проведения – 16 неделя
Литература
1.
2.
3.
4.
5.
6.
7.
8.
1.
2.
3.
4.
5.
6.
5.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Основная литература (ОЛ)
Канатников А.Н., Крищенко А.П. Линейная алгебра: Учеб. для вузов / Под ред. B.C. Зарубина, А.П.
Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. – 336 с. (Сер. Математика в техническом
университете, вып. IV).
Канатников А.Н., Крищенко А.П., Четвериков В.Н. Дифференциальное исчисление функций многих
переменных: Учеб. для вузов / Под ред. B.C. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э.
Баумана, 2003. – 456 с. (Сер. Математика в техническом университете, вып. V).
Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Физматлит, 2005.
Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 1. – М.: Интеграл-Пресс, 2006. –
416 с.
Бугров Я.С., Никольский С.М. Высшая математика. Т. 2. Дифференциальное и интегральное исчисление. –
М.: Дрофа, 2003. – 512 с.
Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа: Учеб.
пособие для втузов / Под ред. А.В. Ефимова, Б.П. Демидовича. – М.: Наука, 1993. – 478 с.
Сборник задач по математике для втузов. Ч. 2. Специальные разделы математического анализа: Учеб.
пособие для втузов / Под ред. А.В. Ефимова, Б.П. Демидовича. – М.: Наука, 1986. – 368 с.
Задачи и упражнения по математическому анализу для втузов / Под ред. Б.П. Демидовича. – М.: Астрель
2005. – 416 с.
Дополнительная литература (ДЛ)
Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Физматлит, 2007. – 307 с.
Кудрявцев Л.Д. Курс математического анализа. Т. 2. – М.: Высш. шк., 1981. – 584 с.
Сборник задач по линейной алгебре / Под ред. С.К. Соболева. – М.: МГТУ, 1991. –154 с.
Вся высшая математика: Учебник для втузов: В 6 т. / Краснов М.Л., Киселев А.И., Макаренко и др. – Т. 1. –
М.: Эдиториал УРСС, 2000. – 327 с.
Вся высшая математика: Учебник для втузов: В 6 т. / Краснов М.Л., Киселев А.И., Макаренко Г.И. и др. – Т.
2. – М.: Эдиториал УРСС, 2000. – 184 с.
Беклемишева Л.А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной
алгебре. Под ред. Д.В. Беклемишева. – М.: Наука, 1987. – 496 с.
4.
Методические пособия
Крищенко А.П. Линейные пространства. Линейные операторы: Учеб.пособие. – М.: МГТУ, 1988. – 49 с.
Гришина Г.В., Козлов М.Е., Пашовкин Е.М., Подобряев В.Н. Методические указания к самостоятельной
работе студентов по разделам “Математический анализ” и ”Линейная алгебра”, под ред. Гришиной Г.В.
Учеб.пособие. – М.: МГТУ, 1990.–38 с.
Ильичев А.Т., Крапоткин В.Г., Савин А.С. Линейные операторы. Методические указания к выполнению
типового расчета. – М.: МГТУ, 2003. – 36 с.
Пугачев О.В., Стась Г.П, Чередниченко А.В. Квадратичные формы и их геометрические приложения.
Методические указания к выполнению типового расчета. – М.: МГТУ, 2004. – 59 с.
Гришина Г.В., Демин А.И., Михайлова О.В. Функции многих переменных. Методические указания к
выполнению домашнего задания. – М.: МГТУ, 2003. – 44 с.
Богомолов В.Г., Матвеев М.В., Филиновский А.В. Дифференциальное исчисление функций нескольких
переменных. – М.: МГТУ, 1993. – 52 с.
Богомолов В.Г., Матвеев М.В., Филиновский А.В. Прикладные задачи дифференциального исчисления
функций нескольких переменных. – М.: МГТУ, 1993. – 56 с.
Дерябина Г.С., Чуев В.Ю. Вектор-функция нескольких переменных. – М: МГТУ, 2002, – 26 с.
Гласко А.В., Покровский И.Л., Станцо В.В. Системы линейных алгебраических уравнений – М, МГТУ им.
Баумана, 2004.
Сидняев Н.И.. Феоктистов В.В. Линейные и евклидовы пространства. – М,: МГТУ им. Баумана, 2008.
30
Павельева Е.Б., Томашпольский В.Я. Линейная алгебра. Методические указания к выполнению типового
расчета (ЭУИ). – М.: МГТУ им. Баумана, 2010.
Феоктистов В.В., Сидняев Н.И. Линейные и евклидовы пространства. Методические указания к выполнению
домашнего задания. ─ М.:МГТУ, 2008, -71 с.
11.
12.
Рекомендуемые Интернет-сайты:
3. Канатников А.Н., Крищенко А.П.
4.
Конспект лекций по линейной алгебре и функциям нескольких
переменных http://mathmod.bmstu.ru/
http://www.mathelp.spb.ru - лекции по высшей математике
ЛИНЕЙНАЯ АЛГЕБРА И ФУНКЦИИ НЕСКОЛЬКИХ
ПЕРЕМЕННЫХ
для ИБМ
Дисциплина состоит из двух учебных модулей
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-8
8
Упражнения
1-8
16
Домашние задания текущие
1-8
10
9
2
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
9-17
9
Упражнения
9-17
18
Домашние задания текущие
9-17
10
17
2
Контроль по модулю №1
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Контроль по модулю №2
Примечание
Вычисление скалярного произведения и нормы
вектора в ортонормированном базисе.
Лекция 2. Линейные операторы и их матрицы
(определение, примеры). Преобразование матрицы
линейного оператора при переходе к новому базису.
Собственные векторы и собственные значения
линейного
оператора.
Характеристический
многочлен
линейного
оператора.
Свойство
множества собственных векторов, отвечающих
одному и тому же собственному значению.
Алгебраическая и геометрическая кратности
собственного значения, связь между ними.
Линейная независимость собственных векторов,
ЛЕКЦИИ
Модуль 1 ЛИНЕЙНАЯ АЛГЕБРА
Лекция 1. Линейные пространства и их
подпространства. Базис и размерность линейного
пространства, примеры. Матрица перехода к новому
базису, преобразование координат вектора при
переходе к новому базису. Евклидово пространство,
аксиомы и примеры. Норма вектора. Неравенство
Коши – Буняковского и неравенство треугольника.
Ортогональность векторов. Линейная независимость
ортогональной системы ненулевых векторов.
Ортонормированный базис евклидова пространства.
31
отвечающих различным собственным значениям.
Существование базиса из собственных векторов в
случае действительных и некратных корней
характеристического
уравнения.
Матрица
линейного оператора в базисе, состоящем из его
собственных векторов.
Лекция 3. Линейные операторы в евклидовых
пространствах. Самосопряженный оператор, его
матрица в ортонормированном базисе. Свойства
корней
характеристического
многочлена
самосопряженного оператора: вещественность и
равенство алгебраических и геометрических
кратностей. Ортогональность собственных векторов
самосопряженного
оператора,
отвечающих
различным собственным значениям. Существование
ортонормированного базиса из собственных
векторов
самосопряженного
оператора.
Ортогональные
преобразования
координат,
ортогональные
матрицы
и
их
свойства.
Диагонализация
симметрической
матрицы
ортогональным преобразованием.
Лекция 4. Квадратичные формы. Координатная и
матричная формы записи. Преобразование матрицы
квадратичной формы при переходе к новому базису.
Знакоопределенные квадратичные формы, критерий
Сильвестра. Канонический вид квадратичной
формы. Приведение квадратичной формы к
каноническому
виду
ортогональным
преобразованием. Приведение уравнений кривых
второго порядка к каноническому виду с помощью
ортогонального преобразования.
дифференциала
функции
двух
переменных.
Экстремум
ФНП.
Необходимое
условие
существования экстремума. Достаточные условия
экстремума (формулировка с помощью матрицы
Гессе).
Лекция 8. Условный экстремум ФНП, его
геометрическая интерпретация (при n  2 ), функция
Лагранжа. Необходимое условие существования
условного экстремума. Достаточные условия.
Векторная ФНП как отображение F : R n  R m .
Матрица Якоби векторной ФНП, якобиан (при
m  n ). Производная сложной векторной ФНП в
матричной форме.
УПРАЖНЕНИЯ
МОДУЛЬ 1: ЛИНЕЙНАЯ АЛГЕБРА
Занятие 1. Линейное пространство. Линейная
зависимость. Базис и размерность пространства.
Переход к новому базису.
Ауд.: ОЛ-6, гл. 4: 4.1–4.9 (неч.), 4.15, 4.17, 4.21, 4.24,
4.28, 4.30, 4.37 или
ДЛ-3, гл. 3: 7–17 (неч.), 21–25 (неч.), 29–33 (неч.),
40, 53–57(неч.), 63.
Дома: ОЛ-6, гл. 4: 4.2–4.10 (четн.), 4.16, 4.18, 4.19,
4.25, 4.31 или
ДЛ-3, гл. 3: 8–14 (четн.), 22–26 (четн.), 30–34 (четн.),
42, 54–58 (четн.), 64.
Занятие 2. Ранг системы векторов. Линейная
оболочка системы векторов. Подпространство
линейного пространства.
Ауд.: ОЛ-6, гл. 4: 4.45–4.53 (неч.) или
ДЛ-3, гл. 3: 73–77 (неч.), 87–91 (неч.), 95–99 (неч.).
Дома: ОЛ-6, гл. 4: 4.46, 4.48, 4.52, 4.54 или
ДЛ-3, гл. 3: 74–78 (четн.), 88–92 (четн.), 96–100
(четн.), гл. 4: 6–12 (четн.), 32, 38.
Занятие 3. Евклидовы пространства. Процесс
ортогонализации Грама – Шмидта.
Ауд.: ОЛ-6, гл. 4: 4.63 (а), 4.64 (а), 4.65 (а,б), 4.67–
4.76 (неч.), или
ДЛ-3, гл. 4: 5–12 (неч.), 17– 24 (неч.), 31, 37, 39, 47,
49, 53, 57, 59.
Дома: ОЛ-6, гл. 4: 4.63 (б), 4.64 (б), 4.65 (в), 4.67–
4.76 (четн.) или
ДЛ-3, гл. 4: 5–12 (четн.) 17–24 (четн.), 32, 38, 48, 50,
54, 58, 60.
Занятие 4. Линейные операторы и их матрицы.
Преобразование матрицы линейного оператора при
переходе к новому базису. Действия над линейными
операторами.
Ауд.: ОЛ-6, гл. 4: 4.83 – 4.99 (неч.), 4.103, 4.106 (б),
4.107, 4.110, 4.113 или
ДЛ-3, гл. 5: 1, 5, 7, 21, 23, 25, 32 (а), 33 (а), 44, 45 (а),
47, 49, 51 (а, б), 71.
Дома: ОЛ-6, гл. 4: 4.84, 4.86, 4.90 – 4.100 (четн.),
4.102, 4.104, 4.108, 4.110(б), 4.118 или
ДЛ-3, гл. 5: 6, 8, 22, 24, 32 (6), 33 (б), 43, 45 (б), 48,
51 (в, г), 72.
Занятие 5. Собственные векторы и собственные
значения линейного оператора. Диагонализация
симметричных
матриц
ортогональным
преобразованием.
Модуль 2. ФУНКЦИИ НЕСКОЛЬКИХ
ПЕРЕМЕННЫХ
Лекция 5. Метрика и окрестности в R n . Граница
множества. Открытые, замкнутые, ограниченные и
связные множества в R n . Скалярная функция
нескольких
переменных
(ФНП).
Линии
и
поверхности уровня. Предел и непрерывность ФНП
в точке, на множестве. Свойства ФНП, непрерывной
на: (а) связном множестве; (б) замкнутом и
ограниченном множестве. Частные производные
ФНП, геометрическая интерпретация для n  2 .
Частные производные высших порядков, теорема о
независимости смешанных частных производных
высших порядков от порядка дифференцирования.
Матрица Гессе.
Лекция
6.
Дифференцируемость
ФНП.
Необходимые условия, достаточное условие
дифференцируемости. Полный дифференциал ФНП.
Необходимые и достаточные условия того, что
выражение P( x, y)dx  Q( x, y)dy является полным
дифференциалом необходимость с доказательством.
Производная сложной функции. Частная и полная
производные ФНП. Инвариантность формы первого
дифференциала. Неявные функции. Теорема о
существовании (без док-ва) и дифференцируемости
неявной ФНП. Градиент и производная ФНП по
направлению, их свойства.
Лекция 7. Касательная плоскость и нормаль к
поверхности, их уравнения. Геометрический смысл
32
Ауд.: ОЛ-6, гл. 4: 4.129, 4.131, 4.135–4.143 (неч.),
4.174, 4.183, 4.191 или
ДЛ-3, гл. 5: 75–80 (неч.). 89–100 (неч.), 155–162
(неч.).
Дома: ОЛ-6, гл. 4: 4.130, 4.132, 4.134–4.142 (четн.),
4.176, 4.184, 4.186 или
ДЛ-3, гл. 5: 75–80 (четн). 89–100 (четн.), 156–162
(четн.).
Занятие 6. Квадратичные формы, критерий
Сильвестра. Преобразование матрицы квадратичной
формы при переходе к новому базису.
Ауд.: ОЛ-6, гл. 4: 4.218–4.225 (четн.) или
ДЛ-3, гл. 6: 13, 15, 43, 45.
Дома: ОЛ-6, гл. 4: 4.218–4.233 (неч.) или
ДЛ-3, гл. 6: 14, 16, 44, 46.
Занятия 7–8. Приведение квадратичной формы к
каноническому виду методом Лагранжа и
ортогональным
преобразованием.
Приведение
кривых второго порядка к каноническому виду.
Ауд.: ОЛ-6, гл. 4: 4.210, 4.211, 4.213, 4.215, 4.226,
4.228, 4.231 или
ДЛ-3, гл. 6: 19, 21, 23 (б), 29, 31, 35, 47, 49, 55.
Дома: ОЛ-7, гл. 4: 4.212, 4.214, 4.216, 4.227, 4.229,
4.230 или
ДЛ-3, гл. 6: 20, 22, 23 (а), 30, 32, 36, 48, 50, 56.
Занятие 9. Рубежный контроль по модулю 1.
ОЛ-6, гл. 7: 7.7, 7.9, 7.13, 7.20 (построить линии и
поверхности уровня), 7.33, 7.34, 7.45, 7.47, 7.51.
Занятие 11. Частные производные 1-го порядка.
Частные
производные
высших
порядков.
Дифференциал первого и второго порядка ФНП.
Ауд.: ОЛ-7: 1801–1825 (неч), 1892, 1894, 1897, 1834,
1838, 1844, 1917, 1924 или
ОЛ-6, гл. 7: 7.57, 7.60, 7.61, 7.63, 7.66, 7.87, 7.89,
7.91, 7.103, 7.105, проверить функцию

 x 4  x 2  y 4 ; x 2  y 2  0;
на
f ( x, y )  
x 2  y 2  0.

0;
дифференцируемость в точке (0,0).
Дома: ОЛ-7: 1801–1825 (четн.), 1891, 1893, 1898,
1838, 1840, 1845, 1916, 1925 или
ОЛ-6, гл. 7: 7.56, 7.58, 7.59, 7.62, 7.64, 7.67, 7.88,
7.90, 7.92, 7.102, 7.107.
Занятия 12-13. Производная сложной и неявной
ФНП. Производная по направлению и градиент
ФНП. Касательная плоскость и нормаль к
поверхности.
Ауд.: ОЛ-7: 1856, 1861, 1864, 1865, 1870, 1944, 1946,
1948, 1950, 1955, 1876, 1878, 1882 (а), 1886, 1889,
1981 (а), 1982, 1985, 1986 или
ОЛ-6, гл. 7: гл. 7: 7.114, 7.119, 7.122, 7.129, 7.135,
7.141, 7.145, 7.149, 7.152, 7.229 (а), 7.233 (а), 7.232,
7.234, 7.239 (а); ОЛ-6 гл. 10: 10.31–10.43 (неч.).
Дома: ОЛ-7: 1857, 1862, 1863, 1871, 1943, 1947,
1949, 1956, 1877, 1879, 1882 (6), 1883, 1888, 1981 (б),
1984, 1987, 1990 или
ОЛ-6, гл. 7: 7.116, 7.118, 7.123, 7.130, 7.136, 7.140,
7.146, 7.150, 7.151; 7.229 (б), 7.233 (б, в), 7.235,
7.239 (б); ОЛ-6 гл. 10: 10.32–10.44 (четн.).
Занятия 14-15. Безусловный и условный экстремум
ФНП.
Ауд.: ОЛ-7: 2008, 2010, 2012, 2016, 2016.1, 2021–
2024, 2031 или
ОЛ-6, гл. 7: 7.187–7.195 (неч.), 7.201, 7.205, 7.214.
Дома: ОЛ-8: 2009, 2011, 2014, 2016.2, 2023, 2024,
2033 или
ОЛ-6, гл. 7: 7.187–7.195 (четн.), 7.202–7.204, 7.210–
7.213.
Занятие 16. Рубежный контроль по модулю 2.
МОДУЛЬ 2. ФУНКЦИИ НЕСКОЛЬКИХ
ПЕРЕМЕННЫХ
Занятие 10. Область определения ФНП. Линии и
поверхности уровня. Предел и непрерывность ФНП.
Ауд.: ОЛ-7: 1792 (в), 1793 (г), 1794 (в), 1795 (а),
1796 (в), 1797 (б, в), 1788 (в), найти предел
lim ( x 3  3 y 2 )  e( x
x 
y 
2
 y2 )
, проверить функцию
 x3  3 y 4 2
, x  y2  0

f ( x, y )   x 2  y 2
 0,
x2  y2  0

на непрерывность в точке (0; 0) или
ОЛ-6, гл. 7: 7.6, 7.8, 7.10, 7.19, 7.21 (построить
линии и поверхности уровня), 7.32, 7.35, 7.44, 7.46,
7.50, 7.55.
Дома: ОЛ-7 гл. 4: 1792 (е, и), 1793 (б, в), 1794(г, ж),
1796 (а, б), 1797 (г, е), 1799 (б) или
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, подготовке к выполнению
контрольных работ и рубежных контролей, выполнении индивидуальных ДЗ.
Контрольные мероприятия
Модуль 1: Линейная алгебра
1. Домашнее задание №1 «Линейная алгебра» состоит из 7 задач по темам: линейные и евклидовы
пространства, линейные операторы, квадратичные формы и их геометрические приложения. Сроки
выполнения: выдача– 1 неделя, прием – 7 неделя.
2. Рубежный контроль № 1 по теме «Линейная алгебра», практика. Билет содержит 4-5 задач. Срок
проведения – 8 неделя.
33
3. Рубежный контроль № 1 по теме «Линейная алгебра», теория. Задание содержит 2-3 теоретических
вопроса. Срок проведения – 9 неделя.
Модуль 2. Дифференциальное исчисление функций нескольких переменных
4. Домашнее задание № 2 состоит из задач по темам: геометрическое изображение ФНП, дифференцирование
сложной и неявной ФНП, дифференциалы 1 и 2 порядка, касательная плоскость и нормаль, экстремум ФНП.
Сроки выполнения: выдача – 10 неделя, прием – 15 неделя.
5. Рубежный контроль № 2 по теме: Функции нескольких переменных, практика. Билет содержит 4-5 задач.
Срок проведения – 16 неделя.
6. Рубежный контроль № 2 по теме: Функции нескольких переменных, теория. Задание содержит 2-3
теоретических вопроса. Срок проведения – 17 неделя.
Литература
Основная литература (ОЛ)
3. Канатников А.Н., Крищенко А.П. Линейная алгебра: Учеб. для вузов / Под ред. B.C. Зарубина, А.П.
Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. – 336 с. (Сер. Математика в техническом
университете, вып. IV).
4. Канатников А.Н., Крищенко А.П., Четвериков В.Н. Дифференциальное исчисление функций многих
переменных: Учеб. для вузов / Под ред. B.C. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э.
Баумана, 2003. – 456 с. (Сер. Математика в техническом университете, вып. V).
5. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Физматлит, 2005.
6. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 1. – М.: Интеграл-Пресс, 2006.
– 416 с.
7. Бугров Я.С., Никольский С.М. Высшая математика. Т. 2. Дифференциальное и интегральное исчисление. –
М.: Дрофа, 2003. – 512 с.
8. Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа: Учеб.
пособие для втузов / Под ред. А.В. Ефимова, Б.П. Демидовича. – М.: Наука, 1993. – 478 с.
9. Задачи и упражнения по математическому анализу для втузов /Под ред. Б.П. Демидовича/. – М.: Астрель
2005, – 416 с.
Дополнительная литература (ДЛ)
7. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Физматлит, 2007,– 307 с.
8. Кудрявцев Л.Д. Курс математического анализа. Т. 2. – М.: Высш. шк., 2001. – 584 с.
9. Сборник задач по линейной алгебре / Под ред. С.К. Соболева. – М.: МГТУ, 1991. –154 с.
10. Вся высшая математика: Учебник для втузов: В 6 т. / Краснов М.Л., Киселев А.И., Макаренко и др. – Т. 1. –
М.: Эдиториал УРСС, 2000. – 327 с.
11. Вся высшая математика: Учебник для втузов: В 6 т. / Краснов М.Л., Киселев А.И., Макаренко Г.И. и др. – Т.
2. – М.: Эдиториал УРСС, 2000. – 184 с.
12. Беклемишева Л.А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной
алгебре. Под ред. Д.В. Беклемишева. – М.: Наука, 1987. – 496 с.
Методические пособия, изданные в МГТУ (МП)
13. Ильичев А.Т., Крапоткин В.Г., Савин А.С. Линейные операторы. Методические указания к выполнению
типового расчета. – М.: МГТУ, 2003. – 36 с.
14. Пугачев О.В., Стась Г.П, Чередниченко А.В. Квадратичные формы и их геометрические приложения.
Методические указания к выполнению типового расчета. – М.: МГТУ, 2004. – 59 с.
15. Гришина Г.В., Демин А.И., Михайлова О.В. Функции многих переменных. Методические указания к
выполнению домашнего задания. – М.: МГТУ, 2003. – 44 с.
16. Богомолов В.Г., Матвеев М.В., Филиновский А.В. Дифференциальное исчисление функций нескольких
переменных. – М.: МГТУ, 1993. – 52 с.
17. Богомолов В.Г., Матвеев М.В., Филиновский А.В. Прикладные задачи дифференциального исчисления
функций нескольких переменных. – М.: МГТУ, 1993. – 56 с.
18. Дерябина Г.С., Чуев В.Ю. Вектор-функция нескольких переменных. – М: МГТУ, 2002, – 26 с.
19. Сидняев Н.И.. Феоктистов В.В. Линейные и евклидовы пространства. – М.: МГТУ им. Баумана, 2008.
Электронные ресурсы:
1. Павельева Е.Б., Томашпольский В.Я. Линейная алгебра. Методические указания к выполнению типового
расчета (ЭУИ). – М.: МГТУ им. Баумана, 2010, http://hoster.bmstu.ru/~fn1/?page_id=30.
34
ЛИНЕЙНАЯ АЛГЕБРА
Дисциплина состоит из 2-х учебных модулей и экзамена
Модуль 1
Сроки
проведения или
выполнения,
недели
Трудоёмкость,
часы
Лекции
1-10
30
Упражнения
1-11
33
Домашние задания текущие
1-10
12
11
6
Сроки
проведения или
выполнения,
недели
Трудоёмкость,
часы
Лекции
11-17
21
Упражнения
12-17
18
Домашние задания текущие
11-17
12
17
6
Виды аудиторных занятий
и самостоятельной работы
Контроль по модулю №1
Примечание
Модуль 2
Виды аудиторных занятий
и самостоятельной работы
Контроль по модулю №2
Примечание
Модуль 1: Линейные пространства, теория линейных операторов
Лекции
подпространств.
Разложение
линейного
пространства в прямую сумму подпространств.
Линейные оболочки систем векторов. Нахождение
базиса и размерности суммы и пересечения
подпространств, заданных как линейные оболочки
некоторых систем векторов. Факторпространства
линейных пространств.
ОЛ2: Гл. 1, §§1-2, ОЛ3: Гл. 2.
Лекции 5-6 – Линейные операторы. Определение
и основные свойства линейных операторов. Ядро,
образ, ранг и дефект линейного оператора.
Основные неравенства для ранга и дефекта
линейного оператора. Матричная запись линейных
операторов. Преобразование матрицы линейного
оператора при переходе от одного базиса к
другому.
Лекции 1-2 – Предварительные сведения.
Множества
и
отображения.
Отношения
эквивалентности, факторизация множеств и
отображений. Отношения порядка, упорядоченные
множества. Понятие числового поля. Основные
свойства многочленов над полями вещественных и
комплексных чисел.
ОЛ1: Гл. 1, §§5-6. Гл. 5, §1, ДЛ8: Гл. 2, §§1-2.
Лекции 3-4 – Линейные пространства.
Определение и основные свойства линейных
пространств. Линейная зависимость элементов
линейного пространства. Базис и координаты в
линейном пространстве, преобразование координат
при преобразовании базиса. Размерность линейного
пространства. Изоморфизм линейных пространств.
Подпространства,
сумма
и
пересечение
35
ОЛ2: Гл. 2, §§1-2, ОЛ3: Гл. 5, §§1-3.
Лекция 7 – Линейные функционалы и
билинейные формы. Линейные функционалы,
полуторалинейные и билинейные функции в
линейных
пространствах,
их
матричное
представление и основные свойства.
ОЛ2: Гл. 2, §§1-2, ОЛ3: Гл. 5, §§1-3.
Лекции 8-9 – Двойственное пространство.
Двойственное пространство и его свойство.
Теорема о существовании двойственного базиса.
Примеры. Теорема о существовании канонического
изоморфизма
X→X**.
Критерии
линейной
независимости. Сопряженный оператор и его
свойства.
ОЛ2: Гл. 1, §3.
Лекции 10-12 – Теория линейных операторов.
Инвариантные
подпространства
линейных
операторов. Минимальный и характеристический
многочлены линейного оператора, их свойства.
Собственные значения и собственные векторы
линейных операторов, их свойства. Существование
инвариантных
подпространств
у
линейных
операторов в вещественном и комплексном
пространствах.
Теорема
Гамильтона-Кэли.
Циклические векторы линейных операторов.
ОЛ2: Гл. 2, §§2-3.
Лекции 13-14 – Канонический вид линейных
операторов. Собственные и присоединенные
векторы, собственные и корневые инвариантные
подпространства
линейных
операторов,
их
свойства. Теорема о приведении оператора к
жордановой
нормальной
форме.
Структура
матрицы
жордановой
нормальной
формы
линейного оператора.
ОЛ2: Гл. 2, §4, ОЛ3: Гл. 5, §8.
Упражнения
Дома: ОЛ4: 39.1(неч.), 39.2, 39.5(неч.), 39.10(б),
39.15(неч.), 39.18, 39.21, 39.22, 39.23(б).
Занятие 8. Двойственное пространство.
Сопряженный оператор
Ауд.: ОЛ4: 36.9(а,б), Аналог задачи 3 ДЗ№1,
43.14(а).
Дома: ОЛ4: 36.9(в), 36.10, 43.14(б).
Занятия
9-10.
Собственные
значения
и
собственные векторы линейных операторов.
Ауд.: ОЛ4: 40.1(неч.), 40.2, 40.6, 40.7, 40.8(а), 40.9,
40.15(чет.).
Дома: ОЛ4: 40.1(чет.), 40.4, 40.5, 40.8(б), 40.10,
40.15(неч.).
Занятие
11.
Инвариантные
и
корневые
подпространства линейных операторов.
Ауд.: ОЛ4: 40.16(1,3), 40.19, 40.20, 40.22, 40.24,
40.31(а), 40.35(а,б).
Дома: ОЛ4: 40.16(2,4), 40.17, 40.21, 40.25, 40.30,
40.31(б), 40.35(в,г).
Занятия 12-13. Жорданова форма и ее приложения.
Ауд.: ОЛ4: 41.1(неч.), 41.3, 41.5, 41.6, 41.10(а,б),
41.16, 41.17, 41.19.
Дома: ОЛ4: 41.1(чет.), 41.2, 41.4, 41.10(в,г), 41.20,
41.22.
Занятие 14. Контроль по модулю 1.
Занятия 1-2. Матричные вычисления.
Комплексные числа. Свойства отображений.
Ауд.: ОЛ4: 7.1(а,б), 8.1 (а,б), 8.4 (а,б), 9.2 (а,и),
Вычислить определитель Вандермонда, 11.10(а),
18.11(а), 2.1, 2.5, 20.1(а, ж), 20.4(а), 20.8, 21.1(д,к),
21.4(а), 21.8, 21.11(а,б).
Дома: ОЛ4: 7.1(в,г), 8.1(в,г), 8.1(в,г), 9.2 (б,к),
11.10(б,в), 18.11(б), 2.6, 2.7, 20.1(б,з), 20.4(д), 20.10,
21.1(а,п), 21.4, 21.11(в,г), 22.2, 22.4, 22.5, 22.7(з,о).
Занятие 3. Линейные пространства.
Ауд.: ОЛ4: 34.2(а), 34.3(б,г), 34.4(б), 34.11(а), 34.12,
34.13(а), 34.14(а,б).
Дома: ОЛ4: 34.2(б), 34.3(а,в,ж), 34.4(а,в), 34.11(б),
34.13(б,в), 34.14(в,г).
Занятие 4. Линейные пространства.
Ауд.: ОЛ4: 35.1(г,д,ж), 35.3(а,б,д), 35.6(б,в),
35.11(а), 35.12(а,б), 35.13(а,б), 35.14(а,б).
Дома: ОЛ4: 35.1(а,и,к), 35.3(в,г,е), 35.6(а,г),
35.11(б), 35.12(в), 35.13(в,г), 35.14(б).
Занятие 5. Линейные пространства.
Ауд.: ОЛ4: 35.16(а), 35.18, 35.21, 35.22.
Дома: ОЛ4: 35.16(б), 35.17, 35.19, 35.21, 35.23.
Занятия 6-7. Линейные операторы. Матрица
линейного оператора
Ауд.: ОЛ4: 39.1(чет.), 39.3, 39.5(чет.), 39.6, 39.10(а),
39.15(чет.), 39.17, 39.20, 39.23(а).
Модуль 2: Евклидовы и эрмитовы пространства, тензоры
Лекции
ортогонального
дополнения.
Изоморфизм
конечномерных
евклидовых
пространств.
Эрмитовы пространства и их основные свойства.
Неравенство Коши-Буняковского в вещественном и
комплексном случаях. Теоремы об общем виде
линейного функционала и полуторалинейной
функции в эрмитовом пространстве. Норма
линейного оператора и ее свойства.
ОЛ2: Гл. 3, §§1-2, ОЛ3: Гл. 4.
Лекции 1-2 – Евклидовы и эрмитовы
пространства. Определение и основные свойства
скалярного
произведения
и
вещественного
евклидова пространства. Ортонормированный
базис конечномерного евклидова пространства и
его свойства. Матрица Грама и ее свойства.
Процесс ортогонализации Грама-Шмидта. QRразложение. Разложение евклидова пространства в
прямую
сумму
подпространства
и
его
36
квадратов. Методы Лагранжа и Якоби приведения
квадратичной формы к сумме квадратов. Закон
инерции квадратичных форм. Индексы инерции
квадратичных форм, классификация квадратичных
форм. Критерий Сильвестра знакоопределенности
квадратичной формы.
ОЛ2: Гл. 1, §4, ОЛ3: Гл. 7, §§1-6.
Лекции 8-9 – Уравнения гиперповерхностей
второго порядка и их аффинная классификация.
Общее уравнение гиперповерхности второго
порядка. Преобразование общего уравнения
гиперповерхности второго порядка при аффинных
преобразованиях. Инварианты общего уравнения
гиперповерхности
второго
порядка.
Центр
гиперповерхности второго порядка. Классификация
уравнений
центральных
и
нецентральных
гиперповерхностей второго порядка.
ОЛ3: Гл. 7, §7.
Лекция 10-11 – Тензоры. Основы тензорного
исчисления (понятие о тензорах, операции над
тензорами, произведение тензоров, координаты
тензора, тензоры в разных системах координат,
тензорное произведение пространств). Свёртка,
симметризация и альтернирование тензоров.
Симметричные и кососимметричные тензоры.
ОЛ2: Гл. 6, §§1-2.
Лекции 3-4 – Линейные операторы в эрмитовых
и эвклидовых пространствах. Самосопряженные
операторы. Матрица самосопряженного оператора.
Необходимые
и
достаточные
условия
самосопряженности. Свойства собственных чисел и
собственных
векторов
самосопряженных
операторов.
Спектральное
разложение
самосопряженных операторов. Положительные
операторы. Корни k-ой степени из операторов.
Эрмитовы формы и их основные свойства.
Билинейные формы и самосопряженные операторы
в евклидовых пространствах.
ОЛ2: Гл. 1, §4, Гл. 3, §3, ОЛ3: Гл. 5, §§4-6.
Лекция 5 – Нормальные, унитарные и
ортогональные
операторы.
Нормальные
операторы и их свойства. Критерии нормальности.
Спектральное разложение нормальных операторов.
Унитарные и ортогональные операторы, их
свойства.
Комплексификация
вещественных
евклидовых пространств и линейных операторов.
Канонический вид ортогональных операторов.
ОЛ2: Гл. 2, §4, ОЛ3: Гл. 5, §§7-8.
Лекции 6-7 – Квадратичные формы в
евклидовых
пространствах.
Квадратичные
формы. Теоремы о приведении квадратичной
формы и пары квадратичных форм к сумме
Упражнения
Занятие 1-2. Евклидовы и эрмитовы пространства.
Ауд.: ОЛ5: 25.2(чет.), 25.4, 25.10, 25.26(1,4), 25.29,
26.5, 26.9, 26.28(чет.), 26.35.
Дома: ОЛ5: 25.2(неч.), 25.3, 25.5, 25.26(2,3), 25.32,
26.4, 26.12, 26.28(неч.), 26.36.
Занятие 3. Евклидовы и эрмитовы пространства.
Ауд.: ОЛ4: 43.4(а,б), 43.7(а,б), 43.16(а), 43.18(а),
43.22, 43.24.
Дома: ОЛ4: 43.4(в,г), 43.7(в,г), 43.16(б,в),
43.18(б,в), 43.23, 43.25, 43.29, 43.31, 43.35.
Занятия 4-5. Самосопряженные операторы.
Ауд.: ОЛ4: 44.1 (г,д,е), 44.2, 44.4, 44.6, 44.9 (а,в).
Дома: ОЛ4: 44.1 (а,б,в), 44.3, 44.5, 44.7, 44.11.
Занятие 6. Нормальные и ортогональные
операторы.
Ауд.: ОЛ4: 44.24, 44.27, 45.2, 45.4(б,д), 45.11, 46.3,
46.10(а,б).
Дома: ОЛ4: 44.25, 44.26, 45.3, 45.4(в,г), 45.10, 45.12,
46.4, 46.10(в,г).
Занятие 7-8. Билинейные и квадратичные формы.
Ауд.: ОЛ5: 32.1(3,7), 32.5, 32.7(1,3), 32.8(4,6),
32.36(6,14), 32.38, ОЛ5: 32.13(1,3,4), 32.15, 32.17,
32.18(1,3), 32.21, 52.20(а), .52.21(м), 52.22(у).
Дома: ОЛ5: 32.1(4,5,6), 32.6, 32.7(5,6,7), 32.8(12,14),
32.36(8,11), 32.37, ОЛ5: 32.13(2,5,6), 32.16,
32.18(2,4,5), 32.22, 52.20(б), 52.21(н), 52.22(ф).
Занятие 9-10. Тензоры
Ауд.: ОЛ4: §§47-48 (четные).
Дома: ОЛ4: §§47-48 (нечетные).
Занятие 11. Контроль по модулю 2.
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке рекомендованной литературы, материала
лекций, выполнении домашних заданий и в подготовке к контрольным работам.
Контрольные мероприятия и сроки их проведения
Модуль 1
1. Домашнее задание №1. Срок выдачи – 2 неделя, срок сдачи – 10 неделя.
2. Контрольная работа №1. Срок проведения – 11 неделя.
Модуль 2
1. Домашнее задание №2. Срок выдачи – 9 неделя, срок сдачи – 16 неделя.
2. Контрольная работа №2. Срок проведения – 17 неделя.
Литература
37
Основная литература
1. Кострикин А.И. Введение в алгебру. Часть I. Основы алгебры. – М.: Физматлит, 2004. – 272 с.
2. Кострикин А.И. Введение в алгебру. Часть 2. Линейная алгебра. – М.: Физматлит, 2000. – 268 с.
3. Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Наука, 1978. – 304 с.
4. Кострикин А.И. (ред.) Сборник задач по алгебре – М.: Физматлит, 2001. – 464 с.
5. Беклемишева Л.А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной
алгебре. – М.: Физматлит, 2004. – 496 с.
Дополнительная литература
1. Мальцев А.И. Основы линейной алгебры. – М.: Наука, 1975. – 400 с.
2. Ван дер Варден Б.Л. Алгебра. – М.: Наука, 1976.
3. Зорич В.А. Математический анализ. Часть I. – М.: МЦНМО, 2002. – 664 с.
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Дисциплина состоит из 2 учебных модулей и экзамена.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-8
16
Упражнения
1-9
28
Домашние задания текущие
1-9
12
Контроль по модулю №1
10
6
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
9-17
18
Упражнения
10-17
23
Домашние задания текущие
10-17
12
16
6
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Контроль по модулю №2
Примечание
Модуль 1: Интегралы
Лекции
Лекция 1. Первообразная и ее свойства.
Неопределенный интеграл, его свойства, связь с
дифференциалом.
Таблица
основных
неопределенных интегралов.
ОЛ-1 §1.1-1.4, ОЛ-3 гл. X, §1-3, §10-14, ОЛ-5
гл.5 §5.1-5.8.
Лекция 2.
Интегрирование подстановкой и
заменой переменного. Интегрирование по частям.
Интегрирование
выражений,
содержащих
квадратный трехчлен.
ОЛ-1 §1.1-1.6, ОЛ-3 гл. X, §4-9, ОЛ-5 гл.5 §5.25.8.
38
Лекция 3.
Дробно-рациональные функции.
Разложение правильной рациональной дроби на
сумму простейших. Интегрирование простейших
дробей и дробно-рациональных функций.
ОЛ-1 §2.1-2.4, ОЛ-3 гл. X §4-9, ОЛ-5 гл.5 §5.25.6, ОЛ-6 §22,24,25.
Интегрирование
периодических
функций,
интегрирование четных и нечетных функций на
отрезке, симметричном относительно начала
координат.
ОЛ-1 §6.9-6.10, ОЛ-3 гл. XI §4-6, ОЛ-5 гл.6
§6.3,6.4, ОЛ-6 §29,30.
Лекция 4. Интегрирование функций, рационально
зависимых от тригонометрических функций.
Интегрирование
иррациональных
функций.
Примеры интегралов, не выражающихся через
элементарные функции.
ОЛ-1 гл.3,4, ОЛ-3 гл. X §10-14, ОЛ-5 гл.2 §5,7,
ОЛ-6 §26.
Лекции 8-9. Несобственные интегралы по
бесконечному промежутку (1-го рода). Несобственные интегралы от неограниченных функций на
отрезке (2-го рода). Признаки сходимости
несобственных интегралов. Абсолютная и
условная сходимости.
ОЛ-1 §7.1-7.6, 7.8, ОЛ-3 гл. XI §7, ОЛ-5 гл.6
§6.8-6.11, ОЛ-6 §33.
Лекции 5-6. Определенный интеграл как предел
интегральных сумм. Суммы и интегралы Дарбу.
Критерий
существования
определенного
интеграла
Римана.
Достаточные
условия
существования
интеграла
Римана.
Геометрическая интерпретация определенного
интеграла. Основные свойства определенного
интеграла. Теоремы об оценке и о среднем
значении.
ОЛ-1 §6.1-6.2, 6.5-6.8, ОЛ-3 гл. XI §1-3, ОЛ-5
гл.6 §6.1,6.2, ОЛ-6 §28,30.
Лекции 10-11. Площадь плоской фигуры.
Вычисление
площадей
плоских
фигур,
ограниченных кривыми, заданными в декартовых
координатах, параметрически и в полярных
координатах. Объем тела. Вычисление объемов
Вычисление
объемов
тел
по
площадям
поперечных сечений и объемов тел вращения.
ОЛ-1 §9.1-9.5, ОЛ-3 гл. XII §1,2,4,5, ОЛ-5 гл.7
§7.1-7.4,7.7,7.8, ОЛ-6 §32.
Лекция 12. Длина дуги кривой. Вычисление
длины дуги кривой. Площадь поверхности.
Вычисление площади поверхности вращения.
ОЛ-1 §9.1-9.5, ОЛ-3 гл. XII §1,2,4,5, ОЛ-5 гл.7
§7.1-7.4,7.7,7.8, ОЛ-6 §32.
Лекция 7. Определенный интеграл с переменным
верхним пределом и его производная. Формула
Ньютона-Лейбница. Вычисление определенных
интегралов заменой переменного и по частям.
Упражнения
Занятие 1. Непосредственное интегрирование по
таблице. Интегрирование методом подстановки.
Ауд.: ОЛ-8, гл.6, §1: 6.15, 6.23, 6.24, 6.27, 6.29,
6.35, 6.37, 6.40, 6.42, 6.43, 6.44, 6.48 6.52, 6.53,
6.56, 6.60, 6.62, 6.65, 6.74, 6.79, 6.83, 6.89, 6.95,
6.98, 6.100, 6.102, 6.107 или
ОЛ-9, гл.4, §1: 1032, 1040, 1044, 1046, 1050, 1062,
1063, 1065, 1066, 1073, 1075, 1080, 1093, 1082,
1086, 1095, 1104, 1119, 1133, 1137, 1145,
1149,1153, 1159, 1163, 1167, 1179, 1189.
Дома: ОЛ-8, гл.6, § 1: 6.20, 6.22, 6.25, 6.32, 6.38,
6.39, 6.41 6.45, 6.46, 6.47, 6.49, 6.54, 6.57, 6.61,
6.66, 6.68, 6.72, 6.76, 6.80, 6.85, 6.86, 6.92, 6.97,
6.101, 6.104, 6.106, 6.112 или
ОЛ-9, гл.4, § 1: 1037, 1041, 1057, 1069, 1070, 1074,
1077, 1083, 1085, 1094, 1108, 1096, 1101, 1114,
1120, 1130, 1146, 1152, 1154, 1162, 1172 1182,
1188.
Занятие 2. Интегрирование по частям.
Ауд.: ОЛ-8, гл. 6, § 1: 6.129, 6.130, 6.132, 6.135,
6.124, 6.128, 6.136, 6.143, 6.151, 6.157, 6.144,
6.146, 6.147, 6.155, 6.156 или
ОЛ-9, гл. 4, § 3: 1214, 1219, 1236, 1231, 1213,
1223, 1227, 1234, 1235, 1252, 1253, 1245, 1237,
1228, 1242, 1246.
Дома: ОЛ-8, гл. 6, § 1: 6.125, 6.131, 6.140, 6.142,
6.127, 6.138, 6.145, 6.152, 6.153, 6.154, 6.137, 6.141
или
ОЛ-9, гл. 4, § 3: 1215, 1217, 1229, 1232, 1244,
1237, 1241, 1254, 1239, 1249, 1222, 1226.
Занятие
3.
Интегрирование
выражений,
содержащих квадратный трёхчлен.
Ауд.: ОЛ-8, гл. 6, § 2: 6.158, 6.161, 6.163, 6.165,
6.271, 6.250, 6.254, 6.255, 6.257, 6.259, 6.260,
6.264, 6.275 или ОЛ-9, гл. 4, § 4: 1225, 1259, 1261,
1262, 1265, 1266, 1269, 1271, 1272, 1274, 1277,
1278, 1279.
Дома: ОЛ-8, гл. 6, § 2:, 6.159, 6.160, 6.162, 6.164,
6.251, 6.252, 6.253, 6.256, 6.258, 6.265, 6.280 6.276,
6.277 или ОЛ-9, гл. 4, § 4: 1258, 1260, 1263, 1267,
1270, 1268, 1273, 1275, 1276.
Занятие 4. Интегрирование рациональных
дробей.
Ауд.: ОЛ-8, гл. 6, § 2: 6.167, 6.168, 6.177, 6.171,
6.179, 6.178, 6.174, 6.185, 6.186, 6.188 или
ОЛ-9, гл. 4, § 5: 1282, 1284, 1286, 1289, 1290,
1298, 1308, 1313, 1314.
Дома: ОЛ-8, гл. 6, § 2: 6.129, 6.170, 6.173, 6.180,
6.181, 6.184, 6.187, 6.189 или
ОЛ-9, гл. 4, § 5: 1283, 1285, 1292, 1295, 1296,
1297, 1305, 1307, 1311.
Занятие 5. Интегрирование тригонометрических
функций.
Ауд.: ОЛ-8, гл. 6, § 2: 6.190, 6.191, 6.195, 6.197,
6.198, 6.201, 6.203, 6.206, 6.209, 6.212, 6.213, 6.216
или
39
ОЛ-9, гл. 4, § 7: 1338, 1341, 1345, 1347, 1350,
1351, 1355, 1359, 1365, 1366.
Дома: ОЛ-8, гл. 6, § 2: 6.192, 6.194, 6.196, 6.199,
6.202, 6.204, 6.208, 6.210, 6.211, 6.214, 6.215, 6.217
или
ОЛ-9, гл. 4, § 7: 1339, 1340, 1344, 1346, 1348,
1352, 1358, 1362, 1367, 1368, 1372.
Занятие 6. Интегрирование тригонометрических
функций и некоторых иррациональных функций.
Ауд.: ОЛ-8, гл. 6, § 2: 6.219, 6.222, 6.225, 6.226,
6.238, 6.240, 6.242, 6.244, 6.261, 6.262, 6.264,
6.266, 6.267 или
ОЛ-9, гл. 4, § 6, 7: 1377, 1382, 1388, 1380, 1389,
1318, 1320, 1322, 1325, 1403, 1405, 1407, 1411,
1412.
Дома: ОЛ-8, гл. 6, § 2: 6.218, 6.223, 6.224, 6.227,
6.239, 6.241, 6.243, 6.245, 6.263, 6.256, 6.268, 6.269
или
ОЛ-9 гл. 4 § 6, 7: 1373, 1378, 1381, 1389, 1387,
1315, 1317, 1319, 1321, 1323, 1324, 1404, 1406,
1408, 1413.
Занятие
7.Контрольная
работа
«Техника
интегрирования».
Занятие
8.
Вычисление
определённого
интеграла. Его свойства и геометрическая
интерпретация.
Ауд.: ОЛ-8, гл. 6, § 4: 6.326, 6.337, 6.340, 6.346,
6.350, 6.379, 6.387, 6.390, 6.395, 6.399, 6.406,
6.364(б, в), 6.365 (а, в), 6.366 (а, г), 6.369, 6.370,
6.378 (в задачах 6.326, 6.337, 6.340, 6.399, 6.406
дать геометрическую интерпретацию) или
ОЛ-9, гл. 5, § 2, 4–6: 1521, 1529, 1534, 1536, 1538,
1576, 1587, 1590, 1592, 1598, 1592, 1598, 1599,
1600, 1610(а, б), 1611 (а, в), 1612, 1614, 1619, 1621
(в задачах 1521, 1529, 1536, 1599, 1600 дать
геометрическую интерпретацию).
Дома: ОЛ-8, гл. 6, § 4: 6.328, 6.336, 6.341, 6.347,
6.386, 6.394, 6.400, 6.403, 6.464 (а), 6.365 (б), 6.366
(б, в), 6.368, 6.371 (в задачах 6.336, 6.338, 6.341,
6.399, 6.347 дать геометрическую интерпретацию)
или
ОЛ-9, гл.5, § 2, 4–6: 1522, 1527, 1537, 1539, 1541,
1589, 1591, 1593, 1601, 1602, 1610 (в), 1611 (б),
1613, 1618, 1620 (в задачах 1527, 1537, 1541, 1601
дать геометрическую интерпретацию).
Занятие 9. Вычисление площади плоской
фигуры в декартовой и полярной системах
координат.
Ауд.: ОЛ-8, гл. 6, § 6: 6.453, 6.456, 6.467, 6.478,
6.479, 6.483, 6.486, 6.488 или
ОЛ-9, гл. 5, § 7: 1623, 1624, 1633, 1638, 1650,
1655, 1658, 1663.
Дома: ОЛ-8, гл. 6, § 6: 6.457, 6.464, 6.468, 6.480,
6.481, 6.484, 6.487, 6.492 или
ОЛ-9, гл. 5, § 7: 1626, 1634, 1636, 1645, 1653,
1656, 1657, 1661.
Занятия 10-11. Исследование несобственных
интегралов на сходимость. Вычисление объёмов
тел
по
площадям
поперечных
сечений,
вычисление объёмов тел вращения. Приложения
определённого интеграла в физике.
Ауд.: ОЛ-8, гл. 6, § 5, 6: 6.411, 6.417, 6.419, 6.424,
6.433, 6.435, 6.437, 6.441, 6.426, 6.428, 6.430,
6.432, 6.443, 6.445, 6.447, 6.449, 6.451, 6.533,
6.535, 6.536, 6.538, 6.540, 6.541, 6.543, 6.560,
6.573, 6.581 или
ОЛ-9, гл.5, § 3, 9: 1551, 1552, 1555, 1556, 1560,
1562, 1546, 1549, 1550, 1558, 1559, 1570, 1573,
1571, 1707, 1708, 1688, 1691, 1692, 1694, 1701 (в),
1702, 1703.
Дома: ОЛ-, гл. 6, § 5, 6: 6.412, 6.418, 6.420, 6.434,
6.436, 6.439, 6.429, 6.431, 6.442, 6.444 6.446, 6.448,
6.534, 6.537, 6.542, 6.544, 6.561, 6.574, 6.582 или
ОЛ-9, гл. 5, § 3, 9: 1554, 1559, 1563, 1565, 1547,
1557, 1566, 1567, 1572, 1646, 1683, 1691 (а), 1697,
1709, 1689, 1695, 1697, 1701 (б) 1704.
Занятия 12-13. Вычисление длины дуги и
площади поверхности вращения.
Ауд.: ОЛ-8, гл. 6, § 6: 6.494, 6.500, 6.506, 6.507,
6.509, 6.519 (а), 6.523 (б), 6.527, 6.530 или
ОЛ-9, гл.5, § 8, 10: 1665, 1667, 1669, 1676, 1680,
1715, 1722 (б), 1723 (в), 1725.
Дома: ОЛ-8, гл. 6, § 6: 6.499, 6.504, 6.511, 6.519
(б), 6.523 (а), 6.526, 6.529, 6.531 или
ОЛ-9 гл. 5 § 8, 10: 1666 1670, 1678, 1679, 1716,
1722(а), 1723(б), 1726.
Занятие 14. Контроль по модулю 1 (РК №1).
Модуль 2: Функции многих переменных
Лекции
Лекции 13-14. Функции нескольких переменных
ОЛ-3 гл. 8, §1-4, ОЛ-5 гл.8 §1-3, 11, 12, ОЛ-12
гл.1.
как отображения R  R . Скалярные и
векторные функции. График функции нескольких
переменных. Примеры функций нескольких
переменных и их геометрическое представление.
Линии и поверхности уровня. Окрестности,
n
m
Лекция 15. Частные производные и частные
дифференциалы скалярной функции нескольких
переменных и их геометрическая интерпретация.
Понятие
дифференцируемости
функции.
Необходимые
и
достаточные
условия
дифференцируемости.
ОЛ-3 гл. 8, §5, 6, ОЛ-5 гл.8 §4, 5, ОЛ-12 гл.2.
n
открытые и замкнутые множества в R . Линейно
связные
множества,
области.
Предел
и
непрерывность функции нескольких переменных.
Свойства
функций,
непрерывных
на
ограниченном и замкнутом множестве Rn.
40
Лекция
16.
Частные
производные
и
дифференциалы высших порядков скалярной
функции.
Матрица
Гессе.
Теорема
о
независимости смешанной производной от
последовательности
выполнения
дифференцирования.
ОЛ-3 гл. 8, §5, 6, ОЛ-5 гл.8 §4, 5, ОЛ-12 гл. 3.
непрерывно
дифференцируемой
функции.
Примеры для функции двух переменных.
ОЛ-3 гл. 8, § 17; ОЛ-5 гл.8 §16-18, ОЛ-12 гл. 6.
Лекция 21. Условный экстремум скалярной
функции двух переменных. Функция Лагранжа.
Необходимое
и
достаточное
условия
существования
условного
экстремума.
Нахождение наибольшего и наименьшего
значений функции двух переменных в замкнутой
области.
Обобщение
теории
условного
экстремума на скалярные функции
n
переменных.
ОЛ-3 гл. 8, § 18; ОЛ-5 гл.8 §19 ОЛ-12 гл.7.
Лекция 17. Полный дифференциал. Необходимые
и
достаточные
условия,
при
которых
дифференциальная форма является полным
дифференциалом. Дифференцируемость сложной
функции. Инвариантность формы первого
дифференциала.
Дифференциалы высших
порядков.
ОЛ-3 гл. 8, §7-10; ОЛ-5 гл.8 §6-9, ОЛ-12 гл.2.6,
2.7.
Лекция
22.
Частные
производные
и
дифференцируемость векторной функции, ее
полный дифференциал и матрица Якоби.
Дифференцируемость
сложной
векторной
функции. Теорема о неявной функции для
векторных функций многих переменных. Теорема
о существовании
и дифференцируемости
обратной для векторной функции.
ОЛ-12 гл. 1, 2, 4.
Лекции 18-19. Неявно заданные функции.
Теорема
о
существовании
и
дифференцируемости неявно заданной функции.
Производная по направлению скалярной функции
нескольких переменных. Градиент функции и его
свойства. Уравнения касательной и нормали к
линии уровня для функции двух переменных.
Касательная плоскость и нормаль к поверхности.
Формула Тейлора для функции двух и
n
переменных.
ОЛ-3 гл. 8, §10, 11, 14, 15, 17; ОЛ-5 гл.8 §7, 8, 9,
13 -16, ОЛ-12 гл. 4, 5, 3.4.
Лекции 23-24. Определенные интегралы,
зависящие от параметра. Дифференцирование и
интегрирование интегралов по параметру.
Равномерная сходимость несобственных
интегралов. Признаки равномерной сходимости
несобственных интегралов. Непрерывность и
дифференцируемость несобственных интегралов
по параметру. Интегрирование несобственных
интегралов по параметру.
ОЛ-1 гл. 8.
Лекция 20. Локальный экстремум скалярной
функции нескольких переменных. Необходимое
условие локального экстремума непрерывно
дифференцируемой
функции.
Достаточное
условие
локального
экстремума
дважды
Упражнения
Занятия 15-16. Область определения ФНП.
Линии и поверхности уровня. Предел и
непрерывность ФНП. Частные производные
первого порядка.
Ауд. ОЛ-8 гл.7: 7.6 7.8 7.10 7.19 7.21 (в этих
задачах также построить линии и поверхности
уровня); 7.12 7.14 7.15 7.18 7.32 7.35 7.38 7.39
7.41 7.43 7.44 7.46 7.50 7.52; 7.55 7.57 7.61
7.63 (только производные 1-го порядка) или:
ОЛ-10: 1792(в) 1793(г) 1795(а) 1796(в) 1797(б,
в) 1799(в) 1803 1805 1807 1812
Дома. ОЛ-8 гл.7:
7.7 7.9 7.13 7.20 (в этих
задачах также построить линии и поверхности
уровня) 7.33 7.34 7.45 7.47 7.51; 7.56 7.58 7.60
7.62 7.64 (только производные 1-го порядка) или:
ОЛ-10: 1792(е, и) 1793(б, в) 1794(г, ж) 1796(а, б)
1797(г, е) 1799(б) 1804 1806 1810 1813
Ауд. ОЛ-8 гл.7: 7.65 7.66 7.70 7.87 7.89
7.103 7.105 или: ОЛ-10: 1892 1894 1897
1838 1844 1917 1925
Дома. ОЛ-8 гл.7: 7.67 7.68 7.71 7.88 7.90
7.102 7.107 или: ОЛ-10: 1891 1893 1898
1840 1845 1016 1925
7.91
1834
7.92
1838
Занятия 18-19. Восстановление функции по ее
полному дифференциалу. Производная сложной и
неявной функции.
Ауд. ОЛ-9 гл.9: 9.98 - 9.104 (четн.), ОЛ-8 гл. 7:
7.114 7.119 7.122 7.129 7.135 7.141 7.145 7.149
7.150 7.157 7.161 или: ОЛ-10: 1926 1928 1930
2803 2806 1856 1861 1864 1865 1870 1944
1946 1948 1950 1955
Дома. ОЛ-9 гл.9: 9.99 - 9.105 (неч.), ОЛ-8 гл. 7:
7.116 7.118 7.123 7.130 7.136 7.140 7.146 7.150
7.151 7.158 7.160 или:
ОЛ-10:
1927 1929 1931 2802 2804
1857 1862 1863 1871 1943 1947 1949
Занятие 17. Частные производные высших
порядков. Дифференциалы первого и второго
порядков ФНП.
41
Занятия 20-21. Производная по направлению и
градиент ФМП. Касательная плоскость и нормаль
к поверхности. Экстремум ФМП.
Ауд. ОЛ-8 гл. 7: 7.229(а) 7.233(а) 7.232 7.234
7.239(а) 7.187-7.195 (неч.), ОЛ-9 гл.10: 10.3110.43 (неч.) или:
ОЛ-10: 1876 1878
1882(а) 1886 1889 1981(а) 1982 1985 1986
2008 2010 2012 2016 2016.1 (1999 2001 2003)
Дома. ОЛ-8 гл. 7: 7.229(б) 7.233(б, в) 7.235
7.239(б) 7.188-7.194(четн.) (7.179 7.183 7.184),
ОЛ-9 гл. 10:10.32-10.44 (четн.) или:
ОЛ10:
1877 1879 1882(б) 1883 1888 1981(б)
1984 1987 1990 2009 2011 2014 2016.2 (1997
2002 2004)
Занятие 22. Условный экстремум ФМП.
Ауд. ОЛ-10: 2021-2024 2031 или
ОЛ-8 гл. 7: 7.201-7.205 7.214.
Дома. ОЛ-8 гл. 7: 7.206-7.209, 7.213.
Занятие 23-24. Интегралы с параметрами.
Ауд. ОЛ-1 гл. 8: 8.1 (а, б) 8.3 (а, б) 8.4 8.6 (а)
8.7
Дома. ОЛ-1 гл. 8: 8.1 (в) 8.3 (в) 8.5 8.6 (б) 8.8
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, выполнении домашних заданий,
подготовке к контрольным работам и рубежным контролям.
Контрольные мероприятия и сроки их проведения
Модуль 1.
1. ДЗ №1 «Определённый интеграл и его приложения»
Срок выдачи 5 неделя, срок сдачи – 10 неделя
2. КР №1 «Техника интегрирования»
Срок проведения - 6 неделя
3. Контроль по модулю №1 (РК №1) «Определённый интеграл и его приложения».
Срок проведения – 10 неделя
Модуль 2.
1. Контроль по модулю №2 (РК №2) «Функции многих переменных».
Срок проведения – 15 неделя
Литература
Основная литература (ОЛ)
1.
2.
3.
4.
5.
6.
7.
8.
Зарубин В.С., Иванова Е.Е., Кувыркин Г.Н. Интегральное исчисление функций одного переменного: Учеб. для
вузов / Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. – 528 с. (Сер.
Математика в техническом университете, вып. VI).
Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 1. – М.: Интеграл-Пресс, 2006. –
416 с.
Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 2. – М.: Интеграл-Пресс, 2006. –
544 с.
Бугров Я.С., Никольский С.М. Высшая математика. Т. 2. Дифференциальное и интегральное исчисление. – М.:
Дрофа, 2003. – 512 с.
Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа: Учеб.
пособие для втузов / Под ред. А.В. Ефимова, Б.П. Демидовича. – М.: Наука, 1993. – 478 с.
Канатников А.Н., Крищенко А.П., Четвериков В.Н. Дифференциальное исчисление функций многих переменных.
– М.: Изд-во МГТУ им. Н.Э. Баумана, 2000. – 456 с.
Сборник задач по математике для втузов. Ч. 2. Специальные разделы математического анализа: Учеб. пособие для
втузов / Под ред. А.В. Ефимова и Б.П. Демидовича. – М.: Наука, 1986. – 368 с.
Задачи и упражнения по математическому анализу для втузов / Под ред. Б.П. Демидовича. – М.: Интеграл-Пресс,
1997. – 416 с.
Дополнительная литература (ДЛ)
1.
2.
Вся высшая математика: Учебник для втузов: В 6 т. / Краснов М.Л., Киселев А.И., Макаренко и др. – Т. 2. – М.:
Эдиториал УРСС, 2000. – 184 с.
Вся высшая математика: Учебник для втузов: В 6 т. / Краснов М.Л., Киселев А.И., Соболев С. К. и др. – Т. 3. – М.:
Эдиториал УРСС, 2001. – 237с.
42
1.
2.
3.
4.
5.
6.
1.
2.
3.
Методические пособия
Ахметова Ф.Б., Добрица Б.Т., Сырцов А.В. Неопределенный интеграл. – М.: МГТУ, 2008.
Галкин С.В. Интегральное исчисление и дифференциальные уравнения. – М.: Изд-во МГТУ, 2007. – 160 с.
Добрица Б.Т., Роткова О.В., Шахов Е.М. Неопределенный интеграл. – М.: МГТУ, 1988.
Копаев А.В., Маркелов Г.Е., Тесалина А.А. Определенный интеграл. Методические указания для выполнения
домашнего задания. – М.: Изд-во МГТУ, 2002. – 69 с.
Минеева О.М., Неклюдов А.В., Скуднева О.В. Несобственные интегралы. Методические указания для выполнения
домашнего задания. – М.: Изд-во МГТУ, 2003. – 41 с.
Ковалев Я.Г., Киреева Ю.Г., Лунева М.С., Тесалина А.А. Определенный интеграл. Методические указания для
выполнения домашнего задания. – М.: МВТУ, 1987.
Рекомендуемые интернет-сайты:
Иванков П.Л. Конспект лекций по интегралам и дифференциальным уравнениям. http://mathmod.bmstu.ru
http://www.mathelp.spb.ru - лекции по высшей математике.
http://www.BauMO.narod.ru/MA2.pdf - конспект лекций по интегралам и функциям многих переменных.
ЛИНЕЙНАЯ АЛГЕБРА И ГЕОМЕТРИЯ для специальности ИУ9
ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
для ИУ9
Литература
Основная литература (ОЛ)
Канатников А.Н., Крищенко А.П. Линейная алгебра: М.: Изд. МГТУ им. Н.Э. Баумана, 2002. 335 с.
Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа / Под
ред. А.В. Ефимова, Б.П. Демидовича. М.: Наука, 1993. 478 с.
Сборник задач по алгебре / Под ред. Кострикина А.И. М.: Наука, 1987. 352 с.
Александров П.С. Курс аналитической геометрии и линейной алгебры: М.: Наука, 1979. 512 с.
Кострикин А.И. Введение в алгебру, часть II. М.: Физматлит, 2004.
Дополнительная литература (ДЛ)
Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. М.: Наука, 1987. 336 с.
Винберг Э.Б. Курс алгебры. М.: Факториал, 1999. 528 с.
Моденов П.С., Пархоменко А.С. Сборник задач по аналитической геометрии. Москва-Ижевск, Регулярная
и хаотическая динамика, 2002. 384 с.
Проскуряков И.В. Сборник задач по линейной алгебре. М.: Наука, 2006. 384 с.
Гельфанд И.М. Лекции по линейной алгебре. М.: Наука, 1966. 280 с.
Лекции
Модуль 1. Линейные пространства. Линейные функции
Лекция 1. Линейные пространства и линейные подпространства. Примеры. Линейная зависимость, базис
(повторение). Преобразование координат. Свойства матриц перехода.
ОЛ-1, п. 1; ДЛ-1, гл. VI, §1, ДЛ-2, гл. 2, §2.
Лекция 2. Сумма и пересечение подпространств. Прямая сумма. Формула Грассмана.
ОЛ-1, п. 2; ДЛ-1, гл. VI, §2, ДЛ-2, гл. 5, §1.
Лекция 3. Линейные функции. Сопряженное пространство. Сопряженный (двойственный) базис,
преобразование координат двойственного базиса. Изоморфизмы
линейные функции.
ОЛ-1, п. 10.1, ДЛ-1, гл. VI, §5, ДЛ-2, гл. 5, §2.
43
V  V * и V  V ** . Подпространства и
Модуль 2. Евклидовы пространства. Билинейные и квадратичные функции
Лекция 4. Евклидовы пространства. Неравенство Коши — Буняковского. Матрица Грама. Ортогональный
базис. Ортогонализация Грама — Шмидта. Ортогональные матрицы. Теорема о QR -разложении.
ОЛ-1, пп. 3.1—3.8, 11.2; ДЛ-1, гл. VII, §1, ДЛ-2, гл. 5, §4.
Лекция 5. Ортогональное дополнение. Теорема об ортогональном разложении. Теорема Пифагора. Угол и
расстояние между вектором и подпространством. Изоморфизм линейных пространств
евклидовых пространств.
V и V * в случае
ОЛ-1, п. 3.9; ДЛ-1, гл. VII, §1, ДЛ-2, гл. 5, §4.
Лекция 6. Билинейные функции. Связь между матрицами билинейной функции в разных базисах. Ранг
билинейной функции. Симметрические билинейные функции. Теорема о том, что для произвольной
симметрической билинейной функции существует базис пространства, в котором матрица функции диагональна.
ОЛ-1, пп. Д.8.1; ДЛ-1, гл. VI, §6.1, ДЛ-2, гл. 5, §3.
Лекция 7. Квадратичные формы. Процедура поляризации. Приведение квадратичной формы к сумме
квадратов. Канонический вид. Метод Лагранжа. Формула Якоби.. Нормальный вид над R и над
. Закон
инерции.
ОЛ-1, пп. 8.1-8.5; ДЛ-1, гл. VI, §6.2-6.3, ДЛ-2, гл. 5, §3.
Лекция 8. Положительно определенная квадратичная форма. Критерий Сильвестра. Следствие для матрицы
Грама. Полуторалинейные функции, эрмитовы квадратичные формы. Унитарные пространства. Вывод свойств,
аналогичных свойствам евклидова пространства.
ОЛ-1, пп. 8.6; ДЛ-1, гл. VI, §6.3-6.4, гл. VII, §4.1-4.2, ДЛ-2, гл. 5, §3-5.
Модуль 3. Линейные операторы
Лекция 9. Линейные отображения. Их матрицы при замене базиса. Инвариантность ранга. Теорема о
dim Ker  + dim Im  = dim V . Линейные операторы и их матрицы. Ранг и определитель линейного
оператора. Алгебра линейных операторов. Изоморфизм End V  Mn (F) . Многочлены от линейных
операторов.
ОЛ-1, п. 4; ДЛ-1, гл. VI, §3, ДЛ-2, гл. 6, §1.
Лекция 10. Вид матрицы линейного оператора при наличии инвариантных подпространств. Собственные
векторы и значения. Корректность определения характеристического многочлена. Линейная независимость
собственных векторов, отвечающих различным собственным значениям. Инвариантные подпространства
линейного оператора над R и над .
ОЛ-1, п. 5; ДЛ-1, гл. VI, §4.1-4.5, ДЛ-2, гл. 6, §2.
Лекция 11. Собственные подпространства. Критерий существования базиса из собственных векторов
линейного оператора. Существование базиса, в котором матрица линейного оператора A конечномерного
линейного пространства V над алгебраически замкнутым полем F треугольна. Теорема Гамильтона-Кэли.
ДЛ-1, гл. VI, §4.6-4.9, §7.1 , ДЛ-2, гл. 6, §2.
Лекция 12. Аннулирующие многочлены. Минимальный многочлен и его свойства. Жордановы клетки и
матрицы, их характеристические и минимальные многочлены. Существование жорданова базиса.
ОЛ-1, пп. Д.5.1; ДЛ-1, гл. VI, §7.2-7.5, ДЛ-2, гл. 6, §4-5.
Лекция 13. Единственность жордановой нормальной формы. Корневые подпространства. Значение
многочлена от жордановой клетки. Вычисление функции от матрицы (без доказательства).
ОЛ-1, пп. Д.5.1; ДЛ-1, гл. VI, §7.2-7.5, ДЛ-2, гл. 6, §4-5.
Лекция 14. Связь между линейным оператором и билинейной функцией в евклидовом пространстве.
Сопряженный соператор. Симметрический оператор. Канонический вид симметрического оператора.
ОЛ-1, п. 6; ДЛ-1, гл. VII, §2.1-2.2, §3.2-3.3, ДЛ-2, гл. 6, §3.
Лекция 15. Ортогональный оператор. Канонический вид ортогонального оператора. Приведение
квадратичной формы к главным осям в евклидовом пространстве. Одновременное приведение пары квадратичных
форм к сумме квадратов. Полярное разложение невырожденного линейного оператора евклидова пространства.
Приведение эрмитова и унитарного оператора к каноническому виду в унитарном пространстве.
44
ОЛ-1, п. 7.1-7.3; ДЛ-1, гл. VII, §2.4-2.6, §3.3, §4, ДЛ-2, гл. 6, §3.
Модуль 4. Аффинные и проективные пространства. Тензоры
Лекция 16. Аффинные пространства. Примеры. Изоморфизм аффинных пространств одной размерности.
Аффинная система координат. Аффинные подпространства, их взаимное расположение. Задание аффинного
подпространства как множества решений СЛАУ.
ДЛ-1, гл. VIII, §1, ДЛ-2, гл. 7, §1.
Лекция 17. Геометрически независимые системы точек. Барицентрические координаты. Симплексы.
Выпуклые множества.
ДЛ-2, гл. 7, §1-2.
Лекция 18. Аффинное отображение. Его матрица, изменение матрицы при переходе к новой системе
координат. Действие аффинного преобразования на n+1 точке. Аффинная группа и ее подгруппы.
ДЛ-1, гл. IV, §1-3, ДЛ-2, гл. 7, §3.
Лекция 19. Аффинное евклидово пространство, расстояние между двумя аффинными подпространствами.
Движения и аффинные ортогональные операторы.
ДЛ-2, гл. 7, §3.
Лекция 20. Разложение движения аффинного евклидова пространства в произведение движения с
неподвижной точкой и сдвига. Следствия для двумерного и трехмерного аффинного евклидова пространства.
ДЛ-1, гл. IV, §3, ДЛ-2, гл. 7, §3.
Лекция 21. Аффинно-квадратичные функции, их матрицы, изменение при замене координат. Условие
центральности аффинно-квадратичной функции. Приведение аффинно-квадратичной функции к нормальному
виду.
ДЛ-2, гл. 7, §4.
Лекция 22. Приведение аффинно-квадратичной функции к главным осям. Аффинные квадрики. Аффинная
классификация квадрик. Ортогональная классификация квадрик. Эквивалентность относительно группы
преобразований. Строение аффинного преобразования плоскости и пространства.
ОЛ-1, п. 9, ДЛ-1, гл. VIII, §1,
ДЛ-2, гл. 7, §4.
Лекция 23. Модели проективной плоскости. Проективная система координат. Принцип двойственности.
Теорема Дезарга.
ДЛ-2, гл. 7, §5.
Лекция 24. Проективные преобразования проективной плоскости. Действие проективного оператора на
четырех точках. Кривые второго порядка на проективной плоскости.
ДЛ-2, гл. 7, §5.
Лекция 25. Полилинейные функции. Изменение коэффициентов полилинейной функции при переходе к
другому базису. Определение тензора. Примеры. Размерность пространства тензоров типа (p,q) .
ОЛ-1, п. 10.2-10.4, ДЛ-1, гл. IX, §1.1-1.4, ДЛ-2, гл. 9, §1-3.
Лекция 26. Операция тензорного произведения и его свойства. Тензорная алгебра векторного пространства.
Симметрические тензоры. Операция симметрирования. Кососимметрические тензоры. Операция альтернирования.
ОЛ-1, п. 10.4, , ДЛ-1, гл. IX, §1.5-1.10, ДЛ-2, гл. 9, §1-3.
Лекция 27. Другие операции над тензорами.
ОЛ-1, п. 10.4, , ДЛ-1, гл. IX, §2, ДЛ-2, гл. 9, §1-3.
Лекции 28–29. Резерв.
Практические занятия
Модуль 1. Линейные пространства. Линейные функции
Занятие 1. Линейные пространства. Размерность. Базис. Переход к новому базису.
Ауд.: ОЛ-2 №№ 4.1-9(неч), 10, 15, 17, ОЛ-3 №№ 1.1.3(а,в), 1.1.4(а).
45
Дома: ОЛ-2 №№ 4.2, 4, 6, 8, 16, 18,ОЛ-3 №№ 1.1.5
Занятие 2. Линейные пространства (продолжение). Линейные подпространства. Ранг системы векторов.
Ауд.: ОЛ-2 №№ 4.23, 24, 28, 30, 37, 21, 45, 47, 49.
Дома: ОЛ-2 №№ 4.25, 31, 46, 47(до конца), 48, 50.
Занятие 3. Линейные подпространства (продолжение). Линейная оболочка системы векторов. Описания
подпространств.
Ауд.: ОЛ-2 №№ 4.51, 52; ОЛ-3 №№ 1.2.10(а,б,в); разработка кафедры.
Дома: ОЛ-2 №№ 4.53, 54; ОЛ-3 №№ 1.2.13, 1.2.10(г,д); разработка кафедры
Занятие 4. Сумма и пересечение подпространств. Прямая сумма.
Ауд.: ОЛ-3 №№ 1.2.14, 1.2.19, 1.2.18; разработка кафедры
Дома: разработка кафедры.
Занятие 5. Сопряженное пространство.
Ауд.: разработка кафедры.
Дома: разработка кафедры.
Модуль 2. Евклидовы пространства. Билинейные и квадратичные функции
Занятие 6. Евклидовы пространства. Процесс ортогонализации.
Ауд.: ОЛ-2 №№ 4.63(а), 67, 69, (71), 73, (75); ОЛ-3 № 4.1.31; ОЛ-1 № 3.5.
Дома: ОЛ-2 №№ 4.63(б), 64(б), 70, 74.
Занятие 7. Ортогональное дополнение.
Ауд.: ОЛ-2 №№ 4.79; разработка кафедры.
Дома: разработка кафедры
Занятия 8–9. Билинейные функции. Квадратичные формы. Критерий Сильвестра. Метод Лагранжа.
Полуторалинейные функции.
Ауд.: ОЛ-2 №№ 4.204, 218, 220, 221, 210, 212; разработка кафедры.
Дома: ОЛ-2 №№ 4.222, 223, 224,211, 212; разработка кафедры.
Модуль 3. Линейные операторы
Занятие 10. Линейные операторы и их матрицы. Преобразование матрицы линейного
переходе к новому базису.
оператора при
Ауд.: ОЛ-2 №№ 4.83, 85, 87, 89, 91, 93, 97, 113, 106(а).
Дома: ОЛ-2 №№ 4. 84, 86, 90, 95, 97, 106(б), 108, 112; разработка кафедры.
Занятие 11. Собственные значения и собственные векторы. Приведение матрицы линейного оператора к
диагональному виду.
Ауд.: ОЛ-2 №№ 4.135, (137, 139, 141, 143), 4.176, 179, 180(б); ОЛ-3 №№ 3.2.16(б).
Дома: ОЛ-2 №№ 4.136, 139, (134, 138, 140, 142), 148, 172, 175, 180(а).
Занятие 12. Инвариантные подпространства. След. Подобие матриц.
Ауд.: ОЛ-3 №№ 3.2.27, 3.2.29; разработка кафедры.
Дома: ОЛ-3 №№ 3.2.28, 3.2.22, 3.2.30; разработка кафедры.
Занятия 13-15. Нахождение жордановой нормальной формы. Нахождение жорданова базиса. Функции от
матриц. Аннулирующие и минимальные многочлены.
Ауд.: ОЛ-3 №№ 3.3.1(б,д), 3.3.3, 3.3.19(а), 3.3.7, 3.3.43, 3.3.45, 3.3.21, 3.3.22, 3.3.24(а), 3.3.26.
46
Дома: ОЛ-3 №№ 3.3.1(б,в), 3.3.3(б)*, № 3.3.1(в) — найти жорданов базис, 3.3.10(а), 3.3.19(б),
3.3.43(а), 3.3.27,3.3.30, 3.3.24.
Занятия 16-17. Самосопряженные и ортогональные операторы. Диагонализация симметрических матриц
ортогональным преобразованием. Приведение матрицы ортогонального оператора к каноническому виду.
Проекторы.
Ауд.: ОЛ-2 №№ 4.151, 168(а, б)+171, 170, 191, 183; ОЛ-3 №№ 4.4.5(а, б);
Дома: ОЛ-2 №№ 4.152, 168(в)+171, 184, 186; ОЛ-3 №№ 4.4.5(в), 4.3.3; разработка кафедры.
Модуль 4. Аффинные и проективные пространства. Тензоры
Занятия 18-19. Аффинные пространства. Способы задания плоскостей. Взаимное расположение плоскостей.
Евклидовы пространства.
Ауд.: ОЛ-3 №№ № 6.1.10(а), 6.1.16(б), 6.1.20(а), 6.3.6(а); ДЛ-4 №№ 1877, 1887, 1337, 1339
(формулировка), 1340, 1374;
Дома: ОЛ-3 №№ 6.1.10(б), 6.1.16(а, в), 6.3.7(а); ДЛ-4 №№ 1338, 1339(доказать), 1341, 1885.
Занятие 20. Аффинные преобразования.
Ауд.: ОЛ-3 №№ 6.1.30, 6.1.31(а), 6.1.33(а), 6.1.28*; ДЛ-3 №№ 1157, 1176.
Дома: ОЛ-3 №№ 6.1.31(б), 6.1.33(б); ДЛ-3 №№ 1156, 1160, 1182.
Занятие 21. Ортогональные преобразования квадратичных форм. Приведение кривых и поверхностей 2-го
порядка к каноническому виду.
Ауд.: ОЛ-2 №№ 4.214, 216, 226, 228, 231, (235, 237, 234).
Дома: ОЛ-2 №№ 4.213, 215, 227, 229, 230, (233, 236).
Занятия 22-23. Проективное пространство. Проективные преобразования.
Ауд.: ОЛ-3 №№ 6.5.1(а), 6.5.3(а); ДЛ-3 №№ 1310, 1307, 1397, 1389, 1392.
Дома: ОЛ-3 №№ 6.5.1(б), 6.5.3(б); ДЛ-3 №№ 1310, 1307, 1397, 1389, 1392.
Занятия 24-25. Определение тензоров. Операции над тензорами. Матричная запись тензоров.
Ауд.: разработка кафедры.
Дома: разработка кафедры.
Занятия 26-28. Резерв.
Вопросы для подготовки к экзамену
Модуль 1. Линейные пространства. Линейные функции
1. Линейные (векторные) пространства. Базис. Матрица перехода. Изменение координат
вектора при переходе от базиса к базису.
2. Докажите, что два векторных пространства V и W изоморфны тогда и только тогда, когда
dim V = dim W .
3. Линейные подпространства. Сумма и пересечение подпространств. Формула Грассмана.
4. Когда сумма V1 +V2 +...+Vm подпространств линейного пространства V является прямой?
5. Линейные функции. Сопряженное пространство. Для любого конечномерного пространства
V имеем dim V = dim V* .
6. Пусть даны два базиса E и F линейного пространства V , T — матрица перехода от E к F .
Рассмотрим двойственные базисы E и F . Какова матрица перехода от F к E ?
7. Всякое подпространство есть пересечение ядер некоторого множества линейных функций.
47
Модуль 2. Евклидовы пространства. Билинейные и квадратичные функции
8. Евклидово пространство. Неравенство Коши — Буняковского. Свойство углов и длин в
евклидовом пространстве.
9. Расскажите о матрице Грама и ее свойствах.
10. Докажите линейную независимость системы ненулевых ортогональных векторов. Как
вычисляется скалярное произведение в ортонормированном базисе? Опишите процесс
ортогонализации Грама — Шмидта.
11. Ортогональные матрицы как матрицы перехода от одного ортонормированного базиса к
другому. Группа O(n) .
12. Обосновать QR -разложение.
13. Доказать, что V=U  U  , в частности, U U  = 0 и dim U  = n - dim U , где n = dim V .
14. Вывести свойства операции взятия ортогонального дополнения.
15. Теорема Пифагора. Угол и расстояние между вектором и подпространством.
16. Изоморфизм линейных пространств V и V * в случае евклидовых пространств.
17. Пусть  - билинейная функция на линейном пространстве V , B и B ' - ее матрицы в
базисах E и E ' , соответственно. Какова связь этих матриц?
18. Докажите, что ранг билинейной функции не зависит от выбора базиса.
19. Для произвольной симметрической билинейной функции существует базис пространства, в
котором матрица функции диагональна.
20. Любая квадратичная форма линейной заменой переменных приводится к виду, в котором
ненулевые коэффициенты имеют лишь квадраты переменных.
21. Опишите процедуру поляризации.
22. Опишите алгоритм Лагранжа.
23. Докажите формулу Якоби.
24. К какому виду приводится любая квадратичная форма невырожденным линейным
преобразованием над полем комплексных и действительных чисел?
25. Докажите закон инерции.
26. Докажите критерий Сильвестра.
27. Определение полуторалинейных функций, эрмитовых квадратичных форм, унитарного
пространства и вывод свойств, аналогичных
свойствам евклидова пространства.
28. Совокупность U (n) унитарных матриц порядка n - группа.
Модуль 3: Линейные операторы
29. Линейные отображения, матрицы, замена базисов, инвариантность ранга.
30. dim Ker  + dim Im  = dim V .
31. Изменение матрицы линейного оператора при переходе к новому базису. Ранг и
определитель линейного оператора.
48
32. Алгебра линейных операторов. Изоморфизм End V  Mn (F) для линейного пространства
V над полем F размерности n , dim End V = (dim V)2 .
33. Вид матрицы линейного оператора при наличии инвариантных подпространств.
34. Докажите, что определение характеристического многочлена корректно, то есть не зависит
от выбора базиса.
35. Собственные векторы и значения. Число   F является собственным для линейного
оператора A: V  V тогда и только тогда, когда  - корень характеристического многочлена.
36. Любой линейный оператор над полем действительных чисел обладает одномерным или
двумерным инвариантным подпространством.
37. Собственные подпространства. Если k - кратность собственного значения  линейного
оператора A , то dimV  k .
38. Докажите, что система собственных векторов линейного оператора, отвечающих попарно
различным собственным значениям, линейно независима.
39. Критерий существования базиса из собственных векторов линейного оператора.
40. Пусть A: V  V - линейный оператор конечномерного линейного пространства V над
алгебраически замкнутым полем F . Тогда существует базис, в котором матрица линейного
оператора A треугольна.
41. Теорема Гамильтона — Кэли.
42. Минимальный многочлен и его свойства.
43. Линейный оператор A: V  V линейного пространства V над алгебраически замкнутым
полем F диагонализируем тогда и только тогда, когда его минимальный многочлен не имеет
кратных корней.
44. Жордановы клетки и матрицы, их характеристические и минимальные многочлены.
Жорданов базис.
45. Пусть
— линейный оператор линейного пространства V над алгебраически
замкнутым полем F . Тогда в V имеется жорданов базис для A .
46. Единственность жордановой нормальной формы.
47. Пусть A: V  V - линейный оператор линейного пространства V над алгебраически
замкнутым полем F . Тогда V распадается в прямую сумму корневых подпространств,
соответствующих всем (различным) собственным значениям оператора A .
48. Значение многочлена от жордановой клетки. Вычисление функции от матрицы (без
доказательства).
49. Связь между линейным оператором и билинейной функцией в евклидовом пространстве.
50. В евклидовом пространстве любому линейному оператору отвечает сопряженный оператор
и притом только один. Связь операции перехода от оператора к сопряженному оператору с
операциями сложения и умножения линейных операторов.
51. Матрица симметрического и ортогонального оператора в ортонормированном базисе.
52. Пусть V - евклидово пространство, A: V  V - ортогональный или симметрический
линейный оператор линейного пространства V , U  V - A -инвариантное подпространство,
W = U  - ортогональное дополнение к U . Тогда W - A -инвариантное подпространство.
49
53. Канонический вид симметрического оператора евклидова пространства.
54. Канонический вид ортогонального оператора евклидова пространства.
55. Приведение квадратичной формы к главным осям в евклидовом пространстве.
56. Одновременное приведение пары квадратичных форм к сумме квадратов.
57. Полярное разложение невырожденного линейного оператора евклидова пространства.
58. Приведение эрмитова и унитарного оператора к каноническому виду в унитарном
пространстве.
Модуль 4. Аффинные и проективные пространства. Тензоры
59. Определение и простейшие свойства аффинных пространств.Примеры. Изоморфизм
аффинных пространств одной размерности.
60. Система координат в аффинном пространстве. Формулы перехода от одной системы к
другой.
61. Аффинные подпространства, их взаимное расположение. Размерность аффинной оболочки
двух аффинных подпространств.
62. Задание аффинного подпространства как множества решений СЛАУ.
63. Геометрически независимые системы точек. Барицентрические координаты.
64. Симплексы. Выпуклые множества.
65. Аффинное отображение. Его матрица, изменение матрицы при переходе к новой системе
координат. Действие аффинного преобразования на n+1 точке.
66. Аффинная группа и ее подгруппы.
67. Аффинное евклидово пространство, расстояние между двумя аффинными
подпространствами.
68. Движения и аффинные ортогональные операторы.
69. Разложение движения аффинного евклидова пространства в произведение движения с
неподвижной точкой и сдвига. Следствия для двумерного и трехмерного аффинного евклидова
пространства.
70. Аффинно-квадратичные функции, их матрицы, изменение при замене координат. Условие
центральности аффинно-квадратичной функции.
71. Приведение аффинно-квадратичной функции к нормальному виду и к главным осям.
72. Аффинные квадрики и их классификация.
73. Строение аффинного преобразования плоскости и пространства.
74. Модели проективной плоскости.
75. Принцип двойственности. Теорема Дезарга.
76. Проективные преобразования проективной плоскости. Действие проективного оператора на
четырех точках.
77. Кривые второго порядка на проективной плоскости.
78. Полилинейные функции. Изменение коэффициентов полилинейной функции при переходе
к другому базису.
50
79. Определение тензора. Примеры. Размерность пространства тензоров типа (p,q) .
80. Операция тензорного произведения и его свойства. Тензорная алгебра векторного
пространства.
81. Симметрические тензоры. Операция симметрирования.
82. Кососимметрические тензоры. Операция альтернирования.
83. Другие операции над тензорами.
Контрольные мероприятия
Модуль 1. Линейные пространства. Линейные функции (4 неделя, максимум 10 баллов,
минимум 5 баллов).
Рубежный контроль по модулю 1 (4 неделя).
Модуль 2. Евклидовы пространства. Билинейные и квадратичные функции (7 неделя,
максимум 12 баллов, минимум 6 баллов).
Рубежный контроль по модулю 2 (7 неделя).
Модуль 3: Линейные операторы (11 неделя, максимум 26 баллов, минимум 14 баллов)
Рубежный контроль по модулю 3 (11 неделя).
Модуль 4. Аффинные и проективные пространства. Тензоры (17 неделя, максимум
12 баллов, минимум 6 баллов).
Рубежный контроль по модулю 4 (17 неделя).
Экзамен максимум 30 баллов, минимум 15 баллов.
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
для ИУ9
Литература
Основная литература (ОЛ)
Зарубин В.С., Иванова Е.Е., Кувыркин Г.Н. Интегральное исчисление функций одного переменного: Учеб.
для вузов / Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. – 528 с. (Сер.
Математика в техническом университете, вып. VI).
Канатников А.Н., Крищенко А.П., Четвериков В.Н. Дифференциальное исчисление функций многих
переменных: Учеб. для вузов / Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана,
2000. – 456с. (Сер. Математика в техническом университете, вып. V).
Зорич В.А. Математический анализ. Ч. I. – М.: Наука, 1981. – 544с.
Иванова Е.Е. Дифференциальное исчисление функций одного переменного: Учеб. для вузов / Под ред. В.С.
Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1998. – 408с. (Сер. Математика в техническом
университете, вып. II).
Демидович Б.П. Сборник задач и упражнений по математическому анализу. – М.: Наука, 1977. – 528с.
Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа: Учеб.
пособие для втузов / Под ред. А.В. Ефремова, Б.П. Демидовича. – М.: Наука, 1993. – 478 с.
Сборник задач по математике для втузов. Ч. 2. Специальные разделы математического анализа: Учеб. пособие
для втузов / Под ред. А.В. Ефремова и Б.П. Демидовича. – М.: Наука, 1986. – 368 с.
Задачи и упражнения по математическому анализу. / И. А. Виноградова, С. Н. Олехник, В. А. Садовничий.
Под общ. ред. В. А. Садовничего. — М.: Изд-во Моск. ун-та, 1988. - 416с.
51
Задачи и упражнения по математическому анализу для втузов. / Под ред. Б.П.Демидовича. – М.: ИнтегралПресс, 1997. – 416 с.
Архипов Г.И., Садовничий В.А., Чубариков В.Н. Лекции по математическому анализу / Под ред. В.А.
Садовничего. – М.: Высш. шк., 1999. – 695с.
Дополнительная литература (ДЛ)
Вся высшая математика: Учебник для втузов: В 6 т. / Краснов М.Л., Киселев А.И., Соболев С. К. и др. – Т. 3. –
М.: Эдиториал УРСС, 2001. – 237с.
Гелбаум Б., Олмстед Дж. Контрпримеры в анализе. – М.: Мир, 1967. – 252с.
Ляшко И.И., Боярчук А.К., Гай Я.Г., Головач Г.П. Математический анализ: введение в анализ, производная
интеграл. Справочное пособие по высшей математике. Т. 1. – М.: Едиториал УРСС, 2001. – 360с.
Неструев Дж. Гладкие многообразия и наблюдаемые. – М.: МЦНМО, 2000. – 300с.
Рудин У. Основы математического анализа. – М.: Мир, 1978. – 320с.
Методические и учебные пособия (МП)
Добрица Б.Т., Роткова О.В., Шахов Е.М. Неопределенный интеграл. – М.: МГТУ, 1988.
Копаев А.В., Маркелов Г.Е., Тесалина А.А. Определенный интеграл. Методические указания для выполнения
домашнего задания. – М.: Изд-во МГТУ, 2002. – 69 с.
Минеева О.М., Неклюдов А.В., Скуднева О.В. Несобственные интегралы. Методические указания для
выполнения домашнего задания. – М.: Изд-во МГТУ, 2003. – 41 с.
Ковалев Я.Г., Киреева Ю.Г., Лунева М.С., Тесалина А.А. Определенный интеграл. Методические указания
для выполнения домашнего задания. – М.: МВТУ, 1987.
Лекции
Модуль 1. Неопределенный интеграл
Лекция 1. Первообразная и ее свойства. Неопределенный интеграл, его свойства, связь с дифференциалом.
Таблица основных неопределенных интегралов. Интегрирование подстановкой и заменой переменной.
Интегрирование по частям.
ОЛ-1, § 1.1–1.6.
Лекция 2–3. Рациональные дроби. Разложение правильной рациональной дроби в сумму простейших.
ОЛ-1, § 2.1, 2.3.
Лекция 4. Интегрирование выражений, содержащих квадратный трехчлен. Интегрирование простейших
дробей. Интегрирование рациональных функций. Интегрирование функций, рационально зависимых от
тригонометрических функций. Интегрирование иррациональных функций. Примеры интегралов, не
выражающихся через элементарные функции. Практические советы для овладения техники интегрирования.
ОЛ-1, § 2.2, 2.4, 3.1, 3.2, 3.5, 4.1, 4.2.
Модуль 2. Приложения определенного интеграла
Лекция 5. Примеры задач, приводящих к понятию определенного интеграла. Определенный интеграл как
предел по базе.
ОЛ-3, гл.6, § 1.
Лекция 6. Необходимое условие
интерпретация определенного интеграла.
интегрируемости.
Критерий
интегрируемости.
Геометрическая
ОЛ-3, гл.6, § 1.
Лекция 7–8. Основные свойства определенного интеграла: линейность и аддитивность, оценка модуля
интеграла, теорема об оценке, две теоремы о среднем значении.
ОЛ-3, гл.6, § 2.
Лекция 9. Вычисление определенного интеграла. Интеграл с переменным верхним пределом, теоремы о его
непрерывности и о его производной. Формула Ньютона — Лейбница. Вычисление определенных интегралов
52
заменой переменной (подстановкой) и по частям. Интегрирование периодических функций, интегрирование
четных и нечетных функций на отрезке, симметричном относительно начала координат.
ОЛ-3, гл.6, § 3.
Лекция 10. Геометрические приложения интеграла. Вычисление площадей плоских фигур, ограниченных
кривыми, заданными в декартовых координатах, параметрически и в полярных координатах. Вычисление объемов
тел по площадям поперечных сечений и объемов тел вращения.
ОЛ-1, § 9.1, 9.3, 9.4; ОЛ-3, гл.6, § 4.
Лекция 11. Кривые в пространстве. Векторные функции скалярного аргумента и их пределы. Кривая как
годограф векторной функции. Касательная к кривой и производная векторной функции. Достаточное условие
существования касательной. Геометрический и механический смысл производной векторной функции. Правила
дифференцирования векторных функций.
ОЛ-4, § 9.1–9.3; ОЛ-10, гл.10, § 1; ОЛ-3, гл.6, § 4.
Лекция 12–13. Длина дуги спрямляемой кривой. Достаточное условие спрямляемости кривой. Натуральная
параметризация кривой. Формулы для длины дуги плоской кривой.
ОЛ-1, § 9.2; ОЛ-10, гл.8, § 6, гл.10, § 1–2; ОЛ-3, гл.6, § 4; ДЛ-15, гл.6, п.6.35.
Лекция 14. Кривизна кривой. Формулы для вычисления в пространственном и плоском случаях. Радиус,
круг и центр кривизны. Эволюта и эвольвента. Свойства эволюты. Механический способ построения по заданной
кривой одной из ее эвольвент.
ОЛ-4, § 9.4, 9.5, дополнение 9.1.
Лекция 15. Несобственные интегралы по бесконечному промежутку (I-го рода). Несобственные интегралы
от неограниченных функций на отрезке (II-го рода). Их свойства. Несобственные интегралы с несколькими
особенностями.
ОЛ-1, § 7.1, 7.2, 7.4, 7.5, 7.9; ОЛ-3, гл.6, § 5.
Лекция 16. Признаки сходимости несобственных интегралов. Абсолютная и условная сходимости. Пример
условно сходящегося интеграла.
ОЛ-1, § 7.3, 7.6, 7.8; ОЛ-3, гл.6, § 5.
Модуль 3. Дифференциальное исчисление функций нескольких
переменных
Лекция 17. Топология в n-мерном арифметическом пространстве Rn. Евклидова норма, окрестности,
ограниченные, открытые, замкнутые и связные множества, области в Rn.
ОЛ-3, гл.7, § 1, гл.8, § 1; ОЛ-2, § 1.1.
Лекция 18. Компакты в Rn.
ОЛ-3, гл.7, § 1.
Лекция 19. Скалярные и векторные функции многих переменных. Координатные функции векторной
функции. График функции многих переменных. Линии и поверхности уровня. Последовательности в Rn и их
пределы. Критерий Коши сходимости последовательности. Определение предела функции многих переменных по
базе. Свойства предела функции.
ОЛ-3, гл.7, § 2; ОЛ-2, § 1.2, 1.3.
Лекция 20. Непрерывность функции многих переменных. Локальные свойства непрерывных функций.
Свойства функций, непрерывных на ограниченных и замкнутых подмножествах Rn. Связность образа связного
множества при непрерывном отображении.
ОЛ-3, гл.7, § 2; ОЛ-2, § 1.4, 1.5, 1.7.
Лекции 21. Дифференцируемость и дифференциал функции многих переменных. Частные производные и их
геометрическая интерпретация. Матрица Якоби.
ОЛ-3, гл.8, § 2; ОЛ-2, § 2.1–2.3, 2.7.
Лекции 22. Два необходимых и одно достаточное условия дифференцируемости.
53
ОЛ-3, гл.8, § 2; ОЛ-2, § 2.4, 2.5.
Лекция 23. Правила дифференцирования. Линейность операции дифференцирования. Правило Лейбница.
Дифференцируемость сложной функции. Цепное правило. Инвариантность формы первого дифференциала.
ОЛ-2, § 2.6.
Лекция 24. Частные производные второго порядка. Матрица Гессе. Теорема о совпадении смешанных
производных.
ОЛ-2, § 3.1.
Лекция 25. Производные и дифференциалы высших порядков. Формула Тейлора. Остаточные члены в
форме Лагранжа и Пеано. Линейное приближение функции и формула конечных приращений.
ОЛ-2, § 3.2–3.5.
Лекция 26. Геометрические приложения. Производная по направлению. Градиент и его свойства.
Касательная плоскость и нормаль к поверхности. Достаточное условие их существования. Геометрическая
интерпретация дифференциал функции двух переменных.
ОЛ-2, § 5.1–5.3.
Лекция 27. Неявно заданные функции. Теорема о существовании и дифференцируемости неявно заданных
функций.
ОЛ-2, § 4.1, 4.2.
Модуль 4. Безусловные и условные экстремумы
Лекция 28. Локальный экстремум функции многих переменных. Необходимые и достаточные условия
локального экстремума.
ОЛ-2, § 6.1–6.4.
Лекция 29–30. Условный экстремум скалярной функции многих переменных. Метод множителей Лагранжа.
Необходимые и достаточные условия для условного экстремума. Нахождение наибольшего и наименьшего
значений функции многих переменных в замкнутой области.
ОЛ-2, § 7.1–7.4.
Лекция 31. Теорема о существовании и дифференцируемости обратного отображения (существовании
диффеоморфизма). Вывод теоремы о неявных функциях из теоремы об обратном отображении.
ОЛ-2, § 4.3.
Лекция 32. Резервная.
Практические занятия
Модуль 1. Неопределенный интеграл
Занятие 1. Интегрирование по таблице, подведением под знак дифференциала и по частям.
Ауд.: ОЛ-8, стр. 178–181: 3, 13, 29, 27, 81, 41, 20, 52, 61, 64, 79, 70,
73,107, 110, 113, 115.
Дома: ОЛ-8, стр. 178–181: 5, 12, 26, 30, 42, 54, 69, 112.
Занятие 2. Интегрирование по частям и интегрирование выражений, содержащих квадратный трёхчлен.
Ауд.: ОЛ-8, стр. стр. 181, 194, задачи: 120, 117, 118, 163, 165, 168.
Дома: ОЛ-8, стр. 181–182, 193–194, задачи: 74, 84, 119, 121, 161, 167.
Занятие 3. Интегрирование рациональных дробей.
Ауд.: ОЛ-8, стр. 203–204: 183, 184, 188, 192.
Дома: ОЛ-8, стр. 203–204: 187, 189, 193, 196, 200, 201.
Занятия 4–5. Интегрирование тригонометрических и иррациональных функций.
54
Ауд.: ОЛ-8, стр. 190, 194, 209: 132, 135, 131, 140, 134, 144, 205, 147, 151, 164, 180.
Дома: ОЛ-8, стр. 190, 194, 218–223: 129, 133, 138, 139, 141, 145, 149, 206, 212.
Занятие 6. Подготовка к контрольной работе на технику интегрирования.
Ауд.: ОЛ-8, стр. 194–221: 244, 247, 176, 257, 185, 122, 210, 326.
Дома: ОЛ-8, стр. 194–221: 55, 58, 76, 80, 123, 170, 246, 260, 279, 282, 284, 288, 289, 316, 324, 334.
Занятие 7. Контрольная работа «Техника интегрирования».
Дома: ОЛ-3, стр. 365: 1 (a,b); ОЛ-8, стр. 381–382: 1, 4, 6, 10.
Модуль 2. Приложения определенного интеграла
Занятие 8. Теоретические задачи на определение интеграла Римана и на критерий интегрируемости.
Ауд.: ОЛ-8, стр. 382–387: 17, 18, 45.
Дома: ОЛ-8, стр. 381–389: 19, 41, 42, 51.
Занятие 9. Вычисление определенного интеграла: формулы интегрирования по частям и замены
переменной. Интегрирование синуса и косинуса на отрезке, кратном периоду.
Ауд.: ОЛ-8, стр. 276–277: 1, 8, 13; cтр. 384–388: 20, 23, 24, 30 (a, б), 43.
Дома: ОЛ-8, стр. 276–277: 6, 15; стр. 384–389: 21, 22, 25, 30 (г), 31, 32, 40.
Занятие 10. Вычисление площадей плоских фигур в декартовой и полярной системах координат.
Ауд.: ОЛ-8, стр. 276–278: 20, 25, 36, 57.
Дома: ОЛ-8, стр. 276–278: 34, 38, 58, 61.
Занятие 11. Вычисление объёмов тел вращения.
Ауд.: ОЛ-8, стр. 279–280: 73 (а, б), 90.
Дома: ОЛ-8, стр. 279–280: 75 (в), 76, 92.
Занятие 12. Вычисление длин дуг.
Ауд.: ОЛ-8,стр. 280–282: 102, 114, 127.
Дома: ОЛ-8,стр. 280–282: 106, 110, 122, 132.
Занятие 13. Вычисление площадей поверхностей вращения. Подготовка к контрольной работе на
приложения определенного интеграла.
Ауд.: ОЛ-8,стр. 276–282: 140, 143, 68, 86 в).
Дома: ОЛ-8,стр. 276–282: 137, 148, 151, 35, 37, 59, 78, 107, 120, 69, 84 б).
Занятие 14. Исследование на сходимость несобственных интегралов.
Ауд.: ОЛ-5, стр. 227–229: 2336, 2344, 2359, 2360, 2361, 2362, 2370, 2375, 2381, 2380.1; ОЛ-6, гл.6: 6.425,
6.428, 6.431, 6.442.
Дома: ОЛ-5, стр. 227–229: 2365, 2366, 2355; ОЛ-6, гл.6: 6.427, 6.430, 6.432, 6.446, 6.449.
Занятие 15. Подготовка к контрольной работе на сходимость несобственных интегралов.
Ауд.: ОЛ-5, стр. 227-229: 2371, 2374, 2384, 2356 б), 2364, 2373, 2379, 2376.1, 2372, 2380.2.
Дома: ОЛ-8, стр. 276–279: 134, 141, 146; ОЛ-5,стр. 227-229: 2367, 2370.1.
Занятие 16. Контрольная работа на приложения определенного интеграла и несобственный интеграл.
Модуль 3. Дифференциальное исчисление функций нескольких
переменных
Занятие 17. Область определения ФМП, линии и поверхности уровня, предел.
Ауд.: ОЛ-5, стр. 319–322: 3153, 3169, 3171; ОЛ-8, стр. 401: 8.
55
Дома: ОЛ-5,стр. 319–322: 3161, 3174, 3178, 3181, 3182, 3183.2, 3187; ОЛ-8, стр. 401–402: 9, 10.
Занятие 18. Непрерывность ФМП.
Ауд.: ОЛ-5, стр. 319–322: 3196, 3202; ОЛ-8, стр. 403--406: 33 (а, б), 34 (а), 35, 27; задачи лекции.
Дома: ОЛ-5, стр. 319–322: 3192, 3195, 3197; ОЛ-8, стр. 403--406: 24, 25, 26, 33 (в), 34 (г), 36, 37.
Занятие 19. Частные производные и дифференциал первого порядка ФМП.
Ауд.: ОЛ-8, стр. 351–353: 1, 7, 16, 32 в), 41 б).
Дома: ОЛ-8, стр. 351–353: 2, 6, 12, 19, 41 в).
Занятие 20. Равномерная непрерывность и дифференцируемость ФМП. Производная сложной функции.
Ауд.: ОЛ-8,стр. 403–406: 38, 46; стр. 352: 23, 31.
Дома: ОЛ-8, стр. 403–406: 39, 45; стр. 352: 22, 29.
Занятие 21–22. Частные производные и дифференциалы высших порядков ФМП. Формула Тейлора.
Ауд.: ОЛ-8,стр. 353–363: 38, 42, 48, 51, 120, 130, 200, 212.
Дома: ОЛ-8,стр. 353–363: 39, 44, 47, 56, 119, 123, 125, 213.
Занятие 23. Производная по направлению и градиент ФМП. Касательная плоскость и нормаль к
поверхности.
Ауд.: ОЛ-8,стр. 363–364: 218, 220 (а), 223, 236.
Дома: ОЛ-8,стр. 363–364: 219, 225, 237.
Занятие 24. Производная неявной функции.
Ауд.: ОЛ-8, стр. 351–365: 94, 95, 61, 33, 67, 76, 73, 103, 127, 111, 117, 110, 139, 244.
Дома: ОЛ-8, стр. 407: 51, 53; стр. 351–365: 34 б), 45, 96, 62, 68, 75, 77, 105, 132.
Занятие 25. Подготовка к контрольной работе по ФМП-1.
Решение типового варианта.
Дома: ОЛ-8, стр. 353–365: 46, 77, 98, 115, 110, 121, 221, 240.
Занятие 26. Контрольная работа по ФМП-1.
Модуль 4. Безусловные и условные экстремумы
Занятие 27. Экстремум ФМП.
Ауд.: ОЛ-8,стр. 365–366: 246, 249, 253, 278.
Дома: ОЛ-8,стр. 365–366: 248, 247, 254, 279.
Занятие 28. Условный экстремум ФМП.
Ауд.: ОЛ-8,стр. 366–367: 287, 285, 295, 307.
Дома: ОЛ-8,стр. 366–367: 286, 290, 296, 311.
Занятие 29. Контрольная работа по ФМП-2.
Занятие 30. Резервное.
Контрольные мероприятия
Модуль 1. Неопределенный интеграл (5 неделя, максимум 12 баллов, минимум 6 баллов).
Рубежный контроль по модулю 1 (5 неделя)
Модуль 2. Приложения определенного интеграла (10 неделя, максимум 24 балла, минимум 13
баллов).
56
Домашнее задание №1 «Приложения определенного интеграла» (выдача 4 неделя, прием — 8
неделя).
Рубежный контроль по модулю 2 (10 неделя).
Модуль 3. Дифференциальное исчисление функций нескольких переменных (14 неделя,
максимум 16 баллов, минимум 8 баллов).
Рубежный контроль по модулю 3 (14 неделя).
Модуль 4. Безусловные и условные экстремумы (17 неделя, максимум 13 баллов, минимум 7
баллов).
Рубежный контроль по модулю 3 (17 неделя).
Типовые задания
Рубежный контроль по модулю 1
Проводится по материалу лекций 1–4 и практических занятий 1–6.
Задача
1
2
3
4
5
6
7
8
Макс
Мин
Макс. оценка
1
1
1
1
2
2
2
2
12
6
Домашнее задание №1 «Приложения определенного интеграла»
Задача
1
2
3
4
5
6
Макс
Мин
Макс. оценка
2
2
2
2
2
2
12
7
57
Рубежный контроль по модулю 2
Проводится по материалу лекций 5–16 и практических занятий 8–16.
Задача
1
2
1
2
3
Макс
Мин
Макс. оценка
2
1
3
3
3
12
6
1. Дать определение интеграла Римана.
2. Привести формулу для вычисления с помощью определенного интеграла площади плоской
фигуры, граница которой задана в полярных координатах.
Рубежный контроль по модулю 3
Проводится по материалу лекций 17–26 и практических занятий 17–26.
Задача
1
2
1
2
3
4
5
Макс
Мин
Макс. оценка
2
2
2
3
2
2
3
16
8
1. Сформулируйте теорему о пределе сложной функции.
2. Дайте определение дифференциалов высших порядков. Сформулируйте теорему Тейлора для
функций многих переменных с остаточным членом в форме Лагранжа.
58
Рубежный контроль по модулю 4
Проводится по материалу лекций 27–31 и практических занятий 27–29.
Задача
1
1
2
Макс
Мин
Макс. оценка
2
4
7
13
7
1. Дайте определение условного локального экстремума и функции Лагража. Сформулируйте
необходимые условия и схему исследования функций на условный экстремум.
1. Исследовать на экстремум функцию z  3x 2  x3  3y 2  4y .
2. Исследовать на экстремум функцию z 
x
при условии 9x 2  4y 2  1.
2y  2
Вопросы для подготовки
Модуль 2. Приложения определенного интеграла
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
Дать определение интеграла Римана.
Сформулировать необходимое условие интегрируемости.
Сформулировать критерий интегрируемости и следствия из него.
Сформулировать свойства линейности и аддитивности определенного интеграла.
Сформулировать теоремы об оценке модуля интеграла и об оценке.
Сформулировать две теоремы о среднем для определенного интеграла.
Сформулировать свойства определенного интеграла: монотонность и теорему о сохранении
интегралом знака подынтегральной функции.
Сформулировать теорему о непрерывности интеграла c переменным верхним пределом.
Сформулировать теорему о производной от интеграла по его верхнему пределу.
Сформулировать теорему о формуле Ньютона-Лейбница для определенного интеграла.
Сформулировать правила интегрирования по частям и подстановкой для определенного
интеграла.
Дать определения длины дуги кривой и спрямляемых кривых.
Сформулировать достаточное условие спрямляемости кривых.
Дать определение кривизны кривой и ее геометрический смысл. Привести формулы для
вычисления кривизны графика функции.
Дать определение радиуса кривизны, круга кривизны и центра кривизны плоской кривой.
Сформулировать геометрический смысл круга кривизны.
Дать определение эволюты и эвольвенты. Сформулировать механический способ
построения по заданной кривой одной из ее эвольвент.
Дать определение несобственного интеграла от непрерывной функции на бесконечном
59
промежутке. Сформулировать признаки сравнения для таких интегралов.
18. Дать определение несобственного интеграла от неограниченной функции на конечном
отрезке интегрирования. Сформулировать признаки сравнения для таких интегралов.
19. Сформулировать свойства несобственного интеграла от непрерывной функции на
бесконечном промежутке.
20. Дать определение абсолютной и условной сходимости несобственного
интеграла.
Сформулировать теорему об их связи.
21. Привести формулу для вычисления с помощью определенного интеграла площади плоской
фигуры в случае, когда ее граница задана в декартовых координатах.
22. Привести формулу для вычисления с помощью определенного интеграла площади плоской
фигуры в случае, когда ее граница задана параметрически.
23. Привести формулу для вычисления с помощью определенного интеграла площади плоской
фигуры, граница которой задана в полярных координатах.
24. Привести формулу для вычисления с помощью определенного интеграла объема тела по
площадям параллельных сечений.
25. Привести формулу для вычисления с помощью определенного интеграла объема тела
вращения вокруг оси OX в декартовой системе координат.
26. Привести формулу для вычисления с помощью определенного интеграла объема тела
вращения вокруг оси OY в декартовой системе координат.
27. Привести формулу для вычисления с помощью определенного интеграла объема тела
вращения вокруг полярной оси в полярной системе координат.
28. Привести формулу для вычисления с помощью определенного интеграла длины дуги
кривой, заданной параметрически.
29. Привести формулу для вычисления с помощью определенного интеграла длины дуги
кривой, заданной в декартовой системе координат.
30. Привести формулу для вычисления с помощью определенного интеграла длины дуги
кривой, заданной в полярной системе координат.
31. Привести формулу для вычисления с помощью определенного интеграла площади
поверхности вращения кривой, заданной в декартовой системе координат.
32. Привести формулу для вычисления с помощью определенного интеграла площади
поверхности вращения кривой, заданной в полярной системе координат.
Модуль 3. Дифференциальное исчисление функций нескольких
переменных
1. Дайте определение внутренних, граничных и предельных точек множеств, открытых и
замкнутых множеств, окрестностей, компактов и областей в Rn. Сформулируйте критерий
компактности множеств в Rn.
2. Дайте определение предела последовательности в Rn, сходящейся, расходящейся и
фундаментальной последовательности. Сформулируйте критерий Коши сходимости
последовательности.
3. Что такое координатные функции векторной функции многих переменных? Дайте
определение предела функции многих переменных по базе. Сформулируйте теорему о
покоординатной сходимости векторной функции многих переменных.
4. Сформулируйте теорему о пределе сложной функции.
5. Сформулируйте теорему о пределе ограничения функции на подмножество.
6. Дайте определение непрерывной функции многих переменных в точке и точек разрыва
функции. Сформулируйте локальные свойства непрерывных функций.
7. Дайте определение функции, непрерывной на множестве в Rn. Сформулируйте теорему о
непрерывных отображениях компактов и линейно связных множеств. Сформулируйте
свойства функций, непрерывных на компактах и на линейно связных множествах.
8. Дайте определение дифференцируемости и дифференциала функции многих переменных.
Сформулируйте теорему о покоординатной дифференцируемости ФМП.
9. Дайте определение и геометрическую интерпретацию частной производной функции
многих переменных. Дайте определение матрицы Якоби векторной функции.
Сформулируйте первое необходимое условие дифференцируемости.
60
10. Сформулируйте второе необходимое условие и достаточное условие дифференцируемости.
На примерах покажите, что необходимые условия дифференцируемости не являются
достаточными.
11. Сформулируйте свойство линейности и правило Лейбница для дифференциала и частных
производных функции многих переменных.
12. Сформулируйте теорему о дифференцировании сложной функции, цепное правило и
свойство инвариантности дифференциала функции многих переменных.
13. Дайте определение частных производных высших порядков. Что такое матрица Гессе
функции многих переменных? Сформулируйте теорему о равенстве смешанных частных
производных. Приведите пример функции, для которой эта теорема неверна.
14. Дайте определение дифференциалов высших порядков. Сформулируйте теорему Тейлора
для функций многих переменных с остаточным членом в форме Лагранжа.
15. Дайте определение и геометрическую интерпретацию производной по направлению.
Сформулируйте теорему о производной по направлению дифференцируемой функции.
16. Дайте определение градиента функции многих переменных. Сформулируйте его свойства.
17. Дайте определение касательной плоскости и нормали к поверхности. Сформулируйте
теорему об их существовании и уравнениях. Дайте геометрическую интерпретацию
дифференциала функции двух переменных.
Модуль 4. Безусловные и условные экстремумы
1. Дайте определение локального экстремума функции многих переменных, стационарных и
критических точек. Сформулируйте необходимое условие экстремума и схему
исследования функций на экстремум.
2. Сформулируйте достаточные условия экстремума функции многих переменных в общем
случае и в двумерном случае.
3. Дайте определение условного локального экстремума и функции Лагранжа. Сформулируйте
необходимые условия и схему исследования функций на условный экстремум.
4. Сформулируйте достаточные условия условного экстремума в общем случае.
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
для УЦ
Литература
Основная литература (ОЛ)
Иванова Е.Е. Дифференциальное исчисление функций одного переменного: Учеб. для вузов / Под ред.
В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 1998. –408 с.
Зарубин В.С., Иванова Е.Е., Кувыркин Г.Н. Интегральное исчисление функций одного переменного: Учеб.
для вузов / Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. –528 с.
Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – М.: Наука, 1980. – 431 с.
Пискунов Н.С. Дифференциальное и интегральное исчисление. Т.1 – М.: Наука, 1985. – 429 с.
Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа: Учеб.
пособие для вузов / Под ред. А.В. Ефимова и Б.П. Демидовича. 2-е изд., – М.: Наука, 1986. – 428 с.
Задачи и упражнения по математическому анализу для втузов. / Под ред. Б.П. Демидовича. – М.: Наука, 1987.
– 472 с.
Дополнительная литература (ОЛ)
Фролов С.В. Шостак Р.Я. Курс высшей математики. Т.1. – М.: Высшая школа, 1973. – 480 с.
Ильин В.А. Позняк Э.Г. Основы математического анализа. Ч.1. – М.: Наука, 1982. – 616 с.
61
Кудрявцев Л.Д. Курс математического анализа. Т.1. – М.: Высшая школа, 1988. – 712с Методические и
учебные пособия (МП)
Лекции
Модуль 1. Исследование функций и приложения
дифференциального исчисления
Лекции 1–2. Необходимое и достаточное условия монотонности дифференцируемой функции на
промежутке. Экстремум функции. Необходимое условие экстремума. Стационарные и критические точки
функции. Достаточные условия экстремума (по первой и второй производным, по производной высшего порядка).
Наибольшее и наименьшее значение функции на данном отрезке Выпуклость (вверх и вниз) функции, точки
перегиба. Достаточные условия выпуклости дважды дифференцируемой функции. Необходимые и достаточные
условия наличия точки перегиба. Асимптоты графика функции. Схема полного исследования функции и
построения ее графика.
ОЛ-1, гл. 8
Лекция 3. Приложения дифференциального исчисления: формула Тейлора с остаточным членом в формах
Пеано и Лагранжа. Формула Маклорена. Представленеи по формуле Маклорена некоторых элементарных
функций. Использование формулы Тейлора в приближенных вычислениях и для вычисления пределов. Векторная
функция скалярного аргумента: векторная функция скалярногоаргумента со значениями в R3, ее годограф,
уравнения пространственной кривой, винтовая линия. Предел и непрерывность векторной функции. Производная
векторной функции, ее геометрический и механический смысл. Уравнение касательной к пространственной
кривой.
ОЛ-1, гл. 7, § 7.1 - 7,5, гл9.
Модуль 2. Неопределенный интеграл
Лекция 4. Первообразная и ее свойства. Неопределенный интеграл, его свойства, связь с дифференциалом.
Таблица основных неопределенных интегралов. Интегрирование с ипользованеим подведения под знак
дифференциала, замены переменной. Интегрирование по частям. Интегрирование выражений, содержащих
квадратный трехчлен.
ОЛ-2, гл 1 § 1.1–1.6;
Лекция 5. Рациональные дроби. Разложение правильной рациональной дроби в сумму простейших (без
доказательства). Интегрирование простейших дробей. Интегрирование функций, рационально зависимых от
тригонометрических функций. Интегрирование иррациональных функций. Примеры интегралов, не
выражающихся через элементарные функции.
ОЛ-2, гл 2.§ 2.1–2.4, гл 3, гл 4.
Модуль 3. Определенный интеграл
Лекция 6. Определенный интеграл как предел интегральных сумм. Теорема об интегрируемости кусочнонепрерывных функций (без доказательства). Геометрическая интерпретация определенного интеграла. Основные
свойства определенного интеграла. Теоремы об оценке и о среднем значении. Определенный интеграл с
переменным верхним пределом, теорема о его производной. Формула Ньютона — Лейбница. Вычисление
определенных интегралов подстановкой и по частям. Интегрирование периодических функций, интегрирование
четных и нечетных функций на отрезке, симметричном относительно начала координат.
ОЛ-2, гл 6.§ 6.1–6.10.
Лекция 7. Вычисление площадей плоских фигур, ограниченных кривыми, заданными в декартовых
координатах, параметрически и в полярных координатах. Вычисление объемов тел по площадям поперечных
сечений и объемов тел вращения.
ОЛ-2, гл 9 § 9.3, 9.4.
Лекция 8. Дифференциал длины дуги плоской кривой, заданной в декартовых координатах, в полярных
координатах, в параметрическом виде. Вычисление длины дуги кривой и площади поверхности вращения.
Несобственные интегралы по бесконечному промежутку (1-го рода). Несобственные интегралы от неограниченных
функций на отрезке (2-го рода). Признаки сходимости несобственных интегралов. Абсолютная и условная
сходимости. Несобственные интегралы с несколькими особенностями.
ОЛ-2, гл 9 § 9.3, 9.4, 9.1, 9.2, 9.5, гл 7.
62
Практические занятия
Модуль 1. Исследование функций и приложения
дифференциального исчисления
Занятие 1. Исследование функций. Асимптоты графиков функций, интервалы возрастания, убывания,
экстремумы.
Ауд.: ОЛ-5 № 5.454, 5.455, 5.456, 5.406, 5.404, 5.410.
Дома: ОЛ-5 № 5.452, 5.453, 5.457, 5.458, 5.405, 5.408, 5.409 или
Ауд.: ОЛ-6 № 903, 907, 911, 913, 818, 825, 833.
Дома: ОЛ-6 № 904, 906, 908, 910, 815, 819, 821.
Занятие 2. Практические задачи на наибольшее и наименьшее значения функций.
Ауд.: ОЛ-6 № 866, 868, 875, 884, 885, 889.
Дома: ОЛ-6 № 873, 876, 877, 882, 883, 886, 888.
Занятие 3. Исследование функций. Интервалы выпуклости, точки перегиба.
Ауд.: ОЛ-5 № 5.444, 5.446, 5.466, 5.496, 5.516.
Дома: ОЛ-5 № 5.442, 5.445, 5.472, 5.497, 5.517 или
Ауд.: ОЛ-6 № 898, 900, 921, 938, 953.
Дома: ОЛ-6 № 895, 899, 931, 933.
Занятие 4. Исследование функций и построение их графиков. Разбор варианта ДЗ «Исследование функций
и построение их графиков»
Ауд.: ОЛ-5 № 5.493, 5.500, 5.525, 5.427, 5.429, 5,436.
Дома: ОЛ-5 № 5.494, 5.502, 5.526, 5.428, 5.431, 5.437 или
Ауд.: ОЛ-6 № 973, 989, 943, 866, 868, 875.
Дома: ОЛ-6 № 946, 974, 988, 945, 873, 876, 877.
Занятие 5. Формула Тейлора.
Ауд.: ОЛ-5 № 5.383, 5.385, 5.389, 5.391, 5.392, 5.394, 5.395, 5.397 (а,в), 5.400 (а,б).
Дома: ОЛ-5 № 5.382, 5.386, 5.388, 5.390, 5.393, 5.396, 5.397 (б,г), 5.398 (б), 5.400 (в) или
Ауд.: ОЛ-6 № 768, 769, 772 (а), 774, 775.
Дома: ОЛ-6 № 770, 771, 772 (б), 773.
Занятие 6. Подготовка к рубежному контролю по модуль 1.
Ауд.: ОЛ-5 № 5.405, 5.410, 5.443, 5.455, 5.476, 5.489, 5.391, 5.392.
Дома: ОЛ-5 № 5.406, 5.409, 5.444, 5.456, 5.478, 5.490, 5.389, 5.390.
Занятие 7. Рубежный контроль по модулю 1.
Модуль 2. Неопределенный интеграл
Занятие 8. Непосредственное интегрирование по таблице. Интегрирование методом подстановки.
Ауд.: ОЛ-5, гл.6, §1: 6.15, 6.23, 6.24, 6.27, 6.29, 6.35, 6.37, 6.40, 6.42, 6.43, 6.44, 6.48 6.52, 6.53,
6.56, 6.60, 6.62, 6.65, 6.74, 6.79, 6.83, 6.89, 6.95, 6.98, 6.100, 6.102, 6.107 или
ОЛ-6, гл.4, §1: 1032, 1040, 1044, 1046, 1050, 1062, 1063, 1065, 1066, 1073, 1075, 1080, 1093, 1082,
1086, 1095, 1104, 1119, 1133, 1137, 1145, 1149,1153, 1159, 1163, 1167, 1179, 1189.
63
Дома: ОЛ-5, гл.6, § 1: 6.20, 6.22, 6.25, 6.32, 6.38, 6.39, 6.41 6.45, 6.46, 6.47, 6.49, 6.54, 6.57, 6.61,
6.66, 6.68, 6.72, 6.76, 6.80, 6.85, 6.86, 6.92, 6.97, 6.101, 6.104, 6.106, 6.112, или
ОЛ-6, гл.4, § 1: 1037, 1041, 1057, 1069, 1070, 1074, 1077, 1083, 1085, 1094, 1108, 1096, 1101,
1114, 1120, 1130, 1146, 1152, 1154, 1162, 1172, 1182, 1188.
Занятие 9. Интегрирование по частям.
Ауд.: ОЛ-5, гл. 6, § 1: 6.129, 6.130, 6.132, 6.135, 6.124, 6.128, 6.136, 6.143, 6.151, 6.157, 6.144,
6.146, 6.147, 6.155, 6.156 или
ОЛ-6, гл. 4, § 3: 1214, 1219, 1236, 1231, 1213, 1223, 1227, 1234, 1235, 1252, 1253, 1245, 1228,
1242, 1246.
Дома: ОЛ-5, гл. 6, § 1: 6.125, 6.131, 6.140, 6.142, 6.127, 6.138, 6.145, 6.152, 6.153, 6.154, 6.137,
6.141 или
ОЛ-6, гл. 4, § 3: 1215, 1217, 1229, 1232, 1244, 1237, 1241, 1254, 1239, 1249, 1222, 1226.
Занятие 10. Интегрирование выражений, содержащих квадратный трехчлен.
Ауд.: ОЛ-5, гл. 6, § 2: 6.158, 6.161, 6.271, 6.250, 6.254, 6.255, 6.257, 6.259, 6.260, 6.264 или
ОЛ-6, гл. 4, § 4: 1255, 1259, 1261, 1262, 1265, 1266, 1269, 1271, 1272, 1274, 1277, 1278, 1279.
Дома: ОЛ-5, гл. 6, § 2:, 6.159, 6.160, 6.162, 6.164, 6.165, 6.251, 6.252, 6.253, 6.256, 6.258, 6.265,
6.280 6.276, 6.277 или
ОЛ-6, гл. 4, § 4: 1258, 1260, 1263, 1267, 1270, 1268, 1273, 1275, 1276.
Занятие 11. Интегрирование рациональных дробей.
Ауд.: ОЛ-5, гл. 6, § 2: 6.167, 6.168, 6.177, 6.171, 6.179, 6.178, 6.174, 6.185, 6.186, 6.188 или
ОЛ-6, гл. 4, § 5: 1282, 1284, 1286, 1289, 1290, 1298, 1308, 1313, 1314.
Дома: ОЛ-5, гл. 6, § 2: 6.129, 6.170, 6.173, 6.180, 6.181, 6.184, 6.187, 6.189 или
ОЛ-6, гл. 4, § 5: 1283, 1285, 1292, 1295, 1296, 1297, 1305, 1307, 1311.
Занятия 12–13. Интегрирование тригонометрических функций.
Ауд.: ОЛ-5, гл. 6, § 2: 6.190, 6.191, 6.195, 6.197, 6.198, 6.201, 6.203, 6.206, 6.209, 6.212, 6.213,
6.216, 6.219, 6.222, 6.225 или
ОЛ-6, гл. 4, § 7: 1338, 1341, 1345, 1347, 1350, 1351, 1355, 1359, 1365, 1366, 1377, 1382, 1388,
1380, 1389.
Дома: ОЛ-5, гл. 6, § 2: 6.218, 6.223, 6.224, 6.192, 6.194, 6.196, 6.199, 6.202, 6.204, 6.208, 6.210,
6.211, 6.214, 6.215, 6.217 или
ОЛ-6, гл. 4, § 7: 1339, 1340, 1344, 1346, 1348, 1352, 1358, 1362, 1367, 1368, 1372, 1373, 1378,
1381, 1387.
Занятие 14. Интегрирование иррациональных функций.
Ауд.: ОЛ-5, гл. 6, § 2: 6.238, 6.240, 6.242, 6.244, 6.261, 6.262, 6.264, 6.266, 6.267 или
ОЛ-6, гл. 4, § 6, 7: 1318, 1320, 1322, 1325, 1403, 1405, 1407, 1411, 1412
Дома: ОЛ-5, гл. 6, § 2: , 6.227, 6.239, 6.241, 6.243, 6.245, 6.263, 6.256, 6.268, 6.269 или
ОЛ-6 гл. 4 § 6, 7: 1315, 1317, 1319, 1321, 1323, 1324, 1404, 1406, 1408, 1413.
Занятие 15. Подготовка к контрольной работе «Техника интегрирования».
Ауд.: ОЛ-5 № 6.270, 6.272 6.274, 6.276, 6.282, 6.284, 6.286, 6.290, 6.294, 6.296, 6.304, 6.306,
6.310, 6.312, 6.314, 6.316 или
ОЛ-6 № 1432, 1436, 1441, 1447, 1453, 1456, 1459, 1463, 1469, 1473, 1475, 1478, 1479, 1480.
64
Дома: ОЛ-5 № 6.271, 6.273 6.275, 6.277, 6.283, 6.285, 6.287, 6.291, 6.295, 6.297, 6.305, 6.307,
6.311, 6.313, 6.315, 6.319 или
ОЛ-6 № 1433, 1437, 1442, 1448, 1454, 1457, 1460, 1464, 1470, 1474, 1476, 1481, 1482, 1483.
Занятие 16. Рубежный контроль по модулю 2, контрольная работа «Техника интегрирования».
Модуль 3. Определенный интеграл
Занятие 17. Вычисление определенного интеграла. Его свойства и геометрическая интерпретация. Оценка
определенного интеграла.
Ауд.: ОЛ-5, гл. 6, § 4: 6.326, 6.337, 6.340, 6.346, 6.350, 6.379, 6.387, 6.390, 6.395, 6.399, 6.406, (в
задачах 6.326, 6.337, 6.340, 6.399, 6.406 дать геометрическую интерпретацию), § 6: 6.364(б, в),
6.365 (а, в), 6.366 (а, г), 6.369, 6.370, 6.378 или
ОЛ-6, гл. 5, § 2, 4–6: 1521, 1529, 1534, 1536, 1538, 1576, 1587, 1590, 1592, 1598, 1592, 1599, 1600,
(в задачах 1521, 1529, 1536, 1599, 1600 дать геометрическую интерпретацию), § 7: 1598, 1610(а,
б), 1611 (а, в), 1612, 1614, 1619, 1621.
Дома: ОЛ-5, гл. 6, § 4: 6.328, 6.336, 6.341, 6.347, 6.386, 6.394, 6.400, 6.403, (в задачах 6.336,
6.338, 6.341, 6.399, 6.347 дать геометрическую интерпретацию), § 6: 6.364 (а), 6.365 (б), 6.366 (б,
в), 6.368, 6.371 или
ОЛ-6, гл.5, § 2, 4–6: 1522, 1527, 1537, 1539, 1541, 1589, 1591, 1593, 1601, 1602, (в задачах 1527,
1537, 1541, 1601 дать геометрическую интерпретацию), § 7: 1610 (в), 1611 (б), 1613, 1618, 1620.
Занятие 18. Вычисление площади плоской фигуры в декартовой и полярной системах координат. Выдача
домашнего задания по модулю 3 «Приложения определенного интеграла».
Ауд.: ОЛ-5, гл. 6, § 6: 6.453, 6.456, 6.467, 6.478, 6.479, 6.483, 6.486, 6.488 или
ОЛ-6, гл. 5, § 7: 1623, 1624, 1633, 1638, 1650, 1655, 1658, 1663.
Дома: ОЛ-5, гл. 6, § 6: 6.457, 6.464, 6.468, 6.480, 6.481, 6.484, 6.487, 6.492 или
ОЛ-6, гл. 5, § 7: 1626, 1634, 1636, 1645, 1646, 1653, 1656, 1657, 1661.
Занятие 19. Вычисление объемов тел по площадям поперечных сечений, вычисление объемов тел
вращения.
Ауд.: ОЛ-5, гл. 6, § 5, 6: 6.533, 6.535, 6.536, 6.538, 6.540, 6.541, 6.543 или
ОЛ-6, гл.5, § 3, 9: 1691(б), 1692, 1694, 1701 (в), 1702, 1703, 1707, 1708, 1688.
Дома: ОЛ-5, гл. 6, § 5, 6: 6.534, 6.537, 6.542, 6.544 или
ОЛ-6, гл. 5, § 3, 9: 1691 (а), 1697, 1709, 1689, 1695, 1697, 1701 (б), 1704.
Занятия 20–21. Вычисление длины дуги и площади поверхности вращения.
Ауд.: ОЛ-5, гл. 6, § 6: 6.494, 6.500, 6.506, 6.507, 6.509, 6.519 (а), 6.523 (б), 6.527, 6.530 или
ОЛ-6, гл.5, § 8, 10: 1665, 1667, 1669, 1676, 1680, 1715, 1722 (б), 1723 (в), 1725.
Дома: ОЛ-5, гл. 6, § 6: 6.499, 6.504, 6.511, 6.519 (б), 6.523 (а), 6.526, 6.529, 6.531 или
ОЛ-6 гл. 5 § 8, 10: 1666, 1670, 1678, 1679, 1683, 1716, 1722(а), 1723(б), 1726.
Занятие 22. Несобственные интегралы. Исследование несобственных интегралов на сходимость.
Ауд.: ОЛ-5, гл. 6, § 5, 6: 6.411, 6.417, 6.419, 6.424, 6.433, 6.435, 6.437, 6.441, 6.426, 6.428, 6.430,
6.432, 6.443, 6.445, 6.447, 6.449, 6.451 или
ОЛ-6, гл.5, § 3, 9: 1551, 1552, 1555, 1556, 1560, 1562, 1546, 1549, 1550, 1558, 1559, 1570, 1573,
1571.
Дома: ОЛ-5, гл. 6, § 5, 6: 6.412, 6.418, 6.420, 6.434, 6.436, 6.439, 6.429, 6.431, 6.442, 6.444, 6.446,
6.448 или
65
ОЛ-6, гл. 5, § 3, 9: 1554, 1559, 1563, 1565, 1547, 1557, 1566, 1567, 1572.
Занятие 23. Подготовка к рубежному контролю по модулю 3.
Ауд.: ОЛ-5 № 6.454, 6.482, 6.484, 6.489, 6.495, 6.504, 6.520, 6.529, 6.539, 6.544, 6.425, 6.427,
6.444.
Дома: ОЛ-5 № 6.455, 6.481, 6.485, 6.492, 6.498, 6.506, 6.521, 6.523, 6.426, 6.428, 6.439, 6.447.
Занятие 24. Рубежный контроль по модулю 3.
Занятие 25. Резерв.
Контрольные мероприятия
Модуль 1. Исследование функций скалярного аргумента и приложения дифференциального
исчисления (7 неделя, максимум 22 балла, минимум 11 баллов).
Домашнее задание №1 «Исследование функций и построение графиков» (выдача 3 неделя,
прием 6 неделя).
Рубежный контроль по модулю 1 (7 неделя).
Модуль 2. Неопределенный интеграл (12 неделя, максимум 38 баллов, минимум 19 баллов).
Рубежный контроль по модулю 2 (12 неделя).
Модуль 3. Определенный интеграл (16 неделя, максимум 30 баллов, минимум 16 баллов).
Домашнее задание №2 «Приложения определенного интеграла» (выдача 13 неделя, прием 16
неделя).
Рубежный контроль по модулю 3 (16 неделя).
СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.
ЛИНЕЙНАЯ АЛГЕБРА.
для УЦ
ЛИТЕРАТУРА
Основная литература (ОЛ)
Канатников А.Н., Крищенко А.П. Линейная алгебра: Учеб. для вузов / Под ред. B.C. Зарубина, А.П.
Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. – 336 с. (Сер. Математика в техническом университете,
вып. IV).
Канатников А.Н., Крищенко А.П., Четвериков В.Н. Дифференциальное исчисление функций многих
переменных: Учеб. для вузов / Под ред. B.C. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана,
2003. – 456 с. (Сер. Математика в техническом университете, вып. V).
Ильин В.А., Позняк Э.Г. Линейная алгебра. – М.: Физматлит, 2005.
Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 1. – М.: Интеграл-Пресс, 2006. –
416 с.
Бугров Я.С., Никольский С.М. Высшая математика. Т. 2. Дифференциальное и интегральное исчисление. –
М.: Дрофа, 2003. – 512 с.
Сборник задач по математике для втузов. Ч. 1. Линейная алгебра и основы математического анализа: Учеб.
пособие для втузов / Под ред. А.В. Ефремова, Б.П. Демидовича. – М.: Наука, 1993. – 478 с.
Сборник задач по математике для втузов. Ч. 2. Специальные разделы математического анализа: Учеб. пособие
для втузов / Под ред. А.В. Ефремова, Б.П. Демидовича. – М.: Наука, 1986. – 368 с.
Задачи и упражнения по математическому анализу для втузов / Под ред. Б.П. Демидовича. – М.: ИнтегралПресс, 1997. – 416 с.
66
Дополнительная литература (ДЛ)
Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1984. – 319 с.
Кудрявцев Л.Д. Курс математического анализа. Т. 2. – М.: Высш. шк., 1981. – 584 с.
Сборник задач по линейной алгебре / Под ред. С.К. Соболева. – М.: МГТУ, 1991. –154 с.
Вся высшая математика: Учебник для втузов: В 6 т. / Краснов М.Л., Киселев А.И., Макаренко и др. – Т. 1. –
М.: Эдиториал УРСС, 2000. – 327 с.
Вся высшая математика: Учебник для втузов: В 6 т. / Краснов М.Л., Киселев А.И., Макаренко и др. – Т. 2. –
М.: Эдиториал УРСС, 2000. – 184 с.
Беклемишева Л.А., Петрович А.Ю., Чубаров И.А. Сборник задач по аналитической геометрии и линейной
алгебре. Под ред. Д.В. Беклемишева. – М.: Наука, 1987. – 496 с.
Методические пособия, изданные в МГТУ (МП)
Крищенко А.П. Линейные пространства. Линейные операторы: Учеб. пособие. – М.: МГТУ, 1988. – 49 с.
Ильичев А.Т., Крапоткин В.Г., Савин А.С. Линейные операторы. Методические указания к выполнению
типового расчета. – М.: МГТУ, 2003. – 36 с.
Пугачев О.В., Стась Г.П, Чередниченко А.В. Квадратичные формы и их геометрические приложения.
Методические указания к выполнению типового расчета. – М.: МГТУ, 2004. – 59 с.
Богомолов В.Г., Матвеев М.В., Филиновский А.В. Дифференциальное исчисление функций нескольких
переменных. – М.: МГТУ, 1993. – 52 с.
Богомолов В.Г., Матвеев М.В., Филиновский А.В. Прикладные задачи дифференциального исчисления
функций нескольких переменных. – М.: МГТУ, 1993. – 56 с.
Гришина Г.В., Демин А.И., Михайлова О.В. Функции многих переменных. Методические указания к
выполнению домашнего задания. – М.: МГТУ, 2003. – 44 с.
Дерябина Г.С., Чуев В.Ю. Вектор-функция нескольких переменных. – М: МГТУ, 2002, – 26 с.
ЛЕКЦИИ
Модуль 1: Матрицы и системы линейных алгебраических уравнений
Лекция 1. Пространство арифметических векторов. Линейная зависимость и линейная независимость
арифметических векторов, необходимое и достаточное условие линейной зависимости. Минор матрицы. Базисный
минор. Теорема о базисном миноре и её следствие для квадратной матрицы.
ОЛ-1 гл.6 п.6.7; гл.8 п.8.4-8.5; ОЛ-4 гл.1 пар.3 п.1-2; ОЛ-5 гл.5 пар. 4.
Лекция 2. Ранг матрицы. Теорема о ранге матрицы (без док-ва). Инвариантность ранга матрицы
относительно элементарных преобразований (без док-ва). Методы вычисления ранга матрицы. Системы линейных
алгебраических уравнений (СЛАУ). Координатная, матричная и векторная форма записи. Критерий КронекераКапелли совместности неоднородной системы линейных уравнений.
ОЛ-1 гл.8 п.8.4 – 8.6; гл.9 п.9.1-9.3; ОЛ-4 гл.1 пар.3; гл.3 пар.1; ОЛ-5 гл.5 пар. 4-5.
Лекции 3–4. Решение систем линейных алгебраических уравнений. Однородные системы линейных
алгебраических уравнений. Свойства решений однородной системы. Теорема о числе линейно независимых
решений однородной СЛАУ. Фундаментальная система решений однородной СЛАУ. Теорема о структуре общего
решения неоднородной СЛАУ. Свойства решений неоднородной и соответствующей однородной системы.
Построение нормальной фундаментальной системы решений системы линейных однородных уравнений и
частного решения совместной неоднородной системы линейных уравнений.
ОЛ-1 гл.9 п.9.5 – 9.7; ОЛ-4 гл.3 пар.2; ОЛ-5 гл.5 пар. 5.
Модуль 2: Линейные и евклидовы пространства
Лекция 5. Аксиоматика линейного пространства. Примеры линейных пространств. Следствия из аксиом.
Линейные комбинации векторов, линейно зависимые и линейно независимые системы векторов, критерий
линейной зависимости и независимости векторов. Свойства линейно зависимых и линейно независимых систем
векторов. Размерность и базисы линейного пространства. Разложение вектора по базису, единственность
разложения. Конечномерные линейные пространства.
ОЛ-2 гл.1 п.1.1 – 1.7; ОЛ-4 гл.2 пар.1-2; ОЛ-5 гл.6 пар. 1.
Лекция 6. Координаты вектора. Линейные операции над векторами в координатной форме. Переход к
новому базису, матрица перехода. Преобразование координат вектора при переходе к другому базису.
67
Подпространства линейных пространств, их свойства, размерность. Линейная оболочка системы векторов. Ранг
системы векторов.
ОЛ-2 гл.1 п.1.6, 1.8; гл.2 п.2.1-2.2, 2.4-2.6; ОЛ-4 гл.2 пар.2-4; ОЛ-5 гл.6 пар. 1-2.
Лекция 7. Аксиоматика евклидова пространства, скалярное произведение. Примеры евклидовых
пространств. Неравенство Коши-Буняковского. Нормированное пространство. Норма вектора и её свойства. Угол
между векторами. Ортогональные векторы, линейная независимость ортогональной системы векторов.
ОЛ-2 гл.3 п.3.1 –3.5; ОЛ-4 гл.4 пар.1-3; ОЛ-5 гл.7 пар.1.
Лекция 8. Ортонормированный базис евклидова пространства, его построение из произвольного базиса с
помощью процесса ортогонализации Грама-Шмидта. Скалярное произведение векторов в произвольном и
ортонормированном базисах. Матрица Грама и её свойства.
ОЛ-2 гл.3 п.3.6 – 3.8; ОЛ-4 гл.4 пар.2 п.1-4; ОЛ-5 гл.7 пар. 1,3.
Лекция 9. Ортогональные матрицы и их свойства. Теорема о матрице перехода от ортонормированного
базиса к ортонормированному базису. Изоморфизм линейных и евклидовых пространств. Теорема об изоморфизме
конечномерных линейных пространств. Теорема об изоморфизме конечномерных евклидовых пространств.
ОЛ-2 гл.7 п.7.1, 7.3; гл.4 п.4.2; ОЛ-5 гл.7 пар.1 п.6; гл.6 пар.3 п.3.
Модуль 3: Линейные операторы
Лекция 10. Понятие линейного оператора. Примеры. Матрица линейного оператора, ее преобразование при
замене базиса. Подобные матрицы. Линейные операции над линейными операторами. Произведение линейных
операторов. Связь между операциями с линейными операторами и операциями с их матрицами. Обратный
оператор и его матрица.
ОЛ-2 гл.4 п.4.1 – 4.5; ОЛ-4 гл.5 пар.1-2; ОЛ-5 гл.6 пар.3.
Лекция 11. Собственные значения и собственные векторы линейного оператора, их нахождение.
Характеристический многочлен, его инвариантность относительно выбора базиса. Линейная независимость
собственных векторов, соответствующих различным собственным значениям. Матрица линейного оператора в
базисе из собственных векторов.
ОЛ-2 гл.5 п.5.1 – 5.5; ОЛ-4 гл.5 пар.3; ОЛ-5 гл.6 пар. 4.
Лекция 12. Линейные операторы в евклидовых пространствах. Сопряженный оператор. Линейность
сопряженного оператора. Матрица сопряженного оператора в ортонормированном базисе. Свойства сопряженного
оператора.
ОЛ-2 гл.6 п.6.1; ОЛ-4 гл.5 пар.5 п.1; ОЛ-5 гл.7 пар. 2.
Лекция 13. Самосопряженный (симметрический оператор), симметричность его матрицы
в
ортонормированном базисе. Свойства собственных значений и собственных векторов самосопряженного
линейного оператора. Существование ортонормированного базиса евклидова пространства из собственных
векторов самосопряженного оператора.
ОЛ-2 гл.6 п.6.2 – 6.3; ОЛ-4 гл.5 пар.5 п.2; ОЛ-5 гл.7 пар. 2.
Лекция 14. Ортогональный оператор. Свойства ортогонального оператора. Теорема об ортогональности его
матрицы в ортонормированном базисе. Ортогональные преобразования координат. Приведение матрицы
самосопряженного оператора к диагональному виду с помощью ортогонального преобразования.
ОЛ-2 гл.7 п.7.2 – 7.4; ОЛ-4 гл.5 пар.9; ОЛ-5 гл.7 пар.2.
Модуль 4: Квадратичные формы
Лекции 15–16. Квадратичная форма в евклидовом пространстве и связанный с ней симметричный оператор.
Изменение матрицы квадратичной формы при замене переменных. Канонический вид квадратичной формы.
Приведение квадратичной формы к каноническому виду с помощью ортогонального преобразования.
Канонический вид квадратичной формы в ортонормированном базисе из собственных векторов этого оператора.
Метод Лагранжа приведения квадратичной формы к каноническому виду. Закон инерции квадратичных форм (без
док-ва). Знакоопределенность квадратичных форм и их матриц. Критерий Сильвестра (без док-ва).
ОЛ-2 гл.8 п.8.1 – 8.6; ОЛ-4 гл.7 пар.2-4, 6; ОЛ-5 гл.8 пар. 2-3.
Лекция 17. Общие уравнения кривых и поверхностей второго порядка, их приведение к каноническому
виду. Классификация кривых и поверхностей второго порядка.
ОЛ-2 гл.9 п.9.1 – 9.6; ОЛ-4 гл.7 пар.6-7.
68
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Модуль 1: Матрицы и системы линейных алгебраических уравнений
Занятие 1. Нахождение ранга матрицы.
Ауд.: ОЛ-3 гл.3: № 3.150; 3.154; 3.156; 3.159; 3.163; 3.166.
Дома: ОЛ-3 гл.3: № 3.151; 3.153; 3.157; 3.165; 3.168.
Занятие 2. Решение систем линейных однородных уравнений.
Ауд.: ОЛ-3 гл.3: № 3.223; 3.224; 3.225; 3.228; 3.235; 3.230.
Дома: ОЛ-3 гл.3: № 3.226; 3.227; 3.229; 3.231; 3.232; 3.234.
Занятия 3–4. Решение систем линейных неоднородных уравнений.
Ауд.: ОЛ-3 гл.3: № 3.206; 3.210; 3.208; 3.239; 3.218; 3.220.
Дома: ОЛ-3 гл.3: № 3.207; 3.209; 3.211; 3.212; 3.236; 3.238; 3.219; 3.221.
Занятие 5. Рубежный контроль по модулю 1.
Модуль 2: Линейные и евклидовы пространства
Занятие 6. Линейные пространства, размерность, базис. Матрица перехода от одного базиса к другому.
Изменение координат вектора при переходе к новому базису.
Ауд.: ОЛ-3 гл.4: № 4.1 – 4.9 (неч); 4.15; 4.17; 4.18; 4.23; 4.25; 4.30; 4.37.
Дома: ОЛ-3 гл.4: № 4.2 – 4.10 (чет); 4.16; 4.20; 4.24; 4.28; 4.31; 4.38.
Занятие
7.
Ранг
системы
векторов.
Линейная
оболочка
системы
векторов.
Подпространство линейного пространства.
Ауд.: ОЛ-3 гл.4: № 4.19; 4.21; 4.45; 4.47; 4.52; 4.54.
Дома: ОЛ-3 гл.4: № 4.46; 4.48; 4.51; 4.53.
Занятие 8. Евклидово пространство. Процесс ортогонализации.
Ауд.: ОЛ-3 гл.4: № 4.67; 4.71; 4.74.
Дома: ОЛ-3 гл.4: № 4.69; 4.72; 4.76.
Занятие 9. Рубежный контроль по модулю 2.
Модуль 3: Линейные операторы
Занятие 10. Линейные операторы и их матрицы.
Ауд.: ОЛ-3 гл.4: № 4.86; 4.89; 4.90; 4.91; 4.94; 4.97.
Дома: ОЛ-3 гл.4: № 4.85; 4.87; 4.92; 4.93; 4.95; 4.99.
Занятие 11. Преобразование матрицы линейного оператора при переходе к новому базису. Собственные
значения и собственные векторы линейного оператора.
Ауд.: ОЛ-3 гл.4: № 4.106(а); 4.107; 4.135; 4.137; 4.139; 4.140.
Дома: ОЛ-3 гл.4: № 4.106 (б); 4.134; 4.136; 4.138; 4.141.
Занятие 12. Матрица сопряженного оператора. Приведение матрицы линейного оператора к диагональному
виду.
Ауд.: ОЛ-3 гл.4: № 4.151; 4.176; 4.175; 4.183; 4.186.
Дома: ОЛ-3 гл.4: № 4.152; 4.177; 4.174; 4.184.
69
Занятие 13. Рубежный контроль по модулю 3.
Модуль 4: Квадратичные формы
Занятие 14. Приведение квадратичной формы к каноническому виду с помощью ортогонального
преобразования.
Ауд.: ОЛ-3 гл.4: № 4.213; 4.214; 4.215.
Дома: ОЛ-3 гл.4: № 4.216.
Занятие 15. Приведение уравнения линии второго порядка и поверхности второго порядка к каноническому
виду.
Ауд.: ОЛ-3 гл.4: № 4.226; 4.228; 4.235; 4.237.
Дома: ОЛ-3 гл.4: № 4.227; 4.229; 4.233; 4.239.
Занятие 16. Контрольная работа «Квадратичные формы».
Занятие 17. Приведение квадратичной
Знакоопределенность квадратичной формы.
формы
методом
Лагранжа
к
нормальному
виду.
Ауд.: ОЛ-3 гл.4: № 4.210; 4.211; 4.218; 4.221; 4.223.
Дома: ОЛ-3 гл.4: № 4.212; 4.219; 4.220; 4.224.
Контрольные мероприятия
Модуль 1: Матрицы и системы линейных алгебраических уравнений (5 неделя, максимум 16
баллов, минимум 8 баллов).
Рубежный контроль по модулю 1 (5 неделя).
Модуль 2: Линейные и евклидовы пространства (9 неделя, максимум 20 баллов, минимум 10
баллов).
Домашнее задание №1 «Линейные и евклидовы пространства» (выдача 6 неделя, прием 9
неделя).
Рубежный контроль по модулю 2 (9 неделя).
Модуль 3: Линейные операторы (13 неделя, максимум 26 баллов, минимум 14 баллов).
Рубежный контроль по модулю 2 (13 неделя).
Модуль 4: Квадратичные формы (17 неделя, максимум 28 баллов, минимум 14 баллов)
Домашнее задание №2 «Приложения квадратичных форм» (выдача 13 неделя, прием 17 неделя).
Рубежный контроль по модулю 2 (17 неделя).
Типовые задания
Домашнее задание №1. «Линейные и евклидовы пространства»
Модуль 2, литература МП-1, МП-2.
Задача 1 (2 балла). В линейном пространстве V3 свободных векторов выбран правый ортонормированный базис i , j , k . Этот базис поворачивается вокруг заданного вектора a (это один
из базисных векторов) на заданный угол  в указанном направлении (положительном или
отрицательном), а затем вокруг вектора b (один из базисных векторов в новом положении) на
заданный угол  в указанном направлении. В результате получается новый базис i  , j  , k .
Найти матрицу перехода из старого базиса в новый.
70
Вариант: a  i ,   135 , b  k ,    .
Задача 2 (4 балла). В евклидовом пространстве R 4 задан базис a1 , a2 , a3 , a4 (координаты этих
векторов определены в стандартном базисе) и два вектора p и q (их координаты определены в
заданном базисе {ai } ).
1. Применяя процесс ортогонализации, построить по базису {ai } новый ортонормированный
базис {bi } .
2. Найти матрицу перехода от нового базиса {bi } к старому базису {ai } .
3. Найти координаты векторов p и q в базисе {bi } .
4. Вычислить скалярное произведение ( p, q) .
5. Вычислить угол между векторами p и q .
Вариант:
 4
 
0
a1    ,
 3
 
0
1
 
0
a2    ,
7
 
0
 1 
 
5
a3    ,
 7 
 
 0
1
 
5
a3    ,
7
 
5
1
 
0
[ p]a    ,
 3
 
 3
0
 
1
[q]a   
 2
 
 2
Домашнее задание №2 «Приложения квадратичных форм»
Модуль 4, литература МП-1, МП-2, МП-3.
Уравнение а) линии второго порядка на плоскости в системе координат Oxy и уравнения б)
поверхности второго порядка в пространстве в системе координат Oxyz привести к
каноническому виду, указав:
1) одно из преобразований перехода от заданной системы координат к канонической системе
координат (собственные числа ортогонального преобразования расположить в порядке
возрастания) ;
2) канонический вид уравнения линии и поверхности, значения всех параметров,
характеризующих форму линии и поверхности ;
3) на плоскости построить исходную систему координат Oxy , каноническую систему
координат Oxy , эскиз линии; для центральной линии найти координаты центра, вершин,
фокусов, уравнения асимптот (для гиперболы), а для параболы — координаты вершины,
фокуса, уравнение директрисы;
4) поверхность построить в канонической системе координат.
Вариант:
а) 8 xy  16 x 2  y 2  6 17 x  10 17 y  51  0 ; — 4 балла
б) x 2  2 y 2  2 z 2  6 xz  4 x  2 2 y  2 2 z  25  0 .— 6 баллов
Рубежный контроль по модулю 1
Проводится в форме контрольной работы по лекциям 1–4 и практическим занятиям 1–4.
71
1. Дать определение базисного минора (2 балла)
2. Дать определение однородной СЛАУ. Доказать свойства решений однородной системы.
Определение ФСР (6 баллов)
4. Найти ранг матрицы A при всех значениях параметра 
 1 6 4 11
A   3   1 7  (3 балла)
1 5 3 9 


5. Указать ранг и базисный минор матрицы СЛАУ, ФСР, базисные и свободные
переменные. Найти общее решение СЛАУ
2 x1  4 x2  x 3 5 x4  0 (3 балла)
6. Исследовать СЛАУ на совместность. Указать ранги и базисные миноры матрицы СЛАУ и ее
расширенной матрицы, ФСР соответствующей однородной СЛАУ, базисные и свободные
переменные. Найти общее решение СЛАУ
 2 x1  x2  3x3
x 
2 x3  x 4
 1

x 2  2 x3  3 x 4

 x1 
3 x3  2 x 4
 3,
 1,
 8,
(6 баллов)
 4.
Рубежный контроль по модулю 2
Проводится в форме контрольной работы по лекциям 5–9 и практическим занятиям 5–8.
1. Дать определение ортогональной системы векторов евклидова пространства. (2 балла).
2. Вывести неравенство Коши – Буняковского. (4 балла)
3. Доказать, что в R5 множество всех векторов вида x   0, c1 , c1  c2 , c2 , 0  , c1 , c2  R , есть
подпространство. Найти размерность этого подпространства. (4 балла)
4. В линейном пространстве L задан базис (e1 , e2 ) . Доказать, что система векторов e1  e1  e2 ,
e2  e1  3e2 образует базис. Найти координаты вектора x  3e1  5e2 в базисе (e1, e2 ) . (4 балла)
5. Найти расстояние от вектора g до линейной оболочки векторов f1 , f 2 , f 3 в евклидовом
пространстве
4
, если g  (1; 4;3;1) , f1  (2; 2;1;0) , f2  (2;2;0; 1) , f3  (1;0; 2; 2) . (4 балла)
Рубежный контроль по модулю 3
Проводится в форме контрольной работы по лекциям 10–14 и практическим занятиям 10–12.
1. Формула для преобразования матрицы линейного оператора при замене базиса. (2 балла)
2. Определение ортогонального оператора. Сформулировать свойства ортогонального
оператора. Доказать теорему об ортогональности его матрицы в ортонормированном базисе. (6
баллов)
3. Доказать, что преобразование A : R 3  R 3 , заданное формулой Ax  ( x, a ) a , где a имеет
координаты a  (1,2,3)T в ортонормированном базисе e  (e1 , e2 , e3 ) , является линейным
оператором и найти его матрицу в базисе e . (3 балла)
72
1 0 
T
4. Линейный оператор A : R 2  R 2 в базисе e1  1,4 T , e2   3,8 имеет матрицу A  
.
2 1 
T
T
Найти матрицу этого оператора в базисе f1  1,1 , f 2   2, 4  . (3 балла)
5. Найти собственные числа и собственные векторы линейного оператора, заданного в
некотором базисе своей матрицей
1 2 3 
4 5 6


7 8 9


Можно ли построить базис из собственных векторов данного оператора? (6
баллов)
Рубежный контроль по модулю 4
Проводится в форме контрольной работы по лекциям 15–16 и практическим занятиям 14–15.
1. Дать определение ранга квадратичной формы. (2 балла)
2. Вывести формулу преобразования матрицы квадратичной формы при переходе к новому
базису. (4 балла)
4. Исследовать на знакоопределенность квадратичную форму x12  15 x22  4 x1 x2  2 x1 x3  6 x2 x3 . (4
балла)
5. Уравнение кривой 6 xy  3x 2  5 y 2  8 10 y  80  0 ортогональным преобразованием
привести к каноническому виду. Указать связь между исходной и канонической системами
координат. Назвать кривую. (6 баллов).
ВВЕДЕНИЕ В СПЕЦИАЛЬНОСТЬ
для ФН-2
Дисциплина состоит из 2-х учебных модулей и зачета.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Лекции
Упражнения
Домашние задания
текущие
Контроль по модулю №1
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
1-10
30
–
–
1-10
20
10
6
73
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Лекции
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
11-17
21
–
–
11-17
14
17
6
Упражнения
Домашние задания
текущие
Контроль по модулю №2
Примечание
Модуль 1: Введение в историю математики
Лекции
Лекция 1. История высшего математического
образования в России и в МГТУ им. Н.Э. Баумана.
Введение в курс. Общие сведения о становлении
высшего математического образования в России.
Высшая математика в Московском Университете.
Научная деятельность А.В. Летникова и образование
кафедры высшей математики в ИМТУ. Краткие
сведения об истории математических кафедр МГТУ
им. Н.Э. Баумана. Выдающиеся ученые-математики,
работавшие в МГТУ им. Н.Э. Баумана.
проблема экзафлопных вычислений. Технологии
параллельного программирования.
Лекции 6. Системы компьютерной алгебры.
Компьютерная алгебра и искусственный интеллект.
История появления систем компьютерной алгебры,
их назначение и возможности. Система Wolfram
Mathematica. Демонстрация возможностей системы.
Лекции 7. Использование пакетов прикладных
программ. Системы геометрического моделирования.
Препроцессоры
(сеткопостроители).
Пакеты
математических программ (MathCAD, Mathematica,
MATLAB). CAD/CAE-системы. Пакеты обработки
результатов расчетов, графопостроители, системы
визуализации.
Лекция 2. Направление подготовки «Прикладная
математика». О подготовке специалистов на кафедре
«Прикладная математика». Структура учебного
плана. Направления специализации, филиалы
кафедры. Возможные направления деятельности
специалистов, окончивших вуз и получивших
специальность «Прикладная математика».
Лекции 8. Вопросы поиска научной информации.
Поиск информации как первый шаг решения
поставленной задачи. Поиск информации в
интернете, формирование запросов в стандартных
поисковых
машинах.
Научные
журналы.
Классические
и
электронные
библиотеки.
Современные базы данных (ScienceDirect, Scopus, elibrary и др.), поиск информации в них. Системы
цитирования.
Лекция 3. Краткие сведения об истории создания
некоторых разделов математики. Становление
современных курсов математического анализа,
аналитической геометрии, линейной алгебры.
Линейная алгебра и вычислительная математика.
Комплексные числа. Специальные разделы высшей
математики.
Лекции 9. Вопросы научной этики и защиты
авторских прав. Понятие об авторском праве.
Авторское право и научные публикации. Плагиат и
цитирование.
Оформление
библиографических
ссылок, пристатейных и прикнижных списков
литературы.
Лекция 4. Вычислительная математика. Краткие
сведения из истории вычислительной техники. Закон
Мура и его особенности. Роль ИПМ им. М.В.
Келдыша в развитии вычислительной математики в
нашей
стране.
Языки
программирования,
используемые при решении задач вычислительного
характера.
Особенности
вычислительной
математики, необходимость их учета при разработке
алгоритмов решения задач.
Лекции 10-12. Основоположники современной
математики. Биографические сведения творцов
современной математики и их вклад в становление
отдельных математических дисциплин: Евклид, Н.И.
Лобачевский и Б. Риман, И. Ньютон и Г.В. Лейбниц,
Р. Декарт, П. Ферма, семейство Бернулли, Л. Эйлер,
Ж.Л. д’Аламбер, П.С. Лаплас и Ж.Л. Лагранж, О.Л.
Коши, К.Ф. Гаусс и К. Вейерштрасс, Д. Гильберт и
др.
Лекции 5. Современная вычислительная техника.
Суперкомпьютеры.
Пути
повышения
производительности
вычислительных
машин.
Суперкомпьютеры:
история
и
современное
состояние, кластерные системы. Особенности
проведения
расчетов
на
суперкомпьютерах;
74
Лекции 13-14. Обзор научных направлений,
развиваемых на кафедре «Прикладная математика».
Научные направления, развиваемые на кафедре и в ее
филиалах.
Научная
школа
В.С.
Зарубина.
Математическое моделирование термомеханических
процессов в материалах и элементах конструкций.
Математическое моделирование процессов тепло- и
массообмена
в
неоднородных
средах.
Математическое
моделирование
процессов
взаимодействия
сплошной
среды
с
электромагнитным
полем.
Математическое
моделирование
динамических
процессов
взаимодействия конструкций с потоком жидкости и
газа. Функциональный анализ и теория вероятностей.
Теория
функций
и
ее
приложения.
Высокопроизводительные
вычисления
и
параллельные вычислительные алгоритмы решения
задач механики сплошной среды.
Лекции
15.
Обзор
научных
направлений,
развиваемых
на
кафедре
«Математическое
моделирование». Научные направления, развиваемые
на кафедре и в ее филиалах. Научная школа А.П.
Крищенко. Теория управления. Математическое
моделирование процессов управления. Устойчивость
динамических систем. Методы синтеза нелинейных
систем
и
нелинейная
теория
управления.
Прикладные задачи теории управления.
Модуль 2: Введение в математическое моделирование
Лекции
Лекция
1.
Понятие
о
математическом
моделировании и вычислительном эксперименте.
Смысл математического моделирования, основные
этапы математического моделирования. Виды
математических моделей. Роль математического
моделирования в деятельности современного
инженера. Использование вычислительной техники
на разных этапах математического моделирования.
Связь между вычислительным и натурным
экспериментом.
Лекция 5. Обзор научных направлений, развиваемых
в филиале кафедры «Прикладная математика» в
ИПМ им. М.В. Келдыша РАН. Разработка численных
методов, вопросы построения сеток, исследования в
области
магнитной
гидродинамики,
тепломассопереноса, взаимодействия сплошной
среды
с
электромагнитным
полем.
Высокопроизводительные вычисления; работа в
области обоснования численных методов.
Лекции 6. Обзор научных направлений, развиваемых
в филиале кафедры «Прикладная математика» в
ИПМех им. А.Ю. Ишлинского РАН. Решение
классических и неклассических задач механики
сплошной среды, исследования в области динамики
систем и теории колебаний.
Лекция 2. Обзор исследований, выполняемых в
рамках
научной
школы
В.С.
Зарубина.
Математическое моделирование термомеханических
процессов в материалах и элементах конструкций.
Современные
композитные
материалы;
математическое моделирование их структуры и
оценка свойств.
Лекции 7. Обзор научных направлений, развиваемых
в филиале кафедры «Прикладная математика» в
ЦИАМ им. П.И. Баранова. Математическое
моделирование работы авиационных двигательных
систем,
проблемы
динамики
и
прочности,
надежности, ресурса.
Лекции 3. Обзор исследований, выполняемых в
рамках
научной
школы
А.П.
Крищенко.
Математическое
моделирование
процессов
управления. Общие сведения о нелинейных
динамических системах. Процессы управления и их
математическое моделирование.
Лекции 8-10. Обзор исследований молодых ученых
кафедр
«Прикладная
математика»
и
«Математическое моделирование». Исследования,
проводимые на кафедрах «Прикладная математика»
и «Математическое моделирование» магистрантами,
аспирантами и молодыми учеными. Научные
семинары и конференции, школы молодых ученых.
Обзор
возможных
направлений
научной
деятельности студентов.
Лекции
4.
Математическое
моделирование
динамических
процессов
взаимодействия
конструкций с потоком жидкости и газа. Некоторые
сведения из аэрогидроупругости, актуальность
проблемы. Результаты исселедований в области
анализа
устойчивости
и
математического
моделирования течений.
Самостоятельная подготовка
Самостоятельная работа студента заключается в проработке материала лекций, выполнении реферата, подготовке
к контрольным работам и рубежным контролям.
Контрольные мероприятия и сроки их проведения
Модуль 1.
75
1. Контроль по модулю №1 (РК №1) «Введение в историю математики».
Срок проведения – 10 неделя
Модуль 2.
1. Реферат
Срок сдачи – 14 неделя
2. Контроль по модулю №2 (РК №2) «Введение в математическое моделирование».
Срок проведения – 17 неделя
Литература
Основная литература (ОЛ)
10. Панов В.Ф. Введение в специальность «математика». Учебное Пособие. М.: Изд-во МГТУ им. Н.Э Баумана,
2004.
11. Панов В.Ф. Математика древняя и юная / Под ред. В.С. Зарубина. – 2-е изд., испр. – М.: Изд-во МГТУ им.
Н.Э. Баумана, 2006. – 646 с.
12. Панов В.Ф. Современная математика и ее творцы / Под ред. В.С. Зарубина. – М.: Изд-во МГТУ им. Н.Э.
Баумана, 2011. – 646 с.
Дополнительная литература (ДЛ)
5. Курант Р., Роббинс Г. Что такое математика. Элементарный очерк идей и методов / Пер. с англ. М. – Л.:
ОГИЗ, Государственное издательство технико-экономической литературы, 1947
6. Тихонов А.Н., Костомаров Д.П. Вводные лекции по прикладной математике. – М.: Главная редакция физикоматематической литературы, 1984. – 192 с.
7. Рыбников К.А. История математики. – М.: Изд-во Московского университета, 1974. – 456 с.
8. Бурбаки Н. Очерки по истории математики / Пер. с франц. М.: Изд-во иностр. Лит, 1963. – 292 с.
9. Клайн М. Математика. Поиск истины: Пер. с англ. М.: Мир, 1988.
10. Клайн М. Математика. Утрата определенности: Пер. с англ. М.: Мир, 1984.
ХИМИЯ
для бакалавров
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
1.
Лекции
2.
Лабораторные работы
3.
Домашние задания
текущие
4.
Рубежный контроль №1
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
1-7
14
1-7
28
1-7
15
8
2
76
Примечание
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
5.
Лекции
8-11
8
6.
Лабораторные работы
9-12
12
7.
Домашние задания
текущие
8-12
8
8.
Рубежный контроль №2
13
2
Примечание
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
9.
Лекции
12-17
12
10.
Лабораторные работы
14-16
12
11.
Домашние задания
текущие
13-16
8
12.
Рубежный контроль №3
17
2
Примечание
Модуль 1: Строение вещества, химия элементов и их соединений.
Лекции
Лекция1.
Химия
как
раздел
ОЛ – 1, Гл.3; ОЛ – 2, Гл.1; ОЛ- 3, Гл.1;
естествознания, значение химии для
ОЛ – 4, Гл.1.
науки и технологии. Вещество и его
Лекция2.
Химическая
связь.
строение.
Понятие
о
квантовоХарактеристики связи: энергия, длина,
механической модели атома водорода.
валентныйугол. Типы связи. Полярность
Вероятностный характер процессов в
связи. Понятие о мето демолекулярных
микромире: принцип неопределенности
орбиталей. Энергетические диаграммы
Гейзенберга, волна де-Бройля, волновое
молекулярных орбиталей для бинарных
уравнение
Шредингера.
Квантовые
гомоядерных молекул, σ – и πчисла. Атомная орбиталь. Формы
молекулярные
орбитали.
Диаи
орбиталей. Строение много электронных
парамагнитные молекулы. Понятие о
атомов. Принцип минимальной энергии.
методе валентных связей. Гибридизация
Принцип Паули. Правила Хунда и
атомных орбиталей. σ- и π-связи.
Клечковского.Э
лектронные
Геометрическая конфигурация молекул.
конфигурации атомов. Энергетические
Электрический момент диполя молекулы.
характеристики
атомов:
энергия
Лекция3. Ионная связь и ее особенности.
ионизации, сродство к электрону,
Межмолекулярные
взаимодействия.
электроотрицательность.
Водородная связь. Химическая связь в
комплексных соединениях. Строение
77
вещества в конденсированном состоянии.
кислородом, азотом, серой, галогенами.
Аморфное и кристаллическое состояние
Химия воды. Жесткость воды. Основные
вещества. Типы химической связи в
виды жесткости. Методы определения
кристаллах. Общие представления о
жесткости, способы устранения.
строении
кристаллов:
элементы
Лекция6. Физико-химические свойства d
симметрии,
кристаллографические
– элементов. Закономерности изменения
системы,
элементарная
ячейка
свойств по группам и периодам.
кристаллов кубической системы и ее
Особенности химического поведения.
характеристики.
Химические
свойства
соединений
ОЛ – 1, Гл.4; ОЛ – 2, Гл.3-5; ОЛ – 3, Гл.3различных степеней окисления d –
5; ОЛ - 4, Гл.2-3.
элементов. Комплексные соединения.
Лекция4.
Периодическийзакон
Химические
свойства
некоторых
Д.И.Менделеева и периодическая система
металлов- хрома, марганца, элементов
элементов.
Периодические
свойства
семейства железа, меди, цинка.
элементов и их соединений. s-,p-,d-,f –
Лекция7. Физико-химическиесвойства p
элементы. Расположение металлов в
– элементов III, IV и V групп
периодической
системе
элементов.
периодической системы, относящихся к
Особенности электронного строения
металлам. Закономерности изменения
атомов металлов. Общие физические и
химических
свойств
в
группах,
химические
свойства
металлов,
взаимодействие с простыми и сложными
нахождение
в
природе.
Методы
веществами.
Химические
свойства
получения.
некоторых
соединений:
гидридов,
Лекция5. Физико - химические свойства
оксидов, галогенидов. Полупроводники.
s – элементов, взаимодействие с
Получение и применение кремния и
простыми и сложными веществами.
германия.
Щелочные
и
щелочноземельные
ОЛ – 1, Гл.3; ОЛ – 2, Гл.1; ОЛ- 3, Гл.1;
металлы.
Химические
свойства
ОЛ – 4, Гл.1, 7,8; ОЛ - 5, Гл.1,11,12; ОЛ соединений s – элементов с водородом,
6, Р.1,2; ДЛ12,Ч1-3.
Лабораторные занятия
Занятие1. Правила работы в химической
Занятие5. Определение жесткости воды.
лаборатории. Основные понятия и законы
Занятие6. Химические свойства d–
химии. Вводное тестирование.
металлов – Mn, Cu, Fe,Со.
Занятие2.
Важнейшие
классы
Занятие7. Химические свойства p –
химических соединений.
элементов – Al, Sn, Pb.
Занятие3.
ОкислительноЗанятие 8. Защита модуля 1.
восстановительные реакции.
Занятие4. Строение атома. Химическая
связь.
МОДУЛЬ 2: Общие закономерности протекания химических процессов
Лекции
Лекции8-9.
Элементы
химической
Объединенное уравнение первого и
термодинамики.
Первый
закон
второго законов. Термодинамические
термодинамики.
Термодинамические
критерии направленности химических
функции: энтальпия и внутренняя
процессов. Энергия Гиббса. Энергия
энергия. Тепловой эффект реакции. Закон
Гельмгольца. Химическое равновесие в
Гесса. Термохимические расчеты. Второй
гомогенной
системе.
Константа
закон термодинамики. Понятие об
равновесия.
Уравнения
изотермы,
энтропии.
Изменение
энтропии
в
изобары, изохоры химической реакции.
процессах. Третий закон термодинамики.
Особенности равновесия в гетерогенных
Расчет
абсолютных
значений
системах. Фазовые равновесия. Правило
стандартных
энтропий
веществ.
фаз.
78
ОЛ – 1,Гл.3,5;ОЛ – 2,Гл.6-9;ОЛ – 3,Гл.69;ОЛ – 4,Гл.4;ОЛ – 5,Гл.5-6.
Лекция10-11. Элементы химической
кинетики. Понятие о скорости реакции.
Зависимость скорости реакции от
концентрации. Закон действующих масс.
Молекулярность и порядок реакции.
Кинетические
уравнения
реакций
нулевого, 1-го и 2-го порядков.
Кинетические
кривые.
Зависимость
скорости реакции от температуры.
Температурный коэффициент скорости
реакции. ПравилоВант-Гоффа. Уравнение
Аррениуса.
Понятие
об
энергии
активации. Энергетическая диаграмма
реакции.
Особенности
кинетики
гетерогенных процессов. Понятие о
диффузии и адсорбции. Понятие о теории
активированного комплекса. Гомогенный
и гетерогенный катализ.
ОЛ – 1, Гл. 4; ОЛ – 2, Гл.10; ОЛ – 3, Гл.10;
ОЛ – 4, Гл.5; ОЛ – 5, Гл.7.
Лабораторные занятия
Занятие9. Химическое равновесие в
гомогенных и гетерогенных системах.
Занятие10.
Кинетика
гомогенных
химических реакций.
Занятие11. Закономерности протекания
химических процессов.
Занятие12.
Гетерогенные
каталитические реакции.
Занятие13. Защита модуля 2.
и
МОДУЛЬ3:Химические и электрохимические процессы в растворах
Лекции
Лекции12-14. Растворы неэлектролитов и
элемент Даниэля-Якоби. Определение
электролитов. Классификация растворов.
направления
окислительноЭнергетика
образования
растворов.
восстановительных реакций. Электролиз.
Понятие об идеальных растворах. Закон
ЗаконыФарадея.
Кинетика
Рауля для неэлектролитов и электролитов.
электрохимических процессов. Понятие о
Понятие об осмосе. Слабые электролиты.
поляризации
перенапряжении.
Теория электролитической диссоциации
Применение
электрохимических
Аррениуса. Степень и коэффициент
процессов в технике. Химические
диссоциации. Константа диссоциации.
источники тока, первичны еэлементы и
Электролитическая диссоциация воды.
аккумуляторы.
Ионное произведение воды. Водородный
ОЛ-1, Гл. 6,7; ОЛ – 2, Гл.11-14,16-20; ОЛ
и гидроксидный показатели- pH, pOH.
– 3, Гл.11-14,16-17; ОЛ – 4, Гл.6; ОЛ – 5,
Понятие о сильных электролитах.
Гл.8-9.
Активность и коэффициент активности.
Лекции15-16.
Коррозия и
защита
Ионное равновесие в системе раствор –
металлов. Классификация коррозионных
осадок. Произведение растворимости.
процессов по виду разрушений и
Диссоциация
комплексных
ионов.
активности коррозионных сред. Типы
Константа нестойкости. Реакции обмена
коррозионных процессов. Показатели
в
электролитах.
Гидролиз
солей.
коррозии:
глубинный,
массовый,
Электрохимические
процессы
в
объемный,
токовый.
Химическая
электролитах. Возникновение двойного
коррозия.
Механизм
электрического слоя на границе металлвысокотемпературной газовой коррозии.
электролит. Электродный потенциал.
Кинетика окисления металлов. Защитные
Уравнение Нернста для электродного
свойства пленок. Электрохимическая
потенциала и электродвижущей силы
коррозия. Механизм электрохимической
(ЭДС)
электрохимической
цепи.
коррозии: анодное окисление металла,
Стандартный водородный электрод. Ряд
катодное восстановление окислителя.
стандартных электродных потенциалов.
Водородная
и
кислородная
Типы
электродов.
Гальванический
деполяризация.
Термодинамическая
79
устойчивость металлов в водной среде.
Понятие од иаграмме Пурбе. Влияние
различных
факторов
на
скорость
коррозии.
Примеры
коррозионных
процессов. Методы защиты металлов от
коррозии:
рациональное
конструирование,
обработка
коррозионной среды, создание защитных
пленок, электрохимическая защита.
ОЛ – 1, Гл. 8; ОЛ – 2, Гл.21-22; ОЛ – 3,
Гл.18; ОЛ – 5, Гл.10.
Лекция17. Обзорная лекция. Некоторые
представления о нанохимии.
ОЛ – 1, Гл. 7; ОЛ – 2, Гл.19; ОЛ – 3, Гл.17;
ОЛ – 5, Гл.15.
Лабораторные занятия
Занятие14. Растворы электролитов.
Занятие15.
Электрохимические
процессы.
Занятие16. Коррозия и защита металлов
от коррозии.
Занятие17. Защита модуля3.
Самостоятельнаяработа
Самостоятельная работа студента заключается в проработке материала лекций, подготовке к
выполнению лабораторных работ, входному контролю готовности к выполнению лабораторной
работы, оформлении отчетов по лабораторным работам;
выполнении индивидуального задания по тематике лабораторной работы, которое
расценивается как защита лабораторной работы. Индивидуальное задание включает в себя 4-6
практических и расчетных задач. Самостоятельная работа является как домашней, так и
аудиторной (в том числе под контролем преподавателя на консультациях).
Домашнее задание (ДЗ1): Строение вещества, химия элементов и их соединений (модуль 1)
выдается на 1 неделе, сдача на 7 неделе .
Домашнее задание (ДЗ2) : Общие закономерности протекания химических процессов (модуль
2) выдача на 8 неделе, сдача на 12 неделе.
Домашнее задание (ДЗ3):Химические и электрохимические процессы в растворах. (модуль 2)
выдача на 13 неделе, сдача на 16 неделе.
Литература
Основная литература (ОЛ)
1.ГуровА.А.,Бадаев Ф.З., Овчаренко Л.П., Шаповал В.Н. Химия. М.: Изд-во МГТУ им.
Н.Э. Баумана, 2004. -748 с.
2.Горбунов А.И., Гуров А.А.. Филиппов Г.Г., Шаповал В.Н. Теоретические основы общей
химии. – М.: МГТУ, 2001-719с.
3Горбунов А.И., Филиппов Г.Г., Федин В.И. Химия. М.:Изд-во МГТУ им. Н.Э. Баумана,
2007. - 687 с.
4.Карапетьянц М.Х., Дракин С.И. Общая и неорганическаяхимия. М.: Химия,2000 –593 с.
5.Ермолаева В.И., Горшкова В.М., Слынько Л.Е. Химияэлементов. Учеб. пособие. - М.:
Изд-во МГТУ им. Н.Э. Баумана, 2007.- 176 с.
Дополнительная литература (ДЛ))
6.Фадеев Г.Н., Двуличанская Н.Н., Степанов М. Б., Матакова С.А. Решениезадачпокурсу
«Химия» длянехимическихвузов. Ч. 2 - М.:Домпедагогики, 2008. – 64 с.
7.Задачипообщей и неорганическойхимии: учеб.пособиедлястудентоввысш. учеб.
заведений / Р.А. Лидин, В.А. Молочко, Л.Л. Андреева; подред. Р.А. Лидина. –
М.:Гуманитар. изд. центрВладос, 2004. – 383 с.
80
8.Задачи и вопросыпообщей и неорганическойхимии с ответами и решениями / Ю.М.
Коренев, А.Н. Григорьев, Н.Н. Желиговская, К.М. Дунаева. – М.:Мир, 2004. – 368 с.
6.
7. Методические пособия
9.Березина С.Л., Голубев A.M., Горшкова В.М. и др. Лабораторный практикум по курсу
химии для технических университетов, ч. 1, ч.2: Методические указания. /Под ред.
Фадеева Г.Н./ – М.: МГТУ, 2005, 2009.
10.Романко О.И., Смирнов А.Д., Батюк В.А. Методическиеуказания к
выполнениюдомашнегозаданияпобазовомукурсухимии (примерырешения). Ч.1. - М.:Издво МГТУ им. Н.Э. Баумана, 2001,с. 15.
11.Методическиеуказания к выполнениюдомашнегозаданияпокурсу общейхимии./Под
ред.Ермолаевой В.И./ – М.: Изд-во МГТУ им. Н.Э. Баумана ,2003, с.48.
12.Сборникконтрольныхвопросов и задачдлязащитылабораторныхработпокурсухимии:
Метод. указания /С.Л. Березина, А.М. Голубев, Е.Е. Гончаренко и др.;Подред. А.М.
Голубева - М.: Изд-во МГТУ им.Н.Э. Баумана, 2009. – 84 с.
Электронные учебные пособия (ЭП)
13.Современная химия в техническом университете. Химия элементов и их соединений:
электронное учебное пособие / Ермолаева В.И., Волков А.А., Горшкова В.М., Слынько
Л.Е.- ФГУП НТЦ «Информрегистр», № 0320801585, от 4.08.08
Интернет-ресурсы
14. http://window.edu.ru/catalog?p_rubr=2.2.74.7
15. http://www.ximicat.com/index.php?razdel=obs
16. http://rushim.ru/books/books.htm
НЕОРГАНИЧЕСКАЯХИМИЯ
для бакалавровЭ-9
Дисциплина состоит из 2-х учебных модулей
Модуль 1
Виды аудиторных занятий и Сроки проведения или
выполнения, недели
самостоятельной работы
Лекции
1-6
Лабораторные работы
1-6
Домашнее задание текущее
1-6
Контроль по модулю 1
6
Трудоемкость, Примечания
часы
6
6
11
2
Модуль 2
Сроки проведения или
выполнения, недели
7 - 17
7 - 17
8 - 15
16
Трудоемкость, Примечания
часы
6
6
12
2
Виды аудиторных занятий и
самостоятельной работы
Лекции
Лабораторные работы
Домашнее задание текущее
Контроль по модулю 2
МОДУЛЬ1: Закономерности протекания реакций в растворах
Лекции
Лекция1. Растворы. Классификация растворов.
Способы выражения состава раствора.
Растворимость.
Энергетика
образования
растворов.
Коллигативные
свойства
разбавленных растворов Закон Раулядляне
электролитов. Понятие об осмосе. Осмотическое
81
давление. Уравнение Вант-Гоффа .Изотонические
растворы. Отклонение свойств растворов кислот,
оснований и солей от закона Рауля и уравнения
Вант-Гоффа.
ОЛ — 1, Гл.6; ОЛ — 2, Гл.11-12; ОЛ-3, Гл.6
Лекция2. Растворы электролитов. Электрическая
проводимость
электролитов.
Слабые
электролиты.
Теория
электролитической
диссоциации Аррениуса. Степень и коэффициент
диссоциации. Закон Рауля для электролитов.
Уравнение Вант-Гоффа для электролитов.
Равновесие
диссоциации
в
растворах
электролитов. Константа диссоциации. Закон
разбавления
Оствальда.
Электролитическая
диссоциация воды. Ионное произведение воды.
Водородный игидроксидный показатели-pH, pOH.
Буферные растворы.
Лекция3. Понятие о сильных электролитах.
Активность и коэффициент активности. Ионное
равновесие в системе раствор – осадок.
Произведение растворимости. Реакции обмена в
электролитах. Гидролиз солей.
ОЛ — 1, Гл.6; ОЛ — 2, Гл.13-14; ОЛ-3, Гл.7
Лабораторные работы
Занятие1. Определение концентрации раствора методом кислотно-основного титрования.
Занятие2. Растворы электролитов.
Занятие3. Закономерности протекания реакций в растворах неэлектролитов и электролитов.
Занятие4. Контроль модуля 1.
МОДУЛЬ2: Электрохимические процессы в электролитах
Лекции
Лекция4.
Окислительно-восстановительные
реакции в электролитах.
Окислители и
восстановители.
Возникновение
скачка
потенциала на границе металл — электролит.
Электродные процессы.
Электрохимические
цепи
обратимые
и
необратимые
Понятие
об
электроде
и
электродном потенциале. Уравнение Нернста для
электродного потенциала и электродвижущей
силы (ЭДС) электрохимической цепи. Типы
электродов. Стандартный водородный электрод.
Ряд стандартных электродных потенциалов.
Определение
направления
окислительновосстановительных реакций.
ОЛ — 1, Гл.6; ОЛ — 2, Гл.16-17; ОЛ-3, Гл.16, 17
Лекция5.
Гальванический
элемент.
Классификация
гальванических
элементов.
Химические и концентрационные гальванические
элементы. Элемент Даниэля – Якоби. Расчет
электродного потенциала и электродвижущей
силы гальванического элемента. Химические
источники тока (ХИТ). Первичные и вторичные
ХИТ. Аккумуляторы.
Лекция6. Электролиз. Потенциал разложения
электролита. Последовательность разряда ионов
на электродах. Законы Фарадея. Применение
электрохимических процессов в технике.
ОЛ — 1, Гл.6; ОЛ — 2, Гл.16-17; ОЛ-3, Гл 16, 17
Лекция7. Коррозия и защита металлов.
Классификация коррозионных процессов по виду
разрушений и активности коррозионных сред.
Типы коррозионных процессов. Показатели
коррозии: глубинный, массовый, объемный,
токовый. Химическая коррозия. Кинетика
окисления металлов. Защитные свойства пленок.
Лекция8.
Электрохимическая
коррозия.
Механизм
электрохимической
коррозии.
Водородная и кислородная деполяризация.
Влияние различных факторов на скорость
коррозии. Примеры коррозионных процессов.
Методы защиты металлов от коррозии.
ОЛ —1, Гл.6; ОЛ — 2, Гл.18; ОЛ-3, Гл.18, 19
Лабораторные работы
Занятие5. Окислительно-восстановительные реакции.
Занятие6. Коррозия и защита металлов.
Занятие7. Электрохимические процессы.
Занятие8. Контроль модуля 2.
Домашние задания
ДЗ 1. Закономерности протекания реакций в растворах. Выдача - 1 неделя, сдача-7неделя.
ДЗ 2. Электрохимические процессы вэлектролитах. Выдача - 8 неделя, сдача - 15неделя.
Самостоятельная работа
Самостоятельная работа студента заключается в проработке материала лекций, подготовке к выполнению
лабораторных работ, входному контролю готовности к выполнению лабораторной работы, выполнении
индивидуального задания по тематике лабораторной работы, которое расценивается как защита лабораторной
82
работы. Индивидуальное задание включает в себя 3-5 практических и расчетных задач. Самостоятельная работа
является как домашней, так и аудиторной под контролем преподавателя (КСР).
ЛИТЕРАТУРА
Основнаялитература(ОЛ)
1. КарапетьянцМ.Х., ДракинС.И. Общаяинеорганическаяхимия.М.:Химия,2000 –593с.
2. ГорбуновА.И.,ФилипповГ.Г.,ФединВ.И.Химия.М.:Изд-воМГТУим.Н.Э.Баумана,2007.– 586 с.
3. ГуровА.А.,БадаевФ.З.,ОвчаренкоЛ.П.,ШаповалВ.Н.Химия.М.:Изд-воМГТУим.Н.Э.Баумана,2004.-748с.
Методическиепособия,изданныевМГТУ(МП)
4. Методическиеуказанияквыполнениюлабораторныхработпонеорганическойхимии/В.И.Ермолаева,Н.Н.Двул
ичаская,В.М.Горшкова,Л.Е.Слынько. – М.:Изд-воМГТУим.Н.Э.Баумана,2009. –103с.
5. Теоретическиеосновынеорганическойхимии:метод.указания/В.И.Ермолаева,Н.Н.Двуличанская.-М.:ИздвоМГТУим.Н.Э.Баумана,2011.-61с.
6. Методическиеуказанияквыполнениюдомашнегозаданияпокурсунеорганическойхимии/ЕрмолаеваВ.И.,Дву
личанскаяН.Н.,ХмарцеваЛ.А.идр.-М.:Изд-воМГТУим.Н.Э.Баумана,2003. – 48с.
7. Сборникконтрольныхвопросовизадачдлязащитылабораторныхработпокурсухимии:Метод.указания/С.Л.Бе
резина,А.М.Голубев,Е.Е.Гончаренкоидр.;Подред.А.М.Голубева-М.:Изд-воМГТУим.Н.Э.Баумана,2009. –
84с.
Электронныеучебныепособия(ЭП)
8. Методическиеуказанияквыполнениюдомашнегозаданияпокурсунеорганическойхимии:электронноеучебное
пособие/ЕрмолаеваВ.И.,ДвуличанскаяН.Н.,ХмарцеваЛ.А.-ФГУПНТЦ«Информрегистр»,
№
0321000438,от14.12.2010
9. Теоретическиеосновыхимии:электронноеучебноеиздание:Методическиеуказаниякрешениюзадачпокурсу«
Неорганическаяхимия»/ЕрмолаеваВ.И.,ДвуличанскаяН.Н.-ФГУПНТЦ«Информрегистр»,
№
0321002540,от14.12.2010
Интернет – источники
1. http://window.edu.ru/catalog?prubr=2.2.74.7.4
2. http://www.ximicat.com/index.php?razdel=neo
3. http://rushim.ru/books/books.htm
ХИМИЯ
для специалистов Ф-та «Э»
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
13.
Лекции
14.
Лабораторные работы
15.
Домашние задания
текущие
16.
Рубежный контроль №1
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
1-5
10
1-4
Примечание
16
1-4
8
5
2
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
17.
Лекции
18.
Лабораторные работы
19.
Домашние задания
текущие
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
6-12
14
6-11
20
5-11
83
11
Примечание
20.
Рубежный контроль №2
12
2
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
21.
Лекции
12-17
12
22.
Лабораторные работы
14-16
12
23.
Домашние задания
текущие
13-16
10
24.
Рубежный контроль №3
17
2
Примечание
МОДУЛЬ 1: Общие закономерности протекания химических процессов
Лекции
Лекция 1.
Основные понятия и
изотермы, изобары, изохоры химической
определения химической термодинамики.
реакции.
Особенности
равновесия
в
Первый
закон
термодинамики.
гетерогенных
системах.
Фазовые
Термодинамические функции: энтальпия и
равновесия. Правило фаз.
внутренняя энергия. Тепловой эффект
ОЛ-1, Гл.6, 10; ОЛ-3, Гл. 9; ОЛ – 4, Гл.4.
реакции. Закон Гесса. Термохимические
Лекция4.Элементы химической кинетики.
расчеты. Второй закон термодинамики.
Понятие о скорости реакции. Зависимость
Понятие об энтропии. Изменение энтропии
скорости реакции от концентрации. Закон
в процессах.
действующих масс. Молекулярность и
ОЛ-1, Гл.6; ОЛ-3, Гл. 6, 7; ОЛ – 4, Гл.4.
порядок реакции. Кинетические уравнения
Лекция 2.Третий закон термодинамики.
реакций нулевого, 1-го и 2-го порядков.
Расчет абсолютных значений стандартных
Кинетические кривые.
энтропий веществ. Объединенное уравнение
ОЛ-1, Гл.7; ОЛ-3, Гл. 10; ОЛ – 4, Гл.5.
первого
и
второго
законов.
Лекция5.Зависимость скорости реакции от
Термодинамические
критерии
температуры. Температурный коэффициент
направленности химических процессов.
скорости реакции. Правило Вант-Гоффа.
Энергия Гиббса. Энергия Гельмгольца.
Уравнение Аррениуса. Понятие об энергии
Химическое равновесие в гомогенной
активации.
Энергетическая
диаграмма
системе. Константа равновесия.
реакции.
Особенности
кинетики
ОЛ-1, Гл.6, 10; ОЛ-3, Гл. 8, 9; ОЛ – 4, Гл.4.
гетерогенных
процессов.
Понятие
о
Лекция3.
Эмпирические константы
диффузии и адсорбции. Гомогенный и
равновесия. Принцип смещения равновесия
гетерогенный катализ.
Ле-Шателье – Брауна.
Уравнения
ОЛ-1, Гл.6; ОЛ-3, Гл. 6; ОЛ – 4, Гл.10.
Лабораторные работы
Занятие 1. Химические равновесие в
Занятие 4. Гетерогенные и каталитические
гомогенных
и
гетерогенных
реакции.
Занятие 5 Защита модуля 1.
системах.Занятие 2.Кинетика гомогенных
химических реакций.
Занятие 3.Закономерности протекания
химических процессов.
84
МОДУЛЬ 2: Химические и электрохимические процессы в растворах
Лекции
Лекция6.
Растворы неэлектролитов.
ионов. Константа нестойкости. Реакции
Классификация
растворов.
Энергетика
обмена в электролитах. Гидролиз солей.
образования
растворов.
Понятие
об
ОЛ-1, Гл.13; ОЛ-3, Гл. 13; ОЛ – 4, Гл.6.
идеальных растворах. Закон Рауля для
Лекция10.
Электрохимические процессы
неэлектролитов. Температуры кипения и
в
электролитах.
Законы
Фарадея.
замерзания растворов. Понятие об осмосе.
Потенциалы электрохимической системы.
ОЛ-1, Гл.13; ОЛ- 3, Гл. 11, 12; ОЛ – 4, Гл.6.
Возникновение двойного электрического
Лекция7.
Растворы в металлических
слоя на границе металл - электролит.
системах, сплавы и диаграммы плавкости.
Электродный
потенциал.
Уравнение
Эвтектические
сплавы.
Сплавы
с
Нернста для электродного потенциала.
образованием твердых растворов. Сплавы с
Стандартный водородный электрод.
образованием
интерметаллических
ОЛ-1, Гл.16; ОЛ-2, Гл. 16; ОЛ-3, Гл. 16.
соединений. Образование сплавов в твердом
Лекция 11. Электродвижущая сила (ЭДС)
состоянии.
электрохимической цепи. Ряд стандартных
ОЛ-3, Гл. 11; ОЛ – 4, Гл.6.
электродных
потенциалов.
Типы
Лекция8.Растворы
электролитов.
электродов. Диаграммы Пурбе. Химические
Электропроводность электролитов. Слабые
и
концентрационные
гальванические
электролиты. Теория электролитической
элементы.
Гальванический
элемент
диссоциации
Аррениуса.
Степень
и
Даниэля-Якоби.
коэффициент
диссоциации.
Константа
ОЛ-1, Гл.16; ОЛ-2, Гл. 17; ОЛ – 3, Гл.17,
диссоциации.
Электролитическая
18.
диссоциация воды. Ионное произведение
Лекция 12.Термодинамика окислительноводы.
Водородный
и
гидроксидный
восстановительных
реакций
в
показатели - pH, pOH.
гальваническом элементе. Практическое
ОЛ-1, Гл.13; ОЛ-3, Гл. 13; ОЛ – 4, Гл.6.
применение химических источников тока.
Лекция9.
Понятие о сильных
Электролиз. Кинетика электрохимических
электролитах. Активность и коэффициент
процессов. Понятие о поляризации и
активности. Ионное равновесие в системе
перенапряжении.
раствор
–
осадок.
Произведение
ОЛ-1, Гл.16; ОЛ-2, Гл. 17; ОЛ – 3, Гл.17,
растворимости. Диссоциация комплексных
18.
Лабораторные работы
Занятие 6. Определение концентрации
Занятие 9. Гальванические элементы.
раствора методом кислотно-основного
Занятие 10. Электрохимические процессы.
титрования.
Занятие 11.Электролиз.
Занятие 7.Растворы электролитов (часть 1).
Занятие 12.Защита модуля 2.
Занятие 8.Растворы электролитов (часть 2).
МОДУЛЬ 3: Коррозия и защита металлов от коррозии
Лекции
Лекция 13. Коррозия. Классификация
ОЛ-1, Гл.18; ОЛ-2, Гл. 21; ОЛ – 3, Гл.18.
коррозионных процессов по
виду
Лекция 14. Электрохимическая коррозия.
разрушений и активности коррозионных
Механизм электрохимической коррозии:
сред. Типы коррозионных процессов.
анодное окисление металла, катодное
Показатели
коррозии:
глубинный,
восстановление окислителя. Водородная и
массовый, объемный, токовый. Химическая
кислородная
деполяризация.
коррозия.
Механизм
Термодинамическая устойчивость металлов
высокотемпературной газовой коррозии.
в водной среде. Влияние различных
Кинетика окисления металлов. Защитные
факторов на скорость коррозии. Примеры
свойства коррозионных пленок.
коррозионных процессов.
85
ОЛ-1, Гл.18; ОЛ-2, Гл. 21; ОЛ – 3, Гл. 18.
Лекция 15. Методы защиты металлов от
коррозии: рациональное конструирование,
легирование металлов, создание защитных
покрытий,
обработка коррозионной
среды, электрохимическая защита.
ОЛ-1, Гл.19; ОЛ-2, Гл. 22; ОЛ – 3, Гл. 18.
Лекция 16. Полимерные и композиционные
материалы. Физико-химические свойства,
получение и применение.
ОЛ – 6.
Лекция17.Фундаментальные и прикладные
аспекты нанохимии.
Лабораторные работы
Занятие 13. Коррозия.
Занятие 17.Защита модуля 3.
Занятие 14. Защита металлов от коррозии.
Занятие
15.
Химические
и
электрохимические процессы при коррозии.
Занятие 16. Получение наночастиц
химических соединений.
Самостоятельная работа
Самостоятельная работа студента заключается в проработке материала лекций,
подготовке к выполнению лабораторных работ, входному контролю готовности к
выполнению лабораторной работы, выполнении индивидуального задания по тематике
лабораторной работы, которое расценивается как защита лабораторной работы.
Индивидуальное задание включает в себя 4-6 практических и расчетных задач.
Самостоятельная работа является как домашней, так и аудиторной (в том числе под
контролем преподавателя на консультациях).
Домашнее задание
ДЗ1: Общие закономерности протекания химических процессов. Выдача на 1 неделе,
сдача на 4 неделе.
ДЗ2: Химические и электрохимические процессы в растворах. Выдача на 5 неделе, сдача
на 11 неделе.
ДЗ3: Коррозия и защита металлов от коррозии. Выдача на 12 неделе, сдача на 16 неделе.
ЛИТЕРАТУРА
Основная литература (ОЛ)
1. Гуров А.А., Бадаев Ф.З., Овчаренко Л.П., Шаповал В.Н. Химия. М.: Изд-во МГТУ
им. Н.Э. Баумана, 2004. -748 с.
2. Горбунов А.И., Гуров А.А.. Филиппов Г.Г., Шаповал В.Н. Теоретические основы
общей химии. – М.: МГТУ, 2001-719с.
3. Горбунов А.И., Филиппов Г.Г., Федин В.И. Химия. М.: Изд-во МГТУ им. Н.Э.
Баумана, 2007. - 687 с.
4. Карапетьянц М.Х., Дракин С.И. Общая и неорганическая химия. М.: Химия,2000
–593 с.
5. Ермолаева В.И., Горшкова В.М., Слынько Л.Е. Химия элементов. Учеб. пособие.
- М.: Изд-во МГТУ им. Н.Э. Баумана, 2007.- 176 с.
86
6. Двуличанская Н.Н., Слынько Л.Е., Пясецкий В.Б. Композиционные материалы.
Физико-химические свойства. Учеб.пособие.- М.: Изд-во МГТУ им. Н.Э. Баумана,
2008.- 47 с.
Дополнительная литература (ДЛ)
7. Фадеев Г.Н., Двуличанская Н.Н., Степанов М. Б., Матакова С.А. Решение задач
по курсу «Химия» для нехимических вузов. Ч. 2 - М.: Дом педагогики, 2008.– 64с.
8. Задачи по общей и неорганической химии: учеб. пособие для студентов высш.
учеб. заведений / Р.А. Лидин, В.А. Молочко, Л.Л. Андреева; под ред. Р.А. Лидина.
– М.: Гуманитар. изд. центр Владос, 2004. – 383 с.
9. Задачи и вопросы по общей и неорганической химии с ответами и решениями /
Ю.М. Коренев, А.Н. Григорьев, Н.Н. Желиговская, К.М. Дунаева. – М.: Мир, 2004. –
368 с.
Методические пособия, изданные в МГТУ (МП)
10. Березина С.Л., Голубев A.M., Горшкова В.М. и др. Лабораторный практикум по
курсу химии для технических университетов, ч. 1, ч.2: Методические указания.
/Под ред. Фадеева Г.Н. – М.: МГТУ, 2005, 2009.
11. Ермолаева В.И., Романко О.И., Смирнов А.Д., Батюк В.А. Методические
указания к выполнению домашнего задания по базовому курсу химии (примеры
решения). Ч.1. - М.: Изд-во МГТУ им. Н.Э. Баумана, 2001. – 27 с. 15.
12.Методические разработки кафедры к лабораторным работам.
13. Сборник контрольных вопросов и задач для защиты лабораторных работ по
курсу химии: Метод. указания /С.Л. Березина, А.М. Голубев, Е.Е. Гончаренко и др.;
Под ред. А.М. Голубева - М.: Изд-во МГТУ им.Н.Э. Баумана, 2009. – 84 с.
Электронные учебные пособия (ЭП)
14.Современная химия в техническом университете. Химия элементов и их
соединений: электронное учебное пособие / Ермолаева В.И., Волков А.А.,
Горшкова В.М., Слынько Л.Е.- ФГУП НТЦ «Информрегистр», № 0320801585, от
4.08.08
Интернет-ресурсы
15. http://window.edu.ru/catalog?p_rubr=2.2.74.7
16. http://www.ximicat.com/index.php?razdel=obs
17. http://rushim.ru/books/books.htm
ХИМИЯ
ДЛЯ СПЕЦИАЛИСТОВ Ф-ТА «ПСО»
Модуль 1
87
Виды аудиторных занятий и
самостоятельной работы
Лекции
Лабораторные работы
Домашнее задание текущее
Контроль по модулю 1
Сроки проведения или
выполнения, недели
1-9
1-9
1-9
10
Трудоемкость, Примечания
часы
10
8
16
2
Виды аудиторных занятий и
самостоятельной работы
Лекции
Лабораторные работы
Домашнее задание текущее
Контроль по модулю 1
Модуль 2
Сроки проведения или
выполнения, недели
10 - 17
10 - 16
10 - 17
17
Трудоемкость, Примечания
часы
7
7
20
2
МОДУЛЬ 1: Химия элементов и их соединений.
Лекции.
Лекция 1. Периодический закон Д.И. Менделеева и периодическая система
элементов. Периодические свойства элементов и их соединений. s -, p -, d -, f –
элементы. Расположение металлов в периодической системе элементов.
Особенности электронного строения атомов металлов. Общие физические и
химические свойства металлов, нахождение в природе. Методы получения.
Лекция 2.Физико - химические свойства s –металлов, взаимодействие с простыми
и сложными веществами. Щелочные и щелочноземельные металлы. Химические
свойства соединений s – элементов с водородом, кислородом, азотом, серой,
галогенами. Жесткость воды. Основные виды жесткости. Методы определения
жесткости, способы устранения.
Лекции 3.Физико - химические свойства d – металлов. Закономерности изменения
свойств по группам и периодам. Особенности химического поведения. Кислотноосновные и окислительно-восстановительные свойствасоединений d – металлов
различных степеней окисления.
Лекция 4.
Комплексные соединения d – металлов. Получение, свойства,
применение. Химические свойства некоторых металлов - хрома, марганца,
элементов семейства железа, меди, цинка. Металлообразные соединения d –
металлов.
Лекция 5. Физико - химические свойства p – элементов 13, 14 и 15 групп
периодической системы, относящихся к металлам. Закономерности изменения
химических свойств в группах, взаимодействие с простыми и сложными
веществами. Химические свойства некоторых соединений: гидридов, оксидов,
галогенидов. Полупроводники. Получение и применение кремния и германия.
ОЛ – 1, Гл.3; ОЛ – 2, Гл.1; ОЛ- 3, Гл.1; ОЛ – 4, Гл.1, 7,8; ОЛ - 5, Гл.1,11,12; ОЛ -6,
Р.1,2.
Лабораторные работы
Занятие1.Определениежесткости воды.МП-10 ч.2 с.19-27
Занятие 2. Химические свойства d – металлов –Сr, Mn, Cu.ОЛ -4, Гл.7,8; ОЛ -6,
с.60-79; МП-10 ч.2 с.36-47
Занятие 3.Химические свойства d – металлов – Fe, Со, Zn.ОЛ -4, Гл.7,8; ОЛ -6,
с.60-79; МП-10 ч.2 с.47-52
Занятие 4.Химические свойства p – элементов – Al, Sn, Pb.МП-10 ч.2 с.28-35
Занятие 5.Контроль выполнения модуля 1.
88
МОДУЛЬ 2: Коррозия и защита металлов от коррозии.
Лекции.
Лекция 6. Коррозия. Классификация коррозионных процессов по
виду
разрушений и активности коррозионных сред. Типы коррозионных процессов.
Показатели коррозии: глубинный, массовый, объемный, токовый. Химическая
коррозия.
Механизм высокотемпературной газовой коррозии. Кинетика
окисления металлов. Защитные свойства коррозионных пленок.ОЛ-1, Гл.18; ОЛ-2,
Гл. 21; ОЛ – 3, Гл.18.
Лекция 7. Электрохимическая коррозия. Механизм электрохимической коррозии:
анодное окисление металла, катодное восстановление окислителя. Водородная и
кислородная деполяризация. Термодинамическая устойчивость металлов в водной
среде. Влияние различных факторов на скорость
коррозии. Примеры
коррозионных процессов.ОЛ-1, Гл.18; ОЛ-2, Гл. 21; ОЛ – 3, Гл. 18.
Лекция 8. Методы защиты металлов от коррозии: рациональное конструирование,
легирование металлов, создание защитных покрытий,
обработка коррозионной
среды, электрохимическая защита.ОЛ-1, Гл.19; ОЛ-2, Гл. 22; ОЛ – 3, Гл. 18.
Лекция 9. Полимерные и композиционные материалы. Физико-химические
свойства, получение и применение.ОЛ – 6.
Лабораторные работы
Занятие6. Коррозия.МП-10 ч.2 с.53-60
Занятие 7. Защита металлов от коррозии.МП-10 ч.2 с.60-66
Занятие 8. Химические и электрохимические процессы при коррозии.ОЛ-1, Гл.8
Занятие9.Защита модуля 3.
Самостоятельная работа
Самостоятельная работа студента заключается в проработке материала лекций,
подготовке к выполнению лабораторных работ, входному контролю готовности к
выполнению лабораторной работы, выполнении индивидуального задания по
тематике лабораторной работы, которое расценивается как защита лабораторной
работы. Индивидуальное задание включает в себя 4-6 практических и расчетных
задач. Самостоятельная работа является как домашней (в том числе под контролем
преподавателя с помощью современных информационных технологий), так и
аудиторной (под контролем преподавателя на консультациях ).
Домашнее задание (ДЗ1):Химия элементов и их соединений (модуль 1) выдается
на 1 неделе, сдача на 8 неделе .
Домашнее задание (ДЗ2): Коррозия и защита металлов от коррозии (модуль 2)
выдача на 9 неделе, сдача на 16 неделе.
ЛИТЕРАТУРА
Основнаялитература (ОЛ)
1. ГуровА.А.,Бадаев Ф.З., Овчаренко Л.П., Шаповал В.Н. Химия. М.: Изд-во МГТУ
им. Н.Э. Баумана, 2004. -748 с.
2. Горбунов А.И., Гуров А.А.. Филиппов Г.Г., Шаповал В.Н. Теоретические основы
общей химии. – М.: МГТУ, 2001-719с.
3. ГорбуновА.И.,Филиппов Г.Г., Федин В.И. Химия. М.: Изд-во МГТУ им. Н.Э.
Баумана, 2007. - 687 с.
4. КарапетьянцМ.Х.,Дракин С.И. Общая и неорганическаяхимия. М.: Химия,2000 –
593 с.
5. ЕрмолаеваВ.И.,Горшкова В.М., Слынько Л.Е. Химияэлементов. Учеб. пособие. М.: Изд-во МГТУ им. Н.Э. Баумана, 2007.- 176 с.
89
6. Двуличанская Н.Н., Слынько Л.Е., Пясецкий В.Б. Композиционные материалы.
Физико-химические свойства. Учеб.пособие.- М.: Изд-во МГТУ им. Н.Э. Баумана,
2008.- 47 с.
Дополнительнаялитература (ДЛ)
7. Фадеев Г.Н., Двуличанская Н.Н., Степанов М. Б., Матакова С.А.
Решениезадачпокурсу «Химия» длянехимическихвузов. Ч. 2 - М.:Домпедагогики,
2008.– 64с.
8. Задачи по общей и неорганической химии: учеб.пособие для студентов высш.
учеб. заведений / Р.А. Лидин, В.А. Молочко, Л.Л. Андреева; под ред. Р.А. Лидина.
– М.:Гуманитар. изд. центрВладос, 2004. – 383 с.
9. Задачи и вопросыпообщей и неорганическойхимии с ответами и решениями /
Ю.М. Коренев, А.Н. Григорьев, Н.Н. Желиговская, К.М. Дунаева. – М.: Мир, 2004.
– 368 с.
Методические пособия, изданные в МГТУ (МП)
10. Березина С.Л., Голубев A.M., Горшкова В.М. и др. Лабораторный практикум по
курсу химии для технических университетов, ч. 1, ч.2: Методические указания.
/Под ред. Фадеева Г.Н. – М.: МГТУ, 2005, 2009.
11. Ермолаева В.И., Романко О.И., Смирнов А.Д., Батюк В.А. Методические
указания к выполнению домашнего задания по базовому курсу химии (примеры
решения). Ч.1. - М.:Изд-во МГТУ им. Н.Э. Баумана, 2001. – 27 с. 15.
12.Методические разработки кафедры к лабораторным работам.
13. Сборник контрольных вопросов и задач для защиты лабораторных работ по
курсу химии: Метод.указания /С.Л. Березина, А.М. Голубев, Е.Е. Гончаренко и др.;
Под ред. А.М. Голубева - М.: Изд-во МГТУ им.Н.Э. Баумана, 2009. – 84 с.
Электронные учебные пособия (ЭП)
14.Современная химия в техническом университете. Химия элементов и их
соединений: электронное учебное пособие / Ермолаева В.И., Волков А.А.,
Горшкова В.М., Слынько Л.Е.- ФГУП НТЦ «Информрегистр», № 0320801585, от
4.08.08
Интернет-ресурсы
15. http://window.edu.ru/catalog?p_rubr=2.2.74.7
16. http://www.ximicat.com/index.php?razdel=obs
17. http://rushim.ru/books/books.htm
ОБЩАЯ И НЕОРГАНИЧЕСКАЯ ХИМИЯ
для бакалавров ИУ – 4
Дисциплина состоит из 2-х учебных модулей
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Лекции
Лабораторные работы
Домашнее задание текущее
Контроль по модулю 1
Сроки проведения или
выполнения, недели
1-6
1-6
1-6
7
Модуль 2
90
Трудоемкость, Примечания
часы
12
10
10
2
Виды аудиторных занятий и
самостоятельной работы
Лекции
Лабораторные работы
Домашнее задание текущее
Контроль по модулю 2
Сроки проведения или
выполнения, недели
8 - 17
8 - 17
9 - 15
16
Трудоемкость, Примечания
часы
18
8
6
2
МОДУЛЬ 1:Электрохимические процессы в электролитах. Коррозия и защита металлов
Лекции
Лекция
1.Электрохимические
процессы.
Электрохимические
цепи
обратимые
и
необратимые. Процессы в гальваническом
элементе.
Классификация
гальванических
элементов.
ОЛ –1, Раздел VII, §16; ОЛ-4, Гл. 16
Лекция2.Процессы при электролизе. Потенциал
разложения электролита. Законы Фарадея.
Последовательность разряда ионов на электродах.
Понятие
о
кинетике
электрохимических
процессов. Поляризация электродов.
ОЛ – 1, Раздел VII, §17 ; ОЛ-4, Гл. 17.2
Лекция3.Применение
электрохимических
процессов. Химические источники тока (ХИТ).
Первичные и вторичные ХИТ. Применение
электролиза
ОЛ – 1, Раздел VII, §17 ; ОЛ-4, Гл. 17.3
Лекция
4.Коррозия
и защита
металлов.
Классификация коррозионных процессов по виду
разрушений и активности коррозионных сред.
Типы коррозионных процессов. Показатели
коррозии: глубинный, массовый, объемный,
токовый. Химическая коррозия. Термодинамика
и кинетика окисления металлов. Защитные
свойства пленок. Фактор Пиллинга — Бедвордса.
ОЛ -1, Раздел VIII; ОЛ – 4, Гл. 18
Лекция5.Электрохимическая коррозия. Механизм
электрохимической коррозии. Водородная и
кислородная деполяризация. Влияние различных
факторов на скорость коррозии. Термодинамика
и кинетика электрохимической коррозии. Расчет
электродвижущей силы (ЭДС) коррозионного
элемента в аэрированных и деаэрированных
средах.Примеры коррозионных процессов.
ОЛ -1, Раздел VIII; ОЛ – 4, Гл. 18
Лекция6.Методы защиты металлов от коррозии.
Повышение коррозионной стойкости металлов и
сплавов.
Изменение
состава
и
свойств
коррозионной среды. Применение защитных
покрытий. Электрохимическая защита, виды и
механизм действия
ОЛ -1, Раздел VIII; ОЛ – 4, Гл. 18
Лабораторные работы
Занятие 1.Электрохимические процессы в растворах электролитов
Занятие 2. Коррозия и защита металлов и сплавов
Занятие 3. Защита металлов от коррозии
Занятие 4. Контроль выполнения модуля 1
МОДУЛЬ 2: Химия элементов и их соединений
Лекции
Лекция7.Периодическая система элементов: s - , p
- , d - , f – элементы. Физические и химические
свойства элементов как периодическая функция
заряда ядра и электронной конфигурации атомов.
Простые и сложные вещества. Металлы и
неметаллы.
Расположение
металлов
в
периодической системе элементов: s - , p - , d - , f
— металлы. Понятие о металлической связи.
Общие физические и химические свойства
металлов. Основные методы получения металлов
из руд.
ОЛ — 1, Раздел II, § 3.8, 3.9; ОЛ — 2, Раздел 1,
§1.1
Лекция 8.Химия s –элементов 1 группы
периодической системы. Щелочные металлы.
Физико-химические свойства, нахождение в
природе, методы получения. Взаимодействие
металлов с простыми и сложными веществами.
Соединения металлов с кислородом, водородом,
галогенами, свойства соединений. Применение
щелочных металлов и их соединений в технике
ОЛ — 2, Раздел 1, §1.2; ОЛ — 3, Гл. 7, §§ 7.1, 7.2;
ОЛ — 4, Гл. 19
Лекция 9.Химия s –элементов 2 группы
периодической системы. Физико-химические
свойства, нахождение в природе, методы
получения. Взаимодействие металлов с простыми
и сложными веществами. Соединения металлов с
кислородом, водородом, галогенами, свойства
соединений. Отличие свойств бериллия и магния.
Подгруппа
щелочноземельных
металлов.
Применение металлов и их соединений в технике.
Химия воды. Проблемы водоподготовки. Понятие
о жесткости воды. Основные виды жесткости.
Методы устранения и снижения
91
ОЛ — 2, Раздел 1, §1.2; ОЛ — 3, Гл. 7, §§ 7.1, 7.2;
ОЛ — 4, Гл. 19
Лекция10. Химия d–элементов. Переходные
металлы.
Физико-химические
свойства,
нахождение в природе, методы получения.
Закономерности в изменении электронных
конфигураций атомов элементов по группам и
периодам. Особенности химического поведения
d–элементов. Характерные степени окисления.
Сопоставление
кислотно-основных
и
окислительно-восстановительных
свойств
соединений в различных степенях окисления d–
элемента.
ОЛ — 2, Раздел 1, §§1.3-1.4; ОЛ — 3, Гл. 8, §§
8.1- 8.9; ОЛ — 4, Гл. 21
Лекция11. Химические свойства некоторых
металлов - медь, цинк, хром, марганец, элементы
семейства
железа,
платиновые
металлы.
Металлоподобные
и
интерметаллические
соединения d – элементов. Применение металлов
и их соединений в технике.
ОЛ — 2, Раздел 1, §§1.3-1.4; ОЛ — 3, Гл. 8, §§
8.1- 8.9; ОЛ — 4, Гл. 21
Лекция12.Понятие о комплексных соединениях.
Образование комплекса с позиций метода
валентных связей.
ОЛ — 2, Раздел 1, §§1.3-1.4; ОЛ — 3, Гл. 8, §§
8.1- 8.9; ОЛ — 4, Гл. 21
Лекция 13. Химия
p–элементов. Общая
характеристика
p–элементов,
нарастание
неметаллического характера свойств элементов
по периоду. Общая характеристика свойств p–
элементов 13 (IIIА) группы (В, Al, Ga, In, Tl).
Общая характеристика свойств p–элементов 14
(IVА) группы (C, Si, Ge, Sn, Pb).
ОЛ — 2, Раздел 2, §§2.1-2.6; ОЛ — 3, Гл. 7, §§
7.3- 7.8; ОЛ — 4, Гл. 22
Лекция14.Физические и химические свойства p–
элементов 15 (N, P, As, Sb, Bi) и 16 (O, S, Se, Te,
Po) групп. Распространенность в природе, методы
получения. Химические свойства некоторых
соединений: оксидов, гидридов, галогенидов.
Применение в технике
ОЛ — 2, Раздел 2, §§2.1-2.6; ОЛ — 3, Гл. 7, §§
7.3- 7.8; ОЛ — 4, Гл. 22
Лекции 15 - 16. Элементарные и бинарные
алмазоподобные полупроводники. Механизм
собственной и примесной проводимости кремния
и германия с позиций теории химической связи.
Физико-химические
свойства
кремния
и
германия. Свойства соединений типа AIIIBVи
AIIBVI.
Методы
получения
и
очистки
полупроводников.
ОЛ — 5, §§1-8
92
Лабораторные работы
Занятие 5. Свойства s-металлов. Определение жесткости воды
Занятие6. Химические свойства d – металлов (Mn, Cu,Fe, Co)
Занятие7. Химические свойства p – элементов (B, Al, Sn, Pb)
Занятие8.Контроль выполнения модуля 2
Домашние задания
ДЗ 1.Электрохимические процессы. Коррозия и защита металлов. Выдача - 1 неделя, сдача - 5 неделя
ДЗ 2.Химия элементов и их соединений. Выдача - 6 неделя, сдача - 16 неделя
Самостоятельнаяработа
Самостоятельная работа студента заключается в проработке материала лекций, подготовке к выполнению
лабораторных работ, входному контролю готовности к выполнению лабораторной работы, выполнении
индивидуального задания по тематике лабораторной работы, которое расценивается как защита
лабораторной работы. Индивидуальное задание включает в себя 3-5 практических и расчетных задач.
Самостоятельная работа является как домашней, так и аудиторной под контролем преподавателя (КСР)
ЛИТЕРАТУРА
Основная литература (ОЛ)
1.
2.
3.
4.
5.
Гуров А.А., Бадаев Ф.З., Овчаренко Л.П., Шаповал В.Н. Химия. М.: Изд-во МГТУ им. Н.Э.
Баумана, 2004. -748 с.
Ермолаева В.И., Горшкова В.М., Слынько Л.Е. Химия элементов. Учеб.пособие. - М.: Изд-во МГТУ
им. Н.Э. Баумана, 2007.- 176 с.
Карапетьянц М.Х., Дракин С.И. Общая и неорганическая химия. М.: Химия,2000 –593 с.
Горбунов А.И., Филиппов Г.Г., Федин В.И. Химия. М.: Изд-во МГТУ им. Н.Э. Баумана, 2007. - 687
с.
Ермолаева В.И., Двуличанская Н.Н., Горшкова В.М. Учеб.пособие. - Физико-химические свойства
полупроводниковых материалов. М.: Изд-во МГТУ им. Н.Э. Баумана, 2006.- 43 с.
6.
Дополнительная литература (ДЛ)
7.
8.
Двуличанская Н.Н., Слынько Л.Е., Пясецкий В.Б. Композиционные материалы. Физико-химические
свойства: Учеб.пособие. - М.: Изд-во МГТУ им. Н. Э. Баумана, 2008. – 48 с.
Задачи и вопросы по общей и неорганической химии с ответами и решениями / Ю.М. Коренев, А.Н.
Григорьев, Н.Н. Желиговская, К.М. Дунаева. – М.: Мир, 2004. – 368 с.
9.
Методические пособия, изданные в МГТУ (МП)
Лабораторный практикум по курсу химии для технических университетов: Методические указания.
/ С.Л. Березина, A.M. Голубев, В.М. Горшкова и др. Под ред. Фадеева Г.Н. – Ч.2 - М.: Изд-во МГТУ
им.Н.Э.Баумана, 2009.– 87с.
11.
Теоретические основы неорганической химии: метод.указания к решению задач / В.И. Ермолаева,
Н.Н. Двуличанская.-М.: Изд-во МГТУ им. Н.Э. Баумана,2011.-61 с.
12.
Сборник контрольных вопросов и задач для защиты лабораторных работ по курсу химии:
Метод.указания /С.Л. Березина, А.М. Голубев, Е.Е. Гончаренко и др.; Под ред. А.М. Голубева - М.: Изд-во
МГТУ им.Н.Э. Баумана, 2009. – 84 с.
13.
Интернет – источники
10.
14.
15.
16.
http://window.edu.ru/catalog?prubr=2.2.74.7
http://www.ximicat.com/index.php?razdel=neo
http://rushim.ru/books/books.htm
93
ХИМИЯ
Для ЮР
Дисциплина состоит из 3-х учебных модулей
Модуль 1
Виды аудиторных
занятий и
самостоятельной
работы
Лекции
Лабораторные работы
Домашнее задание
текущее
Контроль по модулю 1
Сроки проведения
или выполнения,
недели
Трудоемко
сть, часы
1 –7
1 –7
2–7
8
14
12
7
4
Примеча
ния
Модуль 2
Виды аудиторных
занятий и
самостоятельной
работы
Лекции
Лабораторные работы
Домашнее задание
текущее
Контроль по модулю 2
Сроки проведения
или выполнения,
недели
Таблица 8.3.2
Трудоемко Примеча
сть, часы
ния
8– 12
8– 12
8 – 12
10
10
12
12
4
Модуль 3
Виды аудиторных
занятий и
самостоятельной
работы
Лекции
Лабораторные работы
Домашнее задание
текущее
Контроль по модулю 1
Сроки проведения
или выполнения,
недели
Трудоемко
сть, часы
13 – 17
13 – 17
13 – 16
16
10
12
17
4#
94
Примеча
ния
МОДУЛЬ1:Строение вещества. Основные законы химии
Лекции
Лекция1.Химия как раздел естествознания, значение химии для науки и технологии. Вещество и его
строение. Понятие о квантово-механической модели атома водорода. Вероятностный характер процессов в
микромире: принцип неопределенности Гейзенберга, волна де-Бройля, волновое уравнение Шредингера.
Квантовые числа. Атомная орбиталь. Формы орбиталей.
ОЛ – 1, Гл.3; ОЛ – 2, Гл. 1; ОЛ − 3, Р-л I: Гл. 2; ОЛ – 4, Гл. 1; ДЛ − 6, 10.
Лекция2.Строение многоэлектронных атомов. Принцип Паули. Правила Хунда и Клечковского. Принцип
минимальной энергии. Электронные конфигурации атомов. Энергетические характеристики атомов: энергия
ионизации, сродство к электрону, электроотрицательность. Периодические свойства элементов.
Периодический закон Д.И. Менделеева.
ОЛ – 1, Гл.3; ОЛ – 2, Гл. 1; ОЛ − 3, Р-л I: Гл. 2; ОЛ – 4, Гл. 2.
Лекция3.Химическая связь. Характеристики связи: энергия, длина, валентный угол, полярность. Типы связи.
Понятие о методе валентных связей. Гибридизация атомныхорбиталей. σ - и π - связи. Геометрическая
конфигурация молекул. Электрический момент диполя молекулы. Метод Гиллеспи.
ОЛ – 1, Гл. 4; ОЛ – 3, Р-л II: Гл. 3, Р-л II: Гл. 1, 3; ОЛ - 4, Гл. 2.
Лекция 4. Ионная связь и ее особенности. Межмолекулярные взаимодействия. Водородная связь.
Металлическая связь и особенности строения металлов. Основные физические и химические свойства
металлов.
ОЛ – 1, Гл. 4; ОЛ – 3, Р-л II: Гл. 4, Р-л II: Гл. 4, 5; ОЛ - 4, Р-л IV: Гл. 11; ДЛ − 5, 10.
Лабораторные работы
Занятие1.Основные понятия и законы химии
Занятие2.Основные классы неорганических соединений
Занятие3.Определение концентрации раствора методом титрования
Занятие4. Жесткость воды
Занятие 5. Строение атомов и химическая связь
Занятие 6. Химические свойства металлов и их соединений
Занятие 7.Контроль модуля1
МОДУЛЬ2:Основные закономерности протекания химических процессов
(термодинамика, кинетика)
Лекции
Лекция5.Элементы химической термодинамики. Первый закон термодинамики. Термодинамические
функции: энтальпия и внутренняя энергия. Тепловой эффект реакции. Закон Гесса. Термохимические
расчеты.
ОЛ – 1, Гл. 5; ОЛ – 2, Гл. 6; ОЛ – 3, Р-л V: Гл. 1; ОЛ – 4, Гл. 5; ДЛ − 6, 8.
Лекция 6. Второй закон термодинамики. Понятие об энтропии. Изменение энтропии в процессах. Третий
закон термодинамики. Расчет абсолютных значений стандартных энтропий веществ. Объединенное
уравнение первого и второго законов. Термодинамические критерии направленности химических процессов.
Энергия Гиббса.
ОЛ – 1, Гл. 6; ОЛ – 2, Гл. 7; ОЛ – 3, Р-л V: Гл. 2; ОЛ – 4, Гл. 5; ДЛ − 6, 8.
Лекция 7.Химическое равновесие в гомогенной системе. Константа равновесия. Уравнения изотермы,
изобары, изохоры химической реакции. Особенности равновесия в гетерогенных системах.
ОЛ – 1, Гл. 10 − 12; ОЛ – 2, Гл. 10 − 12; ОЛ – 3, Р-л V: Гл. 3; ОЛ – 4, Гл. 6; ДЛ − 6, 8.
Лекция 8. Элементы химической кинетики. Понятие о скорости реакции. Зависимость скорости реакции от
концентрации (закон действующих масс). Кинетические уравнения реакций нулевого, 1-го и 2-го порядков.
Лекция 9. Зависимость скорости реакции от температуры. Правило Вант-Гоффа. Уравнение Аррениуса.
Понятие об энергии активации. Энергетическая диаграмма реакции. Особенности кинетики гетерогенных
процессов. Гомогенный и гетерогенный катализ.
ОЛ – 1, Гл. 7 – 9; ОЛ – 2, Гл. 10; ОЛ – 3, Р-л V: Гл. 4; ОЛ – 4, Гл. 7; ДЛ − 6, 10.
Лабораторные работы
Занятие8.Химическая термодинамика
Занятие9.Химическое равновесие в гомогенных системах
Занятие10.Закономерности протекания химических процессов
95
Занятие 11. Химическая кинетика
Занятие12.Контрольмодуля2
МОДУЛЬ3:Основыэлектрохимических процессов
Лекции
Лекции 10. Растворы. Классификация растворов. Энергетика образования растворов. Понятие о
термодинамике идеальных растворах. Закон Рауля и следствия из него. Осмос. Растворы электролитов.
ОЛ – 1, Гл. 13; ОЛ – 2, Гл. 11; ОЛ – 3, Р-л III: Гл. 2; ОЛ – 4, Гл. 8; ДЛ − 8.
Лекция 11. Теория электролитической диссоциации Аррениуса. Сильные и слабые электролиты. Степень
диссоциации. Константа диссоциации. Закон разбавления Оствальда. Электролитическая диссоциация воды.
Ионное произведение воды. Водородный (рН) и гидроксидный (рОН) показатели. Активность и
коэффициент активности.
ОЛ – 1, Гл. 14; ОЛ – 2, Гл.12, 13; ОЛ – 3, Р-л III: Гл. 2; ОЛ – 4, Гл. 8; ДЛ − 6, 10.
Лекция 12. Ионное равновесие в системе раствор – осадок. Произведение растворимости. Диссоциация
комплексных ионов. Константа нестойкости. Реакции обмена в электролитах. Гидролиз солей.
ОЛ – 1, Гл. 14; ОЛ – 2, Гл. 13; ОЛ – 3, Р-л III: Гл. 2; ОЛ – 4, Гл. 8; ДЛ − 6.
Лекция 13. Возникновение двойного электрического слоя на границе металл - электролит. Электродный
потенциал. Уравнение Нернста для электродного потенциала и электродвижущей силы (ЭДС)
электрохимической цепи. Стандартный водородный электрод. Ряд стандартных электродных потенциалов.
Гальванический элемент Даниэля-Якоби.
ОЛ – 1, Гл. 16 – 17; ОЛ – 2, Гл. 17 – 18; ОЛ – 4, Гл. 9; ДЛ − 5, 10.
Лекция 14. Электролиз. Ряды разряжаемости ионов. Законы Фарадея. Химические источники тока,
первичные элементы и аккумуляторы. Коррозия металлов. Классификация коррозионных процессов по виду
разрушений и активности коррозионных сред.
ОЛ – 1, Гл. 17; ОЛ – 2, Гл. 13; ОЛ – 4, Гл. 9; ДЛ − 6, 8.
Лекция 15-16. Электрохимическая коррозия. Механизм электрохимической коррозии. Водородная и
кислородная деполяризация. Контактная коррозия и коррозия сплавов. Влияние различных факторов на
скорость коррозии. Примеры коррозионных процессов. Защита металлов и сплавов от коррозии.
Механические и электрохимические методы защиты.
ОЛ – 1, Гл. 18 – 19; ОЛ – 2, Гл. 22 – 23; ОЛ – 4, Гл. 9; ДЛ − 6, 8.
Лекция 17. Обзорная лекция. Практическое применение химических процессов. Химия и экология.
Безотходные химические производства.
ОЛ – 4; ДЛ – 9
Лабораторные работы
Занятие13.Окислительно-восстановительные реакции
Занятие14. Растворы электролитов
Занятие15.Закономерности протекания электрохимических процессов
Занятие 16. Коррозия металлов и защита металлов от коррозии
Занятие17.Контроль модуля 3
Домашние задания
ДЗ 1.Строение атомов и химическая связь. Химические свойства металлов. Выдача -2неделя, сдача-7неделя.
ДЗ 2.Закономерности протекания химических процессов (термодинамика, равновесие, кинетика). Выдача - 8
неделя, сдача - 12неделя.
ДЗ 3. Электрохимические явления и процессы (электролиты, гальванические элементы, электролиз,
коррозия металлов). Выдача − 13 неделя, сдача – 16 неделя.
Самостоятельная работа
Самостоятельная работа студента заключается в проработке материала лекций, подготовке к
выполнению лабораторных работ, входному контролю готовности к выполнению лабораторной работы,
выполнении индивидуального задания по тематике лабораторной работы, которое расценивается как защита
лабораторной работы. Индивидуальное задание включает в себя 2−4 практических и расчетных задач.
Самостоятельная работа является как домашней, так и аудиторной под контролем преподавателя (КСР).
Литература
96
Основная литература (ОЛ)
Гуров А.А., Бадаев Ф.З., Овчаренко Л.П., Шаповал В.Н. Химия. М.: Изд-во МГТУ им. Н.Э. Баумана, 2004. −
748 с.
Горбунов А.И., Гуров А.А.. Филиппов Г.Г., Шаповал В.Н. Теоретические основы общей химии. – М.:
МГТУ, 2001. − 719 с.
Ахметов Н.С. Общая и неорганическая химия. М.: Высшая школа, 1998. – 743 с.
Коровин Н.В. Общая химия. М.: Высшая школа, 1998. – 557 с.
Дополнительная литература (ДЛ)
Лидин Р.А., Молочко В.А., Андреева Л.Л. Химические свойства неорганических соединений. – М.: Химия,
1996.
Лидин Р.А., Молочко В.А., Андреева Л.Л. Задачи по общей и неорганической химии. – М.: Гуманитар. Изд.
Центр ВЛАДОС, 2004.
Фримантл М. Химия в действии. М.: Мир. – 1998. Т.1 – 528 с., Т.2. – 620 с.
Задачи по общей и неорганической химии: учеб.пособие для студентов высш. учеб. заведений / Р.А. Лидин,
В.А. Молочко, Л.Л. Андреева; под ред. Р.А. Лидина. – М.: Гуманитар. изд. центр Владос, 2004. – 383 с.
Сборник задач и упражнений по общей и неорганической химии: учеб. Пособие для студентов высш.
учеб.заведений / под ред. Павлова Н.Н. – М.: Дрофа, 2005. – 240 с.
Пузаков С.А., Попков В.А., Филиппова А.А. Сборник задач и упражнений по общей химии: учеб.пособие
для студентов высш. учеб. Заведений. − М.: Высшая школа, 2004. – 254 с.
Методические пособия, изданные в МГТУ (МП)
Березина С.Л., Голубев A.M., Горшкова В.М. и др. Лабораторный практикум по курсу химии для
технических университетов, ч. 1, ч. 2: Методические указания. /Под ред. Фадеева Г.Н. – М.: МГТУ, 2005,
2009.
Сборник контрольных вопросов и задач для защиты лабораторных работ по курсу химии: Метод.указания
/С.Л. Березина, А.М. Голубев, Е.Е. Гончаренко и др.; Под ред. А.М. Голубева - М.: Изд-во МГТУ им.Н.Э.
Баумана, 2009. – 84 с.
Методические указания к выполнению домашнего задания по курсу общей химии: Методические указания /
Бадаев Ф.З., Голубев А.М., Горшкова В.М. и др.; под ред. Ермолаевой В.И. − М.: МГТУ, 2003. − 48 с.
Методические разработки кафедры к лабораторным работам.
Интернет – источники
http://window.edu.ru/catalog?prubr=2.2.74.7.4
http://www.ximicat.com/index.php?razdel=neo
http://rushim.ru/books/books.htm
ФИЗИЧЕСКАЯ ХИМИЯ
для бакалавров ФН-4
Дисциплина состоит из 3-х учебных модулей
Модуль 1
Виды аудиторных занятий
и самостоятельной работы
Лекции
Лабораторные работы
Домашнее задание текущее
Контроль по модулю 1
Сроки проведения или
выполнения, недели
8
8
Не предусмотрено
8
Трудоемкость
, часы
18
10
Примечания
2
Модуль 2
Виды аудиторных занятий
и самостоятельной работы
Лекции
Лабораторные работы
Домашнее задание текущее
Контроль по модулю 2
Сроки проведения или
выполнения, недели
13
13
Не предусмотрено
13
97
Трудоемкость
, часы
9
4
2
Примечания
Модуль 3
Виды аудиторных занятий
и самостоятельной работы
Лекции
Лабораторные работы
Контроль по модулю 2
Сроки проведения или
выполнения, недели
17
17
17
Трудоемкость
, часы
7
3
2
Примечания
МОДУЛЬ 1: Физико-химическое состояние вещества
Лекции
МОДУЛЬ 1: Физико-химическое
состояние вещества
Лекции
Лекции
14.
Химическая
термодинамика.
Функции
состояния
–
внутренняя энергия, энтальпия.
Функции процесса – теплота,
работа. Расчет функций состояния
в изопроцессах. Закон Гесса и
следствия из него. Первый закон
термодинамики.
Температурная
зависимость
стандартного
теплового эффекта реакции. Закон
Кирхгофа. Второй и третий законы
термодинамики.
Энтропия.
Уравнение Клаузиуса. Зависимость
энтропии от температуры, давления
и объема. Изменение энтропии в
процессах. Уравнение Больцмана.
Температурная
зависимость
стандартной энтропии химической
реакции. Критерии направленности
процесса. Уравнение Гиббса –
Гельмгольца.
Методы
расчета
стандартной
энергии
Гиббса
химических реакций. Системы
переменного состава. Химический
потенциал. Условия равновесия.
Лекции 5 – 6. Фазовые равновесия.
Фаза,
компонент,
число
термодинамических
степеней
свободы. Правило фаз Гиббса.
Однокомпонентные
гомогенные
системы.
Расчет
термодинамических
функций
идеальных газов по их спектрам.
Определение параметров молекул
по
спектральным
данным.
Химический потенциал компонента
в идеальных газовых растворах.
Реальные
газы.
Уравнение
состояния
с
вириальными
коэффициентами. Другие формы
уравнения состояния. Принцип
соответственных
состояний.
Фугитивность
и
активность.
Химический потенциал реального
газа. Фазовые равновесия в
однокомпонентных гетерогенных
системах.
Температурная
зависимость
давления
насыщенного пара. Уравнение
Клапейрона
–
Клаузиуса.
Эмпирическое правило Трутона.
Примеры
фазовых
диаграмм.
Применение правила фаз Гиббса.
Фазовые переходы: первого и
второго рода, монотропные и
энантиотропные.
Двухкомпонентные системы.
Метод
физико-химического
анализа. Применение правила фаз
Гиббса. Виды равновесий. Физикохимические основы перегонки
растворов. Равновесие «жидкий
98
раствор – кристалл». Расчеты по
диаграммам состояния.
Трехкомпонентные системы.
Применение правила фаз Гиббса.
Графическое изображение состава.
Типы диаграмм состояния.
Лекции 7 – 10. Растворы
Классификация
растворов.
Межмолекулярное и химическое
взаимодействие.
Парциальные
молярные величины. Уравнение
Гиббса
–
Дюгема.
Теплоты
растворения
и
разбавления.
Давление
насыщенного
пара
компонента над раствором. Законы
Рауля и Генри. Растворимость
газов. Коллигативные свойства.
Идеальные,
неидеальные,
предельно разбавленные растворы.
Экстракция.
Активность.
Коэффициент активности. Первое и
второе стандартные состояния.
Методы определения активности и
коэффициента
активности
компонентов раствора.
Лекции 11 — 13. Химическое
равновесие
Термодинамическая
теория
химического сродства. Химическая
переменная. Закон действующих
масс.
Стандартная
термодинамическая
константа
равновесия и способы ее расчета.
Статистический метод расчета
констант равновесия газофазных
реакций. Эмпирические константы
равновесия,
их
связь
со
стандартной термодинамической
константой равновесия. Расчет
состава
равновесной
смеси.
Уравнения изотермы, изобары и
изохоры химической реакции.
Влияние внешних факторов на
смещение химического равновесия.
Химическое
равновесие
в
гетерогенных системах.
Лабораторные работы
Занятие 1. Исследование веществ методом электронного парамагнитного
резонанса
Занятие 2. Спектрофотометрическое определение концентрации веществ в
растворах
Занятие 3. Физико-химическое равновесие в системе фенол – вода.
Контроль выполнения модуля 1. Срок – 8 неделя.
МОДУЛЬ 2: Физико-химическое описание химических процессов
Лекции
МОДУЛЬ 2: Физико-химическое
описание химических процессов
Дебая
–
Хюккеля.
Термодинамические
свойства
ионов.
Движение
ионов
в
электрическом поле. Электрическая
проводимость
растворов
электролитов.
Электрическая
подвижность
ионов.
Числа
переноса. Уравнение Кольрауша.
Кондуктометрия и ее применение.
Константа и степень диссоциации
Лекции
Лекции 14 — 16. Электрохимия.
Растворы
электролитов.
Электролитическая диссоциация.
Средняя
ионная
активность
электролита.
Коэффициент
активности.
Электростатическая
теория
сильных
электролитов
99
слабого
электролита.
Закон
последовательные.
Метод
разведения Оствальда.
лимитирующей стадии. Метод
Электрохимические реакции.
стационарных
концентраций.
Термодинамическая теория ЭДС.
Теории химической кинетики:
Электродные
потенциалы.
активных
столкновений
и
Уравнения Нернста и Петерса.
активированного
комплекса.
Типы
электродов
и
Мономолекулярные реакции в
электрохимических
цепей.
газовой фазе. Схема Линдемана.
Диаграмма
Пурбе.
Цепные
реакции
и
их
Потенциометрия
и
ее
механизм.
Неразветвленные
и
применение.
Типы
разветвленные
процессы.
электрохимических
источников
Предельные
явления
в
тока и топливных элементов.
разветвленных
процессах.
Лекции 17 — 19. Химическая
Фотохимические
реакции.
кинетика.
Гомогенные реакции в жидкой
Кинетика
гомогенных
фазе. Быстрые и медленные
реакций. Кинетические кривые.
реакции.
Уравнение
Скорость, молекулярность, порядок
Смолуховского.
Уравнение
и константа скорости реакции.
Бренстеда – Бьеррума.
Факторы, влияющие на скорость
Гетерогенные
реакции.
реакции. Формальная кинетика.
Кинетика
зародышеобразования
Элементарные
необратимые
новой фазы. Уравнения степенного
реакции
различных
порядков.
типа,
Ерофеева
–
Аврами.
Время полупревращения. Методы
Гетерогенные
процессы
с
определения частного порядка
диффузионным лимитированием.
реакции по компоненту. Сложные
реакции: обратимые, параллельные,
Лабораторные работы
Занятие
4.
Экспериментальное
определение
термодинамических
характеристик гальванического элемента.
Занятие 5. Потенциометрическое титрование
Занятие 6. Кинетика разложения пероксида водорода при гомогенном
катализе
Контроль выполнения модуля 2. Срок – 13 неделя.
МОДУЛЬ 3: Управление физико-химическими процессами
Лекции
МОДУЛЬ 3: Управление физикохимическими процессами
Лекции 20 — 25. Катализ
Активность и селективность
катализатора.
Механизмы
каталитического
действия.
Автокатализ,
ингибирование.
Гомогенный
катализ.
Кинетическое описание кислотноосновного катализа. Уравнение
Бренстеда. Катализ комплексами
переходных
металлов.
Ферментативный
катализ.
Уравнение Михаэлиса – Ментен.
Гетерогенный
катализ.
Основные стадии процесса. Роль
100
адсорбции. Закон действующих
стадии гетерогенно-каталитической
поверхностей. Изотерма адсорбции
реакции. Механизм Ридиэла – Или.
Лэнгмюра. Уравнение Лэнгмюра –
Хиншельвуда.
Лимитирующие
Лабораторные работы
Занятие 7. Изучение адсорбции уксусной кислоты на активированном угле.
Контроль выполнения модуля 3. Срок – 17 неделя.
Домашние задания
не предусмотрено
Самостоятельная работа
Самостоятельная работа студента заключается в проработке материала
лекций; подготовке к выполнению и защите лабораторных работ;
выполнении индивидуального домашнего задания. Каждое домашнее задание
включает в себя 5 практических и расчетных задач. Самостоятельная работа
является как домашней, так и аудиторной (в том числе под контролем
преподавателя на консультациях, где разбираются трудные вопросы из
материала лекций, типовые варианты домашних и контрольных заданий, а
также демонстрируются возможности использования математических
программ при обработке результатов лабораторных работ).
Самостоятельная работа является как домашней, так и аудиторной под
контролем преподавателя (КСР)
Зачетная работа
Итоговый контроль по дисциплине проводится на 17 неделе для студентов,
которые неудовлетворительно освоили содержание модулей (т.е. для
студентов, набравших менее 60 баллов).
ЛИТЕРАТУРА
Основная литература (ОЛ)
1.
Стромберг А.Г., Семченко Д.П. Физическая химия. М.: Высшая
школа.1999. 528 с.
2.
Физическая химия. Под ред. К.С.Краснова. М.: Высшая школа. 1995. Т.
1. 512 с. Т. 2. 320 с.
Дополнительная литература (ДЛ)
1.
Краткий справочник физико-химических величин. Под ред.
А.А.Равделя, А.М.Пономаревой. Л.: Химия. 1983.
2.
Задачи по физической химии / В. В. Еремин, С. И. Каргов, И. А.
Успенская и др. – М.: Изд-во “Экзамен”, 2003. – 320 с.
3.
Методические разработки кафедры к лабораторным работам
Методические пособия, изданные в МГТУ (МП)
1.
Химическая термодинамика. Методические указания. / Е. Е.
Гончаренко, В. А. Батюк, Н. М. Елисеева и др. М.: Изд-во МГТУ, 1994.
2.
Сборник контрольных вопросов и задач для защиты лабораторных
работ по курсу химии: Метод. указания /С.Л. Березина, А.М. Голубев, Е.Е.
101
Гончаренко и др.; Под ред. А.М. Голубева - М.: Изд-во МГТУ им.Н.Э.
Баумана, 2009. – 84 с.
Электронные учебные пособия (ЭП)
1.
Современная химия в техническом университете. Химия элементов и
их соединений: электронное учебное пособие / Ермолаева В.И., Волков А.А.,
Горшкова В.М., Слынько Л.Е.- ФГУП НТЦ «Информрегистр», №
0320801585, от 4.08.08
Интернет – источники
1.
2.
3.
http://window.edu.ru/catalog?p_rubr=2.2.74.7
http://www.ximicat.com/index.php?razdel=obs
http://rushim.ru/books/books.htm
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
для студентов ИУ2
Дисциплина во втором семестре состоит из 3-х учебных модулей и экзамена.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-3
6
Семинары
1-4
8
Домашнее задание
Письменная работа
1-5
5
4
4
Контроль по модулю №1
Примечание
6
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
4-10
14
Семинары
5-12
16
Домашнее задание № 2
Письменная работа № 2
Домашнее задание № 3
Письменная работа № 3
5-9
9
9-12
12
6
3
4
3
Контроль по модулю №2
13
102
Примечание
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
11-17
14
Семинары
13-17
10
Домашнее задание № 4
Письменная работа № 4
13-15
15
7
3
Контроль по модулю №3
16
Примечание
Модуль 4. Экзамен
МОДУЛЬ 1: КИНЕМАТИКА ТОЧКИ. ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Лекции
Лекция 1. Предмет теоретической механики.
Кинематика
точки.
Способы
задания
движения точки. Векторный способ задания
движения. Траектория, скорость, ускорение
точки.
Задание
движения
точки
в
прямоугольных декартовых координатах.
Траектория, скорость и ускорение точки.
Пример Л5-12.13.
ОЛ-1, ГЛ. 1, §§ 1.1-1.4.
Лекция 2. Дифференцирование вектора
постоянного
модуля
по
скалярному
аргументу. Задание движения точки на
плоскости
в
полярных
координатах.
Траектория, скорость, ускорение точки.
Пример. Естественный способ задания
движения точки. Скорость и ускорение точки.
Разложение ускорения по осям естественного
трехгранника. Демонстрация прибора ТМ-8.
ОЛ-1, гл. 1, § 1.5.
Лекция 3. Кинематика твердого тела. Задание
движения твердого тела, число степеней
свободы. Теорема о проекциях скоростей двух
точек твердого тела на прямую, проходящую
через эти точки. Поступательное движение
твердого тела, число степеней свободы.
Траектории, скорости и ускорения точек тела.
Вращение твердого тела вокруг неподвижной
оси. Уравнение движения, число степеней
свободы. Угловая скорость и угловое
ускорение. Векторы угловой скорости и
углового ускорения. Векторные и скалярные
формулы для скоростей и ускорений точек
тела. Демонстрация приборов ТМ-63, ТМ-47.
ОЛ-1, гл. 2, §§ 2.1-2.3.
Семинары
Занятие 1. Задание движения точки в
прямоугольных декартовых координатах.
Траектория, скорость и ускорение точки.
Ауд.: ОЛ5-10.12, 10.13, 12.14, 12.17
Дома: ОЛ4-3.2, 3.7(3.3),3.8(3.4), МП 1-4
Занятие 2. Задание движения точки на
плоскости
в
полярных
координатах.
Траектория, скорость, ускорение точки.
Естественный способ задания движения
точки.
Ауд.: ОЛ4-3.18(3.10), 3.27 (3.20)
Дома: ОЛ4-3.21(3.13),3.22(3.15)
Занятие 3. Поступательное движение
твердого тела. Траектории, скорости и
ускорения точек тела. Вращение твердого
тела вокруг неподвижной оси. Уравнение
движения, угловая скорость и угловое
ускорение. Скорости и ускорения точек тела.
Ауд.: ОЛ5-13.6,13.12,14.5
Дома: ОЛ4-4.5,4.9, ДЗ №1, МП 1-4, 14
Занятие 4. Решение задач типа ДЗ-1.
Ауд.: Задачи типа ДЗ-1.
Дома: ДЗ-1.
103
МОДУЛЬ 2: ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
Лекции
Лекции 4-5. Плоское движение твердого тела
движения
свободного
твердого
тела.
и движение плоской фигуры в ее плоскости.
Разложение движения на поступательное
Уравнения
плоского
движения,
число
вместе с полюсом и вращательное вокруг
степеней свободы. Разложение движения на
полюса. Уравнения движения. Скорости и
поступательное вместе с полюсом и
ускорения точек тела.
вращательное вокруг оси, проходящей через
ОЛ-1, гл. 4, гл. 5.
полюс. Соотношение между скоростями двух
Лекции 8-9.
Сложное движение точки,
любых точек плоской фигуры. Мгновенный
основные понятия и определения. Полная и
центр скоростей – МЦС; методы его
локальная производные вектора, формула
нахождения. Определение скоростей точек с
Бура. Теорема о сложении скоростей. Теорема
помощью
МЦС.
Различные
способы
о сложении ускорений – теорема Кориолиса.
определения угловой скорости. Соотношение
Ускорение Кориолиса, правило Жуковского.
между ускорениями двух любых точек
Частные случаи. Примеры: Л4-7.9, 7.18.
плоской фигуры. Понятие о мгновенном
Сложное движение твердого тела. Сложение
центре ускорений. Различные способы
поступательных
движений,
сложение
нахождения
углового
ускорения.
вращений вокруг пересекающихся осей.
Демонстрация приборов ТМ-26, ТМ-30.
ОЛ-1, гл. 6, гл. 7, §§ 7.1, 7.2, 7.4.
Пример ОЛ4-5.14.
Студенты самостоятельно изучают тему
ОЛ-1, гл. 3, §§ 3.1-3.9.
«Сложение вращений вокруг параллельных
Лекции 6-7. Вращение твердого тела вокруг
осей, пара вращений».
неподвижной точки. Число степеней свободы.
ОЛ-1, гл. 7, § 7.3.
Углы
Эйлера.
Уравнения
движения.
Лекция 10. Понятие о криволинейных
Мгновенная ось вращения. Векторы угловой
координатах. Определение скорости и
скорости и углового ускорения. Скорости
ускорения точки при задании ее движения в
точек тела: векторная и скалярная формулы
цилиндрических и сферических координатах.
Эйлера. Формулы Пуассона. Ускорения точек
ОЛ-1, гл. 1, § 1.4.
тела. Пример Л5-19.4. Общий случай
Семинары
Занятие 5. Определение скоростей точек
твердого тела при его плоском движении.
Мгновенный центр скоростей – МЦС; методы
его нахождения. Определение скоростей
точек с помощью МЦС, определение угловой
скорости тела.
Ауд.: ОЛ5-16.29, Л4-5.6,5.7,5.14.
Дома: ОЛ4-5.8,5.15,5.20.
Занятие 6. Определение ускорений точек
плоской фигуры по соотношению между
ускорениями двух любых ее точек и с
помощью мгновенного центра ускорений.
Различные способы определения углового
ускорения.
Ауд.: ОЛ5-18.11, Л4-5.26,5.30.
Дома: ОЛ4-5.21, 5.28.
Занятие 7 Определение скоростей и
ускорений точек твердых тел при плоском
движении в системах с одной степенью
свободы.
Ауд.: ОЛ4-5.38, 5.37.
Дома: ОЛ4-5.39, 5.43.
Занятие 8 Определение скоростей и
ускорений точек твердых тел при плоском
движении в системах с одной степенью
свободы.
Ауд.: ОЛ4-5.40.
Дома: ОЛ4-5.41.
Занятие 9. Решение задач типа ДЗ-2
«Кинематика плоского движения твердого
тела»
Ауд.: Задачи типа ДЗ-2.
Дома: ДЗ-2, МП 5-7.
104
Занятие 10. Определение скоростей и
ускорений точек при заданных переносном и
относительном ее движениях.
Ауд.: ОЛ5-23.18,23.27,23.30, ОЛ4-7.17.
Дома: ОЛ4-7.6(7.3),7.16(7.13).
Занятие 11. Определение скоростей и
ускорений точек в сложном движении при
известной траектории ее абсолютного
движения.
Ауд.: ОЛ5-23.18,23.27,23.30, ОЛ4-7.17.
Дома: ОЛ4-7.6(7.3),7.16(7.13).
Занятие 12. Решение задач типа ДЗ-3
«Сложное движение точки»
Ауд.: ОЛ4-7.34 (7.29). Задачи типа ДЗ-3.
Дома: ДЗ №3, МП 8-10.
Модуль 3: Статика
Лекции
Лекция 11. Статика, основные понятия и
определения. Аксиомы статики. Основные
виды связей и их реакции: гладкая
поверхность,
цилиндрический
шарнир,
шаровой шарнир, подпятник, гибкая нить,
шарнирный стержень.
ОЛ-1, гл. 8, §§ 8.1, 8.2.
Лекция 12. Система сходящихся сил, условия
равновесия. Алгебраический и векторный
моменты силы относительно точки. Момент
силы относительно оси. Связь векторного
момента силы относительно точки с моментом
силы относительно оси, проходящей через эту
точку.
Аналитические
выражения
для
моментов силы относительно осей координат.
Пара сил. Теорема о сумме моментов сил,
составляющих пару, относительно любой
точки или оси. Векторный и алгебраический
моменты пары.
ОЛ-1, гл. 8, §§ 8.3-8.5.
Лекция 13. Эквивалентность пар. Сложение
пар. Условие равновесия системы пар сил.
Лемма о параллельном переносе силы.
Теорема о приведении произвольной системы
сил к силе и паре сил – основная теорема
статики.
ОЛ-1, гл. 8, § 8.6.
Лекция 14. Главный вектор и главный момент
системы сил. Формулы для их вычисления.
Условия равновесия произвольной системы
сил. Частные случаи: система параллельных
сил, плоская система сил – основная форма.
Теорема
Вариньона
о
моменте
равнодействующей, распределенные силы.
Примеры: Л5-4.26,
Л4-2.17. Зависимость
между главными моментами системы сил
относительно двух центров приведения.
ОЛ-1, гл. 8, § 8.6, гл. 9, § 9.1.
Лекции 15-16. Инварианты системы сил.
Частные случаи приведения. Равновесие
системы тел. Силы внешние и внутренние.
Свойства внутренних сил. Задачи статически
определенные и статически неопределенные.
Равновесие тела на шероховатой поверхности.
Трение скольжения. Законы Кулона. Угол и
конус трения. Пример Л5-5.29. Трение
качения. Коэффициент трения качения.
ОЛ-1, гл. 9, § 9.2, гл. 10.
Лекция 17. Центр системы параллельных сил.
Формулы для радиус-вектора и координат
центра системы параллельных сил. Центр
тяжести тела: объема, площади, линии.
Методы нахождения центра тяжести: метод
симметрии, метод разбиения на части, метод
отрицательных масс. Примеры.
ОЛ-1, гл. 11.
Семинары
Занятие 13. Определение реакций при
равновесии плоской системы тел.
Ауд.: ОЛ5-2.19,2.29,4.17,4.25.
Дома: Л4-1.3, 1.5.
Занятие 14. Определение реакций при
равновесии плоской системы тел.
Ауд.: ОЛ4-1.14,1.15,1.17.
Дома: Л4-1.12, 1.16, МП 11,14.
Занятие 15. Определение реакций при
равновесии произвольной пространственной
системы сил.
Ауд.: ОЛ4-1.26, Л5-8.17, 8.19.
105
106
Дома: ОЛ4-1.24,1.25,1.29.
Занятие 16 Определение реакций при
равновесии произвольной пространственной
системы сил. Решение задач типа ДЗ-4.
Ауд.: ОЛ5-8.26, Л4-2.12,2.18,2.19.
Дома: ОЛ4-2.16, ДЗ №4, МП 12-14.
Занятие 17.
Определение сил
равновесии с учетом трения.
Ауд.: ОЛ5-5.26,5.28, Л4-1.39 (1.38).
Дома: ОЛ4-1.43(1.42),1.46(1.45).
при
Модуль 4: Экзамен
Экзамен проводится по материалам модулей 1-4.
Самостоятельная подготовка



Проработка курса лекций, учебников, методических пособий по темам лекций 1 – 17,
семинаров 1 – 17
Выполнение домашних заданий №№ 1–4.
Подготовка к письменным работам №№ 1–4 и их написание.
Контрольные мероприятия и сроки их проведения
МОДУЛЬ 1:
Домашнее задание № 1 «Кинематика точки. Простейшие движения твердого тела».
Методические пособия МП – 1-4.
Сроки выполнения: выдача – 1-я неделя, прием – 5 неделя.
Письменная работа 1. Тема работы: определение кинематических характеристик движения точки
и твердого тела. Проводится по материалам лекций 1–3 и семинаров 1–4.
Методические пособия МП 1–4.
Срок проведения – 5 неделя.
Срок выставления общей оценки за модуль 1 – 6 неделя.
МОДУЛЬ 2:
Домашнее задание № 2 «Кинематика плоского движения твердого тела».
Методические пособия МП 5–7.
Сроки выполнения: выдача – 5 неделя, прием – 9 неделя.
Письменная работа № 2. Тема работы: определение кинематических характеристик при плоском
движения твердого тела. Проводится по материалам лекций 4–7 и семинаров 5–9.
Методические пособия МП 5–7.
Срок проведения – 9 неделя.
Домашнее задание № 3 «Кинематика сложного движения точки».
Методические пособия МП 8–10.
Сроки выполнения: выдача – 9 неделя, прием – 12 неделя
Письменная работа № 3 Тема работы: определение кинематических характеристик при сложном
движения точки. Проводится по материалам лекций 8-9 и семинаров 10-12..
Методические пособия МП 8–10.
Срок проведения – 12 неделя.
Срок выставления общей оценки за модуль 2 – 13 неделя.
МОДУЛЬ 3.
Домашнее задание № 4 «Статика»
Методические пособия МП 11-14.
Сроки выполнения: выдача – 13 неделя, прием – 15 неделя.
Письменная работа № 4 Тема работы: определение реакций при равновесии плоской и
пространственной систем сил. Проводится по материалам лекций 11-15, семинаров 13-16.
Методические пособия МП 11-14.
106
Срок проведения 16 неделя.
Срок выставления общей оценки за модуль 3 – 16 неделя.
МОДУЛЬ 4 ИТОГОВЫЙ (экзамен)
Срок выставления оценки за 4 модуль – экзаменационная сессия.
Основная и дополнительная литература
Основная литература (ОЛ)
1.Курс теоретической механики / Под ред. К.С.Колесникова. – М.: Изд. МГТУ, 2000, 2002 2005,
2011.
2.Никитин Н.Н. Курс теоретической механики. – М.: Высшая школа, 1974, 1983, 1990 и более
поздние издания.
3.Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Т. 1, 2. – М.: Наука, 1971,
1985.
4.Сборник задач по теоретической механике / Под ред. К.С.Колесникова – М.: Наука, 1989, 2007,
2008 и более поздние издания.
5.Мещерский И.В. Сборник задач по теоретической механике М.: Наука, 1981, 1986 и более
поздние издания.
Методические пособия, изданные в МГТУ (МП)
1. Виноградов А.Н., Пилюгина Н.Н., Феоктистова О.П. Кинематика точки и простейшие
движения твердого тела. – М.: МГТУ, 1994.
2.Кинематика точки и простейшие движения твердого тела. / Под ред. Пожалостина А.А. –
Изд. МГТУ, 1991.
3.Горина Т.И., Кинелев В.Г. Кинематика точки. Кинематика простейших движений твердого
тела. – Изд. МВТУ, 1979 (для ИУ2 – Авиамоторная).
4. Лапшин В.В. Кинематика точки и простейших движений твердого тела: Метод.указания по
выполнению курсовой работы. – М.: Изд. МГТУ, 2003.
5. Дубинин В.В., Карпачев А.Ю., Назаренко Б.П. Кинематика плоского движения твердого
тела: Методические указания и варианты курсового задания. – М.: МГТУ, 2007.
6. Кинематика плоского движения твердого тела / Под ред. Назаренко Б.П. – Изд. МГТУ,
1989.
7. Горина Т.И., Назаренко Б.П., Русанов П.Г. Метод.указания по выполнению курсовой
работы по разделу «Кинематика плоского движения твердого тела». – Изд. МВТУ, 1982 (для ИУ,
СМ5, ИУ2 – Авиамоторная).
8.Кинематика плоского движения твердого тела: Метод.указания по решению задач и
выполнению курсового задания. / В.В. Дубинин, А.Ю. Карпачев, Б.П. Назаренко, Л.В. Северова. –
М.: Изд. МГТУ, 2004.
9.Занозин П.В., Пилюгина Н.Н., Тушева Г.М. Кинематика сложного движения точки. – Изд.
МВТУ, 1980 (для ИУ, СМ5, ИУ2 - Авиамоторная).
10.
Дубинин В.В., Тушева Г.М., Гатауллина Г.И., Ремизов А.В. Кинематика сложного
движения точки: Методические указания и варианты курсовой работы. – М.: МГТУ, 2007.
11.
В.В. Дубинин, Г.И. Гатауллина, Г.М. Тушева. Методические указания к выполнению
курсовой работы и решению задач по теме: «Кинематика сложного движения точки». – МГТУ,
2005.
12.
Дубинин В.В., Занозин П.В., Солохин Е.Н., Орфаницкая Л.П. Метод.указания к
выполнению курсовой работы и решению задач по теме «Кинематика сложного движения точки».
– Изд. МВТУ, 1985.
107
13.
Дубинин В.В., Борохова Н.В., Ильин М.М., Ремизов А.В. Плоская статика.
Метод.указания и курсовая работа по разделу курса «Теоретическая механика». – Изд. МГТУ,
1998.
14.
Бурмистров Б.А., Кирюшкина И.А., Кокушкин В.В. Пространственная статика.
Метод.указания к разделу курсовой работы по теоретической механике. – Изд. МГТУ, 1994.
15.
Статика и кинематика. Метод.указания по решению задач теоретической механики с
помощью ЭВМ / Под ред. В.В. Дубинина. – Изд. МВТУ, 1989.
16.
Кинематика и статика. Метод.указания по проведению практических занятий с
использованием моделей и приборов по курсу «Теоретическая механика». – Изд. МВТУ, 1986.
17.
Решение задач по курсу «Теоретическая механика» с использованием ЭВМ /
Дубинин В.В., Максимов Г.М., Назаренко Б.П., Русанов П.Г., Солохин Е.Н., Степанчук Ю.М. –
Изд. МГТУ, 1988.
18.
Колесников К.С., Дронг В.И. Теоретическая механика. Статика. – Изд. МГТУ, 1992.
19.
Брусенцова Е.А., Пилюгина Н.Н., Пожалостин А.А. Кинематика точки и простейшие
движения твердого тела. Метод.указания и условия вариантов по выполнению курсовой работы.
Часть 1. – Изд. МВТУ, 1987.
20.
Методические указания к решению задач и выполнению курсовых заданий по теме
«Статика». / Под ред. В.В. Дубинина. – Изд. МГТУ, 2003.
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
для ПС
Во втором семестре дисциплина состоит из 3-х учебных модулей и экзамена.
Модуль 1
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
1-2
4
Семинары
1-4
8
Домашнее задание
Письменная работа
1-5
5
4
4
Контроль по модулю №1
Примечание
6
Модуль 2
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
4-10
14
Семинары
5-12
16
Домашнее задание № 2
Письменная работа № 2
Домашнее задание № 3
Письменная работа № 3
5-9
9
9-12
12
6
3
4
3
Контроль по модулю №2
13
108
Примечание
Модуль 3
Виды аудиторных занятий и
самостоятельной работы
Сроки проведения или
выполнения, недели
Трудоёмкость,
часы
Лекции
11-17
14
Семинары
13-17
10
Домашнее задание № 4
Письменная работа № 4
13-15
15
7
3
Контроль по модулю №3
16
Примечание
Модуль 4: Экзамен
Модуль 1: Кинематика точки и кинематика
простейших движений твёрдого тела
Лекции
Лекция 1. Предмет теоретической
механики. Кинематика точки. Способы
задания движения точки. Векторный
способ задания движения. Траектория,
скорость, ускорение точки. Задание
движения точки в прямоугольных
декартовых координатах. Траектория,
скорость и ускорение точки. Пример Л512.13.
ОЛ-1, гл. 1, §§ 1.1-1.4.
Лекция 2. Дифференцирование вектора
постоянного модуля по скалярному
аргументу. Задание движения точки на
плоскости в полярных координатах.
Траектория, скорость, ускорение точки.
Пример. Естественный способ задания
движения точки. Скорость и ускорение
точки. Разложение ускорения по осям
естественного трехгранника.
Демонстрация прибора ТМ-8.
ОЛ-1, гл. 1, § 1.5.
Лекция 3. Кинематика твердого тела.
Задание движения твердого тела, число
степеней свободы. Теорема о проекциях
скоростей двух точек твердого тела на
ось, проходящую через эти точки.
Поступательное движение твердого тела,
число степеней свободы. Траектории,
скорости и ускорения точек тела.
Вращение
твердого
тела
вокруг
неподвижной оси. Уравнение движения,
число степеней свободы. Угловая
скорость и угловое ускорение тела.
Векторные и скалярные формулы для
скоростей и ускорений точек тела.
Демонстрация приборов ТМ-63, ТМ-47.
ОЛ-1, гл. 2, §§ 2.1-2.3.
Семинары
Занятие 1. Задание движения точки в
прямоугольных декартовых координатах.
Траектория, скорость и ускорение точки.
Ауд.: ОЛ5-10.12, 10.13, 12.14, 12.17
Дома: ОЛ4-3.2, 3.7(3.3),3.8(3.4), МП 1-4
Занятие 2. Задание движения точки на
плоскости
в
полярных
координатах.
Траектория, скорость, ускорение точки.
Естественный способ задания движения
точки.
Ауд.: ОЛ4-3.18(3.10), 3.27 (3.20)
109
Дома: ОЛ4-3.21(3.13),3.22(3.15)
Занятие 3. Поступательное движение
твердого тела. Траектории, скорости и
ускорения точек тела. Вращение твердого
тела вокруг неподвижной оси. Уравнение
движения, угловая скорость и угловое
ускорение. Скорости и ускорения точек тела.
Ауд.: ОЛ5-13.6,13.12,14.5
Дома: ОЛ4-4.5,4.9, ДЗ №1, МП 1-4, 14
Занятие 4. Решение задач типа ДЗ-1.
Ауд.: Задачи типа ДЗ-1.
Дома: ДЗ-1.
Модуль 2: Плоское движение твердого тела. Сложное движение точки
Лекции
Лекции 4-5. Плоское движение твердого тела
и движение плоской фигуры в ее плоскости.
Уравнения плоского движения, число
степеней свободы. Разложение движения на
поступательное вместе с полюсом и
вращательное вокруг оси, проходящей через
полюс. Соотношение между скоростями двух
любых точек плоской фигуры. Мгновенный
центр скоростей – МЦС; методы его
нахождения. Определение скоростей точек с
помощью
МЦС.
Различные
способы
определения угловой скорости. Соотношение
между ускорениями двух любых точек
плоской фигуры. Понятие о мгновенном
центре ускорений. Различные способы
определения углового ускорения. Пример
ОЛ4-5.14.
ОЛ-1, гл. 3, §§ 3.1-3.9.
вместе с полюсом и вращательное вокруг
полюса. Уравнения движения. Скорости и
ускорения точек тела.
ОЛ-1, гл. 4, гл. 5.
Лекции 8-9.
Сложное движение точки,
основные понятия и определения. Полная и
локальная производные вектора, формула
Бура. Теорема о сложении скоростей.
Теорема о сложении ускорений – теорема
Кориолиса. Ускорение Кориолиса, правило
Жуковского. Частные случаи. Примеры: Л47.9, 7.18. Сложное движение твердого тела.
Сложение
поступательных
движений,
сложение вращений вокруг пересекающихся
осей.
ОЛ-1, гл. 6, гл. 7, §§ 7.1, 7.2, 7.4.
Студенты самостоятельно изучают тему
«Сложение вращений вокруг параллельных
осей, пара вращений».
ОЛ-1, гл. 7, § 7.3.
Лекции 6-7. Вращение твердого тела вокруг
неподвижной
точки.
Число
степеней
свободы. Углы Эйлера. Уравнения движения.
Мгновенная ось вращения. Векторы угловой
скорости и углового ускорения. Скорости
точек тела: векторная и скалярная формулы
Эйлера. Формулы Пуассона. Ускорения точек
тела. Пример Л5-19.4. Общий случай
движения
свободного
твердого
тела.
Разложение движения на поступательное
Лекция 10. Понятие о криволинейных
координатах. Определение скорости и
ускорения точки при задании ее движения в
цилиндрических и сферических координатах.
ОЛ-1, гл. 1, § 1.4.
Семинары
Занятие 5. Определение скоростей точек
твердого тела при его плоском движении.
Мгновенный центр скоростей – МЦС; методы
его нахождения. Определение скоростей
точек с помощью МЦС, определение угловой
скорости тела.
Ауд.: ОЛ5-16.29, Л4-5.6,5.7,5.14.
Дома: ОЛ4-5.8,5.15,5.20.
Занятие 6. Определение ускорений точек
плоской фигуры по соотношению между
ускорениями двух любых ее точек и с
помощью мгновенного центра ускорений.
Различные способы определения углового
ускорения.
Ауд.: ОЛ5-18.11, Л4-5.26,5.30.
Дома: ОЛ4-5.21, 5.28.
Занятие 7 Определение скоростей и
ускорений точек твердых тел при плоском
движении в системах с одной степенью
свободы.
110
Ауд.: ОЛ4-5.38, 5.37.
Дома: ОЛ4-5.39, 5.43.
Занятие 8 Определение скоростей и
ускорений точек твердых тел при плоском
движении в системах с одной степенью
свободы.
Ауд.: ОЛ4-5.40.
Дома: ОЛ4-5.41.
Занятие 9. Решение задач типа ДЗ-2
«Кинематика плоского движения твердого
тела»
Ауд.: Задачи типа ДЗ-2.
Дома: ДЗ-2, МП 5-7.
Занятие 10. Определение скоростей и
ускорений точек при заданных переносном и
относительном ее движениях.
Ауд.: ОЛ5-23.18,23.27,23.30, ОЛ4-7.17.
Дома: ОЛ4-7.6(7.3),7.16(7.13).
Занятие 11. Определение скоростей и
ускорений точек в сложном движении при
известной траектории ее абсолютного
движения.
Ауд.: ОЛ5-23.18,23.27,23.30, ОЛ4-7.17.
Дома: ОЛ4-7.6(7.3),7.16(7.13).
Занятие 12. Решение задач типа ДЗ-3
«Сложное движение точки»
Ауд.: ОЛ4-7.34 (7.29). Задачи типа ДЗ-3.
Дома: ДЗ №3, МП 8-10.
Модуль 3: Статика
Лекции
Лекция 11. Статика, основные понятия и
определения. Аксиомы статики. Основные
виды связей и их реакции: гладкая
поверхность,
цилиндрический
шарнир,
шаровой шарнир, подпятник, гибкая нить,
шарнирный стержень.
ОЛ-1, гл. 8, §§ 8.1, 8.2.
вычисления.
Условия
равновесия
произвольной системы сил. Частные случаи:
система параллельных сил, плоская система
сил – основная форма. Теорема Вариньона о
моменте равнодействующей, распределенные
силы.
Примеры:
Л5-4.26,
Л4-2.17.
Зависимость между главными моментами
системы сил относительно двух центров
приведения.
ОЛ-1, гл. 8, § 8.6, гл. 9, § 9.1.
Лекция 12. Система сходящихся сил,
условия равновесия. Алгебраический и
векторный моменты силы относительно
точки. Момент силы относительно оси. Связь
векторного момента силы относительно
точки с моментом силы относительно оси,
проходящей через эту точку. Аналитические
выражения для моментов силы относительно
осей координат. Пара сил. Теорема о сумме
моментов
сил,
составляющих
пару,
относительно любой точки или оси.
Векторный и алгебраический моменты пары.
ОЛ-1, гл. 8, §§ 8.3-8.5.
Лекции 15-16. Инварианты системы сил.
Частные случаи приведения. Равновесие
системы тел. Силы внешние и внутренние.
Свойства внутренних сил. Задачи статически
определенные и статически неопределенные.
Равновесие
тела
на
шероховатой
поверхности. Трение скольжения. Законы
Кулона. Угол и конус трения. Пример Л55.29. Трение качения. Коэффициент трения
качения.
ОЛ-1, гл. 9, § 9.2, гл. 10.
Лекция 13. Эквивалентность пар. Сложение
пар. Условие равновесия системы пар сил.
Лемма о параллельном переносе силы.
Теорема о приведении произвольной системы
сил к силе и паре сил – основная теорема
статики.
ОЛ-1, гл. 8, § 8.6.
Лекция 17. Центр системы параллельных
сил. Формулы для радиус-вектора и
координат центра системы параллельных сил.
Центр тяжести тела: объема, площади, линии.
Методы нахождения центра тяжести: метод
симметрии, метод разбиения на части, метод
отрицательных масс. Примеры.
ОЛ-1, гл. 11.
Лекция 14. Главный вектор и главный
момент системы сил. Формулы для их
111
Семинары
Занятие 13. Определение реакций при
равновесии плоской системы тел.
Ауд.: ОЛ5-2.19,2.29,4.17,4.25.
Дома: Л4-1.3, 1.5.
Занятие 14. Определение реакций при
равновесии плоской системы тел.
Ауд.: ОЛ4-1.14,1.15,1.17.
Дома: Л4-1.12, 1.16, МП 11,14.
Занятие 15. Определение реакций при
равновесии произвольной пространственной
системы сил.
Ауд.: ОЛ4-1.26, Л5-8.17, 8.19.
Дома: ОЛ4-1.24,1.25,1.29.
Занятие 16 Определение реакций при
равновесии произвольной пространственной
системы сил. Решение задач типа ДЗ-4.
Ауд.: ОЛ5-8.26, Л4-2.12,2.18,2.19.
Дома: ОЛ4-2.16, ДЗ №4, МП 12-14.
Занятие 17.
Определение сил
при
равновесии с учетом трения.
Ауд.: ОЛ5-5.26,5.28, Л4-1.39 (1.38).
Дома: ОЛ4-1.43(1.42),1.46(1.45).
Модуль 4: Экзамен
Экзамен проводится по материалам модулей 1-4.
Самостоятельная подготовка



Проработка курса лекций, учебников, методических пособий по темам лекций 1 – 17,
семинаров 1 – 17
Выполнение домашних заданий №№ 1–4.
Подготовка к письменным работам №№ 1–4 и их написание.
Контрольные мероприятия и сроки их проведения
МОДУЛЬ 1:
Домашнее задание № 1 «Кинематика точки. Простейшие движения твердого тела».
Методические пособия МП – 1-4.
Сроки выполнения: выдача – 1-я неделя, прием – 5 неделя.
Письменная работа 1. Тема работы: определение кинематических характеристик
движения точки и твердого тела. Проводится по материалам лекций 1–3 и семинаров 1–4.
Методические пособия МП 1–4.
Срок проведения – 5 неделя.
Срок выставления общей оценки за модуль 1 – 6 неделя.
МОДУЛЬ 2:
Домашнее задание № 2 «Кинематика плоского движения твердого тела».
Методические пособия МП 5–7.
Сроки выполнения: выдача – 5 неделя, прием – 9 неделя.
Письменная работа № 2. Тема работы: определение кинематических характеристик при
плоском движения твердого тела. Проводится по материалам лекций 4–7 и семинаров 5–9.
Методические пособия МП 5–7.
Срок проведения – 9 неделя.
Домашнее задание № 3 «Кинематика сложного движения точки».
Методические пособия МП 8–10.
Сроки выполнения: выдача – 9 неделя, прием – 12 неделя
112
Письменная работа № 3 Тема работы: определение кинематических характеристик при
сложном движения точки. Проводится по материалам лекций 8-9 и семинаров 10-12..
Методические пособия МП 8–10.
Срок проведения – 12 неделя.
Срок выставления общей оценки за модуль 2 – 13 неделя.
МОДУЛЬ 3.
Домашнее задание № 4 «Статика»
Методические пособия МП 11-14.
Сроки выполнения: выдача – 13 неделя, прием – 15 неделя.
Письменная работа № 4 Тема работы: определение реакций при равновесии плоской и
пространственной систем сил. Проводится по материалам лекций 11-15, семинаров 13-16.
Методические пособия МП 11-14.
Срок проведения 15 неделя.
Срок выставления общей оценки за модуль 3 – 16 неделя.
МОДУЛЬ 4. ЭКЗАМЕН
▼ Основная и дополнительная литература
1.
2.
3.
4.
5.
1.
2.
3.
4.
5.
6.
7.
Основная литература (ОЛ)
Курс теоретической механики / Под ред. К.С.Колесникова. – М.: Изд. МГТУ, 2000,
2002 2005, 2011.
Добронравов В.В., Никитин Н.Н., Дворников А.Л. Курс теоретической механики. – М.:
Высшая школа, 1974, 1983, 1990 и более поздние издания.
Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Т. 1, 2. – М.:
Наука, 1971, 1985.
Сборник задач по теоретической механике / Под ред. К.С.Колесникова – М.: Наука,
1989, 2007, 2008 и более поздние издания.
Мещерский И.В. Сборник задач по теоретической механике М.: Наука, 1981, 1986 и
более поздние издания.
Методические пособия, изданные в МГТУ (МП)
Виноградов А.Н., Пилюгина Н.Н., Феоктистова О.П. Кинематика точки и простейшие
движения твердого тела. – М.: МГТУ, 1994.
Кинематика точки и простейшие движения твердого тела. / Под ред. Пожалостина
А.А. – Изд. МГТУ, 1991.
Горина Т.И., Кинелев В.Г. Кинематика точки. Кинематика простейших движений
твердого тела. – Изд. МВТУ, 1979 (для ИУ2, ф-т ПС).
Лапшин В.В. Кинематика точки и простейших движений твердого тела:
Метод.указания по выполнению курсовой работы. – М.: Изд. МГТУ, 2003.
Дубинин В.В., Карпачев А.Ю., Назаренко Б.П. Кинематика плоского движения
твердого тела: Методические указания и варианты курсового задания. – М.: МГТУ,
2007.
Горина Т.И., Назаренко Б.П., Русанов П.Г. Метод.указания по выполнению курсовой
работы по разделу «Кинематика плоского движения твердого тела». – Изд. МВТУ,
1982 (для ИУ, СМ5, ИУ2, ф-т ПС).
Кинематика плоского движения твердого тела: Метод.указания по решению задач и
выполнению курсового задания. / В.В. Дубинин, А.Ю. Карпачев, Б.П. Назаренко, Л.В.
Северова. – М.: Изд. МГТУ, 2004.
113
8. Занозин П.В., Пилюгина Н.Н., Тушева Г.М. Кинематика сложного движения точки. –
Изд. МВТУ, 1980 (для ИУ, СМ5, ИУ2, ф-т ПС).
9. Дубинин В.В., Тушева Г.М., Гатауллина Г.И., Ремизов А.В. Кинематика сложного
движения точки: Методические указания и варианты курсовой работы. – М.: МГТУ,
2007.
10. В.В. Дубинин, Г.И. Гатауллина, Г.М. Тушева. Методические указания к выполнению
курсовой работы и решению задач по теме: «Кинематика сложного движения точки». –
МГТУ, 2005.
11. Дубинин В.В., Борохова Н.В., Ильин М.М., Ремизов А.В. Плоская статика.
Метод.указания и курсовая работа по разделу курса «Теоретическая механика». – Изд.
МГТУ, 1998.
12. Бурмистров Б.А., Кирюшкина И.А., Кокушкин В.В. Пространственная статика.
Метод.указания к разделу курсовой работы по теоретической механике. – Изд. МГТУ,
1994.
13. Статика и кинематика. Метод.указания по решению задач теоретической механики с
помощью ЭВМ / Под ред. В.В. Дубинина. – Изд. МВТУ, 1989.
14. Колесников К.С., Дронг В.И. Теоретическая механика. Статика. – Изд. МГТУ, 1992.
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
для СМ5
Дисциплина состоит из 4-х учебных модулей.
Модуль 1
Виды аудиторных
занятий и
Самостоятельной
работы
Лекции
Сроки
проведения или
выполнения,
недели
1-3
Трудоёмкость, Примечание
часы
6
Упражнения
1-4
8
Домашние задания
1-4
4
5
2
текущие
Контроль по модулю № 1
114
Модуль 2
Виды аудиторных
занятий и
Самостоятельной
работы
Лекции
Сроки
проведения или
выполнения,
недели
4-6
Трудоёмкость, Примечание
часы
6
Упражнения
5-9
10
Домашние задания
5-9
5
8-9
2
текущие
Контроль по модулю № 2
Модуль 3
Виды аудиторных
занятий и
Самостоятельной
работы
Лекции
Сроки
проведения или
выполнения,
недели
7-10
Трудоёмкость, Примечание
часы
8
Упражнения
10-12
6
Домашние задания
10-12
3
12-13
2
текущие
Контроль по модулю № 3
Модуль 4
Виды аудиторных
занятий и
Самостоятельной
работы
Лекции
Сроки
проведения или
выполнения,
недели
11-17
Трудоёмкость, Примечание
часы
14
Упражнения
13-17
10
Домашние задания
13-17
5
17
2
текущие
Контроль по модулю № 4
115
Модуль 1: Кинематика точки и кинематика
простейших движений твёрдого тела
ЛЕКЦИИ
Лекция 1. Предмет теоретической
механики.
Кинематика
точки.
Способы задания движения точки.
Векторный
способ
задания
движения. Траектория, скорость,
ускорение
точки.
Задание
движения точки в прямоугольных
декартовых
координатах.
Траектория, скорость и ускорение
точки. Пример Л5-12.13.
ОЛ-1, гл. 1, §§ 1.1-1.4.
Лекция 2. Дифференцирование
вектора постоянного модуля по
скалярному аргументу. Задание
движения точки на плоскости в
полярных
координатах.
Траектория, скорость, ускорение
точки.
Пример.
Естественный
способ задания движения точки.
Скорость и ускорение точки.
Разложение ускорения по осям
естественного
трехгранника.
Демонстрация прибора ТМ-8.
ОЛ-1, гл. 1, § 1.5.
Лекция 3. Кинематика твердого
тела. Задание движения твердого
тела, число степеней свободы.
Теорема о проекциях скоростей
двух точек твердого тела на ось,
проходящую через эти точки.
Поступательное движение твердого
тела, число степеней свободы.
Траектории, скорости и ускорения
точек тела. Вращение твердого тела
вокруг
неподвижной
оси.
Уравнение
движения,
число
степеней
свободы.
Угловая
скорость и угловое ускорение тела.
Векторные и скалярные формулы
для скоростей и ускорений точек
тела. Демонстрация приборов ТМ63, ТМ-47.
ОЛ-1, гл. 2, §§ 2.1-2.3.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Занятие 1.
В аудитории: ОЛ-5: 13.6, 13.12, 14.5
Дома: ОЛ-4: 4.5, 4.9, ДЗ №1, МП 1-4
В аудитории: ОЛ-5: 10.12, 10.13,
12.14, 12.17
Дома: ОЛ-4: 3.2, 3.7(3.3),3.8(3.4),
МП 1-4
Занятие 2.
В аудитории: ОЛ-4: 3.18(3.10), 3.27
(3.20)
Дома: ОЛ-4: 3.21(3.13),3.22(3.15)
Занятие 3.
Занятие 4.
В аудитории: Задачи типа ДЗ 1
Дома: ДЗ №1
Модуль 2: Кинематика плоского движения твёрдого тела
116
ЛЕКЦИИ
Лекции 4-5. Плоское движение
твердого тела и движение плоской
фигуры в ее плоскости. Уравнения
плоского движения, число степеней
свободы. Разложение движения на
поступательное вместе с полюсом и
вращательное
вокруг
оси,
проходящей
через
полюс.
Соотношение между скоростями
двух любых точек плоской фигуры.
Мгновенный центр скоростей –
МЦС; методы его нахождения.
Определение скоростей точек с
помощью
МЦС.
Различные
способы
определения
угловой
скорости. Соотношение между
ускорениями двух любых точек
плоской фигуры. Понятие о
мгновенном центре ускорений.
Различные способы нахождения
углового ускорения. Демонстрация
приборов ТМ-26, ТМ-30. Пример
ОЛ4-5.14.
ОЛ-1, гл. 3, §§ 3.1-3.9.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Занятие 5.
В аудитории: ОЛ-4: 5.38, 5.37
Дома: ОЛ-4: 5.39, 5.43
Занятие 8.
В аудитории: ОЛ-5: 16.29, ОЛ-4: 5.6,
5.7, 5.14
Дома: ОЛ-4: 5.8, 5.15, 5.20
Занятие 6.
В аудитории: ОЛ-5: 18.11, ОЛ-4: 5.26,
5.30
Дома: ОЛ-4: 5.21, 5.28
Занятие 7.
В аудитории: ОЛ-4: 5.40
Дома: ОЛ-4: 5.41, ДЗ №2, МП 5-8
Занятие 9.
В аудитории: Задачи типа ДЗ 2
Дома: ДЗ № 2
Модуль 3: Кинематика сложного движения точки
ЛЕКЦИИ
Лекции 6-7. Вращение твердого тела
Ускорения точек тела. Пример Л5вокруг неподвижной точки. Число
19.4. Общий случай движения
степеней свободы. Углы Эйлера.
свободного
твердого
тела.
Уравнения движения. Мгновенная ось
Разложение
движения
на
вращения. Векторы угловой скорости
поступательное вместе с полюсом и
и углового ускорения. Скорости точек
вращательное
вокруг
полюса.
тела: векторная и скалярная формулы
Уравнения движения. Скорости и
Эйлера.
Формулы
Пуассона.
ускорения точек тела.
117
ОЛ-1, гл. 4, гл. 5.
Лекции 8-9.
Сложное движение
точки,
основные
понятия
и
определения. Полная и локальная
производные вектора, формула Бура.
Теорема о сложении скоростей.
Теорема о сложении ускорений –
теорема
Кориолиса.
Ускорение
Кориолиса, правило Жуковского.
Частные случаи. Примеры: Л4-7.9,
7.18. Сложное движение твердого
тела.
Сложение
поступательных
движений,
сложение
вращений
вокруг пересекающихся осей.
ОЛ-1, гл. 6, гл. 7, §§ 7.1, 7.2, 7.4.
Студенты самостоятельно изучают
тему «Сложение вращений вокруг
параллельных осей, пара вращений».
ОЛ-1, гл. 7, § 7.3.
Лекция
10.
Понятие
о
криволинейных
координатах.
Определение скорости и ускорения
точки при задании ее движения в
цилиндрических
и
сферических
координатах.
ОЛ-1, гл. 1, § 1.4.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Занятие 10.
Дома: ОЛ-4: 7.23(7.18), 7.26(7.21)
Занятие 12.
В аудитории: ОЛ-5: 23.18, 23.27,
23.30
Дома: ОЛ-4: 7.6(7.3), 7.16(7.13)
Занятие 11.
В аудитории: ОЛ-4:
7.17(7.14),7.29(7.24), ОЛ-5: 23.62
В аудитории: ОЛ-4: 7.34 (7.29).
Задачи типа ДЗ3
Дома: ДЗ № 3, МП 9-12
Модуль 4: Статика
ЛЕКЦИИ
Лекция 11,12. Статика, основные
понятия и определения. Аксиомы
статики. Основные виды связей и их
реакции:
гладкая
поверхность,
цилиндрический шарнир, шаровой
шарнир, подпятник, гибкая нить,
шарнирный стержень.
Система сходящихся сил, условия
равновесия.
Алгебраический
и
векторный моменты силы относительно
точки. Момент силы относительно оси.
Связь векторного момента силы
относительно точки с моментом силы
относительно оси, проходящей через
118
эту точку. Аналитические выражения
для моментов силы относительно осей
координат. Пара сил. Теорема о сумме
моментов сил, составляющих пару,
относительно любой точки или оси.
Векторный и алгебраический моменты
пары. Эквивалентность пар (без
вывода). Сложение пар. Условие
равновесия системы пар сил. Лемма о
параллельном переносе силы. Теорема
о приведении произвольной системы
сил к силе и паре сил – основная
теорема статики.
ОЛ-1, гл. 8, § 8.1-8.5.
Лекция 13. Главный вектор и главный
момент системы сил. Формулы для их
вычисления.
Условия
равновесия
произвольной системы сил. Частные
случаи: система параллельных сил,
плоская система сил – основная форма.
Теорема
Вариньона
о
моменте
равнодействующей,
распределенные
силы. Примеры: Л5-4.26,
Л4-2.17.
Зависимость
между
главными
моментами системы сил относительно
двух центров приведения.
ОЛ-1, гл. 8, § 8.6, гл. 9, § 9.1.
Лекции 14-15. Инварианты системы
сил. Частные случаи приведения.
Равновесие системы тел. Силы внешние
ДЛ -1
и внутренние. Свойства внутренних
сил. Задачи статически определенные и
статически неопределенные. Примеры
решения
задач типа
домашнего
задания.
Равновесие
тела
на
шероховатой поверхности. Трение
скольжения. Законы Кулона. Угол и
конус трения. Пример Л5-5.29. Трение
качения. Коэффициент трения качения.
Центр системы параллельных сил.
Формулы
для
радиус-вектора
и
координат
центра
системы
параллельных сил. Центр тяжести тела:
объема, площади, линии. Методы
нахождения центра тяжести: метод
симметрии, метод разбиения на части,
метод отрицательных масс. Примеры.
ОЛ-1, гл. 9, § 9.2, гл. 10, гл. 11.
Лекция
16-17.
(Читается
по
согласованию
с
выпускающей
кафедрой).
Постановка
задач
статического
расчета
элементов
приборов. Задачи инженерного расчета
конструкций. Модели механических
элементов приборов.
Основные
понятия механики деформируемого
тела. Деформации и перемещения.
Прочность, жесткость и устойчивость
элементов конструкций. Напряжения
при различных видах деформаций.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Занятие 13.
В аудитории: ОЛ-4: 1.26, ОЛ-5: 8.17,
8.19
Дома: ОЛ-4: 1.24, 1.25, 1.29
В аудитории: ОЛ-5: 2.19, 2.29, 4.17,
4.25
Дома: ОЛ-4: 1.3, 1.5
Занятие 14.
В аудитории: ОЛ-4: 1.14, 1.15, 1.17
Дома: ОЛ-4: 1.12, 1.16, МП 13, 18
Занятие 15.
Занятие 16.
В аудитории: ОЛ-5: 8.26, ОЛ-4: 2.12,
2.18, 2.19
119
Дома: ОЛ-4: 2.16, ДЗ № 4, МП 12-15
Занятие 17.
В аудитории: ОЛ-5: 5.26, 5.28, ОЛ-4:
1.39(1.38)
Дома: ОЛ-4: 1.43(1.42), 1.46(1.45)
САМОСТОЯТЕЛЬНАЯ ПОДГОТОВКА
Самостоятельная работа студента заключается в проработке материала
лекций, в выполнении текущих еженедельных заданий, получаемых
студентом
на семинарских занятиях для закрепления пройденного
материала, в выполнении ДЗ, в подготовке к контрольным мероприятиям по
модулям.
Контрольные мероприятия и сроки их проведения
ДЗ № 1 - «Кинематика точки и простейшие движения твёрдого тела».
Сроки выполнения: выдача 1-я неделя, прием – 5 неделя.
Контроль по модулю 1: срок проведения – 5 неделя.
ДЗ №2 – «Кинематика плоского движения твёрдого тела». Сроки
выполнения: выдача 5-я неделя, прием – 9 неделя.
Контроль по модулю 2: срок проведения – 8-9 неделя.
ДЗ № 3 - «Кинематика сложного движения точки». Срок выдачи - 9
неделя, срок сдачи – 13 неделя.
Контроль по модулю 3: срок проведения – 12-13 неделя.
ДЗ № 4 – «Статика». Сроки выполнения: выдача 13-я неделя, прием – 16
неделя.
Контроль по модулю 4: срок проведения – 17 неделя.
Литература
Основная литература (ОЛ)
1. Курс теоретической механики / Под ред. К.С.Колесникова. – М.: Изд.
МГТУ, 2000, 2002 2005, 2011.
2. Никитин Н.Н. Курс теоретической механики. Изд. 4-е и посл. – М.:
Высшая школа, 1983, 1990, 2003.
3. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Т.
1, 2. – М.: Наука, 1998.
4. Сборник задач по теоретической механике / Под ред. К.С.Колесникова –
М.: Наука, 1989, 2007, 2008 и более поздние издания.
5. Мещерский И.В. Сборник задач по теоретической механике М.: Наука,
1981, 1986 и более поздние издания.
120
Дополнительная литература (ДЛ)
1. Феодосьев В.И. Сопротивление материалов. Изд. 14 и посл. М.: Изд.
МГТУ, 2007.
Методические пособия, изданные в МГТУ (МП)
1. Виноградов А.Н., Пилюгина Н.Н., Феоктистова О.П. Кинематика точки и
простейшие движения твердого тела. – М.: МГТУ, 1994.
2. Кинематика точки и простейшие движения твердого тела. / Под ред.
Пожалостина А.А. – Изд. МГТУ, 1991.
3. Лапшин В.В. Кинематика точки и простейших движений твердого тела:
Метод.указания по выполнению курсовой работы. – М.: Изд. МГТУ, 2003.
4. Дубинин В.В., Карпачев А.Ю., Назаренко Б.П. Кинематика плоского
движения твердого тела: Методические указания и варианты курсового
задания. – М.: МГТУ, 2007.
5. Кинематика плоского движения твердого тела / Под ред. Назаренко Б.П. –
Изд. МГТУ, 1989.
6. Горина Т.И., Назаренко Б.П., Русанов П.Г. Метод.указания по
выполнению курсовой работы по разделу «Кинематика плоского
движения твердого тела». – Изд. МВТУ, 1982 (для ИУ, СМ5, ИУ2 –
Авиамоторная).
7. Кинематика плоского движения твердого тела: Метод.указания по
решению задач и выполнению курсового задания. / В.В. Дубинин, А.Ю.
Карпачев, Б.П. Назаренко, Л.В. Северова. – М.: Изд. МГТУ, 2004.
8. Занозин П.В., Пилюгина Н.Н., Тушева Г.М. Кинематика сложного
движения точки. – Изд. МВТУ, 1980 (для ИУ, СМ5, ИУ2 - Авиамоторная).
9. Дубинин В.В., Тушева Г.М., Гатауллина Г.И., Ремизов А.В. Кинематика
сложного движения точки: Методические указания и варианты курсовой
работы. – М.: МГТУ, 2007.
10.В.В. Дубинин, Г.И. Гатауллина, Г.М. Тушева. Методические указания к
выполнению курсовой работы и решению задач по теме: «Кинематика
сложного движения точки». – МГТУ, 2005.
11.Дубинин В.В., Занозин П.В., Солохин Е.Н., Орфаницкая Л.П.
Метод.указания к выполнению курсовой работы и решению задач по теме
«Кинематика сложного движения точки». – Изд. МВТУ, 1985.
12.Дубинин В.В., Борохова Н.В., Ильин М.М., Ремизов А.В. Плоская статика.
Метод.указания и курсовая работа по разделу курса «Теоретическая
механика». – Изд. МГТУ, 1998.
13.Бурмистров Б.А., Кирюшкина И.А., Кокушкин В.В. Пространственная
статика. Метод.указания к разделу курсовой работы по теоретической
механике. – Изд. МГТУ, 1994.
14.Брусенцова Е.А., Пилюгина Н.Н., Пожалостин А.А. Кинематика точки и
простейшие движения твердого тела. Метод.указания и условия вариантов
по выполнению курсовой работы. Часть 1. – Изд. МВТУ, 1987.
15.Методические указания к решению задач и выполнению курсовых
заданий по теме «Статика». / Под ред. В.В. Дубинина. – Изд. МГТУ, 2003.
121
Рекомендуемые Интернет-сайты
1. http://hoster.bmstu.ru/~fn3/
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
для СМ (кроме СМ5), РК4, 5. 9, 10
Дисциплина состоит из 4-х учебных модулей.
Модуль 1
Виды аудиторных
занятий и
Самостоятельной
работы
Лекции
Сроки
проведения или
выполнения,
недели
1-3
Трудоёмкость, Примечание
часы
6
Упражнения
1-4
8
Домашние задания
1-4
4
5
2
текущие
Контроль по модулю № 1
Модуль 2
Виды аудиторных
занятий и
Самостоятельной
работы
Лекции
Сроки
проведения или
выполнения,
недели
4-6
Трудоёмкость, Примечание
часы
6
Упражнения
5-9
10
Домашние задания
5-9
5
текущие
122
Контроль по модулю № 2
8-9
2
Модуль 3
Виды аудиторных
занятий и
Самостоятельной
работы
Лекции
Сроки
проведения или
выполнения,
недели
7-10
Трудоёмкость, Примечание
часы
8
Упражнения
10-12
6
Домашние задания
10-12
3
12-13
2
текущие
Контроль по модулю № 3
Модуль 4
Виды аудиторных
занятий и
Самостоятельной
работы
Лекции
Сроки
проведения или
выполнения,
недели
11-17
Трудоёмкость, Примечание
часы
14
Упражнения
13-17
10
Домашние задания
13-17
5
17
2
текущие
Контроль по модулю № 4
123
МОДУЛЬ 1. КИНЕМАТИКА ТОЧКИ.
ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
ЛЕКЦИИ
Лекция 1. Предмет теоретической
механики.
Кинематика
точки.
Способы задания движения точки.
Векторный
способ
задания
движения. Траектория, скорость,
ускорение
точки.
Задание
движения точки в прямоугольных
декартовых
координатах.
Траектория, скорость и ускорение
точки. Пример Л5-12.13.
Л-1, ГЛ. 1, §§ 1.1-1.4.
Лекция 2. Дифференцирование
вектора постоянного модуля по
скалярному аргументу. Задание
движения точки на плоскости в
полярных
координатах.
Траектория, скорость, ускорение
точки.
Пример.
Естественный
способ задания движения точки.
Скорость и ускорение точки.
Разложение ускорения по осям
естественного
трехгранника.
Демонстрация прибора ТМ-8.
Л-1, гл. 1, § 1.5.
Лекция 3. Кинематика твердого
тела. Задание движения твердого
тела, число степеней свободы.
Теорема о проекциях скоростей
двух точек твердого тела на ось,
проходящую через эти точки.
Поступательное движение твердого
тела, число степеней свободы.
Траектории, скорости и ускорения
точек тела. Вращение твердого тела
вокруг
неподвижной
оси.
Уравнение
движения,
число
степеней
свободы.
Угловая
скорость и угловое ускорение тела.
Векторные и скалярные формулы
для скоростей и ускорений точек
тела. Демонстрация приборов ТМ63, ТМ-47.
Л-1, гл. 2, §§ 2.1-2.3.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Занятие 1.
В аудитории: Л-4: 3.18(3.10), 3.27
(3.20)
Дома: Л-4: 3.21(3.13),3.22(3.15)
Занятие 3.
В аудитории: Л-5: 10.12, 10.13, 12.14,
12.17
Дома: Л-4: 3.2, 3.7(3.3),3.8(3.4), МП
1-4
Занятие 2.
В аудитории: Л-5: 13.6, 13.12, 14.5
Дома: Л-4: 4.5, 4.9, ДЗ №1, МП 1-4,
19
124
Дома: ДЗ №1
Занятие 4.
В аудитории: Задачи типа ДЗ 1
МОДУЛЬ 2. ПЛОСКОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
Лекции 4-5. Плоское движение
твердого тела. Уравнения плоского
движения, число степеней свободы.
Разложение
движения
на
поступательное вместе с полюсом и
вращательное
вокруг
оси,
проходящей
через
полюс.
Соотношение между скоростями
двух любых точек плоской фигуры.
Мгновенный центр скоростей –
МЦС; методы его нахождения.
Определение скоростей точек с
помощью
МЦС.
Различные
способы
определения
угловой
скорости. Соотношение между
ускорениями двух любых точек
плоской фигуры. Понятие о
ЛЕКЦИИ
мгновенном центре ускорений.
Различные способы определения
углового ускорения. Демонстрация
приборов ТМ-26, ТМ-30. Пример
Л4-5.14.
Л-1, гл. 3, §§ 3.1-3.9.
Лекция 6. Вращение твердого тела
вокруг неподвижной точки. Число
степеней свободы. Углы Эйлера.
Уравнения движения. Мгновенная
ось вращения. Векторы угловой
скорости и углового ускорения.
Скорости точек тела: векторная и
скалярная
формулы
Эйлера.
Формулы Пуассона.
Л-1, гл. 4, гл. 5.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Занятие 5.
В аудитории: Л-5: 16.29, Л-4: 5.6, 5.7,
5.14
Дома: Л-4: 5.8, 5.15, 5.20
Занятие 6.
В аудитории: Л-5: 18.11, Л-4: 5.26,
5.30
Дома: Л-4: 5.21, 5.28
Занятие 7.
Занятие 8.
В аудитории: Л4-5.40
Дома: Л4-5.41, ДЗ №2, МП 5-7
Занятие 9.
В аудитории: Задачи типа ДЗ 2
Дома: ДЗ № 2
В аудитории: Л-4: 5.38, 5.37
Дома: Л-4: 5.39, 5.43
125
МОДУЛЬ 3. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
ЛЕКЦИИ
Лекция 7. Ускорения точек
твердого тела при сферическом
движении. Осестремительное и
вращательное ускорения. Пример
Л5-19.4. Общий случай движения
свободного
твердого
тела.
Разложение
движения
на
поступательное вместе с полюсом и
вращательное (сферическое) вокруг
полюса. Уравнения движения.
Скорости и ускорения точек тела.
Л-1, гл. 4, гл. 5.
Лекции 8-9. Сложное движение
точки,
основные
понятия
и
определения. Полная и локальная
производные вектора, формула
Бура.
Теорема
о
сложении
скоростей. Теорема о сложении
ускорений – теорема Кориолиса.
Ускорение Кориолиса, правило
Жуковского.
Частные
случаи.
Примеры: Л4-7.9, 7.18. Сложное
движение твердого тела. Сложение
поступательных
движений,
сложение
вращений
вокруг
пересекающихся осей.
Л-1, гл. 6, гл. 7, §§ 7.1, 7.2,
7.4.
Студенты
самостоятельно
изучают тему «Сложение вращений
вокруг параллельных осей, пара
вращений».
Л-1, гл. 7, § 7.3.
Лекция
10.
Понятие
о
криволинейных
координатах.
Определение скорости и ускорения
точки при задании ее движения в
цилиндрических и сферических
координатах.
Л-1, гл. 1, § 1.4.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Занятие 10.
Занятие 12.
В аудитории: Л-5: 23.18,23.27,23.30
Дома: Л-4: 7.6(7.3), 7.16(7.13)
Занятие 11.
В аудитории: Л-4:
7.17(7.14),7.29(7.24), Л-5: 23.62
Дома: Л-4: 7.23(7.18), 7.26(7.21)
В аудитории: Л-4: 7.34 (7.29).
Задачи типа ДЗ3
Дома: ДЗ № 3, МП 8-10
МОДУЛЬ 4. СТАТИКА
Лекция 11. Статика. Основные
понятия и определения. Аксиомы
статики. Основные виды связей и
их реакции: гладкая поверхность,
цилиндрический шарнир, шаровой
шарнир, подпятник, гибкая нить,
шарнирный стержень. Система
ЛЕКЦИИ
сходящихся
сил,
условия
равновесия.
Л-1, гл. 8, §§ 8.1, 8.2.
Лекция 12. Алгебраический и
векторный
моменты
силы
относительно точки. Момент силы
относительно
оси.
Связь
126
векторного
момента
силы
относительно точки с моментом
силы
относительно
оси,
проходящей через эту точку.
Аналитические выражения для
моментов силы относительно осей
координат. Пара сил. Теорема о
сумме
моментов
сил,
составляющих пару, относительно
любой точки или оси. Векторный и
алгебраический моменты пары.
Л-1, гл. 8, §§ 8.3-8.5.
Лекция 13. Эквивалентность пар
сил. Сложение пар сил. Условие
равновесия системы пар сил.
Лемма о параллельном переносе
силы. Теорема о приведении
произвольной системы сил к силе и
паре сил – основная теорема
статики.
Л-1, гл. 8, § 8.6.
Лекция 14. Главный вектор и
главный момент системы сил.
Формулы для их вычисления.
Условия равновесия произвольной
системы сил. Частные случаи:
система параллельных сил, плоская
система сил – основная форма.
Теорема Вариньона о моменте
равнодействующей,
распределенные силы. Примеры:
Л5-4.26,
Л4-2.17. Зависимость
между
главными
моментами
системы сил относительно двух
центров приведения.
Л-1, гл. 8, § 8.6, гл. 9, § 9.1.
Лекции
15-16.
Инварианты
системы сил. Частные случаи
приведения. Равновесие системы
тел. Силы внешние и внутренние.
Свойства внутренних сил. Задачи
статически
определенные
и
статически
неопределенные.
Равновесие тела на шероховатой
поверхности. Трение скольжения.
Законы Кулона. Угол и конус
трения. Пример Л5-5.29. Трение
качения. Коэффициент трения
качения.
Л-1, гл. 9, § 9.2, гл. 10.
Лекция 17. Центр системы
параллельных сил. Формулы для
радиус-вектора и координат центра
системы
параллельных
сил.
Формулы для нахождения центра
тяжести однородного тела. Методы
нахождения центра тяжести: метод
симметрии, метод разбиения на
части, метод отрицательных масс.
Примеры.
Л-1, гл. 11.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Занятие 13.
В аудитории: Л-5: 2.19, 2.29, 4.17,
4.25
Дома: Л-4: 1.3, 1.5
Занятие 14.
В аудитории: Л-4: 1.14, 1.15, 1.17
Дома: Л-4: 1.12, 1.16, МП 13, 18
Занятие 15.
В аудитории: Л-4: 1.26, Л5-8.17, 8.19
Дома: Л-4: 1.24, 1.25, 1.29
Занятие 16.
В аудитории: Л-5: 8.26, Л-4: 2.12,
2.18, 2.19 Дома: Л-4: 2.16, ДЗ № 4,
МП 11-13
Занятие 17.
В аудитории: Л-5: 5.26, 5.28, Л-4:
1.39(1.38)
Дома: Л-4: 1.43(1.42), 1.46(1.45)
127
САМОСТОЯТЕЛЬНАЯ ПОДГОТОВКА
Самостоятельная работа студента заключается в проработке материала
лекций, в выполнении текущих еженедельных заданий, получаемых
студентом
на семинарских занятиях для закрепления пройденного
материала, в выполнении ДЗ, в подготовке к контрольным мероприятиям по
модулям.
Контрольные мероприятия и сроки их проведения
ДЗ № 1 - «Кинематика точки и простейшие движения твёрдого тела».
Сроки выполнения: выдача 1-я неделя, прием – 5 неделя.
Контроль по модулю 1: срок проведения – 5 неделя.
ДЗ №2 – «Кинематика плоского движения твёрдого тела». Сроки
выполнения: выдача 5-я неделя, прием – 9 неделя.
Контроль по модулю 2: срок проведения – 8-9 неделя.
ДЗ № 3 - «Кинематика сложного движения точки». Срок выдачи - 9
неделя, срок сдачи – 13 неделя.
Контроль по модулю 3: срок проведения – 12-13 неделя.
ДЗ № 4 – «Статика». Сроки выполнения: выдача 13-я неделя, прием – 16
неделя.
Контроль по модулю 4: срок проведения – 17 неделя.
Литература
Основная учебная литература (Л)
1.
Курс теоретической механики. Под ред. К.С. Колесникова. – М.: Изд. МГТУ,
2000, 2002, 2005, 2011.
2.
Никитин Н.Н. Курс теоретической механики. Изд. 4-е и посл. –
М.: Высшая школа, 1983, 1990, 2003.
3.
Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической
механики. Т. 1, 2. – М.: Наука, 1998.
4.
Сборник задач по теоретической механике. Под ред. К.С.
Колесникова. – М.: Наука, 1983, 1989, 2007, 2008.
5.
Мещерский И.В. Сборник задач по теоретической механике. – М.:
Наука, 1981, 1986.
128
Методические пособия, изданные в МГТУ (МП)
1. Брусенцова Е.А., Пилюгина Н.Н., Пожалостин А.А. Кинематика точки
и простейшие движения твердого тела. Метод.указания и условия вариантов
по выполнению курсовой работы. Часть 1. – Изд. МВТУ, 1987.
2. Болотникова Я.А., Панкратов А.А., Пожалостин А.А., Шкапов П.М.
Кинематика точки и простейшие движения твердого тела. / Под ред.
Пожалостина А.А. – Изд. МГТУ, 1991.
3. Виноградов А.Н., Пилюгина Н.Н., Феоктистова О.П. Кинематика точки
и простейшие движения твердого тела. – М.: МГТУ, 1994.
4. Лапшин В.В. Кинематика точки и простейших движений твердого тела:
Метод.указания по выполнению курсовой работы. – М.: Изд. МГТУ, 2003.
5. Дубинин В.В., Карпачев А.Ю., Назаренко Б.П. Кинематика плоского
движения твердого тела: Методические указания и варианты курсового
задания. – М.: МГТУ, 2007.
6. Кинематика плоского движения твердого тела / Под ред. Назаренко
Б.П. – Изд. МГТУ, 1989.
7. Кинематика плоского движения твердого тела: Метод.указания по
решению задач и выполнению курсового задания. / В.В. Дубинин, А.Ю.
Карпачев, Б.П. Назаренко, Л.В. Северова. – М.: Изд. МГТУ, 2004.
8. Занозин П.В., Пилюгина Н.Н., Тушева Г.М. Кинематика сложного
движения точки. – Изд. МВТУ, 1980 (для ИУ, СМ5, ИУ2 - Авиамоторная).
9. Дубинин В.В., Тушева Г.М., Гатауллина Г.И., Ремизов А.В.
Кинематика сложного движения точки: Методические указания и варианты
курсовой работы. – М.: МГТУ, 2007.
10.
В.В. Дубинин, Г.И. Гатауллина, Г.М. Тушева. Методические
указания к выполнению курсовой работы и решению задач по теме:
«Кинематика сложного движения точки». – МГТУ, 2005.
11.
Дубинин В.В., Борохова Н.В., Ильин М.М., Ремизов А.В. Плоская
статика. Метод.указания и курсовая работа по разделу курса «Теоретическая
механика». – Изд. МГТУ, 1998.
12.
Бурмистров Б.А., Кирюшкина И.А., Кокушкин В.В.
Пространственная статика. Метод.указания к разделу курсовой работы по
теоретической механике. – Изд. МГТУ, 1994.
13.
Методические указания к решению задач и выполнению
курсовых заданий по теме «Статика». / Под ред. В.В. Дубинина. – Изд.
МГТУ, 2003.
Рекомендуемые Интернет-сайты
1. http://hoster.bmstu.ru/~fn3/
129
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА
для факультетов МТ, Э
Дисциплина состоит из 3-х учебных модулей и экзамена
Модуль 1
Виды аудиторных
занятий и
Самостоятельной
работы
Лекции
Сроки
Трудоёмкость, Примечание
проведения или часы
выполнения,
недели
1-3
6
Упражнения
1-4
8
Домашние задания
1-4
4
5
2
текущие
Контроль по модулю
(письменная работа № 1)
Модуль 2
Виды аудиторных
занятий и
Самостоятельной
работы
Лекции
Сроки
проведения или
выполнения,
недели
5-10
Трудоёмкость, Примечание
часы
12
Упражнения
5-12
16
Домашние задания
5-12
8
12-13
4
текущие
Контроль по модулю:
письменная работа № 2
письменная работа № 3
130
Модуль 3
Виды аудиторных
занятий и
Самостоятельной
работы
Лекции
Сроки
проведения или
выполнения,
недели
11-17
Трудоёмкость, Примечание
часы
14
Упражнения
13-17
10
Домашние задания
13-17
5
17
2
текущие
Контроль по модулю №
3
Модуль 4
Экзамен (в сроки экзаменационной сессии)
Модуль 1: Кинематика точки и кинематика
простейших движений твёрдого тела
ЛЕКЦИИ
Лекция 1. Предмет теоретической
механики.
Кинематика
точки.
Способы задания движения точки.
Векторный
способ
задания
движения. Траектория, скорость,
ускорение
точки.
Задание
движения точки в прямоугольных
декартовых
координатах.
Траектория, скорость и ускорение
точки. Пример Л5-12.13.
ОЛ-1, гл. 1, §§ 1.1-1.4.
Лекция 2. Дифференцирование
вектора постоянного модуля по
скалярному аргументу. Задание
движения точки на плоскости в
полярных
координатах.
Траектория, скорость, ускорение
точки.
Пример.
Естественный
способ задания движения точки.
Скорость и ускорение точки.
Разложение ускорения по осям
естественного
трехгранника.
Демонстрация прибора ТМ-8.
ОЛ-1, гл. 1, § 1.5.
Лекция 3. Кинематика твердого
тела. Задание движения твердого
тела, число степеней свободы.
Теорема о проекциях скоростей
двух точек твердого тела на ось,
проходящую через эти точки.
Поступательное движение твердого
тела, число степеней свободы.
131
Траектории, скорости и ускорения
точек тела. Вращение твердого тела
вокруг
неподвижной
оси.
Уравнение
движения,
число
степеней
свободы.
Угловая
скорость и угловое ускорение тела.
Векторные и скалярные формулы
для скоростей и ускорений точек
тела. Демонстрация приборов ТМ63, ТМ-47.
ОЛ-1, гл. 2, §§ 2.1-2.3.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Занятие 1.
В аудитории: ОЛ-5: 13.6, 13.12, 14.5
Дома: ОЛ-4: 4.5, 4.9, ДЗ №1, МП 1-4,
19
В аудитории: ОЛ-5: 10.12, 10.13,
12.14, 12.17
Дома: ОЛ-4: 3.2, 3.7(3.3),3.8(3.4),
МП 1-4
Занятие 2.
В аудитории: ОЛ-4: 3.18(3.10), 3.27
(3.20)
Дома: ОЛ-4: 3.21(3.13),3.22(3.15)
Занятие 3.
Занятие 4.
В аудитории: Задачи типа ДЗ 1
Дома: ДЗ №1
Модуль 2: Кинематика плоского движения твёрдого тела
и кинематика сложного движения точки
Лекции 4-5. Плоское движение
твердого тела. Уравнения плоского
движения, число степеней свободы.
Разложение
движения
на
поступательное вместе с полюсом и
вращательное
вокруг
оси,
проходящей
через
полюс.
Соотношение между скоростями
двух любых точек плоской фигуры.
Мгновенный центр скоростей –
МЦС; методы его нахождения.
Определение скоростей точек с
помощью
МЦС.
Различные
способы
определения
угловой
скорости. Соотношение между
ускорениями двух любых точек
ЛЕКЦИИ
плоской фигуры. Понятие о
мгновенном центре ускорений.
Различные способы определения
углового ускорения. Демонстрация
приборов ТМ-26, ТМ-30. Пример
Л4-5.14.
ОЛ-1, гл. 3, §§ 3.1-3.9.
Лекции 6-7. Вращение твердого
тела вокруг неподвижной точки.
Число степеней свободы. Углы
Эйлера.
Уравнения
движения.
Мгновенная
ось
вращения.
Векторы угловой скорости и
углового ускорения. Скорости
точек тела: векторная и скалярная
формулы
Эйлера.
Формулы
132
Пуассона.
Ускорения
точек
твердого тела при сферическом
движении. Осестремительное и
вращательное ускорения. Пример
Л5-19.4. Общий случай движения
свободного
твердого
тела.
Разложение
движения
на
поступательное вместе с полюсом и
вращательное (сферическое) вокруг
полюса. Уравнения движения.
Скорости и ускорения точек тела.
ОЛ-1, гл. 4, гл. 5.
Лекции 8-9. Сложное движение
точки,
основные
понятия
и
определения. Полная и локальная
производные вектора, формула
Бура.
Теорема
о
сложении
скоростей. Теорема о сложении
ускорений – теорема Кориолиса.
Ускорение Кориолиса, правило
Жуковского.
Частные
случаи.
Примеры: Л4-7.9, 7.18. Сложное
движение твердого тела. Сложение
поступательных
движений,
сложение
вращений
вокруг
пересекающихся осей.
ОЛ-1, гл. 6, гл. 7, §§ 7.1, 7.2,
7.4.
Студенты
самостоятельно
изучают тему «Сложение вращений
вокруг параллельных осей, пара
вращений».
ОЛ-1, гл. 7, § 7.3.
Лекция
10.
Понятие
о
криволинейных
координатах.
Определение скорости и ускорения
точки при задании ее движения в
цилиндрических и сферических
координатах.
ОЛ-1, гл. 1, § 1.4.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Занятие 5.
В аудитории: Задачи типа ДЗ 2
Дома: ДЗ № 2
Занятие 10.
В аудитории: ОЛ-5: 16.29, ОЛ-4:
5.6, 5.7, 5.14
Дома: ОЛ-4: 5.8, 5.15, 5.20
Занятие 6.
В аудитории: ОЛ-5: 18.11, ОЛ-4:
5.26, 5.30
Дома: ОЛ-4: 5.21, 5.28
Занятие 7.
В аудитории: ОЛ-5:
23.18,23.27,23.30
Дома: ОЛ-4: 7.6(7.3), 7.16(7.13)
Занятие 11.
В аудитории: ОЛ-4:
7.17(7.14),7.29(7.24), ОЛ-5: 23.62
Дома: ОЛ-4: 7.23(7.18), 7.26(7.21)
Занятие 12.
В аудитории: ОЛ-4: 5.38, 5.37
Дома: ОЛ-4: 5.39, 5.43
Занятие 8.
В аудитории: ОЛ-4: 7.34 (7.29).
Задачи типа ДЗ3
Дома: ДЗ № 3, МП 8-10
В аудитории: ОЛ-4: 5.40
Дома: ОЛ-4: 5.41, ДЗ №2, МП 5-7
Занятие 9.
133
Модуль 3: Статика
ЛЕКЦИИ
Лекция 11. Статика. Основные
понятия и определения. Аксиомы
статики. Основные виды связей и
их реакции: гладкая поверхность,
цилиндрический шарнир, шаровой
шарнир, подпятник, гибкая нить,
шарнирный стержень. Система
сходящихся
сил,
условия
равновесия.
ОЛ-1, гл. 8, §§ 8.1, 8.2.
Лекция 12. Алгебраический и
векторный
моменты
силы
относительно точки. Момент силы
относительно
оси.
Связь
векторного
момента
силы
относительно точки с моментом
силы
относительно
оси,
проходящей через эту точку.
Аналитические выражения для
моментов силы относительно осей
координат. Пара сил. Теорема о
сумме
моментов
сил,
составляющих пару, относительно
любой точки или оси. Векторный и
алгебраический моменты пары.
ОЛ-1, гл. 8, §§ 8.3-8.5.
Лекция 13. Эквивалентность пар
сил. Сложение пар сил. Условие
равновесия системы пар сил.
Лемма о параллельном переносе
силы. Теорема о приведении
произвольной системы сил к силе и
паре сил – основная теорема
статики.
ОЛ-1, гл. 8, § 8.6.
Лекция 14. Главный вектор и
главный момент системы сил.
Формулы для их вычисления.
Условия равновесия произвольной
системы сил. Частные случаи:
система параллельных сил, плоская
система сил – основная форма.
Теорема Вариньона о моменте
равнодействующей,
распределенные силы. Примеры:
Л5-4.26,
Л4-2.17. Зависимость
между
главными
моментами
системы сил относительно двух
центров приведения.
ОЛ-1, гл. 8, § 8.6, гл. 9, § 9.1.
Лекции
15-16.
Инварианты
системы сил. Частные случаи
приведения. Равновесие системы
тел. Силы внешние и внутренние.
Свойства внутренних сил. Задачи
статически
определенные
и
статически
неопределенные.
Равновесие тела на шероховатой
поверхности. Трение скольжения.
Законы Кулона. Угол и конус
трения. Пример Л5-5.29. Трение
качения. Коэффициент трения
качения.
ОЛ-1, гл. 9, § 9.2, гл. 10.
Лекция 17. Центр системы
параллельных сил. Формулы для
радиус-вектора и координат центра
системы
параллельных
сил.
Формулы для нахождения центра
тяжести однородного тела. Методы
нахождения центра тяжести: метод
симметрии, метод разбиения на
части, метод отрицательных масс.
Примеры.
ОЛ-1, гл. 11.
134
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
Занятие 13.
В аудитории: ОЛ-5: 2.19, 2.29, 4.17,
Занятие 16.
4.25
В аудитории: ОЛ-5: 8.26, ОЛ-4: 2.12,
Дома: ОЛ-4: 1.3, 1.5
2.18, 2.19 Дома: ОЛ-4: 2.16, ДЗ № 4,
Занятие 14.
МП 11-13
В аудитории: ОЛ-4: 1.14, 1.15, 1.17
Занятие 17.
Дома: ОЛ-4: 1.12, 1.16, МП 13, 18
В аудитории: ОЛ-5: 5.26, 5.28, ОЛ-4:
Занятие 15.
1.39(1.38)
В аудитории: ОЛ-4: 1.26, Л5-8.17,
Дома: ОЛ-4: 1.43(1.42), 1.46(1.45)
8.19
Дома: ОЛ-4: 1.24, 1.25, 1.29
САМОСТОЯТЕЛЬНАЯ ПОДГОТОВКА
Самостоятельная работа студента заключается в проработке материала лекций, в
выполнении текущих еженедельных заданий, получаемых студентом
на
семинарских занятиях для закрепления пройденного материала, в выполнении ДЗ, в
подготовке к контрольным мероприятиям по модулям.
1.
2.
3.
4.
5.
6.
7.
8.
9.
Контрольные мероприятия и сроки их проведения
ДЗ № 1 - «Кинематика точки и простейшие движения твёрдого тела». Сроки
выполнения: выдача 1-я неделя, прием – 5 неделя.
Контроль по модулю 1 (письменная работа № 1): срок проведения – 5 неделя.
ДЗ №2 – «Кинематика плоского движения твёрдого тела». Сроки выполнения:
выдача 5-я неделя, прием – 9 неделя.
Контроль по модулю 2 (письменная работа № 2): срок проведения – 9-10
неделя.
ДЗ № 3 - «Кинематика сложного движения точки». Срок выдачи - 9 неделя,
срок сдачи – 13 неделя.
Контроль по модулю 2 (письменная работа № 3): срок проведения – 12-13
неделя.
ДЗ № 4 – «Статика». Сроки выполнения: выдача 13-я неделя, прием – 16
неделя.
Контроль по модулю 3 (письменная работа № 4): срок проведения – 17 неделя.
Экзамен: срок проведения – в экзаменационную сессию
Литература
Основная учебная литература (ОЛ)
1. Курс теоретической механики. Под ред. К.С. Колесникова. – М.: Изд. МГТУ,
2000, 2002, 2005, 2011.
2. Никитин Н.Н. Курс теоретической механики. Изд. 4-е и посл. – М.: Высшая
школа, 1983, 1990, 2003.
135
3. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики. Т. 1, 2. –
М.: Наука, 1998.
4. Сборник задач по теоретической механике. Под ред. К.С. Колесникова. – М.:
Наука, 1983, 1989, 2007, 2008.
5. Мещерский И.В. Сборник задач по теоретической механике. – М.: Наука,
1981, 1986.
Методические пособия, изданные в МГТУ (МП)
1. Брусенцова Е.А., Пилюгина Н.Н., Пожалостин А.А. Кинематика точки и
простейшие движения твердого тела. Метод.указания и условия вариантов по
выполнению курсовой работы. Часть 1. – Изд. МВТУ, 1987.
2. Болотникова Я.А., Панкратов А.А., Пожалостин А.А., Шкапов П.М.
Кинематика точки и простейшие движения твердого тела. / Под ред.
Пожалостина А.А. – Изд. МГТУ, 1991.
3. Виноградов А.Н., Пилюгина Н.Н., Феоктистова О.П. Кинематика точки и
простейшие движения твердого тела. – М.: МГТУ, 1994.
4. Лапшин В.В. Кинематика точки и простейших движений твердого тела:
Метод.указания по выполнению курсовой работы. – М.: Изд. МГТУ, 2003.
5. Дубинин В.В., Карпачев А.Ю., Назаренко Б.П. Кинематика плоского
движения твердого тела: Методические указания и варианты курсового
задания. – М.: МГТУ, 2007.
6. Кинематика плоского движения твердого тела / Под ред. Назаренко Б.П. –
Изд. МГТУ, 1989.
7. Кинематика плоского движения твердого тела: Метод.указания по решению
задач и выполнению курсового задания. / В.В. Дубинин, А.Ю. Карпачев, Б.П.
Назаренко, Л.В. Северова. – М.: Изд. МГТУ, 2004.
8. Занозин П.В., Пилюгина Н.Н., Тушева Г.М. Кинематика сложного движения
точки. – Изд. МВТУ, 1980 (для ИУ, СМ5, ИУ2 - Авиамоторная).
9. Дубинин В.В., Тушева Г.М., Гатауллина Г.И., Ремизов А.В. Кинематика
сложного движения точки: Методические указания и варианты курсовой
работы. – М.: МГТУ, 2007.
10.В.В. Дубинин, Г.И. Гатауллина, Г.М. Тушева. Методические указания к
выполнению курсовой работы и решению задач по теме: «Кинематика
сложного движения точки». – МГТУ, 2005.
11.Дубинин В.В., Борохова Н.В., Ильин М.М., Ремизов А.В. Плоская статика.
Метод.указания и курсовая работа по разделу курса «Теоретическая
механика». – Изд. МГТУ, 1998.
12.Бурмистров Б.А., Кирюшкина И.А., Кокушкин В.В. Пространственная
статика. Метод.указания к разделу курсовой работы по теоретической
механике. – Изд. МГТУ, 1994.
13.Методические указания к решению задач и выполнению курсовых заданий по
теме «Статика». / Под ред. В.В. Дубинина. – Изд. МГТУ, 2003.
Рекомендуемые Интернет-сайты
1. http://hoster.bmstu.ru/~fn3/
136
ФИЗИЧЕСКАЯ КУЛЬТУРА
2 семестр
Теория
Лекция
Принципы и методика занятий физическими упражнениями.
Общая и специальная физическая подготовка в образовательном процессе по
физическому воспитанию. Методические принципы физического воспитания.
Основы и этапы обучения движениям. Развитие физических качеств. Формирование
психических качеств в процессе физического воспитания.
Общая физическая подготовка, ее цели и задачи. Специальная (спортивная)
подготовка, ее цели и задачи. Зоны интенсивности и энерготраты при различных
физических нагрузках. Значение мышечной релаксации. Коррекция физического
развития, телосложения, двигательной и функциональной подготовленности
средствами физической культуры.
Краткая характеристика основных групп видов спорта и систем физических
упражнений. Индивидуальный выбор студентом вида спорта или систем физических
упражнений для регулярных занятий (2 часа).
В течение семестра
По графику учебного отделения
- Методика и особенности занятий избранным видом спорта или системой
физических упражнений, 1 час (по тематике учебных отделений).
Практика
17 недель
- Занятия по планам учебных отделений (видов спорта) (4 часа в неделю).
Контрольные упражнения
В течение семестра
- контрольные упражнения вида спорта по графику учебного отделения.
ЗАЧЕТНЫЕ ТРЕБОВАНИЯ
По системе балльно-рейтинговой оценки результатов успеваемости студентов
университета проставляются с учетом модулей.
Внимание!
Медицинская справка не является основанием для освобождения от занятий и
получения зачета по физическому воспитанию.
Студенты, освобожденные по состоянию здоровья от практических занятий на
длительный срок, зачисляются в специальное учебное отделение для освоения
доступных им разделов учебной программы с начала учебного семестра или сразу
после получения медицинской справки.
Студенты, находящиеся на дообследовании должны зарегистрироваться в
специальном отделении до получения ими мед.заключения (справки).
137