исследование влияния режимов термической и химико
реклама

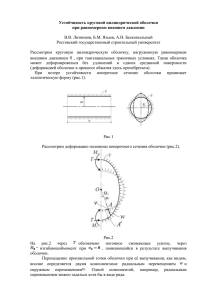
РАСЧЁТ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ РЕЗЕРВУАРА ПЕРЕМЕННОЙ ТОЛЩИНЫ Жигилий Д.А., ассистент; Жулёв А.А., студент Оболочечные конструкции имеют широкое применение в строительстве. Наиболее распространены резервуары для хранения жидкостей и сыпучих веществ в виде круговой цилиндрической оболочки переменной толщины. Рассмотрим задачу о напряженно-деформированном состоянии круговой цилиндрической оболочки переменной толщины под действием осесимметричного гидростатического давления. Принимаем, что для оболочки справедлива гипотеза недеформируемых нормалей. Согласно этой гипотезе прямолинейный элемент, нормальный к координатной поверхности оболочки, остается прямолинейным и нормальным к деформированной поверхности, сохраняя при этом свою длину. Пренебрегаем нормальными напряжениями на площадках, параллельных координатной поверхности, по сравнению с аналогичными напряжениями на площадках, перпендикулярных координатной поверхности. Используем линейную теорию оболочек, т. е. предполагаем, что перемещения малы по сравнению с толщиной оболочки, а углы поворота — по сравнению с единицей. Выбираем в качестве основных следующие функции: где Y N , N , Sˆ , M , u , u , , , N N cos Qˆ sin , r z s r z s r s s N z N s sin Q̂s cos , u r u cos w sin , u z u sin w cos . N r , N z радиальное и осевое погонные усилия соответственно; u r , u z - аналогичные перемещения, s - угол поворота нормали в осевом сечении. Система обыкновенных дифференциальных уравнений в нормальной dY A(s)Y f (s) , форме: ds где Y N r , N z , Ŝ, Ms , u r , u z , , s , A(s) a ij (s) (i, j 1, 2, , 8) , f f1, f 2 , , f8 . В алгоритме решения рассматриваемого класса задач предусматриваются следующие этапы: вычисление матрицы разрешающей системы и вектора ее свободных членов по исходным данным о геометрических параметрах координатной поверхности, толщинах и механических характеристиках материала и поверхностной нагрузки; численное решение краевой задачи для разрешающей системы уравнений вычисление всех характеристик напряженно-деформированного состояния оболочки в заданных точках. Решение двух - точечных краевых задач для систем линейных обыкновенных дифференциальных уравнений производится методом дискретной ортогонализации С.К. Годунова, сводящим решение краевой задачи к решению задач Коши, в данном случае численным методом Кутта - Мерсона 4-го порядка точности. В алгоритм метода дискретной ортогонализации для преодоления проблемы вырожденности матрицы системы алгебраических уравнений, возникающей при поиске произвольных постоянных, а также проблемы неограниченного экспоненциального роста погрешностей, вводятся механизмы ортогонализации и нормирования компонент решения в дискретном наборе точек интервала решения. В системе компьютерной алгебры MathCAD создана программа расчёта напряженнодеформированного состояния тонких осесимметричных оболочек находящихся под действием осесимметричных нагрузок. Приняты следующие параметры цилиндрического резервуара: - геометрические характеристики оболочки: R 2 м , l 4 м , h 0.005 (6 z) м ; - упругие постоянные материала: E 2 1011 Па , 0.3 ; Н . м3 Получены компоненты напряженно-деформированного состояния цилиндрической оболочки (в частности рисунке). - параметры поверхностной нагрузки: p r (l z) Па , 9810 200 3 810 3 610 0 Ym 0 100 200 300 200 3 410 Ym 3 400 3 210 600 0 100 200 3 300 800 210 m m а) б) Рисунок - Погонные внутренние силовые факторы вдоль меридиана оболочки (ось абсцисс – номер узла ортогонализации, разбиение равномерно по длине): а) б) осью. N r (Н/м) - внутреннее погонное усилие в радиальном направлении; M s (Н) - внутренний погонный момент в плоскости, образованной образующей цилиндра и его