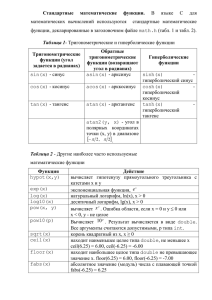
Гиперболические функции
реклама

Гиперболические функции Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Гиперболические функции были введены Винченцо Риккати (Vincenzo Riccati) в 1757 году («Opusculorum», том I). Он получил их из рассмотрения единичной гиперболы. Дальнейшее исследование свойств гиперболических функций было проведено Ламбертом. Риккати применял для гиперболических функций обозначения Sh и Ch. В дальнейшем в обозначениях гиперболических функций утвердился некоторый разнобой. Например, в Энциклопедии Брокгауза и Эфрона используются обозначения sinhyp, coshyp, в русскоязычной литературе закрепились обозначения sh, ch, в англоязычной закрепились sinh,cosh. Гиперболические функции часто встречаются при вычислении различных интегралов. Некоторые интегралы от рациональных функций и от функций, содержащих радикалы, довольно просто выполняются с помощью замен переменных с использованием гиперболических функций. Гиперболические функции задаются следующими формулами: гиперболический синус: (в англоязычной литературе обозначается sinh(x)) гиперболический косинус: гиперболический тангенс: (в англоязычной литературе обозначается tanh(x)) гиперболический котангенс: , Иногда также определяются гиперболические секанс и косеканс: , . В связи с особенностями написания операторов гиперболических функций в русском языке появился ряд жаргонных наименований этих функций. Простейшее (и наиболее распространённое) словообразование использует уточняющую приставку «гипер-» к названиям тригонометрических функций. Также существуют такие жаргонные названия: — «ши́нус», «сихинус». — «чо́синус», «коши́нус», «коси́хинус», «чуби́нус», «чи́нус», «чихо́нус». — «ча́нгенс», «та́шинус», «та́хинус», «таха́нгенс». — «кочангенс», «кота́хинус». sh(x), ch(x), th(x), cth(x) Геометрическое определение Ввиду соотношения ch²t-sh²t=1, гиперболические функции дают параметрическое представление гиперболы x2 − y2 = 1 (x=cht, y=sht). При этом аргумент t = 2S, где S — площадь криволинейного треугольника OQR, взятая со знаком «+», если сектор лежит выше оси OX, и «−» в противоположном случае. Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом. Связь с тригонометрическими функциями Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента. . . sin (х) = Im(e) cos(x) = Re(e), где e ix = cos (x) + i sin(x). Функция Гудермана, названная в честь Кристофа Гудермана (1798—1852), связывает тригонометрические функции и гиперболические функции без привлечения комплексных чисел. Она определяется как При этом . Имеют место также следующие тождества: , , , Важные тождества 1. 2. Чётность: 1. 2. 3. 3. Формулы сложения: 1. 2. 3. 4. Формулы двойного угла: 1. 2. 3. 4. 5. 6. 5. Формулы кратных углов: , 6. Произведения 1. 2. 3. 4. 7. Суммы 1. 2. 3. 4. 8. Формулы понижения степени 9. Производные: 10. Интегралы: 1. 2. 3. 4. 5. Неравенства При всех выполняется: , Разложение в степенные ряды (Ряд Лорана) Здесь B2n — числа Бернулли. Обратные гиперболические функции Читаются ареа… (-синус и т. д.) — от лат. «area» — «площадь». — обратный гиперболический синус, гиперболический арксинус, ареасинус: — обратный гиперболический косинус, гиперболический арккосинус, ареакосинус. — обратный гиперболический тангенс, гиперболический арктангенс, ареатангенс. — обратный гиперболический котангенс, гиперболический арккотангенс, ареакотангенс. — обратный гиперболический секанс, гиперболический арксеканс, ареасеканс. — обратный гиперболический косеканс, гиперболический арккосеканс, ареакосеканс. Связь между некоторыми обратными гиперболическими и обратными тригонометрическими функциями: где i — мнимая единица. Эти функции имеют следующее разложение в ряд: В зарубежной литературе обратные гиперболические функции часто обозначают посредством знака минус первой степени: например, пишут как (причём обозначает другую функцию — ), и т. д.