Использование пакета Gretl для нахождения критических значений
реклама
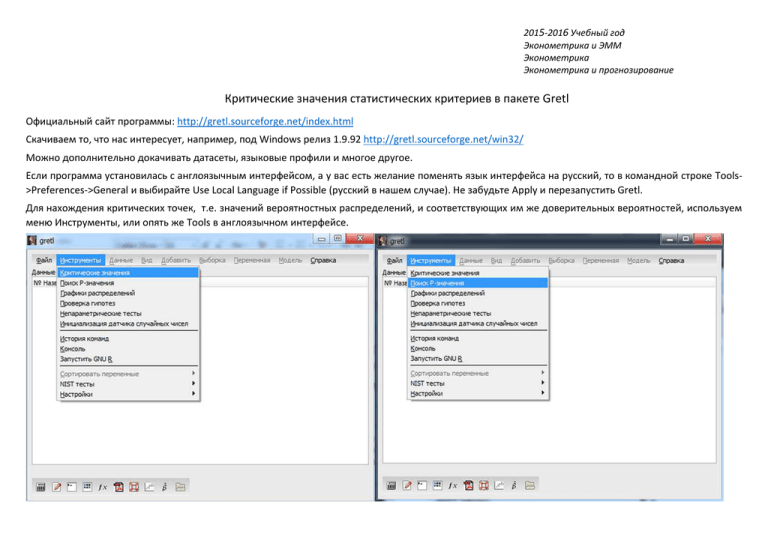
2015-2016 Учебный год Эконометрика и ЭММ Эконометрика Эконометрика и прогнозирование Критические значения статистических критериев в пакете Gretl Официальный сайт программы: http://gretl.sourceforge.net/index.html Скачиваем то, что нас интересует, например, под Windows релиз 1.9.92 http://gretl.sourceforge.net/win32/ Можно дополнительно докачивать датасеты, языковые профили и многое другое. Если программа установилась с англоязычным интерфейсом, а у вас есть желание поменять язык интерфейса на русский, то в командной строке Tools>Preferences->General и выбирайте Use Local Language if Possible (русский в нашем случае). Не забудьте Apply и перезапустить Gretl. Для нахождения критических точек, т.е. значений вероятностных распределений, и соответствующих им же доверительных вероятностей, используем меню Инструменты, или опять же Tools в англоязычном интерфейсе. Food расходы на питание, тыс. руб. Wage размер заработнойплаты, тыс. руб. Save сбережения(депозиты, наличные рубли и валюта), тыс. руб. Pay обязательные платежи, тыс. руб. n 100 (перекрестные данные, количествообследованных домохозяйств ) Foodt 97,45 0,724 Waget 0,14 Savet 0,358 Payt et S 45,93 0,04 0,08 0,29 R 2 0,818 Например, вам необходимо проверить статистическую значимость коэффициента 2 при переменной Save . Вы формулируете гипотезу, находите значение наблюдаемой t статистики: H0 : 2 0 T b2 0,14 1,75 S b2 0,08 Для проверки гипотезы вам необходимо найти критическое значение распределения Стьюдента при уровне значимости для двухсторонней критической области / 2 и степенями свободы n m 1 , т.е. t ( 2 ; n m 1) . Задаем / 2 0,005; 0,025; 0,05 и n m 1 100 3 1 96 . Gretl не может определить, одностороннюю или двухстороннюю вероятность вы хотите узнать, поэтому ему необходимо задать уровень значимости для «правой» критической точки (если мы выбираем одностороннюю вероятность, как при проверке гипотезы о равенстве коэффициента числу, то это 0,01 ; а если двухстороннюю, как при проверке статистической значимости коэффициента, то «правой» точке соответствует / 2 0,01 / 2 0,005 . Представляют интерес распределения: нормальное N, Стьюдента Т, Хи-квадрат 2 , Фишера F, Дарбина-Уотсона DW (тут только для 0,05 ). В меню Инструментов есть также и Графики распределений, и даже возможность Проверки гипотез (речь про гипотезы для математического ожидания и дисперсии, семинар (1)). Выбираем критическое значение, т.е. t (0,005;96) 2,62802 . Вероятности выше даны вам для того, чтобы исключить ошибку с вашей стороны: точку t (96) 2,62802 можно использовать при проверке двухсторонней гипотезы при 0,01 ; или односторонней гипотезы при 0,005 . Аналогично находим t (0,025;96) 1,98498 ; t (0,05;96) 1,66088 . Проверяем: T 1,75 t (0,005;96) 2,62802 H 0 T 1,75 t (0,025;96) 1,98498 H 0 T 1,75 t (0,05;96) 1,66088 H 1 Общий вывод: коэффициент при переменной Save слабо статистически значим; т.к. согласно t статистике коэффициент 2 статистически незначим при уровнях значимости 0,01; 0,05, но статистически значим при 0,10 . Гипотезу можно проверить, используя доверительную вероятность или P значение: H 0 : P value H : P value 0 Находим значение доверительной вероятности, используя то, что T 1,75 : Здесь также приводятся два значения доверительной вероятности, для проверки односторонней гипотезы P 0,0416568 и для проверки двухсторонней гипотезы P 0,0833135 (как и в случае и / 2 , значение двухсторонней доверительной вероятности в два раза больше, т.е. это как бы сумма двух вероятностей попадания в левостороннюю и правостороннюю критические области, которые равны). Таким образом, 2 –– статистически значим при уровне значимости, начиная с 0,09 (т.е. и для большего уровня – 0,10 ), т.к. 0,09 P 0,0833135 . При уровнях значимости 0,01 и 0,05 коэффициент 2 статистически незначим, т.к. 0,05 P 0,0833135 и тем более 0,01 P 0,0833135 .