Подготовка к ЕГЭ. Задания С1 с решениями

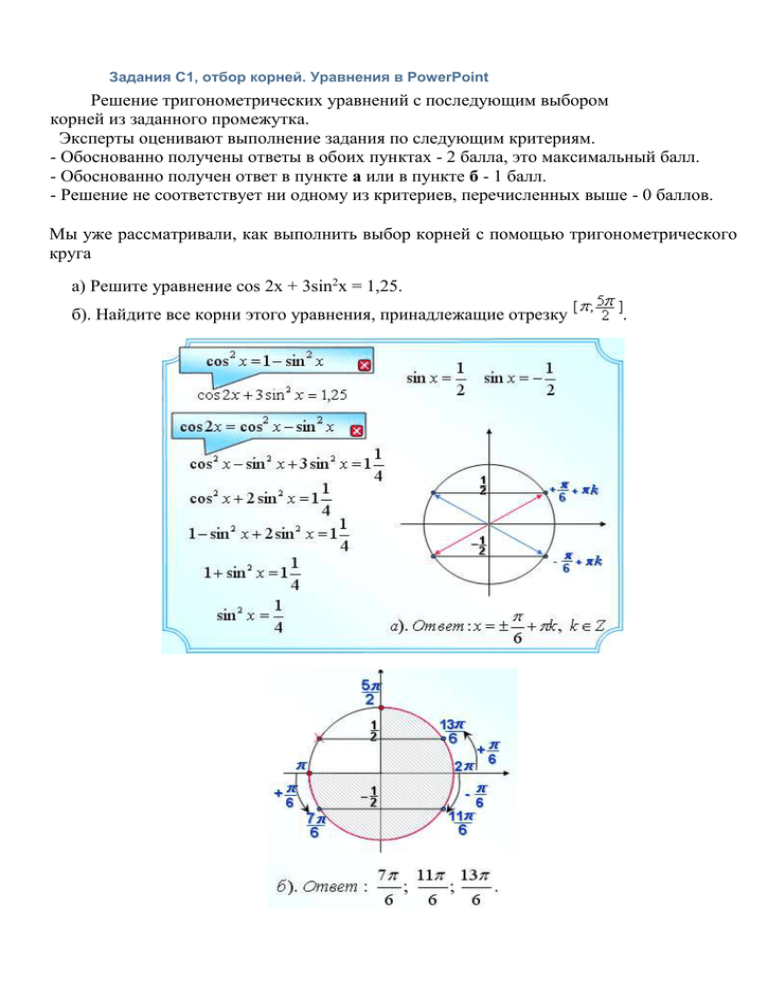
Задания С1, отбор корней. Уравнения в PowerPoint
Решение тригонометрических уравнений с последующим выбором
корней из заданного промежутка.
Эксперты оценивают выполнение задания по следующим критериям.
- Обоснованно получены ответы в обоих пунктах - 2 балла, это максимальный балл.
- Обоснованно получен ответ в пункте а или в пункте б - 1 балл.
- Решение не соответствует ни одному из критериев, перечисленных выше - 0 баллов.
Мы уже рассматривали, как выполнить выбор корней с помощью тригонометрического
круга
а) Решите уравнение cos 2x + 3sin2x = 1,25.
б). Найдите все корни этого уравнения, принадлежащие отрезку
.
>>>. Но это не единственный способ отбора корней. Иногда бывает не просто найти
заданный промежуток на тригонометрическом круге. Если вы не понимаете, как
работать с помощью тригонометрического круга, то можно делать выбор корней с
помощью решения двойных неравенств. При этом можно найти номера n тех корней,
которые принадлежат заданному промежутку. Зная число n, уже несложно вычислить и
сами
корни.
Примеры заданий.
1. а) Решите уравнение 6cos2x – 7cosx – 5 = 0.
б). Найдите все корни этого уравнения, принадлежащие отрезку [– ; 2 ].
Решение [скачать, 275 Kb]
2. а). Решите уравнение 4sin2x – 12sinx + 5 = 0.
б). Найдите все корни этого уравнения, принадлежащие отрезку [– ; 2 ].
Решение
[скачать, 306 Kb]
3. а). Решите уравнение sin2x –2 sin2x + 4cosx – 4 sinx = 0
б). Найдите корни этого уравнения, принадлежащие отрезку [– ; ].
Решение [скачать, 239 Kb].
4. а). Решите уравнение 7tg2x –
+1=0
б). Найдите корни этого уравнения, принадлежащие отрезку [–
Решение
[скачать, 191 Kb].
5. а). Решите уравнение 4tg2x +
+3=0
б). Найдите корни этого уравнения, принадлежащие отрезку [
Ответ: а). 2 n + , n Z б). 3
6. а). Решите уравнение cos3x =
;– ]
;4 ]
sin4x + cos5x
б). Найдите корни этого уравнения, принадлежащие отрезку
Решение
[скачать, 464 Kb].
7. а). Решите уравнение
б). Найдите корни этого уравнения, принадлежащие отрезку [ 2 ;
]
Решение
[скачать, 457 Kb] .
8. а). Решите уравнение 2sin2(
+ x) =
cosx
б). Найдите корни этого уравнения, принадлежащие промежутку [–
Решение [скачать, 305 Kb].
9. а). Решите уравнение
;–2 ].
sin2( +x) = – cosx
б) Найдите корни этого уравнения, принадлежащие промежутку [–
Решение [скачать, 319 Kb]
;– ]
10. Решите уравнение (2cos2x – 5cosx + 2) log3(–sinx)= 0.
б). Найдите корни этого уравнения, принадлежащие промежутку [ ;
Решение
[скачать, 389 Kb]
]
11. Тригонометрическое уравнение с выбором корней методом перебора и оценки.
Решите уравнение 4cos2x – 8sinx + 1 = 0 и найдите все корни, принадлежащие
отрезку [–3 ; – ].
Решение [скачать, 207 Kb].