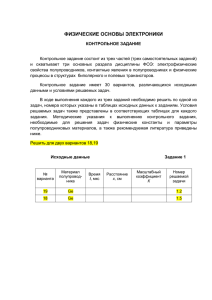
КОНТРОЛЬНЫЕ ЗАДАНИЯ 1. Образец кремния n-типа, находящийся в состоянии термодинамического
реклама

КОНТРОЛЬНЫЕ ЗАДАНИЯ 1. Образец кремния n-типа, находящийся в состоянии термодинамического равновесия при температуре 300К, характеризуется следующими параметрами: удельное сопротивление (Ом•см), подвижность электронов n (см 2 ( В с)) , подвижность дырок p , концентрация собственных носителей ni (см-3) и эффективная плотность состояний в зоне проводимости Nc (см-3). Определить: концентрацию электронов и дырок, положение уровня Ферми, вероятность событий, состоящих в том, что донорный уровень занят и свободен. Известно, что энергия ионизации донорной примеси d равна 0,05эВ. =10 Омсм, n 1200 см 2 ( В с) , p 800 см 2 ( В с) , ni 2 1010 см-3, N c 10 20 см-3, 2. Примесный полупроводник n-типа имеет концентрацию собственных носителей ni (см-3) при температуре 300К. Известно, что концентрация электронов в зоне проводимости n X N d , где N d - концентрация донорной примеси. Определить отношение N d n i , а также концентрацию основных (n) и неосновных (p) носителей, если дано: ni 4 1010 см-3 X =1,005, 3. Определить время жизни электронно-дырочных пар , если в момент времени t1(с) после выключения генерации неравновесная концентрация носителей оказалась в K раз больше, чем в момент времени t2(с). 2 t1= 10-5 c, t2= 10-4 c, K=5, 4. Определить диффузионную длину носителей заряда, если их избыточная концентрация на расстоянии Х1(мм) от точки генерации равна n1 (см-3), а на расстоянии Х2(мм), соответственно, n2 (см-3). Х1= 2 мм, Х2= 4,3 мм, n1 =1014 см-3, n2 =1013 см-3, E=400 В м , 5. Образец примесного полупроводника p-типа с размерами: длиной l , толщиной d и шириной a имеет сопротивление R , измеренное между торцами наименьшего сечения. Подвижности электронов и дырок равны n и p , соответственно, а концентрация собственных носителей ni . Определить в образце концентрацию основных и неосновных носителей заряда и отношение электронной проводимости к дырочной. l =6 мм d =2 мм a =3 мм R =200 Ом n =0,12 м 2 ( В с) p =0,025 м 2 ( В с) ni =1016 м-3 6. Сравнить концентрации электронов в собственном германии и кремнии при температурах Т1 и Т2. Считать, что эффективные плотности состояний N c и N v не зависят от температуры. Ширину запрещенной зоны в германии и кремнии принять равной 0,7 и 1,1 эВ, соответственно. Вычислить значения удельных проводимостей при указанных температурах. Удельное сопротивление чистых образцов при комнатной температуре 290К принять равными 0,5 и 1000 Омм, соответственно. Т1=50 С Т2=100 С j0 =1 А м 2 3 7. Определите, как уменьшится барьерная емкость диода с резким переходом при увеличении модуля напряжения смещения на величину U (В), если известно, что при U=X(В) C бар Y(пФ). U =2 В, X=3 В, Y=40 пФ, 8. Вычислите эффективность эмиттера, коэффициент переноса и коэффициент передачи тока в схеме с общим эмиттером для транзистора n-pn с однородной базой, имеющего следующие параметры: концентрации примесей ( N d и N a ), толщина базы ( Wб ), соотношение коэффициентов диффузии дырок и электронов ( D p 0.5Dn ), диффузионные длины носителей ( L p и Ln ). N d 1018 см-3, N a 1016 см-3, W=0,5 мкм, L p =1 мкм, Ln =10 мкм, ПРИМЕР ОФОРМЛЕНИЯ КОНТРОЛЬНОГО ЗАДАНИЯ Тема: Вычисление проводимости полупроводника. 3 Задача: Чистый кристаллический германий содержит 4,51028 атомов м . При температуре 300К один атом из каждых 2 109 атомов ионизирован. Подвижности электронов и дырок при этой температуре равны 0,4 и 0,2 м 2 ( В с) . Определите проводимость чистого германия. Определите проводимость примесного германия при 300К, причем на каждые 107 атомов германия приходится один примесный атом. Решение: При 300К один из 2109 атомов ионизирован. Поэтому, чтобы найти концентрацию собственных носителей ni в германии следует разделить общую концентрацию атомов на 2109, т.е. ni 4,5 10 23 (2 10 9 ) 2.25 1019 м-3. Используем известное соотношение для проводимости собственного полупроводника [1]: i ni q n p 2.25 1019 1.6 10 19 (0.4 0.2) 2.16 Ом-1м-1, где q-заряд электрона, а n и p - подвижности электронов и дырок. 4 Электропроводность чистого германия при температуре 300К и заданных условиях получилась i =2,16 Ом-1м-1. Полупроводник легированный трехвалентным элементом при 300К является материалом p-типа. Концентрация акцепторов N a равна: N a 4,5 1018 10 7 4.5 10 21 м-3 Электропроводность полупроводника p-типа рассчитывается по qn n p p , формуле [1]: где n-концентрация электронов в зоне проводимости, p-концентрация дырок в валентной зоне. Обычно можно считать, что при 300К все атомы примеси ионизированы. Полагая, что каждый атом примеси принимает один электрон, считаем, что p N a . Поскольку полупроводник не вырожден, то справедлив закон p n ni2 . действующих масс C учетом последних двух соотношений определяем: 12 2 38 ni n 0.4 19 4.5 10 0.2 2.25 10 1.6 10 q N a p 21 Na 4.5 10 1.6 10 19 9 10 20 4.5 1016 144 Ом-1м-1.