теоретическая часть C

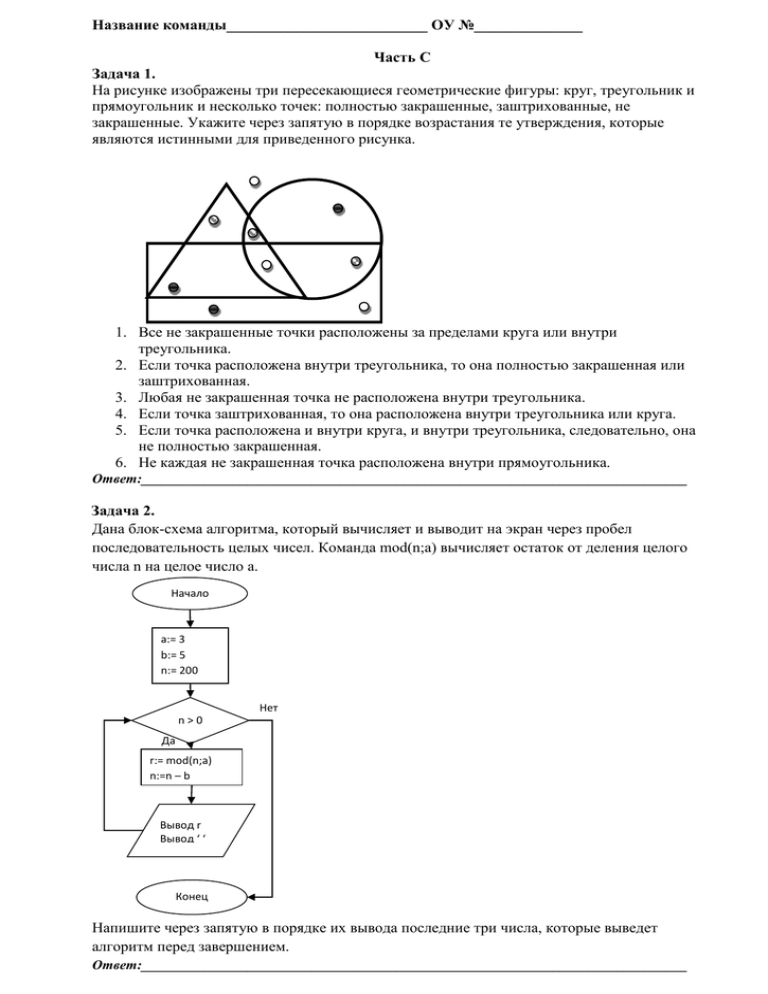
Название команды__________________________ ОУ №______________
Часть С
Задача 1.
На рисунке изображены три пересекающиеся геометрические фигуры: круг, треугольник и
прямоугольник и несколько точек: полностью закрашенные, заштрихованные, не
закрашенные. Укажите через запятую в порядке возрастания те утверждения, которые
являются истинными для приведенного рисунка.
1. Все не закрашенные точки расположены за пределами круга или внутри
треугольника.
2. Если точка расположена внутри треугольника, то она полностью закрашенная или
заштрихованная.
3. Любая не закрашенная точка не расположена внутри треугольника.
4. Если точка заштрихованная, то она расположена внутри треугольника или круга.
5. Если точка расположена и внутри круга, и внутри треугольника, следовательно, она
не полностью закрашенная.
6. Не каждая не закрашенная точка расположена внутри прямоугольника.
Ответ:_____________________________________________________________________________
Задача 2.
Дана блок-схема алгоритма, который вычисляет и выводит на экран через пробел
последовательность целых чисел. Команда mod(n;a) вычисляет остаток от деления целого
числа n на целое число a.
Начало
а:= 3
b:= 5
n:= 200
Нет
n>0
Да
r:= mod(n;a)
n:=n – b
Вывод r
Вывод ‘ ‘
Конец
Напишите через запятую в порядке их вывода последние три числа, которые выведет
алгоритм перед завершением.
Ответ:_____________________________________________________________________________
Задача 3.
Имеется текстовый документ, содержащий 40 страниц формата А5, полностью заполненных
текстом таким образом, что на каждой ровно 500 символов. Для кодирования символов
использовался двухбайтный Unicode.
Документ переформатировали на страницы формата А4 и одновременно перекодировали
символы в однобайтный ASCII, при этом объем всей текстовой информации уменьшился на
10 000 байт. Сколько приходится символов (знаков) на одну страницу формата А4, если в
переформатированном документе количество страниц уменьшилось ровно на 25 по
сравнению с форматом А5 и все страницы формата А4 оказались полностью заполнены?
Ответ:_____________________________________________________________________________
Задача 4.
Три брата Билли, Вилли, Дилли собирали гербарий: кленовые, березовые и дубовые листья.
Братья хотели определить, сколько всего листьев они собрали, но никак не могли собрать все
листья вместе. Они парами считали сколько листьев собрал каждый из них.
По итогам этих визитов они построили следующие три отчета в виде трех нормированных
гистограмм с накоплением:
100%
90%
80%
70%
60%
50%
40%
30%
20%
10%
0%
Вилли
Билли
100%
90%
80%
70%
60%
50%
40%
30%
20%
10%
0%
Дилли
Билли
100%
90%
80%
70%
60%
50%
40%
30%
20%
10%
0%
Дилли
Вилли
Помогите братьям определить общее количество листьев, если известно, что Вилли собрал 4
дубовых листьев, Дилли 6 березовых, Билли 8 кленовых. В ответ запишите целое число,
соответствующее общему количеству листьев, собранных всеми братьями.
Ответ:_____________________________________________________________________________
Задача 5.
Дана таблица некоторых изделий магазина аксессуаров.
№
Наименование
Цвет (RGB)
Количество
1. Ободок
(0, 0, 0)
18
2. Заколка
(0, 20, 20)
17
3. Шарф
(0, 0, 70)
25
4. Перчатки
(150, 0, 180)
10
5. Браслет
(200, 200, 200)
30
6. Подвеска
(10, 40, 100)
16
7. Резинка для волос
(255, 255, 255)
34
8. Зажим для волос
(30, 200, 255)
56
9. Серьги
(255, 140, 0)
33
В таблице провели сортировку по возрастанию количества товара в магазине.
На какой позиции после сортировки окажется оранжевый аксессуар?
Ответ:_____________________________________________________________________________