ИДЗ Д
реклама
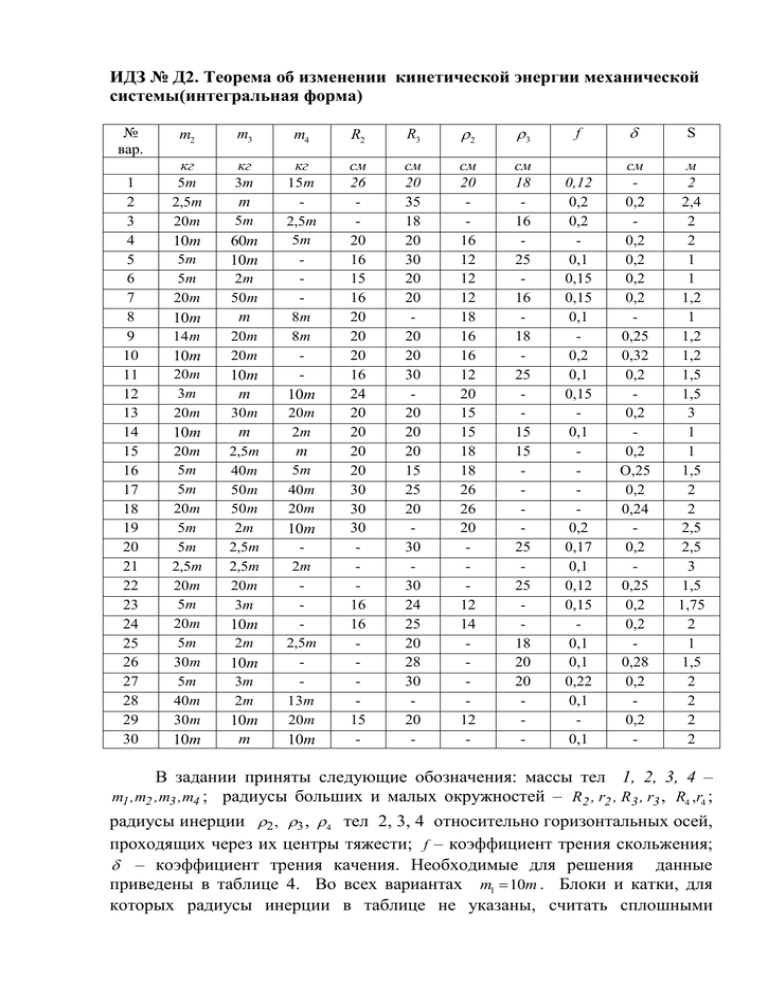
ИДЗ № Д2. Теорема об изменении кинетической энергии механической системы(интегральная форма) № вар. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 m2 m3 m4 R2 R3 2 3 f S кг 5m 2,5m 20m кг 3m кг 15m 2,5m 5m 8m 8m - см 26 20 16 15 16 20 20 20 16 24 20 20 20 20 30 30 30 16 16 15 - см 20 35 18 20 30 20 20 20 20 30 20 20 20 15 25 20 30 30 24 25 20 28 30 20 - см 20 16 12 12 12 18 16 16 12 20 15 15 18 18 26 26 20 12 14 12 - см 18 16 25 16 18 25 15 15 25 25 18 20 20 - 0,12 0,2 0,2 0,1 0,15 0,15 0,1 0,2 0,1 0,15 0,1 0,2 0,17 0,1 0,12 0,15 0,1 0,1 0,22 0,1 0,1 см 0,2 0,2 0,2 0,2 0,2 0,25 0,32 0,2 0,2 0,2 O,25 0,2 0,24 0,2 0,25 0,2 0,2 0,28 0,2 0,2 - м 2 2,4 2 2 1 1 1,2 1 1,2 1,2 1,5 1,5 3 1 1 1,5 2 2 2,5 2,5 3 1,5 1,75 2 1 1,5 2 2 2 2 10m 5m 5m 20m m 5m 60m 10m 2m 50 m 10m m 14 m 20m 20m 10m 20m 3m 20m 10m m 10m m 20m 5m 5m 20m 5m 5m 2,5m 20m 5m 20m 5m 30 m 5m 40m 30 m 2,5m 40m 50 m 50 m 2m 2,5m 2,5m 20m 3m 10m 30 m 10m 2m 10m 3m 2m 10m m 10m 20m 2m m 5m 40m 20m 10m 2m 2,5m 13m 20m 10m В задании приняты следующие обозначения: массы тел 1, 2, 3, 4 – m1 ,m2 ,m3 ,m4 ; радиусы больших и малых окружностей – R2 , r2 , R3 , r3 , R4 ,r4 ; радиусы инерции 2 , 3 , 4 тел 2, 3, 4 относительно горизонтальных осей, проходящих через их центры тяжести; f – коэффициент трения скольжения; – коэффициент трения качения. Необходимые для решения данные приведены в таблице 4. Во всех вариантах m1 10m . Блоки и катки, для которых радиусы инерции в таблице не указаны, считать сплошными однородными цилиндрами. В варианте 17 тележка 4 на четырёх одинаковых колёсах 3 . Наклонные участки нитей параллельны соответствующим наклонным плоскостям. Пример выполнения задания. Дано (Рис. 2, а): m1 – масса груза 1, m2 2 m1, m3 m1, m4 0,5m1 , m5 20m1 , R2 R3 12 см, r2 0,5R2 , r3 0,75R3 , R5 20 см , AB l 4 R3 , 2 8 см, 3 10 см, 30 , f 0,1, = 0,2 см, s = 0,06 м. Сопротивление качению тела 2 не учитывать. Шатун 4 считать тонким однородным стержнем; каток 5 – однородный сплошной цилиндр. Массами звена BC 5 и ползуна В пренебречь. На рисунке 2, а) показана механическая система в начальном положении. Рис. 2 Найти: V1 – скорость груза 1 в конечном положении. Решение. Применим теорему об изменении кинетической энергии системы: T T0 Ake Aki , (1) где T0 и T – кинетическая энергия системы в начальном и конечном положениях; Aki Ake – сумма работ внешних сил, приложенных к системе; – сумма работ внутренних сил системы. Для систем, состоящих из абсолютно твёрдых тел, соединённых нерастяжимыми нитями, Aki = 0. Так как в начальном положении система находится в покое, то T0 0 . Уравнение (1) принимает вид: T Ake . (2) Кинетическая энергия T системы в конечном её положении (рис. 2, б) равна сумме кинетических энергий тел 1, 2, 3, 4, 5: T =T1 T2 T3 T4 T5 . (3) Кинетическая энергия груза 1 T1 m1 V12 2 (4) . Кинетическая энергия катка 2, совершающего плоское движение, T2 2 m 2 V С2 2 J 2 22 , 2 (5) где VC2 – скорость центра тяжести C 2 катка 2 VC2 V1 , (6) J 2 – момент инерции катка 2 относительно его центральной оси C2 J 2 m2 22 , (7) 2 – угловая скорость катка 2. Так как каток катится без скольжения, то мгновенный центр скоростей катка находится в точке Р2. Поэтому 2 VC2 V 1 . C2 P2 R2 (8) Подставляя (6) – (8) в формулу (5), получаем m2 22 V12 m2 V12 1 T2 m2 2 2 2R22 2 2 1 22 V1 . (9) R2 Кинетическая энергия звена 3, вращающегося вокруг неподвижной оси Ох, J 2 T3 3x 3 , 2 (10) где J 3x – момент инерции звена 3 относительно оси Ох: 2 , J 3x m3 3x (11) 3 – угловая скорость звена 3: 3 VE . r3 (12) Скорость точки E звена 3 равна скорости точки D катка, которую можно найти из соотношения: (r 2 R 2 ) VD ; VC 2 R2 а так как VD 3 3 , VE VD V1 . 2 V1 2 то VC 2 V1 , R2 2 r 2 , (13) Подставляя (13) в (12), получаем 3 3 V1 . 2 r3 (14) После подстановки (11) и (14) в (10) выражение кинетической энергии звена 3 принимает вид: 2 m3 32x 3V1 T3 , или 2r3 2 T3 2 V 2 9 m3 3x 1 . 8 r 32 (15) Кинетическая энергия шатуна 4 , совершающего плоское движение, T4 1 1 2 m4 V C J 4 42 , 4 2 2 где VC 4 – скорость центра тяжести C 4 шатуна 4, J 4 – момент инерции шатуна относительно центральной оси C4 , 4 – угловая скорость шатуна 4. Для определения скорости VC 4 и угловой скорости 4 найдём конечное положение шатуна 4. Когда груз 1 пройдёт путь s 0, 06 (м), барабан 3 повернётся на угол 3 . Этот угол можно определить на основании формулы (14), заменяя в ней 3 d 3 ds , V1 , dt dt получаем d3 3 ds , или d 3 3 ds ; dt 2r3 dt 2 r3 после интегрирования (при нулевых начальных условиях) 3 3 s . 2 r3 Видно, что линейные и угловые перемещения находятся в такой же зависимости, как соответствующие линейные и угловые скорости. Вычислим угол 3 0, 06 2 0, 09 3 радиан . Значит, барабан 3 повернётся на 180 ; при этом шатун 4 из начального положения A0 B0 перейдёт в конечное положение АВ (рис. 2, б). Так как скорости точек А и В шатуна в этот момент параллельны, мгновенный центр скоростей шатуна находится в бесконечности. Угловая скорость шатуна 4 = 0, а скорости всех его точек равны между собой. Кинетическая энергия шатуна 4 T4 где 2 m4 V C 4 , 2 (16) VC 4 VA . (17) Скорость точки А звена 3 VA 3 R 3 (18) или с учётом (14) VA Поскольку r 3 С учётом (17) 3 R3 V 1 . 2 r3 3 R 3 , получим VA 2 V1 . 4 VC 4 2 V1 . (19) После подстановки (19) в (16) выражение кинетической энергии шатуна 4 принимает вид: T4 1 m 4 (2V 1) 2 2 m 4 V 12 . 2 (20) Кинетическая энергия катка 5 T5 1 1 2 m5 V C J 5 52 , 5 2 2 где V C 5 – скорость центра тяжести C5 катка 5; J 5 – момент инерции катка 5 (однородного сплошного цилиндра) относительно его центральной оси C5 ; 1 J 5 m 5 R 52 , 5 – угловая скорость катка 5. 2 Так как каток катится без скольжения, то мгновенный центр скоростей находится в точке P 5 (рис. 2, б), поэтому 5 VC 5 , R5 T5 2 1 1 m 5 R 52 V C 2 5 3 m V2 . m5 V C 5 5 C5 2 2 4 2 R 52 Так как звено BC 5 совершает поступательное движение, то VC5 VB ; но VB VC 4 2V 1 , т.е., VC 5 2 V 1 . Кинетическая энергия катка 5 принимает вид: T5 3 m 5 (2 V 1) 2 3 m 5 V12 . 4 (21) По формуле (3) с учётом (4), (9), (15), (20), (21): m1 V 12 T 2 1 m2 2 22 2 9 32x 1 2 V 1 m 3 2 V 12 2 m 4 V 12 3 m 5 V 12 . R 8 r3 2 Подставляя сюда заданные значения масс и радиусов, получаем m V2 T 129 1 1 . 2 (22) Найдём сумму работ всех внешних сил, приложенных к системе, на заданном её перемещении. Покажем внешние силы (рис. 2, в). Работа силы тяжести G 1 : AG1 G1 h1 m1 g s sin . (23) Работа силы трения скольжения F ТР. : A FТР. F ТР. s . Так как F ТР. f N 1 f G1 cos , то A F ТР. f m1 g s cos . Работа силы тяжести G 2 : AG 2 G 2 h C 2 m 2 g s sin . (24) (25) Работа сил сцепления F сц 2, F сц5 катков 2 и 5 равна нулю, так как эти силы приложены в мгновенных центрах скоростей катков. Работа силы тяжести G 4 : AG 4 G 4 h C 4 , где h C 4 – вертикальное перемещение центра тяжести C 4 шатуна 4 из начального положения в его конечное положение (рис. 2, г): h C 4 R 3 ; AG 4 m 4 g R 3 . (26) Работа пары сил сопротивления качению катка 5: A M C M C 5 , (27) где M C N 5 G 5 – момент пары сил сопротивления качению катка 5, 5 – угол поворота катка 5. Так как каток 5 катится без скольжения, то угол его поворота 5 SC 5 R5 , где SC – перемещение центра тяжести катка 5. Работу пары сил сопротивления качению вычислим, как сумму работ этой пары при качении катка 5 влево при повороте тела 3 на угол / 2 и качении вправо, когда тело 3 повернётся ещё на угол / 2 . Путь, 5 пройденный центром тяжести C 5 катка 5 равен сумме перемещений ползуна В влево и вправо: SC 2 Bo B . (29) Определим перемещение B0 B при повороте тела 3 на угол / 2 . За начало отсчёта координаты точки В выберем неподвижную точку К плоскости (рис. 2, г). При этом повороте тела 3 шатун из положения A0 B0 перейдёт в положение K B . Тогда B 0 B K B 0 K B , 5 где K B 0 K O O B 0 R 3 A 0 B 0 2 A 0O 2 R 3 l 2 R 32 , K B A B l 4 R 3 . Следовательно, B0 B R 3 l 2 R 32 l R 3 4 R3 2 R 32 4 R 3 0,88 R 3 , (30) Подставляя (30) в (29), а затем в (28), находим полный угловой путь катка 5: 5 1, 76 R3 . R5 (31) Работа пары сил сопротивления качению по (27): A M C m 5 g 1, 76 R3 . R5 (32) Сумма работ внешних сил определится сложением работ, вычисляемых по формулам (23) – (26) и (32): R Ake m1gs sin f m1g s cos m2 gs sin m4 gR3 m5 g 1,76 R3 5 Подставляя заданные значения масс, получаем R3 20 1,76R3 e , A m g s sin f cos 2 sin k 1 2 s R s 5 или Ake 1,51m1 g s . Приравняем значения T (33): 129 V1 (33) и Ake , определяемые по формулам (22) и m1 V12 1,51 m1 g s , откуда 2 2 1,51 g s 3,02 9,81 0,06 0,2 м / с . 129 129 Механическая система под действием сил тяжести приходит в движение из состояния покоя; начальное положение системы показано на схемах в таблице 3. Учитывая трение скольжения тела 1 (варианты 1–3, 5-8, 10-12, 14, 19–23, 25-28, 30) и сопротивление качению тела 3, катящегося без скольжения (варианты 2, 4-7, 9–11, 13, 15–18, 20, 22–24, 26, 27, 29), определить скорость тела 1 в тот момент, когда пройденный им путь станет равным s. Схемы механизмов ИДЗ № Д1 задание №1 задание №2 задание №3 задание №4 задание №5 задание №6 задание №7 задание №8 задание №9 задание №10 задание №11 задание №12 задание №13 задание №14 задание №15 задание №16 задание №17 задание №18 задание №19 задание №20 задание №21 задание №22 задание №23 задание №24 задание №25 задание №26 задание №27 задание №28 задание №29 задание №30


