Контрольная работа для студентов 1 курса фармацевтического

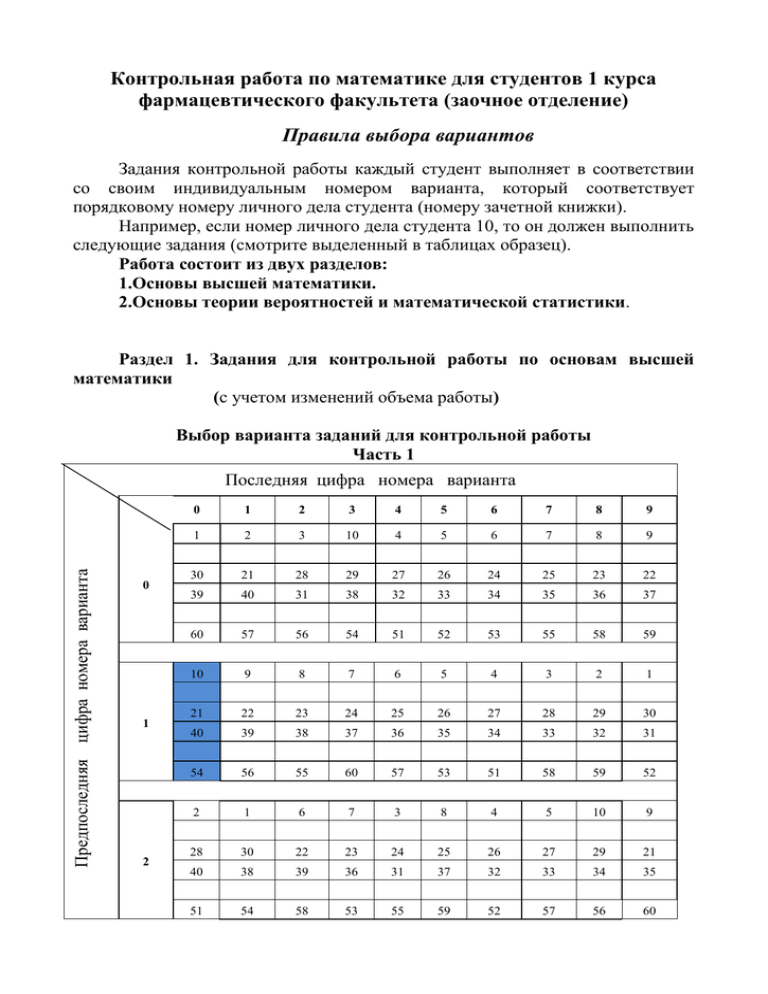
Контрольная работа по математике для студентов 1 курса
фармацевтического факультета (заочное отделение)
Правила выбора вариантов
Задания контрольной работы каждый студент выполняет в соответствии
со своим индивидуальным номером варианта, который соответствует
порядковому номеру личного дела студента (номеру зачетной книжки).
Например, если номер личного дела студента 10, то он должен выполнить
следующие задания (смотрите выделенный в таблицах образец).
Работа состоит из двух разделов:
1.Основы высшей математики.
2.Основы теории вероятностей и математической статистики.
Раздел 1. Задания для контрольной работы по основам высшей
математики
(с учетом изменений объема работы)
Выбор варианта заданий для контрольной работы
Часть 1
Предпоследняя цифра номера варианта
Последняя цифра номера варианта
0
1
2
0
1
2
3
4
5
6
7
8
9
1
2
3
10
4
5
6
7
8
9
30
21
28
29
27
26
24
25
23
22
39
40
31
38
32
33
34
35
36
37
60
57
56
54
51
52
53
55
58
59
10
9
8
7
6
5
4
3
2
1
21
22
23
24
25
26
27
28
29
30
40
39
38
37
36
35
34
33
32
31
54
56
55
60
57
53
51
58
59
52
2
1
6
7
3
8
4
5
10
9
28
30
22
23
24
25
26
27
29
21
40
38
39
36
31
37
32
33
34
35
51
54
58
53
55
59
52
57
56
60
3
4
Предпоследняя цифра номера варианта
5
6
7
8
9
10
7
6
5
4
3
1
8
2
30
29
28
27
26
25
24
23
21
22
39
40
37
38
31
32
33
34
35
36
54
56
55
59
58
57
60
52
51
53
3
2
1
4
5
7
9
10
6
8
27
29
30
21
22
24
25
26
28
23
31
33
32
34
35
36
39
37
40
38
51
56
57
54
55
53
60
52
58
59
8
7
10
5
4
6
2
1
9
3
22
23
24
25
21
27
28
29
30
26
38
31
32
33
34
35
36
37
39
40
58
56
57
60
52
59
53
55
51
54
7
6
9
10
3
2
1
8
5
4
23
24
25
26
27
28
29
30
22
21
37
38
31
32
33
34
35
36
40
39
54
55
58
56
60
52
59
53
51
57
6
10
8
9
7
1
2
3
4
5
24
26
27
28
29
30
21
22
23
25
36
37
40
31
32
33
34
35
39
38
54
60
57
55
53
58
52
59
56
51
5
4
3
2
1
10
7
9
8
6
25
27
28
30
29
21
22
23
24
26
40
32
33
34
35
36
37
31
38
39
2
9
51
55
60
52
59
57
53
58
56
54
4
3
2
1
8
9
10
6
5
7
26
28
29
30
21
22
23
24
25
27
32
31
34
35
36
37
38
33
39
40
53
60
59
52
58
56
55
54
57
51
Выбор варианта заданий для контрольной работы
Часть 2
Последняя цифра номера варианта
Предпоследняя цифра номера варианта
0
1
2
3
4
5
0
1
2
3
4
5
6
7
8
9
5
2
9
4
1
6
7
8
3
10
16
19
12
17
20
15
14
13
18
11
26
29
22
27
30
25
24
23
28
21
38
32
39
34
31
37
36
35
33
40
5
4
7
3
9
6
2
10
1
8
16
15
20
14
19
17
11
18
12
13
26
25
28
24
30
27
22
29
23
21
31
32
36
33
39
35
38
40
34
37
6
5
2
10
1
4
3
8
9
7
14
20
13
17
15
12
16
18
11
19
27
25
28
24
29
23
26
22
30
21
34
33
37
32
38
35
40
36
39
31
4
1
9
7
5
8
6
10
3
2
20
12
19
17
16
14
18
16
15
11
27
21
25
23
22
30
24
26
29
28
33
37
31
34
40
38
35
32
39
36
6
4
3
9
1
10
2
8
7
5
16
17
14
13
20
12
18
14
15
11
24
24
29
28
30
22
21
27
26
25
35
39
36
31
33
32
38
34
37
40
10
6
7
1
9
8
2
3
5
4
15
17
20
11
19
18
12
13
15
14
27
26
22
29
23
24
30
28
25
21
3
6
32
39
36
35
34
33
38
40
31
37
8
10
6
9
5
7
1
3
4
2
17
11
20
16
19
18
12
15
14
13
21
23
24
22
25
27
30
28
26
29
36
37
33
38
39
40
35
31
32
34
Продолжение таблицы на след странице
7
8
9
8
6
3
7
10
9
5
1
4
2
14
15
11
20
13
12
16
17
18
19
28
24
30
23
27
25
26
21
22
29
38
36
31
33
32
34
40
35
37
39
9
2
7
10
6
5
4
3
8
1
20
12
17
14
16
15
19
13
18
11
21
24
25
26
28
30
27
29
23
22
35
38
37
34
36
39
31
40
33
32
10
7
8
4
3
2
6
1
5
9
12
11
19
15
16
17
13
18
14
20
21
29
28
27
30
25
24
23
22
26
37
38
39
32
31
35
34
33
40
36
Предпоследняя цифра номер
варианта
Выбор варианта заданий для контрольной работы
Часть 3
Последняя цифра номера варианта
0
1
2
3
0
1
2
3
4
5
6
7
8
9
15
14
13
12
11
16
20
19
18
17
25
27
28
30
29
21
22
23
24
26
14
15
13
26
28
29
12
30
17
21
16
22
11
23
20
24
19
25
18
27
11
30
12
21
13
28
20
29
14
27
15
26
16
24
17
25
18
23
19
22
11
12
13
14
15
16
17
18
19
20
4
4
21
22
23
24
25
26
27
28
29
30
12
28
13
30
14
22
11
23
19
24
16
25
15
26
17
27
20
29
18
21
Продолжение таблицы на след странице
19
30
18
29
20
28
17
27
16
26
15
25
14
24
12
23
13
21
11
22
6
13
27
17
29
15
30
16
21
14
22
12
24
18
25
11
26
20
28
19
23
7
18
22
19
23
17
24
20
25
12
21
14
27
13
28
15
29
11
30
16
26
8
17
23
18
24
19
25
16
26
20
27
11
28
12
29
14
30
13
22
15
21
9
16
24
15
26
14
27
13
28
12
29
20
30
18
21
19
22
17
23
11
25
Вариант контрольной работы определяется по таблице в зависимости от
двух последних цифр номера личного дела студента. В колонке таблицы по
вертикали расположены цифры от 0 до 9, каждая из которых – предпоследняя
цифра номера личного дела. В верхней строке по горизонтали размещены
цифры от 0 до 9, каждая из которых – последняя цифра номера личного дела.
Пересечение вертикальной и горизонтальной линий определяет номера
заданий контрольной работы. Например, по последним двум цифрам личного
дела «10» находим вариант контрольной работы на пересечении строк с цифрой
1 и столбца с цифрой 0. Это номера:
Часть 1 – 10, 21, 40, 54.
Часть 2 – 5, 16, 26, 31.
Часть 3 - 14, 26.
Будьте внимательны при выборе варианта. Работа, выполненная не
по своему варианту, возвращается без проверки.
5
Задачи для контрольной работы (Часть 1)
Дифференциальное исчисление функций
Задачи 1-10
Найти производные следующих функций
1 x
1. y  cos 2
;
1 x
2
2. y  log 3 x 2  4 x  5 ;


3. y  e ln x  sin x ;
4. y  sin 2 x3  e x  ;
5. y  sin 3 arctge 3 x ;
6. y  101sin 3 x ;
4
7. y  3 ln sin
x3
;
4
8. y  5sin (3x 8) ;
3
2
x3
ln x
9. y  2 ;
10. y  ctg sin(sin x) ;
Задачи 21-30
Найти дифференциал функции
21. y  ln 1  2 x 2
22.
y = e x (x 2 - 2x  2)
7
3
23. y  ( x  x  1) lg x
24.
y
25. y  ( x
26. y  sin(3 x  1) cos 3
2
29. y =
2
2
28. y  x 1 x
1
x
sin 2 x
sin x
ln x
x
 3) 5 ln 2 x
27. y  (2x  1)(x 2  1)  e x
2 cos x
x
30. y = e (1 ctg 2 )
2
Задачи 31-40
Найти частные производные и полный дифференциал функции
32. z  xexy
31. z  sin x cos y
6
x
33. z  ln y 
xy
35.
z = ln(e
37.
z  u2 x2 
34.
 x  y)
36.
x2  1
u
z = tg(x2 y3 )
z=
1
x 1
ln
4 y 2 1
38. z  e
sin 5 x
 y cos4 x
y
40. z  ln sin( x )
39. z = ln(sin x3 y 2 )
Задачи 51-60
Решить задачу
51. После введения лекарственного препарата в
препарата в организме убывает по закону
скорость выведения препарата через 2 часа?
уменьшится вдвое?
52. Рост числа N клеток популяции со временем
N
53.
54.
55.
56.
57.
58.
организм человека масса
M  M 0 e  t / 2 . Какой будет
За какое время препарат
t описывается уравнением
5N 0
, где N 0 - начальный размер популяции, k - const.
(5  N 0 )e kt  N 0
Получите формулу для скорости роста численности популяции.
Кисть человека при ходьбе совершает гармонические колебания по закону
x  20 sin 1,5  t , (см). Определите максимальную скорость и ускорение при
движении.
Масса лекарственного вещества в крови уменьшается вследствие
выведения из организма по закону m(t )  20e t / 2 . Во сколько раз скорость
выведения через час отличается от скорости спустя 3 часа.
Пишущий элемент регистрирующего прибора совершает колебания по
закону x  2 sin  (t  0,8) см. С какой скоростью пишущий элемент
проходит через положение равновесия.
Движение летчика при катапультировании приближенно можно описать
формулой S  (3,7t 3  ln t  19t ) м. Определить скорость и ускорение летчика
через 2 сек. после катапультирования.
Вычислить скорость роста бактерий в условиях ограниченности
пространства, если закон увеличения числа бактерий имеет вид N  N 0 e kt ,
где k - const. Возрастает или убывает скорость со временем?
Численность
ограниченной
внешними
ресурсами
популяции
увеличивается по закону N  N 0
1 b
, где b и k = const. Определите
1  be  kt
скорость роста популяции и время, в течение которого скорость
увеличивается.
7
 kt
59. Рост клеток определяется законом N  N 0 e be , где b и k – const.
Определить момент времени, до которого скорость роста увеличивается.
60. Закон изменения температуры Т тела в зависимости от времени t
выражается формулой T  2,5t 2 . С какой скоростью нагревается тело в
момент времени t = 2 сек ? Через какое время скорость нагревания
увеличится вдвое?
Задачи для контрольной работы (Часть 2)
Интегральное исчисление функций
Задачи 1-10
Найти неопределенные интегралы
1.  e x sin e x  x 2 dx ;
.
x 1
 x dx ;
x
3.  sin 2 dx ;
 1 x 
4.   x  dx ;
2.
2
2
dx
5.  2  3 x 2 ;

6.
(3 x  1)dx
x2  1
.
2
7.
 (1  x )
8.
 cos2 x
9.
e3x  1
 e x dx ;
10)
 1 x 2
x dx
3 3
;
xtgxdx
;
arctgx
dx
.
Задачи 11-20
Вычислить определенный интеграл

4
1
11.
x 2 dx
0 1  x 2
12.
8

1

  cos x  sin 2 x dx

2
6.

ln 2
13.

2
e  x dx
14.
 sin
3
x cos xdx
0
0
3
15.

2
x
3
e dx
16.

  x
1 
dx
x4 
2

x
 x 2 )dx
1
0
e
17.

3
1
dx
x
18.
2
1
ln 2
19.

 (2
e x  1  dx
20.
0

2
 x sin xdx
0
Применение интегралов к решению практических задач
Задачи 21-30
Вычислить площадь фигуры, ограниченной заданными линиями. Изобразите
эту площадь графически.
23.
y1  x 3 и y 2  4 x
y  4  x2 и y  x  2
y  4  x2 и y  x  2
24.
y  x  4 , y  16  x 2 и осью ОХ
21.
22.
2
27.
y  x 2 , осью ОХ, прямыми х=1 и х=3
y  4 x 2  x 3 и осью ОХ
y  x 2 и y  x3
28.
y
25.
26.
29.
30.
x и yx
1
2
и y  3 x
x
y  sin x и y  0 на отрезке 0,  
y
Задачи 31-40
Решить задачу
31. В любой момент времени ускорение тела
a

3 2
t м / с2
2
 . Найти зависимость
пройденного пути от времени движения, если тело начало двигаться из
состояния покоя с начальной скоростью 8 м/с.
2
32. Тело движется прямолинейно с ускорением a  5см / с . Начальная
скорость тела v0  2 м / c . Выведите закон движения тела и вычислите путь,
пройденный им за первые 10 минут движения.
9
33. Пузырек воздуха поднимается со дна сосуда с жидкостью со скоростью
v  ( 0,5t  1) мм/с. Какой должна быть высота уровня жидкости, чтобы
пузырек достиг поверхности за 4 сек.?
34. Скорость тела задана формулой v  1  t м/с. Найти путь, пройденный
телом за первые 8 сек. после начала движения. За какое время тело
пройдет половину этого пути?
35. При гармоническом колебательном движении скорость задается формулой
dx
2
 
 2  t
, где Т-период колебаний, Т=const. Найти
v

cos


dt
T

T
2
положение тела в момент времени t=Т, если в момент времени t=0 оно
находилось в точке х=1.
36. Угловая скорость вращения барабана кимографа   6t 2  4t  5 . Найти угол
поворота  (t ) , если за t=2 сек. был совершен поворот на   2 рад.
37. Сила, действующая на тело, в направлении движения меняется со
временем по закону F=6t (H). Найти скорость тела в любой момент
времени, если в момент начала отсчета она была равна 1 м/с. Масса тела 3
кг, F (t )  m  a(t ) .
38. Найти закон изменения скорости тела, если уравнение ускорения имеет
вид a  3t 2  4t  4 м / с 2 , и если через 2 сек. скорость тела была 16 м/с.
39. Скорость укорочения мышцы описывается уравнением
dx
 B ( x0  x) , где
dt
x 0 - полное укорочение мышцы, В - постоянная , зависящая от нагрузки.
Записать закон сокращения мышцы х=х(t), если при t=0 укорочение было
равно нулю.
40. Ток в цепи, содержащей конденсатор, меняется с течением времени по
закону I=Imaxsin  t , где Imax и  известные постоянные величины.
Определить, как изменяется со временем заряд конденсатора, если в
момент времени, когда ток максимален, заряд конденсатора равен нулю.
(Сила тока равна скорости изменения заряда).
Задачи для контрольной работы (Часть 3)
Дифференциальные уравнения и их применение
Задачи 11-20
Найти частное решение уравнения
11.
1  x y  y  0 ,
12.
yx  2  3 y если у=0 при х=0
13.
(1  e x ) yy   e x
2
y (1)  1
если у=2 при х=0
10
14.
y   2 x  y если у= 0 при х=2
15.
ctg (ln y )
ex

если
ydx
dy(1  e x )
sin 3 x
y  e  / 2 при х=0

16.
yx 
17.
y( x2  1) cos y  2 x sin 2 y если y 
18.
19.
20.
cos5 y
xt
cos2 t 4
xy  

если y 
2
при х=0.

2
при х=1
t3
x если х=0 при t  0
ln 5 x
2
cos y
если y 

2
при х=1
( x 2  1) cos y (sin 2 y)2 x


если у =
при х =0
2
y
2
Задачи 21-30
Решить задачу.
21. Скорость растворения лекарственного вещества в таблетках
пропорциональна количеству m лекарства в таблетке. Известно, что при
m  m0 . Найти закон растворения таблетки, если период
t 0
полурастворения таблетки Т.
22. Популяция бактерий растет так, что скорость ее роста в момент времени t
равна 0,1 от размера популяции x(t). Опишите этот процесс с помощью
дифференциального уравнения и найдите размер популяции через 10
часов, если x(0)=1000.
23. Скорость выведения лекарственного препарата из организма человека
пропорциональна концентрации этого вещества в крови в данный момент
времени. Определите зависимость концентрации этого вещества от
времени, если в начальный момент она была равна 0,2мг/л, а через 23 часа
уменьшилась вдвое.
24. Световой поток, поглощаемый стекловидным телом глаза пропорционален
толщине тела и падающему потоку  . Выведите закон поглощения и
определите, какая доля падающего потока дойдет до сетчатки если
известно, что в слое dx поглощается часть светового потока величиной
( d ).
25. Скорость охлаждения тела в воздухе пропорциональна разности
температур тела (Т) и воздуха ( T0 ). При температуре воздуха 20 0 C тело в
течении 20 минут охладилось от 1000 C до 60 0 C . Через сколько времени
температура тела станет равной 30 0 C ?
11
dx
26. Скорость укорочения мышцы описывается уравнением: dt  B( x0  x) ,где
x0 - полное укорочение мышцы; х - укорочение мышцы в данный момент;
B - постоянная, зависящая от
нагрузки. Записать закон сокращения
мышцы x  x(t ) , если в момент времени t  0 укорочение мышцы стало
равно нулю.
27. Известно, что скорость распада радия пропорциональна его наличному
количеству и что половина его первоначального количества распадается в
течение 1600 лет. Определить, какой процент данного количества радия
распадется в течение 100 лет?
Е
28. Абсолютное изменение громкости звука
пропорционально
относительному изменению интенсивности
I
звуковой волны. Составить
I
дифференциальное уравнение и найти его частное решение при условии,
что вблизи порога слышимости E  0 , I  I 0 , k  const .
29. Скорость распада, т.е. скорость количества нераспавшихся атомов,
пропорциональна их количеству N (t ) в данный момент времени. Составить
дифференциальное уравнение радиоактивного распада и найти его
решение при условии, что первоначальное количество нераспавшихся
атомов равнялось N 0 .
30. Популяция бактерий увеличивается таким образом, что удельная скорость
роста в момент t (час) составляет величину
1
. Допустим, что начальной
1  2t
популяции соответствует х(0)=1000. Какой будет популяция после 4-х
часов роста?
Раздел 2. Задания для контрольной работы по основам теории
вероятностей и математической статистики.
(с учетом изменений объема работы)
Правила выбора вариантов
Задания для контрольной работы каждый студент выполняет в
соответствии со своим индивидуальным номером варианта, который
соответствует порядковому номеру личного дела( зачетной книжки) студента.
12
Например, если номер личного дела( зачетной книжки) студента 10, то он
должен выполнить следующие задания (смотрите выделенный в таблицах
образец).
Вариант контрольной работы определяется по таблице в зависимости от
двух последних цифр личного дела студента, зачетной книжки. В колонке
таблицы по вертикали расположены цифры от 0 до 9, каждая из которых –
предпоследняя цифра личного дела, зачетной книжки. В верхней строке по
горизонтали размещены цифры от 0 до 9, каждая из которых – последняя
цифра личного дела, зачетной книжки.
Пересечение вертикальной и горизонтальной линий определяет номера
заданий контрольной работы. Например, по последним двум цифрам личного
дела, зачетной книжки «10» находим вариант контрольной работы на
пересечении строк с цифрой 1 и столбца с цифрой 0. Это номера:
Часть 1 – 11, 21, 40, 43, 54.
Часть 2 – 16, 31.
.
Будьте внимательны при выборе варианта. Работа, выполненная не
по своему варианту, возвращается без проверки.
Выбор варианта заданий для контрольной работы
Часть 1
Предпоследняя цифра номера варианта
Последняя цифра номера варианта
0
0
1
2
3
4
5
6
7
8
9
11
12
13
20
14
15
16
17
18
19
30
21
28
29
27
26
24
25
23
22
39
40
31
38
32
33
34
35
36
37
44
41
46
45
49
47
50
48
43
42
60
57
56
54
51
52
53
55
58
59
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
39
38
37
36
35
34
33
32
31
43
44
45
46
47
48
49
50
41
42
54
56
55
60
57
53
51
58
59
52
0
1
2
3
4
5
6
7
8
9
2
1
6
7
3
8
4
5
10
9
12
13
14
11
19
16
15
17
20
18
28
30
22
23
24
25
26
27
29
21
40
38
39
36
31
37
32
33
34
35
10
1
2
13
3
4
Предпоследняя цифра номера варианта
5
6
7
8
45
46
42
41
43
44
50
47
48
49
51
54
58
53
55
59
52
57
56
60
19
18
20
17
16
15
14
12
13
11
30
29
28
27
26
25
24
23
21
22
39
40
37
38
31
32
33
34
35
36
42
41
43
44
45
46
47
48
49
50
54
56
55
59
58
57
60
52
51
53
13
17
15
16
14
12
18
11
20
19
27
29
30
21
22
24
25
26
28
23
31
33
32
34
35
36
39
37
40
38
46
45
47
48
50
49
41
42
43
44
51
56
57
54
55
53
60
52
58
59
18
19
17
20
12
14
13
15
11
16
22
23
24
25
21
27
28
29
30
26
38
31
32
33
34
35
36
37
39
40
42
46
45
49
48
47
50
41
43
44
58
56
57
60
52
59
53
55
51
54
17
18
19
16
20
11
12
14
13
15
23
24
25
26
27
28
29
30
22
21
37
38
31
32
33
34
35
36
40
39
49
50
48
47
41
42
43
44
45
46
54
55
58
56
60
52
59
53
51
57
16
15
14
13
12
20
18
19
17
11
24
26
27
28
29
30
21
22
23
25
36
37
40
31
32
33
34
35
39
38
49
50
41
42
43
44
45
46
47
48
54
60
57
55
53
58
52
59
56
51
0
1
2
3
4
5
6
7
8
9
15
14
13
12
11
16
20
19
18
17
25
27
28
30
29
21
22
23
24
26
14
9
40
32
33
34
35
36
37
31
38
39
48
47
50
49
44
45
46
41
43
42
51
55
60
52
59
57
53
58
56
54
14
15
13
12
17
16
11
20
19
18
26
28
29
30
21
22
23
24
25
27
32
31
34
35
36
37
38
33
39
40
47
48
49
50
42
43
44
45
46
41
53
60
59
52
58
56
55
54
57
51
Выбор варианта заданий для контрольной работы
Часть 2
Последняя цифра номера варианта
Предпоследняя цифра номера варианта
0
1
2
3
4
0
1
2
3
4
5
6
7
8
9
5
2
9
4
1
6
7
8
3
10
16
19
12
17
20
15
14
13
18
11
38
32
39
34
31
37
36
35
33
40
5
4
7
3
9
6
2
10
1
8
16
15
20
14
19
17
11
18
12
13
31
32
36
33
39
35
38
40
34
37
6
5
2
10
1
4
3
8
9
7
14
20
13
17
15
12
16
18
11
19
34
33
37
32
38
35
40
36
39
31
4
1
9
7
5
8
6
10
3
2
20
12
19
17
16
14
18
16
15
11
33
37
31
34
40
38
35
32
39
36
0
1
2
3
4
5
6
7
8
9
6
4
3
9
1
10
2
8
7
5
16
17
14
13
20
12
18
14
15
11
35
39
36
31
33
32
38
34
37
40
15
Предпоследняя цифра номера варианта
5
6
7
8
9
10
6
7
1
9
8
2
3
5
4
15
17
20
11
19
18
12
13
15
14
32
39
36
35
34
33
38
40
31
37
8
10
6
9
5
7
1
3
4
2
17
11
20
16
19
18
12
15
14
13
36
37
33
38
39
40
35
31
32
34
8
6
3
7
10
9
5
1
4
2
14
15
11
20
13
12
16
17
18
19
38
36
31
33
32
34
40
35
37
39
9
2
7
10
6
5
4
3
8
1
20
12
17
14
16
15
19
13
18
11
35
38
37
34
36
39
31
40
33
32
10
7
8
4
3
2
6
1
5
9
12
11
19
15
16
17
13
18
14
20
37
38
39
32
31
35
34
33
40
36
Задачи для контрольной работы (Часть 1)
Теория вероятностей
Задачи 11-20
11. Вероятность того, что студент в летнюю сессию не сдаст вовремя первый
экзамен, равна 0,2; второй – 0,1; третий – 0,15. Найти вероятность того, что
студентом будут сданы вовремя:
a) только 2-ой экзамен;
b) все 3 экзамена;
c) ни одного экзамена.
12. Вероятность того, что в летнюю сессию студент сдаст первый экзамен,
равна 0,8; второй – 0,9; третий – 0,8. Найти вероятность того, что студент:
16
a) не сдаст только первый экзамен;
b) сдаст только первый и третий;
c) хотя бы один экзамен сдаст.
13. Для сигнализации об аварии установлены два независимо работающих
сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна
0,95 для первого сигнализатора и 0,9 – для второго. Найдите вероятность того,
что при аварии:
а)все сигнализаторы сработают;
b)сработает только один сигнализатор;
c)сработает хотя бы один сигнализатор.
14. Производительности трёх конвейеров, выпускающих одинаковые
лекарственные препараты на фармацевтическом заводе, относятся как 1:3:6. Из
нерассортированной партии выпущенных препаратов взяты наудачу два.
Какова вероятность того, что:
а) один из них выпущен со второго конвейера;
б) оба выпущены с одного конвейера;
в) хотя бы один выпущен с первого конвейера.
15. Экспедиция издательства отправила вестники с информацией в три
медицинских учреждения. Вероятность своевременной доставки информации в
первое учреждение равна 0,9, во второе – 0,7 и в третье – 0,8. Найти
вероятность следующих событий:
a) только одно учреждение получит информацию вовремя;
b) хотя бы одно учреждение получит информацию с опозданием;
c) по крайней мере два учреждения получат информацию вовремя.
16. Студент разыскивает нужную ему информацию в трех справочниках.
Вероятность того, что она содержится в первом, втором и третьем
справочниках, равна соответственно 0,7; 0,73 и 0,76. Найти вероятность того,
что эта информация содержится:
a) не менее чем в двух справочниках;
b) во всех трех справочниках;
c) хотя бы в одном справочнике.
17. Спортсменом произведено три выстрела по цели. Вероятность попадания
при первом выстреле равна 0,75; при втором – 0,9; при третьем – 0,8.
Определить вероятность того, что будет:
a) три промаха;
b) хотя бы одно попадание;
c) по крайней мере два попадания.
18.
Вероятность
своевременного
выполнения
студентом-заочником
контрольной работы по каждой из трех дисциплин равна соответственно 0,9;
0,75 и 0,8. Найти вероятность своевременного выполнения контрольной
работы студентом:
a) только по одной дисциплине;
b) хотя бы по двум дисциплинам;
c) по всем трем дисциплинам.
17
19. Оператор обслуживает 4 установки, работающие независимо друг от друга.
Вероятность того, что первая установка в течение смены потребует внимания,
равна 0,25; вторая – 0,5; третья – 0,4 и четвертая – 0,1. Найти вероятность того,
что в течение смены:
a) хотя бы одна установка потребует внимания оператора;
b) все три установки не потребуют внимания оператора;
c) только одна установка потребует внимание оператора.
20. Экспертной организацией послан курьер за различными документами в
четыре архива. Вероятность наличия документов в первом архиве равна 0,6; во
втором – 0,7; в третьем – 0,8; в четвертом – 0,9. Найти вероятность того, что
нужные документы окажутся:
a) только в двух архивах;
b) хотя бы в двух архивах;
c) ни в одном архиве не окажется нужных документов.
Задачи 21-30
21. В специализированную больницу поступают в среднем 60% больных с
заболеванием К, 25% – с заболеванием L, 15% – с заболеванием М. Вероятность
полного излечения болезни К равна 0,7; для болезней L и М эти вероятности
соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был
выписан здоровым. Определить, каким вероятнее всего заболеванием страдал
больной.
22. Расследуют причины неудачной операции, по поводу которой можно
высказать 4 предположения (гипотезы): H1 , H 2 , H 3 , H 4 . По данным статистики
P( H1 )  0,2; P( H 2 )  0,4; P( H 3 )  0,3; P( H 4 )  0,1 . В ходе расследования обнаружено,
что произошло массивное кровотечение ( A ). Условные вероятности события А
по той же статистике P( A / H1 )  0,9; P( A / H 2 )  0; P( A / H 3 )  0,2; P( A / H 4 )  0,3 .
Какая из гипотез наиболее вероятна при данных условиях?
23. В поликлинике ведут прием 3 врача. Первый врач принимает 50% больных,
второй – 20% больных и третий – 30% больных. Одному из пациентов
поставлен ошибочный диагноз. Вероятность врачебной ошибки первого врача
составляет 1%; второго – 8%; третьего – 3%. Найти, какой врач вероятнее всего
поставил ошибочный диагноз.
24.
Однотипные
лекарственные
препараты
выпускаются
тремя
фармацевтическими заводами в количественном отношении 1:2:3, причем
вероятности несоответствия стандарту для этих же заводов соответственно
равны 3%, 2%, 1%. Препарат, выбранный НИИ для исследования оказался не
соответствующим стандарту. Определить какому заводу вероятнее всего
принадлежит препарат.
18
25. При вызове по телефону специальной бригады скорой педиатрической
помощи на основе простых признаков диспетчер должен отличить детей с
крайне тяжелым состоянием, чтобы предоставить им приоритет в очередности
направления бригады. Признак A1 – окраска кожи, A2 – длительность
гипертермии, A3 – возраст ребенка. Имеем две гипотезы: H 1 – крайне тяжелое
состояние, H 2 – все другие состояния. По статистическим данным P(H1 )  0,01 ;
P( H 2 )  0,99 . Условные вероятности наблюдения признаков: P( A1 / H1 )  0,59 ;
P( A1 / H 2 )  0,13 ; P( A2 / H1 )  0,73 ; P( A2 / H 2 )  0,14 ; P( A3 / H1 )  0,4 ; P( A3 / H 2 )  0,1 .
Вычислить вероятность угрожаемого состояния по каждому признаку отдельно,
пользуясь формулой Байеса. Сравнить эти вероятности, сделать вывод.
26. В некоторой популяции животных 20% являются самцами, 70% самками и
10% детёнышами. Вероятность гибели в течение периода наблюдения равна
для самца – 0,012; для самки – 0,007; для детёныша – 0,035. Какова вероятность
того, что первое погибшее животное самец или самка?
27. В 7 аптечках находятся одинаковые по массе и размерам таблетки. В трёх –
по 7 зеленых и 3 желтых таблеток (это аптечка состава H 1 ). В двух других
аптечках (состава H 2 ) – по 8 зеленых и 2 желтых таблеток. В двух аптечках
(состава H 3 ) – 5 зеленых и 5 желтых таблеток. Наудачу выбирается аптечка и
из нее извлекается таблетка, которая оказалась зеленой. Какой аптечке
вероятнее всего принадлежит извлеченная таблетка?
28. Пациенты попадают на УЗИ-обследование к одному из двух диагностов.
Вероятность того, что пациент попал к первому диагносту 0,8; ко второму – 0,2.
Вероятность того, что заболевание будет обнаружено первым – 0,94; вторым –
0,98. Пациенту при обследовании поставили верный диагноз. Найти
вероятность того, что пациента проверил первый диагност.
29. В аптеку поступили ингаляторы от трёх поставщиков в отношении 1:4:5.
Практика показала, что ингаляторы, поступившие от первого, второго и
третьего поставщиков, не потребуют ремонта в течение гарантийного срока
соответственно в 98%, 88% и 92 % случаев. Проданный ингалятор потребовал
ремонта в течение гарантийного срока. От какого поставщика вероятнее всего
поступил этот ингалятор?
30. Для участия в конкурсе на поставку медикаментов приглашены организации
трех регионов: 6 организаций – из I-го региона, 8 – из II-го и 5 – из III-го. По
предварительным данным вероятность быть выбранными по конкурсу для
организаций I-го региона оценивается в 0,6; для организаций II-го региона –
0,7; для организаций III-го региона – 0,8. Наудачу названная организация
оказалась выбранной по конкурсу. Какому региону вероятнее всего
принадлежит названная организация?
19
Задачи 31-40
31. Найти дисперсию, среднее квадратическое отклонение данной случайной
величины Х, зная закон ее распределения. Построить многоугольник
распределения.
Х 0,1 2
10
20
Р 0,4 0,2 0,15 0,25
32. Найти дисперсию, среднее квадратическое отклонение данной случайной
величины Х, зная закон ее распределения. Построить многоугольник
распределения.
Х
Р
1
0,4
2
0,1
3
0,3
4
0,2
величины Х, M ( X 2 ) , D(3 X  2) .
.
33. Даны законы распределения двух независимых случайных величин X и Y
соответственно:
X
0
1
3
Р 0,2 0,5
?
Y
2
3
Р
0,4
?
Найти вероятности, с которыми случайные величины принимают значение
равное 3. Найти математическое ожидание, дисперсию, среднее квадратическое
отклонение случайной величины Z  X  3Y .
34. Найти p2  P( X  1) , математическое ожидание и дисперсию случайной
величины Х, зная закон ее распределения. Построить многоугольник
распределения. Найти математическое ожидание случайной величины
Y  2 X 2  1.
Х
Р
1
0,19
2
p2
20
3
0,25
4
0,05
35. Найти дисперсию случайной величины Х, зная закон ее распределения.
Построить многоугольник распределения.
Х
Р
-1
0,48
1
0,01
2
0,09
3
0,42
Найти M (5 X 2 ) , D( X  2) .
36. Известен закон распределения дискретной случайной величины Х.
Построить многоугольник распределения.
Х
–1
1
2
3
Р
0,19
0,51
0,25
0,05
Найти математическое ожидание, дисперсию случайной величины X, M ( X 2 ) ,
D(3 X  2)
37. Найти дисперсию случайной величины Х, зная закон ее распределения.
Построить многоугольник распределения
Х
0,1
2
10
20
Р
0,4
0,2
0,15
0,25
Найти дисперсию, среднее квадратическое отклонение случайной величины
Y  X 2  3.
38. Дискретная случайная величина Х имеет закон распределения:
Х
Р
0,2
0,4
0,2
p1
0,6
0,4
0,8
0,2
1
0,1
Чему равна вероятность p1  P( X  0,2) ? Построить многоугольник
распределения. Найти математическое ожидание и дисперсию случайной
величины Y  2 X 2  1 .
39. Дискретная случайная величина Х имеет закон распределения:
Х
Р
3
p1
4
0,25
5
р3
6
0,15
7
0,35
Найти вероятность р1  Р( Х  3) и р2  Р( Х  5) , если известно, что р3 в 4 раза
больше p1 . Построить многоугольник распределения. Найти математическое
ожидание и дисперсию случайной величины Х, М (3 Х 2 ) , D(5  X ) .
21
40. Задают ли закон распределения дискретной случайной величины каждая
из таблиц. Если «да», то найти дисперсию случайной величины Х,
дисперсию случайной величины Y  3X  5 , дисперсию случайной величины
Y  3X  5 .
1.
Х
Р
0
0,05
1
0,15
2
0,20
3
0,25
4
0,35
2.
Х
Р
5
0,1
6
0,2
7
0,3
8
0,4
9
0,5
3.
Х
Р
0
0,13
1
0,34
2
0,51
3
0,12
4.
Х
Р
0
0,15
1
0,50
2
0,25
Задачи 41-50
41. В группе шесть человек, из них четверо здоровы. Для участия в
соревнованиях выбирают наугад 2 человека. Составить закон распределения
случайной величины Х. Построить многоугольник распределения.
Определить математическое ожидание, дисперсию, среднее квадратическое
отклонение данной случайной величины:
Х – число больных среди отобранных для участия в соревнованиях;
42. Вероятность поражения вирусным заболеванием куста земляники равна
0,2. Составить закон распределения случайной величины Х. Построить
многоугольник распределения. Определить математическое ожидание,
дисперсию, среднее квадратическое отклонение данной случайной величины:
Х – число кустов земляники, пораженных вирусом, из четырёх кустов;
43. Устройство электрофизиотерапии состоит из трех независимо
работающих элементов. Вероятность отказа каждого элемента в одном опыте
равна 0,1. Составить закон распределения случайной величины Х. Построить
многоугольник распределения. Определить математическое ожидание,
дисперсию, среднее квадратическое отклонение данной случайной величины:
Х – число не отказавших (работающих) элементов в одном опыте;
44. В партии 20% неисправных приборов. Наудачу отобраны 3 прибора.
Составить закон распределения дискретной случайной величины Х.
Построить многоугольник распределения. Определить математическое
22
ожидание, дисперсию, среднее квадратическое отклонение данной случайной
величины:
Х – число неисправных приборов среди 3-х отобранных;
45. Спортсмен ведёт стрельбу по цели с вероятностью попадания при каждом
выстреле 0,4. За каждое попадание он получает 5 очков, а в случае промаха
очков ему не начисляют. Составить закон распределения дискретной
случайной величины Х. Построить многоугольник распределения.
Определить математическое ожидание, дисперсию, среднее квадратическое
отклонение этой случайной величины:
Х – число очков, полученных спортсменом за 3 выстрела;
. 46. Вероятность того, что в течение недели прибор для определения
распадаемости таблеток выйдет из строя, равна 0,3. Составить закон
распределения дискретной случайной величины Х. Построить многоугольник
распределения. Определить математическое ожидание, дисперсию, среднее
квадратическое отклонение данной случайной величины:
Х – число поломок за 3 недели;
47. Экзаменатор задает студенту вопросы. Как только число правильных
ответов достигнет трёх либо студент ответит неправильно, экзаменатор
прекращает задавать вопросы. Вероятность правильного ответа на один
вопрос равна 0,75. Составить закон распределения дискретной случайной
величины Х. Построить многоугольник распределения. Определить
математическое ожидание, дисперсию, среднее квадратическое отклонение
данной случайной величины:
Х – число заданных вопросов;
48. В коробке находятся 3 ампулы с новокаином, изготовленных на первом
заводе, и 7 – на втором заводе. Из коробки по одной достают ампулы.
Составить закон распределения числа вынутых ампул. Построить
многоугольник распределения. Определить математическое ожидание,
дисперсию, среднее квадратическое отклонение данной случайной величины.
Х- число ампул, изготовленных на первом заводе;
49. Контрольная работа состоит из трёх вопросов. На каждый вопрос
приведено 4 ответа, один из которых правильный. Составить закон
распределения дискретной случайной величины Х. Построить многоугольник
распределения Определить математическое ожидание, дисперсию, среднее
квадратическое отклонение данной случайной величины:
Х – число правильных ответов при простом угадывании;
50. В билете три задачи. Вероятность правильного решения первой задачи
равна 0,9; второй – 0,8; третьей – 0,7. Составить закон распределения
23
дискретной
случайной
величины
Х.
Построить
многоугольник
распределения. Определить математическое ожидание, дисперсию, среднее
квадратическое отклонение данной случайной величины.
a) Х – число правильно решённых задач;
Задачи 51-60
51. Рост взрослой женщины является случайной величиной, распределенной
по нормальному закону с параметрами а  164 см и   5,5 см. Вычислить
вероятность того, что:
хотя бы одна из наудачу отобранных трех женщин будет иметь рост от
175 до 180 см;
52. Рост взрослых мужчин является случайной величиной, распределенной
по нормальному закону. Пусть математическое ожидание ее равно 175 см, а
среднее квадратическое отклонение – 6 см. Определить вероятность того,
что:
хотя бы один из двух наудачу выбранных мужчин будет иметь рост от 170 до
180 см;
53. Случайные ошибки измерения подчинены нормальному закону со
средним квадратическим отклонением   20 мм и математическим
ожиданием а  0 . Найти вероятность того, что из трех независимых
измерений:
ошибка хотя бы одного не превзойдет по абсолютной величине 4 мм;
54. При изготовлении таблеток их масса распределена по нормальному
закону с математическим ожиданием 0,5 г и средним квадратическим
отклонением 0,01 г. Найти:
интервал симметричный относительно математического ожидания,
вероятность попадания в который равна 0,93;
55. Установлено, что распределение диаметров эритроцитов хорошо
описывается нормальным законом распределения с математическим
ожиданием а  8мкм и средним квадратическим отклонением   0,6 мкм .
Найти:
симметричный относительно а интервал диаметров, в который попадает
90 % эритроцитов;
56. Масса взрослого животного некоторого вида является нормально
распределенной случайной величиной со средним значением 100 кг и
стандартным отклонением 8 кг. Наудачу выбирают взрослое животное.
Найти вероятность следующих событий:
24
масса животного не достигает 100 кг;
57. Цена некой ценной бумаги нормально распределена с математическим
ожиданием 98 ден.ед. и средним квадратическим отклонением 12 ден.ед.
Найти:
интервал симметричный относительно математического ожидания, в
который с вероятностью 0,87 попадает цена ценной бумаги
58. Высота данного лекарственного растения имеет нормальное
распределение с математическим ожиданием 20 см и средним
квадратическим отклонением 5 см. Найти:
долю растений, высота которых попадает в интервал (15;20);
59. Станок прессует таблетки со средним диаметром 9 мм. Полагая, что
диаметр распределен по нормальному закону со средним квадратическим
отклонением0,2 мм,
найти:
в какой интервал диаметров, симметричный относительно математического
ожидания, укладывается 99 % таблеток;
60. Распределение массы плодов некоторого растения достаточно хорошо
описывается нормальным законом. Математическое ожидание массы одного
плода 97 г. Среднее квадратическое отклонение 20 г. Найти:
в какой интервал, симметричный относительно математического
ожидания, попадает 84 % плодов;
Задачи для контрольной работы (Часть 2)
Задачи 1-10
1. Из продукции, произведенной фармацевтической фабрикой за месяц,
случайным образом отобраны 20 коробочек некоторого гомеопатического
препарата, количество таблеток в которых оказалось равным соответственно
50, 47, 50, 51, 49, 50, 51, 48, 52, 51, 50, 49, 50, 52, 48, 50, 47, 50, 51, 49.
Построить вариационный ряд количества таблеток. Построить
полигон
относительных
частот.
Вычислить
числовые
характеристики выборки.
Представить эти данные в виде интервального статистического ряда.
Построить гистограмму относительных частот. Вычислить числовые
характеристики выборки.
2. Станок-автомат изготавливает таблетки. Для контроля произвели
взвешивание 30 таблеток (в г): 0,47; 0,49; 0,51; 0,50; 0,48; 0,52; 0,50; 0,51;
25
0,47; 0,49; 0,51; 0,47; 0,46; 0,49; 0,48; 0,48; 0,50; 0,50; 0,48; 0,50; 0,49; 0,50;
0,49; 0,50; 0,51; 0,51; 0,50; 0,49; 0,51; 0,50.
Построить вариационный ряд массы таблеток. Построить полигон
относительных частот. Вычислить числовые характеристики
выборки.
Представить эти данные в виде интервального статистического ряда.
Построить гистограмму относительных частот. Вычислить числовые
характеристики выборки.
3. Провели измерения высоты 30 штук некоторого лекарственного растения
(в см): 20; 18; 17; 16; 21; 19; 20; 22; 22; 18; 22; 19; 22; 18; 17; 19; 24; 21; 19; 22;
16; 21; 22; 19; 20; 21; 18; 21; 20; 20.
Построить вариационный ряд высот. Построить полигон
относительных частот. Вычислить числовые характеристики
выборки.
Представить эти данные в виде интервального статистического ряда.
Построить гистограмму относительных частот. Вычислить числовые
характеристики выборки.
4. Измеряли размер 30 плодов некоторого растения (в см): 7; 4; 5 6; 8; 4; 2; 5;
6; 4; 8; 3; 7; 6; 3; 3; 4; 5; 6; 3; 6; 4; 4; 3; 5; 4; 6; 3; 6; 5.
Построить вариационный ряд размера плодов некоторого растения.
Построить полигон относительных частот. Вычислить числовые
характеристики выборки.
Представить эти данные в виде интервального статистического ряда.
Построить гистограмму относительных частот. Вычислить числовые
характеристики выборки.
5. Рост 30 мальчиков в возрасте 2 лет (в см) равен: 92, 91, 96, 93, 97, 93, 91,
92, 90, 97, 95, 94, 92, 98, 96, 90, 95, 93, 94, 89, 91, 89, 96, 94, 94, 92, 93, 95, 87,
94.
Построить вариационный ряд роста мальчиков в возрасте 2 лет.
Построить полигон относительных частот. Вычислить числовые
характеристики выборки.
Представить эти данные в виде интервального статистического ряда.
Построить гистограмму относительных частот. Вычислить числовые
характеристики выборки.
6. Для изучения урожайности лекарственного растения поляна разбита на
30 площадок по 1 м 2 . Подсчитали количество растений на каждом из
участков: 6, 6, 4, 4, 5, 6, 6, 7, 5, 5, 5, 2, 6, 5, 5, 4, 5, 5, 5, 8, 5, 4, 6, 7, 3, 6, 5, 5, 6,
4.
Построить вариационный ряд количества растений на 1 м 2 .
Построить полигон относительных частот. Вычислить числовые
характеристики выборки.
26
Представить эти данные в виде интервального статистического ряда.
Построить гистограмму относительных частот. Вычислить числовые
характеристики выборки.
7. Станок прессует таблетки. Измерили диаметр 30 таблеток (в мм): 8,8; 9,1;
9,0; 8,9; 9,2; 9,2; 9,3; 9,0; 9,3; 8,9; 8,8; 9,1; 9,2; 9,0; 9,0; 9,1; 9,1; 9,0; 8,8; 8,8;
8,8; 8,7; 9,0; 9,1; 9,1; 9,0; 9,2; 8,7; 9,1; 8,9.
Построить вариационный ряд диаметров таблеток. Построить
полигон
относительных
частот.
Вычислить
числовые
характеристики выборки.
Представить эти данные в виде интервального статистического ряда.
Построить гистограмму относительных частот. Вычислить числовые
характеристики выборки.
8. Изучались данные о количестве больных поступающих в терапевтическое
отделение в течение суток: 6, 5, 7, 8, 7, 9, 6, 10, 9, 9, 6, 10, 8, 5, 9, 8, 7, 5, 8, 10,
11, 10, 10, 8, 9, 6, 9, 7, 12, 9.
Построить вариационный ряд количества больных. Построить
полигон
относительных
частот.
Вычислить
числовые
характеристики выборки.
Представить эти данные в виде интервального статистического ряда.
Построить гистограмму относительных частот. Вычислить числовые
характеристики выборки.
9. Измеряли давление у 30 практически здоровых женщин в возрасте 6065 лет (в мм рт. ст.): 100, 75, 140, 140, 150, 150, 140, 160, 140, 130, 110, 80, 90,
110, 95, 90, 130, 120, 120, 130, 130, 140, 140, 150, 150, 150, 160, 160, 130, 130.
Построить вариационный ряд количества больных. Построить
полигон
относительных
частот.
Вычислить
числовые
характеристики выборки.
Представить эти данные в виде интервального статистического ряда.
Построить гистограмму относительных частот. Вычислить числовые
характеристики выборки.
10. Исследования показали, что здоровые люди значительно отличаются по
содержанию в крови фермента каталазы. Приведены данные содержания
фермента каталазы в крови 30 человек: 5; 5; 3,5; 5; 4; 4; 5; 5; 4,5; 4,5; 4; 3,5;
4,5; 4,5; 5; 5,5; 6; 6,5; 5; 5; 5,5; 5,5; 5,5; 5,5; 5; 5; 4; 4; 6; 6.
Построить вариационный ряд содержания каталазы. Построить
полигон
относительных
частот.
Вычислить
числовые
характеристики выборки.
Представить эти данные в виде интервального статистического ряда.
Построить гистограмму относительных частот. Вычислить числовые
характеристики выборки.
27
Задачи 11-20
11. Измеряли скорость оседания эритроцитов (СОЭ) у 30 человек:
7
7
3
5
7
9
1
5
5
7
9
1
7
5
9
7
1
7
5
5
7
3
9
9
5
7
1
3
9
9
Дайте точечную и интервальную (с доверительной вероятностью 0,95)
оценку средней скорости оседания эритроцитов.
12. Наблюдения за сахаром в крови у 50 человек дали такие результаты:
3,94
3,82
3,81
3,92
3,91
3,84
3,94
3,71
3,89
3,62
3,86
3,98
4,16
4,02
4,18
4,06
3,57
3,76
4,17
4,26
3,67
3,87
4,00
3,72
4,03
3,97
4,07
3,46
4,09
4,14
3,76
3,99
4,08
3,78
3,72
3,61
3,69
3,88
4,02
4,33
3,96
3,76
4,01
3,73
3,82
4,04
3,71
3,93
3,52
4,03
Дайте точечную и интервальную (с доверительной вероятностью 0,95)
оценку среднего содержания сахара в крови.
13. Приведены данные длительности интервалов RR (в мс) по ЭКГ здорового
человека:
787 801 869 923 872 764 822 943 868 918 881 771 827 907 843
826 826 763 775 873 883 887 896 802 916 925 854 857 764 802
Дайте точечную и интервальную (с доверительной вероятностью 0,95)
оценку средней длительности интервалов RR (в мс) по ЭКГ всех здоровых
людей.
14. Приведены данные длительности интервалов RR (в мс) по ЭКГ больной с
диагнозом «Мерцательная аритмия»:
676 793 827 734 955 730 489 1074 846 757 921 856 785 741
1020 805 875 712 1026 928 861 802 844 715 743 651 1075 902
Дайте точечную и интервальную (с доверительной вероятностью 0,9) оценку
средней длительности интервалов RR (в мс) по ЭКГ всех больных с
диагнозом «Мерцательная аритмия».
28
15. Изучалась длительность интервалов RR (в мс) по ЭКГ больной с
диагнозом «Синусовая тахикардия» (больная на 1-е сутки после
нейрохирургического вмешательства):
50
0
49
2
49
2
49
2
49
2
49
2
49
6
48
8
49
6
48
8
49
6
49
2
50
0
49
2
49
6
49
2
49
6
49
2
49
2
49
2
49
2
48
8
49
6
49
2
49
6
49
2
49
2
49
2
Дайте точечную и интервальную (с доверительной вероятностью 0,95)
оценку средней длительности интервалов RR (в мс) по ЭКГ всех больных с
диагнозом «Синусовая тахикардия».
16. Изучалась длительность интервалов RR (в мс) по ЭКГ больной с
диагнозом «Желудочковая экстрасистолия» (больная на 6-е сутки после
нейрохирургического вмешательства):
720 724 720 420 1004 728 728 728 728 440 1044 752 748
420 1096 776 736 740 740 424 1096 760 744 736 744 736
Дайте точечную и интервальную (с доверительной вероятностью 0,95)
оценку средней длительности интервалов RR (в мс) по ЭКГ всех больных с
диагнозом «Желудочковая экстрасистолия».
17. Приведены данные о систолическом давлении крови (в мм рт ст) у
практически здоровых женщин в возрасте 60-69.
121
137
118
138
152
143
113
148
81
133
122
151
101
98
150
120
134
102
141
130
142
132
136
131
73
136
136
141
159
129
106
115
112
115
110
122
113
111
124
128
127
106
125
132
126
109
134
140
95
109
139
143
101
134
111
144
Дайте точечную и интервальную (с доверительной вероятностью 0,95)
оценку среднего систолического давления крови (в мм рт ст) у всех женщин
в возрасте 60-69.
18. Изучалось артериального давления крови (в мм рт ст) у 50 женщин в
возрасте 60-69 лет с диагнозом «гипертоническая болезнь» составляют:
192 185 171 119 172 186 193 126 173 187 194 145 149 151
144 173 194 137 187 175 166 156 153 175 196 161 162 165
154 164 159 177 182 161 165 179 172 158 148 164 169 171
29
Дайте точечную и интервальную (с доверительной вероятностью 0,95)
оценку среднего артериального давления крови (в мм рт. ст.) у всех женщин
в возрасте 60-69 лет с диагнозом «гипертоническая болезнь».
19. При подсчете количества листьев на каждом из 30 лекарственных
растений определенного вида получены следующие результаты:
10
9
10
13
10
13
11
11
13
11
12
11
7
11
7
10
10
10
9
9
9
10
0
10
11
12
11
10
8
8
Дайте точечную и интервальную (с доверительной вероятностью 0,95)
оценку среднего количества листьев всех лекарственных растений данного
вида.
20. При измерении роста студентов получены следующие результаты (в см):
173
186
174
186
177
169
166
170
185
175
189
177
179
197
183
181
179
175
169
190
178
194
171
191
187
158
182
173
166
181
Дайте точечную и интервальную (с доверительной вероятностью 0,95)
оценку среднего роста всех студентов (в см).
Задачи 31-40
31. Изучались затраты на рекламу медицинской техники в усл.ден.ед. (Х) и
количество учреждений, воспользовавшихся услугами фирмы «Медтехника»
(Y). Данные исследования приведены в таблице:
Х 8 8 8 9 9 9 9 10 10 10 10 11 11 11 11
У 80 85 72 85 80 88 82 90 100 92 95 90 120 115 100
a)
b)
c)
Построить корреляционное поле, установить, наличие связи между
данными признаками.
Найти коэффициент корреляции и проверить его значимость при
p  0,95 . Сделать вывод о тесноте корреляционной связи.
Предположить вид корреляционной зависимости, найти параметры
уравнения регрессии, построить линию регрессии. Определить
ожидаемое значение У для Х=20.
30
32. Признак Х – число детей ни разу не болевших в течение первого года
жизни, в группе наблюдения; признак У – средняя продолжительность
грудного вскармливания детей в данной группе.
Х 10 12 4 8 15 6 11 6 3 10
У 10 10 5 11 12 6 9 5 2 11
Построить корреляционное поле, установить, наличие связи между
данными признаками.
b) Найти коэффициент корреляции и проверить его значимость при
p  0,95 . Сделать вывод о тесноте корреляционной связи.
c) Предположить вид корреляционной зависимости, найти параметры
уравнения регрессии, построить линию регрессии. Определить
ожидаемое значение У для Х=15.
33. Признак Х – число детей, находившихся на грудном вскармливании до
6 месяца в группах наблюдения; признак У – частота заболеваемости среди
этих детей (число обращений).
a)
Х 40 32 50 44 28 51 38 42 63 51
У 20 13 23 15 13 21 15 12 26 22
a)
b)
c)
Построить корреляционное поле, установить, наличие связи между
данными признаками.
Найти коэффициент корреляции и проверить его значимость при
p  0,95 . Сделать вывод о тесноте корреляционной связи.
Предположить вид корреляционной зависимости, найти параметры
уравнения регрессии, построить линию регрессии. Определить
ожидаемое значение У для Х=60.
34. Признак Х – число лиц, прошедших профилактический осмотр в течение
периода, У – число лиц, вновь обратившихся в поликлинику по поводу
заболеваний.
Х 100 130 150 120 100 180 95 114 187 150
У 10 12 13 10 8
16 10 12 15 12
a)
b)
c)
Построить корреляционное поле, установить, наличие связи между
данными признаками.
Найти коэффициент корреляции и проверить его значимость при
p  0,95 . Сделать вывод о тесноте корреляционной связи.
Предположить вид корреляционной зависимости, найти параметры
уравнения регрессии, построить линию регрессии. Определить
ожидаемое значение У для Х=160.
31
35. В эксперименте на 13 кошках получены следующие данные об
интрасклеральном (Х) и внутриглазном давлении (У).
19,
8
32,
У
5
Х
7,8
16,
1
12,
7
21,
3
13,
4
26,
8
10,
3
23,
4
13,
7
19,
7
16,
2
29,
9
15,
4
22,
2
15,
4
22,
6
21,
5
17,
6
8,1
14,
3
11,
7
18,
6
7,6
21,
4
Построить корреляционное поле, установить, наличие связи между
данными признаками
b) Найти коэффициент корреляции и проверить его значимость при
p  0,95 . Сделать вывод о тесноте корреляционной связи.
c) Предположить вид корреляционной зависимости, найти параметры
уравнения регрессии, построить линию регрессии. Определить
ожидаемое значение У для Х=20.
36. У 10 человек были исследованы проницаемость сосудов сетчатки (Х) и ее
электрическая активность (У).
a)
Х 19,5 15,0 13,5 23,3 6,3
2,5
1,8
6,5
1,8
У 0,0 38,5 59,0 97,4 119,2 198,7 248,7 318,0 438,5
a)
b)
c)
Построить корреляционное поле, установить, наличие связи между
данными признаками.
Найти коэффициент корреляции и проверить его значимость при
p  0,95 . Сделать вывод о тесноте корреляционной связи.
Предположить вид корреляционной зависимости, найти параметры
уравнения регрессии, построить линию регрессии. Определить
ожидаемое значение У для Х=18.
37. У взрослых мужчин были измерены рост (Х) и масса (У).
Х (см) 165 176 175 168 167 172 175 180
У (кг) 56 75 70 61 62 63 72 80
a)
b)
c)
Построить корреляционное поле, установить, наличие связи между
данными признаками.
Найти коэффициент корреляции и проверить его значимость при
p  0,95 . Сделать вывод о тесноте корреляционной связи.
Предположить вид корреляционной зависимости, найти параметры
уравнения регрессии, построить линию регрессии. Определить
ожидаемое значение У для Х=185.
38. Получены следующие данные зависимости
растворимого азотнокислотного Na (m) от t0 раствора.
32
наибольшей
массе
t(0C) 0
4,0 10,0 15,0 21,0 29,0 36,0
m(г) 66,7 71,0 76,3 80,6 85,7 92,9 99,4
a)
b)
c)
Построить корреляционное поле, установить, наличие связи между
данными признаками.
Найти коэффициент корреляции и проверить его значимость при
p  0,95 . Сделать вывод о тесноте корреляционной связи.
Предположить вид корреляционной зависимости, найти параметры
уравнения регрессии, построить линию регрессии. Определить
ожидаемое значение m для t=30.
39. При измерении активности (А)  -препарата с помощью газоразрядного
счетчика через равные промежутки времени (t) были получены данные.
T(мин) 0 2 4 6 8 10 12 14 16 18
A, c 1
12 23 17 36 9 19 25 7 16 26
a)
b)
c)
Построить корреляционное поле, установить, наличие связи между
данными признаками.
Найти коэффициент корреляции и проверить его значимость при
p  0,95 . Сделать вывод о тесноте корреляционной связи.
Предположить вид корреляционной зависимости, найти параметры
уравнения регрессии, построить линию регрессии. Определить
ожидаемое значение A для T=3.
40. При изучении завести после преломления (n) от концентрации в ней соли
(c) получены следующие результаты:
c(г/см3) 0,000 0,025 0,050 0,10 0,20
0,4
0,8
n
1,333 1,338 1,340 1,350 1,377 1,377 1,389
a)
b)
c)
Построить корреляционное поле, установить, наличие связи между
данными признаками.
Найти коэффициент корреляции и проверить его значимость при
p  0,95 . Сделать вывод о тесноте корреляционной связи.
Предположить вид корреляционной зависимости, найти параметры
уравнения регрессии, построить линию регрессии. Определить
ожидаемое значение n для c=0,6.
33
34
35