Фрагмент рабочей тетради

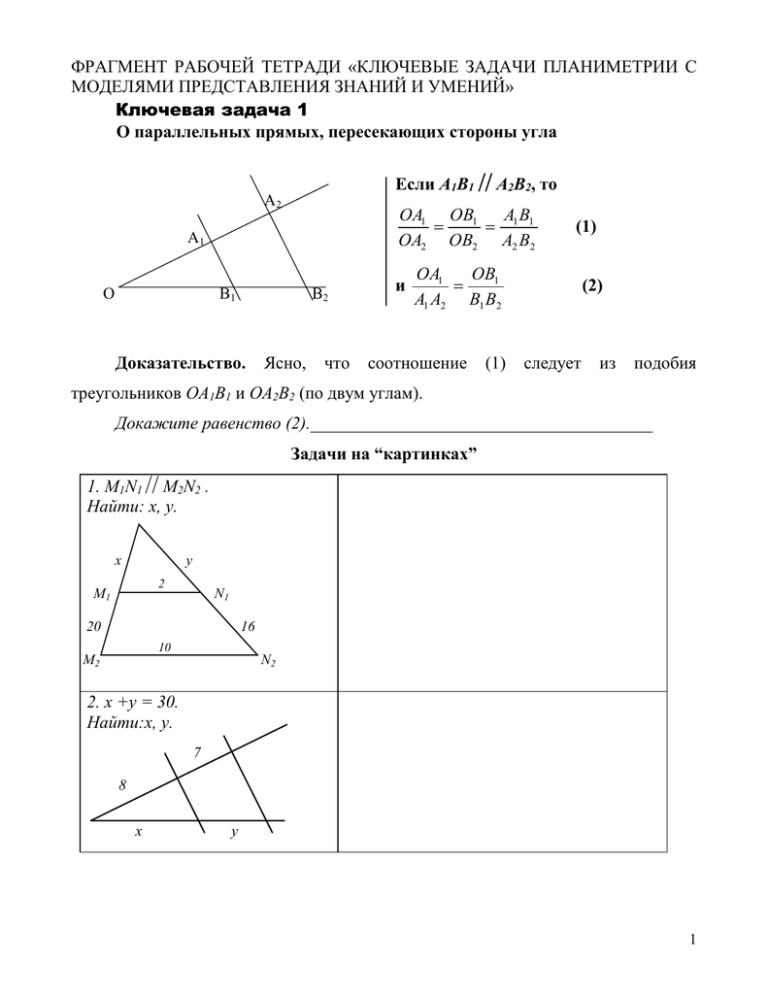
ФРАГМЕНТ РАБОЧЕЙ ТЕТРАДИ «КЛЮЧЕВЫЕ ЗАДАЧИ ПЛАНИМЕТРИИ С
МОДЕЛЯМИ ПРЕДСТАВЛЕНИЯ ЗНАНИЙ И УМЕНИЙ»
Ключевая задача 1
О параллельных прямых, пересекающих стороны угла
Если А1В1  А2В2, то
A2
ОА1 ОВ1
АВ

 1 1
ОА2 ОВ2 А2 В2
A1
O
B1
B2
Доказательство.
Ясно,
что
и
(1)
ОА1
ОВ1

А1 А2 В1 В2
соотношение
(1)
(2)
следует
из
подобия
треугольников ОА1В1 и ОА2В2 (по двум углам).
Докажите равенство (2)._______________________________________
Задачи на “картинках”
1. M1N1  M2N2 .
Найти: x, y.
x
y
2
M1
N1
20
16
10
M2
N2
2. х +у = 30.
Найти:x, y.
7
8
x
y
1
3.
Cтороны
угла
параллельными прямыми.
пересечены
Найти: x, y, z, t.
49
x
7
O
z
20
у
t
12
28
4. ABCD - трапеция, EF  AB.
DE  DA = 2 : 3.
Найти: x.
х
D
E
36
A
45
C
F
B
5. a  l  b.
Найти: x.
b
l
a
10
х
6
8
10
а2
1.1. Построить отрезок х  , где а и b заданные отрезки.
b
Решение.
построение,
четырех
как
этапов:
Решение
правило,
анализ,
задачи
на
состоит
из
A2
построение,
A1
доказательство, исследование.
1. Анализ. На этом этапе предполагается,
что искомый отрезок найден. Рассмотрим
O
B1
B2
2
произвольный угол с вершиной О, стороны которого пересекают параллельные
прямые А1В1 и А2В2.
Как
в
виде
пропорции
следует
записать
равенство
а2
х ?
b
___________________________________________________________________
Какое равенство ключевой задачи следует использовать для решения этой
задачи?______________________________________________________
Укажите на рисунке, каким образом следует расположить отрезки а, а, в и
х на сторонах угла.
2. Построение. Опишите шаги построения искомого отрезка.
1)______________________
4)___________________
2)______________________
5)___________________
3)______________________
6)___________________
7)______________________
3. Доказательство. Докажите, что построенный отрезок удовлетворяет
условиям задачи.
_________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________
________________________________________________________
4. Исследование. Очевидно, что существует единственное решение для
любых отрезков a и b.
Придумайте задачи на построение с использованием соотношения (2)
a 3 abc
ключевой задачи 1. Например: построить отрезки 2 ,
.
de
b
_________________________________________
_________________________________________
_________________________________________
_________________________________________
3
_________________________________________
_________________________________________
1.2. Высота CD треугольника АВС делит медиану ВМ в соотношении 31,
считая от вершины В. В каком соотношении CD делит сторону АВ, считая от
вершины А?
Решение. Эта задача примечательна тем, что для использования ключевой
задачи 1 требуется провести дополнительные построения.
Строим МК  CD. Ясно, что МК  АВ.
С
Рассмотрим угол CAD, стороны которого
пересекают параллельные прямые MK и
М
CD. Тогда, поскольку АМ=МС, то АK=KD
L
(следует из ключевой задачи 1, равенство
А
( ).
Рассмотрим
угол
МВА,
К
стороны
D
которого пересекают параллельные прямые МК и CD.
ключевой задачи 1, равенство ( )). Т.е.
B
BL BD
(следует из

LM KD
BD 3
AD 2 KD 2

 .
 ; BD=3KD. Тогда
BD 3KD 3
KD 1
Ответ:
2
.
3
1.3. В остроугольном треугольнике АВС длины медиан ВМ, CN и высоты
АН равны соответственно 4, 5 и 6. Найти площадь треугольника АВС.
А
Решение.
1. ВМ=4, CN=5, AH=6 (по условию).
ВМ  CN=O.
2.
Для
нахождения
площади
1
S= AHBC нужно найти длину ВС.
2
N
АВС
M
O
B
T
H
K
C
4
3. Каждая из медиан ВМ и CN делится точкой О в отношении 21, считая от
вершин В и С (следует из _____________).
8
10
ВО= _______________________  ; СО= _______________________  .
3
3
Из точки О опустим перпендикуляр ОК на ВС, тогда из прямоугольных
треугольников ОВК и ОСК по теореме Пифагора, найдем
2
2
8
 10 
2
2
ВК     ОК  , СК     ОК  .
 3
3
4. Следующим шагом должно стать нахождение длины ОК. Применяя ключевую
задачу 1 к углу NCT, получим: ОК=
______
1
NT, а NT= АН . Таким образом,
2
ОК= _________ АН, ВК=_______________________________________
СК=_________________________________________________________
1
5. Таким образом, ВС=ВК+КС= _______________. SABC=  АН  ВС  2 7  8 .
2
(Из этой задачи выделим факт, который можно использовать в дальнейшем:
расстояние от точки пересечения медиан до стороны треугольника в 3 раза
меньше высоты, опущенной на эту сторону.)
Ответ: 2 7  8 .
Задачи для самостоятельного решения
1. В равнобедренном АВС (АВ=ВС) точка пересечения высот делит пополам
расстояние между центром описанной окружности и основанием. Определить
cosABC.
Ответ:
2
.
3
5
2. Длина основания АС треугольника АВС равна 3, медиана AD  4. Высота ВЕ
делит медиану AD пополам. Найти площадь АВС.
Ответ: 6 3 .
Проведите анализ и обобщение решения задач данного раздела. Опишите
построение модели представления знаний (рис.25) по следующим вопросам:
1. Что общего в решении задач данного раздела?
2. Что представляет собой каркас ключевой задачи 1? (К1-
каркас
ключевой задачи)
3. По каким признакам можно определить, что при решении задачи
используется ключевая задача 1? (К2 - признаки присутствия)
4. Какие способы используются при решении задач? (К3 -
способы
решения)
5. Какие геометрические фигуры участвуют в сюжете задачи? (К4 геометрические фигуры)
6. На какие основные геометрические факты (определения, теоремы,
свойства, признаки) опирается решение задач данного раздела? (К5 –
используемые элементы теории)
7. Какие типы задач (вычислительные, на построение, на доказательство) вы
рассматривали? (К6 - типы задач)
8. Какие следствия, полезные для решения задач в дальнейшем, можно
выделить? (К7 - «полезные» следствия)
9. Какие задачи можно отнести к обязательному минимуму, т.е. те, которые
обязательно надо уметь решать? (К8 - практический минимум)
Рассмотренную модель представления «знаний» можно использовать в
качестве «мини-энциклопедии» или «шпаргалки» геометрических фактов и задач,
которая позволяет выделять и распознавать используемую ключевую задачу.
Под руководством учителя рассмотрите следующую, более сложную,
модель: модель представления «умений» (рис. 26). Здесь выделяются каркас
6
ключевой задачи, его элементы и связи между ними, построение соответственно
возможных задачных ситуаций, а также шаги решения задачи с помощью
ключевой задачи. Изначально в условии задана геометрическая фигура, это
может быть треугольник, или четырехугольник, или окружность (координата К1).
В данной фигуре выделяется каркас используемой ключевой задачи, в нашем
случае угол, стороны которого пересекают две параллельные прямые, а также его
известные и неизвестные элементы: a, b, c, d, x, y (координаты К2). В
зависимости
от
того,
какие
из
них
являются
известными
и
наличия
дополнительных условий (координата К3), и какое выбрано отношение
(координата К4) можно построить различные задачные ситуации, имеющие
своим ответом одно или много значений для неизвестного элемента. Выделение
типов задачных ситуаций есть анализ типов связей между элементами каркаса.
Описанная в координате К5, последовательность шагов решения есть
программа действий учащегося по решению задачи, в которой реализуется
ориентировочная основа деятельности по решению задачи.
Опишем 1-ю задачную ситуацию. Дан треугольник, стороны которого
пересечены прямой параллельно какой-либо стороне. Заданы отрезки x, y, b, т.е.
известны их длины. Найти длину отрезка а. Сравнивая чертеж треугольника с
каркасом ключевой задачи, видим, что дополнительных построений не требуется,
при решении будет использоваться отношение (1)
связывает названные элементы. Отсюда а 
a x
 , т.к. именно оно
b y
bx
.
y
10. Опишите самостоятельно 2 – 5-ые задачные ситуации.
11. Что общего и различного в рассмотренных задачных ситуациях?
12. Проверьте работу этой модели на одной из решенных задач.
7