Урок проверки коррекции знаний по теме: &quot

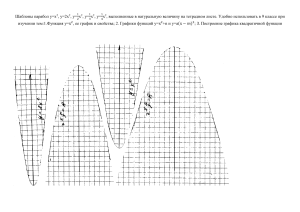
Урок проверки коррекции знаний по теме: " Квадратичная функция у=ах2+вх+с и ее свойства
Цель урока: обобщить и систематизировать знания учащихся о квадратичной функции: повторить
изученные приемы исследования свойств функции, методы построения графиков; закрепить и
упрочить умения и навыки учащихся по данной теме, показать ее прикладной характер, ориентировать
на использование полученных знаний при дальнейшем изучении математики.
Задачи:
Образовательные: проверка и коррекция умений строить график квадратичной функции по точкам и с
помощью шаблона; выработка навыков исследования свойств функции по графику; повторение
решения
уравнений;
Развивающие: развитие познавательного интереса к обучению математики посредством использования
ИКТ, развитие вычислительных навыков, логического мышления, формирование математической речи
учащихся и оформление решения задач.
Воспитательные: воспитывать аккуратность при построении чертежей и работе на доске, умение
работать в группе.
Формы работы учащихся: фронтально, групповая, индивидуальная.
I. Организационный момент.
Сообщить учащимся, что по данной теме они должны знать:- что является графиком квадратичной
функции;- как находятся координаты вершины параболы;- как определяется направление ветвей;
уметь:-строить график квадратичной функции по точкам и с помощью шаблона; определять
координаты вершины параболы;
II.Фронтальный опрос учащихся :
1 .Какая функция называется квадратичной?
2 Что является графиком этой функции?
3.От чего зависит направление «ветвей» параболы?
4. Как найти координаты вершины параболы?
5. Какая прямая является осью параболы?
По ходу ответов на доске записи.
На закрепление устно выполнить следующее задание:
Не выполняя построения графика функции
у= 2х2- 4х + 3, ответить на следующие вопросы:
1)
Куда направлены «ветви» параболы?
2)
Какие координаты имеет вершина параболы?
3)
Какая прямая является осью параболы?
III. Работа в группах.
Задание группам:
Построить график функции y = |x2 – 4x + 3|. Какие виды преобразований необходимо выполнить,
чтобы получить данный график из графика функции y = x2.
Решение:
Виды преобразований:
• смещение вправо на 2 единицы;
• смещение вниз на 1 единицу;
• симметрия относительно оси Ох отрицательной части графика.
Дополнительно: Построить график функции у = 3х2 + 6|х| + 6.
IV. Индивидуальные задания на карточках (ученики выполняют на доске, объясняют решение классу
после работы по группам):
1. Найти наибольшее значение функции у = - 1,5(х – 1)2 на отрезке [0; 2]
.
2. Найти наименьшее значение функции у = 2(х +3)2 на отрезке [– 4; 1]
3. По графику у = ах2 + bx + c определите знаки чисел a, b, c. (рисунок 4)
Решение:
• ветви вниз a < 0
• > 0, a < 0 b > 0
• при x = 0 y = c > 0
Рисунок 4
V. Физминутка.
VI. Обобщение и проверка знаний учащихся
Тест.
Вариант I
1. Какая линия является графиком функции у = – (х – 3)2 + 2?
А. Прямая, проходящая через начало координат.
Б. Прямая, не проходящая через начало координат.
В. Парабола.
Г. Гипербола.
2. График функции у = 2(х + 2)2 получается из графика функции у =2х2 сдвигом на две единицы:
А. Вправо.
Б. Влево.
В. Вверх.
Г. Вниз.
3. Найдите наименьшее значение функции у = 3(х – 2)2 на отрезке [–2; 5].
А. 0.
Б. –12.
В. 12.
Г. 27.
4. Какая из перечисленных функций является ограниченной сверху?
А. у = 2х2 – 5х + 3.
Б. у = 3х2 – 1.
В. у = -3х2 + х + 1.
Г. у = .
5. Уравнение оси симметрии параболы у = –3х2 + 5х + 1 имеет вид:
А. .
Б. .
В. .
Г. .
Вариант II
1. Какая линия является графиком функции у = – (х + 2)2 - 4?
А. Прямая, проходящая через начало координат.
Б. Прямая, не проходящая через начало координат.
В. Парабола.
Г. Гипербола.
2. График функции у = 3х2 – 2 получается из графика функции у =3х2 сдвигом на две единицы:
А. Вправо.
Б. Влево.
В. Вверх.
Г. Вниз.
3. Найдите наименьшее значение функции у = 3(х + 2)2 на отрезке [–2; 1].
А. 0.
Б. –12.
В. 12.
Г. 27.
4. Какая из перечисленных функций является ограниченной снизу?
А. у = –2х2 – 5х + 3.
Б. у = 3х2 – 1.
В. у = -3х2 + х + 1.
Г. у = .
5. Уравнение оси симметрии параболы у = 2х2 – 7х + 1 имеет вид:
А. .
Б. .
В. .
Г. .
Взаимопроверка с использованием ключа к ответам.
Вариант I: Г Б Г Б В
Вариант II: Б А А В В
VII.
VIII.
IX.
Рефлексия (“Что знаю?”, “Чего не знаю?”, “Что получилось?”, “Что нет?”).
Подведение итогов урока.
Домашнее задание.