Контрольная работа по курсу:
ТЕОРИЯ ЭЛЕКТРИЧЕСКОЙ СВЯЗИ
Вариант 43.
𝑚 = 8, 𝑛 = 7.
Задание 1.
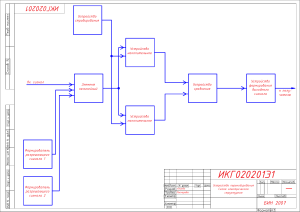
Разработайте и нарисуйте обобщенную структурную схему системы
связи. Кратко опишите назначение отдельных блоков и операций над
сигналами в системе связи. Нарисуйте качественно временные диаграммы
сигналов на выходе каждого блока структурной схемы.
Решение.
Рисунок 1.
Обобщенная структурная схема системы связи для
передачи и приема непрерывных сообщений.
1
Источник сообщения - устройство конечного пользователя (микрофон, видеокамера и пр.). Формирует сигнал, который должен быть передан
получателю.
Кодер по исходному сигналу в соответствии с некоторым алгоритмом формирует модулирующий сигнал, который передается в модулятор.
При этом кодер может преобразовывать исходный сигнал с учетом требований сжатия информации и помехозащищенности. Модулятор модулирует несущее колебание, поступающее от генератора, модулирующим сигналом. В результате формируется модулированный сигнал радиочастоты
(на рисунке - амплитудная модуляция), который можно передавать на
дальние расстояния по радиоканалу либо по другому каналу связи (коаксиальный или симметричный кабель и пр.). Выходное устройство формирует из электрического сигнала (ток/напряжение) на его входе сигнал в
виде электромагнитных колебаний в среде распространения (в линии
связи). Например, в случае радиорелейной линии выходное устройство это усилитель и антенна.
На стороне приемника выполняются обратные операции. Входное
устройство принимает сигнал из линии связи, усиливает его и преобразует
его в электрический сигнал ток/напряжение. Демодулятор из сигнала радиочастоты выделяет кодированный сигнал. Декодер по кодированному
сигналу восстанавливает исходное сообщение и передает сообщение получателю.
2
Задание 2.
Нарисуйте принципиальную схему амплитудного модулятора и постройте вольт-амперную характеристику (ВАХ) нелинейного элемента модулятора, которая аппроксимирована линейно-ломаной функцией:
𝑖 = 𝑆 ∙ (𝑢 − 𝐸0 )
𝑖=0
{
𝐸0 = 𝑚 − 𝑛 = 4 − 3 = 1
𝑆 =𝑚+1=4+1=5
при
𝑢 ≥ 𝐸0
при
𝑢 < 𝐸0
напряжение отсечки
В
мА/В крутизна наклона ВАХ
Рассчитайте статическую модуляционную характеристику (СМХ) амплитудного модулятора. Выберите рабочий участок на СМХ и рабочую
точку. Определите параметры АМ сигнала на выходе модулятора и запишите аналитическое выражение сигнала АМ для определенных числовых
значений параметров модуляции.
Амплитуда несущего колебания на входе модулятора равна 𝑈𝑚 = 1
В,
частота несущей равна 𝑓0 = (200 + 𝑛) = 200 + 7 = 207 кГц,
частота модулирующего сигнала равна 𝐹 = (𝑚 + 3) = 8 + 3 = 11
кГц,
сопротивление контура равно 𝑅 = (𝑚 + 2) = 8 + 2 = 10 кОм.
Определите добротность колебательного контура модулятора.
Решение.
Основа амплитудного модулятора - нелинейный элемент. В нашей
схеме рисунок 2 [1, стр. 94] это 𝑛𝑝𝑛-транзистор. На базу транзистора
подается сумма модулирующего сигнала и ВЧ сигнала от генератора
несущего колебания. Пользуясь полиномиальной аппроксимацией для характеристики 𝑖к = 𝑓(𝑢бэ ), можно записать:
2
𝑖к = 𝑎0 + 𝑎1 ∙ (𝑢вч + 𝑢мод ) + 𝑎2 ∙ (𝑢вч + 𝑢мод ) + ⋯ =
2
= 𝑎0 + 𝑎1 ∙ (𝑢вч + 𝑢мод ) + 𝑎2 ∙ ((𝑢вч )2 + 2 ∙ 𝑢вч ∙ 𝑢мод + (𝑢мод ) ) + ⋯ .
Для АМ сигнала полезным продуктом является слагаемое: 2 ∙ 𝑎2 ∙
𝑢вч ∙ 𝑢мод .
3
Рисунок 2.
Принципиальная схема амплитудного модулятора.
В коллекторную цепь включен контур, настроенный на радиочастоту,
для фильтрации посторонних гармоник.
Статическая модуляционная характеристика (СМХ) амплитудного
модулятора - это зависимость амплитуды первой гармоники выходного
тока модулятора от напряжения смещения при постоянной амплитуде
несущей и амплитуде модулирующего сигнала, равной нулю.
Пределы изменения напряжения смещения:
𝐸0 − 𝑈𝑚 < 𝐸 < 𝐸0 + 𝑈𝑚
1−1<𝐸 <1+1
т. е. 0 В < 𝐸 < 2 В
𝐸 −𝐸
𝑐𝑜𝑠(𝜃) = 0
𝑈𝑚
;
;
;
.
Амплитуда первой гармоники выходного тока модулятора:
𝐼1 = |𝑆 ∙ 𝑈𝑚 ∙ 𝛾1 (𝜃)|
,
где:
4
𝛾1 (𝜃) =
ники.
𝜃−𝑠𝑖𝑛(𝜃)∙𝑐𝑜𝑠(𝜃)
𝜋
-
коэффициент Берга для первой гармо-
Расчет выполнен в таблице 1.
Таблица 1. Расчет СМХ амплитудного модулятора.
𝐸, В
0
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6
1,8
2
𝑐𝑜𝑠(𝜃)
1
0,8
0,6
0,4
0,2
0
-0,2
-0,4
-0,6
-0,8
-1
Рисунок 3.
𝜃, (град)
0
36,87
53,13
66,422
78,463
90
101,537
113,578
126,87
143,13
180
𝛾1 (𝜃)
0
0,052
0,1424
0,2523
0,3735
0,5
0,6265
0,7477
0,8576
0,948
1
𝐼1 , мА
0
0,26
0,712
1,262
1,868
2,5
3,132
3,738
4,288
4,74
5
СМХ амплитудного модулятора.
Рабочий участок - линейный участок СМХ. Границы рабочего
участка:
5
𝐸𝑚𝑖𝑛 = 0,4
В
,
𝐸𝑚𝑎𝑥 = 1,6
В
,
𝐼𝑚𝑖𝑛 = 1,281
мА
,
𝐼𝑚𝑎𝑥 = 7,719
мА
,
Ток в рабочей точке:
𝐼рт = 4,5
мА
.
Минимальная, максимальная и средняя амплитуды несущей:
𝑈𝑚𝑖𝑛 = 𝐼𝑚𝑖𝑛 ∙ 𝑅 = 1,281 ∙ 10 = 12,814
В
;
𝑈𝑚𝑎𝑥 = 𝐼𝑚𝑎𝑥 ∙ 𝑅 = 7,719 ∙ 10 = 77,186
В
.
𝑈0 = 𝐼рт ∙ 𝑅 = 4,5 ∙ 10 = 45 В
.
Глубина модуляции:
𝐼
𝑀а = 𝑚𝑎𝑥
−𝐼𝑚𝑖𝑛
𝐼𝑚𝑎𝑥 +𝐼𝑚𝑖𝑛
=
7,719−1,281
7,719+1,281
= 0,715
.
Аналитическое выражение для сигнала АМ:
-
в общем виде:
𝑢ам (𝑡) = 𝑈0 ∙ (1 + 𝑀а ∙ 𝑐𝑜𝑠(𝛺 ∙ 𝑡)) ∙ 𝑐𝑜𝑠(𝜔0 ∙ 𝑡) ;
-
для наших значений параметров:
𝛺 = 2 ∙ 𝜋 ∙ 𝐹 = 2 ∙ 𝜋 ∙ 11 ∙ 103 = 6,912 ∙ 104
с−1
;
𝜔0 = 2 ∙ 𝜋 ∙ 𝑓0 = 2 ∙ 𝜋 ∙ 207 ∙ 103 = 1,301 ∙ 106 с−1
.
𝑢ам (𝑡) = 𝑈0 ∙ (1 + 𝑀а ∙ 𝑐𝑜𝑠(𝛺 ∙ 𝑡)) ∙ 𝑐𝑜𝑠(𝜔0 ∙ 𝑡) =
= 45 ∙ (1 + 0,715 ∙ 𝑐𝑜𝑠(6,912 ∙ 104 ∙ 𝑡)) ∙ 𝑐𝑜𝑠(1,301 ∙ 106 ∙ 𝑡)
В
.
Для получения неискаженной модуляции нужно, чтобы колебательный контур модулятора выделял из всего спектра тока только полосу
частот [𝜔0 − 𝛺; 𝜔0 + 𝛺] [2, стр. 80]. Поэтому требуемую добротность
колебательного контура можно оценить как:
𝑄=
𝜔0
𝛺
=
1,301∙106
6,912∙104
= 18,818 .
6
Задание 3.
Нарисуйте принципиальную схему частотного модулятора и рассчитайте статическую модуляционную характеристику (СМХ) частотного модулятора, если емкость варикапа, подключенного параллельно емкости
резонансного контура частотно-модулируемого генератора, зависит от
напряжения смещения:
𝐶в =
𝑛+2
𝐸
=
7+2
𝐸
=
9
𝐸
[пФ] при 1 В < 𝐸 < 2 В.
Емкость контура генератора равна:
𝐶 = 100 + 𝑚 = 100 + 8 = 108
пФ
;
индуктивность:
𝐿 = 100 − 𝑛 = 100 − 7 = 93 мкГн .
Выберите рабочий участок на СМХ и рабочую точку, определите
параметры ЧМ сигнала на выходе модулятора, запишите аналитическое
выражение для ЧМ сигнала.
Амплитуда ЧМ колебания на выходе модулятора равна:
𝑈𝑚 = (𝑚 + 1) = 8 + 1 = 9
В
,
частота модулирующего сигнала равна:
𝐹 = (𝑛 + 1) = 7 + 1 = 8
кГц .
Решение.
Статическая модуляционная характеристика (СМХ) частотного модулятора - это зависимость частоты, генерируемой модулятором, от напряжения смещения.
Пределы изменения напряжения смещения:
1 В<𝐸<2 В
.
Емкость варикапа:
7
𝐶в =
9
пФ
𝐸
.
Частота, генерируемая генератором:
𝑓=
1
2∙𝜋∙√𝐿∙(𝐶+𝐶в )
.
Расчет выполнен в таблице 2.
Рабочий участок - линейный участок СМХ. Границы рабочего
участка:
𝐸𝑚𝑎𝑥 = 2
В
𝑓𝑚𝑎𝑥 = 1,556
МГц ,
,
𝐸𝑚𝑖𝑛 = 1,6
В
𝑓𝑚𝑖𝑛 = 1,548
МГц .
;
Частота в рабочей точке:
𝑓0 = 1,552 МГц .
Рисунок 4.
Принципиальная схема частотного модулятора.
Девиация частоты:
𝑓д = 𝑓𝑚𝑎𝑥 − 𝑓0 = 𝑓0 − 𝑓𝑚𝑖𝑛 = 1,556 ∙ 106 − 1,552 ∙ 106 =
= 3,861 ∙ 103
Гц
.
8
Таблица 2. Расчет СМХ частотного модулятора.
𝐸, В
1
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2
𝐶в , пФ
9
8,182
7,57
6,923
6
5,625
5,294
5
4,737
4,5
5,625
𝐶 + 𝐶в , пФ
117
116,182
115,5
114,923
114,429
114
113,625
113,294
113
112,737
112,5
𝑓, Гц
1,526
1,531
1,536
1,539
1,543
1,546
1,548
1,551
1,553
1,554
1,556
Индекс ЧМ:
𝑓
3,861
𝐹
8
𝑀ч = д =
= 0,483
Рисунок 5.
.
СМХ амплитудного модулятора.
Аналитическое выражение для сигнала ЧМ:
9
-
в общем виде:
𝑢чм (𝑡) = 𝑈𝑚 ∙ 𝑐𝑜𝑠(𝜔0 ∙ 𝑡 + 𝑀ч ∙ 𝑠𝑖𝑛(𝛺 ∙ 𝑡))
-
;
для наших значений параметров:
𝛺 = 2 ∙ 𝜋 ∙ 𝐹 = 2 ∙ 𝜋 ∙ 8 ∙ 103 = 5,027 ∙ 104
с−1
;
𝜔0 = 2 ∙ 𝜋 ∙ 𝑓0 = 2 ∙ 𝜋 ∙ 1,552 ∙ 106 = 9,752 ∙ 106
с−1
.
𝑢чм (𝑡) = 𝑈𝑚 ∙ 𝑐𝑜𝑠(𝜔0 ∙ 𝑡 + 𝑀ч ∙ 𝑠𝑖𝑛(𝛺 ∙ 𝑡)) =
= 9 ∙ 𝑐𝑜𝑠(9,752 ∙ 106 ∙ 𝑡 + 0,483 ∙ 𝑠𝑖𝑛(5,027 ∙ 104 ∙ 𝑡))
10
В
.
Задание 4.
В соответствии с выполненными в п.п. 2, 3 расчетами постройте в
масштабе три временные диаграммы (модулирующий сигнал, АМ сигнал
и ЧМ сигнал), укажите числовые значения параметров сигналов; три
спектральные диаграммы (спектр модулирующего и несущего гармонических сигналов, спектр АМ сигнала и спектр ЧМ сигнала). На графиках
спектров укажите значения амплитуд и частот гармоник и параметры АМ
и ЧМ сигналов.
Сравните энергетические и спектральные характеристики АМ и ЧМ
сигналов.
Решение.
Поскольку частота заполнения во много раз выше частоты модулирующего сигнала, то построить в реальном масштабе зависимость напряжения от времени в наглядном виде невозможно. Поэтому на временных
диаграммах АМ и ЧМ сигналов масштаб по времени не соблюден.
Для построения спектральных диаграмм преобразуем выражения для
АМ- и ЧМ-сигналов с помощью тригонометрических соотношений:
𝑢ам (𝑡) = 45 ∙ (1 + 0,715 ∙ 𝑐𝑜𝑠(6,912 ∙ 104 ∙ 𝑡)) ∙ 𝑐𝑜𝑠(1,301 ∙ 106 ∙ 𝑡) =
= 45 ∙ 𝑐𝑜𝑠(1,301 ∙ 106 ∙ 𝑡) +
+45 ∙ 0,715 ∙ 0,5 ∙ 𝑐𝑜𝑠((1,301 ∙ 106 − 6,912 ∙ 104 ) ∙ 𝑡) +
+45 ∙ 0,715 ∙ 0,5 ∙ 𝑐𝑜𝑠((1,301 ∙ 106 + 6,912 ∙ 104 ) ∙ 𝑡) =
= 45 ∙ 𝑐𝑜𝑠(1,301 ∙ 106 ∙ 𝑡) +
+16,093 ∙ 𝑐𝑜𝑠((1,301 ∙ 106 − 6,912 ∙ 104 ) ∙ 𝑡) +
+16,093 ∙ 𝑐𝑜𝑠((1,301 ∙ 106 + 6,912 ∙ 104 ) ∙ 𝑡) В
.
𝑢чм (𝑡) = 9 ∙ 𝑐𝑜𝑠(9,752 ∙ 106 ∙ 𝑡 + 0,483 ∙ 𝑠𝑖𝑛(5,027 ∙ 104 ∙ 𝑡))
ЧМ-сигнал можно представить в виде бесконечного ряда:
11
В
.
𝑖
𝑢чм (𝑡) = 𝐴0 ∙ 𝑐𝑜𝑠(𝜔0 ∙ 𝑡) + ∑∞
𝑖=1(−1) ∙ 𝐴𝑖 ∙ 𝑐𝑜𝑠((𝜔0 − 𝑖 ∙ 𝛺) ∙ 𝑡) +
+ ∑∞
𝑖=1 𝐴𝑖 ∙ 𝑐𝑜𝑠((𝜔0 + 𝑖 ∙ 𝛺) ∙ 𝑡)
,
где:
𝐴0 = 𝑈0 ∙ 𝐽0 (𝑀ч ) = 9 ∙ 𝐽0 (0,483) = 8,483 В
𝐴𝑖 = 𝑈0 ∙ 𝐽𝑖 (𝑀ч ) = 9 ∙ 𝐽𝑖 (0,483)
𝐽𝑖 (𝑀ч )
;
;
функция Бесселя первого рода 𝑖-го порядка.
-
При построении амплитудного спектра мы будем учитывать только
те составляющие, для которых выполняется условие |𝐴𝑖 | ≥ 0,05 ∙ |𝐴0 |, или
|𝐽𝑖 (𝑀ч )| ≥ 0,05 ∙ |𝐽0 (𝑀ч )|.
Результаты расчетов для правой части спектральной диаграммы запишем в виде таблицы (левая часть диаграммы построена с учетом симметрии спектра относительно 0):
Таблица 3. Спектр ЧМ-сигнала.
𝑖
𝜔, рад/с
𝐽𝑖 (𝑀ч )
𝑈ч , В
0
9,752 ∙ 106
0,943
8,483
1
9,802 ∙ 106
0,234
2,109
2
9,853 ∙ 106
0,029
0,257
Сравним энергетические и спектральные характеристики АМ и ЧМ
сигналов. Ширина спектра АМ сигнала всегда равна 𝛥𝐹ам = 2 ∙ 𝐹 - удвоенной верхней частоте в спектре первичного сигнала. Полезная мощность
АМ сигнала определяется боковыми составляющими, дающими информацию о частоте первичного сигнала и его интенсивности, и составляет:
(𝑀а )2
2
=
0,7152
2
= 0,256
(𝑀а )2
0,7152
2+(𝑀а
2+0,7152
=
)2
= 0,204
-
от мощности несущей или
-
от общей средней мощности.
Ширина спектра ЧМ сигнала определяется индексом ЧМ. Обычно
для практических целей принимают [1, стр. 98]:
𝛥𝐹чм = 2 ∙ 𝐹 ∙ (1 + 𝑀) .
12
В нашем случае, приблизительно, 𝛥𝐹чм = 4 ∙ 𝐹. Расчет показывает,
что для угловых частот ±3 амплитуда составляет 2,4 % от амплитуды
на частоте, на рисунке 7 в они не показаны.
Полезная мощность ЧМ сигнала также определяется боковыми составляющими и составляет:
𝑖
𝑚𝑎𝑥(𝐽 (𝑀 ))
2∙∑𝑖=1
𝑖
ч
(𝐽0 (𝑀ч ))
-
2
2
2
=
2
(𝐽0 (0,483))
= 0,125
от мощности несущей или
2
2
2
𝑖
𝑚𝑎𝑥 (𝐽 (𝑀 ))
2∙∑𝑖=1
𝑖
ч
𝑖
2
𝑚𝑎𝑥 (𝐽 (𝑀 ))
(𝐽0 (𝑀ч )) +2∙∑𝑖=1
𝑖
ч
-
2
2∙((𝐽1 (0,483)) +(𝐽2 (0,483)) )
=
2
2∙((𝐽1 (0,483)) +(𝐽2 (0,483)) )
2
2
2
(𝐽0 (0,483)) +2∙((𝐽1 (0,483)) +(𝐽2 (0,483)) )
= 0,111
от общей средней мощности.
Из свойств функций Бесселя следует, что полезная мощность ЧМ
сигнала увеличивается с увеличением индекса модуляции M.
Таким образом, спектр ЧМ сигнала шире спектра АМ, а доля полезной мощности ЧМ сигнала больше АМ.
а
13
б
в
Рисунок 6.
Временные диаграммы:
а
модулирующий сигнал;
б
АМ сигнал;
в
ЧМ сигнал.
14
а
б
15
в
Рисунок 7.
Спектральные диаграммы:
а
спектр модулирующего сигнала и несущей;
б
спектр АМ сигнала;
в
спектр ЧМ сигнала.
16
Задание 5.
Модулированный сигнал поступает на вход приемного устройства в
сумме с аддитивным нормальным белым шумом со спектральной плотностью энергии:
𝐺0 = (𝑚 + 𝑛 + 1) ∙ 10−6 = (8 + 7 + 1) ∙ 10−6 = 16 ∙ 10−6 В2 /Гц
.
Рассчитайте функцию корреляции белого шума на выходе идеального полосового фильтра с полосой пропускания, соответствующей ширине спектра и несущей сигнала АМ, определенной в п. 2. Запишите
выражение для функции плотности вероятности (ФПВ) шума на выходе
идеального полосового фильтра, определите дисперсию шума и постройте
график ФПВ. Рассчитайте вероятность того, что значения шума превысят
0 В, 𝜎 В и 1 В.
Решение.
Энергетический спектр шума на выходе идеального полосового
фильтра:
𝐺вых (𝜔) = 𝐺0 ∙ (𝐾0 )2
при 𝜔0 − 𝛺 < 𝜔 < 𝜔0 + 𝛺 .
Функция корреляции выходного шума:
𝐵(𝜏) =
1
2∙𝜋
𝐺 ∙(𝐾0 )2
= 0
2∙𝜋
𝐺 ∙(𝐾0 )2
= 0
∙ (−
1
𝑗∙𝜏
2∙𝜋
+∞
∙ ∫−∞ 𝐺вых (𝜔) ∙ 𝑒 𝑗∙𝜔∙𝜏 ∙ 𝑑𝜔 =
−𝜔 +𝛺
0
𝐺 ∙(𝐾0 )2
2∙𝜋
𝐺 ∙(𝐾0 )2
= 0
𝜋∙𝜏
0
∙
∙ 𝑒 𝑗∙𝜏∙(−𝜔0−𝛺) +
= 0
𝜔 +𝛺
∙ (∫−𝜔 0−𝛺 𝑒 𝑗∙𝜔∙𝜏 ∙ 𝑑𝜔 + ∫𝜔 0−𝛺 𝑒 𝑗∙𝜔∙𝜏 ∙ 𝑑𝜔) =
∙
1
𝑗∙𝜏
1
𝑗∙𝜏
∙ 𝑒 𝑗∙𝜏∙(−𝜔0 +𝛺) −
1
𝑗∙𝜏
∙ 𝑒 𝑗∙𝜏∙(𝜔0−𝛺) +
1
𝑗∙𝜏
∙ 𝑒 𝑗∙𝜏∙(𝜔0+𝛺) ) =
∙ (𝑒 −𝑗∙𝜏∙𝜔0 + 𝑒 𝑗∙𝜏∙𝜔0 ) ∙ (𝑒 𝑗∙𝜏∙𝛺 − 𝑒 −𝑗∙𝜏∙𝛺 ) =
∙ 𝑐𝑜𝑠(𝜔0 ∙ 𝜏) ∙ 𝑠𝑖𝑛(𝛺 ∙ 𝜏)
.
Дисперсия шума на выходе фильтра (примем 𝐾0 = 1):
17
𝜎 2 = 𝐵(0) =
2∙𝐺0 ∙(𝐾0 )2 ∙𝛺
𝜋
В2
= 0,704
= 4 ∙ 𝐺0 ∙ 𝐹 = 4 ∙ 16 ∙ 10−6 ∙ 11 ∙ 103 =
.
Процесс на выходе фильтра является нормальным со средним значением, равным нулю, и с дисперсией 𝜎 2 . Тогда можно записать ФПВ
шума на выходе фильтра:
𝑓(𝑢) =
1
√2∙𝜋∙𝜎
∙𝑒
𝑢2
2∙𝜎2
−
=
1
2∙√2∙𝜋∙𝐺0 ∙𝐹
∙𝑒
𝑢2
8∙𝐺0 ∙𝐹
−
.
Подставим численные значения:
𝑓(𝑢) =
1
√2∙𝜋∙𝜎
∙𝑒
𝑢2
2∙𝜎2
−
=
1
√2∙𝜋∙0,704
∙𝑒
𝑢2
2∙0,704
−
= 0,475 ∙ 𝑒
𝑢2
1,408
−
В−1 .
Рисунок 8.
Функция плотности вероятности (ФПВ) шума на
выходе идеального полосового фильтра.
Вероятность того, что значение шумового напряжения превысит уровень 𝑈0 , определяется интегралом от ФПВ шума:
18
∞
𝑈
𝑃(𝑢 > 𝑈0 ) = ∫𝑈 𝑓(𝑢) ∙ 𝑑𝑢 = 1 − ∫−∞0 𝑓(𝑢) ∙ 𝑑𝑢 =
0
2
𝑈
2
𝑡
0
𝑈0 − 𝑢 2
1
𝑈
−
𝜎
2∙𝜎
=1−
∙ ∫−∞ 𝑒
∙ 𝑑𝑢 = 1 −
∙ ∫−∞ 𝑒 2 ∙ 𝑑𝑡 = 1 − Ф ( 0)
𝜎
√2∙𝜋∙𝜎
√2∙𝜋
1
где
Ф( )-
,
функция Лапласа.
Рассчитаем вероятность того, что значения шума превысит:
1)
0 В. Поскольку Ф(0) = 0,5, то 𝑃(𝑢 > 0) = 0,5. Этот результат
понятен, поскольку шум - нормальный процесс с нулевым средним.
2)
0,159.
3)
𝜎 В. Положим
𝑈0
𝑈0 = 𝜎;
𝜎
1 В. 𝑃(𝑢 > 1 В) = 1 − Ф (
= 1;
1
√0,704
19
Ф(1) = 0,841;
) = 0,117.
𝑃(𝑢 > 𝜎) =
Задание 6.
Модулированные сигналы АМ и ЧМ поступают на вход соответственно амплитудного детектора и частотного детектора. Начертите принципиальные схемы амплитудного диодного детектора и частотного детектора на расстроенных контурах. Поясните принципы работы амплитудного
и частотного детекторов.
Рассчитайте спектр тока через диод для АМ детектора (этот расчет
справедлив для каждого из диодов частотного детектора). ВАХ диода
аппроксимирована отрезками прямых:
𝑖=0
при 𝑢 < 0
𝑖 =𝑆∙𝑢
при 𝑢 ≥ 0
{
= 𝑚 + 5 = 8 + 5 = 13
мА/В
.
Сопротивление нагрузки детектора:
𝑅 = (𝑚 + 10) = 8 + 10 = 18
кОм .
Параметры входного АМ сигнала из п. 2:
𝑢ам (𝑡) =
= 45 ∙ (1 + 0,715 ∙ 𝑐𝑜𝑠(6,912 ∙ 104 ∙ 𝑡)) ∙ 𝑐𝑜𝑠(1,301 ∙ 106 ∙ 𝑡)
В
.
Рассчитайте спектр напряжения на выходе 𝑅𝐶-фильтра детектора,
выбрав постоянную времени 𝑅𝐶-фильтра нижних частот так, чтобы амплитуда несущей составляла не более 0,1 от амплитуды полезного сигнала.
Рассчитайте значение емкости 𝑅𝐶-фильтра.
Постройте графики спектров тока и напряжения на выходе детектора, на которых укажите значения амплитуд и частот гармоник спектров.
Решение.
Принцип работы амплитудного диодного детектора аналогичен принципу работы обычного однополупериодного выпрямителя. В течение времени, когда разность потенциалов между точками 1 и 2 (рисунок 9)
выше, чем напряжение на конденсаторе, через диод протекает ток, заряжающий конденсатор. В течение остального времени ток через диод не
20
протекает, и конденсатор разряжается в цепь нагрузки. Если выбрать
постоянную времени 𝑅𝐶-цепочки таким образом, что:
1
𝜔0
≪𝑅∙𝐶 ≪
1
𝛺
,
то напряжение на конденсаторе будет успевать отслеживать изменение
модулирующего сигнала и сглаживать высокочастотные колебания.
Рисунок 9.
тектора.
Принципиальная схема амплитудного диодного де-
Работа частотного детектора основана на том, что если резонансная
частота контура отличается от средней частоты модулированного колебания, то изменение амплитуды напряжения на контуре повторяет (в некоторых пределах) изменение частоты входного напряжения. В схеме детектора на двух расстроенных контурах (рисунок 10) выходное напряжение
есть разность двух выпрямленных напряжений 𝑈01 и 𝑈02 , создаваемых на
сопротивлениях 𝑅1 и 𝑅2 транзисторами 𝑇1 и 𝑇2 .
При частоте входного сигнала 𝜔0 напряжения на 𝑅1 и 𝑅2 одинаковы.
При увеличении частоты на амплитуда напряжения на контуре, настроенном на более высокую частоту, возрастает, следовательно, возрастает и
21
напряжение на 𝑅1 (и соответственно, убывает на 𝑅2 ). Разность этих
напряжений и дает НЧ сигнал, при малых отклонениях частоты от 𝜔0
приблизительно пропорциональный.
Рисунок 10.
Принципиальная схема частотного детектора на расстроенных контурах.
Представим ток через диод в виде ряда Фурье:
𝑖 = 𝐼0 + 𝐼1 ∙ 𝑐𝑜𝑠(𝜔0 ∙ 𝑡) + 𝐼2 ∙ 𝑐𝑜𝑠(2 ∙ 𝜔0 ∙ 𝑡) + 𝐼3 ∙ 𝑐𝑜𝑠(3 ∙ 𝜔0 ∙ 𝑡) + ⋯
Рассчитываем амплитуды гармоник тока:
𝐼𝑘 = 𝑆 ∙ 𝑈0 ∙ (1 + 𝑀а ∙ 𝑐𝑜𝑠(𝛺 ∙ 𝑡)) ∙ 𝛾𝑘 (𝜃) .
Определим 𝜃 из соотношения:
𝑡𝑔(𝜃) − 𝜃 =
𝜋
𝑆∙𝑅
;
𝑆 ∙ 𝑅 = 13 мА/В 18 кОм = 234
𝑡𝑔(𝜃) − 𝜃 =
𝜋
𝑆∙𝑅
=
𝜋
234
;
= 13,426 ∙ 10−3
;
откуда
𝜃 = 0,337 рад = 19,3370
;
𝛾0 (𝜃) = 7,269 ∙ 10−3
𝛾1 (𝜃) = 14,302 ∙ 10−3 .
,
22
.
Требуется выполнить расчет только для частот: 0, 𝛺, 𝜔0 − 𝛺, 𝜔0 ,
𝜔0 + 𝛺.
𝑢ам (𝑡) =
= 45 ∙ (1 + 0,715 ∙ 𝑐𝑜𝑠(6,912 ∙ 104 ∙ 𝑡)) ∙ 𝑐𝑜𝑠(1,301 ∙ 106 ∙ 𝑡)
В
.
𝐼0 = 𝑆 ∙ 𝑈0 ∙ 𝛾0 (𝜃) ∙ (1 + 𝑀а ∙ 𝑐𝑜𝑠(𝛺 ∙ 𝑡)) =
= 0,013 ∙ 45 ∙ 7,269 ∙ 10−3 ∙ (1 + 0,715 ∙ 𝑐𝑜𝑠(6,912 ∙ 104 ∙ 𝑡)) =
= 4,253 ∙ 10−3 ∙ (1 + 0,715 ∙ 𝑐𝑜𝑠(6,912 ∙ 104 ∙ 𝑡))
мА
;
𝐼1 = 𝑆 ∙ 𝑈0 ∙ 𝛾1 (𝜃) ∙ (1 + 𝑀а ∙ 𝑐𝑜𝑠(𝛺 ∙ 𝑡)) =
= 0,013 ∙ 45 ∙ 14,302 ∙ 10−3 ∙ (1 + 0,715 ∙ 𝑐𝑜𝑠(6,912 ∙ 104 ∙ 𝑡)) =
= 8,367 ∙ 10−3 ∙ (1 + 0,715 ∙ 𝑐𝑜𝑠(6,912 ∙ 104 ∙ 𝑡))
мА
.
Достаточно рассчитать две гармоники, так как остальные гармоники
дадут частоты выше 𝜔0 + 𝛺.
Воспользуемся формулой:
𝑐𝑜𝑠(𝛼) ∙ 𝑐𝑜𝑠(𝛽) = 0,5 ∙ (𝑐𝑜𝑠(𝛼 + 𝛽) ∙ 𝑐𝑜𝑠(𝛼 − 𝛽))
.
Тогда искомые гармонические составляющие тока можно записать в
виде:
𝐼 = 4,253 ∙ 10−3 + 3,042 ∙ 10−3 ∙ 𝑐𝑜𝑠(𝛺 ∙ 𝑡) + 8,367 ∙ 10−3 ∙ 𝑐𝑜𝑠(𝜔0 ∙ 𝑡) +
+2,992 ∙ 10−3 ∙ 𝑐𝑜𝑠((𝜔0 − 𝛺) ∙ 𝑡) +
+2,992 ∙ 10−3 ∙ 𝑐𝑜𝑠((𝜔0 + 𝛺) ∙ 𝑡)
А
.
Выберем постоянную RC-фильтра таким образом, что:
1
𝜔0
1
𝜔0
≪𝑅∙𝐶 ≪
=
1
1,301∙106
1
𝛺
;
= 7,689 ∙ 10−7 с
;
23
1
𝛺
=
1
6,912∙104
= 1,447 ∙ 10−5
с
.
Амплитуда напряжения на выходе 𝑅𝐶-фильтра равна:
𝑈𝜔 =
𝑅∙𝐼𝜔
√1+(𝜔∙𝐶∙𝑅)2
.
Расчет показывает, что при заданном соотношении частот одновре𝑈 (𝜔 )
менно удовлетворить условию (*) и условию 𝜔 (𝛺)0 < 0,1 не удается.
𝑈𝜔
Для этого нужно использовать фильтр более высокого порядка.
Пусть 𝑅𝐶 = 2,16 ∙ 10−5 с (𝑅 = 18 кОм, 𝐶 = 1,2 нФ).
Результаты расчетов запишем в виде таблицы:
Таблица 4. Спектр напряжения и тока на выходе 𝑅𝐶-фильтра.
𝜔
𝜔, рад/с
𝐼, мА
𝑈, В
0
0
4,253
76,546
Рисунок 11.
𝛺
6,912104
3,042
30,469
𝜔0 − 𝛺
1,232106
2,992
2,023
𝜔0
1,301106
8,367
5,357
Спектр тока на выходе 𝑅𝐶-фильтра.
24
𝜔0 + 𝛺
1,37106
2,992
1,819
Рисунок 12.
Спектр напряжения на выходе 𝑅𝐶-фильтра.
25
Литература.
1.
Теория электрической связи: Учебник для вузов/А. Г. Зюко,
Д. Д. Кловский, В. И. Коржик, М. В. Назаров; Под редакцией Д. Д.
Кловского. - Москва: Радио и связь, 1999 г.
2.
Андреев В. С. Теория нелинейных электрических цепей: Учебное пособие для вузов. - Москва: Радио и связь, 1982 г.
26