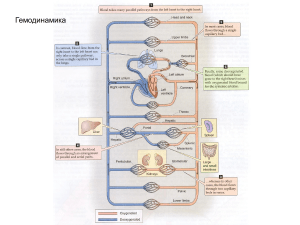
Статья - МАТЕМАТИЧЕСКИЕ МОДЕЛИ ГЕМОДИНАМИКИ КРОВОТОКА С УЧЕТОМ РАБОТЫ РАСПРЕДЕЛЕННОГО СЕРДЦА
реклама

Мезо-, нано-, биомеханика и механика природных процессов Вестник Нижегородского университета им. Н.И. Лобачевского, 2011, № 4 (2), с. 423–424 423 УДК 539.3 МАТЕМАТИЧЕСКИЕ МОДЕЛИ ГЕМОДИНАМИКИ КРОВОТОКА С УЧЕТОМ РАБОТЫ РАСПРЕДЕЛЕННОГО СЕРДЦА 2011 г. А.В. Доль, Ю.П. Гуляев Саратовский госуниверситет им. Н.Г. Чернышевского dzero@pisem.net Поступила в редакцию 15.06.2011 Представлены математические модели движения крови в крупных кровеносных сосудах с учетом работы распределенного сердца. Рассмотрена модель в рамках одномерной теории течения вязкой несжимаемой жидкости. Представлена модель кровотока в трехмерном случае. Ключевые слова: биомеханика, гемодинамика, математическое моделирование, уравнения Навье − Стокса, артерия. Основная замкнутая система уравнений течения вязкой несжимаемой жидкости Вопросы моделирования гемодинамики крупных кровеносных сосудов приобретают в последнее время все большую актуальность. Это связано с медицинскими проблемами реконструкции сосудистого русла при атеросклеротических поражениях и необходимостью прогнозирования возможного поведения сосуда в ближайшие и отдаленные периоды после оперативного вмешательства. Построим математическую модель динамики кровотока. Движение крови по сосуду предполагается осесимметрическим, поэтому будем рассматривать его в цилиндрической системе координат. Ось z направляем по оси сосуда, полярную ось r направим по его радиусу. Поле скоростей с компонентами vr , vz зависит от переменных z, r, t. Уравнения Навье − Стокса в цилиндрической системе координат имеют вид: ∂v ∂v ∂v ρ r + vr r + v z r = ∂ t ∂ r ∂z ∂2 v 1 ∂vr v r ∂ 2 vr ∂P , =− + µ 2r + − + ∂r ∂r r ∂r r 2 ∂z 2 (1) ∂v ∂v ∂v ρ z + v r z + v z z = ∂ t ∂ r ∂z ∂2 v 1 ∂v z ∂ 2 v z ∂P =− + µ 2z + + 2 , ∂r ∂z r ∂r ∂z ∂ ( rv r ) ∂ ( rv z ) + = 0, ∂r ∂z (2) (3) где ρ − плотность крови, µ − вязкость крови, P − давление. Получим уравнения движения цилиндрической оболочки. На стенки трубы действует трансмуральное давление, состоящее из среднего давления P0 и пульсационной составляющей P′. Оболочка находится в предварительно натянутом состоянии. Кроме трансмурального давления на стенки действуют силы вязкого трения и силы упругой податливости окружающих сосуд тканей в осевом и радиальном направлении соответственно: S 1 = −K 2u , P1 = = −K1w, K1, K2 − коэффициенты податливости тканей. В поперечном сечении действует продольная сила: S = S0 + S′, где S0 − средняя сила продольного натяжения, S′ − пульсационная составляющая продольной силы. В окружном направлении на элемент действует поперечная сила натяжения T = T0 + T ′, где T0 − средняя сила поперечного натяжения сосуда, T ′ − пульсационная составляющая поперечной силы. Уравнение изменения количества движения элемента оболочки в осевом направлении имеет вид: ∂2u ∂S ′ S0 − T0 ∂w (4) + − K 2 u, R ∂z ∂z ∂t где w − радиальное смещение стенки, R − радиус сосуда. Уравнение изменения количества движения элемента в радиальном направлении: P ∂2 w ∂2 w T′ ρh 2 = P ′ + 0 w − + S 0 2 − K1 w. (5) R R ∂t ∂z Используя закон Гука, получим уравнения для усилий: ρh 2 = А.В. Доль, Ю.П. Гуляев 424 Eh ∂u w + ν , 2 R 1 − ν ∂x ∂u Eh w + ν , T′ = (6) 2 ∂x 1− ν R ν − коэффициент Пуассона. Система (1)−(6) представляет собой замкнутую систему уравнений динамики кровотока в артериальном русле. S′ = Одномерная теория Для вывода уравнений одномерной теории нужно усреднить уравнения Навье − Стокса по радиусу трубы. Если ввести объемный расход по формуле вью можно назвать распределенным (вторичным) сердцем. Из этой системы получается уравнение для объемного кровотока с учетом реактивного перемещения стенок сосуда, возникающего под действием волны давления: ρ ∂Q ∂P 8πµ = − πR 2 − 2 (Q − πR 2 v0 ), ∂t ∂z πR (8) где v0 − средняя скорость продольного перемещения стенки сосуда за счет мышечной реакции. Дальнейшая процедура построения решения задачи о пульсации кровотока представлена в работе [1]. Трехмерная теория R Q = ∫ 2 πrv z dr, 0 а также пренебречь конвективной составляющей ускорения частиц жидкости, инерционными силами, действующими на элемент оболочки, из замкнутой системы уравнений (1)−(6) получается более простой вариант системы уравнений динамики кровотока: ∂Q ∂p ′ 8πµ − ρ = − πR 2 Q, ∂z π R 2 ∂t ∂w 1 ∂Q =− , ∂t 2πR ∂z (7) ∂ 2w T0 T S 0 2 + p ′ + 2 w − = 0, R ∂z R Eh w . T= 1− ν2 R Пульсовая волна давления, распространяясь по сосуду, вызывает ответную реакцию мышечных слоев сосудистой стенки. Эта реакция выражается в принудительном продольном растяжении мышечных волокон, которые приводят к дополнительному перемещению сосудистой стенки. В силу наличия вязкости крови, последняя увлекается стенкой. В результате средняя скорость кровотока возрастает. Такую схему взаимодействия стенки сосуда с кро- В трехмерном случае система уравнений (1)−(6) при определенных упрощениях методом разделения переменных сводится к системе обыкновенных дифференциальных уравнений относительно амплитуд пульсирующего кровотока. При этом амплитуда продольных скоростей в жидкой части системы будет удовлетворять уравнению Бесселя нулевого порядка: v z 0 1 v z 0 iρω + − (9) v = 0, ∂r r ∂r µ z0 где vz0 − проекция скорости течения крови на ось z; ω − круговая частота. Работа «распределенного сердца» моделируется с помощью функции дополнительных продольных реактивных перемещений стенок сосуда, инициированных пульсовой волной. Предложенные математические модели динамики кровотока достаточно точно описывают течение крови в сужающихся сосудах и могут применяться для решения задач динамики кровотока в артериальном дереве различной геометрической конфигурации. Список литературы 1. Гуляев Ю.П., Коссович Л.Ю. Математические модели биомеханики в медицине. Саратов: Изд-во СГУ, 2001. 49 с. MATHEMATICAL MODELS OF HAEMODYNAMICS WITH TAKING INTO ACCOUNT THE WORK OF A DISTRIBUTED HEART A.V. Dol, Yu.P. Gulyaev The paper describes mathematical models of blood flow in large-scale vessels with taking into account the work of a distributed heart. The mathematical model of a viscous incompressible liquid flow is considered. A 3-dimentional mathematical model is described. Keywords: biomechanics, haemodynamics, mathematical modeling, Navier − Stokes, artery.