СОДЕРЖАНИЕ
Дискретная математика ....................................................................................... 5
1. Разложение по столбцу в таблице покрытий, дерево процесса решения. 7
2. Приближенное решение задачи о покрытии. Метод минимального столбца —
максимальной строки. .......................................................................................... 8
3. Метод ветвей и границ в задаче о покрытии. .............................................. 9
4. Отношение совместимости и совместимые подмножества. Метод граничного
перебора построения максимальных совместимых подмножеств................ 13
5. Комбинаторика. Основные виды наборов. Компоненты связности. Определение
связности графа. Построение компонент связности в неориентированном графе. 14
6. Компоненты связности. Определение связности графа. Построение компонент
связности в ориентированном графе. ............................................................... 14
7. Остов, система фундаментальных циклов, система независимых циклов,
построение произвольного остова. ................................................................... 17
8. Остов, система фундаментальных циклов, система независимых циклов,
построение минимального остова нагруженного графа. ............................... 19
9. Кратчайшая раскраска графа — основные определения. Внутренне и внешне
устойчивые множества вершин графа. ............................................................ 21
10. Реализация булевых функций формулами. Основные свойства элементарных
булевых функций. ............................................................................................... 24
11. Совершенные дизъюнктивные и конъюнктивные нормальные формы (СДНФ,
СКНФ). ................................................................................................................ 24
12. Геометрическая форма представления и графический способ минимизации
булевых функций ................................................................................................ 24
13. Матричные формы представления и метод карт Карно минимизации булевых
функций в классе ДНФ и КНФ. ........................................................................ 24
14. Интервальные формы представления булевых функций. Основные
определения. ....................................................................................................... 24
15. Минимизация булевых функций методом Квайна-Мак-Класки в классе ДНФ и
КНФ. .................................................................................................................... 25
16. Типовые задачи по дискретной математике ........................................... 25
Теория вероятностей и математическая статистика ................................... 26
1. Понятие случая. Классическая формула для вычисления вероятности случайного
события. Статистическая вероятность случайного события. ........................ 26
2. Интерпретация основных понятий теории вероятностей на основе теории
множеств. Алгебра событий. Аксиомы теории вероятностей. ...................... 26
3. Формула полной вероятности. Формула Байеса. ...................................... 27
4. Закон распределения случайной величины. Статистический ряд. ......... 27
5. Определение функции распределения случайной величины. Свойства функции
распределения. .................................................................................................... 28
6. Плотность распределения. Свойства плотности распределения. ........... 29
7. Числовые характеристики дискретных и непрерывных случайных величин. 30
8. Биномиальное распределение..................................................................... 31
9. Равномерное распределение непрерывной случайной величины. ......... 31
10.
Показательное распределение непрерывной случайной величины. ... 32
11.
Нормальное распределение. Стандартное нормальное распределение.32
12. Геометрическое распределение. Понятие простейшего потока. Свойства
простейшего потока. Связь простейшего потока с распределением Пуассона.
32
13. Статистические оценки. Точечные оценки параметров распределения. Свойства
оценок. ................................................................................................................. 33
14.
Критерии проверки статистических гипотез. Критерий согласия Пирсона. 33
Моделирование вычислительных процессов и систем ............................... 35
1. Определение понятия модель. .................................................................... 35
2. Аналитическое и имитационное моделирование. .................................... 35
3. Характеристики обслуживания заявок в системах массового обслуживания
(СМО). ................................................................................................................. 35
4. Стационарный режим. Формулы Литтла. Нотация СМО. ....................... 36
5. СМО с неограниченной очередью. Уравнения для вероятностей состояний.
Основные характеристики для многоканальных и одноканальных СМО. .. 36
6. СМО типа СИМ/1. Формула Поллячека - Хинчина. ................................ 38
7. Характеристики СМО при многомерном входящем потоке. СМО с
относительными приоритетами. ....................................................................... 40
8. Характеристики СМО с абсолютными приоритетами. Смешанные приоритеты.
Закон сохранения времени ожидания для СМО без потерь. ......................... 41
9. Стохастические сети массового обслуживания и их параметры.
Экспоненциальные сети. Характеристики разомкнутых стохастических сетей.
Основы системного анализа .............................................................................. 44
1. Определение системы. ................................................................................. 45
2. Принципы системного анализа. ................................................................. 45
3. Классификация систем. ............................................................................... 45
4. Свойства сложных систем........................................................................... 47
5. Методы системного анализа. Анализ и синтез. ........................................ 48
6. Технологии и инструменты системной аналитики................................... 49
Системное программирование ......................................................................... 50
1. Линейные структуры данных: массив, список, очередь, стек, дек. ........ 50
2. Таблицы. Неупорядоченная, двоичная упорядоченная и хеш-таблицы. 50
3. Деревья. Двоичные, сбалансированные и Б- деревья. ............................. 51
4. Классификация систем программирования. ............................................. 52
42
5. Однопросмотровый, двухпросмотровый и многопросмотровый Ассемблеры.
Компоненты ассемблера. Алгоритм работы ассемблера. .............................. 53
6. Однопросмотровый и многопросмотровый макропроцессоры. Таблицы
макропроцессора. Алгоритм работы макропроцессора. ................................ 54
7. Загрузчики. Абсолютный, перемещающий и связывающий загрузчики.55
Базы данных ......................................................................................................... 56
1. Основные концепции баз данных (БД). Информационная система, банк данных,
база данных, структурирование данных, СУБД.............................................. 56
2. СУБД и ее основные функции, приложения. Классификация СУБД. Критерии
выбора СУБД пользователем, Краткая характеристика современных сетевых СУБД,
56
3. Современные подходы к моделированию данных. Виды моделей данных и их
характеристики. .................................................................................................. 56
4. Реляционная модель данных. Основные понятия. Отношение, домен, атрибут,
кортеж. Типы данных в БД. Целостность реляционных данных. Потенциальный
ключ отношения, первичный ключ, внешний ключ. ...................................... 56
5. Связывание таблиц. Основные виды связей между таблицами. Контроль
целостности связей. Уровни определения ограничений ссылочной целостности. 56
6. SQL. Запросы на модификацию данных в таблицах: INSERT, DELETE, UPDATE.
56
7. SQL. Простые формы оператора SELECT - запросы на выборку данных из одной
таблицы. Использование операторов BETWEEN, LIKE, IS [NOT] NULL, END, OR,
NOT в условиях отбора кортежей. Скалярные выражения в списке атрибутов запроса.
Сортировка кортежей. ........................................................................................ 56
8. Агрегатные функции SQL. Запросы с группировкой и отбором групп. 56
9. SQL. Запросы на выборку данных из нескольких таблиц. Способы объединения
таблиц. Соединение таблицы со своей копией. Простые запросы с подзапросами.
56
10. SQL. Запросы с коррелированными подзапросами. Алгоритм выполнения.
Кванторы [NOT] EXISTS$, ANY, ALL. ............................................................ 56
11.
Нормальные формы (НФ): 1НФ, 2НФ, ЗНФ. Нормальная форма Бойса-Кодда.
56
12. Построение логической модели предметной области. Алгоритм перехода от
диаграммы «сущность-связь» к отношениям реляционной базы данных. .. 56
13. Понятие функциональной зависимости между атрибутами отношения.
Замыкание множества функциональных зависимостей отношения. Неприводимое
множество функциональных зависимостей. Тривиальная функциональная
зависимость. Транзитивная функциональная зависимость. Зависимости,
определяющие избыточность данных в отношении. Декомпозиция без потерь. 56
14. Логический уровень проектирования баз данных. Метод нормальных форм.
Дублирование данных. Аномалии обновления, добавления, удаления данных. 56
ЭВМ и периферийные устройства, Архитектура ЭВМ ............................... 57
1. Архитектура системы команд. Основные типы команд. Способы адресации.
Форматы команд. ................................................................................................ 57
2. Структурная организация и методы проектирования управляющих автоматов с
жесткой логикой. Методы синхронизации. ..................................................... 57
3. Структурная организация управляющих автоматов с программируемой логикой.
Естественная адресация. Смешанное микропрограммирование. ................. 58
4. Центральный процессор. Структурная организация и функциональное
назначение блоков процессора. Цикл процессора .......................................... 58
5. Арифметико-логическое устройство. Структурная организация. Типы
обрабатываемых данных и особенности исполнения команд. ...................... 59
6. Внутренняя память ЭВМ. Статические и динамические запоминающие
устройства. Структурная организация SRAM и DRAM. Режимы работы. .. 60
7. Организация защиты памяти ЭВМ. Назначение. Возможные схемные решения.
60
Операционные системы ..................................................................................... 61
1. Объекты ядра в ОС Windows. Управление процессами в Windows. ...... 61
2. Управление процессами в ОС Unix. Методы организации виртуальной памяти.
Алгоритмы замещения страниц. ....................................................................... 61
3. Файловая система NTFS. ............................................................................. 62
4. Виртуальная файловая система VFS UNIX. .............................................. 62
5. Взаимодействие процессов в рамках компьютерной сети. Удаленный вызов
подпрограмм. ...................................................................................................... 63
Дискретная математика
Таблица – Определения
№ Определение
1 Покрытие называется безызбыточным, если при удалении из него хотя бы
одного элемента оно перестает быть покрытием. Иначе – покрытие избыточно.
2
Покрытие называется минимальным, если его цена
– наименьшая
среди всех покрытий данной задачи.
3 Покрытие называется кратчайшим, если количество l сборников – наименьшее
среди всех покрытий задачи.
4 Объяснением термина «покрытие» служит то, что совокупность множеств
содержит все элементы множества , т.е. покрывает множество .
Таблица – теоремы задач о покрытии
№ Название теоремы
Описание
1
Если P – покрытие, то
– тоже покрытие, т.е.
множество всех возможных покрытий вогнуто.
2
Минимальные и кратчайшие покрытия – безызбыточны
3
Если в столбце таблицы покрытий единственная единица,
то строка с этой единицей входит во все покрытия; такие
Ядро покрытия
строки называются ядерными и заранее выделяются для
введения во все покрытия
4
Если после удаления ядерных строк и покрытых ими
столбцов в строке не остается единиц, то такая строка не
Антиядро покрытия
входит ни в одно безызбыточное покрытие; такие строки
называются антиядерными и вычеркиваются
5 О поглощающих
Можно вычеркнуть все поглощающие столбцы (векторы)
столбцах
без ущерба для построения всех безызбыточных покрытий
6 Р поглощаемых строках
Если нужно найти хотя бы одно кратчайшее покрытие, то
при поиске одного
можно удалять все поглощаемые строки
кратчайшего покрытия
7 О поглощаемых
Если нужно гарантировать построение всех (хотя бы
строках при построении одного) минимальных покрытий, то можно вычеркивать
минимальных
поглощаемую строку, если ее цена больше или равна цене
покрытий
поглощающей строки
1) В столбцах b3 и b4 по одной 1 в каждом, поэтому строки A3 и A5,
содержащие эти 1, являются ядерными. Эти строки запоминаем для введения
во все безызбыточные покрытия этой таблицы и после удаления этих строк и
всех покрытых ими столбцов, таблица покрытий сократится до следующей:
2) В полученной таблице строка A6 не содержит 1, поэтому она является
антиядерной и вычеркивается из таблицы без запоминания.
3) Также столбец b1 >= b2, поэтому поглощающий столбец b7вычеркивается.
Получаем следующую таблицу:
4) В полученной таблице строка A2 поглощается строкой A1 (A2 <= A1 ).
Поэтому возможно несколько разветвлений процесса решения:
a. Если нужно построить все безызбыточные покрытия, то нельзя более
проводить никакие сокращения строк и полученная таблица далее не
сокращается.
b. Если нужно найти минимальные покрытия, то согласно теореме 7
нужно обратить внимание на цены ai строк: A2 <= A1 и a2 <= a1,
поэтому строку A2 нельзя вычеркивать и таблица также не упрощается.
c. Если ищем одно кратчайшее покрытие, то:
i. строку A2, как поглощаемую, можно вычеркнуть.
ii. Строка A1 становится ядерной, так как в столбце b2 останется
единственная единица.
iii. Строка A1 добавляется ко множеству ядерных строк - { A1, A3,
A5}
iv. Таблица покрытий упрощается: вычеркивается строка A1 и
покрытые ею столбцы b2 и b6.
Получается следующая таблица, которая уже не упрощается:
Резюмируя все вышесказанное, можно утверждать, что, используя теоремы 3.3 –
3.7, можно получить ядро покрытия (запомнив ядерные строки). После чего возможны
два исхода процесса решения:
Таблица покрытий после упрощения становится пустой (т.е. вычеркнуты все
столбцы). В этом случае множество ядерных строк и является требуемым
покрытием (решением). 2)
2) Остаток таблицы покрытий более не упрощается посредством применения
теорем 3 – 7. Получается циклический остаток таблицы покрытий. Покрытия
для циклического остатка можно строить методами перебора покрытий:
граничным перебором или разложением по столбцу (который будет рассмотрен
позже). Когда к ядерным строкам добавляются строки покрытия циклического
остатка, получается покрытие исходной таблицы покрытий.
1)
1. Разложение по столбцу в таблице покрытий, дерево процесса решения.
Основная идея метода разложения по столбцу:
Каждый столбец таблицы покрытий должен быть покрыт и покрывается только
за счет строк, содержащих единицу в этом столбце.
Шаги процесса решения:
1) Выбор очередного столбца с меньшим числом единиц для разложения.
2) Поиск вариантов покрытия выбранного столбца, добавление в покрытие одной
строки, содержащей единицы в этом столбце, в порядке уменьшения числа
единиц в них.
3) Сокращение таблицы покрытий: вычеркивание выбранной строки и покрытых
ею столбцов.
4) Исключение выбранных для предыдущих вариантов разложения строк из
следующих вариантов.
5) Применение алгоритма сокращения таблицы покрытий к остатку таблицы.
6) Выделение ядерных строк и приписывание их к выбранной для данного
варианта строке.
7) Фиксация процесса решения в виде дерева, с записью введенных в решение
строк и соответствующего циклического остатка в каждой вершине.
8) Начальная вершина (корень) дерева содержит циклический остаток и множество
ядерных строк исходной таблицы покрытий.
9) Построение ветвей дерева: из вершины выходит ветвей, где - число единиц в
выбранном для разложения столбце.
10)
Достройка дерева разложением циклического остатка в вершинах, где
разложение еще не проведено.
11)
Нумерация конечных листов дерева, в которых остаток пуст, римскими
цифрами.
Пример: построения дерева решения
1) Ядерных и антиядерных строк нет. Столбец b1 ( )является поглощающим и
поэтому вычеркивается. Циклический остаток представлен следующей
таблицей:
2) Множество ядерных строк пусто (нет ядра покрытия). Все столбцы содержат
по две единицы, поэтому выбираем первый – b2. Ветвление ведется по двум
строкам и.
3) В каждом из этих вариантов таблица сокращается (выделяется
соответствующая ядерная строка, присоединяемая к множеству строк при
соответствующей вершине). Т.к. остатки таблиц покрытий после этого
становятся пустыми, процесс разложения заканчивается.
Первое покрытие – минимальное. Оба покрытия – кратчайшие
2. Приближенное решение задачи о покрытии. Метод минимального столбца
— максимальной строки.
Покрытие, близкое к кратчайшему, дает следующий простой алгоритм
преобразования таблицы покрытий.
Алгоритм метода минимального столбца – максимальной строки:
1) Исходная таблица считается текущей преобразуемой таблицей покрытий, а
множество строк покрытия – пустым.
2) В текущей таблице выделяется столбец с наименьшим числом единиц. Среди
строк, содержащих единицы в этом столбце, выделяется одна с наибольшим
числом единиц. Эта строка включается в покрытие, текущая таблица
сокращается вычеркиванием всех столбцов, в которых выбранная строка имеет
единицы. Если в таблице есть невычеркнутые столбцы, то снова выполняется
п.2, иначе – покрытие построено. Заметим, что при подсчете числа единиц в
строке учитываются единицы в невычеркнутых столбцах.
1) Решение задачи сводится к выбору столбца b2 и строки A2, как имеющей три
единицы, после чего остаются только столбцы b3 и b5.
2) Очевидно, что из всех строк выбирается A1, покрывающая оба оставшихся
столбца. Покрытие – {A1, A2}.
3) Выбираем столбец (две единицы) и строку A1 (четыре единицы). Получаем
следующую таблицу:
4) Выбираем столбец (три единицы) и строку A2 (три единицы). Получаем
следующую таблицу:
5) Таким образом, получено решение {A1, A2, A5}, которое на одну строку
больше кратчайшего покрытия.
3. Метод ветвей и границ в задаче о покрытии.
Метод ветвей и границ в задаче о покрытии включает в себя три основных
преобразования:
1) Разложение исходной задачи на подзадачи;
2) Вычисление оценок качества решения для каждой подзадачи;
3) Оптимизация процесса рассмотрения подзадач путем организации и сокращения
их количества.
Общая идея метода:
1) Исходная задача и ее оценка приписываются корню дерева;
2) Если есть вершины без окончательного решения, выбирается вершина с
минимальной оценкой, и происходит разложение на подзадачи (построение
новых ветвей);
3) Если подзадача упрощается до конкретного результата, вычисляется значение
функции качества, и все вершины с худшими оценками удаляются из дерева;
4) Шаги 2 и 3 повторяются до достижения оптимального решения.
Процедуры разложения и оценки должны быть эффективными и учитывать
особенности конкретного класса задач. В данном случае рассматривается их
применение к задаче покрытия.
Рисунок – Оценка при построении кратчайших покрытий (Обозначается буквой О)
Рисунок – Пример оценки при построении кратчайших покрытий
Рисунок – Пример оценки при построении кратчайших покрытий
Рисунок – Оценка при построении минимальных покрытий
Рисунок – Пример оценки при построении минимальных покрытий
Рисунок – Пример оценки при построении минимальных покрытий
Рисунок – Пример процесса решения при использовании оценки ОБМ
4. Отношение совместимости и совместимые подмножества. Метод
граничного перебора построения максимальных совместимых
подмножеств.
Рисунок – Задача о совместимых подмножествах
Алгоритм граничного перебора построения максимальных совместимых
подмножеств
1) Текущее подмножество
2) Находим наибольший номер такой, что
. Рассматриваем следующие
ситуации:
a. Если
то выполняем п.4
b. Если
то выполняем п.3
c. Если
то удаляем элемент
и если
, то
выполняем п.2, если
то выполняем п.7.
3) Удаляем элемент из
4)
и если
то выполняем п.5, иначе проверяем совместимость
элемента
элемента
со всеми элементами множества Если хотя бы для одного
то выполняем п.4, иначе, если для всех
, то вводим элемент
, выполняем п.4.
5) Если
, то выполняем п.6, иначе проверяем на поглощение множество
множествами
.
6)
выполняется п.2. Если да, то выполняем п.2, иначе п.6
с
7) Построение всех максимальных совместимых подмножеств
закончено.
Наиболее наглядно алгоритм граничного перебора выполняется в векторном
представлении подмножеств Y:
Рисунок – Пример граничного перебора
Таким образом, построены четыре максимальных совместимых подмножества:
5. Комбинаторика. Основные виды наборов.
Комбинаторика - это раздел дискретной математики, который изучает методы
подсчета различных конечных множеств. Основные виды наборов в комбинаторике:
1) Перестановки (Permutations): Это упорядоченные наборы, в которых порядок
элементов имеет значение. Количество перестановок из n элементов вычисляется
по формуле: P(n) = n!.
2) Размещения (Arrangements): Это упорядоченные наборы, в которых порядок
элементов важен, но количество элементов в наборе меньше, чем общее
количество элементов. Количество размещений из n элементов по k элементов
вычисляется по формуле: A(n,k) = n! / (n-k)!.
3) Сочетания (Combinations): Это неупорядоченные наборы, в которых порядок
элементов не имеет значения. Количество сочетаний из n элементов по k
элементов вычисляется по формуле: C(n,k) = n! / (k! * (n-k)!).
4) Размещения с повторениями: Это упорядоченные наборы, в которых элементы
могут повторяться. Количество размещений с повторениями из n элементов по k
элементов вычисляется по формуле: A(n+k-1,k) = (n+k-1)! / (k! * (n-1)!).
5) Сочетания с повторениями: Это неупорядоченные наборы, в которых элементы
могут повторяться. Количество сочетаний с повторениями из n элементов по k
элементов вычисляется по формуле: C(n+k-1,k) = (n+k-1)! / (k! * (n-1)!).
6. Компоненты связности. Определение связности графа. Построение
компонент связности в ориентированном графе.
Таблица – Определения
№
Определение
1 Графом G (V, E) называется совокупность двух множеств – непустого
множества V (множества вершин) и множества Е его двухэлементных
подмножеств множества V (Е – множество ребер).
2 Если ребрам графа приданы направления от одной вершины к другой, то такой
граф называется ориентированным.
3 Ребра ориентированного графа называются дугами.
4 Соответствующие вершины ориентированного графа называют началом и
концом.
5 Если направления ребер не указываются, то граф называется
неориентированным (или просто графом).
6 Неориентированный граф называется связным, если каждая пара различных
вершин может быть соединена, по крайней мере, одной цепью.
7 Ориентированный граф называется сильно связным, если для любых двух его
вершин xi и xj существует хотя бы один путь, соединяющий xi с xj .
8 Ориентированный граф называется односторонне (слабо) связным, если для
любых двух его вершин, по крайней мере, одна достижима из другой.
9 Компонентой связности неориентированного графа называется его связный
подграф, не являющийся собственным подграфом никакого другого связного
подграфа данного графа (максимально связный подграф).
10 Компонентой сильной связности ориентированного графа называется его
сильно связный подграф, не являющийся собственным подграфом никакого
другого сильно связного подграфа данного графа (максимально сильно
связный подграф).
11 Компонентой односторонней (слабой) связности неориентированного
графа называется его односторонне связный подграф, не являющийся
собственным подграфом никакого другого односторонне связного подграфа
данного графа (максимально односторонне (слабо) связный подграф).
Рисунок – Пример графа
Рисунок – Пример ориентированного графа
Рисунок – Пример неориентированного графа
Алгоритм построения компонент связности в ориентированном графе включает в
себя два основных шага:
1) Преобразование исходного ориентированного графа в неориентированный граф
без изменения сильной связности вершин. Это достигается заменой всех
встречных дуг (дуги, направленные в противоположные стороны между двумя
вершинами) на ребра.
2) Применение алгоритма поиска компонент связности для неориентированного
графа (описанного в пункте 5.3.2).
Процедура преобразования ориентированного графа в неориентированный
осуществляется следующим образом:
1) Заменить все встречные дуги на ребра.
2) Если в графе больше нет дуг, процедура завершена. В противном случае,
выбрать произвольную оставшуюся дуга (xi, xj).
3) Проверить наличие пути от xj к xi. Если такой путь существует, заменить дугу
(xi, xj) и все дуги пути (xj, xi) на ребра. Если пути нет, удалить дугу (xi, xj) из
графа, так как она не влияет на сильную связность.
4) Повторять шаги 2 и 3, пока все дуги не будут обработаны.
В результате этих преобразований получается неориентированный граф,
сохраняющий сильную связность исходного ориентированного графа, для которого
можно найти компоненты связности с помощью алгоритма, описанного в пункте 5.3.2.
Рисунок – Исходный граф
Рисунок - Преобразованный неориентированный граф
7. Остов, система фундаментальных циклов, система независимых циклов,
построение произвольного остова.
Таблица – определения касательно циклов
Термин
Определение
Цикл называется линейно зависимым от других циклов, если его
Линейная
можно получить комбинацией этих циклов с учетом удаления
зависимость циклов
пройденных ребер туда и обратно.
Линейная
Результатом векторной операции сложения по модулю два для
комбинация
двоичных векторов, соответствующих циклам.
Система
Максимальная линейно независимая совокупность циклов в
независимых циклов графе.
Число циклов в системе независимых циклов для графа.
Цикломатическое
Определяется формулой: ϒ = m - n + p, где m - число ребер, n число (ϒ)
число вершин, p - число компонент связности.
Цикломатическое число графа:
Указывает на наименьшее число ребер, которые нужно удалить, чтобы граф стал
ациклическим;
Всегда неотрицательно.
Таблица – теоремы касательно циклов
Теорема
Содержание
Мощность ϒ системы независимых циклов в графе
Мощность системы
определяется формулой Эйлера: ϒ = m - n + p, где m – число
независимых циклов
ребер; n – число вершин; p – число компонент связности.
Края конечных граней планарного графа образуют систему
Планарные графы
независимых циклов.
Рисунок – пример подсчета цикломатического числа
Рисунок – пример подсчета цикломатического числа
Термин
Определение
Связный граф без циклов; эквивалентно, связный граф с
Неориентированное дерево
n вершинами и n-1 ребрами; граф, где любые две
(или просто дерево)
вершины соединены простой цепью.
Термин
Лес
Листья
Корень дерева
Теорема о числе деревьев
Остовное дерево (Остов)
Определение
Несвязный граф без циклов, каждая связная компонента
которого является деревом.
Вершины дерева, инцидентные только одному ребру.
Выбранная вершина дерева, которая может быть
родительской для других вершин.
Существует различных деревьев на n вершинах.
Частичный граф связного графа G, содержащий все
вершины G и являющийся деревом.
Рисунок – Примеры остовов для графа G
Алгоритм построения произвольного остова:
1) Для каждой компоненты i графа выполняются п.2 и п.3
2) Строим частичный граф, содержащий все вершин компоненты и не содержащий
ребер (нулевой граф).
3) Если в текущий частичный граф включены уже ребер, то остов для компоненты i
построен, иначе выбираем очередное не рассмотренное ребро компоненты и
пытаемся его включить в текущий граф. Если это не приводит к образованию
цикла, то ребро включаем, иначе – нет. Выполняем п.3.
8. Остов, система фундаментальных циклов, система независимых циклов,
построение минимального остова нагруженного графа.
Алгоритм построения минимального остовного дерева для нагруженного графа
(Алгоритм Краскала)
1) Установка начальных значений. Вводится матрица длин ребер C графа G.
2) Выбрать в графе G ребро минимальной длины. Построить граф G2, состоящий
из данного ребра и инцидентных ему вершин. Положить i = 2.
3) Если i = n, где n – число ребер графа, то закончить работу (задача решена), в
противном случае перейти к п. 4.
4) Построить граф Gi + 1, добавляя к графу Gi новое ребро минимальной длины,
выбранное среди всех ребер графа G, каждое из которых инцидентно какойнибудь вершине графа Gi и одновременно инцидентно какой-нибудь вершине
графа G, не содержащейся в Gi. Вместе с этим ребром включаем в Gi + 1 и
инцидентную ему вершину, не содержащуюся в Gi. Присваиваем i: = i + 1 и
переходим к п. 3.
Пример. Найдем минимальное остовное дерево для графа:
Рисунок – граф для разбора примера
1) Шаг 1. Установка начальных значений. Введем матрицу длин ребер C:
2) Шаг 2. Выберем ребро минимальной длины. Минимальная длина ребра равна
единице. Таких ребер три: (x1, x2), (x1, x4), (x2, x4).
В этом случае можно взять любое. Возьмем (x1, x2).
Построим граф G2, состоящий из данного ребра и инцидентных ему вершин x1 и
x2. Положим i = 2.
3) Шаг 3. Так как n = 5, то i ≠ n, поэтому переходим к шагу 4.
4) Шаг 4. Строим граф G3, добавляя к графу G2 новое ребро минимальной длины,
выбранное среди всех ребер графа G, каждое из которых инцидентно одной из
вершин x1, x2 и одновременно инцидентно какой–нибудь вершине графа G, не
содержащейся в G2, т.е. одной из вершин x3, x4, x5. Таким образом, нужно
выбрать ребро минимальной длины из ребер (x1, x4), (x1, x5), (x2, x3), (x2, x4),
(x2, x5). Таких ребер длины единица два: (x1, x4) и (x2, x4).
Можно выбрать любое. Возьмем (x1, x4). Вместе с этим ребром включаем в G3
вершину x4, не содержащуюся в G2. Полагаем i = 3 и переходим к шагу 3.
5) Шаг 3. Так как i ≠ n, поэтому переходим к шагу 4.
6) Шаг 4. Строим граф G4, добавляя к графу G3 новое ребро минимальной длины
из ребер (x1, x5), (x2, x3), (x2, x5), (x4, x5). Такое ребро длины два одно: (x2, x3).
Вместе с этим ребром включаем в G4 вершину x3, не содержащуюся в G3.
Полагаем i = 4 и переходим к шагу 3.
7) Шаг 3. Так как i ≠ n, поэтому переходим к шагу 4.
8) Шаг 4. Строим граф G5, добавляя к графу G3 новое ребро минимальной длины
из ребер (x1, x5), (x2, x5), (x4, x5). Таких ребер длины три два: (x2, x5) и (x4, x5).
Возьмем (x2, x5). Вместе с этим ребром включаем в G5 вершину x5, не
содержащуюся в G4. Полагаем i = 5 и переходим к шагу 3.
9) Шаг 3. Так как i = n, то граф G5 – искомое минимальное остовное дерево.
Суммарная длина ребер равна 1 + 1 + 2 + 3 = 7.
Процесс построения минимального остовного дерева изображен на рисунке:
Рисунок – Процесс построения минимального остовного дерева
9. Кратчайшая раскраска графа — основные определения. Внутренне и
внешне устойчивые множества вершин графа.
Термин
Раскраска графа
Правильная
раскраска
Хроматическое
число (G)
Внутренне
устойчивое
множество
Внешне
устойчивое
множество
Определение
Задание цветов вершинам графа G так, что смежные вершины
имеют различные цвета.
Раскраска, где образы любых двух смежных вершин различны.
Минимальное число цветов, необходимое для раскраски графа G.
Подмножество
то есть:
вершин графа G(X), где вершины не смежны,
Подмножество
вершин графа G(Х), где каждая вершина xi
удовлетворяет хотя бы одному из условий:
Рисунок – пример раскраски графа
Теорема. Для плоских (планарных) графов хроматическое число ≤ 4.
Рисунок – пример касательно внутренне устойчивых множеств
Рисунок – пример касательно внешне устойчивых множеств
Алгоритм построения минимальных внешне устойчивых множеств вершин графа:
1) Матрица отношения графа транспонируется (получается отношение ).
Диагональные элементы приравниваются к единице (сама вершина себя
защищает).
2) Решается задача построения покрытий строками матрицы преобразованного
отношения всех ее столбцов.
Пример:
Матрица G:
Матрица G-1с единицами в диагональных элементах:
Решаем задачу нахождения хотя бы одного кратчайшего покрытия:
Разложение по столбцу х1:
Таким образом построены три кратчайших покрытия, которые служат внешне
устойчивыми множествами вершин заданного графа. Для поиска всех минимальных
внешне устойчивых множеств необходимо решать задачу построения всех
безызбыточных покрытий.
10.Реализация булевых функций формулами. Основные свойства
элементарных булевых функций.
11.Совершенные дизъюнктивные и конъюнктивные нормальные формы
(СДНФ, СКНФ).
12.Геометрическая форма представления и графический способ минимизации
булевых функций
13.Матричные формы представления и метод карт Карно минимизации
булевых функций в классе ДНФ и КНФ.
14.Интервальные формы представления булевых функций. Основные
определения.
15.Минимизация булевых функций методом Квайна-Мак-Класки в классе
ДНФ и КНФ.
16.Типовые задачи по дискретной математике
Теория вероятностей и математическая статистика
1. Понятие случая. Классическая формула для вычисления вероятности
случайного события. Статистическая вероятность случайного события.
Случай - это любое явление или событие, которое может произойти или не произойти
в результате некоторого эксперимента или испытания.
Вероятностью события А называется отношение числа М элементарных исходов,
благоприятствующих наступлению данного события, к числу всех элементарных
исходов испытания:
Статистическая вероятность события A - это предел отношения частоты
наступления события A к общему числу испытаний, когда число испытаний стремится
к бесконечности:
P(A) = lim(n->∞) f(A)
2. Интерпретация основных понятий теории вероятностей на основе теории
множеств. Алгебра событий. Аксиомы теории вероятностей.
1) Пространство элементарных исходов Ω:
Пространство Ω рассматривается как универсальное множество, состоящее из
всех возможных элементарных исходов эксперимента.
2) Случайное событие A:
Случайное событие A представляется как подмножество пространства Ω, т.е. A
⊆ Ω.
Элементарные исходы, входящие в A, являются реализациями события A.
3) Объединение событий A ∪ B:
Объединение событий A и B соответствует множественному объединению
подмножеств A и B в пространстве Ω.
A ∪ B = {x | x ∈ A или x ∈ B}
4) Пересечение событий A ∩ B:
Пересечение событий A и B соответствует множественному пересечению
подмножеств A и B в пространстве Ω.
A ∩ B = {x | x ∈ A и x ∈ B}
5) Дополнение события A:
Дополнение события A соответствует дополнению подмножества A в
универсальном множестве Ω.
A' = {x | x ∈ Ω, x ∉ A}
Алгебра событий - это множество всех возможных событий, которые могут произойти
в некотором эксперименте или испытании.
Рисунок – аксиомы теории вероятностей
3. Формула полной вероятности. Формула Байеса.
Рисунок – формула полной вероятности. Формула Байеса
4. Закон распределения случайной величины. Статистический ряд.
Рисунок – понятие случайной величины
Рисунок – закон распределения случайной величины
Рисунок – статистический ряд
5. Определение функции распределения случайной величины. Свойства
функции распределения.
Рисунок – определение функции распределения случайной величины
Рисунок – свойства функции распределения случайной величины
6. Плотность распределения. Свойства плотности распределения.
Рисунок – определение плотности распределения
Рисунок – свойства плотности распределения
Рисунок – свойства плотности распределения
7. Числовые характеристики дискретных и непрерывных случайных
величин.
Случайная величина называется дискретной (прерывной), если множество
значений конечное, или бесконечное, но счетное.
Под непрерывной случайной величиной будем понимать величину, бесконечное
несчетное множество значений которой есть некоторый интервал (конечный или
бесконечный) числовой оси.
Таблица - Характеристики для дискретных случайных величин
Номер
Характеристика
1
2
3
Таблица – характеристики для непрерывной случайной величины
Номер
Характеристика
1
2
3
8. Биномиальное распределение.
Рисунок – биномиальное распределение
9. Равномерное распределение непрерывной случайной величины.
Рисунок – равномерное распределение
10.Показательное распределение непрерывной случайной величины.
Рисунок – показательное распределение
11.Нормальное распределение. Стандартное нормальное распределение.
Рисунок – нормальное и стандартное нормальное распределения
12.Геометрическое распределение. Понятие простейшего потока. Свойства
простейшего потока. Связь простейшего потока с распределением Пуассона.
Рисунок – геометрическое распределение
Рисунок – понятие и свойства простейшего потока.
13.Статистические оценки. Точечные оценки параметров распределения.
Свойства оценок.
Рисунок – статистические оценки
14.Критерии проверки статистических гипотез. Критерий согласия Пирсона.
Статистической гипотезой (гипотезой) называется любое утверждение об изучаемом
законе распределения или характеристиках случайных величин.
Статистический критерий — это математическое правило, в соответствии с которым
принимается или отвергается та или иная статистическая гипотеза с заданным
уровнем значимости.
Рисунок – критерий согласия Пирсона
Моделирование вычислительных процессов и систем
1. Определение понятия модель.
Модель – это упрощенная система, отражающая отдельные характеристики
исследуемого объекта (процесса). Выбор характеристик определяется целью
исследования. Моделирование – это изучение свойств исследуемого объекта (процесса)
путем анализа соответствующих характеристик его модели
2. Аналитическое и имитационное моделирование.
Рисунок – Виды моделирования
3. Характеристики обслуживания заявок в системах массового обслуживания
(СМО).
Системой массового обслуживания (СМО) называется любая система,
предназначенная для обслуживания какого-либо потока заявок.
Характеристики обслуживания заявок в системах массового обслуживания (СМО)
включают в себя:
1) Интенсивность потока заявок (λ) - среднее количество заявок, поступающих
в систему за единицу времени. Чем выше интенсивность, тем больше нагрузка
на СМО.
2) Интенсивность обслуживания (μ) - среднее количество заявок, которые
система может обслужить за единицу времени. Чем выше интенсивность
обслуживания, тем быстрее СМО справляется с поступающими заявками.
3) Коэффициент загрузки (ρ) - отношение интенсивности потока заявок к
интенсивности их обслуживания. Это характеризует загруженность СМО, при
ρ > 1 система не справляется с нагрузкой.
4) Среднее число заявок в системе (L) - среднее количество заявок,
находящихся в СМО (как в очереди, так и в процессе обслуживания).
5) Среднее время ожидания в очереди (Wq) - среднее время, которое заявка
проводит в очереди на обслуживание.
6) Среднее время пребывания заявки в системе (Ws) - среднее время, которое
заявка проводит в СМО (включая время ожидания и время обслуживания).
7) Вероятность отказа (P0) - вероятность того, что поступившая заявка не будет
принята на обслуживание из-за отсутствия свободных каналов.
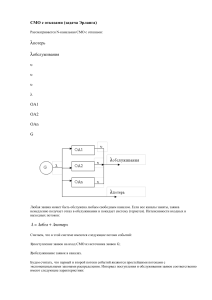
4. Стационарный режим. Формулы Литтла. Нотация СМО.
Свойство стационарности выражает неизменность вероятностного режима потока
по времени. Это значит, что число требований, поступающих в систему в равные
промежутки времени, в среднем, должно быть постоянным
Рисунок – Формулы Литтла
Таблица - Символика (нотация) Д.Кендалла
Обозначение
Описание
m
число обслуживающих каналов
n
количество мест ожидания (емкость накопителя)
k
кол-во источников
AиB
характеризуют соответственно входной поток и поток
обслуживания, задавая функцию распределения интервалов
между заявками во входном потоке и функцию распределения
времен обслуживания.
А и В могут принимать значения:
D
детерминированное распределение
М
показательное
Еr
распределение Эрланга;
Hr
гиперпоказательное;
G
распределение общего вида.
5. СМО с неограниченной очередью. Уравнения для вероятностей состояний.
Основные характеристики для многоканальных и одноканальных СМО.
Одноканальная система с неограниченной очередью:
Имеется одноканальная СМО с очередью, на которую не наложены никакие
ограничения (ни по длине очереди, ни по времени ожидания). Поток заявок,
поступающих в СМО, имеет интенсивность , а поток обслуживании —
интенсивность . Необходимо найти предельные вероятности состояний и показатели
эффективности СМО.
Система может находиться в одном из состояний
, по числу
заявок, находящихся в СМО:
— канал свободен;
— канал занят (обслуживает
заявку), очереди нет;
— канал занят, одна заявка стоит в очереди;
— канал
занят,
заявок стоят в очереди и т.д.
Рисунок – граф состояний СМО
Таблица – характеристики одноканальной СМО с неограниченной очередью
Характеристики
Формулы
Предельные вероятности
Среднее число заявок в
системе
Среднее число заявок в
очереди
Среднее время пребывания
заявки в системе
Среднее время пребывания
заявки в очереди
Многоканальная СМО с неограниченной очередью:
Система может находиться в одном из состояний S0, S1, S2, …? Sk, …, Sn, …,
нумеруемых по числу заявок, находящихся в СМО: S0 — в системе нет заявок (все
каналы свободны); S1 — занят один канал, остальные свободны; S2 — заняты два
канала, остальные свободны; …Sk — занято каналов, остальные свободны; …Sn —
заняты все n каналов (очереди нет); Sn+1 — заняты все n каналов, в очереди одна
заявка; …Sn+r — заняты все n каналов, r заявок стоит в очереди, и т.д.
В отличие от предыдущей СМО, интенсивность потока обслуживании
(переводящего систему из одного состояния в другое справа налево) не остается
постоянной, а по мере увеличения числа заявок в СМО от 0 до увеличивается от
величины до
, так как соответственно увеличивается число каналов
обслуживания. При числе заявок в СМО большем, чем , интенсивность потока
обслуживании сохраняется равной
.
Рисунок – граф состояний СМО
Таблица – характеристики многоканальной СМО с неограниченной очередью
Характеристики
Формулы
Предельные вероятности
Вероятность того, что
заявка окажется в очереди
Среднее число занятых
каналов
Среднее число заявок в
системе
Среднее число заявок в
очереди
Среднее время пребывания
заявки в системе
Среднее время пребывания
заявки в очереди
6. СМО типа G/M/1. Формула Поллячека - Хинчина.
Рисунок – характеристики СМО M/G/1
Рисунок – характеристики СМО M/G/1
Рисунок – характеристики СМО M/G/1
Рисунок – формула Поллячека-Хинчина
7. Характеристики СМО при многомерном входящем потоке. СМО с
относительными приоритетами.
Особенностью СМО с многомерным входящим потоком является то, что
входящий поток заявок образуется с помощью суперпозиции n входящих потоков. Для
каждого потока определены свои интенсивности поступления и времена
обслуживания , а также их вторые начальные моменты
i=1, …, n. Все заявки
поступают в общий накопитель и выбираются из него на обслуживание в порядке
«первый пришел - первый обслужен».
Условие существования стационарного режима – суммарная загрузка СМО
всеми потоками должна быть меньше единицы:
R<1, где R=r1+…+rn и ri=liJi, i=1, …, n.
Основная цель введения приоритетов в системах массового обслуживания это уменьшение времени ожидания заявок одних типов за счет увеличения этого
времени у других.
Приоритет - это преимущество в очереди на обслуживание в канале. Формально
для n-мерного входящего потока приоритет определяется номером i типа заявки: чем
меньше i, тем больше (старше) приоритет.
Для организации обслуживания в СМО с n приоритетами создаются n
накопителей, в которых могут находиться очереди О1, …, Оk, …,On заявок
соответствующих приоритетов. Правило приоритетного обслуживания таково: заявка
из очереди Оk+1 не обслуживается до тех пор, пока есть хотя бы одна заявка в очереди
Оk, k=1,2,…,k-1. В пределах очереди Оk заявки выбираются на обслуживание в
порядке «первый пришел - первый обслужен». Приоритет
называется относительным, если никакая заявка не может прервать обслуживание
любой другой заявки.
Таблица – Характеристики СМО
СМО с многомерным входящим потоком
1) R – среднее число занятых каналов
2) wk - среднее время пребывания заявки k-того
потока (приоритета) в очереди
3) L - среднее число заявок в очереди
СМО с относительными
приоритетами
4) n – среднее число заявок в системе
5) u – среднее время пребывания заявки в системе
8. Характеристики СМО с абсолютными приоритетами. Смешанные
приоритеты. Закон сохранения времени ожидания для СМО без потерь.
СМО с абсолютными и смешанными приоритетами - это системы, в которых
возможно преимущество (приоритет) в обслуживании заявки, причем процесс
обслуживания ранее пришедшей заявки более низкого приоритета прерывается для
абсолютного приоритета, либо используется смешанная дисциплина обслуживания.
Заявка, обслуживание которой прервано, ставится в начало своей очереди и ждёт
момента, когда сложатся условия для её обслуживания. При наличии таковых канал
либо продолжает обслуживать заявку с места, на котором произошло прерывание
(СМО с дообслуживанием), либо начинает её обслуживание с самого начала (СМО с
возобновлением обслуживания).
Для СМО M/G/1 в стационарном режиме действует закон сохранения времени
ожидания: при любой системе приоритетов имеет место равенство:
где
.
Рисунок – Для СМО со абсолютными приоритетами
Рисунок – Для СМО со смешанными приоритетами
9. Стохастические сети массового обслуживания и их параметры.
Экспоненциальные сети. Характеристики разомкнутых стохастических
сетей.
Совокупность взаимосвязанных СМО называется сетью массовогообслуживания
(стохастической сетью).
Параметры стохастических сетей
1. Число систем массового обслуживания n
2. Число каналов обслуживания в каждой СМО ki , i = 1..n
3. Матрица вероятностей (вероятностей перехода из одной системы обслуживания
в другую) передач.
Pij – вероятность того, что после обслуживания в СМО Si заявка
перейдет в СМО Sj.
Pij + Pik = 1
P = ||Pij|| - стохастическая матрица, по строкам сумма элементов
равна 1.
Матрица квадратная.
S0 – бесконечный
источник заявок (в нем
всегда есть заявки)
4. Число заявок, циркулирующих в сети (для замкнутой сети) m
Или интенсивность источника (для разомкнутой сети) 0
5. Среднее время обслуживания заявок в СМО сети 1, 2, …, n
Характеристики разомкнутых стохастических сетей.
Условие стационарности для разомкнутой сети:
Состояния сети и вероятности состояний
Состояние сети связывается с числом заявок в отдельных СМО.
Т.е. можно сказать, что сеть характеризуется состояниями M(M1,M2,…,Mn):
Вероятность P(M1,M2,…,Mn) т.е. вероятность, что в СМО
вычисляется по формуле Джексона:
,
где
Таблица - Характеристики систем в сети
Характеристика
Среднее число заявок в очереди в СМО
Sj
Среднее число заявок в очереди в СМО
(очередь + обслуживание)
Среднее время ожидания в очереди. По
формуле Литтла:
Среднее время пребывания в СМО. По
формуле Литтла:
Формула
Таблица – Характеристики сети
Характеристика
В очередях
Среднее число заявок
Среднее время
В сети
Основы системного анализа
1. Определение системы.
Система есть упорядоченная совокупность взаимосвязанных и
взаимодействующих элементов, закономерно образующих единое целое.
2. Принципы системного анализа.
Принципы системного анализа – это обобщенный опыт работы со сложными
системами, который можно использовать как руководство при анализе и
проектировании систем. Эти принципы включают в себя:
Таблица – Принципы системного анализа
Принцип
Описание
конечной цели
приоритет глобальной цели, формулировка цели исследования,
анализ с учетом основной функции системы.
измерения
оценка эффективности системы относительно целей более
общей системы, частью которой она является.
эквифинальности
достижение требуемого состояния системы различными
путями и при разных начальных условиях.
единства
рассмотрение системы как целого и как совокупности частей.
связности
выявление внутренних и внешних связей системы,
рассмотрение системы как части более крупной системы.
модульного
исследование системы через входные и выходные воздействия,
построения
абстрагирование от излишних деталей.
иерархии
разделение системы на части и их ранжирование для
упрощения разработки.
функциональности приоритет функций над структурой, пересмотр структуры при
добавлении новых функций.
развития(адаптации) учет изменяемости и способности системы к развитию,
наращиванию и замене частей.
историчности
необходимость изменений и взаимодействия с внешней средой
(открытости)
для функционирования системы во времени и пространстве.
децентрализации
сочетание
централизованного
и
децентрализованного
управления с минимальной степенью централизации для
достижения цели.
неопределенности
учет неопределенностей и случайностей в структуре,
функционировании или внешних воздействиях на систему.
3. Классификация систем.
Таблица – Виды классификации систем
Признак
Наименование
классификации
систем
систем
Содержание систем
Изолированные
системы
(искусственные)
Степень
взаимодействия
системы с внешней
средой
Закрытые системы
Открытые системы
Малые системы
Средние системы
Размер системы
Большие сложные
системы
Виды систем
Степень свободы
системы по
отношению к
внешней среде
Космические
системы
Биологические
системы
Технические
системы
Системы, не имеющие с внешней
средой прямой и обратной связи (без
входа и выхода) (например
биологическая система (животное),
испытуемая в полностью закрытой
емкости, - дельфин)
Системы, имеющие с внешней средой
одностороннюю связь (вход или выход)
(например, часы)
Системы, имеющие с внешней средой
прямую и обратную связи (вход и
выход) (например, страна, фирма,
человек или машина)
Системы с числом единичных
компонентов менее 30 (например,
фирма с численностью сотрудников 25
человек или авторучка)
Системы с числом единичных
компонентов от 31 до 300 (например,
фирма с численностью сотрудников 250
человек или пылесос)
Системы с числом единичных
компонентов свыше 301 (например,
корпорация с численностью
сотрудников 15 000 человек,
автомобиль или человек)
Солнечная система
Живые организмы
Изделия, состоящие из сборочных
единиц и деталей, выполняющие
заданые функции
СоциальноКомплексные структуры, состоящие из
экономические
экономических, производственносистемы (в том числе технических и социальных структур,
производственные)
выполняющие различные (например,
город или организация).
Относительно
Системы, функционирующие
самостоятельные,
самостоятельно и выполняющие
юридически и
заданные функции
физически
независимые
системы
Несамостоятельные Системы (подсистемы), входящие в
системы
глобальную систему жестко как
(подсистемы)
неотъемлемый компонент (например,
сотрудник отдела или двигатель
автомобиля)
Комплексные
Системы, выполняющие весь комплекс
системы
функций или работ по стадиям
жизненного цикла объекта (например,
комплексное производственное
объединение, выполняющее все работы
по стадиям жизненного цикла
Уровень
выпускаемых товаров (кроме идущих
специализации
на собственное потребление)
системы
Специализированные Системы, специализирующиеся на
системы
выполнении одной функции или
работы на одной стадии жизненного
цикла объекта (например, банк,
маркетинговая организация или
сборочное предприятие)
Системы
Системы, функционирующие короткий
кратковременного
промежуток времени, или разового
действия (жизни)
применения (например, биологическая
система – мотылек или техническая –
шприц)
Продолжительность Дискретные системы Системы, функционирующие
функционирования
определенный промежуток (интервал)
системы
времени (например, автомобиль или
человек)
Долговременные
Системы, длительность
системы
функционирования которых
практически не ограничена (например,
Солнечная система)
Детерминированные Системы, поведение которых точно
(функциональные)
описывается однозначной функцией
Стохастические
Системы, поведение которых
Способ описания
(вероятностные)
описывается в терминах распределения
системы
случайных величин или вероятностей
Нечеткие
Системы, поведение которых
(описательные)
описывается качественно, а не
количественно
Физические
Системы, имеющие вещественную
Тип величин,
субстанцию
используемых в
Абстрактные
Системы, имеющие логическую,
субстанции
математическую и другие виды
системы
невещественной субстанции
4. Свойства сложных систем.
Таблица – свойства сложных систем
Свойство
№
Описание
сложных систем
Сложная система рассматривается как целостная совокупность
Целостность и
1
взаимосвязанных и взаимодействующих элементов, при этом
членимость
возможна декомпозиция на подсистемы с подчиненными целями
Наличие устойчивых связей между элементами, превосходящих
2 Связи
по силе связи с внешней средой; "связи" означают обмен
веществом, энергией или информацией
Наличие определенной структуры и упорядоченности связей и
элементов во времени и пространстве; сложность функций,
3 Организация
управление, информационные сети, взаимодействие с внешней
средой
Наличие свойств у системы в целом, отсутствующих у
Интегративные
4
отдельных элементов; свойства системы зависят, но не
качества
определяются полностью свойствами элементов
5. Методы системного анализа. Анализ и синтез.
Таблица - состав задач системного анализа
Задача
№ системного
Описание
анализа
Представление системы в виде подсистем, состоящих из более
1 Декомпозиция
мелких элементов; рассматривается как часть анализа
Нахождение свойств системы или окружающей среды; целью
2 Анализ
может быть определение закона преобразования информации,
описывающего поведение системы
Построение системы, реализующей заданный закон
3 Синтез
преобразования, в соответствии с определенным алгоритмом и
классом элементов
Таблица – этапы анализа, обеспечивающего детальное представление системы
№ Этап анализа
Описание задач
1
Уточнение состава и законов
Функционально-структурный
функционирования элементов, алгоритмов и
анализ
взаимовлияния подсистем
2 Разделение управляемых и
неуправляемых характеристик
3 Задание пространства состояний и
параметрического пространства
4 Анализ целостности системы
5 Формулирование требований к
создаваемой системе
6 Морфологический анализ
Анализ взаимосвязи компонентов
№ Этап анализа
7
Генетический анализ
8
Анализ аналогов
9
Анализ эффективности
10
Формирование требований
Описание задач
Анализ предыстории и причин развития
ситуации, построение прогнозов
Выявление и изучение аналогичных систем или
решений
Выбор шкалы измерения, формирование
показателей и критериев эффективности,
оценка результатов
Определение критериев оценки и ограничений
для создаваемой системы
Таблица – этапы синтеза
№ Этап синтеза
Описание задач
1 Разработка модели
Выбор математического аппарата, моделирование, оценка
системы
адекватности и соответствия модели
2 Синтез
Поиск и предложение различных структур системы для
альтернативных
решения проблемы
структур
3
Определение параметров системы для достижения
Синтез параметров
требуемых результатов
4
Обоснование схемы оценивания, проведение
Оценивание вариантов экспериментов, обработка и анализ результатов, выбор
оптимального варианта
6. Технологии и инструменты системной аналитики.
Системное программирование
1. Линейные структуры данных: массив, список, очередь, стек, дек.
Линейные структуры данных - это набор основных абстрактных типов данных,
которые используются для хранения и управления последовательностью элементов.
Основные линейные структуры данных включают:
Массив (Array): Упорядоченная коллекция элементов одного типа, хранящихся в
непрерывной области памяти. Массивы имеют фиксированный размер и
предоставляют быстрый случайный доступ к элементам.
Список (List): Упорядоченная коллекция элементов, в которой каждый элемент
содержит ссылку на следующий элемент. Списки имеют динамический размер и
эффективны для вставки/удаления элементов в начале или середине списка.
Очередь (Queue): Линейная структура данных, в которой элементы добавляются
в конец очереди (enqueue) и извлекаются из начала очереди (dequeue). Очереди
используются для организации процессов, ожидающих обслуживания,
например, в операционных системах.
Стек (Stack): Линейная структура данных, в которой элементы добавляются и
извлекаются в соответствии с принципом LIFO (Last In, First Out). Стеки
используются для отслеживания вызовов функций, обработки выражений и
реализации откатов.
Дек (Deque): Линейная структура данных, которая позволяет добавлять и удалять
элементы как с начала, так и с конца. Деки могут использоваться как очереди
или стеки, в зависимости от требуемой операции.
2. Таблицы. Неупорядоченная, двоичная упорядоченная и хеш-таблицы.
Таблицы - это линейные структуры данных, которые используются для
эффективного хранения и поиска элементов. Существует несколько основных типов
таблиц:
1. Неупорядоченная таблица - это простейший тип таблицы, в которой элементы
хранятся в произвольном порядке. Поиск элементов в неупорядоченной таблице
имеет линейную сложность O(n), поскольку требуется последовательно
просматривать все элементы, чтобы найти искомый.
2. Двоичная упорядоченная таблица - В этом типе таблицы элементы хранятся в
упорядоченном виде, обычно с использованием двоичного дерева поиска. Это
позволяет выполнять поиск, вставку и удаление элементов с логарифмической
сложностью O(log n). Двоичные упорядоченные таблицы обеспечивают
эффективный доступ к элементам в отсортированном порядке.
3. Хеш-таблица - использует хеш-функцию для отображения ключей элементов в
индексы массива, в котором и хранятся элементы. Хорошая хеш-функция
позволяет обеспечить практически константную сложность O(1) для
большинства операций, таких как поиск, вставка и удаление. Хеш-таблицы
эффективно используются для реализации ассоциативных массивов, словарей и
кэширования.
3. Деревья. Двоичные, сбалансированные и Б- деревья.
Деревья являются иерархическими структурами данных, состоящими из узлов,
связанных родительско-дочерними отношениями.
Основные типы деревьев:
1) Двоичные деревья (Binary Trees): Деревья, в которых каждый узел имеет не
более двух дочерних узлов (левый и правый). Двоичные деревья могут быть
реализованы с использованием массивов или связанных списков и используются
для хранения и поиска данных.
2) Сбалансированные деревья (Balanced Trees): Это разновидность двоичных
деревьев, в которых высота левого и правого поддеревьев каждого узла
отличается не более чем на 1. Примерами сбалансированных деревьев являются
AVL-деревья и красно-черные деревья. Они обеспечивают логарифмическую
сложность O(log n) для большинства операций.
3) Б-деревья (B-Trees): Б-деревья - это многоуровневые сбалансированные деревья,
в которых каждый узел может содержать несколько ключей. Они
оптимизированы для работы с большими данными, хранящимися на внешних
устройствах (например, жестких дисках). Б-деревья обеспечивают эффективный
поиск, вставку и удаление элементов, сохраняя сбалансированность дерева.
4. Классификация систем программирования.
Система
программирования
1. Операционная
система
Назначение и
состав
Используемые
языки
Языки
разработки
Предназначена для
обеспечения
работоспособности
компьютера,
выполнения
Языки управления
программ,
заданиями
организации
обмена данными и
управления
памятью.
Assembler, C
(для
визуализации)
2. Системы
программирования
низкого уровня
Предназначены
для обеспечения
разработки и
выполнения
несложных
программ.
Состав: ассемблер Ассемблер (+ иногда Ассемблер, в
(транслятор),
дополнительные
настоящее
редактор связей
языки)
время С
(компоновщик),
загрузчик, простой
текстовый
редактор,
отладчики,
библиотека.
3. Системы
программирования
на универсальных
языках
Предназначены
для разработки
программных
продуктов в
различных
областях.
Языки высокого
уровня (C, Paskal)
Раньше
Ассемблер,
сейчас С,
Pasсal
Разработка
4. Системы
прикладных
программирования
программ. Состав: Специализированные
Универсальные
на
СУБД, САПР,
языки (SQL, FoxPro,
языки
специализированных системы
GPSS, HTML и т.д.)
языках
удаленного
доступа.
5. Прикладные
программы
Предназначены
для решения
конкретных задач
пользователя.
Специализированные языки, реже –
универсальные языки
5. Однопросмотровый, двухпросмотровый и многопросмотровый Ассемблеры.
Компоненты ассемблера. Алгоритм работы ассемблера.
Однопросмотровый,
двухпросмотровый
и
многопросмотровый
ассемблеры
представляют собой различные подходы к решению проблемы обработки операторов,
содержащих ссылки на впереди определённые метки и переменные.
Однопросмотровый ассемблер:
Проблема трансляции возникает, если ссылка предшествует метке или
переменной, и в этом случае невозможно сформировать полный код команды.
Однопросмотровый ассемблер решает эту проблему, формируя неполный код
команды, где значение метки или переменной принимается равным 0.
Информация о месте значения и имени ссылки записывается в таблицу ссылок
(таблицу неразрешённых ссылок).
После обработки программы просматриваются записи в таблице ссылок, и
производится модификация неполных кодов команд путем дописывания
требуемых значений.
Если в таблице символических имен не найдено имя ссылки, то это означает, что
метка или переменная не определена, что соответствует ошибке в программе.
Двухпросмотровый ассемблер:
Первый просмотр: распределение памяти, определение длин команд и данных,
заданных операторами; определение значений, меток и адресов переменных.
Второй просмотр: формирование кодов команд и данных; формирование
объектного кода; формирование протокола трансляции.
Многопросмотровый ассемблер:
Многопросмотровый ассемблер разрешает использовать в выражениях
аргументы, которые будут определены далее.
Реализуется несколько просмотров для определения значений в таблице
символических имен, и последний просмотр используется для формирования кода
команды.
Просмотры для определения значений переменных и констант продолжаются до
тех пор, пока все значения не будут определены или пока на очередном просмотре
не будет определено ни одно новое значение (что указывает на ошибку в
программе).
Компоненты ассемблера:
Постоянные: таблица регистров, таблица форматов команд, таблица директив.
Переменные: таблица символических имен, таблица литералов.
Алгоритм работы ассемблера:
1. Открытие исходного и результирующих файлов.
2. Выделение памяти для временных структур и инициализация переменных.
3. Последовательный просмотр операторов исходной программы.
4. Для каждого оператора: разделение строки, определение типов операндов,
определение команды, формирование кода команды (для двух- и
многопросмотрового ассемблера), увеличение счетчика на длину команды.
5. Формирование объектного кода и протокола трансляции (для двух- и
многопросмотрового ассемблера).
6. Закрытие файлов и завершение работы.
6. Однопросмотровый и многопросмотровый макропроцессоры. Таблицы
макропроцессора. Алгоритм работы макропроцессора.
Макропроцессор (макрогенератор) – предназначен для текстовой замены
фрагментов текста программы с учетом параметров.
7. Загрузчики. Абсолютный, перемещающий и связывающий загрузчики.
Загрузчики - это программы, которые копируют готовый к выполнению модуль в
основную память по команде операционной системы. Существуют разные типы
загрузчиков: абсолютные, перемещаемые и связывающие.
Абсолютные загрузчики просты и быстры. Они записывают объекты программы в ОП
и передают управление по адресу начала ее исполнения. Однако их недостаток в том,
что адрес начала загрузки программы должен быть определен до ее ассемблирования.
Перемещаемые загрузчики обеспечивают эффективное разделение ресурсов
компьютера при одновременном выполнении нескольких независимых программ. Они
могут использовать аппаратные средства для перемещения программ в ОП.
Перемещаемые загрузчики используют таблицы символов для определения и
использования внешних ссылок в сегменте.
Связывающие загрузчики выполняют связывание и перемещение во время загрузки.
Они разделяют работу на две части: выработка загрузочного модуля и загрузка модуля
в основную память с настройкой адресов. Связывающие загрузчики используют
таблицу внешних имен (ESTAB) для хранения информации о внешних ссылках и их
адресов.
Базы данных
1. Основные концепции баз данных (БД). Информационная система, банк данных,
база данных, структурирование данных, СУБД.
2. СУБД и ее основные функции, приложения. Классификация СУБД. Критерии
выбора СУБД пользователем, Краткая характеристика современных сетевых
СУБД,
3. Современные подходы к моделированию данных. Виды моделей данных и их
характеристики.
4. Реляционная модель данных. Основные понятия. Отношение, домен, атрибут,
кортеж. Типы данных в БД. Целостность реляционных данных. Потенциальный
ключ отношения, первичный ключ, внешний ключ.
5. Связывание таблиц. Основные виды связей между таблицами. Контроль
целостности связей. Уровни определения ограничений ссылочной целостности.
6. SQL. Запросы на модификацию данных в таблицах: INSERT, DELETE, UPDATE.
7. SQL. Простые формы оператора SELECT - запросы на выборку данных из одной
таблицы. Использование операторов BETWEEN, LIKE, IS [NOT] NULL, END,
OR, NOT в условиях отбора кортежей. Скалярные выражения в списке атрибутов
запроса. Сортировка кортежей.
8. Агрегатные функции SQL. Запросы с группировкой и отбором групп.
9. SQL. Запросы на выборку данных из нескольких таблиц. Способы объединения
таблиц. Соединение таблицы со своей копией. Простые запросы с подзапросами.
10.SQL. Запросы с коррелированными подзапросами. Алгоритм выполнения.
Кванторы [NOT] EXISTS$, ANY, ALL.
11.Нормальные формы (НФ): 1НФ, 2НФ, ЗНФ. Нормальная форма Бойса-Кодда.
12.Построение логической модели предметной области. Алгоритм перехода от
диаграммы «сущность-связь» к отношениям реляционной базы данных.
13.Понятие функциональной зависимости между атрибутами отношения.
Замыкание множества функциональных зависимостей отношения.
Неприводимое множество функциональных зависимостей. Тривиальная
функциональная зависимость. Транзитивная функциональная зависимость.
Зависимости, определяющие избыточность данных в отношении. Декомпозиция
без потерь.
14.Логический уровень проектирования баз данных. Метод нормальных форм.
Дублирование данных. Аномалии обновления, добавления, удаления данных.
ЭВМ и периферийные устройства, Архитектура ЭВМ
1. Архитектура системы команд. Основные типы команд. Способы адресации.
Форматы команд.
o
o
Система команд является набором инструкций, которые понимает и выполняет
процессор. Каждая команда состоит из опкода (код операции) и одного или
нескольких операндов.
Основные типы команд включают в себя арифметические и логические
команды, команды передачи данных, командные и управляющие команды.
o Арифметические и логические команды выполняют операции над
данными, например, сложение, вычитание, логическое И, ИЛИ, НЕ.
o
Команды передачи данных используются для перемещения данных между
регистрами процессора, памятью и периферийными устройствами.
wśród них команды загрузки и сохранения.
Командные и управляющие команды координируют выполнение
программы, включая ветвление, вызов подпрограмм и управление
потоком.
Способы адресации определяют, как операнды команд обращаются к памяти
или регистрам. Некоторые распространенные способы адресации включают в
себя:
o Прямая адресация использует непосредственное указание адреса
операнда в команде.
o
o
o
Непрямая адресация использует регистр указателя для косвенного
обращения к операнду.
o
Адресация по регистру использует содержимое регистра в качестве
операнда.
Адресация по стеку использует стековый регистр для доступа к
операндам, расположенным в стеке.
Форматы команд определяют структуру и длину команд. Они могут
варьироваться в зависимости от архитектуры процессора. Некоторые
процессоры используют фиксированную длину команд, в то время как другие
используют переменную длину. Форматы команд могут включать в себя поля
для опкода, модификаторов, регистровых адресов и константных операндов.
o
o
2. Структурная организация и методы проектирования управляющих
автоматов с жесткой логикой. Методы синхронизации.
o
Управляющие автоматы (УА) используются для управления
последовательностью выполнения команд в компьютере. Они могут быть с
жесткой или программируемой логикой.
Жесткая логика означает, что логика управления фиксирована и
реализована с помощью физических компонентов, таких как логические
вентили и мультиплексоры.
Структурная организация УА с жесткой логикой включает в себя:
o Блок управления, который генерирует сигналы управления для других
блоков процессора.
o
o
o
Блок декодирования, который декодирует опкоды команд и генерирует
соответствующие сигналы управления.
o
Регистры, которые хранят данные, адреса и флаги состояния.
Арифметико-логическое устройство (АЛУ), которое выполняет
арифметические и логические операции.
Методы проектирования УА с жесткой логикой включают в себя
использование логических схем, таких как схемы Карно, карты Кью, или
логических синтезаторов для реализации необходимой логики.
Методы синхронизации используются для координации работы различных
блоков процессора. Они включают в себя использование тактового сигнала,
синхронизацию по переднему или заднему фронту тактового сигнала, а также
асинхронный дизайн.
o
o
o
3. Структурная организация управляющих автоматов с программируемой
логикой. Естественная адресация. Смешанное микропрограммирование.
o
Управляющие автоматы с программируемой логикой используют
микропрограммы для реализации логики управления. Это обеспечивает гибкость
и возможность изменения логики управления путем изменения
микропрограммы.
o
Естественная адресация является методом адресации, используемым в
микропрограммировании. Он позволяет обращаться к ячейкам памяти
микропрограммы с помощью относительных адресов, что упрощает написание и
изменение микропрограмм.
o
Смешанное микропрограммирование сочетает в себе преимущества жесткой
и программируемой логики. Некоторые часто используемые команды могут
быть реализованы с помощью жесткой логики для повышения скорости, в то
время как более сложные или редко используемые команды могут быть
реализованы с помощью микропрограмм.
4. Центральный процессор. Структурная организация и функциональное
назначение блоков процессора. Цикл процессора
o
o
Центральный процессор (ЦП) является основным компонентом компьютера,
ответственным за выполнение команд и обработку данных.
Структурная организация ЦП включает в себя:
o Арифметико-логическое устройство (АЛУ), которое выполняет
арифметические и логические операции.
o
Регистры, которые хранят данные, адреса и флаги состояния.
o
Блок управления, который генерирует сигналы управления для
координации работы процессора.
Кэш-память, которая используется для хранения часто используемых
данных и команд, обеспечивая быстрый доступ к ним.
Функциональное назначение блоков процессора:
o АЛУ выполняет арифметические и логические операции над данными.
o
o
o
Регистры используются для хранения промежуточных результатов,
адресов памяти и флагов состояния, которые указывают на результат
выполнения операции (например, нуль или переполнение).
o
Блок управления декодирует команды, генерирует необходимые сигналы
управления и координирует работу других блоков процессора.
o
Кэш-память обеспечивает быстрый доступ к часто используемым данным
и командам, сокращая время доступа к основной памяти.
5. Арифметико-логическое устройство. Структурная организация. Типы
обрабатываемых данных и особенности исполнения команд.
o
o
Арифметико-логическое устройство (АЛУ) выполняет арифметические и
логические операции над данными.
Структурная организация АЛУ включает в себя:
o Арифметический блок, который выполняет арифметические операции,
такие как сложение, вычитание, умножение и деление.
o
Регистры флагов, которые хранят информацию о результате операции,
например, нуль, знак, переполнение или перенос.
Типы обрабатываемых данных включают в себя целые числа, числа с
плавающей запятой, символы и битовые поля.
Особенности исполнения команд зависят от конкретной реализации АЛУ.
Некоторые АЛУ могут выполнять операции над одним или двумя операндами
одновременно, в то время как другие могут поддерживать более сложные
операции, такие как умножение или деление с плавающей запятой.
o
o
o
Логический блок, который выполняет логические операции, такие как И,
ИЛИ, НЕ и исключающее ИЛИ.
6. Внутренняя память ЭВМ. Статические и динамические запоминающие
устройства. Структурная организация SRAM и DRAM. Режимы работы.
o
o
Внутренняя память (основная память) ЭВМ используется для хранения
данных и команд, к которым процессор имеет прямой доступ.
Статические запоминающие устройства (СЗУ) сохраняют данные до тех пор,
пока к ним подается питание. Они включают в себя SRAM (статическая память с
произвольным доступом) и флеш-память.
o SRAM (Static Random-Access Memory) состоит из флип-флопов, что
обеспечивает высокую скорость доступа и низкое энергопотребление.
DRAM (Dynamic Random-Access Memory) хранит данные в виде зарядов
в конденсаторах и требует периодического обновления. Она предлагает
большую емкость при более низкой стоимости и энергопотреблении.
Режимы работы внутренней памяти включают в себя режимы чтения и
записи, а также различные варианты циклов обновления для DRAM.
o
o
7. Организация защиты памяти ЭВМ. Назначение. Возможные схемные
решения.
o
Защита памяти используется для предотвращения несанкционированного
доступа к данным и обеспечения целостности и безопасности системы.
o
Назначение защиты памяти включает в себя предотвращение повреждения
данных, защиту от вредоносного программного обеспечения и обеспечение
безопасного выполнения программ.
o
Возможные схемные решения для защиты памяти включают в себя:
o Страничная защита памяти использует таблицы страниц для
управления доступом к памяти. Каждая страница имеет набор атрибутов,
определяющих права доступа.
o
Сегментная защита памяти разделяет память на сегменты с различными
правами доступа.
o
Использование аппаратных средств, таких как MMU (Memory
Management Unit), которая обеспечивает трансляцию адресов и защиту
памяти на аппаратном уровне.
o
Использование операционной системы, которая обеспечивает
управление доступом к памяти и реализует механизмы защиты на
программном уровне.
Операционные системы
1. Объекты ядра в ОС Windows. Управление процессами в Windows.
o
Ядро Windows отвечает за управление аппаратным обеспечением, памятью и
процессами в системе. Основными объектами ядра являются процессы, потоки,
разделы памяти и объекты синхронизации.
o Процессы в Windows представлены структурой EPROCESS, которая
содержит информацию о состоянии процесса, его приоритет, учетные
данные безопасности и управление памятью.
o
Потоки являются базовыми единицами исполнения, и каждый процесс
может иметь один или несколько потоков. Они представлены структурой
ETHREAD.
o
Разделы памяти используются для управления доступом к памяти и
включают в себя код, данные и стек процесса.
Объекты синхронизации включают в себя мьютексы, семафоры и
события, которые помогают координировать доступ к общим ресурсам.
Управление процессами в Windows включает в себя создание и завершение
процессов, переключение контекста, установку приоритетов и управление
ресурсами. Оно осуществляется с помощью функций ядра, таких
как NtCreateProcess, NtTerminateProcess и KeSwitchProcess. Приоритет процессов
может быть динамически изменен с помощью
функций NtSetPriorityProcess или NtAdjustPriorityThread.
o
o
2. Управление процессами в ОС Unix. Методы организации виртуальной
памяти. Алгоритмы замещения страниц.
o
В Unix-подобных системах управление процессами включает в себя создание,
приостановку, возобновление и завершение процессов. Эти операции
осуществляются с помощью системных вызовов, таких
как fork(), exec(), wait() и exit().
o
Виртуальная память используется для абстрагирования физического
адресного пространства и предоставления каждому процессу собственного
адресного пространства. Она организуется с помощью страниц и таблиц
страниц.
o
Алгоритмы замещения страниц используются для управления страницами в
виртуальной памяти. Некоторые популярные алгоритмы включают в себя:
o Оптимальное замещение страниц (OPT): выбирает для вытеснения
страницу, которая будет использоваться через самое долгое время.
o
Алгоритм Least Recently Used (LRU): вытесняет наименее недавно
использованную страницу.
o
Алгоритм First In First Out (FIFO): вытесняет страницу, которая
находится в памяти дольше всего.
o
Алгоритм Second Chance: модификация алгоритма FIFO, которая
предоставляет странице второй шанс, перемещая ее в начало очереди
перед вытеснением.
3. Файловая система NTFS.
o
NTFS (New Technology File System) является основной файловой системой в ОС
Windows. Она обеспечивает надежное хранение данных, эффективное
использование дискового пространства и расширенные функции безопасности.
o
Основные характеристики NTFS:
o Поддержка больших объемов данных: NTFS может поддерживать
файловые системы размером до 256 терабайт.
o
Безопасность на уровне файлов и папок: NTFS позволяет устанавливать
права доступа для конкретных пользователей или групп.
o
Журналирование: NTFS использует журналирование транзакций, что
обеспечивает целостность файловой системы в случае сбоя системы.
o
Компрессия и шифрование файлов: NTFS может сжимать и шифровать
файлы для экономии дискового пространства и защиты данных.
o
Распределенные файловые системы: NTFS поддерживает распределенные
файловые системы, позволяя нескольким компьютерам совместно
использовать один и тот же том.
4. Виртуальная файловая система VFS UNIX.
o
VFS (Virtual File System) является абстракцией, используемой в Unix-подобных
системах для унификации работы с различными типами файловых систем. Она
позволяет операционной системе обращаться к различным файловым системам
(таким как ext4, XFS или NFS) с помощью единого интерфейса.
o
Основные преимущества VFS:
o
Унификация вызовов файловой системы: приложения могут использовать
стандартный набор системных вызовов для работы с любыми файловыми
системами.
o
Абстракция аппаратных различий: VFS скрывает различия в структуре и
организации различных файловых систем, предоставляя единое
представление.
Поддержка различных типов файловых систем: VFS позволяет системе
одновременно поддерживать несколько типов файловых систем, включая
локальные и сетевые.
VFS состоит из двух частей: верхнего уровня, представляющего собой
унифицированный интерфейс, и набора модулей нижнего уровня, которые
реализуют конкретные файловые системы.
o
o
5. Взаимодействие процессов в рамках компьютерной сети. Удаленный вызов
подпрограмм.
o
Взаимодействие процессов в компьютерной сети позволяет процессам,
работающим на разных компьютерах, обмениваться данными и координировать
свою работу. Это достигается с помощью сетевых протоколов, таких как TCP/IP.
o
Удаленный вызов подпрограмм (RPC) является механизмом, позволяющим
программе вызвать подпрограмму, расположенную на другом компьютере, как
если бы она была локальной. RPC абстрагирует сетевые детали, позволяя
программисту работать с удаленными функциями так же, как и с локальными.
o
Основные компоненты RPC:
o Клиент: программа, которая вызывает удаленную подпрограмму.
o
Сервер: программа, предоставляющая удаленную подпрограмму.
o
Протокол обмена сообщениями: определяет формат и семантику
сообщений, передаваемых между клиентом и сервером.
o
Система именования: позволяет клиенту идентифицировать и находить
серверы в сети.