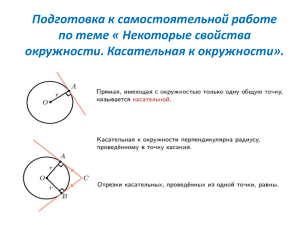
Отрезок, соединяющий две точки на окружности, называется хордой. Самая большая хорда проходит через центр окружности и называется диаметром. 𝛽 𝛼 Центральный угол - угол, вершина которого лежит в центре окружности. Центральный угол равен дуге, на которую опирается. Угол 𝛽 тоже можно назвать центральным углом. Он опирается на дугу, которая больше 180°. Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность. Вписанный угол равен половине дуги, на которую опирается. Центральный угол в два раза больше вписанного угла, опирающегося на ту же дугу. Равные хорды окружности стягивают равные дуги. Вписанные углы, опирающиеся на одну и ту же дугу, равны (˪F=˪M=˪N=˪B, они опираются на одну и ту же дугу AC) Вписанный угол, опирающийся на диаметр равен 90° Угол между пересекающимися хордами окружности равен полусумме дуг, заключенных между ними: 𝟏 𝜶 = (AB + CD) 𝟐 Прямая, имеющая с окружностью только одну общую точку, называется касательной. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания. Отрезки касательных, проведенных из одной точки, равны: АВ = АС Угол между касательной и хордой, проходящей через точку касания, равен половине дуги, заключенной между ними (или равен вписанному углу, опирающемуся на эту дугу): 𝟏 𝜶 = ∪ АВ = ˪АСВ 𝟐 Угол между секущими, проведенными из одной точки к окружности, равен полуразности дуг, заключенных между ними: 𝟏 𝜶 = (∪ АВ - ∪ CD) 𝟐 Если радиус перпендикулярен хорде, то он делит ее пополам. Произведения отрезков пересекающихся хорд равны: АО ∙ ОС = ВО ∙ OD Если окружность вписана в угол, то ее центр лежит на биссектрисе этого угла. В любой треугольник можно вписать окружность. Ее центром является точка пересечения биссектрис треугольника. Если в четырехугольник можно вписать окружность, то суммы противоположных сторон четырехугольника равны: а+с=в+d Центр вписанной пересечении четырехугольника. окружности биссектрис лежит на углов Если в параллелограмм можно вписать окружность, то он является ромбом. Центр окружности лежит на пересечении диагоналей (рис. 1) Если в прямоугольник можно вписать окружность, то он является квадратом. Центр окружности лежит на пересечении диагоналей. У прямоугольного треугольника центр описанной окружности лежит на середине гипотенузы. Отношение длины стороны треугольника к синусу противолежащего угла равно двум радиусам описанной около треугольника окружности: Если около четырехугольника можно описать окружность, то сумма его противоположных углов равна 180° 1.Если около параллелограмма можно описать окружность, то он является прямоугольником. 2.Если около ромба можно описать окружность, то он является квадратом. 3.Если около трапеции можно описать окружность, то она является равнобедренной.