Поурочное планирование. Алгебра 10 класс.

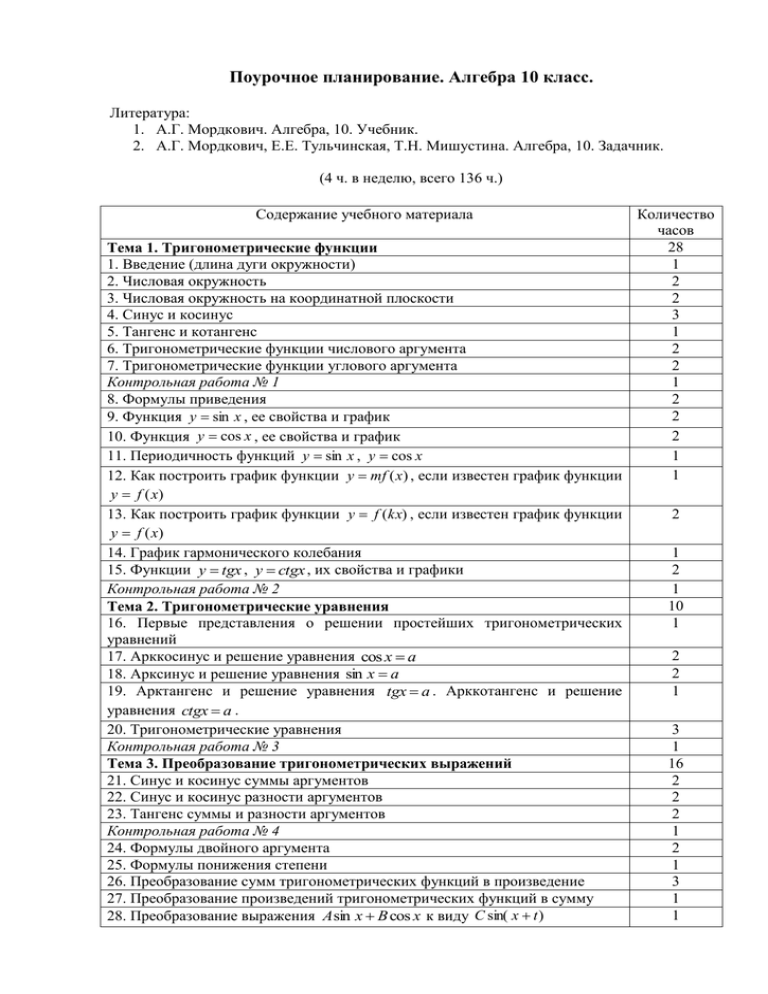
Поурочное планирование. Алгебра 10 класс.
Литература:
1. А.Г. Мордкович. Алгебра, 10. Учебник.
2. А.Г. Мордкович, Е.Е. Тульчинская, Т.Н. Мишустина. Алгебра, 10. Задачник.
(4 ч. в неделю, всего 136 ч.)
Содержание учебного материала
Количество
часов
28
Тема 1. Тригонометрические функции
1. Введение (длина дуги окружности)
1
2. Числовая окружность
2
3. Числовая окружность на координатной плоскости
2
4. Синус и косинус
3
5. Тангенс и котангенс
1
6. Тригонометрические функции числового аргумента
2
7. Тригонометрические функции углового аргумента
2
Контрольная работа № 1
1
8. Формулы приведения
2
2
9. Функция y  sin x , ее свойства и график
2
10. Функция y  cos x , ее свойства и график
1
11. Периодичность функций y  sin x , y  cos x
1
12. Как построить график функции y  mf (x) , если известен график функции
y  f (x)
2
13. Как построить график функции y  f (kx) , если известен график функции
y  f (x)
14. График гармонического колебания
1
2
15. Функции y  tgx , y  ctgx , их свойства и графики
Контрольная работа № 2
1
10
Тема 2. Тригонометрические уравнения
16. Первые представления о решении простейших тригонометрических
1
уравнений
2
17. Арккосинус и решение уравнения cos x  a
2
18. Арксинус и решение уравнения sin x  a
1
19. Арктангенс и решение уравнения tgx  a . Арккотангенс и решение
уравнения ctgx  a .
20. Тригонометрические уравнения
3
Контрольная работа № 3
1
16
Тема 3. Преобразование тригонометрических выражений
21. Синус и косинус суммы аргументов
2
22. Синус и косинус разности аргументов
2
23. Тангенс суммы и разности аргументов
2
Контрольная работа № 4
1
24. Формулы двойного аргумента
2
25. Формулы понижения степени
1
26. Преобразование сумм тригонометрических функций в произведение
3
27. Преобразование произведений тригонометрических функций в сумму
1
1
28. Преобразование выражения A sin x  B cos x к виду C sin( x  t )
Контрольная работа № 5
Тема 4. Производная
29. Числовые последовательности (определение, примеры, свойства)
30. Предел числовой последовательности:
1) понятие предела последовательности
2) вычисление пределов последовательностей
3) сумма бесконечной геометрической прогрессии
31. Предел функции:
1) предел функции на бесконечности
2) предел функции в точке
3) приращение аргумента, приращение функции
32. Определение производной:
1) задачи, приводящие к понятию производной
2) определение производной, ее геометрический и физический смысл
3) алгоритм отыскания производной
33. Вычисление производных:
1) формулы дифференцирования (для функций y  C , y  kx  m , y 
1
37
1
1
1
1
2
2
1
1
1
2
1
,
x
y  x 2 , y  x , y  sin x , y  cos x )
2) правила дифференцирования (сумма, произведение, частное;
дифференцирование функций y  x n , y  tgx , y  ctgx )
3) дифференцирование функции y  f (kx  m)
Контрольная работа № 6
34. Уравнение касательной к графику функции
35. Применение производной для исследования функций:
1) исследование функций на монотонность
2) отыскание точек экстремума
3) построение графиков функций
36. Отыскание наибольших и наименьших значений функций:
1) отыскание наибольшего и наименьшего значений непрерывной
функции на промежутке
2) задачи на отыскание наибольших и наименьших значений величин
Контрольная работа № 7
Повторение
2
3
1
1
2
2
2
3
3
3
2
11
Контрольная работа № 1
(Определение тригонометрических функций)
Вариант 1
1. Вычислите: а) sin
7
 13 
 5 
; б) cos 
 ; г) ctg13,5 .
 ; в) tg  
3
 6 
 4 
3
1
; б) cos t  
.
2
2
3. Упростите выражение ctgt  sin( t )  cos( 2  t ) .
ctgt
4. Докажите тождество
 cos 2 t .
tgt  ctgt
2. Решите уравнения: а) sin t 
5. Вычислите 2 sin 870  12  cos 570  tg 2 60 .
4 
6. Известно, что sin t  ,  t   . Вычислите: cos t , tgt , ctgt .
5 2
1
2
7. Решите неравенство: а) sin t 
; б) cos t  .
2
2
8. Расположите в порядке возрастания числа 1; cos 7; sin 7; ctg 7.
Вариант 2
1. Вычислите: а) cos
5
11
 7 
; б) tg
; в) sin  
 ; г) ctg (3,5 ) .
6
3
 4 
3
1
2. Решите уравнения: а) sin t   ; б) cos t 
.
2
2
3. Упростите выражение tg (t )  cos t  sin( 4  t ) .
4. Докажите тождество ctgt  sin 2 t  (tgt  ctgt) 1 .
5. Вычислите 4 cos 840  48  sin 600  ctg 2 30 .
4
3
6. Известно, что cos t   ,   t 
. Вычислите: sin t , tgt , ctgt .
5
2
3
2
7. Решите неравенство: а) sin t 
; б) cos t  
.
2
2
8. Расположите в порядке возрастания числа tg 10; sin 10; cos 10; ctg 10.
Вариант 3
1. Вычислите: а) sin
9
5
 4 
 7 
; б) cos 
.
 ; в) tg  
 ; г) ctg
4
4
 3 
 6 
1
2
; б) cos t   .
2
2
3. Упростите выражение tgt  cos( t )  sin(   t ) .
tgt
4. Докажите тождество
 sin 2 t .
tgt  ctgt
2. Решите уравнения: а) sin t 
5. Вычислите 4 sin 2 120  2 cos 600  27tg 660 .
3 
6. Известно, что sin t  ,  t   . Вычислите: cos t , tgt , ctgt .
5 2
3
1
7. Решите неравенство: а) sin t   ; б) cos t 
.
2
2
8. Расположите в порядке возрастания числа 1; cos 7,5; sin 7,5; tg 7,5.
Вариант 4
1. Вычислите: а) cos
2
17
 11 
 
; б) sin  
; г) ctg   .
 ; в) tg
3
6
 4 
 4
1
3
; б) cos t  .
2
2
3. Упростите выражение ctg (t )  sin t  cos(  t ) .
2. Решите уравнения: а) sin t  
4. Докажите тождество tgt  cos 2 t  (tgt  ctgt) 1 .
5. Вычислите 4 sin 690  8 cos 2 210  27ctg 660 .
3 
6. Известно, что cos t   ,  t   . Вычислите: sin t , tgt , ctgt .
5 2
1
2
7. Решите неравенство: а) sin t  
; б) cos t  .
2
2
8. Расположите в порядке возрастания числа tg 10,5; cos 10,5; sin 10,5; ctg 10,5.
Контрольная работа № 2
(Свойства и графики тригонометрических функций)
Вариант 1
1. Найдите наименьшее и наибольшее значения функции:
 2  
  7 
;
а) y  sin x на отрезке  ;  . б) y  cos x на отрезке 
.
 3 2 
6 6 


sin   t tg (t )
2 
2. Упростите выражения: а) cos 2 (  t )  cos 2 (  t ) ; б)
.


cos  t 
2 
cos x
3. Исследуйте функцию y  4
на четность-нечетность.
x  x2  1


4. Постройте график функции y  cos x    2 .
3

2
5. Известно, что f ( x)  2 x  3x  2 . Докажите, что f (sin x)  3 sin x  2 cos 2 x .
sin x
6. Постройте график функции y 
.
| sin x |
Вариант 2
1. Найдите наименьшее и наибольшее значения функции:
  5 
 3  
;  .
а) y  cos x на отрезке  ;  . б) y  sin x на отрезке 
6
6 3 
 3


cos  t ctg (t )

2




2. Упростите выражения: а) sin 2   t   sin 2 (  t ) ; б)
.

2




sin   t 
2 
3
sin x
3. Исследуйте функцию y  2
на четность-нечетность.
x 1


4. Постройте график функции y  sin  x    1 .
6

2
5. Известно, что f ( x)  3x  2 x  3 . Докажите, что f (cos x)  2 cos x  3 sin 2 x .
tgx
6. Постройте график функции y 
.
| tgx |
Вариант 3
1. Найдите наименьшее и наибольшее значения функции:
  5 
  
а) y  sin x на отрезке  ;  . б) y  cos x на отрезке  ;   .
4 4 
 3 


cos  t 
2  .
2. Упростите выражения: а) sin 2 (  t )  sin 2 (  t ) ; б)
sin(   t )tg (t )
tg 5 x
3. Исследуйте функцию y  4
на четность-нечетность.
3x  x 2  1


4. Постройте график функции y  sin  x    1 .
6

2
5. Известно, что f ( x)  3x  2 x  1 . Докажите, что f (sin x)  2 sin x  3 cos 2 x  2 .
cos x
6. Постройте график функции y 
1.
| cos x |
Вариант 4
1. Найдите наименьшее и наибольшее значения функции:
 2 
  5 
;0 .
а) y  sin x на отрезке  ;  . б) y  cos x на отрезке 
 3 
4 3 


cos  t ctg (t )
 3

2 
 t  ; б)
2. Упростите выражения: а) cos 2 2  t   cos 2 
.


 2

sin   t 
2 
2
ctg x
3. Исследуйте функцию y  4
на четность-нечетность.
x  2x2  2


4. Постройте график функции y  cos x    2 .
3

2
5. Известно, что f ( x)  2 x  3x  1 . Докажите, что f (cos x)  3 cos x  2 sin 2 x  1 .
| sin x |
 1.
6. Постройте график функции y 
sin x
Контрольная работа № 3
(Тригонометрические уравнения)
Вариант 1
Решите уравнения:
1. 2 sin x  2  0 .
x 
2. cos    1  0 .
2 4
 3

 x  1.
3. Решите уравнение cos( 2  x)  sin 
 2

2
2
4. sin x cos x  2 sin x  cos x .
5. Найдите корни уравнения sin 2 x  2 cos x  2  0 на отрезке [5 ; 3 ] .
6. Решите уравнение 3 sin 2 x  4 sin x cos x  5 cos 2 x  2 .
7. Найдите корни уравнения sin 3x  cos 3x , принадлежащие отрезку [0; 4].
Вариант 2
Решите уравнения:
1. 2 cos x  3  0 .


2. sin  2 x    1  0 .
3

 3

 x 1  0 .
3. Решите уравнение sin( 2  x)  cos
 2

2
2
4. 3 sin x  2 sin x cos x  cos x .
5. Найдите корни уравнения cos 2 x  3 sin x  3  0 на отрезке [2 ; 4 ] .
6. Решите уравнение 5 sin 2 x  2 sin x cos x  cos 2 x  4 .
7. Найдите корни уравнения sin 2 x  3 cos 2 x , принадлежащие отрезку [-1; 6].
Вариант 3
Решите уравнения:
1. 2 sin x  1  0 .


2. cos 2 x    1  0 .
6



3. Решите уравнение sin   x   cos  x   1  0 .
2

2
2
4. 3 sin x  4 sin x cos x  cos x  0 .
5. Найдите корни уравнения 6 sin 2 x  5 cos x  5  0 на отрезке [3 ; 5 ] .
6. Решите уравнение sin 2 x  9 sin x cos x  3 cos 2 x  1 .
7. Найдите корни уравнения 3 sin 2 x  cos 2 x , принадлежащие отрезку [-1; 4].
Вариант 4
Решите уравнения:
1. 2 cos x  2  0 .
x 
2. sin     1 .
2 6


3. Решите уравнение cos  x   sin(   x)  1 .
2

2
2
4. 6 sin x  5 sin x cos x  cos x .
5. Найдите корни уравнения cos 2 x  2 sin x  2  0 на отрезке [4 ; 2 ] .
6. Решите уравнение 5 sin 2 x  2 sin x cos x  cos 2 x  1 .
7. Найдите корни уравнения sin 3x  cos 3x  0 , принадлежащие отрезку [0; 6].
Контрольная работа № 4
(Тригонометрические формулы сложения аргументов)
Вариант 1
1. Найдите значения выражений:
а) sin 58 cos 13  cos 58 sin 13 ;

7

7
 sin sin
б) cos cos
.
12
12
12
12
1


cos   sin     .
2
6

3. Докажите тождество sin(    )  sin(    )  2 sin  cos  .
4. Решите уравнение sin 3x cos x  cos 3x sin x  0 .
12
3


5. Зная, что sin    ,    
, найдите tg     .
13
2
4






 

6. Известно, что cos  t   cos  t   p . Найдите cos  t  cos  t  .
4 
4 
4  4 
2. Упростите выражения: а) cos(t  s)  sin t sin s ; б)
Вариант 2
1. Найдите значения выражений:

3

3
 cos sin
а) sin cos
;
5
10
5
10
б) cos 78 cos 108  sin 78 sin 108 .
1


sin   cos    .
2
6

3. Докажите тождество cos(   )  cos(   )  2 cos  cos  .
4. Решите уравнение cos 2x cos x  sin 2x sin x  0 .
12 3


   2 , найдите tg     .
5. Зная, что cos   ,
13 2
4






 

6. Известно, что sin   t   sin   t   p . Найдите sin   t  sin   t  .
3 
3 
3  3 
2. Упростите выражения: а) sin(    )  cos  sin  ; б)
Вариант 3
1. Найдите значения выражений:
а) sin 81 cos 21  cos 81 sin 21 ;
5

5

cos  sin
sin .
б) cos
8
8
8
8
3


2. Упростите выражения: а) cos x cos y  cos( x  y ) ; б) sin     
cos  .
3
 2
3. Докажите тождество sin(    )  sin(    )  2 cos  sin  .
4. Решите уравнение sin 5x cos x  cos 5x sin x  0 .
3
3


5. Зная, что cos    ,    
, найдите tg     .
5
2
4






 

6. Известно, что cos  t   cos  t   p . Найдите cos  t  cos  t  .
6

6 
6
 6 
Вариант 4
1. Найдите значения выражений:
5

5

cos  cos
sin ;
а) sin
14
7
14
7



б) cos 78 cos 18  sin 78 sin 18 .
3


2. Упростите выражения: а) sin  cos   sin(    ) ; б) cos  x  
sin x .
3
 2
3. Докажите тождество cos(   )  cos(   )  2 sin  sin  .
4. Решите уравнение cos 4x cos x  sin 4x sin x  0 .
4 


5. Зная, что sin   ,     , найдите tg     .
5 2
4






 

6. Известно, что sin   t   sin   t   p . Найдите sin   t  sin   t  .
6

6 
6
 6 
Контрольная работа № 5
(Формулы тригонометрии)
Вариант 1
sin 2t cos t
.
2 sin t
2. Решите уравнение sin 5x  sin 3x .
3. Докажите тождество 2 cos 2 (45  4 )  sin 8  1 .
4. Вычислите cos 70  sin 140  cos 10 .
5. Найдите корни уравнения 3 sin x  cos x  1 на отрезке [3 ; 3 ] .
6. Решите уравнение sin 5 x  sin x  2 sin 2 x  1 .
1. Упростите выражение 1 
Вариант 2
cos 2t
 cos t .
cos t  sin t
2. Решите уравнение cos 8x  cos 6x .
3. Докажите тождество 2 sin 2 (45  2t )  sin 4t  1 .
4. Вычислите sin 72  cos 222  sin 12 .
5. Найдите корни уравнения 3 sin x  cos x  1 на отрезке [3 ; 3 ] .
1. Упростите выражение
6. Решите уравнение 2 cos 2 3x  cos 3x  cos 9 x  1 .
Вариант 3
sin 2t sin t
.
2 cos t
2. Решите уравнение sin 7 x  sin 5x .
3. Докажите тождество 2 cos 2 (45  3 )  sin 6  1 .
4. Вычислите cos 50  sin 160  cos 10 .
5. Найдите корни уравнения sin x  3 cos x  1 на отрезке [2 ; 4 ] .
1. Упростите выражение 1 
6. Решите уравнение sin 5 x  sin x  2 sin 2 x  1 .
Вариант 4
cos 2t
 sin t .
cos t  sin t
2. Решите уравнение cos 6x  cos 4x .
1. Упростите выражение
3. Докажите тождество 2 sin 2 (45  3t )  sin 6t  1 .
4. Вычислите sin 84  cos 234  sin 24 .
5. Найдите корни уравнения sin x  3 cos x  1 на отрезке [2 ; 4 ] .
6. Решите уравнение 2 cos 2 2 x  cos 2 x  cos 6 x  1 .
Контрольная работа № 6
(Правила и формулы отыскания производных)
Вариант 1
1. Найдите производную функции:
4
а) y  x 5 ; б) y  3 ; в) y  ; г) y  3  2 x ; д) y  2 x  3 sin x ;
x
tgx
е) y  x cos x ; ж) y 
; з) y  (3x  5) 4 .
x
2. Найдите угол, который образует с положительным лучом оси абсцисс касательная к
x10 x 7
графику функции y 

 x 3  2 в точке x0  1 .
10 7
 
3. Вычислите f '   , если f ( x)  2 sin x  3x 2  2x  3 .
3
4. Прямолинейное движение точки описывается законом s  t 5  t 3 (м). Найдите ее
скорость в момент времени t = 2 c.
5. Найдите все значения x, при которых выполняется неравенство f ' ( x)  0 , если
f ( x)  12 x  x 3 .
6. Найдите все значения x, при которых выполняется равенство f ' ( x)  0 , если
f ( x)  cos 2 x  x 3 и x  [0; 4 ] .
Вариант 2
1. Найдите производную функции:
3
а) y  x 4 ; б) y  4 ; в) y   ; г) y  3x  2 ; д) y  2 cos x  4 x ;
x
ctgx
е) y  x sin x ; ж) y 
; з) y  (2 x  3)5 .
x
2. Найдите угол, который образует с положительным лучом оси абсцисс касательная к
x12 x 3
  x  2 в точке x0  1 .
графику функции y 
12 3
x
 
3. Вычислите f '   , если f ( x)  1,5 x 2   5  4 cos x .
2
6
4. Прямолинейное движение точки описывается законом s  t 4  2t 2 (м). Найдите ее
скорость в момент времени t = 3 c.
5. Найдите все значения x, при которых выполняется неравенство
f ' ( x)  0 , если
f ( x)  6 x 2  x 3 .
6. Найдите все значения x, при которых выполняется равенство
f ' ( x)  0 , если
f ( x)  sin 2 x  x 2 и x  [0; 4 ] .
Вариант 3
1. Найдите производную функции:
5
а) y  x 6 ; б) y  2 ; в) y  ; г) y  3  5 x ; д) y  8 x  0,5 cos x ;
x
sin x
е) y 
; ж) y  xctgx ; з) y  (5 x  1) 7 .
x
2. Найдите угол, который образует с положительным лучом оси абсцисс касательная к
x8 x 5
графику функции y 
  x 3  3 в точке x0  1 .
8
5
x
 
3. Вычислите f '   , если f ( x)  2 cos x  x 2   5 .
3
6
4. Прямолинейное движение точки описывается законом s  t 4  t 2 (м). Найдите ее
скорость в момент времени t = 3 c.
5. Найдите все значения x, при которых выполняется неравенство f ' ( x)  0 , если
f ( x)  81x  3x 3 .
6. Найдите все значения x, при которых выполняется равенство
f ' ( x)  0 , если
f ( x)  cos 2 x  x 3 и x  [0; 4 ] .
Вариант 4
1. Найдите производную функции:
6
x
а) y  x 7 ; б) y  5 ; в) y   ; г) y  4 x  5 ; д) y  sin x 
;
x
2
cos x
е) y 
; ж) y  xtgx ; з) y  (3x  4) 6 .
x
2. Найдите угол, который образует с положительным лучом оси абсцисс касательная к
x9 x6
графику функции y 

 x  3 в точке x0  1 .
9
6
 
3. Вычислите f '   , если f ( x)  1,5x 2  6 sin x  x  4 .
3
4. Прямолинейное движение точки описывается законом s  t 6  4t 4 (м). Найдите ее
скорость в момент времени t = 2 c.
5. Найдите все значения x, при которых выполняется неравенство
f ' ( x)  0 , если
f ( x)  7,5 x 2  x 3 .
6. Найдите все значения x, при которых выполняется равенство
f ( x)  sin 2 x  x и x  [0; 4 ] .
f ' ( x)  0 , если
Контрольная работа № 7 (2ч)
(Применение производной к исследованию функций)
Вариант 1
1. Дана функция y  x 3  3x 2  4 . Найдите:
а) промежутки возрастания и убывания функции;
б) точки экстремума;
в) наибольшее и наименьшее значения функции на отрезке [-1; 4].
2. Постройте график функции y  x 3  3x 2  4 .
3. Составьте уравнение касательной к графику функции y  4 x в точке x = 4.
4. Площадь прямоугольного участка 144 м2. При каких размерах участка длина
окружающего его забора будет наименьшей?
x2  4
5. Постройте график функции y  2
.
x 4
Вариант 2
1. Дана функция y  0,5 x 4  4 x 2 . Найдите:
а) промежутки возрастания и убывания функции;
б) точки экстремума;
в) наибольшее и наименьшее значения функции на отрезке [-1; 3].
2. Постройте график функции y  0,5 x 4  4 x 2 .
6
3. Составьте уравнение касательной к графику функции y  в точке x = 3.
x
2
4. Площадь прямоугольного треугольника 6 см . Найдите наименьшее значение площади
квадрата, построенного на гипотенузе треугольника.
8x
5. Постройте график функции y  2
.
x 4
Вариант 3
1. Дана функция y  x 3  3x 2  4 . Найдите:
а) промежутки возрастания и убывания функции;
б) точки экстремума;
в) наибольшее и наименьшее значения функции на отрезке [-4; 1].
2. Постройте график функции y  x 3  3x 2  4 .
3. Составьте уравнение касательной к графику функции y  2 x в точке x = 1.
4. Площадь прямоугольного треугольника 8 см2. Какими должны быть длины сторон
треугольника, чтобы сумма площадей квадратов, построенных на его сторонах, была
наименьшей?
x2  1
5. Постройте график функции y  2
.
x 1
Вариант 4
1. Дана функция y  0,25 x 4  2 x 2 . Найдите:
а) промежутки возрастания и убывания функции;
б) точки экстремума;
в) наибольшее и наименьшее значения функции на отрезке [-3; 1].
2. Постройте график функции y  0,25 x 4  2 x 2 .
9
3. Составьте уравнение касательной к графику функции y  в точке x = 3.
x
4. Длина, ширина и высота прямоугольного параллелепипеда с квадратным основанием
составляют в сумме 36 см. Чему равен наибольший объем такого параллелепипеда?
4x
5. Постройте график функции y  2
.
x 1
Устные упражнения по алгебре и началам анализа в 10-ом классе.
Сентябрь
1. Вычислите x из уравнения 3x – 5 = 7.
2. Вычислите x из уравнения 19 – 4x = 3
3. Решите уравнение x2 – 8x + 15 = 0
4. Составьте квадратное уравнение, если x1 = 7; x2 = 4.
1
1
1
5. Вычислите 3 - 1 - 1 .
2
4
4
6. Вычислите 352 – 152 .
25  17  17
7. Вычислите
.
17  17  23
8. Решите пропорцию12 : x = 45 : 15
9. Вычислите НОК для (a - 3)2, (a + 3)2 и (a2 - 9)
10. Вычислите 15% от 60.
11. Вычислите x, если 20% от x составляют 12.
12. Вычислите значение выражения (((a + 3)a + 2)a + 3)a – 54, если
a = 2.
13. Упростите (2a + b)(2a - b)(4a2 + b2).
14. Вычислите 29  31, используя формулу разности квадратов.
15. Автомашина прошла S км за t часов. Вычислите среднюю скорость.
16. Не решая уравнения x2 – 3x + 2, составьте другое уравнение, у
которого корни имеют в два раза большее значение.
17. Дополните выражение 4x2 – 12x + ? до квадрата разности.
3
18. Вычислите среднее арифметическое двух чисел 29 и 30,25.
4
2
2
a  2ab  b
19. Сократите дробь
.
a2  b2
20. Вычислите 6% от 150 рублей.
21. Решите квадратное уравнение x2 – 2x – 24 = 0.
22. Вычислите сумму 1+3+5+7+9+11+13+15+17+19.
23. Вычислите a10 прогрессии 3, 7, 11, …, a10.
24. Вычислите разность арифметической прогрессии, если a2 = 7,
a5 = 25.
25. Вычислите знаменатель геометрической прогрессии, если a1 = 12,
a3 = 3.
26. Выразите в радианах 600 и 1350 .
5
2
 и
.
10
6
28. В прямоугольном треугольнике катеты равны. Вычислите синус и
27. Выразите в градусах
косинус острого угла.
29. Определите знак выражения sin450 – cos600.
 
30. Определите знак выражения  .
3 2
4
4
{3; 5}
x2 – 11x + 28 = 0
1
1000
1
4
(a2 - 9)2
9
60
0
16a4 – b4
899
S
км/ч
t
x2 – 6x + 8 = 0
9
30
ab
ab
9р.
{-4; 6}
100
39
6

1
2

3
и 
3
4
1500 и 360
2
2
,
2
2
Положительный
Отрицательный
31. Сколько процентов составляет 5кг от 40кг?
32. Сумма трех последовательных чисел равна 48. Вычислите числа.
33. Составьте квадратное уравнение, если x1 = 5; x2 = -2.
12,5%
15, 16, 17
x2 – 3x – 10 = 0
3
0

2 
34. Вычислите  5  4   .

 3  

35. Вычислите 25  22 : 24.
36. Вычислите sin2  - 1 + cos2  .
1
8
0
1
2
(x - 2)(x - 3)
1x3
37. Вычислите 2sin150 cos150.
38. Разложите на множители x2 – 5x + 6.
39. Решите неравенство x2 – 4x + 3  0.
40. Решите систему уравнений
 x  y  8,

 x  y  4.
(6; 2)
Октябрь
1. Решите квадратное уравнение x2 + 5x – 6 = 0.
2. План выпуска деталей 60 штук, а изготовлено 45. Вычислите
процент выполнения плана.
3. Решите квадратное уравнение х2 - 3х = О.
4. Найдите общий делитель чисел 18, 48 и 36.
5. Решите уравнение 0,1: х = 10.
6. Вычислите 73 + 34 + 27 + 66 – 100.
7. Какие значения может принимать a в равенстве
sinх = a ?
8. Вычислите 20% от 75.
2
9. Запишите в виде бесконечной десятичной дроби.
9
5  3x
10. Найдите область определения функции y 
.
x3
11. Вычислите cos2 30°- sin2 300.
12. Вычислите sin40° cos10° - cos40° sin10°.
13. Вычислите cos25°cos20° - sin250sin 20°.
tg 60 0  tg15 0
14. Вычислите
.
1  tg 60 0 tg15 0
15. Вычислите 4cosl5°sin15°.
(-6; 1)
75%
{О; 3}
6
0,01
100
0а1
15
0.222...
x  3
1/2
1/2
2 /2
1
1
2
1
16. Вычислите   .
2
17. Дано sin  = 1/2. Вычислите соs  , если  - острый угол.
18. Чему равен х в равенстве sinx =  ?
a5a3a
19. Вычислите 4 2 .
a a
20. Решите систему
2 x  y  7,

2 x  y  1.
4
3 /2
Не существует
a3
(2; 3)
4 2  2 0  10
.
22
16
22. Представьте
в виде числа, вводя отрицательные показатели.
27
23. Вычислите х в пропорции 12 : 18 = 2 : х.
24. Вычислите область определения функции у = 2 x  8 .
25. Могут ли tg  и ctg  быть соответственно равными
2- 3 и2+ 3.
26. Решите неравенство х2 - 2х - 3  0.
27. Дано уравнение x2 – 12x +36 = 0. Составьте другое квадратное
уравнение с корнями в три раза меньше.
21. Вычислите
28. Найдите область определения функции y = x 2  4 x .
29. Вычислите cos75°cosl5° + sin75°sinl5°.
tg 25 0  tg 20 0
30. Вычислите
.
1  tg 25 0 tg 20 0
31. 25% от х равно 12,5 м. Вычислите х.


32. Определите знак функции соs   1 .
2

1 6
33. Вычислите 2  .
3 7
34. Вычислите (-1)2n + (- 1)2n-1, где n  N.
35. В семье три сына, каждый имеет одну сестру. Сколько детей в
семье?
36. Какой цифрой оканчивается произведение
11•12•13•... •19?
37. Вычислите ( 7  3 )( 7  3 ).
38. Вычислите sin 330°.
39. Вычислите соs 720°.
40. Вычислите tg2250.
4
24 • 3 -9
3
x 4
Да
–1  x  3
х2 - 4х + 4 = 0
x 0 и x 4
1/2
1
50 м
Минус
2
0
4
Нулем
4
1/2
1
1
Ноябрь
1. Извлеките корень cos 2   2 cos   1 .
1 - соs 
2. Вычислите sin7  .
0
3. Вычислите корни уравнения x2 + 8x + 16 = 0.
-4и-4
4. Вычислите 80 : 23 + 32 • 3-1.
13
5. Вычислите ( 5  3 )( 5  3 ).
2
6. Вычислите 150% от 10.
15
3
7. Известно, что sin  
,  -острый угол. Вычислите cos  .
1/2
2
8. Вычислите sin2 a + tga ctga + cos2 a.
2
1
1
9. Вычислите arcsin +arccos - 2arctg1.
0
2
2
3
10. Может ли быть верным равенство sin2  + cos2  = ?
Нет
2
11. Карандаш и блокнот стоят вместе 80 р. Ручка дешевле блокнота на 10 р.
Вычислите стоимость карандаша и блокнота.
12. Решите уравнение 2sin  - 1= 0.
13. Решите уравнение 5tg х + 5 = 0.
14. Вычислите
4tg

4
.
15. Найдите область определения функции y =
2
x2
.
x 1
16. Извлеките корень 3 a 3  3a 2 b  3ab 2  b 3 .
17. Вычислите (sina - l)(sinа + 1).
18. Вычислите координаты точки пересечения прямой у == 0,5x + 1
с осью ординат.
19. В каких точках парабола у = х2 — 2х — 3 пересекает ось абсцисс?
20. Какие значения принимает функция y = x2 – 2x + 1?
8  0,125  60
21. Вычислите
.
0,5
22. Вычислите cos19  .
10
23. Что будет графиком функции у =
на плоскости?
x
24. Решите неравенство х2 - х - 6  0.

25. Что больше: cos  или sin ?
2
2
x  2x
26. Решите неравенство
>0.
x2
27. По плану следует изготовить 60 деталей, а изготовлено 75.
Вычислите процент выполнения плана.
5x
28. При каких значениях x дробь
не имеет смысла?
2x  6
29. Составьте квадратное уравнение, если х1 = - 2, x2 = 3.
30. Вычислите корни уравнения x2 + 2х + 1 = 0.
31. Решите уравнение 3 x - 3 = 0.


32. Вычислите 2cos2 3 - 2sin2 3 .
33. Решите уравнение х2 - 2х - 15 = 0.
34. Определите четность или нечетность функции y = x2 – 3.
1
35. Решите уравнение 1 - х = 0,125.
8
0,5 : 0,5  9,5
36. Вычислите
.
5
37. Какие знаки имеют корни уравнения 3х2 - 7х + 4 = 0?

или cos 4  ?
4
39. Существует ли такое значение х, чтобы выполнялось равенство
38. Что больше tg
35 р. и 45 р.

x = (-1)k 6 +  k,
kZ

x = - +  k,
4
kZ
x 1
a-b
- cos2а
(0; 1)
(-1; 0)(3; 0)
[0;+  )
120
-1
Гипербола
-2  х  3

sin
2
х>0
125%
При х = 3
х2 - x - 6 = 0
–1 и –1
27
-1
{- 3; 5}
Четная
1
2,1
Оба
положительные
Равны
5
?
8
40. Вычислите 2cos15°cos75°.
Нет
sinx cosx =
1/2
Декабрь
1. Вычислите ( x )2.
|x|
5

6
2. Переведите 150° в радианную меру.
1
или - 1,5?
- 1,5
2
1
4. Решите уравнение х + 60 = 120.
360
6
5. Как изменится произведение, если первый множитель увеличить
в 6 раз, а второй уменьшить в 4 раза?
Увеличится в 1,5 раза
6. Разложите х2 + 2х - 8 на множители.
(х - 2)(х + 4)
7. Что больше: cos  или sin2  ?
sin2 
12
8. Решите неравенство
> 6.
1<x<3
x 1
7
9. Запишите 0,777... в виде обыкновенной дроби.
9
3
10. Определите четность или нечетность функции у = 4х .
Нечетная
11. Решите уравнение 2 x = 10.
25
12. Вычислите arccos1 + arcsin1 + arcsin1.

3. Что больше: - 5
13. Извлеките корень 1  2tgx  tg 2 x .
| 1 – tgx |
1
x1, 2 =
2
14. Решите уравнение 4x2 - 4х + 1 = 0.
10
< 0?
x2
16. Напишите наименьшее общее кратное натуральных четных
однозначных чисел.
15. При каких значеничх x дробь

17. Роешите уравнение x +
= arcsin 2 .
4
0
 ab

 10  .
18. Вычислите  2
2
a b

19. Какие значения может принимать функция у = х 2 - 6х + 9?
20. Найдите область определения функции y = x  x  12 .
21. При каких значениях х функция у = x2 + 4х + 4 принимает
наименьшее значение?
22. Что больше: 45 или 2 5
23. При каких значениях х функция
( x  1)( x  5)
y=
( x  2)( x  3)
не имеет смысла?
24. Составьте пропорцию из чисел 3, 5, 9, 15.
25. Произведение двух чисел равно 150. Первое число в 1,5 раза
2
x<2
24
Нет решения
1
0  y< 
x  -4 и x  3
-2
45
При - 2 и 3
3 : 5 = 9 : 15
больше второго. Вычислите эти числа.
26. Решите уравнение ( 2 x - 1)( 2 x + 1) = x.
27. Колесный трактор вспахивает поле за 6 часов, а гусеничный - за
3 часа. За сколько часов они вспашут поле, работая вместе?
28. Решите систему уравнений
3x  y  36,

 y  3x  0.
29. Вычислите среднее арифметическое чисел 20, 34 и 36.
15, 10
x=1
За 2 часа
x = 6, y = 18
30
30. Вычислите a a .
31. В уравнении х2 - 12х + с = 0 один корень в три раза больше другого.
3
3
2
a
Вычислите с.
27
32. Решите уравнение 5(x - 1)(x + 3) = 0.
33. Сумма двух чисел равна 80. Чему будет равна сумма, если одно
слагаемое увеличить на 20, а другое уменьшить на 30?
34. Костюм стоил К рублей. Сначала его цену уменьшили на 10% ,
а затем повысили на 10% . Как изменилась его цена?
35. Составьте квадратное уравнение, если x1 = -3, x2 = 4.
36. Определите четность или нечетность функции у = 1 + cos х.
37. Одна труба заполняет бассейн за 4 часа, а другая за 2 часа. Какую
часть бассейна две трубы заполнят за час вместе?
38. Делится ли произведение 32 • 27 • 65 на 15?
39. Запишите формулу двухзначного числа.
40. Решите систему уравнений

1 3
,
sin x  cos y 

2
,

sin x  cos y  1  3 .

2
 
если x и y находятся в интервале 0;  .
 2
{-3; 1}
70
На 0,01К рублей
x2 – x - 12 = 0
Четная
3/4
Да
10а + b
  
6 ; 6


Январь
x3  y3
, если x = 3, у = 2.
x 2  xy  y 2
2. Найдите 12% от 250.
1. Вычислите
1
30
3. Вычислите a 4 .
а2
4. Какой знак имеет функция у = cos 2?
Отрицательный
5. Чему равно k в уравнении х2 + kx - 3 = 0, если один его корень
равен -1?
k = -2
1
6. Цену тетради понизили на стоимости. Вычислите первоначальную
8
ее цену, если после снижения тетрадь стоит 210 руб.
240 руб.
7. Под каким углом прямая у == х - 2 пересекает ось абсцисс?
45°
8. Вычислите ординату точки пересечения графика функции у = 2х + 5 с
осью ординат.
y=5
9. Решите уравнение x  3 = 3.
12
10. Сумма двух чисел равна 250. Одно из них равно 25% другого.
Вычислите эти числа.
11. Вычислите область определения функции y = x  2 x  3 .
12. Напишите пять членов последовательности хn = 3n - 2.
13. Вычислите sin 570°.
14. Вычислите 64-1.5.
6
2
15. Решите неравенство sin2 х  1.
50, 200
x  -1 и x  3
1; 4; 7; 10; 13
- 1/2
1
5/ 2

 k , k  Z
2
16. При каких значениях х функция у = 25 - 10х + х2 принимает
наименьшее значение?
17. Вычислите 27 - 2 12 + 3 .
m3  n3
18. Сократите дробь 2
.
m mn  n 2
19. Какое число при делении на а дает в частном Ь и остаток 2?
x2 1
20. Может ли дробь
быть отрицательной?
x2
1
 
21. Для каких значений х взятых в промежутке 0;  sinx < ?
2
 2
22. Что меньше: 7 2 или 72 ?
23. Решите уравнение ( x - 3}( x + 3) = 0.
24. Решите уравнение х2 - 4х - 60 = 0.
25. Определите, четная или нечетная функция у = 5 - х2.
26. Решите неравенство 3(х - 2) > 24.
27. Найдите наименьшее общее кратное чисел 9, 12 и 36.
2x  4
28. При каких значениях х функция у =
будет положительной?
0,5
2
1

29. Решите уравнение
.
x 1 x 1
30. Решите систему уравнений
 x  y  7,

 x  y  13.
5
0
m+n
ab + 2
Нет
0  x<
72
9
{- 6; 10}
Четная
х > 10
72
х>2
3
10, 3
31. При каких значениях х функция у = 2sin х • cos х обращается в
нуль?
32. Вычислите arccos
x=
3
1
+ arcsin .
2
2
33. Вычислите соs 150°.



34. Вычислите 2  cos 2  sin 2  .
6
6

35. В каких точках функция у = х2 +2x – 3 пересекает ось абсцисс?
36. Решите систему уравнений

6

2
k, k  Z
 /3
-
3
2
1
(-3; 0)(1; 0)
x  y
 2  10,

 x  y  2.
 2
37. Упростите 3 + 27 .
38. Решите неравенство | х | < 3.
39. Вычислите знаменатель прогрессии 3; 6; 12; ... .
40. Решите систему уравнений
2 x  y  1,

2 x  y  7.
x = 12; y = 8
4 3
-3 < х < 3
2
x = 2, y = 3
Февраль
2
+ arctg 1.
2
2. Упростите 2 2  32 .
3. Напишите 5 членов последовательности x n = 2 n.
4. В классе 25 учащихся, из них 23 успевают. Вычислите процент
успеваемости.

2
16
2; 4; 8; 16; 32
5. Решите уравнение 36х2 - 1 = 0.
x= 
1. Вычислите arcsin
x2  5
6. При каких значениях х функция у = 2
не имеет смысла?
x 9
7. Укажите координаты точки пересечения графика функции
у = х2 + 3х - 4 осью ординат.
8. Разделите число 70 в отношении 2 : 3 : 5.
1
9. Что больше: 2arctg 1 или 3arcsin ?
2
10. Запишите формулу нечетного числа.
11. Чему равно с в уравнении х2 - 2х + с = 0, если его один корень
равен 6?
12. Решите неравенство 4(x - 3) < 20.
x2  4
13. При каких значениях х функция у =
равна нулю?
2 x
14. Вычислите cos 21  .
5
15. Переведите  в градусную меру.
4
16. Вычислите разность прогрессии, если a1 = 2, a5 = 14.
35  120  120
17. Вычислите
.
11  120  120
18. При каких значениях х функция у = cos2 x – sin2x обращается в нуль?
19. Вычислите 612  60 2 .
20. Функция y = cos 3х четная или нечетная?
21. Вычислите arcsin 1 - arctg 1 - arccos 1.
22. Делится ли число 217356 на 4?
23. Число жителей района на начало года равно а. Прирост населения
92 %
1
6
3
(0; - 4)
14, 21, 35
Равны
2n - 1
- 24
х<8
2
-1
225°
3
3

4


2
k, k  Z
11
Четная

4
Да
a
за год составил Р%. Сколько будет жителей района на конец года?
24. Цену тетради снизили на 10%, т. е. на 70 рублей. Вычислите новую
цену тетради.
25. Вычислите sin 900°.
26. Определите четность или нечетность функции у = sin х + х.
27. Фермер рассчитывал собрать с участка урожай а центнеров, а
собрал b центнеров (b > а). На сколько процентов больше
запланированного собрал он урожай?
aP
100
630 р.
0
Нечетная
ba
 100%
a

28. Решите уравнение cos x = 0.
29. Вычислите производную функции у = 3х2 - 5х - 7.
30. Вычислите sin 40° • cos 5o + cos 40° • sin 5°.
x2 1
31. Вычислите область определения функции y = 2
.
x 1
 k , k  Z
2
6х - 5
2 /2
x  1
32. Вычислите 1  sin 2 x .
| cos х |
33. Вычислите a : a , где а  0.
34. Определите:  -1 больше или меньше 1?
35. Вычислите sin 750°.
а
меньше
1/2
5
3
36. Упростите (1  3 ) 2 .
37. Вычислите arccos 0,5 + arccos (- 0,5).
38. Решите неравенство |x| < 8.
3 -1

-8<х<8
1
39. Вычислите производную функции у = x 4 – 2x.
2
40. Упростите 3 2 + 8 .
2x3 - 2
5 2
Март
1. Вычислите х в пропорции 12 : х = 42 : 14.
3
3
2. Вычислите arcsin
- arccos
.
2
2
3. Вычислите sin 330°.
4. Вычислите sin 0 + cos 0 + tg 0.
5. Решите уравнение ( x + 5)( x - 5) = 0.
6. Найдите область определения функции
у= x3 + x2 .
7. В каких точках график функции у = x2 – 7x + 12 пересекает ось
ординат?
8. Вычислите производную функции у = tg x ctg х.
9. Вычислите cos 25° cos 20° - sin 25° sin 20°.
10. В уравнении х2 - 9х + с = 0 значение одного корня в два раза
больше другого. Вычислите значение с.
11. При каких значениях х функция у = х2 - 7х +12 равна нулю?
4

6
- 1/2
1
25
x3
(0; 12)
0
2 /2
18
3и4
1
0


5


12. Вычислите  2  2   

 12  

13. Вычислите производную функции у = 3х5 - 2x2.
14. Вычислите ( x  2) 2 при х  2.
15. Из 300 яерен при проращивании взошло240. Вычислите процент
всхожести семян.
16. Какой знак имеет функция y = sin3?
17. Решите уравнение x3 – 3x2 + 3x – 1 = 0.

3
.
18. Вычислите sin  arcsin
2 

19. Напишите 5 членов последовательности
n
x n=
.
n 1
20. Решите неравенство |х| > 2.
21. Вычислите (- а2)3, если а = 2.
22. Делится ли число 67341 на 3?
23. Решите неравенство х2 - 5х + 6  0.
24. Округлите до сотых число 5,19507.
25. Вычислите 852 - 152.
1
4
15х4 - 4х
2-х
80%
Положительный
x=1
3
2
1 2 3 4 5
; ; ; ;
2 3 4 5 6
х < -2 и х > 2
- 64
Да
2x3
5,20
7000
26. Решите уравнение sin2 x = 0.
 k, k  Z
27. Упростите 54  24 .
28. 10 кур за 10 дней съедают 10 кг зерна. Сколько зерна съедают 100
кур за 100 дней.
29. Определите четность или нечетность функции у = 2х2 - 3?
30. Вычислите соs 540°.
31. Вычислите производную функции у = 3х2 - 5х + 1.
32. Вычислите значение выражения
у = sin2 400° + cos2 320°.
33. Найдите область определения функции
1
y = x2 – 3x + 1.
5
5 6
34. Вычислите 16

1
2
.
35. Чем отличается график функции у = х2 от графика функции у = | x2|?
36. Вычислите критические точки функции у = x2 - 6х + 5.
24
37. Решите неравенство
> 4.
x3

2
2
.
 arccos
38. Вычислите cos  arcsin

2
2


39. Вычислите cos 40° cos 20° - sin 20° sin 40°.
1т
Четная
-1
6х - 5
1
xR
1
4
Одинаковы
3
3<x<9
1
1/2
Апрель
1. Известно, что налог 6% от зарплаты составил 12 000 рублей. Какова
зарплата?
200 000 руб.
2. Извлеките корень 1 cos 2 x .
| sin x |
3. При каких значениях х функция у = 1 - 2х + x2 возрастает?
х1
4. Упростите 48 : 12 .
2
5. Запишите формулу трехзначного числа.
100а + 10b + с
6. Запишите формулу общего члена последовательности 5; 8; 11; ... .
3n + 2
7. Какой угол образует прямая у = 3 х - 3 c осью абсцисс?
60°
8. Найдите область определения функции у = sin x .
2 k  x    2k , k  Z
9. Укажите наименьшее и наибольшее значения функции
у = 1 + 2cos 2x.
- 1; 3
10. Вычислите производную функции у = 2sin х cos х.
2cos 2х
1
1

11. Вычислите sin  arcsin  arccos  .
1
2
2

1
12. Сколько корней имеет уравнение sin х = ?
Бесчисленное множество
2
13. При каких значениях x функция у = 16 - 8х + х2 принимает
наименьшее значение?
4
14. Что больше: sin 20° или sin 200°?
sin 20o
15. Сколько секунд в часу?
3600 с

1
 1 
16. Вычислите cos  arccos    .
2
 2 

17. Переведите 120° в радианную меру.
2  /3
18. Запишите формулу числа, которое делится на 3 и в остатке
получается 1.
3n +1
1
1

19. Вычислите arcsin
+ arccos
- arctg 1.
2
2
4
20. Извлеките корень 0,0025 .
0,05
2
21. Чему равно с в уравнении x - х - с = 0, если корень х 1 = 3?
6


2
22. Упростите корень 1  3
3 1
23. Вычислите знаменатель прогрессии, если b 2 = 2, b 6 = 32.
±2
24. Запишите формулу общего члена последовательности 1; 4; 9; 16; ... .
n2
25. Решите неравенство | х |  0.
Любое действительное число
26. Определите, четная или нечетная функция у = 2x3 - tg х.
Нечетная


27. Вычислите arctg 1 + .
4
2
28. Вычислите значение выражения (a - b)(а + b), если а = -1, b = 2.
-3
29. Решите неравенство x2 - 2x + 1  0.
Любое действительное число
30. Вычислите критические точки функции у = 2x3 - 6х.
±1
3
31. Упростите 4 2 .
32. Вычислите производную функции
1
y = x3 – 3x2.
3
33. Решите неравенство x2 - 3х  0.
34. Вычислите производную функции у = 0,5,х10.
35. Решите уравнение sin2 х = 0.
1
1
36. Что больше: arcsin
или arccos ?
2
2
8
x2 – 6x
х  0 и х 3
5х9
k , k  Z
1
arccos
2
37. Решите уравнение x3 + 6x2 + 12x + 8 = 0.
38. Вычислите производную функции у = cos2 2x + sin2 2x.
3
39. Известно, что соs  =
. Чему равен sin  в интервале
2
40. Решите уравнение cos х + 1 = 0.
 
0; 2  ?


-2
0
1
2
х =   2n, n  Z
Май
n
 1
1. Напишите пять членов последовательности x n =    .
 2
2. Вычислите производную функции


+ cos x sin .
2
2
1
3. Вычислите 2arcsin
+ 2arctg 1.
2
4. Решите неравенство 4 – x2  0.
y = sin x cos
5. Вычислите 9

1
2
.
1 1 1 1
1
 ; ; ; ;
2 4 8 16 32
- sin x
5
6
-2 x 2
1
3
150° или

6. Решите уравнение tg 2x - 1 = 0.
8


2
k; k  Z
7. Тело движется по закону s = t2 + t - 3 (м). Какова будет его
скорость через t = 2 с?
5 м/с
8. Разделите число 36 Пропорционально числам 5 : 7.
15 и 21
9. Делится ли число 5260 на 6?
Нет
  2k  x  2  2k , k  Z
10. Решите неравенство 3sin х < 0.
11. Вычислите производную функции у = соs2 х – sin2 х.
- 2sin 2x
12. Вычислите производную функции у = х(х - 1).
2x - 1
13. Вычислите критическую точку функции
у = 3х2 - 12x + 5.
х=2

14. Вычислите производную функции y = cos x – sin .
–sin x
6
15. Какое наименьшее значение принимает функция у = х2 – 2x - 3?
-4
1
16. Может ли функция у = 2
обращаться в нуль?
Не может
x  2x
1
17. Решите уравнение 4х2 + 4x + 1 = 0.
x 1, 2 = 2
2
18. При каких значениях х функция у = 3x – 6x убывает?
При х < 1
19. Решите уравнение 1 т = 10x г.
6
2

20. Вычислите производную функции у = ctg 2x.
sin 2 2 x


  2k  x   2k , k  Z
21. Решите неравенство 2cos х  0.
2
2
22. Вычислите разность прогрессий, если а 6 = 25, a 3 = 13.
4
23. Решите неравенство х2 - 9 > 0.
х<-3их>3
24. Вычислите 7  3 7  3 .
4
2
25. При каких значениях х функция у = x + 6x + 9 равна нулю?
-3



26. Решите неравенство соs х  - 0,5.
27. Вычислите 62,52 - 37,52.
28. Переведите 225o в радианную меру.
29. При каких значениях х функция у = х3 - 1 возрастает?
30. Вычислите производную функции у = 2tg 2x.
2
4
 2k  x 
 2k , k  Z
3
3
2500
5  /4
При любых значениях х
4
cos 2 2 x
31. Замените корень степенью с дробным показателем 4 a 6 .
а1, 5
32. При каких значениях х функция у = 3x2 – 6x + 2 имеет минимум?
X=1


  k  x   k , k  Z
33. Решите неравенство tg x  1.
2
4
2
34. Вычислите максимальное значение функции у = 4 - x .
4

 2k , k  Z
35. Решите уравнение sin х = 1.
2
x2 1
x  3; x  2
36. Найдите область определения функции y = 2
.
x  x6
37. Вычислите критические точки функции у = 2х2 - 8х + 5.
2
15
38. Решите неравенство
> 5.
2<х<5
x2
39. При каких значениях х функция у = 2х2 - 4х возрастает?
х1
40. Решите систему уравнений

1 2
,
cos x  cos y 

2

cos x  cos y  1  2 ,

2


 
x ,y
если x и y находятся в интервале 0;  .
3
4
 2