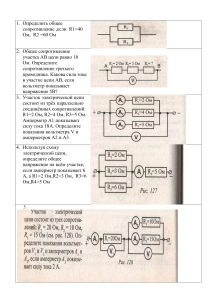
Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Ярославский государственный технический университет» Кафедра «Электротехники» Работа защищена c оценкой_________________ Проверил преподаватель _____________Н.И. Воронина « » 2023 г. РАСЧЁТ ОДНОФАЗНОЙ ЦЕПИ ПЕРЕМЕННОГО ТОКА СМЕШАННОГО СОЕДИНЕНИЯ Контрольная работа по дисциплине «Электроснабжение объектов строительства» ЯГТУ 08.03.01-003 к/р Работу выполнил студент гр. ЗДА-35 _____________ Е.А. Дьяконов « » 2023 г. 2023 г. 2 Задача №2 На рисунке приведена схема однофазных цепей переменного тока смешанного типа. Дано: А В Параметры R1 R2 R3 L2 С1 C3 U f Ед. изм. Ом Ом Ом мГн мГн мкФ В Гц Значение 10 2 10 15,9 100 200 150 50 Определить: 1. Токи во всех ветвях цепи и напряжения на каждом элементе цепи. 2. Составить баланс активной и реактивной мощностей. 3. Построить в масштабе на комплексной плоскости векторную диаграмму. 4. Определить показания вольтметра и активную мощность, измеряемую ваттметром. Решение: 1. Расчёт токов по веткам. 1) Индуктивное сопротивление элементов: 0 𝑥𝐿2 = 2𝜋 ∙ 𝑓 ∙ 𝐿 ∙ 𝑗 = 2𝜋 ∙ 50 ∙ 15,9 ∙ 10−3 ∙ 𝑗 = 𝑗4,995 = 4,995𝑒 𝑗90 Ом. 3 2) Ёмкостное сопротивление элементов: 𝑥С1 = −𝑗 𝑥С3 = −𝑗 1 2𝜋∙𝑓∙С∙ 1 2𝜋∙𝑓∙С∙ = −𝑗 = −𝑗 1 2𝜋∙50∙100∙10−6 ∙ 1 2𝜋∙50∙200∙10−6 ∙ 0 = −𝑗31,831 = 31,831𝑒 −𝑗90 Ом. 0 = −𝑗15,915 = 15,915𝑒 −𝑗90 Ом. 3) Комплексное сопротивление по ветвям, Ом. 0 𝑧1 = 𝑅1 − 𝑗𝑥С1 = 10 − 𝑗31,831 = 33,36𝑒 −𝑗72,56 Ом. 0 𝑧2 = 𝑅2 + 𝑗𝑥𝐿2 = 2 + 𝑗4,995 = 5,38𝑒 𝑗68,18 Ом. 0 𝑧3 = 𝑅3 − 𝑗𝑥С3 = 10 − 𝑗15,915 = 18,79𝑒 −𝑗57,86 Ом. 4) Эквивалентное сопротивление параллельных ветвей, Ом. 𝑧23 = 𝑧2 ∙𝑧3 𝑧2 +𝑧3 0 = 5,38𝑒 𝑗68,18 ∙18,79𝑒 −𝑗57,86 2+𝑗4,995+10−𝑗15,915 0 = 101,09𝑒 𝑗10,32 16,22𝑒 0 −𝑗42,30 0 = 6,23𝑒 𝑗52,62 Ом. 𝑧23 = 6,23 ∙ cos(52,620 ) + 6,23 sin(52,620 ) 𝑗 = 3,78 + 𝑗4,95 Ом. 5) Общее комплексное сопротивление цепи, Ом. 𝑧 = 𝑧1 + 𝑧23 = 10 − 𝑗31,831 + 3,78 + 𝑗4,95 = 13,78 − 𝑗26,88 Ом. 6) Ток на неразветвлённом участке цепи А. 𝐼= 𝑈 𝑧 = 150 13,78−𝑗26,88 150 = 30,21𝑒 −𝑗62,860 0 = 4,965𝑒 𝑗62,86 = 2,26 + 𝑗4,42 А. 7) Напряжение 𝑈𝐴𝐵 (В) на участке АВ: 0 0 0 𝑈𝐴𝐵 = 𝑧23 ∙ 𝐼 = 6,23𝑒 𝑗52,62 ∙ 4,965𝑒 𝑗62,86 = 30,93𝑒 𝑗115,48 = −13,3 + 𝑗27,92 В. 8) Ток 𝐼2 , 𝐼3, (А). 𝐼2 = 𝐼3 = 𝑈𝐴𝐵 𝑧2 𝑈𝐴𝐵 𝑧3 = = 30,93𝑒 𝑗115,48 5,38𝑒 0 𝑗68,180 30,93𝑒 𝑗115,48 18,79𝑒 0 −𝑗57,860 0 = 5,75𝑒 𝑗47,3 = 3,9 + 𝑗4,22 А. 0 = 1,65𝑒 𝑗173,34 = −1,64 + 𝑗0,19 А. 9) Проверка по первому закону Кирхгофа. 𝐼 = 𝐼2 + 𝐼3 ⟹ 2,26 + 𝑗4,42 = 3,9 + 𝑗4,22 − 1,64 + 𝑗0,19 = 2,26 + 𝑗4,41 4 2. Расчёт падений напряжения на элементах цепи. 1) Напряжение 𝑈𝐶1 (В) на индуктивности 𝐶1: 0 0 0 𝑈𝐶1 = 𝑥𝐶1 ∙ 𝐼 = 31,831𝑒 −𝑗90 ∙ 4,965𝑒 𝑗62,86 = 158,04𝑒 −𝑗27,14 = 140,64 − 𝑗72,09 В. 2) Напряжение 𝑈𝑅1 (В) на сопротивлении 𝑅1: 0 0 𝑈𝑅1 = 𝑅1 ∙ 𝐼 = 10 ∙ 4,965𝑒 𝑗62,86 = 49,965𝑒 𝑗62,86 = 22,79 + 𝑗44,46 В. 3) Напряжение 𝑈𝑅2 (В) на сопротивлении 𝑅2 : 0 0 𝑈𝑅2 = 𝑅2 ∙ 𝐼2 = 2 ∙ 5,75𝑒 𝑗47,3 = 11,5𝑒 𝑗47,3 = 7,8 + 𝑗8,45 В. 4) Напряжение 𝑈𝐿2 (В) на сопротивлении 𝐿2 : 0 0 0 𝑈𝐿2 = 𝑥𝐿2 ∙ 𝐼2 = 4,995𝑒 𝑗90 ∙ 5,75𝑒 𝑗47,3 = 28,72𝑒 𝑗137,3 = −21,11 + 𝑗19,48 В. 5) Напряжение 𝑈𝑅3 (В) на сопротивлении 𝑅3 : 0 0 𝑈𝑅3 = 𝑅3 ∙ 𝐼3 = 10 ∙ 1,65𝑒 𝑗173,34 = 16,5𝑒 𝑗173,34 = −16,39 + 𝑗1,91 В. 6) Напряжение 𝑈С3 (В) на сопротивлении С3: 0 0 0 𝑈С3 = 𝑥С3 ∙ 𝐼3 = 15,915𝑒 −𝑗90 ∙ 1,65𝑒 𝑗173,34 = 26,26𝑒 𝑗83,34 = 3,05 + 𝑗26,08 В. 7) Проверка по второму закону Кирхгофа. 𝑈 = 𝐶1 + 𝑅1 + 𝑅2 + 𝐿2 = 𝐶1 + 𝑅1 + 𝑅3 + 𝐶3 140,64 − 𝑗72,09 + 22,79 + 𝑗44,46 + 7,8 + 𝑗8,45 − 21,11 + 𝑗19,48 = 149,48 + 𝑗0,3 В. 140,64 − 𝑗72,09 + 22,79 + 𝑗44,46 − 16,39 + 𝑗1,91 + 3,05 + 𝑗26,08 = 150,09 + 𝑗0,36 В. 3. Баланс мощностей 1) Комплексная мощность 𝑆 (В·А), потребляемая из сети 0 0 𝑆 = 𝑈 ∙ 𝐼 = 150 ∙ 4,965𝑒 𝑗62,86 = 744,75𝑒 𝑗62,86 = 339,73 + 𝑗662,75 = 𝑃 − 𝑗𝑄 𝑃 = 339,73 Вт; 𝑄 = 662,75 ВА. 2) Активная мощность на резисторах 𝑅1 , 𝑅2 , 𝑅3 . 𝑃 = 𝑅1 ∙ 𝐼 2 + 𝑅2 ∙ 𝐼22 + 𝑅3 ∙ 𝐼32 = 10 ∙ 4,9652 + 2 ∙ 5,752 + 10 ∙ 1,652 = 339,86 Вт. 5 3) Реактивная мощность 𝑄𝐶 = 𝑥𝐶1 ∙ 𝐼 2 + 𝑥𝐶3 ∙ 𝐼32 = 31,831 ∙ 4,9652 + 15,915 ∙ 1,652 = 828 ВА. 𝑄𝐿 = 𝑥𝐿2 ∙ 𝐼22 = 4,995 ∙ 5,752 = 165,15 ВА. 𝑄 = 𝑄𝐿 − 𝑄𝐶 = 828 − 165,15 = 662,85 ВА. 4) Определение коэффициента мощности cos 𝜑 = 𝑃 𝑆 = 339,86 √339,732 +662,752 = 0,46 4. Построение векторной диаграммы сил токов и напряжений +J Масштаб 𝐼 − 2,5 ∶ 1 А, 𝑈 − 1 ∶ 2,5 В. Министерство науки и высшего образования Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Ярославский государственный технический университет» Кафедра «Электротехники» Работа защищена c оценкой_________________ Проверил преподаватель _____________Н.И. Воронина « » 2023 г. РАСЧЁТ ТРЁХПРОВОДНОЙ ТРЁХФАЗНОЙ ЦЕПИ С НЕСИММЕТРИЧНОЙ НАГРУЗКОЙ Контрольная работа по дисциплине «Электроснабжение объектов строительства» ЯГТУ 08.03.01-003 к/р Работу выполнил студент гр. ЗДА-35 _____________ Е.А. Дьяконов « » 2023 г. 2023 г. 2 Задача №3 На рисунке 3.6 приведена схема трёхпроводной трёхфазной цепи с несимметричной нагрузкой. Дано: Рисунок 3.6 Параметры UЛ RAB RBC RCA XAB XBC XCA Ед. изм. В Ом Ом Ом Ом Ом Ом Значение 127 8 8 8 6 6 6 Найти: токи в линейных проводниках, построить векторную диаграмму. Решение: При соединении нагрузки треугольником фазные и линейные напряжения равны между собой: 𝑈ф = 𝑈л = 127 В. Комплексы фазных (линейных) напряжений, (В): Запишем симметричную систему трёхфазных напряжений. 0 𝑈𝐴𝐵 = 𝐽𝑈ф = 𝐽127 = 127𝑒 𝐽0 В. 3 0 0 0 0 𝑈𝐵𝐶 = 𝑈𝐴𝐵 ∙ 𝑒 −𝐽120 = 127𝑒 𝐽0 ∙ 𝑒 −𝐽120 = 127𝑒 −𝐽120 = −63,5 − 𝐽109,98 В. 0 0 0 0 𝑈𝐶𝐴 = 𝑈𝐴𝐵 ∙ 𝑒 𝐽120 = 127𝑒 𝐽0 ∙ 𝑒 𝐽120 = 127𝑒 𝐽120 = −63,5 + 𝐽109,98 В. Комплексное эквивалентные сопротивления каждой фазы, (Ом): 0 𝑧𝐴𝐵 = 𝑅𝐴𝐵 − 𝑗𝑥𝐴𝐵 = 8 − 𝑗6 = 10𝑒 −𝑗36,87 Ом. 0 𝑧𝐵𝐶 = 𝑅𝐵𝐶 − 𝑗𝑥𝐵𝐶 = 8 − 𝑗6 = 10𝑒 −𝑗36,87 Ом. 0 𝑧𝐶𝐴 = 𝑅𝐶𝐴 + 𝑗𝑥𝐶𝐴 = 8 + 𝑗6 = 10𝑒 𝑗36,87 Ом. Комплексы фазных токов, (А): 𝐼𝐴𝐵 = 𝐼𝐵𝐶 = 𝐼𝐶𝐴 = 𝑈𝐴𝐵 𝑧𝐴𝐵 𝑈𝐵𝐶 𝑧𝐵𝐶 𝑈𝐶𝐴 𝑧𝐶𝐴 = = = 127𝑒 𝐽0 0 0 0 10𝑒 −𝑗36,87 127𝑒 −𝐽120 0 0 10𝑒 −𝑗36,87 127𝑒 𝐽120 0 0 10𝑒 𝑗36,87 = 12,7𝑒 𝐽36,87 = 10,16 + 𝐽7,62 А. 0 = 12,7𝑒 −𝐽83,13 = 1,52 − 𝐽12,61 А. 0 = 12,7𝑒 𝐽83,13 = 1,52 + 𝐽12,61 А. Линейные токи находим по первому закону Кирхгофа, (А): 𝐼𝐴 = 𝐼𝐴𝐵 − 𝐼𝐶𝐴 = 10,16 + 𝐽7,62 − (1,52 + 𝐽12,61) = 8,64 − 𝐽4,99 А. 𝐼𝐵 = 𝐼𝐵𝐶 − 𝐼𝐴𝐵 = 1,52 − 𝐽12,61 − (10,16 + 𝐽7,62) = −8,64 − 𝐽20,23 А. 𝐼𝐶 = 𝐼𝐶𝐴 − 𝐼𝐵𝐶 = 1,52 + 𝐽12,61 − (1,52 − 𝐽12,61) = 0 + 𝐽25,22 А. Проверка. 𝐼𝐴 + 𝐼𝐵 + 𝐼𝐶 = 8,64 − 𝐽4,99 − 8,64 − 𝐽20,23 + 0 + 𝐽25,22 = 0 Активная мощность цепи, (Вт): 2 2 2 𝑃 = 𝑅𝐴𝐵 ∙ 𝐼𝐴𝐵 + 𝑅𝐵𝐶 ∙ 𝐼𝐵𝐶 + 𝑅𝐶𝐴 ∙ 𝐼𝐶𝐴 = 8 ∙ 10,162 + 8 ∙ 1,522 + 8 ∙ 1,522 = 862,77 Вт. Реактивная мощность цепи, (ВА). 2 2 2 𝑄 = 𝑥𝐴𝐵 ∙ 𝐼𝐴𝐵 + 𝑥𝐵𝐶 ∙ 𝐼𝐵𝐶 + 𝑥𝐶𝐴 ∙ 𝐼𝐶𝐴 = 6 ∙ 10,162 + 6 ∙ 1,522 + 6 ∙ 1,522 = 647,09 ВА. Полная мощность цепи: 𝑆 = √𝑃2 + 𝑄 2 = √862,772 + 647,092 = 1078,47 4 Построение векторной диаграммы линейных и фазных токов и напряжений. +1 +J Масштаб 𝐼 − 1 ∶ 2 А, 𝑈 − 1 ∶ 10 В.