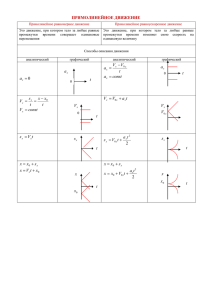
Кинематика Механическое движение – изменение положения тела в пространстве с течением времени относительно других тел. Поступательное движение – движение, при котором все точки тела проходят одинаковые траектории. Материальная точка – тело, размерами которого в данных условиях можно пренебречь, т.к. его размеры пренебрежимо малы по сравнению с рассматриваемыми расстояниями. Траектория – линия движения тела. (Уравнение траектории – зависимость у(х)) Путь l (м) – длина траектории. Свойства: l ≥ 0, не убывает! Перемещение s(м) – вектор, соединяющий начальное и конечное положение тела. sх = х – х0 - модуль перемещения s Свойства: s ≤ l , s = 0 на замкнутой территории. l x xo s l = ; средняя перемещения = ; x ; t t t Скорость (м/с) – 1) средняя путевая 2) мгновенная - скорость в данной точке, может находиться только по уравнению скорости х = 0х + aхt или по графику (t) 2 Ускорение а(м/с ) - изменение скорости за единицу времени. 0 ; à t ах х 0х t x t = прямолинейное а ↑↑ ( F ) если 0 ↑↑ а - движение ускоренное если 0 ↑↓ а - движение замедленное прямолинейное если 0 а - движение по окружности Относительность движения - зависимость от выбора системы отсчета: траектории, перемещения, скорости, ускорения механического движения. Принцип относительности Галилея – все законы механики одинаково справедливы во всех инерциальных системах отсчета. Переход от одной системы отсчета к другой осуществляется по правилу: и отн = 1 - 2 Где 1 - скорость тела относительно неподвижной системы отсчета, 2 – скорость подвижной системы отсчета, отн (υ12) – скорость 1-го тела относительно 2-го. 1 = 2 + отн 2 отн 1 Виды движения. Прямолинейное движение. Прямолинейное равномерное движение. xo =const x Прямолинейное равноускоренное движение. xo xo а const x а const sx sx sx 0 ускоренное 0 замедленное x x = x0 + xt х~t x по оси x0 t против оси x = x0 + 0xt + ахt 2 2 x x х ~ t2 t t ускоренное sx = xt sx=0xt + x = const x ахt 2 2 x= ox+ axt по оси Ох замедленное х 2 0х 2 или sx = x по оси Ох без t! 2а х x t замедленное по Ох υ=0 против оси Ох t t ускоренное ускоренное против оси Ох a=0 ax = const vx ах ах t t t ускоренное движение Криволинейное движение. Движение по окружности с постоянной по модулю скоростью 2R =2πR(м/с) - линейная скорость T 2 =2π(рад/с) – угловая скорость t T l t т.е = ω R aц 2 R 2 R (м/с2) - = t – период (с), N T= Движение по параболе с ускорением свободного падения. x = xo + oxt + g хt 2 ; 2 x= ox+ gxt ; y = yo + oyt + y= oy+ gyt x2 y2 оx = 0 cos gx = 0 центростремительное ускорение T= замедленное движение оy = 0 sin gy = - g 1 y N 1 – частота (Гц=1/с), = t T h x ℓ aц φ s aц g 0 α y s x s g yt 2 2 Частные случаи равноускоренного движения под действием силы тяжести. Движение по вертикали. Движение тела брошенного горизонтально. 1. Если 0 = 0 h gt 2 ; 2 = gt h о 2. Ecли 0 ↑ , тело движется вверх s gt 2 ; = 0 – gt h оt 2 h gt 2 ; s = оt; y= gt 2 Ecли 0 ↑ , тело падает вниз с высоты h - высота, s - дальность полета gt 2 ; = -0 + gt 2 gt 2 3. Ecли 0 ↓ h 0 t ; = 0 + gt 2 (ось Оу направлена вниз) h оt Дополнительная информация для частных случаев решения задач. 1. Разложение вектора на проекции. 2 . Средняя скорость. у 1) по определению ср 1 s у sy yo Модуль вектора может быть найден по теореме Пифагора: S = s x2 s y2 sy sx х х о sx x 2) ср 21 2 1 2 для 2х S; если S1>0 S2<0 5. Движение колеса без проскальзывания. вращ 2 2 3) ср 1 2 ; ср 1 ... n n , 1 2 s1 ≠ s2 3. Метод площадей. 4. Физический смысл производной. Для уравнений координаты х(t) и y(t) → На графике х(t) x = x΄, y = y΄, и площадь фигуры численно равна ах = ΄x = x΄΄, аy = ΄y = y΄΄, t перемещению или х2 у2 пройденному пути. а а х2 а y2 S =S1 - S2 ℓ = S1+ S2 v 1 s1 = s2 если t1 = t2 = … = tn x s s 2 ... s n t1 t 2 ... t n âðàù ïîñò пост 6. Дальность полёта. Дальность полета максимальна при угле бросания 45˚ υ0 = const пост = вращ y (если нет проскальзывания) вращ пост Скорость точки на относительно земли. ободе колеса 60˚45˚30˚ s60=s30 s45 = max x 7. Свойства перемещения для 2) Отношение перемещений сделанных за время от начала отсчета, при o=0 равно: равноускоренного движения при o=0. at 2 a S1 за t =1с S1= = 2 2 Отношение перемещений сделанных за одну секунду, при o=0 равно: 1) s1 s2 s3 s4 0 1s1 1c 3s1 2c 5s1 3c 7s1 4c S1: S2: S3: …: Sn = 1: 3: 5: 7: ….: (2n-1) Sn = S1(2n – 1) = а (2n - 1) 2 0 1s1 1c 4s1 2c 9s1 3c 16s1 4c S1: S2: S3: …: Sn = 12: 22: 32: 42: ….: n2 Sn = S1n2 = а 2 n 2