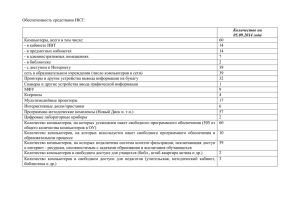
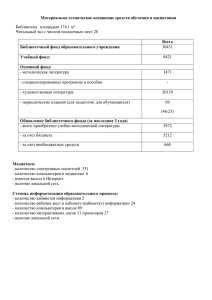
= 7 , =0 , =1 , =1 , =1 , =5 . Задание 9. Студент на экзамене отвечает на 45 тестовых вопросов. Вероятность правильного ответа на один вопрос равна p=0.77. Построить закон распределения СВ Х – оценки студента на экзамене, если 5 ставится за правильные ответы не менее чем на 87 % тестовых вопросов, 4 – если процент правильных ответов лежит в пределах от 73 (включительно) до 87, 3 – если этот процент лежит в пределах от 60 (включительно) до 73. Найти М(Х), D(X), моду Х. В случае получение нецелых значений числа правильных ответов округлять до ближайшего большего целого числа. Решение: 1) закон распределения СВХ. x p 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 1,89563E-29 2,8558E-27 2,10336E-25 1,00931E-23 3,54794E-22 9,73986E-21 2,17382E-19 4,05465E-18 6,44778E-17 8,87426E-16 1,06954E-14 1,13929E-13 1,08068E-12 9,18396E-12 7,02773E-11 4,86237E-10 3,0522E-09 1,74311E-08 9,07763E-08 4,31863E-07 1,87954E-06 7,49093E-06 2,73582E-05 9,15904E-05 0,000281076 0,000790435 0,00203557 0,004795553 0,010320864 0,020254888 0,03616525 0,058584661 0,085807425 0,113166315 0,133715697 0,140692168 0,130836919 0,106545223 0,075093659 0,045123168 0,022659678 0,0092513 0,00294969 0,000688957 0,000104841 7,79979E-06 Шагимарданова Камила 7201-11 x 45*% 5 4 3 2 округл 39,15 32,85 27 0 p 39 33 27 0 0,080785434 0,70004998 0,215928642 0,003235944 2) М(Х)-мат.ожидание М(Х)= 5 ⋅ 0,081 + 4 ⋅ 0,70005 + 3 ⋅ 0,216 + 2 ⋅ 0,003237 = 3,86 3) D(X)-дисперсия 2 D(X)= 𝑀(𝑥 2 ) − (𝑀(𝑥)) =52 ⋅ 0,081 + 42 ⋅ 0,70005 + 32 ⋅ 0,216 + 22 ⋅ 0,003237 - 3,862 = 0,29 4) Так как p(max) = 0,70004998, то мода СВХ = 4. Задание 10. Для нормальной работы дисплейного класса необходима безотказная работа в течение дня как минимум 13 компьютеров. Сколько компьютеров нужно установить, чтобы с вероятностью не меньше 0.95 обеспечить нормальную работу класса, если вероятность отказа компьютера в течение дня равна 0.06 Решение: Безотказная работа: 1-0,06=0,94 Вероятность нормальной работы, при установке 13 компьютеров: 13 13 𝑝(𝑚 ≥ 13) = 𝑃13 = 𝐶13 ⋅ 0,9413 ⋅ 0,060 = 0,447 <0,95 При 14: 13 13 14 14 𝑝(𝑚 ≥ 13) = 𝑃14 + 𝑃14 = 𝐶14 ⋅ 0,9413 ⋅ 0,061 + 𝐶14 ⋅ 0,9414 ⋅ 0,060 = 0,79 <0,95 При 15: 13 14 15 13 14 15 𝑝(𝑚 ≥ 13) = 𝑃15 + 𝑃15 + 𝑃15 = 𝐶15 ⋅ 0,9413 ⋅ 0,062 + 𝐶15 ⋅ 0,9414 ⋅ 0,061 + 𝐶15 ⋅ 0,9415 ⋅ 0,060 =0,94< 0,95 При 16: 13 15 16 13 15 16 14 14 𝑝(𝑚 ≥ 13) = 𝑃16 + 𝑃16 + 𝑃16 + 𝑃16 = 𝐶16 ⋅ 0,9413 ⋅ 0,063 + 𝐶16 ⋅ 0,9414 ⋅ 0,062 + 𝐶16 ⋅ 0,9415 ⋅ 0,061 + 𝐶16 ⋅ 16 0 0,94 ⋅ 0,06 =0,985 > 0,95 Ответ №10: 16 компьютеров 2