Кафедра АСОИУ
–
Афонин В. В.
Лабораторная работа № 4
ГРАФИКА СИСТЕМЫ MATLAB
Цель работы. Изучить основы 2D и 3D графики системы MATLAB.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
С точки зрения вычислительных операций на графику возлагается визуализация результатов. В системе MATLAB предусмотрена двухмерная и трехмерная графика. Справку о графических функциях и командах можно получить
по следующим справкам:
help graph2D
help graph3D
help specgraph
Каждое графическое построение – это работа с графическими объектами.
MATLAB показывает графические объекты в специальных графических окнах,
имеющих в заголовке слово Figure. Нумерация графических окон начинается с
единицы и далее натуральные числа. Большие возможности предоставляются
пользователю по оформлению графиков (2D, 3D) и графических окон. Каждый
графический объект (например, диаграмма) может быть сохранен в традиционных графических форматах, таких как .bmp, .gif, .jpeg, .tiff, .png и в
других.
Графики на плоскости (2D графики) могут быть построены в декартовой
и полярной системах координат.
Диаграммы и графики могут быть изменены по цвету на усмотрение
пользователя. При этом в MATLAB имеются зарезервированные цвета, которые
приведены в табл. 4.1.
Таблица 4.1
Зарезервированные названия цветов в MATLAB
Символ цвета
Английское название
Русское название
Код RGB
y
yellow
желтый
[1, 1, 0]
m
magenta
фиолетовый (сиреневый)
[1, 0, 1]
c
cyan
сине-зеленый (бирюзовый)
[0, 1, 1]
r
red
красный
[1, 0, 0]
g
green
зеленый
[0, 1, 0]
b
blue
синий
[0, 0, 1]
w
white
белый
[1, 1, 1]
k
black
черный
[0, 0, 0]
Кафедра АСОИУ
–
Афонин В. В.
Тип линии (стиль) графиков может быть установлен в соответствии с зарезервированными названиями, которые приведены в табл. 4.2.
Таблица 4.2
Типы (стили) линий
Символ метки или линии
Английское название
Русское название
.
point
точка
o
circle
кружок (окружность)
х
x-mark(cross)
крестик
+
plus
плюс
*
star (asterisk)
звезда (звездочка)
s
square
квадрат
d
diamond
ромб (алмаз)
v
triangle (down)
треугольник (вниз)
^
triangle (up)
треугольник (вверх)
<
triangle (left)
треугольник (влево)
>
triangle (right)
треугольник (вправо)
р
Pentagram
(five-pointed star)
пятиугольник
(пятилучевая звезда)
h
hexagram
(six-pointed star)
шестиугольник
(шестилучевая звезда)
-
solid line
Сплошная линия
:
dotted line
пунктирная (двойная)
линия
-.
dash-dot line
штрих-пунктирная линия
--
dashed line
штриховая линия
none
no line
нет линии
В графической системе MATLAB имеются также функции и команды,
которые позволяют манипулировать графическими объектами. Некоторые из
этих функций и команд будут рассмотрены в практической части, где также будут рассмотрены основные приемы построения графиков. При графических построениях можно рекомендовать создавать М-файлы.
Рассмотрим построение графиков линейных функций вида
y = ax + b;
Первый пример приведен в листинге 4.1
2
Кафедра АСОИУ
%%%
–
Афонин В. В.
Листинг 4.1
clear, clc, close all
%%% Параметры прямой линии
a = 0.5;
b = 2;
x = -7 : 0.01 : 4.2;
y = a*x + b;
line(x, y, 'color', 'r', 'linew', 2 )
%%%% AXIS
xmax = max([max(x), abs(min(x))])*1.1;
ymax = max([max(y), abs(min(y))])*1.2;
%%%% Ось абсцисс
line([-xmax*0.95, xmax], [0, 0], 'color', 'k', 'linew', 1)
%%%% Ось ординат
line([0, 0], [-ymax*0.6, ymax], 'color', 'k', 'linew', 1)
text(xmax, 0, '\bf<', 'rotation', 180)
text(0, ymax, '\bf<', 'rotation', -90)
text(xmax*0.9, -xmax/15, '\it\fontsize{14}\fontname{georgia}x')
text(-xmax/10, ymax*0.95, '\it\fontsize{14}\fontname{georgia}y')
text(-xmax/10, -xmax/15, '\it\fontsize{13}0')
line(0, 0, 'marker', 'o', 'markersize', 5, 'color', 'k',...
'markerfacecolor', 'k')
line(0, b, 'marker', 'o', 'markersize', 5, 'color', 'k',...
'markerfacecolor', 'w')
grid on
axis equal
axis off
set(gcf, 'name', 'Пример построения прямой линии', 'color', 'w')
Результат выполнения программы (скриншот) показан на рис. 4.1.
3
Кафедра АСОИУ
–
Афонин В. В.
Рис. 4.1. График прямой линии y = 0.5x + 2
График можно сохранить в различных графических форматах, чтобы потом вставить, например, в документ типа Word. При этом сохраняться будет
собственно один график без интерфейса графического окна. Для этого следует
в меню File выбрать пункт Save as. Пример выбора графического формата
.bmp для сохранения показан на рис. 4.2.
4
Кафедра АСОИУ
–
Афонин В. В.
Рис. 4.2. Меню выбора графического формата сохранения диаграммы
После выбора графического формата, например, .bmp, можно присвоить
какое-нибудь имя. Пусть это будет «Пример». При этом можно выбрать место
(директорию) для сохранения. Результат выбора показан на рис. 4.3.
Рис. 4.3. Назначение имени для сохранения диаграммы в формате .bmp
5
Кафедра АСОИУ
–
Афонин В. В.
После вставки файла «Пример.bmp» получим график, показанный на
рис. 4.4.
Рис. 4.4. График прямой линии в .bmp формате
Для построения прямой линии, проходящей через две заданные точки,
можно воспользоваться параметрическими уравнениями прямой. Приведем необходимые уравнения:
x − x1
y − y1
=
;
x2 − x1 y2 − y1
x − x1
= t;
x2 − x1
y − y1
= t;
y2 − y1
x = x1 + x2 − x1 t;
y = y1 + y2 − y1 t,
где t [0; 1].
6
Кафедра АСОИУ
–
Афонин В. В.
Рассмотрим второй пример построения прямой линии, проходящей через
две заданные точки (листинг 4.2).
%%%
Листинг 4.2
clear, clc, close all
%%% Координаты точек
x1 = -3.5;
y1 = 4;
x2 = 5.2;
y2 = -4;
%%% Параметр
t = 0 : 0.01 : 1;
x = x1 + (x2 - x1)*t;
y = y1 + (y2 - y1)*t;
line(x, y, 'linew', 2 )
line(x1, y1, 'marker', 'o', 'markersize', 5, 'color', 'b',...
'markerfacecolor', 'b')
line(x2, y2, 'marker', 'o', 'markersize', 5, 'color', 'b',...
'markerfacecolor', 'b')
xlabel('\bf - - - - - - - x - - - - - - -')
ylabel('\bf - - - - - - - y - - - - - - -')
ylim([y2 - 0.5, y1+0.5]);
grid on
axis equal
str = 'Построение прямой линии, проходящей через две точки'
set(gcf, 'name', str)
При изменении параметра за пределы отрезка [0; 1] прямая линия будет
выходить за пределы заданных точек.
Результат выполнения программы показан на рис. 4.5.
7
Кафедра АСОИУ
–
Афонин В. В.
Рис. 4.5. Прохождение прямой линии через две заданные точки
Параметрическое задание уравнений может быть применено для построения окружностей, эллипсов, гипербол. Рассмотрим примеры (листинг 4.3).
%%% Листинг 4.3
clear, clc, close all
%%% Построение окружности
R = 2; %% радиус окружности
%% Координаты центра
x0 = 3.5;
y0 = 3;
%% Параметр
t = 0 : 0.001 : 360;
x = R*cosd(t) + x0;
y = R*sind(t) + y0;
figure(1);
line(x, y, 'linew', 2 ) %% окружность
8
Кафедра АСОИУ
–
Афонин В. В.
line(x0, y0, 'marker', 'o', 'markersize', 5, 'color', 'k',...
'markerfacecolor', 'k')
xlabel('\bf - - - - - - - x - - - - - - -')
ylabel('\bf - - - - - - - y - - - - - - -')
%ylim([y2 - 0.5, y1+0.5]);
grid on
axis equal
str1 = 'Построение окружности: ';
str2 = sprintf('R = %g; x0 = %g; y0 = %g', R,x0,y0)
str = strcat(str1, str2); %% конкатенация строк
set(gcf, 'name', str)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%% Построение эллипса
a = 5.5;
b = 3;
x0 = -2;
y0 = -3;
t = 0 : 0.0001 : 2*pi; %% pi = 3.14...
x = a*cos(t) + x0;
y = b*sin(t) + y0;
figure(2)
line(x, y, 'linew', 2 ) %% эллипс
line(x0, y0, 'marker', 'o', 'markersize', 5, 'color', 'k',...
'markerfacecolor', 'k')
xlabel('\bf - - - - - - - x - - - - - - -')
ylabel('\bf - - - - - - - y - - - - - - -')
grid on
axis equal
str1 = 'Построение эллипса: ';
str2 = sprintf('a = %g; b = %g; x0 = %g; y0 = %g', a, b, x0,y0)
str = strcat(str1, str2); %% конкатенация строк
set(gcf, 'name', str)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%%%% Построение гиперболы
a = 6;
b = 4;
t = 0 : 0.0001 : pi/2; %% pi = 3.14...
x = a*cosh(t); %% косинус гиперболический
y = b*sinh(t); %% синус гиперболический
figure(3)
9
Кафедра АСОИУ
–
Афонин В. В.
line(x, y, 'linew', 2 )
line(x, -y, 'linew', 2 )
line(-x, y, 'linew', 2 )
line(-x, -y, 'linew', 2 )
xlabel('\bf - - - - - - - x - - - - - - -')
ylabel('\bf - - - - - - - y - - - - - - -')
xlim([-max(x)-max(x)/12, max(x) + max(x)/12]);
grid on
axis equal
str = sprintf('Построение гиперболы: a = %g;
set(gcf, 'name', str)
b = %g;
Результат выполнения программы показан на рис. 4.6–4.8.
Рис. 4.6. График окружности
10
', a, b)
Кафедра АСОИУ
–
Рис. 4.7. График эллипса
11
Афонин В. В.
Кафедра АСОИУ
–
Афонин В. В.
Рис. 4.8. График гиперболы
Рассмотрим пример построения фигуры (катеноида) в трехмерном пространстве (листинг 4.4).
%%%
Листинг 4.4
clear, clc, close all
plot3(0,0,0)
hold on
a
u
v
x
y
z
=
=
=
=
=
=
1.8;
-a : 0.08 : a;
linspace(0, 2*pi, length(u) );
cosh(u)' * cos(v);
cosh(u)' * sin(v);
u' * ones(size(v));
mesh(z, x, y) %% катеноид
colormap(0.0*[1,1,1]) %%% цвет
%%%% AXIS
xmax = max(max(x))*1.1;
ymax = max(max(z)) + a*0.9;
12
Кафедра АСОИУ
–
Афонин В. В.
line([-xmax*0.9, xmax], [0, 0], [0, 0], 'color', 'k', 'linew', 1)
line([0, 0], [0, 0], [-ymax*0.95, ymax], 'color', 'k', 'linew', 1)
text(xmax, 0, 0, '\bf\fontsize{10}<', 'rotation', 180)
text(a/70, 0, ymax, '\bf\fontsize{10}<', 'rotation', -90)
text(xmax*0.9, 0, -xmax/12, '\it\fontsize{14}\fontname{georgia}x')
text(-xmax/8, 0, ymax*0.95, '\it\fontsize{14}\fontname{georgia}y')
view(-10, 0) %% точка обзора
alpha(0.95) %% прозрачность фигуры
axis equal
axis off
set(gcf, 'NumberTitle', 'off', 'name', 'Катеноид', 'color', 'w')
Результат выполнения программы показан на рис. 4.9.
Рис. 4.9. Катеноид как фигура вращения
13
Кафедра АСОИУ
–
Афонин В. В.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Пример 1. С помощью функции plot в декартовой системе координат построить и оформить график следующей функции:
y(t) = e–0.2tcos(3t).
Программный код решения примера
%% Очистка памяти, очистка экрана (командного окна),
%% закрытие одного активного графического окна
clear all, clc, close
%% Заданная функция
str = 'exp(-0.2*t)*cos(3*t)';
%% Область изменения аргумента функции
t = 0 : 0.1 : 20;
%% Заданная функция с массивным перемножением .*
y = exp(-0.2*t).*cos(3*t);
% Построение графика красным цветом с толщиной линии в 2 пикселя
plot(t, y, 'r', 'linewidth', 2) %% допустимо 'linew'
%% Выделение номера массива
n = fix(length(y)/3);
%% Нанесение надписи в заданной точке (см. help text)
text(t(n),y(n),'\bf\fontsize{12}\leftarrow y(t)', 'rotation',45)
%% Включение сетки на диаграмме
grid on
%% Заголовок диаграммы (см. help title и help sprintf)
title(sprintf('%sГрафик функции %s','\bf\fontsize{12}', str))
%% Разметка координатных осей (см. help xlabel и help ylabel)
xlabel('\bf\it - - - - - - t - - - - - -')
ylabel('\bf y = f(t)')
%% Установка свойств координатных осей, установка цвета,
%% размера шрифта, жирности шрифта
set(gca, 'color', [1,1,0], 'fontweight', 'bold', 'fontsize', 9)
%% Установка свойств графического окна, установка цвета
set(gcf, 'color','c')
Результат выполнения программы показан на рис. 4.10.
14
Кафедра АСОИУ
–
Афонин В. В.
Рис. 4.10. График функции, заданной массивом точек, в декартовой системе
Задание 4.1
Постройте и оформите графики следующих функций:
y = (x + 1)2.
y = 2 + (x – 1)3.
y = x3 – 3x + 2.
y = 2x3 – x4 .
1
y
.
1 x
x2
y
.
x2
1
yx .
x
2
x
y
.
x 1
15
Кафедра АСОИУ
y
–
Афонин В. В.
10
(локон Аньези).
x 1
2
2x
. (серпантин Ньютона)
x2 1
1
(трезубец Ньютона).
y x2
x
y
y x x (полукубическая парабола).
y x
x
(циссоида Диоклеса).
4 x
y x 25 x 2 .
y = x sin x.
1
y sin x sin 3x.
3
1
y cos x cos 2 x.
2
y sin x .
Пример 2. Постройте в полярной системе координат график следующей функции:
y 3 [1 5sin 2t ], t [0, 2 ]..
Программный код решения примера
clear all, clc,close all
%% Область определения функции в радианах
t = 0 : 0.01 : 2*pi;
%% Функция
y = 3*(1 + 5*sin(2*t));
%% Строчный тип
stry = '3*(1 + 5*sin(2*t))';
%% Создание указателя (дескриптора) на фигуру №1
fig1 = figure(1);
%% Установка свойств
set(fig1, 'name','Полярная систем координат')
%% Обращение к функции полярной системы координат
polar(t,y)
%% Создание указателя (дескриптора) на график функции
g = findobj('type', 'line');
%% Установка свойств линии графика функции
set(g, 'linew', 2, 'color', 'red')
%% Заголовк диаграммы
title(sprintf('%sГрафик функции %s', '\bf\fontsize{12}', stry))
%% Установка свойств (цвета) текущего (активного) объекта
16
Кафедра АСОИУ
–
Афонин В. В.
%% типа фигура - figure
set(gcf,'color','c')
В приведенном программном коде графическая функция polar принимает аргументы (t, y), выраженные в радианах. Результат выполнения программы приведен на рис. 4.11.
Рис. 4.11. Пример графика в полярной системе координат
Задание 4.2
Постройте графики следующих функций в полярной системе координат
(r, ) (r ≥ 0):
1. r = /2 (спираль Архимеда).
2. r = 10 sin 3 (трехлепестковая роза).
3. r = a(1 + cos ) (a > 0) (кардиоида).
4 (1 sin t ) 3 cost
.
4. y
sec t
Пример 3. Постройте график следующей функции, заданной параметрическим
способом:
x = 10 cos3 t, y = 10 sin3 t (астроида).
17
Кафедра АСОИУ
–
Афонин В. В.
Программный код решения примера
clear allclc,close all
t = 0 : 0.1 : 2*pi;
x = 10*cos(t).^3;
y = 10*sin(t).^3;
plot(x,y,'r','linew', 2)
grid on
title('\bfАстроида', 'fontsize',12)
xlabel('\bf\it\fontsize{12} - - - - - - - - x - - - - - - - -')
ylabel('\bf\it\fontsize{12} - - - - - - - - y - - - - - - - -')
axis equal
В программе использована команда axis equal, которая создает оси
координат в равных отношениях по единицам измерений.
Результат выполнения программы показан на рис. 4.12.
Рис. 4.12. График функции, заданной параметрически
Задание 4.3
1. Постройте график функции, заданной параметрическим способом
18
Кафедра АСОИУ
–
x
3a t
Афонин В. В.
3a t 2
(декартов лист).
, y
1 t3
1 t3
Пример 4. Постройте в одной системе координат графики следующих функций:
y 10 x 2 ,
y2 6 x .
Программный код решения примера
clear all, clc,close all
%% Область определения 1-й функции
x = -4 : 0.01 : 4;
%% Массив значений 1-й функции
y = 10 - x.^2;
%% Област определения 2-й функции
x2 = -5 : 0.01 : 6;
%% Массивы значений 2-й функции
y2 = sqrt(6 - x2);
y22 = -sqrt(6 - x2);
%% Диаграмма
plot(x, y, 'r', 'linew', 2)
%% удержание второго и следующих графиков
hold on
plot(x2, y2, 'linew', 2)
plot(x2, y22, 'linew', 2)
%% Координатная сетка
grid on
%% Разметка оси абсцисс
xlabel('\bf\fontsize{12} x')
%% Разметка оси ординат
ylabel('\bf\fontsize{12} y(x)')
%% Создание пояснений на линии графиков
legend('y(x)','y_2(x)','location','best')
В программе используется команда hold on, предназначенная для совмещения графиков в одной системе координат.
Результат выполнения программы показан на рис. 4.13.
19
Кафедра АСОИУ
–
Афонин В. В.
Рис. 4.13. Пример совмещения графиков функций
Задание 4.4
1. Проверьте программу при отсутствии команды hold on и с командой
hold off.
2. Определите графически решение системы уравнений
x2 + y = 10, x + y2 = 6.
3. Нанесите на диаграмму заголовок с выражениями для построенных графиков функций.
4. Задайте номер фигуры (figure) в соответствии с номером компьютера, за
которым выполняется лабораторная работа (1, 2, ).
Пример 5. Постройте графики синусоиды и косинусоиды в одной системе координат с помощью графической функции fplot.(см. help fplot).
20
Кафедра АСОИУ
–
Афонин В. В.
Функция принимает в виде строки выражение, которое следует построить. В ней же вторым аргументом выступает числовой вектор с начальной и конечной точкой изменения аргумента функции.
Программный код решения примера
clear all, clc, close all
%% Определение размеров родительского окна дисплея
g0 = get(0, 'screensize');
%% Установка пользовательского размера графического окна
M = [g0(1) + 100, g0(2) + 50, 0.8*g0(3), 0.7*g0(4)];
set(gcf, 'position',M)
%%% Диаграмма
fplot('sind(t)', [-360, 360], 'r' );
hold on;
fplot('cosd(t)', [-360, 360]);
%% Координатная сетка
grid on
%% Определение типа линии на графике
sc = findobj('type','line');
set(sc(1),'linew', 2, 'linestyle','--')
set(sc(2),'linew', 2)
%% Разметка осей координат
xlabel('\fontsize{12}t')
ylabel('\fontsize{12}f(t)')
%% Установка свойств осей диаграммы
set(gca, 'xtick', -360 : 30 : 360, 'fontsize', 9)
%% Создание пояснений на линии графиков
legend('\bfsin(t)','\bfcos(t)')
В функциях fplot включены гармонические функции от аргумента, задаваемого в градусах угловых. Для удержания двух графиков в одних координатных осях включена команда hold on. Разметка координатной сетки установлена пользователем от –360 до 360 градусов угловых с шагом в 30 градусов
угловых. Для этого используется строка 'xtick' с последующем вектором
числовых значений. Ключевое слово gca – это указатель на объект типа оси
координат.
Результат выполнения программы показан на рис. 4.14.
21
Кафедра АСОИУ
–
Афонин В. В.
Рис. 4.14. Построение графиков с помощью функций fplot
Задание 4.5
1. Постройте графики функций, заданных от аргумента, выраженного в радианах.
2. С помощью функции title включите в заголовок диаграммы аналитическое выражение построенных функций.
3. В функциях fplot в качестве аргумента функций синуса и косинуса введите первые буквы своей фамилии (латинского алфавита).
4. Изучите графическую функцию line и с помощью ее постройте функции синуса и косинуса. Постройте также прямоугольник на диаграмме.
Пример 6. Постройте следующий график функции в логарифмическом масштабе по оси абсцисс:
y = 1/x
Программный код решения примера
clear,clc,close all
x = 0.1 : 0.1 : 1000;
y = 1./x;
22
Кафедра АСОИУ
–
Афонин В. В.
%См. help semilogx
semilogx(x,y,'color',[1 0 0],'linew',3),
grid on,
title('\bf\fontsize{12}Графическая функция semilogx'),
xlabel('\bf\it\fontsize{14} - - - - - - - x - - - - - - -');
ylabel('\bf\fontsize{14} y = f(x)'),
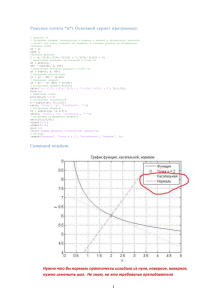
Результат выполнения программы показан на рис. 4.15.
Рис. 4.15. График функции в полулогарифмическом масштабе по оси ОХ
Задание 4.6
1. Постройте график функции y = 1/x с типом линии штрих-пунктир.
2. С помощью графической функции в центр диаграммы внесите вид функциональной зависимости, т. е. y = 1/x.
Пример 7. Постройте следующий график функции в логарифмическом масштабе по оси ординат:
y = 1/x
23
Кафедра АСОИУ
–
Афонин В. В.
Программный код решения примера
clear,clc,close all
x = 0.0001 : 0.0001 : 0.01;
y = 1./x;
% См. help semilohy
semilogy(x,y,'color',[1 0 0],'linew',2),
grid on,
title('\bf\fontsize{12}Графическая функция semilogy'),
xlabel('\bf\it\fontsize{14} - - - - - - - x - - - - - - -');
ylabel('\bf\fontsize{14} y = f(x)'),
set(gca, 'fontsize', 9, 'ytick', [1e1, 1e2, 1e3, 1e4])
ylim([1e1, 1e4]);
В программе применена принудительная оцифровка оси ординат с помощью служебного слова ytick и вектора чисел, представленных в экспоненциальной форме. Функция ylim использует для фиксации границ по оси ординат.
Результат выполнения программы показан на рис. 4.16.
Рис.4.16. График функции в полулогарифмическом масштабе по оси OY
24
Кафедра АСОИУ
–
Афонин В. В.
Пример 8. Постройте следующий график функции в логарифмическом масштабе по обеим осям координат:
y = 1/x
Программный код решения примера
clear,clc,close all
x = 0.001 : 0.001 : 1000;
y = 1./x;
% См. help loglog
loglog(x,y,'color',[1 0 0],'linew',2),
grid on,
title('\bf\fontsize{12}Графическая функция loglog'),
xlabel('\bf\it\fontsize{14} - - - - - - - x - - - - - - -');
ylabel('\bf\fontsize{14} y = f(x)'),
set(gca, 'fontsize', 9)
Пример выполнения программы показан на рис. 4.17.
Рис. 4.17. Пример графика функции в логарифмическом масштабе
25
Кафедра АСОИУ
–
Афонин В. В.
Задание 4.7
1. Постройте в логарифмическом масштабе по обеим осям координат график функции y = 1/x2.
2. Создайте разметку (оцифровку) по обеим осям координат на усмотрение
пользователя (используйте в свойствах осей set(gca, ) служебные
слова xtick, ytick).
Пример 9. Постройте распределение вероятностей Пуассоновского потока с параметром = 1.23 и значения k = 5 на отрезке времени T [0, 18].
Распределение вероятностей потока Пуассона определяется по следующей
формуле:
(T )k T
Pk (T )
e .
k!
Программный код решения примера
clear all, clc, close all
L = 1.23;
k = 5;
T = 0 : 0.5 : 18;
Pkt = ((L*T).^k).*exp(-L*T)./factorial(k);
% См. help stem
stem(T, Pkt, 'fill', 'k')
grid on
% Подготовка форматированной строки
str = sprintf('%s Распределение вероятностей потока Пуассона,%s%g, k = %d, T %s [ 0, %g ]','\bf', ...
'\newline Параметры потока: \fontsize{12}\lambda\fontsize{10} =
',L, k, '\fontsize{12}\in\fontsize{10}', T(end));
title(str);
xlabel('\bf\it - - - - - - - - t - - - - - - - -');
ylabel('\bf\fontsize{12} P_k(t)');
В программе использована графическая функция stem (от английского –
ствол, стебель). Применены также массивные операции возведения в степень,
умножения, деления, которые идут сразу после символа точки.
Пример выполнения программы показан на рис. 4.18.
26
Кафедра АСОИУ
–
Афонин В. В.
Рис. 4.18. Пример распределения вероятностей потока Пуассона
Задание 4.8
1. Постройте распределение вероятностей потока Пуассона для значений k
от нуля до 10 (исключая k = 5). При этом скорректируйте интервал времени так, чтобы было видно стремление к нулю вероятностей.
2. Выберите на свое усмотрение цвет заливки «стержней» в графической
функции stem, т. е. когда используется служебное слово fill.
27