ТРДФ

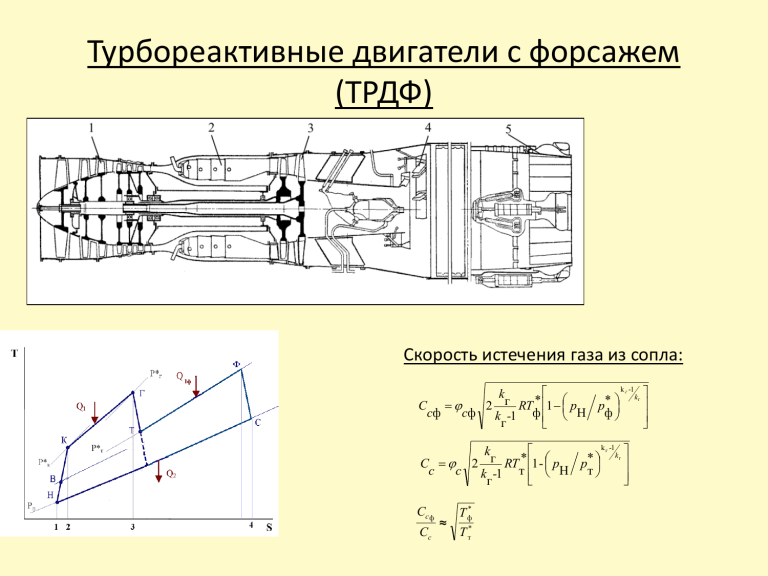
Турбореактивные двигатели с форсажем
(ТРДФ)
Скорость истечения газа из сопла:
k г -1

kг 


*
*
г

С 
2
RT 1   p
p 
сф
сф
k -1 ф   Н ф 

г

k
k г -1

kг 
*
*
г


С  2
RT 1 -  p
p 

с
с
k -1 т   Н т 


г
k
Сс ф
Сс
≈
Т ф*
Т т*
Параметры ТРДФ
Удельная тяга двигателя :
Rуд.ф  Ccф  V  Cc
Rуд.ф 
Rуд.ф
Rуд.
Т ф*
Т т*
 V  Rуд
 Т*

ф

V
 1
*
*


Тт
Тт


Т ф*
*

V  Т ф


 1
*
*

Т т Rуд  Т т


степень
форсирования
двигателя
Т ф*
при взлете:
Т ф*
Rуд.ф 
Т т*
Необходимое увеличение площади
критического сечения сопла
(принимаем условие pт*=const)
Gп  mг
 кр pт*
Т
*
т
Fкр q(кр )  mгф
 крф pт*
(1  g тф ) Т
*
ф
Fкрф q(крф )
откуда
приближенно:
Fкрф 
Fкрф
Fкр

Т ф*
Т т*
2
Параметры ТРДФ
Q1  Q1ф  ср (Т г - Т к )  ср (Т ф - Т т )  ср (Т г - Т в - Lк
Подведенная
теплота
 ср Tф - Tв 
ср
 Т ф - Т г  Lт
ср
)
максимально достижимая температура Тф определяется запасом
кислорода для горения:
 





р
Q
н





Q  Q L0
1 1ф
 1.1....1.15
при Σ=1:
TФ пред  Т в 
 гQнр
С р L0
в стендовых условиях Тф пред≈2200 К; при Мп=2,5 до 2400 К; практически Тф пред =1900 – 2100 К.
Влияние условий полета на Rуд ф и Суд ф
удельный расход топлива:
C удф 
3600Q1  Q1ф 
RудфQнр
   10; Н  11км; Т Г*  1200К
3
Оптимизация параметров двигателей с
форсажем
•
Применение: когда режимы форсажа используются в качестве основных
режимов работы.
• Задача: при заданных условиях полета и постоянстве ТГ и ТФ найти степень
повышения давления в компрессоре, соответствующую максимальной
удельной тяге
• Rуд max достигается при р*Т= р*Тmax,
xк  xк 
  
поскольку рН=const и рВ=const, это соответствует условию
хт
из уравнения
баланса
получаем
в результате
 хт  max

k
x  1 kг
1
RTн* к

RT * т 1  
k 1
к
k -1 г  хт 
г

xк
x 1 

 xк 1  к
хт


т к 

тк  2xк  1  0

xк
 xк 
   0
 хт 
и
 к оптф
 1   тк 


2


k
k 1
4
Оптимизация параметров двигателей с форсажем
с у ТРД и ТРДФ изменяются
одинаково, а температура перед
форсажной камерой по-разному
оптимальные к по удельной тяге и экономичности
совпадают
Q1  Q1ф 
Cp
г
TФ - TH   const
C уд ф 
3600Q1  Q1ф 
RудфQнр
 копт ф
 
1  Т

  1  г
 2  Тн
 

 
 тк

 k  1 2  
MП 
1 
2

  
xl
k k 1
xlf
2
1,264911
1,8
3
1,549193
2,2
4
1,788854
2,6
5
2
3
5
Зависимость показателей ТРДФ при различных
условиях полета от к, Тг и Тф.
•увеличение Тф всегда увеличивает
Rуд и Суд;
•увеличение Тг увеличивает Rуд и
уменьшает Суд;
•при изменении к оба параметра
имеют экстремум, причем , чем
больше Мп, тем меньше копт;
•с ростом Мп влияние параметров
ослабевает, т.к. уменьшается
теплоподвод в основной камере и
растет при сжатии доля
скоростного напора.
Тг=1600 К
Тг= 1200 К
6
Турбовинтовые и турбовальные двигатели
R= Rв+Rc - суммарная тяга
Тяговая работа:
Lтяг  Lтяг в  Lтяг с  Lв в  Cc  V V
Сс2  V 2
Сс2  V 2
Le  Lт  Lк  р 
 Lв 
2
2
( р  0,98  0,985)
Эквивалентная мощность
Nэ  Nв 
RcV
в
7
Показатели ТВД
На взлетном режиме или при работе на стенде
V=0 и в = 0.
Принимают:
Rв / Nв    1216 (Н кВт ) и
N э0  N в0 
Rc 0

Полный КПД двигателя:
п  Lтяг Q  N тяг GQ
1
1
п 
здесь
где
N тяг  N эв , GQ1 
QнрGт ч
3600
3600 N эв 3600в

QнрGт ч
Qнр сe
сe 
Gт ч
Nэ
удельный
расход
топлива
Н=0, Мп= 0
Н=11км, Мп=0,75
8
Оптимальное распределение работы цикла
между винтом и соплом
Тяговая работа:
Lтяг  Lвв  Cc  V V
в качестве переменной введем
отношение скоростей Сс / V
Lтяг

V2

 Le 
2


Работа, передаваемая на винт:

Сс2  V 2 
 мех
Lв   Lе 
2


 Cc  2  


2 C
   1 мехв  V  c  1
V

 V 
 

После дифференцирования:
1
 Cc 

 
 V опт мехв
принимают с=1,15…1,3.
Lтяг
0
 Cc 
 
V 
поскольку Q1 не зависит от
распределения работы,
величина (Сс/V)опт
соответствует также
максимуму полного КПД п .
9
Двухконтурные турбореактивные
двигатели (ТРДД)
Степень двухконтурности
m  GвII
GвI
Полный КПД двигателя:
0  eп
1. В двигателях с реактивной тягой с ростом Тг увеличивается е и скорость Сс.
2. При умеренных скоростях полета (трансзвук) увеличение разности (Сс-V)
снижает полетный КПД п, что тормозит рост полного КПД 0.
3. В двухконтурных двигателях часть полезной работы первого контура
передается вентилятору второго контура. При этом скорость Сс1 уменьшается
и полетный КПД сохраняет приемлемые значения.
4.Воздух второго контура направляется в сопло, что создает дополнительную
тягу, компенсирующую снижение тяги первого контура.
10
Двухконтурные турбореактивные
двигатели (ДТРД, ТРДД)
Схемы ТРДД
а), б), в) – с раздельными контурами; г)- с камерой смешения;
б)- с укороченным вторым контуром; в) – с подпорным компрессором
11
Удельные параметры ТРДД
ТРДД с раздельными контурами
тяга каждого из контуров:
RI  GгI CcI   pcI  pH FcI  GвIV
RII  GгII CcII   pcII  pH FcII  GвIIV
Удельный расход топлива:
GтлI  GтлII
cуд 
RI  RII
суммарная удельная тяга:
RудI  mRуд II
RI  RII
Rуд 

GвI  GвII
1 m
3600g тлI  mgтлII 
cуд 
1  mRуд
ТРДД с камерой смешения (по аналогии с ТРД):
R  GгCc   pcI  pн Fc  GвV
Rуд 
R
Gв
cуд 
Gтл I  Gтл II
R
GтII≠ 0, если во втором контуре также подводится топливо
12
Оптимальное распределение работы цикла в ТРДД с
раздельными контурами
(параметры I контура и степень двухконтурности известны)
Удельная тяга
двигателя:
Rуд 
условие получения
максимальной тяги
Rуд I  mRуд II
Rуд
LкII
1 m

C
C
 cI  m cII  0
LкII
LкII
Удельная работа первого контура:
Баланс энергии во втором контуре:
Тогда:
CcI
m

LкII
СсI
Поскольку:
и
ccI  V  m(ccII  V )
1 m
где LкII - работа,
передаваемая во второй
контур
СсI2  V 2
Le  mLкII 
 f m,V 
2
2
С сII
V 2
LкII II 
2
II - потери во втором
контуре (II=0,78…0,86)
CcII  II

LкII CcII
CcI
C
 m cII  0
LкII
LкII
имеем:
 CcII 

   II  1
 CcI  опт
13
Скорости на срезе каждого из сопел:
CcI   I
k 1


k


2k
p
*
Н
RTТ 1   *  
  pт  
k 1


;
CcII   II
k 1


k


2k
p
* 
Н
 
RTКII 1  
* 

k 1
 II pКII  



σII =0,94-0,96 – полный
контур
σII =0,98-0,99 –
укороченный контур
поскольку Т*т.>T*к II, должно быть р*кII>p*т
m=1; Н=0;V=0;
кΣ=25; Тг=1600К
Распределение работы, соответствующее максимуму удельной тяги,
соответствует также минимуму удельного расхода топлива.
14
Влияние внешних условий
при II=1
2
С сI2  V 2 С сII
V 2

;
2
2
С сI2  V 2
Le  mLкII 
 mLкII  LкII ;
2
L
LкII opt  e
1 m
1.
Увеличение работы внутреннего контура (вследствие роста ТГ или кI) приводит к
возрастанию Lк II и кII..
2.
Скорость полета при дозвуковых скоростях слабо сказывается на Lк I и Lк II ;
3. Увеличение высоты полета приводит к увеличению Lк I и Lк II и тем более кII из-за
снижения температуры Тн.
4. Увеличение степени двухконтурности уменьшает Lк II кII
15
Влияние параметров первого контура и степени
двухконтурности на удельные показатели ТРДД
16
Влияние параметров первого контура и степени
двухконтурности на удельные показатели ТРДД
При кII =кII опт и II=1:
СсI  СсII 
RудI  mRуд II
2Le
2 Le
3600QI
 V 2 ; Rуд 

 V 2  V ; ce 
.
1  mгQнр Rуд
1 m
1 m
1 m
к=20;
2- Н=11км, Мп=0,9; к= 25;
3- Н=11 км, Мп=2, к= 12.
1- Н=0, Мп=0,
17
Влияние степени двухконтурности на показатели ТРДД
принимаем к II= const и
суммарная удельная тяга:
m= var, тогда RудII ≈ const
Rуд 
RудI
1 m

mRуд II
1 m
c ростом m Rуд монотонно
уменьшается из-за уменьшения
первого слагаемого
с ростом m:
•эффективный КПД e уменьшается из-за роста
потерь при передаче энергии во 2-й контур
•полетный КПД п увеличивается в
соответствии с формулой
п 
2V ccI  mccII  m  1V 
,
2
ccI2  mccII
 m  1V 2
где ccII = const, а ccI уменьшается.
cуд 
3600 g тл
1  mRуд
18
Выбор параметров второго контура
в ТРДДсм (с камерой смешения)
Считаем известными для обоих контуров параметры газа (Т*т,р*т,λт) и воздуха
(Т*II,р*IIλII) перед смешением. При дозвуковых скоростях ( λ =0,3-0,5) можно принять рI ≈
рII. Поэтому должно выполняться равенство:
pт* (т )  pII*  (II )
Для камеры смешения выполняются условия сохранения:
энергии
массы
импульса (при Fсм=F1+F2)
из (1) находим Тсм
получаем
GI c pгTт*  GII c pвTк*II  GI  GII c pсмTс*м
(1)
GI  GII  Gсм
(2)
z(I ) Tт*  mz(II ) Tк*II  (1  m) z(см ) Tсм*
(3)
Tт*  mTк*II
T 
1 m
*
см
FI pт* I q(I )
Tт*

(3)
FII pк*II  II q(II )
Tк*II
находим λсм
*

FI  FII  pсм
q(см )

Tсм*
σсм=0,98…0,99
(2)
р*см
19
Оптимизация параметров второго контура в
ТРДДсм
Необходимое требование: минимизация потерь энергии при смешении потоков
перед камерой смешения:
рI=рII ;
при λ I =0,3-0,5 можно принять
тогда скорости газа и воздуха перед
камерой пропорциональны:
скорость выхода из
сопла двигателя:
pI*  pII*
C I ~ Tт* , C II ~ Tв*II .
k 1


k


2k
p
Tт*  mTк*II
* 
*

Н
Ссм  
RTсм 1   * 
 Tсм 
  pсм  
k 1
1 m


отношение удельной тяги ТРДД со смешением потоков к удельной
тяге двигателя с раздельными контурами:
Rуд 
1  mT
T
*
I
*
I
 mT
m T
*
II
*
II
2


1

2
m Tт*  Т кII
T
*
I
m T
*
II


2
2
 1,015...1,025
20
Оптимизация параметров второго контура в
ТРДДсм (с камерой смешения)
Максимальная удельная тяга достигается при минимизации потерь при
смешении потоков. Условием оптимального распределения энергии между
контурами является условие
p*  (0,97...1,05) p*
II
I
таким образом, оптимальное значение πкII здесь ниже,чем в ТРДД с
раздельными контурами
21
Двухконтурные двигатели для сверхзвуковых
скоростей (ТРДДФ)
Форсаж в ТРДД применяют, чтобы распространить их применение на
сверхзвуковые скорости полета.
При отсутствии форсажа наблюдается:
1. Резкое уменьшение Rуд по m. Отсюда – рост расхода
воздуха и миделя двигателя.
2. При больших скоростях - резкое увеличение суд с ростом т.
Форсаж в 2-х контурных двигателях используется при взлете, совершении
маневра и, в основном, для компенсации падения Rуд по скорости полета.
22
Основная схема ТРДДФ - со смешением потоков и
общей форсажной камерой:
для камеры смешения минимум
потерь соответствует условию :
pт*  pк*II
но для многорежимных двигателей
это условие невыполнимо
g тл

*
*
Gтл c p Tф  TН


G
г Qнр

Величина gтлΣ не зависит от кII и от m. Значения
кIIопт по уд. тяге и уд. расходу топлива совпадают
Доказательство:
удельная теплота, подведенная в 1-м контуре

 



Q1 I  c p TГ  TК1   TФ  TT 1   c p  TГ  TН  Lк1    TФ  TГ  Lт   c p  TФ  TН  Lт  Lк1 
c
c
c
c
p
p 
p
p



то же во 2-м контуре
поскольку


L
Q1II  c p TФ  TК2 m  c p  TФ  TН  к2 m
cp 

суммарная теплота
Lт  Lк1  Lк2 m
Q1  c p TФ  TН 1  m 
23
Влияние параметров 1-го контура на Rуд и Суд:
при заданном Тг уменьшение Rуд при увеличении m
происходит из-за уменьшения давления рсм и с.
линия А-А ( изменение Тг при т=const):
при увеличении Тг увеличивается рсм≈рт, т.е.
давление перед соплом, откуда увеличивается Rуд.ф
при этом необходимо увеличение сII.
При заданной тяге уменьшается расход воздуха и
площадь миделя и масса двигателя.
Сохранение значения Rуд при увеличении Тг возможно при одновременном
увеличении т (линия Б-Б). Размеры двигателя сохраняются, но
улучшается экономичность на малых скоростях.
24
Влияние параметров 1-го контура на Rуд и Суд:
Мп=2,
Н=11 км,
т=1
Тф=2000 К
без форсажа
Н= 0 км
Н= 11 км
25
Прямоточные двигатели
(показания к применению)
с ростом скорости и высоты полета:
• растут давление р*в и температура Т*в
перед компрессором, к уменьшается,
работа турбокомпрессора становится
менее эффективной;
• уменьшается приведенный расход воздуха
через компрессор, в связи с тем, что
величина Gв влияет на тягу сильнее, чем Rуд,
тяга двигателя снижается;
• отсутствие турбокомпрессора
существенно облегчает и удешевляет
двигатель, что важно для беспилотных и
одноразовых аппаратов.
Недостаток: необходим разгонный двигатель или катапульта.
26
Зависимость параметров перед компрессором от
скорости полета
27
Основные типы ПВРД
28
Процесс газодинамического сжатия воздуха
работа сжатия воздуха в
воздухозаборнике:
Lсж  с рTн
k 1 2
Mп ,
2
степень повышения давления в
воздухозаборнике:
pв* pн*
 k 1 2 
в 
  вх  1 
Mп 
pн pн
2


работа сжатия, записанная в форме
принятой для компрессоров ГТУ:
k
k 1
 вх
 k  1 2  k 1k
M п  вх  1
1 
  k 1 
2


c T
Lсж  c pTн  в
,
p н
 сж 
сж


k 1
откуда КПД процесса сжатия:
сж
 k  1 2  k 1k 
 1 
M п  вх  1
2



k 1 2
Mп
2
29
Термодинамический цикл ПВРД
эффективный КПД
цикла:




m рсж
k 1 2
e  m
Mп 
 1
k

1
2
2
 1 

M псж
2


k 1 2 

Mп 
  1 
2


k 1 2
Mп
1
2

КПД идеального цикла: t  1 
xв ид 1  k  1 M 2
п
2
приведенные параметры:
Le пр 
Le
Q1
 k 1 2 
;
   1 
Mп 
c pTн
cpTн
2


максимальная работа цикла
достигается при:
xвL  m р сж
связь между  и
идеальный цикл
действительный цикл
:
  k  1 2  Qнрг
Q1  c pTн m  1 
M п  
2
 L0
 
30
Термодинамический цикл ПВРД
если пренебречь потерей давления в камере
сгорания, работа расширения:

1
Lр  сpTг 1   р , где
 xв 
k -1
xв   в
k
.
удельная работа цикла:
Le 
подведенная теплота:
эффективный КПД
цикла:
КПД идеального цикла:
c pTн
сж
 m рсж

 1, где
xв


xв  1
m
сp
cp

 k  1 2 
Q1  cp Tг  Tн*  c pTн m   1 
M п 
2









m


k 1 2
р сж
e  m
Mп 
 1
k

1
2
2
 1 

M псж
2


k 1 2
Mп
1
2
t  1 

xв ид 1  k  1 M 2
п
2
k 1 2 

Mп 
  1 
2


31
Эффективность ПВРД как движителя
для ВРД любого типа полетный КПД:
скорость истечения из сопла:
учитывая, что:
получаем:
Le 
c pTн
сж
п 
1
2
cc
Vп
cc  2 Le  Vп2  Vп
2 Le
Vп2
 1.
 m рсж 
k 1 2
 1, xв  1 
M псж ,
x
2
в


xв  1
Vп  M п kRTн
m р сж
cc

k 1 2
Vп
1
M п сж
2
32
Удельные параметры ПВРД
скорость истечения из сопла
скорость полета
k 1
 p
k

н


cc  2c pгTг 1  
*
p
c
 

удельная тяга
k 1
 p
k

Vп  2c pвTн 1   н *  
  pв  


1  p p* k 1k 


н
c
 1  g тл cc 






Rуд  Vп 
 1  Vп 1  g тл  m
 1
Vп
1  p p* k 1k 




н
в








Удельный импульс тяги–
отношение тяги двигателя к
массовому расходу топлива
двигателем :
J уд






k 1
*

k
1   pн pc 


Rуд


R
1  g тл



 Vп 
m
 1
Gтл g тл
1   p p* k 1k 
 g тл

н
в






Коэффициент тяги - отношение
тяги двигателя с единицы
2 RудGв
площади характерного
Fн
c


2
R
mid
поперечного сечения к величине
 нVп2 Fmid
Fmid
скоростного напора:


k 1
*

k
1   pн pc 






1  g тл  m
 1
k

1


1   p p *  k 
н
в






33
Зависимость удельных параметров ПВРД
от числа скорости и высоты полета
• Для параметров Rуд и Jуд существуют значения
Мп опт;
• значения Мп опт увеличиваются при уменьшении
 или увеличении θ, т.е. при росте Тг;
• причина – в изменении полного КПД, связанного с
влиянием п при умеренных Мп и КПД е при
больших Мп;
• величина сR монотонно снижается из-за роста Т
* и уменьшения степени подогрева
н
С увеличением высоты полета Нп
лобовая тяга, отнесенная к площади
входа в двигатель, падает тем
значительнее, чем меньше  или
больше θ.
RудGв
RF 
 Rуд  нVп
Fн
Мп=4
34
Гиперзвуковые прямоточные воздушнореактивные двигатели (ГПВРД)
сверхзвуковое течение
сохраняется по всей
проточной части
двигателя
Идея: уменьшение степени сжатия во входном
устройстве, в результате чего:
• уменьшаются потери σвх;
• снижаются температура и давление в КС, что
уменьшает теплонапряженность конструкции
35
54
Особенности цикла ГПВРД
• при подводе теплоты к сверхзвуковому
потоку возникают дополнительные потери
• поэтому идеальный цикл ГПВРД (НВГС) не
совпадает с идеальным циклом ПВРД
(НН*Г*о Со )
обозначим:
удельная работа и КПД
для ПВРД


Lt 0  c pTн ( х  1)   1 ;
x


хp

 pн 
*
н
k 1
k
*
p
г
;  кс 
pн*
t 0  1  1 x
для ГПВРД
 
 
 1 
 
Lt  c pTн ( х  1) 




 
 
1
k 1
  k x  


 
 1
x 1




 
 
 1 
x  1  
t 

x



 
 
1
k 1
  k x  


 
 1
x 1




36
Действительный цикл ГПВРД
55
коэффициент полного давления
 вх 
pв*
pн*
;  кс 
pг*
pв*
; с 
pс*
pг*
    вх кс с
с увеличением Мп соотношение
 вх с ГПВРД   вх с ПВРД
 кс ГПВРД   кс ПВРД
растет
быстро
растет
медленно
область применения ГПВРД:
 вх кс с ГПВРД
Удельная работа и КПД:

  p  k 1k   p*  k 1k  


Le  c pTн  1  g тл 1   н *     н 
 1 
    pн    pн 



 


 вх кс с ПВРД  1
k 1
 
 *  k 1k 
k

p
p
 1  g тл 1   н *     н 
 1

p
p
   н    н 





e 
k 1

 pн*  k 

1  g тл     


 pн 


37
Расчет относительных геометрических параметров
ГПВРД
соотношение площадей входа Fн и выхода Fв воздухозаборника:
fв 
Fв q н  1

Fн q в   вх
или
k 1 2
M п 1  2
1
2
fв 
k
k 1
  k 1 2

2
1

M
1



п
с

2


1



где
  св V
статическая температура при
выходе из воздухозаборника:
 k 1 2
Т в  1 
M п 1  2
2


Т

н
38
39
Влияние формы камеры сгорания на показатели ГПВРД
при θ=сonst:
проходное сечение камеры
сгорания:
f кс 
Fв 1  g тл qв  *


Fг
qг  кс
1. камера постоянного
сечения
2. камера постоянного
давления
предельное значение θ*=Тг*/ Тн*
(соответствует λг=1)
3. сужающаяся камера
Для расширения диапазона работы ГПВРД
камера на начальном участке должна иметь
постоянное сечение (вариант 1) до
достижения λг=1, а затем выполняться
расширяющейся для выполнения условия М=1.
40
Параметры реактивного сопла ГПВРД:
степень понижения давления в сопле
определяется скоростью полета:
pг* pн* вх кс
 k 1 2 
с 

  вх кс 1 
Mп 
pн
pн
2


k
k 1
скорость истечения из сопла:
сс  с
  p  k 1k 
2k
RTн* 1   н*   
k 1
  pг  


   k 1k 
2k
p
RTн* 1   н*  
k 1
  pc  


k 1
соотношение между коэффициентами φс и σс,
задающими потери в сопле:
изменение проходного сечения сопла:
f с  f кс

 k
pн

1   *
p



 c2   н в х кс с k1

 k
pн

1   *
p


 н в х кс 
qг 
qс  с
41
Пульсирующие ВРД
Комбинированные двигатели для
больших высот и скоростей полета
Турбопрямоточные двигатели (ТПД)
на основе ТРДФ
решающее преимущество:
высокая эффективность
двигателя в условиях
больших скоростей полета.
на основе ТРДДФ
достигается максимальная
экономичность при
дозвуковых скоростях, но
сохраняется высокая
эффективность на
крейсерских режимах при
М=4,5…5
43
Ракетно-турбинные двигатели (РТД)
со смешением потоков
3,4 – насосы горючего и окислителя;
5 – газогенератор; 7 – стабилизатор;
8 – камера сгорания; 9 -сопло
с раздельными контурами
3,5 – насосы окислителя и горючего;
4 – газогенератор; 7,8 – камеры
сгорания: воздушная и ракетная; 9,10
- сопла
44
Термодинамический цикл РТД
ракетный цикл:
Н-КГ-ПГ –испарение и горение топлива,
ПГ-К – расширение в турбине,
К-К1 – смешение с воздухом (для схемы 1),
К-Г – горение топлива в воздухе,
Г-С – расширенние в сопле
воздушный цикл:
К- КВ - сжатие в компрессоре
Температура ТГ может быть такой же, как в ТРДФ и выше, давление рГ
выше, чем в ТРД при таком же к.
индекс «0» - при H=0, M=0
индекс «расч» – Мп=4, Н>11 км
режимы
1- РТД
2- ПВРД
45
Использование хладоресурса криогеннных топлив
пароводородный РТД
1-насос жидкого водорода,
2- подогреватель водорода,
7- камера сгорания
Тг=1200 К, gтл= 1/38,
к0 max= 5 (на старте)
не используется
хладоресурс водорода
РТД с ожижением воздуха
2- отбор воздуха, 3теплообменник-конденсатор,
4-насос жидкого воздуха, 5насос жидкого водорода, 7водородо-воздушный
генератор
gтл увеличивается в 3-5 раз,
поэтому увеличивается к0max
и величина е.
Результат – более низкая, чем в ТРДФ лобовая масса и более высокая Rуд.
46
Комбинированные двигатели для
больших высот и скоростей полета
Турбопрямоточные двигатели (ТПД)
на основе ТРДФ
решающее преимущество:
высокая эффективность
двигателя в условиях
больших скоростей полета.
на основе ТРДДФ
достигается максимальная
экономичность при
дозвуковых скоростях, но
сохраняется высокая
эффективность на
крейсерских режимах при
М=4,5…5
47
Ракетно-турбинные двигатели (РТД)
со смешением потоков
3,4 – насосы горючего и окислителя;
5 – газогенератор; 7 – стабилизатор;
8 – камера сгорания; 9 -сопло
с раздельными контурами
3,5 – насосы окислителя и горючего;
4 – газогенератор; 7,8 – камеры
сгорания: воздушная и ракетная; 9,10
- сопла
48
Термодинамический цикл РТД
ракетный цикл:
Н-КГ-ПГ –испарение и горение топлива,
ПГ-К – расширение в турбине,
К-К1 – смешение с воздухом (для схемы 1),
К-Г – горение топлива в воздухе,
Г-С – расширенние в сопле
воздушный цикл:
К- КВ - сжатие в компрессоре
Температура ТГ может быть такой же, как в ТРДФ и выше, давление рГ
выше, чем в ТРД при таком же к.
индекс «0» - при H=0, M=0
индекс «расч) – Мп=4, Н>11 км
режимы
1- РТД
2- ПВРД
49
Использование хладоресурса криогеннных топлив
пароводородный РТД
1-насос жидкого водорода,
2- подогреватель водорода,
7- камера сгорания
Тг=1200 К, gтл= 1/38,
к0 max= 5 (на старте)
не используется
хладоресурс водорода
РТД с ожижением воздуха
2- отбор воздуха, 3теплообменник-конденсатор,
4-насос жидкого воздуха, 5насос жидкого водорода, 7водородо-воздушный
генератор
gтл увеличивается в 3-5 раз,
поэтому увеличивается к0max
и величина е.
Результат – более низкая, чем в ТРДФ лобовая масса и более высокая Rуд.
50
Ракетно-прямоточные двигатели (РПД)
с совмещенной камерой смешения и
горения (а), с раздельными камерами (б).
1- воздухозаборник, 2 – газогенератор,
3- сопло газогенератора, 4 – камера
смешения (и сгорания), 5 – корпус
прямоточного контура, 6 – реактивное
сопло.
характерные параметры:
m
Gв
1 коэффициент

Gтл g тл эжекции
*
коэффициент
pпг
p  * ;  пг избытка окислителя
pв
керосин +азотная к-та,
пг=0,8; Σ = 1,25, рֿ=50
с дожиганием
без дожигания
твердое топливо,
рпг= 1,9 МПа, Н=12 км
Jуд
СR
51