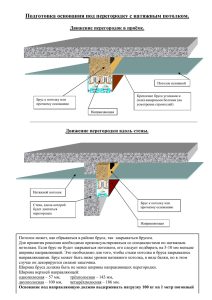
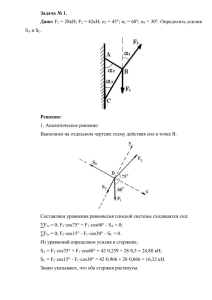
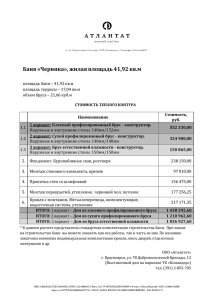
РПР 1. Расчёт ступенчатого бруса δ l2/2 l2/2 l1/2 l1/2 Стальной ступенчатый брус (рис. 1) жёстко защемлён одним концом, другой конец бруса до F1 нагружения находится на расстоянии , от опорной поверхности. Он нагружен силами F1, F3, d2 после чего, его температура повышается на ΔТ. F3 Требуется определить реакции опор и построить эпюры N, , u при следующих данных: Рис.1. F1 = 100 кН, F3 = 100 кН, d1 = 8 см, d2 = 6 см, = 0,2 мм, ΔТ = 20 К, l1 = 1 м, l2 =1 м, , E = 2105 МПа, = 12,510-6 К–1, nт = 1,5 и подобрать марку стали. d1 1 Брус без нижней опорной поверхности 1.1. Делим брус на участки (рис. 2, а): I, II, III, IV (сверху вниз; границами участков являются: начало и конец бруса; сечения, где приложены силы и сечения, где меняется размер поперечного сечения). 1.2. Определяем нормальные силы на каждом участке. Для этого используем метод сечений (нормальная сила в поперечном сечении численно равна сумме проекций на нормаль к сечению одну сторону от этого сечения). N I F1 F 2 100 100 200 кН ; N II F1 100 кН ; N III F1 100 кН ; N IV 0 . Строим эпюру нормальных сил (рис. 2, б). N, кН σ , МПа 4х500 а) 80 100 кН 60 б) + 200 в) + в) 37,79 19,89 u, мм 0,2195 0,3942 0,6076 100 35,37 + 0,7326 100 кН Рисунок 2 – Брус без нижнего основания 1.3. Определяем площади поперечных сечений на каждом участке. d 12 8 2 AI AII 50,27 см 2 ; 4 4 2 d 2 62 AIII AIV 28,27 см 2 . 4 4 1.4. Определим нормальные напряжения на каждом участке: N 200 10 3 I I 37,79 МПа ; AI 50,27 10 4 II N II AII 100 10 3 19,89 МПа ; 50,27 10 4 N IV 100 10 3 0. 35,37 МПа ; IV 4 AIV AIII 28,27 10 Строим эпюру нормальных сил (рис. 2, в). 1.5. Определяем удлинения каждого участка III lI N III N I lI E AI l I T 200 10 3 0,5 2 10 11 50,27 10 4 1,25 10 5 0,5 20 0,2195 мм ; N II l II 100 10 3 0,5 l II l II T E A II 2 10 11 50,27 10 4 1,25 10 5 0,5 20 0,1747 мм ; N III l III 100 10 3 0,5 l III l III T E A III 2 10 11 28,27 10 4 l IV 1,25 10 5 0,5 20 0,2134 мм ; N IV l IV l IV T 0 1,25 10 5 0,5 20 0,1250 мм . E AIV 1.6. Определяем перемещения границ участков бруса и 0 , I 0 (закреплено); и I , II u 0 , I l I 0 0,2195 0,2195 мм; и II , III u I , II l II 0,2195 0,1747 0,3942 мм; и III, IV u II, III l III 0,3942 0,2134 0,6076 мм; и IV, V u III, IV l IV 0,6076 0,125 0,7326 мм. Строим эпюру перемещений (рис. 2, г). 1.7. Назначим марку стали из условия прочности при центральном растяжении-сжатии: т наиб n т 37,79 1.5 56,69 МПа. Этому пределу текучести будет соответствовать самая низкопрочная из сталей, ст.1, у которой σт = 190 МПа. 2 Брус с нижней опорной поверхностью После приложения нагрузки и изменения температуры брус удлинится и коснётся нижней опорной поверхности. В обеих опорных поверхностях, появятся реакции R A и R B (рис. 3, а). 2.1. Определяем степень статической неопределимости (ССН) системы ССН = КН – КНУС = 2 – 1 = 1 – система один раз статически неопределима. Здесь: КН – количество неизвестных реакций опор (в нашем случае – 2); КНУС – количество независимых уравнений статики (в нашем случае – 1, сумма вертикальных проекций всех сил). 2.2. Раскрываем статическую неопределимость. Для этого: 2.2.1. Выражаем нормальные силы на каждом участке через R B (составляем необходимые уравнений статики) N I 200 10 3 R B ; N II N III 100 10 3 R B ; N IV R B . 2.2.2. Составляем уравнение совместности деформаций, выражающее закономерность деформаций всего бруса (в нашем случае – общее удлинение бруса = δ). l I l II l III l IV ; N I lI E AI N II l II E AII N III l III E AIII N IV l IV E AIV (2) ( l I l II l III l IV ) T . 2.2.3. Решаем совместно уравнения (1), (2) и раскрываем статическую неопределимость 200 10 3 R B 0,5 4 100 10 3 R B 0,5 3 R B 0,5 2 10 50,27 10 2 10 50,27 10 2 10 28,27 10 4 R B 0,5 0,2 10 3 1,25 10 5 ( 2 ) 20 ; 2 10 11 28,27 10 4 11 4 100 10 11 11 RB = 194,58 кН. 2.3. Определяем нормальные силы на каждом участке и строим эпюру N (рис. 2, б): N I 200 194,58 5,42 кН ; N II N III 100 194,58 94,58 кН ; N IV 194,58 кН. 2.4. Определим нормальные напряжения на каждом участке и строим эпюру σ (рис. 2, в): N 5,42 10 3 I I 1,079 МПа ; A I 50,27 10 4 A II 94,58 10 3 18,81 МПа ; 50,27 10 4 N, кН σ , МПа u, мм RA а) 80 б) 5,42 в) в) 94,58 18,81 1,079 4х500 N II 100 кН 60 0,2 II 100 кН 194,58 RB 0, 1277 33,46 0,2057 + 68,86 0,2445 0,20003 Рисунок 3 – Брус с нижней опорной поврхностью III N III IV N IV A III AIV 94,58 10 3 33,46 МПа ; 28,27 10 4 194,58 10 3 68,86 МПа . 28,27 10 4 2.5. Определяем удлинения каждого участка N I lI 5,42 10 3 0,5 lI lI T E AI 2 10 11 50,27 10 4 1,25 10 5 0,5 20 0,1277 мм ; N II l II 94,58 10 3 0,5 l II l II T E AII 2 10 11 50,27 10 4 1,25 10 5 0,5 20 0,0780 мм ; N III l III 94,58 10 3 0,5 l III l III T E AIII 2 10 11 28,27 10 4 l IV 1,25 10 5 0,5 20 0,0414 мм ; N IV l IV 194,58 10 3 0,5 l IV T E AIV 2 10 11 28,27 10 4 1,25 10 5 0,5 20 0,0471мм . 2.6. Определяем перемещения границ участков бруса и строим эпюру перемещений (рис. 2, г): и 0 , I 0 (закреплено); и I , II u 0, I l I 0 0,1277 0,1277 мм; и II, III u I , II l II 0,1277 0,078 0,2057 мм; и III, IV u II, III l III 0,2057 0,0414 0,2471 мм; и IV, V u III, IV l IV 0,2471 0,04707 0,20003 мм; Вычислим погрешность решения: u IV.V 100% 0,20003 0,2 100% 0,015 % 3 %. 0,2 Погрешность в пределах допускаемой, следовательно, статическая неопределимость раскрыта верно. 2.7. Назначим марку стали из условия прочности при центральном растяжении-сжатии: т наиб n т 68,86 1.5 103,3 МПа . Этому пределу текучести будет соответствовать самая низкопрочная из сталей, ст.1, у которой σт = 190 МПа. Примечания: 1. Оформление РПР должно соответствовать требованиям: СТО СГАУ 02068410-004-2018. Общие требования к учебным текстовым документам [Текст]. – Самара: Изд-во Самарского университета, 2018. – 31 с. 2. Любые нарушения стандарта, потребует переоформлене работы.