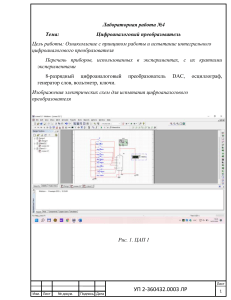
Задача 1. Расчет разветвленной линейной цепи постоянного тока с несколькими источниками электрической энергии Для электрической цепи (рисунок 1) известны ЭДС Е1 , Е2 источников питания, а также сопротивления R1 R6 . Рисунок 1 Параметры элементов схемы приведены в таблице 1. Та б л и ц а 1 Вариант Е1 Е2 R1 R2 R3 В 3 95 R4 R5 R6 5 6 7 Ом 35 9 4 5 Необходимо: 1. Составить систему уравнений для определения токов путем непосредственного применения законов Кирхгофа. Решать эту систему уравнений не следует. 2. Определить токи ветвей методом контурных токов. 3. Составить баланс мощностей. Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 3 Решение 1. Выберем произвольно и укажем положительные направления токов. Определим число ветвей, т.е. число неизвестных токов, и узлов, которые обозначим цифрами (рисунок 2). Определим сколько уравнений нужно составить по первому закону Кирхгофа и сколько по второму. Для схемы (рисунок 2) число ветвей в – 6, число узлов y – 4. По первому закону тока Кирхгофа необходимо составить 3 уравнения, и по второму – 3 уравнения. Рисунок 2 Общее число уравнений равно числу неизвестных токов, т.е. 6. Составим уравнения по первому закону Кирхгофа для узлов 1, 2 и 3: ⎧ I1 I 3 I 6 0, I1 I 2 I 5 0, ⎨ ⎩ I 2 I 4 I 6 0. Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 4 По второму закону Кирхгофа составим 3 уравнения (направление обхода контура примем по направлению часовой стрелки): ⎧ I1 R1 I 5 R5 I 3 R3 E1 , I 2 R2 I 4 R4 I 5 R5 E2 , ⎨ ⎩ I3 R3 I 4 R4 I 6 R6 0. 2. Выполним расчет цепи по методу контурных токов. Выделим в схеме три независимых контура с контурными токами I11, I22, I33. Направление контурных токов можно выбрать произвольно, но для единообразия последующих формул и расчетов зададим контурным токам направления, совпадающие с направлениями обхода контуров (в данном случае с направлением движения часовой стрелки) (рисунок 3). Рисунок 3 Для определения контурных токов цепи составим три уравнения: Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 5 R11I11 R12 I 22 R13 I 33 E11 , ⎧ R21I11 R22 I 22 R23 I 33 E22 , ⎨ ⎩ R31I11 R32 I 22 R33 I33 E33 . где R11, R22, R33 – контурные сопротивления; R12=R21, R13=R31, R23=R32 – взаимные сопротивления контуров; E11, E22, E33 – контурные ЭДС. Контурные сопротивления: R11 = R1 + R3 + R5 = 9 + 5 + 6 = 20 Ом; R22 = R2 + R4 + R5 = 4 + 5 + 6 = 15 Ом; R33 = R3 + R4 + R6 = 5 + 5 + 7 = 17 Ом; Взаимные сопротивления контуров: R12 = R21 = R5 = 6 Ом; R13 = R31 = R3 = 5 Ом; R23 = R32 = R4 = 5 Ом; Контурные ЭДС: E11 E1 95 B; E22 E2 35 B; E33 0 B; Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 6 После подстановки найденные значений в исходную схему получим: ⎧ 20 I11 6 I 22 5I 33 95; 6 I11 15I 22 5I 33 35; ⎨ ⎩ 5I11 5I 22 17 I 33 0. Решим систему относительно неизвестных: R11 R12 R13 20 6 5 R21 R22 R31 R32 R23 15 6 5 3313; R33 17 5 5 E11 1 E22 R12 R22 R13 95 6 5 R23 35 6 5 26295; E33 R32 R33 0 E11 R13 20 95 5 2 R21 R31 E22 E33 R23 15 35 5 23090; R33 17 0 5 R11 3 R21 R12 R22 E11 20 6 95 E22 15 6 35 14525; R11 R31 R32 E33 5 5 17 5 0 Вычислим контурные токи, пользуясь найденными определителями: I11 1 26295 7,94 A; 3313 Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 7 I 22 2 23090 6,97 A; 3313 I 33 3 14525 4,38 A; 3313 Токи ветвей равны алгебраическим суммам контурных токов. При этом знаки у контурных токов определим по следующему правилу: если направление контурного тока совпадает с направлением тока ветви, то он записывается со знаком плюс, если не совпадает – со знаком минус. Найдём токи в отдельных ветвях цепи: I1 I11 7,94 A; I 2 I 22 6,97 A; I 3 I11 I 33 7,94 4,38 3,56 A; I 4 I 22 I 33 6,97 4,38 2,59 A; I 5 I11 I 22 7,94 6,97 0,97 A; I 6 I 33 4,38 A; Выполним проверку. Проверка по первому закону Кирхгофа для узла 1 показала, что расчеты выполнены правильно: I1 I 3 I 6 0; 7,94 3,56 4,38 0; Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 8 3. Cоставим баланс мощностей для исходной схемы, изображенной на рисунке 2. При составлении баланса мощностей найдём вначале мощности источников: Pист I1 E1 I 2 E2 7,94 95 6,97 35 998,3Вт. Найдём мощность, которую потребляют приемники: Pпр I12 R1 I 22 R2 I32 R3 I 42 R4 I 52 R5 I 62 R6 7,942 9 6,97 2 4 3,562 5 2,592 5 0,97 2 6 4,382 7 998,56 Вт; Таким образом, баланс мощностей выполняется. Задача № 2. Расчёт разветвлённой цепи однофазного синусоидального тока Электрическая цепь (рисунок 4), подключенная к сети переменного тока с напряжением U и частотой 50 Гц. Рисунок 4 Параметры элементов схемы приведены в таблице 2. Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 9 Та б л и ц а 2 Вариант U, B R1, Oм С1, мкФ R2, Oм С2, мкФ L3, мГн 3 380 8 400 7 600 15 Необходимо: 1) рассчитать сопротивления реактивных элементов цепи; 2) определить действующие значения токов в ветвях с помощью комплексных чисел; 3) по полученным комплексным изображениям записать выражения для мгновенных значений напряжения на разветвлённом участке цепи и токов в ветвях; 4) составить баланс активных и реактивных мощностей; 5) построить векторную диаграмму, на которой изобразить векторы всех токов и напряжений на участках цепи. Решение 1. Сопротивления реактивных элементов цепи: X L 3 L3 2 f L3 2 50 15 10 3 4,712Ом; X C1 1 1 1 7,958Ом; C1 2 f C1 2 50 400 106 X C2 1 1 1 5,305Ом; C2 2 f C2 2 50 600 10 6 Определим комплексные сопротивления отдельных ветвей цепи: Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 10 Z1 R1 jX C2 8 j 7,958 11, 28 e j 44,85Ом; Z 2 R2 jX C2 7 j5,305 8,783 e j 37,24Ом; Z 3 jX L 3 j 4,712 4,712 e j 90Ом; Преобразованная цепь представлена на рисунке 5. Рисунок 5 Осуществляем эквивалентные преобразования для цепи. Параллельно соединенные элементы Z 2 и Z 3 заменяем одним эквивалентным Z 23 (Z 2 Z3 ) 8,783 e j 37,24 4,712 e j 90 41,14 e j 52,76 Z 23 5,85 e j 57,63 j 4,87 (Z 2 Z3 ) 7 j5,305 j 4,712 7,03 e 3,15 j 4,93Oм; После преобразования схема упрощается и состоит из двух элементов, включенных последовательно (рисунок 6). Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 11 Рисунок 6 Определяем эквивалентное сопротивление всей цепи: Z эк Z1 Z 23 8 j 7,958 3,15 j 4,93 11,15 3,03 j 11,55 e j15,47Ом; 2. Общий ток цепи определяем по закону Ома: I1 U 380·e j 0 31,7 j8,78 32,9 e j15,47 A; j15,47 Z эк 11,55 e Определим напряжение на участке 1-2 цепи: U 1 I1 Z1 32,9 e j15,47 11,28 e j 44,85 323,9 181,2 j 371,1 e j 29,38 B; Определим напряжение на участке 2-3 цепи: U 23 I1 Z 23 32,9 e j15,47 5,85 e j 57,63 55, 2 184, 4 j 192,5 e j 73,1 B; Определим токи в ветвях после разветвления, используя закон Ома: Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 12 U 23 192,5 e j 73,1 I2 7,75 20,64 j 22,05 e j110,34 A; j 37,24 Z 2 8,73 e U 23 192,5 e j 73,1 I3 39,1 11,7 j 40,85 e j16,9 A; j 90 Z3 4,712 e Запишем мгновенные значения токов: i1 2 I1 sin(t i1 ) 2 32,9 sin(t 15, 47) 46,53 sin(t 15, 47) A; i2 2 I 2 sin(t i2 ) 2 22,05 sin(t 110,34) 31,18 sin(t 110,34) A; i3 2 I 3 sin(t i3 ) 2 40,85 sin(t 16,9) 57, 77 sin(t 16,9) A. Запишем мгновенные значения напряжений на участке цепи с параллельным соединением ветвей: u23 2U 23 sin(t u23 ) 2 192,5 sin(t 73,1) 272,2 sin(t 73,1) B. 4. Составим баланс активных и реактивных мощностей. Эти балансы показывают, что активные и реактивные мощности на входе должны быть равны сумме соответственно активных и реактивных мощностей всех потребителей. Комплексная мощность цепи с активным, индуктивным и емкостным сопротивлениями: * S U I. Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 13 S 380 e j 0 32,9 e j15,47 12049 j 3335 B A; Активную мощность потребителей рассчитаем как произведение активного сопротивления участка на квадрат действующего значения тока этого участка. Суммарная активная мощность потребителей: Pпoтр I 21 R1 I 2 2 R2 32,92 8 22,052 7 7772 3055 12063 Вт. Реактивную мощность потребителей определяем как произведение квадрата тока реактивного элемента на его сопротивление. Причем мощность катушки индуктивности положительная, а конденсаторов – отрицательна. Qпoтр X C1 I 21 X C2 I 2 2 I 23 X L3 7,958 32,92 22,052 ( 5,305) 40,852 4,712 3330 вар. Таким образом, баланс активных и реактивных мощностей соблюдается. 5. Векторная диаграмма размещена на комплексной плоскости +1 и +j (рисунок А.1). Задача № 3. Расчёт трёхфазной цепи К трёхфазной симметричной сети с линейным напряжением Uл подключена цепь (рисунок 7). Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 14 Рисунок 7 Значения линейного напряжения Uл, активного R, индуктивного XL и ёмкостного XC сопротивлений приёмников приведены в таблице 3. Та б л и ц а 3 Вариант UЛ, B R1, Oм ХL1, Ом ХС2, Ом R2, Oм ХС3, Ом 3 380 8 4 4 8 4 Необходимо: 1) рассчитать токи при соединении приёмников по схеме «звезда» с включенным и отключенным нейтральным проводом; 2) рассчитать токи при соединении приёмников по схеме «треугольник»; 3) составить баланс мощностей для всех случаев; 4) для всех случаев построить векторные диаграммы токов и топографические диаграммы напряжений. Решение При анализе трехфазных электрических цепей используем метод комплексных чисел. Предварительно определим комплексные сопротивления фаз приемников: Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 15 Z a R1 jX L1 8 j 4 8,94 e j 26,36Ом; Z b R2 jX C 2 8 j 4 8,94 e j 26,36Ом; Z c jX C 3 j 4 4 e j 90Ом. Комплексные сопротивления фаз не равны, следовательно, нагрузка несимметричная. 1. Выполним расчеты при соединении приемников по схеме «звезда» с включенным нейтральным проводом (рисунок 8). Рисунок 8 Сопротивления нейтральных проводов и нейтрального провода примем равным нулю и поэтому не будем их учитывать при расчете. Так как в схеме есть нейтральный провод, то комплексные фазные напряжения приемника будут равны комплексным фазным напряжениям источника: U a U A ;U b U B ;U c U C . Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 16 Действующее значение фазного напряжения источника определим из соотношения: Uф U л 380 220B. 3 3 Учитывая симметричный характер трехфазного источника комплексные фазные напряжения: U A 220 e j 0 220 j 0 B; U B 220 e j120 110 j190 B; U C 220 e j120 110 j190 B. Комплексные токи в линейных проводах (фазные токи нагрузки) определяем по закону Ома: Ua 220 e j 0 I A Ia 24,6 e j 26,36 22,04 j10,9 A; j 26,36 Z a 8,94 e I B Ib Ub Zb 220 e j120 24,6 e j 93,64 1, 46 j 24,56 A; j 26,36 8,94 e Uc 220 e j120 IC I c 55 e j 210 47,5 j 27,7 A. j 90 Zc 4e Ток в нейтральном проводе находим согласно первому закону Кирхгофа: Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 17 I N I a I b I c 22,04 j10,9 1, 46 j 24,56 47,5 j 27,7 26,92 j 63,16 68,66 e j112,87 A. Составим баланс мощностей: S ист S пр . * * * S ист U A I A U B I B U C I C 220 e j 0 24,6 e j 26,36 220 e j120 24,6 e j 93,64 220 e j120 55 e j 210 10831 j 5397 12120,6 e j 26,7 B A; S пр R1I a2 R2 I b2 jX L1 I a2 jX C2 I b2 jX C3 I c2 8 24,6 2 8 24,6 2 j 4 24,62 j 4 24,62 j 4 552 10862 j 5346 12106,3 e j 26,7 B A; Векторная и топографическая диаграммы представлены на рисунке А.2. Построение начнем с расположения векторов фазных напряжений U a ,U b ,U c (векторы сдвинуты друг относительно друга на 120°). При построе- нии векторной диаграммы токов учтем, что токи в фазах сдвинуты относительно фазных напряжений на фазные углы сдвига фаз: a 26,36 – активноиндуктивная нагрузка, b 26,36 – активно-емкостная нагрузка, c 90 – емкостная нагрузка. Действующее значение тока в нейтральном проводе равно 68,66 А, а его начальная фаза N 112,87 . Строим векторы токов с учетом углов сдвига фаз. Вектор тока в нейтральном проводе можно построить двумя способами: Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 18 как сумму векторов в соответствии с выражением I N I a I b I c или I N в соответствии с расчетными данными. 2. Выполним расчеты для случая, когда приёмники соединены по схеме «звезда» с отключенным нейтральным проводом. Так как в схеме с нейтральный провод отсутствует, то фазные напряжения приемника не будут равны фазным напряжением источника из-за смещения нейтрали: U a U A U nN ;U b U B U nN ;U c U C U nN . Напряжение смещения нейтрали: U nN U A Ya U B Yb U C Yc Ya Yb Yc , где Ya , Yb ,Yc – комплексные проводимости фаз приемника, См. Находим комплексные проводимости фаз приемника: Ya 1 1 0,11 e j 26,36 0,099 j 0,049См, j 26,36 Z a 8,94 e Yb 1 1 0,11 e j 26,36 0,099 j 0,049См, j 26,36 Z b 8,94 e Yc 1 1 0, 25 e j 90 0,0002 j 0,25См. j 90 Zc 4 e Определяем напряжение смещения нейтрали: Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 19 U nN 220 e j 0 0,11 e j 26,36 220 e j120 0,11 e j 26,36 220 e j120 0, 25 e j 90 0,11 e j 26,36 0,11 e j 26,36 0, 25 e j 90 213,72 e j165,01 206,68 j 54, 4 B. Найдем напряжения на фазах приемника: U a 220 (206,68 j54,4) 426,68 j54,4 430,13 e j 7,28 B; U b 110 j190 (206,68 j54, 4) 96,68 j135,6 166,54 e j 54,43 B; U c 110 j190 (206,68 j54,4) 96,68 j 244, 4 262,83 e j 68,41 B. Линейные напряжения U ab ,U bc ,U ca в случае генератора большой мощности не изменяются. Токи в линейных проводах (фазные токи нагрузки) определяем по закону Ома: Ua 430,13 e j 7,28 I A Ia 48,11 e j19,36 45,36 j16,04 A; j 26,36 Za 8,94 e Ub 166,54 e j 54,43 I B Ib 18,63 e j 28,07 16,44 j8,77 A; j 26,36 Zb 8,94 e Uc 262,83 e j 68,41 IC Ic 65,7 e j158,41 61,8 j 24,81A; j 90 Zc 4e Выполним проверку расчетов с помощью первого закона Кирхгофа: Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 20 I a I b I c 45,36 j16,04 16, 44 j8,77 61,8 j 24,81 0. Баланс мощностей: S ист S пр . * * * S ист U A I A U B I B U C I C 220 e j 0 48,11 e j19,36 220 e j120 18,63 e j 28,07 220 e j120 65,7 e j158,41 8635,05 j15643,9 17868,8 e j 61,08 B A; S пр R1I a2 R2 I b2 jX L1 I a2 jX C2 I b2 jX C3 I c2 8 48,112 8 18,632 j 4 48,112 j 4 18,632 j 4 65,7 2 21243,6 j 9495,9 23269,4 e j 24,06 B A; Векторные диаграммы представлены на рисунке А.3. Строим симметричную топографическую диаграмму напряжений генератора и вектор смещения нейтрали U nN 213,72 e j165,01 B. Векторы, соединяющие точку n и точки a, b, c соответственно будут векторами фазных напряжений приемника U a ,U b ,U c . Из точки n строим векторы токов I a , Ib , I c с учетом сдвига фаз относительно напряжений a 26,36,b 26,36,c 90. 3. Выполним расчет трехфазной цепи при соединении приемников по схеме «треугольник» (рисунок 9). Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 21 Рисунок 9 При таком соединении каждая фаза приемника оказывается включенной на линейное напряжение источника и эти же напряжения являются фазными напряжениями приемника: U ab U AB ;U bc U BC ;U ca U CA. При известных фазных напряжениях U a ,U b ,U c источника линейные напряжения на выводах несимметричной трехфазной нагрузки, соединенной в треугольник, находим как разность соответствующих фазных напряжений: U AB U A U B ;U BC U B U C ;U CA U C U A . U AB 220 (110 j190) 330 j190 380 e j 30 B; U BC 110 j190 (110 j190) j380 380 e j 90 B; U CA 110 j190 220 330 j190 380 e j150 B. Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 22 Определим комплексные сопротивления фаз приемников: Z ab R1 jX L1 8 j 4 8,94 e j 26,36Ом; Z bc R2 jX C 2 8 j 4 8,94 e j 26,36Ом; Z ca jX C 3 j 4 4 e j 90Ом; Комплексные фазные токи нагрузки определяем по закону Ома: I ab I bc I ca U ab Z ab U bc Zbc U ca Z ca 380 e j 30 42,5 e j 3,64 42,41 j 2,72 A; j 26,36 8,94 e 380 e j 90 42,5 e j 63,64 18,9 j 38,07 A; j 26,36 8,94 e 380 e j150 95 e j 240 47, 4 j82,33 A. j 90 4e Линейные токи определяем согласно первому закону Кирхгофа: I A I ab I ca 42,41 j 2,72 (47,4 j82,33) 89,81 j 85,05 123,7 e j 43,43 A; I B I bc I ab 18,9 j 38,07 (42,41 j 2,72) 23,51 j 40,79 47,08 e j119,75 A; I C I ca I bc 47,4 j82,33 (18,9 j 38,07) 66,3 j 44, 26 79,72 e j146,1 A. Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 23 Баланс мощностей: * * * S ист U A I A U B I B U C I C 220 e j 0 123,7 e j 43,43 220 e j120 47,08 e j119,75 220 e j120 79,72 e j146,1 28815 j 36241 46299,97 e j 51,5 B A; S пр R1I ab2 R2 I bc2 jX L1 I ab2 jX C2 I bc2 jX C3 I ac2 8 42,52 8 42,52 j 4 42,52 j 4 42,52 j 4 952 28900 j 36200 46321,17 e j 51,5 B A; Векторные диаграммы представлены на рисунке А.4. Строим топографическую диаграмму напряжений. Векторы фазных токов I ab , I bc , I ca соответственно откладываем относительно векторов фазных (линейных) напряжений U ab ,U bc ,U ca под углами a 26,36,b 26,36, c 90. Затем строим векторы линейных токов I A , I B , I C . Длина и направление соответствуют расчетным данным. Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 24 СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 1 Жаворонков М. А. Электротехника и электроника : учеб. пособие для студ. спец. вузов, техн. отд-ний гуманит. вузов и вузов неэлектротехн. профиля : доп. УМО по образованию в обл. энергетики и электротехники / М. А. Жаворонков, А. В. Кузин. – М. : Академия, 2005. ‒ 394 с. 2 Касаткин А. С. Электротехника : учеб. для студ. неэлектротехн. спец. вузов : рек. Минобразования России / А. С. Касаткин, М. В. Немцов. – 11-e изд. – М. : Академия, 2007. ‒ 539 с. 3 Немцов М. В. Электротехника / М. В. Немцов, М. Л. Немцова. – М.: Академия, 2013. – 480 с. – ISBN 978-5-4468-0432-0. – Текст : непосредственный. 4 Рекус Г. Г. Сборник задач и упражнений по электротехнике и основам электроники / Г. Г. Рекус, А. И. Белоусов. – М. : Высшая школа, 2001. − 240 с. Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 25 ПРИЛОЖЕНИЕ А (обязательное) Векторные диаграммы Рисунок А.1 Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 26 Рисунок А.2 Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 27 Рисунок А.3 Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 28 Рисунок А.4 Лист КР-02069964-13.03.01-63-23 Изм. Лист № докум. Подпись Дата 29