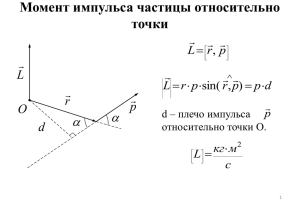
В помощь иностранному студенту Формулы ко 2-му коллоквиуму 1. Система материальных точек. Внутренние и внешние силы. Закон сохранения импульса изолированной системы. Закон сохранения импульса системы: импульс системы остается постоянным, если на нее не действуют внешние силы. 2. Работа силы. Связь работы и энергии. Мощность. Закон сохранения механической энергии. Превращение энергии из одного вида в другой. Примеры. Кинетическая энергия поступательного движения. Потенциальная энергия упруго деформированного тела. Работа A F dS , где F – сила, S – перемещение. Если сила постоянна, то в частном случае: A FS cos , где S – путь, – угол между направлением скорости и силой. dA Мощность N . dt Закон сохранения (изменения) энергии: E A , где A – работа всех сил, кроме консервативных (сила тяжести, сила упругости). m 2 Кинетическая энергия поступательного движения: Ek , где m – масса, – скорость. 2 kx 2 Потенциальная энергия упруго деформированного тела: E p , где k – коэффициент упругости, x – 2 растяжение (сжатие). 3. Потенциальная энергия в однородном поле силы тяжести. E p mgh, где g – ускорение свободного падения, m – масса, h – изменение высоты. 4. Абсолютно упругий и абсолютно неупругий удары (столкновения). Превращение энергии в процессе столкновения. Законы сохранения энергии и импульса. Связь между скоростями соударяющихся тел до и после удара. Убыль механической энергии в неупругом ударе. При абсолютно упругом ударе тела после соударения разлетаются, а при абсолютно неупругом ударе движутся как единое целое. В неупругом ударе происходит выделение теплоты. Законы сохранения импульса и энергии для упругого удара: m11 m2 2 m11 m2 2 m112 m2 22 m112 m1 22 , 2 2 2 2 где 1 , 2 – скорости соударяющихся тел до удара, а 1 , 2 – скорости соударяющихся тел после удара. Законы сохранения импульса и энергии для неупругого удара: m11 m22 m1 m2 , m112 m222 m1 m2 2 Q 2 2 2 где Q – выделившаяся в процессе удара теплота. 5. Понятие абсолютно твердого тела. Поступательное, вращательное и плоскопараллельное движения твердого тела. Связь между угловой и линейной скоростями точек твердого тела. Абсолютно твердым называется тело, которое ни при каких условиях не деформируется. В абсолютно твердом теле расстояние между любыми двумя точками остается постоянным. Векторная формула: , r , где – вектор угловой скорости, r – радиус-вектор. Необходимо уметь находить направление и модуль вектора векторного произведения (см. лекции по механике или по аналитической геометрии). Скалярная формула: R , где R – радиус окружности, по которой движется точка. 6. Центр инерции твердого тела. Связь координат и масс точек твердого тела в системе координат, связанной с центром масс. Лемма о центре масс: n mi ri 0 , где mi i 1 – массы точек твердого тела, ri – их радиус-векторы в системе центра масс. 7. Центр инерции твердого тела. Координаты центра инерции. Закон движения центра инерции твердого тела. n Радиус-вектор центра масс: RC mi ri i 1 m , где m – масса всего тела. d0 Закон движения центра масс: m F , где 0 – скорость центра масс, F – результирующая сила. dt Центр инерции движется так, как если бы в нем была бы сосредоточена вся масса и к нему были бы приложены все силы. 8. Момент силы. Закон динамики вращения тела вокруг неподвижной оси. Момент инерции. Момент силы относительно оси: M Fl , где l – плечо силы (правило определения плеча см. в лекциях или в материалах занятий по решению задач). Закон динамики вращения тела вокруг неподвижной оси (уравнение вращательного движения): M I , где I – момент инерции тела, – угловое ускорение. Момент инерции материальной точки: I mr , где r – расстояние от точки до оси. 2 n Момент инерции твердого тела: I mi ri 2 , где ri – расстояние от i-той точки до оси. i 1 9. Момент импульса. Уравнение моментов (относительно оси). Закон сохранения момента импульса. Момент импульса точки относительно оси: N mr , где r – радиус окружности, которую описывает точка. Момент импульса тела относительно оси: N I , где I – момент инерции тела, где – угловая скорость вращения. Уравнение моментов относительно оси: M dN , где M – момент силы относительно оси, N – dt момент импульса относительно оси . Закон сохранения момента импульса: момент импульса остается постоянным, если момент внешних сил равен нулю. 10. Момент импульса и момент силы относительно точки. Уравнение моментов (относительно точки). Момент импульса точки относительно точки: N r , p , где r – радиус-вектор точки, p – импульс dN точки. Уравнение моментов относительно точки: M , где M – момент силы относительно точки, dt N – момент импульса относительно точки. 11. Кинетическая энергия вращающегося тела. Работа по повороту твердого тела. I 2 , где I – момент инерции, – угловая 2 скорость вращения. Работа по повороту твердого тела: A Md , где M – момент силы относительно Кинетическая энергия вращающегося тела: Eвращ оси, – угол поворота. 12. Аналогия между поступательным движением материальной точки и вращательным движением твердого тела. Поступательное движение N 1 2 Путь S , перемещение Линейная скорость 3 Сила 4 5 Линейное ускорение 6 S Угол Угловая скорость F Масса Вращательное движение M , Момент силы относительно точки M Угловое ускорение Момент силы относительно оси a m Момент инерции I Импульс p N , Момент импульса относительно точки N dN dN Уравнение моментов M , M dt dt Момент импульса относительно оси Второй закон Ньютона, первая формулировка dp F dt Второй закон Ньютона, вторая формулировка 8 F ma m 2 9 Кинетическая энергия Eк 2 10 Работа A FdS 7 Уравнение вращательного движения M I Кинетическая энергия вращательного движения Работа по повороту A Md I 2 Eвращ 2 13. Момент инерции. Вычисление моментов инерции тел (на примере моментов инерции цилиндра, кольца и тонкого кольца, стержня и шара). Сплошной цилиндр: I 1 mR2 2 1 mR12 R22 2 2 Шар: I mR2 5 Полый цилиндр (и кольцо): I Тонкостенный цилиндр (и тонкое кольцо): I mR 2 Стержень: I 1 2 ml 12 14. Момент инерции. Теорема Гюйгенса-Штейнера. I I O ma2 , где I – момент инерции относительно произвольной оси, I O – момент инерции относительно оси, проходящей через центр масс параллельно данной, a – расстояние между осями. 15. Момент импульса относительно точки. Связь между моментом импульса относительно точки и угловой скоростью вращения твердого тела. Тензор инерции. Связь между моментом импульса относительно точки и угловой скоростью вращения твердого тела: N Iˆ Тензор инерции – квадратная матрица 3 на 3: I xx I xy I xz ˆI I yx I yy I yz I I I zx zy zz n Диагональные: I xx mi Ri xi i 1 2 2 n Недиагональные: I xx mi xi yi i 1 Ri – модуль радиус-вектора точки, xi , yi – координаты точки. 16. Теорема о главных осях. Теорема: Для любого тела имеются три взаимно перпендикулярных направления, при вращении вокруг которых вектор момента импульса относительно точки сонаправлен с вектором угловой скорости: N . Такие направления называются главными. 17. Диагонализация тензора инерции. Главные моменты инерции твердого тела. Диагонализация – приведение тензора инерции к диагональному виду. Диагональный вид матрицы – когда вне главной диагонали нули. Тензор инерции принимает диагональный вид, если в качестве координатных осей выбраны главные направления твердого тела. Главные моменты инерции – моменты инерции относительно главных направлений, диагональные элементы тензора, приведенного к диагональному виду. 18. Связь момента инерции твердого тела относительно произвольной оси, проходящей через центр масс, с тензором инерции относительно системы координат, связанной с центром масс. I n n IˆO n , где I n – момент инерции относительно оси, проходящей через центр масс и задаваемой единичным вектором n , IˆO – тензор инерции в системе, связанной с центром масс. 19. Гироскопы. Гироскоп под действием сил (приближенная теория). Прецессия гироскопа. Гироскопические силы. Нутации. Гироскоп – быстро вращающееся симметричное тело, ось которого может менять свое направление в пространстве. Прецессия – вращение оси гироскопа в горизонтальной плоскости. Угловая скорость прецессии: M . N 20. Законы Кеплера. Закон всемирного тяготения. Опыт Кавендиша. 1-й закон Кеплера: Орбиты всех планет являются эллипсами, в одном из фокусов которых находится Солнце. 2-й закон Кеплера: Движение каждой планеты происходит так, что радиус-вектор, проведенный из центра Солнца к планете, за равные промежутки времени «ометает» равные площади. 3-й закон Кеплера: T12 a13 , где T – период обращения планеты, a – большая полуось эллипса орбиты T22 a23 (что такое фокус и полуось эллипса – см. в литературе) Закон всемирного тяготения: F G m1m2 , где G – гравитационная постоянная, m1 , m2 – массы r2 взаимодействующих тел, r – расстояние между центрами этих тел.