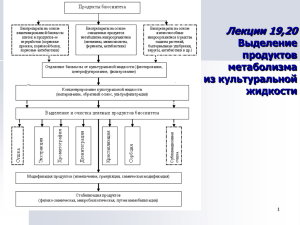
Лекция № 10 Процесс жидкостной экстракции Жидкостная экстракция – процесс с участием двух взаимно нерастворимых (ограниченно растворимых) жидкостей, между которыми распределяется экстрагируемое вещество. В результате взаимодействия разделяемой смеси с экстрагентом в виде отдельных жидких фаз получают два продукта: рафинат и экстракт. Рафинат представляет собой продукт, полученный из разделяемой смеси, из которой в основном удалено экстрагируемое вещество. Экстракт представляет собой экстрагент, который в результате проведения процесса обогащен экстрагируемым веществом. Достоинствами экстракции по сравнению с такими способами разделения как ректификация и выпаривание является низкая температура проведения процесса, низкие затраты тепловой энергии, а также возможность подбора высокоселективных экстрагентов, обеспечивающих глубокое извлечение целевого компонента. Однако необходимость организации регенерации экстрагента усложняет аппаратурно-технологическое оформление процесса. Жидкостная экстракция конкурирует с ректификацией при тонком разделении смесей близкокипящих жидкостей, а также азеотропных смесей. Применение экстракции позволяет вести процессы разделения термочувствительных сред при низких температурах без использования вакуумной техники. Экстракцию применяют для разделения технологических сред на компоненты – целевые продукты (полупродукты), а также для очистки технологических продуктов от вредных примесей, для очистки стоков от вредных примесей и извлечения из них ценных компонентов. 1 Методы жидкостной экстракции При экстракции неорганических веществ из растворов (как правило, из растворов водных) используют один экстрагент. При разделении смесей взаимно растворимых органических веществ в зависимости от конкретных условий применяют либо один, либо два несмешивающихся экстрагента. Экстракцию с применением двух экстрагентов называют фракционной. 1.1 Одноступенчатая экстракция На рис.1 представлена схема, поясняющая процесс одноступенчатой экстракции. Одноступенчатая экстракция может проводиться в периодическом и непрерывном режимах. При этом, как правило, в смесителеэкстракторе 1 осуществляется эмульгирование экстрагента и разделяемой смеси и их взаимодействие. Затем эмульсия направляется в отстойник 2, где она разделяется на экстракт и рафинат. Применима одноступенчатая экстракция при высокой разделяемости исходной смеси. 1 Рис. 1 – Схема процесса одноступенчатой экстракции 1 – смеситель-экстрактор; 2 – отстойник. Обозначение потоков: С – исходная смесь; А и В – компоненты смеси; Э – экстрагент; ЭТ – экстракт; Р – рафинат 1.2 Многоступенчатая перекрестноточная экстракция Многоступенчатую перекрестноточную экстракцию применяют для получения рафината высокой чистоты при возможности применения дешевого экстрагента, не требующего регенерации, при незначительной ценности извлекаемого компонента. Осуществляют многоступенчатую перекрестноточную экстракцию в группе последовательно соединенных по разделяемой смеси смесителей-отстойников, как показано на рис. 2. Э Рис. 2 – Схема перекрестноточной экстракции Обозначение потоков: С – исходная смесь; А и В – компоненты смеси; Э – экстрагент; ЭТ – экстракт; Р – рафинат 2 1.3 Многоступенчатая противоточная экстракция Многоступенчатая противоточная экстракция применяется при необходимости глубокого извлечения распределяемого компонента из разделяемой смеси. Позволяет по сравнению с другими схемами снизить расход экстрагента, получить более насыщенный экстракт. Осуществляют многоступенчатую противоточную экстракцию в каскаде смесителейотстойников, как показано на рис. 3, либо в противоточных колонных экстракторах. Рис. 3 – Схема многоступенчатой противоточной экстракции Обозначение потоков: С – исходная смесь; А и В – компоненты смеси; Э – экстрагент; ЭТ – экстракт; Р – рафинат 1.4 Противоточная многоступенчатая экстракция с флегмой Противоточная многоступенчатая экстракция с флегмой применяется с целью глубокого разделения исходного раствора. Осуществляется в колоннах экстракторах. Схема противоточной многоступенчатой экстракции с флегмой показана на рис. 4. При работе по этой схеме разделяемая смесь подается в среднюю часть экстракционной колонны. Недостатками метода являются увеличенный расход экстрагента, увеличение размеров экстрактора, удорожание установки в целом. Рис. 4 – Схема противоточной многоступенчатой экстракции с флегмой 1 – ступени взаимодействия фаз; 2 – регенератор экстрагента; 3 – ступень питания. Обозначение потоков: С – исходная смесь; А и В – компоненты смеси; Э – экстрагент; ЭТ – экстракт; Р – рафинат; ЭР – регенерированный экстрагент 3 2 Равновесие в системах жидкость-жидкость Фазовые равновесие в системе жидкость-жидкость определяют величины предельных концентраций экстрагируемого вещества в экстракте и рафинате. Количественно взаимосвязь концентраций распределяемого вещества в экстракте и рафинате, находящихся в условиях равновесия, можно выразить зависимостью: m = y*/х где m – коэффициент распределения вещества по фазам; у* и x – концентрации распределяемого вещества в экстракте и рафинате в условиях равновесия, соответственно. Значение m зависит от природы растворителя в исходной смеси, распределяемого вещества, экстрагента, а также от наличия и природы примесей во взаимодействующих фазах. Конкретный вид равновесной зависимости устанавливают экспериментальным путем. Теоретически хорошо разработано описание условия равновесия тройных систем, т.е. систем в которых обе фазы при экстракции представляют двухкомпонентные растворы. Чтобы изобразить процесс экстракции на диаграммах трехкомпонентных систем, необходимо познакомиться с принципом изображения этих систем на плоскости. 2.1 Способы изображения трехкомпонентных систем Для построения полной диаграммы состояния трехкомпонентной системы необходима система координат из пяти взаимно перпендикулярных осей, по которым откладываются температура, давление, мольные объемы различных фаз и мольные доли (или массовые проценты) двух компонентов в фазах. Реально построение такой диаграммы невозможно. Нельзя также построить проекцию этой диаграммы на четырехмерное пространство в осях: температура, давление, мольные доли двух компонентов. Лишь приняв какой-либо из параметров, например, температуру или давление, постоянным, можно построить трехмерную диаграмму, которая будет отображать зависимость числа и состава фаз в равновесных системах от исходного состава и от температуры (при постоянном давлении) или от давления (при постоянной температуре). Часто для еще большего упрощения постоянными принимаются температура и давление одновременно. В этом случае на плоскости составов наносятся проекции сечения трехмерной диаграммы плоскостью T= const или p = const. Двумерные диаграммы отражают различные состояния системы и фазовые переходы только при выбранных значениях p и T. При построении диаграммы состояния трехкомпонентной системы состав ее изображают на плоскости, а в перпендикулярном направлении откладывают температуру ( p= const) или давление ( T= const). Чаще используется первый вариант, так как давление в большинстве случаев при изучаемых 4 превращениях остается постоянным или изменяется немного, а температурные изменения значительны. Состав трехкомпонентной системы обычно изображают, пользуясьтреугольником Гиббса – Розебома (рис. 5). Вершины равностороннего треугольника отвечают чистым компонентам (100%) A, B и C. Каждая из сторон треугольника позволяет описать составы двухкомпонентных систем A + B, B + C, A + C. Все точки внутри треугольника описывают составы трехкомпонентных систем. Метод определения состава по Гиббсу основан на том, что сумма перпендикуляров, опущенных из любой точки равностороннего треугольника на каждую из сторон, равна высоте треугольника. Если принять, что высота треугольника соответствует 100 мольным (или массовым) процентам, то состав тройной системы можно выразить с помощью длин перпендикуляров. При этом содержанию данного компонента отвечает длина перпендикуляра, опущенного на сторону, противоположную соответствующей вершине треугольника. Например, точка о отвечает составу: 20% компонента A (отрезок оа), 30% компонента B (отрезок оb) и 50% компонента C (отрезок оc). Рис. 5 – Треугольник Гиббса – Розебома для изображения состава трехкомпонентной системы 5 Длина перпендикуляра оценивается с помощью координатной сетки, покрывающей треугольник. Высоты треугольника делятся на 10 или 100 равных отрезков и через точки деления проводятся три группы параллельных прямых так, что каждая группа перпендикулярна соответствующей высоте треугольника, при этом длина каждого получающегося отрезка отвечает 10 или 1% содержания данного компонента в смеси. Выражение составов трехкомпонентных систем по Розебому основано на том, что сумма отрезков, проведенных из какой-либо точки внутри треугольника параллельно его сторонам до пересечения с каждой из сторон, равна длине стороны треугольника. Координатная сетка образована тремя группами прямых, параллельных сторонам треугольника. Содержанию каждого компонента отвечает длина отрезка, проведенного к стороне, лежащей против вершины этого компонента. На рис. 1 эти отрезки нанесены пунктиром; длины отрезков oa,ob и oc соответствуют содержаниям компонентов A, B, C. Линии, параллельные одной из сторон треугольника, представляют геометрические места точек, соответствующих смесям с одинаковым содержанием одного из компонентов. Например, линия mn отвечает смесям, в которых содержание компонента B составляет 65%. Линии, проведенные из вершин треугольника до пересечения с противолежащей стороной, являются геометрическими местами точек, соответствующих ряду систем, в которых соотношение между содержанием двух компонентов остается постоянным. Так, например, линия Bх отвечает ряду смесей, в которых процентное содержание A и C сохраняется равным 8:2. К треугольной диаграмме, как и диаграмме бинарных систем, приложимо правило рычага. Если, например, точка р отвечает общему составу системы, а система распадается на две фазы составов k и l, то количество первой фазы относится к количеству второй как длины отрезков pl : pk. На рис. 6 показана фазовая диаграмма трехкомпонентной системы с ограниченной взаимной растворимостью компонентов А и С Смешение компонентов А и С приводит к образованию жидкой системы, состоящей из двух слоев, один из которых представляет собой насыщенный раствор вещества С в растворителе А (точка а1), а другой - насыщенный раствор вещества А в растворителе С (точка b1,. Введенное в систему третье вещество В(точка l2) перераспределяется между слоями. Поскольку растворимость его в веществе А выше, а в веществе С ниже, то соответствующая коннода а2b2 непараллельна стороне АС. Правило Тарасенкова: продолжения всех коннод пересекаются в одной точке (точка О). 6 Добавление следующей порции вещества В (точка 13) приводит к образованию сопряженных слоев, в которых концентрации компонентов можно найти по фигуративным точкам а3 и b3. Постепенно прибавляя вещество В можно дойти до состояния системы, которая соответствует фигуративной точке а4. В этом состоянии исчезает второй слой и образуется гомогенный раствор, в котором растворителем является вещество А, а растворенными веществами компоненты В и С. Таким образом, на одной части кривой расслоения (а1 .к) расположены фигуративные точки состава насыщенных растворов, в которых растворителем является вещество А. В другой части (b1...к) находятся фигуративные точки состава насыщенных растворов в растворителе С. Касательная к кривой расслоения, проведенная из точки О, в точке касания дает точку к. Точка к соответствует составу трехкомпонентной смеси, при котором составы равновесных фаз становятся одинаковыми и система переходит в гомогенное состояние. В Рис. 6 – Фазовая диаграмма трехкомпонентной системы с ограниченной взаимной растворимостью компонентов А и С 2.2 Однократная экстракция для частично растворимых жидкостей Схема установки представлена на рис.7. Материальный баланс F S M RE Соотношение потоков определяется по правилу отрезков на треугольной диаграмме Розебома, которая представлена на рис.8. Из диаграммы следует: F SM R ME ; ; E RM S FM 7 Рис.7 – Однократная экстракция. 1 - экстрактор, 2 - отстойник, F - исходная смесь, S - растворитель, М - смесь двухфазной системы, E - экстракт, R - рафинат. Рис. 8– Изображение однократной экстракции на треугольной диаграмме. 1 - бинодальная кривая, К - критическая точка, 2 - коннода (хорда равновесия). Расход растворителя FM ; SF SM Очевидно, что в точке М1, расход растворителя будет минимальным, а в точке M2 - максимальным. Точка Е' определяет состав экстракта после удаления растворителя. 8 Для более полного извлечения компонента из исходной смеси применяют многократную экстракцию. 2.3 Многократная экстракция для частично растворимых жидкостей Схема установки и треугольная диаграмма представлены на рис.9. Рис. 9 – Схема установки а/ и треугольная диаграмма б/ для многократной экстракции. 1 - экстрактор, 2 - отстойник /сепаратор/. Материальный баланс F S1 M 1 R1 E1 Первая ступень 9 S1 F Вторая ступень FM1 ; M 1S R1 M1 M1E1 ; R1E1 E1 M 1 R1 ; R1 S 2 M 2 R2 E2 R1M 2 M E ; R2 M 2 2 2 ; E2 M 2 R2 ; M 2S R2 E2 Третья ступень R2 S3 M 3 R3 E3 S2 R1 S3 R2 R2 M 3 ;; M 3S R3 M 3 M 3 E3 ; R3 E3 E3 M 3 R3 ; Выход экстракта E E1 E2 E3 Рафината R3 Расход растворителя S S1 S 2 S3 2.4 Противоточная экстракция для частично растворимых жидкостей Схема аппарата представлена на рис. 4 К недостаткам многократной экстракции следует отнести громоздкость аппаратуры и большой расход растворителя. Этих недостатков лишена противоточная экстракция в аппарате колонного типа (Рис. 10). Рис.10 – Колонный аппарат для противоточной экстракции. 10 Для изображения процесса противоточной экстракции на треугольную диаграмму наносят точки F, E1, S и Rк. Соединяют точки F и Е1 , Rk и S. Линии продолжают дальше. Пересечение прмых F Е1 и RkS определяет полюс диаграммы Q. Условным построением коннод R1E1, R2E2, RkE3, определяется число теоретических ступеней /в данном случае Nc = 3/. Диаграмма представлена на рис. 11 Рис. 11 – Треугольная диаграмма для противоточной экстракции. Материальный баланс Для представления материального баланса условно соединют точки F и S 1, Rк и E1. Линия RкE1 не является коннодой. F S M E1 Rk S Rk E1 F Q Потоки: SF FM ; MS M FS; Rk M ME1 ; Rk E1 E1 M Rk ; 11