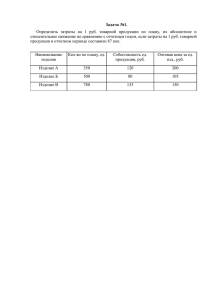
Задание 1. В магазине выставлены для продажи 20 изделий, среди которых 4 изделия некачественных. Какова вероятность того, что взятые случайным образом 5 изделия будут: а) качественными; б) хотя бы одно из них будет качественным; в) ни одного качественного изделия. Решение: а) Пусть событие А – 5 взятых изделий качественные. Общее число случаев выбора 5 изделий из 20 равно 5 n C 20 20! 20! 16 17 18 19 20 16 17 3 19 15504 5!20 5! 5!15! 1 2 3 4 5 Число случаев, благоприятствующих событию А: 5 изделий будут выбраны из 16 качественных изделий – число сочетаний из 16 по 5. m C165 16! 16! 12 13 14 15 16 12 13 14 2 4368 5!16 5! 5!11! 1 2 3 4 5 Тогда P A m 4368 0,2817 n 15504 б) Пусть событие А – хотя бы одно из взятых изделий качественное. Событие А будет противоположным по отношению к событию B – все 5 изделии некачественные. Так как всего 4 изделия являются некачественными, то событие В является невозможным. Вероятность невозможного события равна 0. следовательно, вероятность противоположного события А равна 1. P A 1 в) Вероятность того, что все пять изделий будут некачественными PB 0 Ответ: а) 0,2817; б) 1; в) 0. Задание 2. В партии из N=20 изделий M=4 имеют скрытый дефект. Какова вероятность того, что из взятых наугад n=5 изделий дефектными окажутся m=2 изделия? Решение: Пусть событие А – из выбранных наугад 5 изделий 2 оказались дефектными. Выбрать 5 n C 20 из партии 5 изделия 20! 20! 16 17 18 19 20 16 17 3 19 15504 5!20 5! 5!15! 1 2 3 4 5 Выбрать 2 дефектных изделия можно C 42 способами, n C163 оставшееся изделия 16! 16! 14 15 16 14 5 8 560 3!16 3! 3!13! 1 2 3 из мы можем способами. 4! 4! 1 2 3 4 23 6 2!4 2! 2!12! 1 2 1 2 5 мы можем выбрать способами. Искомая вероятность равна отношению числа благоприятных исходов к общему числу исходов: P A C42 C163 6 560 0,21672 5 C20 15504 Ответ: 0,21672. Задание 3. Студент разыскивает нужную ему формулу в трех источниках. Вероятность того, что формула содержится в первом справочнике p=0,8, во втором – q= 0,7, в третьем – g=0,85. Найти вероятность того, что а) формула содержится хотя бы в одном справочнике; б) формула содержится только в двух учебниках; в) формула содержится в любом учебнике; г) формулы нет ни в одном из учебников. Решение: Пусть событие А1 – формула содержится в первом справочнике; А2 – формула содержится во втором справочнике; А3 – формула содержится в третьем справочнике. Тогда P A1 0,8 , P A2 0,7 , P A3 0,85 . Воспользуемся теоремами сложения и умножения вероятностей. а) формула содержится хотя бы в одном учебнике P P A1 A2 A3 1 P A1 A2 A3 1 1 P A1 1 P A2 1 P A3 1 1 0,8 1 0,7 1 0,85 0,991 б) формула содержится только в двух учебниках: P P A1 A2 A3 A1 A2 A3 A1 A2 A3 P A1 P A2 1 P A3 P A1 1 P A2 P A3 1 P A1 P A2 P A3 0,8 0,7 1 0,85 0,8 1 0,7 0,85 1 0,8 0,7 0,85 0,084 в) формула содержится в любом учебнике: P P A1 A2 A3 P A1 P A2 P A3 0,8 0,7 0,85 0,476 г) формулы нет ни в одном учебнике: P P A1 A2 A3 1 P A1 1 P A2 1 P A3 1 0,8 1 0,7 1 0,85 0,009 Ответ: а) 0,991; б) 0,084; в) 0,476; г) 0,009. Задание 4. В район изделия поставляются тремя фирмами. Известно, что первая фирма поставляет товар с браком в X=0,3%, вторая – Y=0,2%, третья – Z=0,4%. С первой фирмы поступило N=1000, со второй M=2000, с третьей – K=2500 изделий. Найти вероятность, что приобретенное изделие окажется а) стандартным; б) нестандартным; в) какова вероятность, что стандартное изделие поступило с третьей фирмы? Решение: а) Пусть событие А – приобретенное изделие стандартное. Выдвинем три гипотезы: Н1 – изделие поставлено первой фирмой. Н2 – изделие поставлено второй фирмой. Н3 – изделие поставлено третьей фирмой. Тогда PH1 1000 1000 2 0,1818 , PH 1 / A 1 0,003 0,997 1000 2000 2500 5500 11 P H 2 2000 2000 4 0,3636 , 1000 2000 2500 5500 11 PH 2 / A 1 0,002 0,998 P H 3 2500 2500 5 0,4545 , 1000 2000 2500 5500 11 P H 3 / A 1 0,004 0,996 По формуле полной вероятности: P A P H1 P H1 / A P H 2 PH 2 / A P H 3 P H 3 / A 0,1818 0,997 0,3636 0,998 0,4545 0,996 0,18127 0,3629 0,4527 0,9969 б) Пусть событие В – приобретенное изделие нестандартное. Выдвинем три гипотезы: Н1 – изделие поставлено первой фирмой. Н2 – изделие поставлено второй фирмой. Н3 – изделие поставлено третьей фирмой. Тогда PH1 1000 1000 2 0,1818 , PH 1 / B 0,003 1000 2000 2500 5500 11 P H 2 2000 2000 4 0,3636 , 1000 2000 2500 5500 11 PH 2 / B 0,002 P H 3 2500 2500 15 0,4545 , 1000 2000 2500 5500 11 PH 3 / B 0,004 По формуле полной вероятности: P B P H1 P H1 / B P H 2 PH 2 / B P H 3 P H 3 / B 0,1818 0,003 0,3636 0,002 0,4545 0,004 0,000545 0,000727 0,001818 0,003091 в) вероятность поступления стандартного изделия с третьей фирмы: P H 3 / A 0,4545 0,996 0,454131 0,9969 Ответ: а) 0,9969; б) 0,003091; в) 0,454131 Задание 5. В среднем по P=15% договоров страховая компания выплачивает страховую сумму. Найти вероятность того, что из n=10 договоров с наступлением страхового случая будет связано с выплатой страховой суммы: а) три договора; б) менее двух договоров. Решение: Используем формулу Бернулли: n=10 – число опытов р=0,15 – вероятность выплаты страховой суммы q=1–p=0,85 – вероятность не выплаты страховой суммы. Формула Бернулли: Pn m C nm p m q n m Тогда а) вероятность того, что из тринадцати договоров с наступлением страхового случая будет связано с выплатой страховой суммы менее двух договоров, равна: 10! 8 9 10 0,153 0,857 0,153 0,857 3!7! 1 2 3 120 0,003375 0,320577 0,129834 P10 3 C103 p3q10 3 б) вероятность того, что из тринадцати договоров с наступлением страхового случая будет связано с выплатой страховой суммы по трём договорам, равна: 10! 10! 0,150 0,8510 0,151 0,859 0!10! 1!9! 10 9 1 1 0,85 10 0,15 0,85 1 1 0,196874 10 0,15 0,231617 0,196874 0,347425 0,5443 P10 0 P10 1 C100 p 0 q10 0 C101 p1q10 1 Ответ: а) 0,129834; б) 0,5443. Задание 6. Аудиторную работу по теории вероятности успешно выполнило 50% студентов. Найти вероятность того, что из N=400 студентов успешно выполнят: а) M=150 студентов; б) не менее M=150 студентов; в) от M=150 до L=300 студентов. Решение: n = 400 p = 0,5 q = 1 – p = 1 – 0,5 = 0,5 np = 4000,5 = 200 npq = 4000,50,5= 100 npq 100 10 а) M = 150 x M np 150 200 5 10 npq P(m 150) 1 x 0,1 5 0,1 5 0,1 0,0000015 0,00000015 npq б) m1 = 50 x1 M np 150 200 5 10 npq m2 = 300 x2 L np 300 200 10 10 npq P (150 x 300) x2 x1 10 5 10 5 0,499997 0,499997 0,999994 Ответ: а) 0,00000015; б) 0,999994. Задание 7. Задан закон распределения дискретной случайной величины в виде таблицы (в первой строке указаны возможные значения случайной величины, во второй — соответствующие вероятности). Найти: а) функцию распределения; б) математическое ожидание; в) дисперсию; г) среднее квадратическое отклонение; д) коэффициент ассимметрии. xi pi 5 0,1 15 0,2 25 0,3 35 0,2 45 0,2 Решение: а) Составим функцию распределения F(х): F(x≤5) = 0 F(5< x ≤15) = 0,1 F(15< x ≤25) = 0,5 + 0,1 = 0,3 F(25< x ≤35) = 0,3 + 0,3 = 0,6 F(35< x ≤45) = 0,2 + 0,6 = 0,8 F(x>45) = 0,2+0,8=1 x5 0 , 0,1 , 5 x 15 0,3 , 15 x 25 F x 0,6 , 25 x 35 0,8 , 35 x 45 1 , x 45 б) математическое ожидание найдем по формуле M [ x] xi pi . M [ x] 5 0,1 15 0,2 25 0,3 35 0,2 45 0,2 27 в) дисперсию найдем по формуле D[ x] xi2 pi M x 2 . D[ x] 52 0,1 152 0,2 252 0,3 352 0,2 452 0,2 27 2 156 г) среднее квадратическое отклонение σ(x): [ x] Dx 156 12,49 Коэффициент вариации – показывает, какую долю среднего значения этой величины составляет ее средний разброс. v x 12,49 46,26% 27 Поскольку v>30% ,но v<70%, то вариация умеренная. x M x 3 д) коэффициент асимметрии найдем по формуле As As pi 3 5 27 3 0,1 15 27 3 0,2 25 27 3 0,3 35 27 3 0,2 45 27 3 0,2 11,363 144 0,0739 1948,439 Так как As<0, то имеем левостороннюю асимметрию. Задание 9. Исходные данные – результаты выборки непрерывного статистического показателя, Провести группировку, разбив диапазон значений статистического показателя на 5 интервалов, Для выборки необходимо: а) построить гистограмму и секторную диаграмму частот; б) вычислить значения среднего показателя, моды, медианы, дисперсии, среднего квадратического отклонения, коэффициентов асимметрии и эксцесса, Исходные данные: Номера наблюдений Данные для задачи 1 3,1 2 4,3 3 5 4 3,2 5 4,1 6 6,5 7 8,2 8 2,4 9 3,7 10 5,3 11 5,9 12 3,2 13 7,6 14 5,6 15 9,3 16 3,4 17 6,2 18 5,5 19 7,2 20 4,8 Решение: Проведем группировку статистических данных. Число интервалов n= 5, число единиц совокупности N 20 . Величина интервала вычисляется как h x max x min . n xmax – максимальное значение группировочного признака в совокупности. xmin – минимальное значение группировочного признака. Так как xmin 2,4 и xmax 9,3 , то h 9,3 2,4 1,38 . 5 Определим границы групп: Номер группы 1 2 3 4 5 Нижняя граница 2,4 3,78 5,16 6,54 7,92 Верхняя граница 3,78 5,16 6,54 7,92 9,3 Для каждого значения подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого отсортируем таблицу по возрастанию признака, затем подсчитаем количество данных, попавших в каждую группу: Номер группы 1 2 3 4 5 Интервал 2,4 – 3,78 3,78 – 5,16 5,16 – 6,54 6,54 – 7,92 7,92 – 9,3 Количество 6 4 6 2 2 Гистограмма 7 6 5 6 6 4 4 3 2 2 1 2 0 2,4 – 3,78 3,78 – 5,16 5,16 – 6,54 6,54 – 7,92 7,92 – 9,3 Секторная диаграмма частот 0,1; 10% 0,1; 10% 0,3; 30% 2,4 – 3,78 3,78 – 5,16 0,3; 30% 0,2; 20% 5,16 – 6,54 6,54 – 7,92 Составим для расчета показателей вспомогательную таблицу: Группы xi Кол-во, fi xi fi 2,4 – 3,78 3,78 – 5,16 5,16 – 6,54 6,54 – 7,92 7,92 – 9,3 Итого 3,09 4,47 5,85 7,23 8,61 6 4 6 2 2 20 18,54 17,88 35,10 14,46 17,22 103,20 Накоп. |x - xср|f (x - xср)2f (x - xср)3f (x - xср)4f Частость, частота, fi/n S 6 12,42 25,71 -53,22 110,16 0,3 10 2,76 1,90 -1,31 0,91 0,2 16 4,14 2,86 1,97 1,36 0,3 18 4,14 8,57 17,74 36,72 0,1 20 6,9 23,81 82,13 283,34 0,1 30,36 62,85 47,3 432,5 1,0 Для того чтобы рассчитать среднюю арифметическую интервального ряда, надо сначала определить среднюю для каждого интервала, а затем – среднюю для всего ряда. Средняя арифметическая для каждого интервала определяется по формуле средней арифметической простой, т.е. как полусумма верхней и нижней границ. Средняя для всего ряда вычисляется по формуле: n x x i i 1 n f i 1 fi , i где x i – это средние интервалов, f i – частота соответствующих средних (в данном случае, количество предприятий в группе, n – количество групп. n x x f i 1 n i i f i 1 103,20 5,16 20 i Мода – это наиболее часто встречающееся значение признака у единиц данной совокупности. Она соответствует определенному значению признака. Величина моды определяется по формуле: Mo x Mo h где f Mo f ( 1) ( f Mo f ( 1) ) ( f Mo f ( 1) ) хМо – начало модального интервала; h – величина интервала; fМо – частота, соответствующая модальному интервалу; f(-1) – предмодальная частота; f(+1) – послемодальная частота. Сначала определяется модальный интервал как интервал с наибольшей частотой. Это 1-я группа. хМо = 2,4 fМо = 6 f(-1) = 0 f(+1) = 4 h = 1,38 Mo 2,4 1,38 60 3,44 ( 6 0) ( 6 4) Медиана лежит в середине ранжированного ряда и делит его пополам. При нахождении медианы интервального вариационного ряда вначале определяют медианный интервал, в пределах которого находится медиана (интервал, в котором заканчивается одна половина частот f и начинается другая половина), а затем – приближенное значение медианы по формуле: n Me x Me h где 0,5 f i S ( 1) i 1 f Me хМе – нижняя граница медианного интервала; h – величина интервала; S(-1) – накопленная частота интервала, предшествующего медианному; fМе – частота медианного интервала; n f i 1 i – сумма частот или число членов ряда. Медианный интервал в нашей задаче – 2-й, поскольку в этом интервале накопленная частота равна 10, что равно половине общей суммы частот. Следовательно, в этой группе и находится медиана. хМе = 3,78 h = 1,38 S(-1) = 6 fМе = 4 n f i 1 i = 20 Me 3,78 1,38 0,5 20 6 5,16 4 Мода не совпадает со средней арифметической, а медиана и среднее арифметическое равны. Дисперсия индивидуальных представляет значений собой признака средний от их квадрат средней отклонений величины и для сгруппированных данных вычисляется как x n 2 i 1 i x 2 fi n f i 1 i Среднее квадратическое отклонение () равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической. Для сгруппированных данных среднее квадратическое отклонение вычисляется как корень квадратный из дисперсии. 2 62,85 3,1423 20 3,1423 1,7726 Среднее квадратическое отклонение является мерой надежности – чем меньше значение среднего квадратического отклонения (также как и дисперсии), тем однороднее совокупность. x x f As 3 i Коэффициент асимметрии вычисляется как fi i 3 . 47,3 47,3 As 20 3 0,4246 1,7726 20 1,77263 Так как As>0, то имеется правосторонняя асимметрия. x x f Ex i Эксцесс оценивается с помощью показателя эксцесса: 432,5 432,5 Ex 20 4 3 3 2,1901 3 0,8099 1,7726 20 1,77264 Так как Ex<0, то распределение является плосковершинным. i 4 4 fi 3. Задание 10. Найти доверительный интервал для оценки математического ожидания m нормального распределения генеральной совокупности с надежность 0,95, зная выборочное среднее xср, объем выборки n и среднее квадратическое отклонение . Данные взять из таблицы 7. xср= 75,17; n=36; 6 Решение: Для оценки математического ожидания воспользуемся формулой: xв t n a xв t n Найдем t. Из соотношения 2Ф(t) = 0,95 получим: Ф(t) = 0,475. По таблице находим: t = 1,96. Найдем точность оценки t 1,96 6 1,96 n 36 Искомый доверительный интервал: 75,17 1,96 a 75,17 1,96 или 73,21 a 77,13 Ответ: математическое ожидание находится в интервале ( 73,21;77,13 . Задание 7. Найти доверительный интервал для оценки математического ожидания m нормального распределения генеральной совокупности с надежность 0,95, зная выборочное среднее xср, объем выборки n и среднее квадратическое отклонение . Данные взять из таблицы 5. xср= 74,55; n=46; 13 Решение: Для оценки математического ожидания воспользуемся формулой: xв t n a xв t n Найдем t. Из соотношения 2Ф(t) = 0,95 получим: Ф(t) = 0,475. По таблице находим: t = 1,96. Найдем точность оценки t 1,96 13 3,7568 n 46 Искомый доверительный интервал: 74,55 3,7568 a 74,55 3,7568 или 70,7932 a 78,3068 Ответ: математическое ожидание находится в интервале ( 70,79;78,31 .