Лабораторная работа № 2. Выявление различий в уровне исследуемого признака
Задача 1
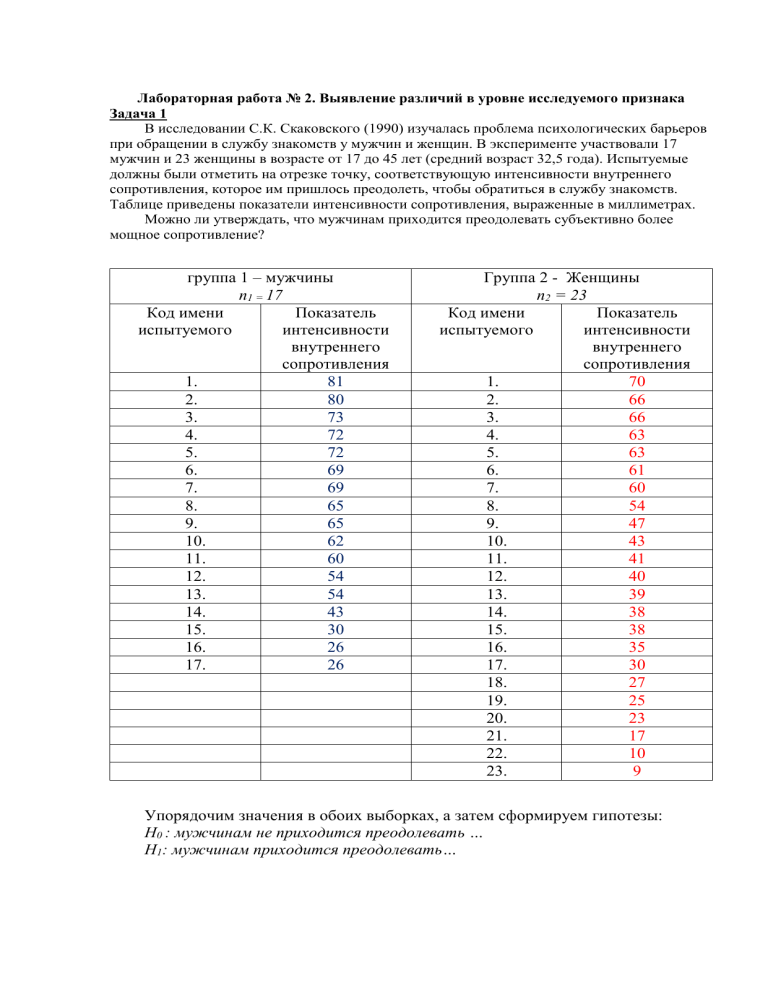
В исследовании С.К. Скаковского (1990) изучалась проблема психологических барьеров
при обращении в службу знакомств у мужчин и женщин. В эксперименте участвовали 17
мужчин и 23 женщины в возрасте от 17 до 45 лет (средний возраст 32,5 года). Испытуемые
должны были отметить на отрезке точку, соответствующую интенсивности внутреннего
сопротивления, которое им пришлось преодолеть, чтобы обратиться в службу знакомств.
Таблице приведены показатели интенсивности сопротивления, выраженные в миллиметрах.
Можно ли утверждать, что мужчинам приходится преодолевать субъективно более
мощное сопротивление?
группа 1 – мужчины
n1 = 17
Код имени
Показатель
испытуемого
интенсивности
внутреннего
сопротивления
1.
81
2.
80
3.
73
4.
72
5.
72
6.
69
7.
69
8.
65
9.
65
10.
62
11.
60
12.
54
13.
54
14.
43
15.
30
16.
26
17.
26
Группа 2 - Женщины
n2 = 23
Код имени
Показатель
испытуемого
интенсивности
внутреннего
сопротивления
1.
70
2.
66
3.
66
4.
63
5.
63
6.
61
7.
60
8.
54
9.
47
10.
43
11.
41
12.
40
13.
39
14.
38
15.
38
16.
35
17.
30
18.
27
19.
25
20.
23
21.
17
22.
10
23.
9
Упорядочим значения в обоих выборках, а затем сформируем гипотезы:
Н0 : мужчинам не приходится преодолевать …
H1: мужчинам приходится преодолевать…
Упорядочим показатели интенсивности внутреннего сопротивления
1 ряд - мужчины
2 ряд – женщины
1.
81
2.
80
3.
73
4.
72
5.
72
1.
70
6.
69
7.
69
2.
66
3.
66
8.
65
9.
65
4.
63
5.
63
10.
62
6.
61
11.
60
7.
60
12.
54
8.
54
13.
54
9.
47
14.
43
10.
43
11.
41
12.
40
13.
39
14.
38
15.
38
16.
35
15.
30
17.
30
18.
27
16.
26
17.
26
19.
25
20.
23
21.
17
22.
10
23.
9
Как видно из таблицы мы правильно обозначили ряды: первый ряд (выше) –
мужчины, второй ряд (ниже) – женщины.
S1=5;
S2=5.
Вычисляем Qэмп по формуле Qэмп = S1 + S2 = 5+5 = 10
По Табл.1 Приложения 1 определяем критические значения для n1 = 17, n2 = 23:
7, 𝑝 ≤ 0,05
𝑄кр = {
9, 𝑝 ≤ 0,01
Ясно, что чем больше расхождения между выборками, тем больше величин Q. H0 отклоняется
при Qэмп ≥ Qкр , а при Qэмп < Qкр мы будем вынуждены принять H0.
𝑄эмп > 𝑄крит (𝑝 ≤ 0,01)
Ответ: H0 отклоняется.
Задание 2.
Для проверки эффективности новой развивающей программы были созданы две группы
детей шестилетнего возраста. Одна группа (экспериментальная) занималась по новой
программе, вторая (контрольная) - по старой. После эксперимента дети обеих групп были
протестированы по методике Керна-Йерасика (школьная зрелость). Результаты тестирования
по вербальной шкале занесены в таблицу. Можно ли сделать заключение об эффективности
новой программы и ее преимуществе перед старой.
Таблица: Результаты тестирования по вербальной шкале (сырые баллы)
№ исп.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
эксп.
12
13
10
8
13
12
15
12
10
11
13
11
11
14
11
13
контр.
14
13
14
14
14
13
12
12
15
13
13
13
13
9
13
13
Решение:
Экспериментальная группа
№ п/п
Показатель
«школьной
зрелости»
1.
7. 15
2.
14. 14
3.
2. 13
4.
5. 13
5.
11. 13
6.
16. 13
7.
1. 12
8.
6. 12
9.
8. 12
10.
10. 11
11.
12. 11
Контрольная группа
№ п/п
Показатель
«школьной
зрелости»
9. 15
1.
1. 14
2.
3. 14
3.
4. 14
4.
5. 14
5.
2. 13
6.
6. 13
7.
10. 13
8.
11. 13
9.
12. 13
10.
13. 13
11.
12.
13.
14.
15.
16.
13. 11
15. 11
3. 10
9. 10
4. 8
12.
13.
14.
15.
16.
15. 13
16. 13
7. 12
8. 12
14. 9
Упорядочим значения в обоих выборках, а затем сформируем гипотезы:
Н0 : … Экспериментальная группа не превосходит контрольную по методике КернаЙерасика
H1: … Экспериментальная группа превосходит контрольную по методике КернаЙерасика.
Упорядочим по убыванию показатели «школьной зрелости»
1 ряд – экспериментальная группа
2 ряд – контрольная группа
n1=16
n2=16
7. 15
9. 15
14. 14
1. 14
2. 13
3. 14
5. 13
4. 14
11. 13
5. 14
16. 13
2. 13
1. 12
6. 13
6. 12
10. 13
8. 12
11. 13
10. 11
12. 13
12. 11
13. 13
13. 11
15. 13
15. 11
16. 13
3. 10
7. 12
9. 10
8. 12
14. 9
4. 8
Как видно из таблицы мы правильно обозначили ряды: первый ряд и второй
ряд – вверху на одном уровне, второй ряд (ниже) – женщины.
S1=0;
S2=1.
Вычисляем Qэмп по формуле Qэмп = S1 + S2 = 0+0 = 0
По Табл.1 Приложения 1 определяем критические значения для n1 = 16, n2 = 16:
6, 𝑝 ≤ 0,05
𝑄кр = {
9, 𝑝 ≤ 0,01
Ясно, что чем больше расхождения между выборками, тем больше величин Q. H0 отклоняется
при Qэмп ≥ Qкр , а при Qэмп < Qкр мы будем вынуждены принять H0.
𝑄эмп > 𝑄крит (𝑝 ≤ 0,01)
Ответ: H0 отклоняется.
Задача 3.
Для проверки эффективности новой развивающей программы были созданы две группы
детей шестилетнего возраста. Одна группа (экспериментальная) занималась по новой
программе, вторая (контрольная) - по старой. После эксперимента дети обеих групп были
протестированы по методике Керна-Йерасика (школьная зрелость). Результаты тестирования
по вербальной шкале занесены в таблицу. Можно ли сделать заключение об эффективности
новой программы и ее преимуществе перед старой.
Таблица: Результаты тестирования по вербальной шкале (сырые баллы)
№ исп
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
эксп.
14
13
11
8
12
13
13
13
11
12
14
13
12
14
10
контр.
13
13
14
12
14
14
12
13
15
13
11
12
14
9
14
Решение:
Упорядочим по убыванию показатели «школьной зрелости»
1 ряд – экспериментальная группа
n1=15
1.
11.
14.
2.
6.
7.
8.
12.
5.
10.
13.
3.
9.
15.
14
14
14
13
13
13
13
13
12
12
12
11
11
10
2 ряд – контрольная группа
n2=15
9. 15
3. 14
5. 14
6. 14
13. 14
15. 14
1. 13
2. 13
8. 13
10. 13
4. 12
7. 12
12. 12
11. 11
14. 9
4.
8
У первой группы значение по выборке ниже, а во второй группе – выше.
Определим количесвто значений второго ряда, которые больше максимального значения
первого ряда: S1 = 1.
Определим количество значений первого ряда, которые меньше максимального значения
второго ряда: S1 = 1.
Вычисляем Qэмп по формуле Qэмп = S1 + S2 = 1+1 = 2
По Табл.1 Приложения 1 определяем критические значения для n1 = 15, n2 = 15:
6, 𝑝 ≤ 0,05
𝑄кр = {
9, 𝑝 ≤ 0,01
Ясно, что чем больше расхождения между выборками, тем больше величин Q. H0 отклоняется
при Qэмп ≥ Qкр , а при Qэмп < Qкр мы будем вынуждены принять H0.
𝑄эмп > 𝑄крит (𝑝 ≤ 0,01)
Сформулируем гипотезы:
H0: Экспериментальная группа не превосходит контрольную по методике Керна-Йерасика
H1: Экспериментальная группа превосходит контрольную по методике Керна-Йерасика.
Ответ:
H0 принимается, экспериментальная группа не превосходит контрольную по методике КернаЙерасика.
H1 не принимается.
Задание 4
В ходе изучения влияния индивидуального стиля профессиональной деятельности педагога на
развитие учебной мотивации учащихся начальной школы были получены следующие
показатели:
Уровень сформированности учебной мотивации учеников 4-го класса А
(индивидуальный
стиль
педагога
–
рассуждающе-методичный)
15,18,24,29,21,24,27,24,26,26,25,28,25,22,25,20, 17,17,18.
Уровень сформированности учебной мотивации учеников 4-го класса Б
(индивидуальный
стиль
педагога
–
эмоционально-методичный)
29,26,19,21,25,27,28,19,30,30,24,28,23,29,21,19,30,20,22,23,23.
Определить: превосходят ли ученики 4 «А» класса по уровню развития сформированности
учебной мотивации учеников 4 «Б» класса.
Решение:
Результаты
№ исп
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
4-А
15
18
24
29
21
24
27
24
26
26
4-Б
29
26
19
21
25
27
28
19
30
30
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
25
28
25
22
25
20
17
17
18
24
28
23
29
21
19
30
20
22
23
23
1 ряд – 4-А класс
n1=19
4. 29
12. 28
7.
9.
10.
11.
13.
15.
3.
6.
8.
27
26
26
25
25
25
24
24
24
14. 22
5. 21
16. 20
2.
19.
17.
18.
1.
Сформируем гипотезы:
18
18
17
17
15
2 ряд – 4-Б класс
n2=21
9. 30
10. 30
17. 30
1.
14.
7.
12.
6.
2.
29
29
28
28
27
26
5.
25
11. 24
13.
20.
21.
19.
4.
15.
18.
3.
8.
16.
23
23
23
22
21
21
20
19
19
19
H0: 4 «А» класс не превосходит 4 «Б» класс по уровню развития сформированности учебной
мотивации
H1: 4 «А» класс превосходит 4 «Б» класс по уровню развития сформированности учебной
мотивации
Определяем количество значений первого ряда, которые больше максимального значения
второго ряда: S1=3. Определяем количество значений второго ряда, которые меньше
минимального значения первого ряда: S2=5. Вычисляем 𝑄эмп
по формуле 𝑄эмп = S1 + S2 = 3+5 = 8
𝑄эмп = 8.
По Табл.1 Приложения 1 определяем критические значения для n1 = 19, n2 = 21:
7, 𝑝 ≤ 0,05
𝑄крит = {
9, 𝑝 ≤ 0,01
𝑄эмп < 𝑄крит (𝑝 ≤ 0,01)
Ответ
H0 принимается, 4 «А» класс не превосходит 4 «Б» класс по уровню развития
сформированности учебной мотивации.
Задача 5
При помощи методики Р. Жиля «Восприятие внутрисемейных отношений» проведено
исследование особенностей восприятия семейных отношений старших подростков,
воспитываемых в семьях и детских домах. Были получены следующие ряды значений:
• подростки, воспитывающиеся в семье: 6,8; 6,9; 6,8; 7,9; 7,8; 7,8; 8,8; 6,8; 6,9; 6,9; 7; 6,8;
7; 7; 7,9; 8; 7,9;
• подростки, воспитывающиеся в условиях детского дома: 6,1; 5,8; 6; 6,2; 6,2; 5,5; 6; 6,4;
5,9; 6,1; 6; 6; 5,8; 6,5; 6.
Определить: превосходят ли подростки, воспитанные в семье, по особенностям
восприятия семейных отношений подростков, воспитывающихся в детских домах.
Решение:
Результаты
№ п/п
в семье
1.
6,8
2.
6,9
3.
6,8
4.
7,9
5.
7,8
6.
7,8
7.
8,8
8.
6,8
9.
6,9
10.
6,9
11.
7
12.
6,8
13.
7
14.
7
15.
7,9
16.
8
17.
7,9
в детдоме
6,1
5,8
6
6,2
6,2
5,5
6
6,4
5,9
6,1
6
6
5,8
6,5
6
1 ряд – подростки, воспитывающиеся в
семье
n1=17
8,8
8
7,9
7,9
7,9
7,8
7,8
7
7
7
6,9
6,9
6,9
6,8
6,8
6,8
6,8
2 ряд – подростки, воспитывающиеся в
детдоме
n2=15
6,5
6,4
6,2
6,2
6,1
6,1
6
6
6
6
6
5,9
5,8
5,8
5,5
Зададим гипотезы:
H0: подростки, воспитанные в семье, превосходят подростков, воспитывающихся в детских
домах, по особенностям восприятия семейных отношений
H1: подростки, воспитанные в семье, не превосходят подростков, воспитывающихся в детских
домах, по особенностям восприятия семейных отношений
Определяем количество значений первого ряда, которые больше максимального значения
второго ряда: S1=17. Определяем количество значений второго ряда, которые меньше
минимального значения первого ряда: S2=15. Вычисляем 𝑄эмп по формуле 𝑄эмп = S1 + S2
=17+15
𝑄эмп = 32.
По Табл.1 Приложения 1 определяем критические значения для n1 = 17, n2 = 15:
7, 𝑝 ≤ 0,05
𝑄крит = {
9, 𝑝 ≤ 0,01
𝑄эмп > 𝑄крит (𝑝 ≤ 0,01)
Ответ
H0 принимается, подростки, воспитанные в семье, превосходят подростков, воспитывающихся
в детских домах, по особенностям восприятия семейных отношений.









