информатика

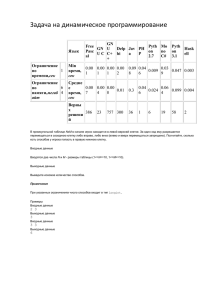
Задания первого этапа республиканской олимпиады по информатике
Бег
№1
(10 баллов)
Костя и Петя занимаются лёгкой атлетикой. Сегодня они точно выяснили, что Костя за 1 час
может пробежать расстояние К1 километров M1 метров, а Петя может пробежать расстояние К2
километров M2 метров. Мальчишки очень устали. Помогите им посчитать, какое будет между ними
расстояние, если они в течение двух часов будут бежать в разные стороны.
Входные данные:
K1 M1 – целые числа (0<=K1<=10, 0<=M1<1000)
K2 M2 – целые числа (0<=K1<=10, 0<=M1<1000)
Выходные данные:
К3 M3 расстояние между ребятами через два часа
Например:
Ввод
Вывод
1 200
4 800
1 200
3 300
12 40
2 720
№2
Небоскрёб
(10 баллов)
В небоскрёбе на каждом этаже расположено по k квартир. Костя живёт в квартире под номером N.
На каком этаже живёт Костя?
Входные данные:
k N – натуральные числа (k<=20, n<=2000)
Выходные данные:
M - этаж, на котором расположена квартира под номером N
Например:
Ввод
Вывод
4 12
3
5 16
4
№3
Домашнее задание
(10 баллов)
Сегодня у Кости сложное домашнее задание по математике. Задание заключается в следующем: из
записанных в ряд K целых чисел, нужно найти сумму первых N1 чисел и сумму последних N2 чисел.
Костя хочет выполнить домашнее задание без ошибок. Помогите Косте.
Входные данные:
K – натуральное число (0<K<=20)
N1, N2 – натуральные числа (0<= N1, N2<=K)
a1, a2, ....., ak, где ai — целые числа (-100<=ai<=100)
Выходные данные:
s1, s2 - сумма первых N1 чисел ряда и сумма последних N2 чисел ряда
Например:
Ввод
Вывод
7
10 -1
3 1
9 -2 3 5 8 7 -1
5
15 44
4 4
1 2 4 8 30
№4
Заблудились
(10 баллов)
Костя и Петя отправились в поход. В день они проходят 15 км. Запас еды у них рассчитан на 7
дней. Побродив по лесам первые 3 дня, они поняли, что заблудились. Однако, когда надежды на
спасение уже практически не осталось, они встретили лесника, который показал им дорогу назад.
Посчитайте, хватит ли еды ребятам, чтобы добраться до дома (Yes/No). Если еды не хватит, то сколько
километров им придётся идти голодными. Двигаются они по прямой.
Входные данные:
x0, y0 - координаты встречи туристов с лесником
x1, y1 - пункт назначения
Все измерения производятся в километрах. Все числа целые (-1000 <= x0, y0, x1, y1 <= 1000 )
Выходные данные:
Yes/No – хватит/не хватит еды
D - расстояние, которое необходимо пройти ребятам без еды, c точностью три знака после запятой
Например:
Ввод
Вывод
50 0
Yes
0 0
50 50
1 -1
No
10,725
№5
Подпоследовательность
(10 баллов)
В заданной последовательности, состоящей из N чисел найти максимально длинную
подпоследовательность (необязательно подряд идущих) чисел такую, что каждый последующий элемент
подпоследовательности не меньше предыдущего (если подпоследовательностей несколько, выведите
любую).
Входные данные:
N – количество чисел в последовательности (1< N <= 40)
a1, a2, ....., an, где ai – натуральные числа ( ai<=1000)
Выходные данные:
K – длина подпоследовательности
b1, b2, ....., bk - элементы подпоследователььности
Например:
Ввод
Вывод
7
4
9258571
2 5 5 7
10
5
5327249857
22457
№6
Пароль
(10 баллов)
Костя забыл новый пароль к своему компьютеру. Он помнит, что его пароль обладал
следующими свойствами:
- пароль – это семизначное число;
- все цифры числа расположены строго по убыванию;
- семизначное число кратно 3.
Петя сказал Косте, что таких вариантов всего 42. Костя смог придумать только два варианта
пароля: 9765432 и 8654310. Остальные 40 вариантов необходимо найти.
Входные данные: входных данных нет
Выходные данные: P1 P2 . . . P42 - найденные пароли
Примечание: каждый найденный вами пароль оценивается 0.25 баллами
№7
Взвешивание
(10 баллов)
На уроке физики Костя получил домашнее задание придумать способы взвешивания грузов на
рычажных весах. На левую чашу весов Костя ложит груз, а на правую чашу гири. У Кости имеются
гири весом 1,2,4,8 грамм. Костя быстро понял, что с таким набором гирь он может взвесить любые
грузы от 1 до 15 грамм. Если бы у Кости была бы ещё гиря 16 грамм, то он смог бы взвешивать грузы
до 31 грамма.
Но тут пришёл Петя и сказал, что гири можно ложить на разные чаши весов. Например, с
помощью гирь 1, 3 и 8 грамм таким образом можно взвесить любые грузы от 1 до 12 грамм.
Помогите Косте разработать минимальный набор гирь (по количеству) для взвешивания грузов
от 1 до k грамм на рычажных весах. Гири можно ложить на обе чаши весов.
Если наборов гирь может быть несколько, то выведите любой.
Входные данные:
k - натуральное число ( k <= 10 000 000)
Выходные данные:
n - количество гирь в минимальном наборе
b1, b2, ....., bn - веса гирь минимального набора
Например:
Ввод
Вывод
4
2
1 3
9
3
1 3 8
Тесты к заданиям
первого этапа республиканской олимпиады по информатике
№1
Бег
(10 баллов)
№ теста
Ввод
Вывод
Баллы
1
1 100
4 600
2
1 200
2
2 800
8 0
2
1 200
3
5 700
22 910
2
5 755
4
7 333
19 998
2
2 666
5
9 150
34 298
2
7 999
№2
Небоскрёб
(10 баллов)
№ теста
Ввод
Вывод
Баллы
1
3 5
2
2
2
3 9
3
2
3
8 89
12
2
4
8 88
11
2
5
1 50
50
2
№3
Домашнее задание
(10 баллов)
№ теста
Ввод
Вывод
Баллы
1
5
3 12
1+1
2 3
1 2 3 4 5
2
3
61 61
1+1
3 3
9 7 45
3
7
9 7
1+1
4 1
8 0 -2 3 4 5 7
4
9
108 -3
1+1
7 6
99 98 97 96 -95 -94 -93 92 91
5
19
15 87
1+1
5 17
1234567890987654321
№4
Заблудились
№ теста
Ввод
1
1 -1
-1 1
2
-25 35
45 55
3
100 0
200 0
4
0 0
0 70
5
50 70
0 0
(10 баллов)
Вывод
Yes
No
12,801
No
40,000
No
10,000
No
26,023
Баллы
2
2
2
2
2
№5
Подпоследовательность
(10 баллов)
№ теста
Ввод
Вывод
Баллы
1
5
3
2
1 3 2 5 4
1 2 4
2
9
5
2
3 2 2 9 5 1 5 8 7
2 2 5 5 7 или (2 2 5 5 8)
3
7
4
2
9 8 9 8 7 8 9
8 8 8 9
4
13
6
2
13 12 17 16 2 7 3 4 5 1 6 8 6
2 3 4 5 6 6 или (2 3 4 5 6 8)
5
27
13
2
3 2 7 2 3 4 3 4 5 4 5 6 5 6 7 6 2 2 3 4 4 5 5 5 6 6 7 7 8
7 8 7 8 1 2 3 5 4 3 2
!!! другие варианты
Примечание: если правильно выдаёт только количество, то 1 балл за тест (но если правильно
выдаёт количество во всех 5 тестах, то 1.5 балла за тест).
№6
Правильные коды:
За каждый правильно выведенный пароль: 0.25 балла (40*0,25=10)
6543210 7653210 7654320 8643210 8654310 8754210
8754321 8763210 8764320 8765310 8765421 8765430
9543210 9654210 9654321 9753210 9754320 9764310
9765210 9765321 9765420 9765432 9843210 9854310
9864210 9864321 9865320 9865410 9865431 9873210
9874320 9875310 9875421 9875430 9876210 9876321
9876420 9876432 9876510 9876531 9876540 9876543
№7
№ теста
1
5
2
40
3
4
5
Ввод
1093
10000
7 174 452
Вывод
3
1 3 9
4
1 3 9
7
1 3 9
10
1 3 9
15
1 3 9
59049
Баллы
2
2
27
2
27 81 243 729
2
27 81 243 729 2187 6561 19683
2
27 81 243 729 2187 6561 19683
177147 531441 1594323 4782969
Примечание:
Правильных ответов может быть несколько
Оптимальный набор гирь: 1 3 9 27 81 243 729 и т.д.
Правильные наборы гирь находим по следующему правилу:
 первая гиря = 1
 вторая гиря = 2 или 3
 каждая следующая гиря не должна превышать удвоенную сумму предыдущих
гирь плюс один (например: 1 2 7 21 63 и т.д.)
 для суммы всех гирь S должно выполняться условие S>=k