МИНОБРНАУКИ РОССИИ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ
ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
«ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)
Кафедра САПР
ОТЧЕТ
по лабораторной работе №1
по дисциплине «Компьютерная графика»
Тема: Отображение фигуры относительно осей с изменением
масштаба
Студенты гр. 8361
Преподаватель
_______________
Кочнев Т.В.
_______________
Самолюк А.А.
_______________
Фам Нгок Ань
_______________
Матвеева И.В.
Санкт-Петербург
2021
1. Цель работы.
Отображение плоского объекта относительно осей координат с
изменением или без изменения масштаба изображения.
2. Теоретические сведения
Рассмотрим треугольник АВС и отразим его относительно осей
координат с изменением масштаба и положения фигуры.
Обшая формула:
𝑥𝐴
[𝑥𝐵
𝑥𝐶
𝑦𝐴
𝑦𝐵 ] * [𝑎
0
𝑦𝐶
𝑎𝑥𝐴
0
] =[𝑎𝑥𝐵
𝑑
𝑎𝑥𝐶
𝑑𝑦𝐴
𝑑𝑦𝐵 ]
𝑑𝑦𝐶
где коэффициент a, d – служат отражения и мастабирование объекта
При a = 1 и d = -1 то выполняется симметричное отражение
относительно оси х.
𝑥𝐴 𝑦𝐴
1
[𝑥𝐵 𝑦𝐵 ] * [
0
𝑥𝐶 𝑦𝐶
𝑥𝐴
0
] =[𝑥𝐵
−1
𝑥
𝐶
−𝑦𝐴
−𝑦𝐵 ]
−𝑦𝐶
При a = -1 и d = 1 то выполняется симметричное отражение
относительно оси y.
𝑥𝐴 𝑦𝐴
−𝑥𝐴
−1
0
] =[−𝑥𝐵
[𝑥𝐵 𝑦𝐵 ] * [
0
1
𝑥𝐶 𝑦𝐶
−𝑥𝐶
𝑦𝐴
𝑦𝐵 ]
𝑦𝐶
При а = d − пропоциональное масштабирование а при a # d −
непропоциональное масштабирование. В данной работе мы использовали
пропоциональное масштабирование. Для a = d > 1 происходит расширение, т.э
увеличение изображения. Если a = d < 1 то равномерное сжатие.
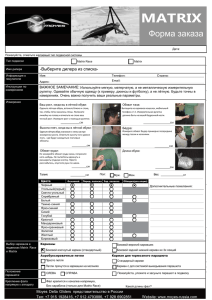
3. Пример выпольнения работы.
В качестве примера рассмотрим треугольник со следующими
координатами:
𝑥𝐴 = −2, 𝑦𝐴 = 1
𝑥𝐵 = −1, 𝑦𝐵 = 2
𝑥𝐶 = −3, 𝑦𝐶 = 3
2
После выбора оси координаты и ввода коэффициента масштабирование
необходимо нажать кнопку «Нарисование». Тогда на графике появили
треугольник и его изображения а также в разделе «Координаты отраженного
треугольника» появились координаты изображения. На следующих картинах
представлены результаты выпольнения примеров работы.
Рисунок 1 – Результат при отражении относительно оси Ox с именеием
масштабирования
Рисунок 2 – Результат при отражения относительно оси Oy с именеием
масштабирования
3
Выводы.
В данной лабораторной работе было рассмотрено и реализовано
отображение треугольника относительно осей Х и Y с изменением его
масштаба.
4
ПРИЛОЖЕНИЕ А
Файл «main.cpp»
#include "mainwindow.h"
#include <QApplication>
int main(int argc, char *argv[])
{
QApplication a(argc, argv);
MainWindow w;
w.show();
return a.exec();
}
5
ПРИЛОЖЕНИЕ Б
Файл «mainwindow.cpp»
#include "mainwindow.h"
#include "ui_mainwindow.h"
#include<QPolygon>
#include<QMessageBox>
int Sx = 40;
int Sy = 40;
MainWindow::MainWindow(QWidget *parent)
: QMainWindow(parent)
, ui(new Ui::MainWindow)
{
ui->setupUi(this);
scene = new QGraphicsScene(-500,-500, 1000,1000,nullptr);
ui->graphicsView->setScene(scene);
ui->graphicsView>setVerticalScrollBarPolicy(Qt::ScrollBarAlwaysOn);
ui->graphicsView>setHorizontalScrollBarPolicy(Qt::ScrollBarAlwaysOn);
SetScene();
ui->dspb_Ax->setValue(0);
ui->dspb_Ay->setValue(0);
ui->dspb_Bx->setValue(0);
ui->dspb_By->setValue(0);
ui->dspb_Cx->setValue(0);
ui->dspb_Cy->setValue(0);
ui->dspb_coeff->setValue(0.4);
ui->rb_x->setChecked(true);
ui->rb_y->setChecked(false);
t = nullptr;
}
6
MainWindow::~MainWindow()
{
delete ui;
delete
scene;
delete t;
}
void MainWindow::on_pbtn_exit_clicked()
{
exit(0);
}
void MainWindow::on_pbtn_draw_clicked()
{
scene->clear();
SetScene();
double A[2], B[2], C[2], coeff, res[3][2];
A[0] = ui->dspb_Ax->value() * Sx;
A[1] = ui->dspb_Ay->value() * Sy;
B[0] = ui->dspb_Bx->value() * Sx;
B[1] = ui->dspb_By->value() * Sy;
C[0] = ui->dspb_Cx->value()* Sx;
C[1] = ui->dspb_Cy->value() * Sy;
coeff = ui->dspb_coeff->value();
t = new Triangle(A,B,C);
if(!t->IsTriangle())
7
QMessageBox::warning(this,"Ошибка", "Сумма двух сторон
треугольника меньше либо равна третьей!");
else
{
QPolygonF pol;
if(ui->rb_x->isChecked())
t->Reflection(0,coeff,res);
else
t->Reflection(1,coeff,res);
ui->line_value_Ax_1->setText(QString::number(res[0][0] *
1.0/Sx));
ui->line_value_Ay_1->setText(QString::number(res[0][1] *
1.0/Sy));
ui->line_value_Bx_1->setText(QString::number(res[1][0]*
1.0/Sx));
ui->line_value_By_1->setText(QString::number(res[1][1]*
1.0/Sy));
ui->line_value_Cx_1->setText(QString::number(res[2][0]*
1.0/Sx));
ui->line_value_Cy_1->setText(QString::number(res[2][1]*
1.0/Sy));
Triangle * tmp = new Triangle(res[0], res[1], res[2]);
scene->addItem(t);
scene->addItem(tmp);
}
}
void MainWindow::SetScene()
{
scene->addLine(-400, 0, 400, 0, QPen(Qt::black));
scene->addLine(0, -400, 0, 400, QPen(Qt::black));
8
QFont p("Times",20);
for(int i = (-400/Sx + 1);i < 400/Sx; i++)
{
QGraphicsTextItem *text1 = scene->addText(QString::number(i));
scene->addLine(Sx * i,3,Sx * i,-3,QPen(Qt::black));
text1->setPos(Sx * i, 4);
}
for(int i = (-400/Sy + 1);i < 400/Sy;i++)
{
if(i != 0)
{
QGraphicsTextItem *text1 = scene->addText(QString::number(i));
scene->addLine(3,- Sy * i,-3, - Sy * i,QPen(Qt::black));
text1->setPos( 8, -Sy * i);
}
}
}
void MainWindow::on_dspb_coeff_valueChanged(double arg1)
{
ui->pbtn_draw->click();
}
9
ПРИЛОЖЕНИЕ В
Файл «triangle.cpp»
#include "triangle.h"
#include "matrix.h"
#include<QPolygon>
Triangle::Triangle()
{
}
Triangle::~Triangle(){}
Triangle::Triangle(double A[2], double B[2], double C[2])
{
matrix[0][0] = A[0];
matrix[0][1] = A[1];
matrix[1][0] = B[0];
matrix[1][1] = B[1];
matrix[2][0] = C[0];
matrix[2][1] = C[1];
}
bool Triangle::IsTriangle()
{
double A = sqrt(pow((matrix[1][0] - matrix[0][0]),2) +
pow((matrix[1][1] - matrix[0][1]),2));
double B = sqrt(pow((matrix[2][0] - matrix[1][0]),2) +
pow((matrix[2][1] - matrix[1][1]),2));
double C = sqrt(pow((matrix[2][0] - matrix[0][0]),2) +
pow((matrix[2][1] - matrix[0][1]),2));
if(A + B <= C || A + C <= B || B + C <= A)
return false;
return true;
}
10
void Triangle::Reflection(int axis, double coefficients, double
res[3][2])
{
double tmp[3][2];
double matrixX[2][2] = {{1,0},{0,-1}};
double matrixY[2][2] = {{-1,0},{0,1}};
double matrixcoeff[2][2] = {{0,0},{0, 0}};
matrixcoeff[0][0] = matrixcoeff[1][1] = coefficients;
TMatrix M;
M.multiply(matrix,matrixcoeff,tmp);
if(axis == 0)
M.multiply(tmp,matrixX,res);
else
M.multiply(tmp,matrixY,res);
}
void Triangle::drawPolygon(QPainter * painter, double
matrix[3][2], QColor color)
{
QPolygonF polygon;
for(int i =0;i < 3;i++)
{
polygon << QPointF(matrix[i][0],matrix[i][1] * (-1));
}
painter->setBrush(color);
painter->drawPolygon(polygon);
}
void Triangle::paint(QPainter *painter, const
QStyleOptionGraphicsItem *option, QWidget *widget)
{
Q_UNUSED(option);
Q_UNUSED(widget);
drawPolygon(painter,matrix,Qt::red);
11
}
QRectF Triangle::boundingRect() const
{
return QRectF(-300,-300,600,600);
area of triangle
}
12
// We are limiting the
ПРИЛОЖЕНИЕ Г
Файл «matrix.cpp»
#include "matrix.h"
matrix::matrix()
{
}
void
matrix::multiply(double
matrix1[3][2],double
matrix2[2][2], double res[3][2]){
int i,j,k;
int N=3;
for (i = 0; i < N; i++)
{
for (j = 0; j < N-1; j++)
{
res[i][j] = 0;
for (k = 0; k < N-1; k++)
res[i][j]
matrix2[k][j];
}
}
}
13
+=
matrix1[i][k]
*