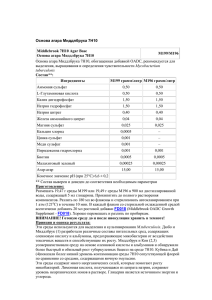
Дано
𝐸 = 420 В
𝑅1 = 320 Ом
𝑅 2 = 600 Ом
𝐿 = 400 мГн = 0,4Гн
𝐶 = 500 мкФ = 0,0005 Ф
Решение:
1. Определим принужденную составляющую тока
𝑖1пр = 𝑖2пр =
𝐸
420
=
= 0,457 А
𝑅1 + 𝑅 2 320 + 600
𝑖3пр = 0
2.Составляем характеристическое уравнение через входное сопротивление
1
𝑗𝑤𝐶
𝑍 = 𝑅1 +
1 , заменяем 𝑗𝑤 на 𝑝
𝑅2 + 𝑗𝑤𝐿 +
𝑗𝑤𝐶
(𝑅2 + 𝑗𝑤𝐿) ∗
1
𝑅 2 + 𝑝𝐿
𝑅 2 + 𝑝𝐿
𝑝𝐶
𝑝𝐶
𝑍(𝑝) = 𝑅1 +
=
𝑅
+
=
𝑅
+
=
1
1
2
1
𝑝𝐶𝑅2 + 𝑝 𝐶𝐿 + 1
𝑝𝐶𝑅2 + 𝑝 2 𝐶𝐿 + 1
𝑅2 + 𝑝𝐿 +
𝑝𝐶
𝑝𝐶
2
(
)
𝑅1 𝑝𝐶𝑅2 + 𝑝 𝐶𝐿 + 1 + 𝑅 2 + 𝑝𝑙 𝑝𝑅1 𝐶𝑅 2 + 𝑝 2 𝑅1 𝐶𝐿 + 𝑅1 + 𝑅 2 + 𝑝𝐿
=
=
=0
𝑝𝐶 𝑅 2 + 𝑝 2 𝐶𝐿 + 1
𝑝𝐶𝑅2 + 𝑝 2 𝐶𝐿 + 1
(𝑅2 + 𝑝𝐿) ∗
𝑍(𝑝) =
𝑝 ∗ 320 ∗ 0.0005 ∗ 600 + 𝑝 2 ∗ 320 ∗ 0.0005 ∗ 0.4 + 320 + 600 + 𝑝 ∗ 0.4
=0
𝑝 ∗ 0.0005 ∗ 600 + 𝑝 2 ∗ 0.0005 ∗ 0.4 + 1
0.064𝑝 2 + 96.4𝑝 + 920 = 0
𝐷 = 𝑏 2 − 4𝑎𝑐 = 96.42 − 4 ∗ 0.064 ∗ 920 =
= 9057.44
−𝑏 ± √𝐷 −96.4 ± √9057.44
𝑝1,2 =
=
=>
2𝑎
2 ∗ 0.064
1
𝑝1 = −1496.65
𝑐
=>
1
𝑝2 = −9.6
𝑐
ОДЗ:
0.0002𝑝 2 + 0.3𝑝 + 1 ≠ 0
𝑝 2 + 1500𝑝 + 5000 ≠ 0
𝐷 = 𝑏 2 − 4𝑎𝑐 = 15002 − 4 ∗ 1 ∗ 5000 =
= 2230000
−𝑏 ± √𝐷 −1500 ± √2230000
𝑝1,2 ≠
=
=>
2𝑎
2
1
𝑝1 ≠ −1496.66
𝑐
=>
1
𝑝2 ≠ −3.34
𝑐
3.Составим выражения тока через индуктивность и находим напряжение на ней.
𝑖2 = 𝑖2пр + 𝑖2св = 0,457 + 𝐴1 𝑒 −1496.65𝑡 + 𝐴 2 𝑒 −9.6𝑡 А
𝑈𝐿 = 𝐿
𝑑𝑖2
= 0.4(−1496.65 ∗ 𝐴1 𝑒 −1496.65𝑡 − 9.6 ∗ 𝐴 2 𝑒 −9.6𝑡 ) =
𝑑𝑡
= −598.66 ∗ 𝐴1 𝑒 −1496.65𝑡 − 3.84 ∗ 𝐴 2 𝑒 −9.6𝑡 В
4. Определим ток на конденсаторе через напряжение на нем
𝑈𝐶 = 𝑈𝐿 + 𝑅2 ∗ 𝑖2 =
= −598.66 ∗ 𝐴1 𝑒 −1496.65𝑡 − 3.84 ∗ 𝐴 2 𝑒 −9.6𝑡 + 600 ∗ (0,457 + 𝐴1 𝑒 −1496.65𝑡 + 𝐴 2 𝑒 −9.6𝑡 ) =
= −598.66 ∗ 𝐴1 𝑒 −1496.65𝑡 − 3.84 ∗ 𝐴 2 𝑒 −9.6𝑡 + 274.2 + 𝐴1 𝑒 −1496.65𝑡 + 600 ∗ 𝐴 2 𝑒 −9.6𝑡 =
= 274.2 − 598.66 ∗ 𝐴1 𝑒 −1496.65𝑡 + 596.16 ∗ 𝐴 2 𝑒 −9.6𝑡 В
𝑖3 = 𝐶
𝑑𝑈𝐶
=
𝑑𝑡
= 0,0005 ∗ (−598.66 ∗ (−1496.65) ∗ 𝐴1 𝑒 −1496.65𝑡 + 596.16 ∗ (−9.6) ∗ 𝐴 2 𝑒 −9.6𝑡 ) =
= 0.0005 ∗ (895984.489 ∗ 𝐴1 𝑒 −1496.65𝑡 − 5723.136 ∗ 𝐴 2 𝑒 −9.6𝑡 ) =
= 447.992 ∗ 𝐴1 𝑒 −1496.65𝑡 − 2.861 ∗ 𝐴 2 𝑒 −9.6𝑡 А
5. Определим ток в неразветвленной части схемы
𝑖1 = 𝑖2 + 𝑖3 =
= 0,457 + 𝐴1 𝑒 −1496.65𝑡 + 𝐴 2 𝑒 −9.6𝑡 + 447.992 ∗ 𝐴1 𝑒 −1496.65𝑡 − 2.861 ∗ 𝐴 2 𝑒 −9.6𝑡 =
= 0,457 + (448.992 ∗ 𝐴1 𝑒 −1496.65𝑡 − 1.861 ∗ 𝐴 2 𝑒 −9.6𝑡 )
6.Определим постоянные интегрирования
{
𝑖2 (0) = 0
0.457 + 𝐴1 + 𝐴 2
=> {
=>
274.2 − 598.66 ∗ 𝐴1 + 596.16 ∗ 𝐴 2
𝑈𝑐 (0) = 0
𝐴1 = −0.457 − 𝐴 2
=> {
274.2 − 598.66 ∗ (−0.457 − 𝐴 2 ) + 596.16 ∗ 𝐴 2
274.2 − 598.66 ∗ (−0.457 − 𝐴 2 ) + 596.16 ∗ 𝐴 2 = 0
547.78 + 1194.82𝐴 2 = 0
1194.82𝐴 2 = 547.78
𝐴 2 = −0.458
𝐴1 = −0.457 − (−0.458) = 0.001
7. Выражение изменения тока от времени в неразветвленной части цепи будет иметь вид
𝑖1 = 0,457 + (448.992 ∗ 0.001 ∗ 𝑒 −1496.65𝑡 − 1.861 ∗ (−0.458) ∗ 𝑒 −9.6𝑡 ) =
= 0,457 + (0.45 ∗ 𝑒 −1496.65𝑡 + 0.85 ∗ 𝑒 −9.6𝑡 )