ilovepdf merged

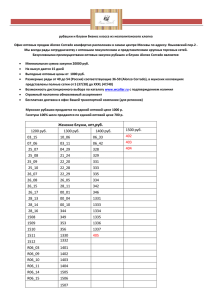
Цифровая обработка сигналов - 1
Title
Digital signal processing
Author
Alexander Kapitanov
Contact
sallador@bk.ru
Project lang
Python
Packages
numpy, scipy, matplotlib
License
GNU GPL 3.0
Введение
Перед вами обучающий материал по основам цифровой обработки сигналов с использованием средств языка
программирования Python. Предполагается, что читатель имеет базовые знания из области высшей математики, а также
владеет языком Python и хотя бы поверхностно знает различные python-библиотеки - numpy/scipy, matplotlib и другие.
Для пользователей MATLAB / GNU Octave освоение материала с точки зрения программного кода не составит труда,
поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из python-библиотек.
Сигналы
Сигналом называется физический процесс, параметры которого изменяются в соответствии с передаваемым сообщением.
Cигнал является материальным носителем информации. По способу представления сигналы разделяются на две группы –
случайные и детерминированные. Их описывают математической моделью или функцией, характеризующей изменение
параметров сигнала.
Случайным сигналом называют функцию времени, значения которой заранее неизвестны и могут быть предсказаны лишь с
некоторой вероятностью. К основным характеристикам случайных сигналов относятся:
закон распределения (относительное время пребывания значения сигнала в определенном интервале),
спектральное распределение мощности.
Детерминированные сигналы описываются аналитической функцией (задаются аналитически), и их поведение полностью
известно в любой момент времени. Детерминированные сигналы в свою очередь бывают периодическими и
непериодическими. Непериодические сигналы, как правило, ограничены во времени.
Периодический сигнал - это сигнал, который повторяется во времени с определенным периодом, то есть для которого
выполняется условие:
s(t) = s(t + kT),
где k – любое целое число, T – период повторения.
Пример периодического сигнала – гармоническое колебание, описываемое следующим выражением:
s(t) = A ⋅ cos(2π⋅tT + ϕ),
где A – амплитуда колебания, φ – начальная фаза.
Известно, что любой сложный периодический сигнал может быть представлен в виде суммы гармонических колебаний с
частотами, кратными основной частоте ω = 2π/T.
Цифровые сигналы
Все сигналы можно разделить на четыре группы:
аналоговые,
дискретные,
квантованные,
цифровые.
Аналоговый сигнал – описывается непрерывной функцией времени. Аналоговый сигнал обеспечивает передачу данных
путем непрерывного изменения во времени амплитуды, частоты или фазы. Практически все физические процессы
описываются непрерывными функциями времени, поэтому представляют собой аналоговые сигналы. Для аналогового
сигнала область значений и определения описывается непрерывным множеством.
сигнала область значений и определения описывается непрерывным множеством.
Для дискретного сигнала свойственно прерывистое (дискретное) изменение сигнала во времени. То есть изменения в
сигнале происходят скачкообразно через некоторые промежутки времени, называемые интервалом дискретизации – Δt или
Td. Дискретизация аналогового сигнала состоит в том, что сигнал представляется в виде последовательности значений,
взятых в дискретные моменты времени, которые называются отсчётами (сэмплами).
Для правильного восстановления аналогового сигнала из цифрового без искажений и потерь используется теорема
отсчетов, известная как теорема Котельникова (Найквиста-Шеннона).
Любой непрерывный сигнал с ограниченным спектром может быть восстановлен однозначно и без потерь по
своим дискретным отсчетам, взятым с частотой строго больше удвоенной верхней частоты спектра
непрерывного сигнала.
Формула теоремы Котельникова:
F s = 1T s > 2F a,
где
F s - частота дискретизации сигнала,
F a - верхняя частота спектра аналогового сигнала.
Такое определение относится к функциям времени, которые состоят из частот от нуля до F a.
В реальных задачах в радиотехнике спектр сигнала может лежать в любом диапазоне частот и начинаться и заканчиваться
на любой частоте, в связи с этим определение Теоремы Котельникова правильно рассматривать относительно ширины
спектра такого сигнала:
Любой непрерывный сигнал с ограниченным спектром может быть восстановлен однозначно и без потерь по
своим дискретным отсчетам, взятым с частотой строго больше удвоенной ширины полосы частот, занимаемой
спектром непрерывного сигнала.
F s = 1T s > 2Δf, где
Δf - ширина спектра непрерывного сигнала.
Квантованные сигналы принимают ряд конечных значений из диапазона непрерывных или дискретных величин. Как
правило, сигналы квантуются по уровню, то есть по амплитуде.
Цифровые сигналы получаются из аналоговых с помощью операций дискретизации и квантования по уровню. Значениям
цифрового сигнала присваивается кодовое слово или набор символов (зачастую двоичных).
Устройства, осуществляющие дискретизацию по времени и квантование по уровню, называются аналого-цифровыми
преобразователями (АЦП). Устройства, переводящие цифровой сигнал в аналоговый называются цифро-аналоговыми
преобразователями (ЦАП).
Для работы с сигналами в Python потребуется ряд предварительных действий.
Необходимо импортировать библиотеку numpy для оперативного и качественного выполнения математических действий, а
также графические средства отображения из библиотеки matplotlib.
In [1]:
import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import fft
%matplotlib inline
Напомним, что магическая функция %matplotlib inline позволяет отображать графики без вызова метода
plt.show()
На приведенном ниже примере представлены сигналы в аналоговой, дискретной и квантованной форме.
Шаг 1: создать ряд временных значений: Функция np.linspace(start, stop, num) задает вектор в диапазоне [start,
stop], а num - количество точек в диапазоне.
Шаг 2: создать сигнал произвольной формы: С помощью функции np.sin() задаём сигнал из набора гармонических
Шаг 2: создать сигнал произвольной формы: С помощью функции np.sin() задаём сигнал из набора гармонических
воздействий. Для простоты амплитуды всех компонент равны 1, а смещение по фазе нулевое.
Шаг 3 Отрисовка графиков. Методы matplotlib задают различный стиль отображения:
plot() - стандартный график, выводит сигнал в аналоговой форме,
stem() - график в виде отсчетов, выводит сигнал в дискретной форме,
step() - график в виде уровней, выводит сигнал в квантованной форме.
Для уменьшения количества кода создана вспомогательная функция plt_sel(s, *args, **kwargs) , которая выбирает
стиль отображения графика. Аргументы *args передают значения по осям ординат и абсцисс, **kwargs используется
для передачи параметров в метод stem() .
In [2]:
n
#
t
#
x
= 40
time vector
= np.linspace(0, 1, n, endpoint=True)
sine wave
= np.sin(np.pi*t) + np.sin(2*np.pi*t) + np.sin(3*np.pi*t) + np.sin(5*np.pi*t)
# Select: plot, stem, bar
def plt_sel(s, *args, **kwargs):
if s == 0:
return plt.plot(*args)
if s == 1:
return plt.stem(*args, **kwargs)
if s == 2:
return plt.step(*args)
# Subplot titles
t_titles = ['Аналоговый', 'Дискретный', 'Квантованный']
# Plot figures
fig = plt.figure(figsize=(16, 4), dpi=80)
for i in range(3):
plt.subplot(1, 3, i+1)
plt.title(t_titles[i])
plt_sel(i, t, x, use_line_collection=True)
plt.xlim([0, 1])
plt.yticks(np.linspace(np.floor(np.min(x)), np.ceil(np.max(x)), 9))
plt.grid(True)
# change plot view
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.spines['bottom'].set_position(('data',0))
plt.tight_layout()
Если шаг квантования и дискретизации выбраны неправильно, преобразование сигнала из аналоговой формы в дискретную
будет происходить с искажениями. Покажем на примере неграмотный выбор шага дискретизации и шага квантования.
Зададим график синуса. Длина сигнала n = 64 отсчетов, на которых укладывается один период гармонического сигнала.
Установим шаг квантования таким образом, чтобы иметь выборку из d = 3, 5, 8 и 32 отсчетов.
In [3]:
n = 64
# time vector
# time vector
t = np.linspace(0, 1, n, endpoint=True)
# sine wave
ds = np.sin(2*np.pi*t)
# discrete step
step_lst = np.array([3, 5, 8, 32])
#plot figure
fig = plt.figure(figsize=(12, 6), dpi=80)
for i in range(4):
tt = np.linspace(0, 1, step_lst[i], endpoint=True)
plt.subplot(2, 2, i+1)
plt.title('Number of points = {}'.format(step_lst[i]))
plt.plot(t, ds, '-', linewidth=2.0)
plt.plot(tt, np.sin(2*np.pi*tt), '--o', linewidth=1.5, markersize=8)
plt.step(tt, np.sin(2*np.pi*tt), linewidth=1.5)
plt.grid()
plt.xlim([0, 1])
plt.tight_layout()
Как видно, наихудшая форма сигнала получилась при большом значении шага дискретизации, то есть большом расстоянии
между соседними отсчетами цифрового сигнала. Чем меньше расстояние между соседними отсчетами (меньше шаг
дискретизации и больше число точек последовательности), тем лучше дискретный сигнал повторяет форму аналогового
сигнала.
Дискретные последовательности
Дискретной последовательностью называется математическая модель дискретного сигнала, представляющая собой
решетчатую функцию: x(nT) = x(n), где T – интервал дискретизации, n = 0, 1, 2, ..., N-1 - отсчёты или сэмплы.
Пример конечной дискретной последовательности x(nT) = {2, 1, -2, 0, 2, 3, 1, 0} . Данная последовательность
выглядит, как показано на рисунке:
In [4]:
# Digital signal
xt = np.array([2, 1, -2, 0, 2, 3, 1, -1])
# Time vector
t = np.linspace(0, xt.size-1, xt.size, endpoint=True)
# Plot figure
fig = plt.figure(figsize=(8, 3), dpi=80)
plt.title('Digital signal')
plt.stem(t, xt, linefmt='C3', markerfmt='D', use_line_collection=True)
plt.stem(t, xt, linefmt='C3', markerfmt='D', use_line_collection=True)
plt.xticks(t)
plt.xlim([np.min(t)-0.2, np.max(t)+0.2])
plt.grid(True)
Дельта-функция
Единичный импульс – простейшая дискретная последовательность. Это дискретная δ-функция δ(nT) Дирака, которая
равна единице при n = 0 и нулю при всех остальных значениях n.
Дискретная δ-функция, смещенная во времени на m тактовых интервалов, записывается следующим образом: δ(nT-mT) .
Единичный скачок
Единичный скачок или функция Хевисайда – еще один вид простых и важных дискретных последовательностей. Он
принимает нулевые значения в отрицательной области времени и единичные значения в положительной.
Математически функция единичного скачка записывается как:
σ(nT) = δ(nT) + δ(nT - T) + δ(nT – 2T) + ...
In [5]:
n = 6
# time vector
t = np.linspace(-n, n-1, 2*n)
# Delta function
xd = np.zeros(2*n)
xd[n] = 1
# Heaviside function
xh = np.heaviside(t, 1)
# Combine them together
xs = [xh, xd]
# Plot results
fig = plt.figure(figsize=(12, 3), dpi=80)
for i, sig in enumerate(xs):
plt.subplot(1, 2, i+1)
plt.stem(t, sig, linefmt='C3', markerfmt='D', use_line_collection=True)
plt.ylabel('Amplitude')
plt.xlabel('Samples')
plt.xticks(t)
plt.xlim([np.min(t)+1, np.max(t)])
plt.grid(True)
plt.tight_layout()
Дискретный единичный скачок σ(n) и дискретная δ-функция δ(n) связаны между собой следующими соотношениями:
δ(nT) = σ(nT) − σ(nT − T) ,
σ(nT) = ∑
+∞k=0
δ(nT − kT) ,
Произвольная дискретная последовательность может быть записана в виде взвешенной суммы δ-функций:
x(nT) = ∑
+∞k=0
x(kT) ⋅ δ(nT − kT) ,
Последовательность x(nT) называется периодической, если она удовлетворяет условию x(nT) = x(nT+mNT) ,
где
m и N – целые числа, m = 0, 1, 2, ..., NT
NT – период дискретной последовательности.
Z-преобразование
Дискретные последовательности очень удобно описывать с помощью Z-формы или Z-преобразований.
Z-преобразование – аналог преобразования Лапласа в дискретной форме. Для дискретной последовательности x(nT)
одностороннее Z-преобразование определяется следующим рядом:
X(z) = Z | x(nT) | = ∑
∞n=0
x(nT)z−n ,
где z = Re(z) + j ⋅ Im(z) - комплексная функция, X(z) - это Z-форма последовательности x(nT).
Z-преобразование связано с преобразованием Лапласа через формулу:
z = esT
Свойства Z-преобразования
1. Линейность
Если последовательность x(nT) можно представить в виде линейной комбинации x(nT) = a · x1(nT) + b · x2(nT),
то X(z) = a · X1(z) + b · X2(z).
Иными словами, Z-преобразование суммы сигналов равно сумме z-образов этих сигналов.
1. Задержка (сдвиг по времени)
Z[x(nT − mT)] = z−m ⋅ X(z).
Задержка входного сигнала на m вносит добавочный множитель z−m .
1. Свертка
Для последовательности y(nT) свертка двух последовательностей равна:
y(nT) = ∑
x (mT) ⋅ x2(nT − mT).
∞m=0 1
или
y(nT) = ∑
x (mT) ⋅ x1(nT − mT).
∞m=0 2
А для Z-формы:
Y(z) = X1(z) ⋅ X2(z).
Z-преобразование свёртки сигналов равно произведению их Z-образов.
Если входной сигнал x(nT) представить в виде взвешенной суммы δ-функций, то Z-форма принимает вид
X(z) = ∑
∞k=0
x(kT) ⋅ z−k.
Примеры
1. Записать Z-форму для последовательности x(nT) = {1,2,3,4,5}
X(z) = 1 + 2z−1 + 3z−2 + 4z−3 + 5z−4.
1. Записать Z-форму для последовательности в виде единичного скачка σ(nT) .
X(z) = 1 + z−1 + z−2 + z−3 + z−4 + . . . = 1(1−z
−1
).
In [6]:
# Digital signal
xt = np.arange(16)
# Plot figure
fig = plt.figure(figsize=(12, 4), dpi=80)
plt.title('Digital signal')
plt.stem(xt, linefmt='C3', markerfmt='D', use_line_collection=True)
plt.ylabel('Amplitude')
plt.xlabel('Samples')
plt.xticks(xt)
plt.xlim([np.min(xt)-0.2, np.max(xt)+0.2])
plt.grid(True)
В следующих главах мы познакомимся с различными формами сигналов, а также с операциями над ними: фильтрация,
свёртка, преобразования в частотную область и обратно.
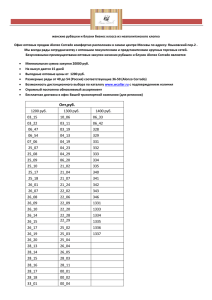
Цифровая обработка сигналов - 2
Title
Digital signal processing
Author
Alexander Kapitanov
Contact
sallador@bk.ru
Project lang
Python
Packages
numpy, scipy, matplotlib
License
GNU GPL 3.0
Введение
Перед вами обучающий материал по основам цифровой обработки сигналов с использованием средств языка
программирования Python. Предполагается, что читатель имеет базовые знания из области высшей математики, а также
владеет языком Python и хотя бы поверхностно знает различные python-библиотеки - numpy/scipy, matplotlib и другие.
Для пользователей MATLAB / GNU Octave освоение материала с точки зрения программного кода не составит труда,
поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из python-библиотек.
Спектр сигнала
Из предыдущей части вы узнали, что сигнал - это физический процесс во времени, параметры которого изменяются в
соответствии с передаваемым сообщением. Мы научились представлять дискретные (цифровые) сигналы во времени. В
этом разделе будет показан переход между временной и частотной областями для дискретных сигналов.
Прямое преобразование Фурье
Чтобы преобразовать сигнал из временной области в частотную и обратно необходимо выполнить операцию под названием
дискретное преобразование Фурье.
Запишем формулу прямого преобразования Фурье для дискретной последовательности x(nT). Прямым дискретным
преобразованием Фурье (ДПФ) называется преобразование последовательности x(n), n = 0, ... , N–1 в
последовательность X(k), k = 0, ..., N–1 по следующей формуле:
$X(k) = \sum_{n=0}^{N-1}x(nT)\cdot e^{(-2\pi j\cdot nk/N)} = \sum_{n=0}^{N-1}x(nT)\cdot W^{-nk}$
где $k = 0, ..., N-1$.
$N$ – количество компонент разложения, число измеренных за период значений сигнала;
$n$ – номер отсчета дискретизированного сигнала, n = 0,1, ... , N–1;
$k$ – номер гармоники компонента преобразования, а T — период времени, в течение которого брались входные
данные;
$W = e^{-2\pi j / N}$ – поворотный множитель.
В этой формуле $X(kT) = X(e^{j\omega T})$ является спектральной плотностью (спектром) дискретной последовательности.
Выражение для спектра дискретной последовательности можно найти, заменив в её Z-форме переменную $z = e^{j\omega
T}$
Для аналоговых сигналов выражение суммы превращается в интеграл.
Используя формулу Эйлера $e^{j\omega T} = cos(\omega T) + j\cdot sin(\omega T)$, можно определить вещественную и
мнимую составляющие, а также модуль и аргумент спектральной плотности, которые связаны с вещественной и мнимой
частями спектра через формулы теории функции комплексного переменного.
Модуль:
$|X(kT)| = \sqrt{Re(X)^2 + Im(X)^2}$
Фаза:
$arg(X(kT)) = \arctan{\frac{Im(X)}{Re(X)}}$
Таким образом, ДПФ для $N$ входных отсчетов сигнала ставит в соответствие N спектральных отсчётов. Из формулы ДПФ
для вычисления одного спектрального отсчета требуется N операций комплексного умножения и сложения. Поскольку таких
операций $N$, то общая вычислительная сложность ДПФ равна $N^2$
операций $N$, то общая вычислительная сложность ДПФ равна $N^2$
Обратное преобразование Фурье
Обратное дискретное преобразование Фурье (ОДПФ) есть перевод последовательности X(k), k = 0, ..., N–1 в
последовательность x(n), n = 0, ... , N–1 по формуле:
$x(nT) = \frac{1}{N}\sum_{n=0}^{N-1}X(k)\cdot e^{(2\pi j\cdot nk/N)} = \frac{1}{N}\sum_{n=0}^{N-1}X(k)\cdot W^{nk}$
где x(n) – измеренная последовательность в дискретных временных точках, значения которой являются исходными
данными для прямого преобразования и выходными для обратного X(k) – N–последовательность комплексных амплитуд
синусоидальных сигналов, образующих исходный сигнал x(n) ; значения последовательности являются выходными
данными для прямого преобразования и входными для обратного
Поскольку амплитуды спектральных отсчетов - комплексные величины, то по ним можно вычислить одновременно и
амплитуду, и фазу сигнала.
Как следует из теоремы Найквиста-Котельникова, ДПФ точно соответствует непрерывному преобразованию Фурье, если
преобразуемая функция есть функция с ограниченным спектром, при этом частота дискретизации Fд должна быть не
меньше удвоенной максимальной частоты спектра Fв. Следует отметить, что для ДПФ справедливы правила и свойства,
которые были рассмотрены для Z-преобразования. Матрицей k * n элементов можно определить ДПФ.
Особенности спектров дискретных сигналов.
1. Спектральная плотность дискретного сигнала – периодическая функция с периодом, равным частоте дискретизации.
2. Если дискретная последовательность вещественная, то модуль спектральной плотности такой последовательности
есть четная функция, а аргумент – нечетная функция частоты.
3. При сдвиге спектра $X(e^{j\omega T})$ последовательности $x(nT)$ по оси частот вправо на величину $\psi$ получим
спектр $Y(e^{j\omega T}) = Y(e^{j(\omega-\psi) T})$ Такому спектру соответствует комплексная последовательность:
$y(nT) = e^{j\psi nT} \cdot x(nT) = \cos{(\psi nT)} \cdot x(nT) + j \sin{(\psi nT)} \cdot x(nT)$
Сдвиг спектра $X(e^{j\omega T})$ последовательности $x(nT)$ по оси частот влево на величину $\psi$ происходит путем
умножения последовательности $x(nT)$ на комплексную экспоненту $e^{j\psi nT}$
1. При сдвиге дискретного сигнала $x(nT)$ вправо по временной оси на m тактов (реализация задержки) получаем сигнал
$x(n) = x(nT - mT)$, Z-преобразование и спектральная плотность которого имеют вид:
$Z[y(nT)] = Z[x(nT-mT)] = X(z)\cdot z^{-m}$
$Y(\omega) = e^{-j\omega mT} \cdot X(e^{j\omega T})$
In [1]:
import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import fft, ifft, fftshift
%matplotlib inline
Пример. Найдите модуль и аргумент спектральной плотности для следующей последовательности x(nT) = {1, 2, 0,
1} .
В библиотеке scipy есть пакет fftpack, который содержит основные функции для вычисления ДПФ (в частности БПФ).
In [2]:
# signal
x = np.array([-1, 2, 0, 1, 3, 3, 2, 0])
# Z-form: X(z) = 1 + 2z^(-1)+z^(-3), where z = exp(-jwT)
# Forward FFT
N = 512
xFFT = fftshift(fft(x, N))
# Magnitude spectrum
xA = np.abs(xFFT)
# Phase spectrum
xF = np.angle(xFFT)
# List of signals
xT = [x, xA, xF]
lst_title = ['Signal', 'Spectrum', 'Phase']
# Plot results
fig = plt.figure(figsize=(12, 6), dpi=80)
for i, sig in enumerate(xT):
plt.subplot(2, 2, int(2**i))
plt.ylabel('Level')
plt.title(lst_title[i])
if i == 0:
plt.stem(sig, use_line_collection=True, basefmt='C0')
plt.xlabel('Time samples')
else:
plt.plot(sig)
plt.xlabel('Freq samples')
plt.xlim([0, N-1])
plt.grid()
plt.tight_layout()
Свойства дискретного преобразования Фурье
1. Линейность: сумма спектров сигналов равна спектру суммы сигналов.
Это свойство говорит о том, что спектр суммы независимых дискретных сигналов равен сумме спектров этих сигналов, а при
умножении дискретного сигнала на константу, его спектр также умножается на эту константу.
1. Сдвиг по отсчетам (по времени)
Циклический сдвиг сигнала на m отсчётов приводит к повороту фазового спектра, а амплитудный спектр при этом не
изменяется.
$X'(k) = X(k) \cdot e^{- \frac{2\pi j}{N} k m} $
1. ДПФ от чётных и нечётных функций
ДПФ четной функции вырождается в косинусное преобразование Фурье
$X(k) = \sum_{n=0}^{N-1}x(n)\cdot \cos{(2\pi nk/N)}$
ДПФ нечетной функции вырождается в синусное преобразование Фурье
$X(k) = \sum_{n=0}^{N-1}x(n)\cdot \sin{(2\pi nk/N)}$
где $k = 0, ..., N-1$.
1. ДПФ циклической свёртки сигналов
Для сигнала $x(n)$, который является результатом циклической свертки двух сигналов $a(b)$ и $b(n)$:
Для сигнала $x(n)$, который является результатом циклической свертки двух сигналов $a(b)$ и $b(n)$:
$x(n) = \sum_{m=0}^{N-1}a(n)\cdot b(n-m)$
N-точечное ДПФ последовательности равно:
$X(k) = A(k) \cdot B(k)$ ,
где $A(k), B(k)$ - спектры сигналов.
Таким образом, спектр циклической свертки двух сигналов равен произведению спектров этих сигналов. Это свойство
позволяет использовать быстрые алгоритмы ДПФ для вычисления свертки.
1. ДПФ произведения сигналов
Для сигнала $x(n)$, который является результатом произведения двух сигналов $a(b)$ и $b(n)$ спектр равен:
$X(k) = \frac{1}{N} \sum_{m=0}^{N-1}A(m)\cdot B(k-m)$
Спектр произведения двух сигналов представляет собой циклическую свертку спектров этих сигналов.
1. Сдвиг по частоте
Аналогично второму свойству (временной сдвиг), если имеется сдвинутый по частоте на m спектр $X(k–m)$, то после ОДПФ
последовательность $x(n)$ принимает следующий вид:
$x'(n) = x(n)\cdot e^{\frac{2\pi j}{N} k m}$
Отсюда следует, что сдвиг спектра осуществляется умножением сигнала на комплексную экспоненту. Это свойсто
используется для переноса частот по диапазону. Заметим, что после умножения на экспоненту сигнал будет комплексным, а
его спектр перестанет быть симметричным.
1. Теорема Парсеваля
Средняя мощность дискретизированной функции времени равна сумме мощностей отдельных спектральных составляющих
и не зависит от их фаз.
Нормированная энергия сигнала $x(n)^2$ равна:
$\sum_{n=0}^{N-1}x^{2}(n) = \frac{1}{N} \sum_{n=0}^{N-1} |{X^{2}(k)}|$
Как видно, свойства ДПФ имеют свойство двойственности, которое заключается в том, что все свойства ДПФ справедливы
как для сигнала, так и для спектра.
Спектр гармонического сигнала
Покажем, как выглядит спектр гармонического сигнала. Для этого зададимся длиной БПФ N = 32 отсчёта. Посмотрим, что
происходит при вычислении ОБПФ для сигнала, который задан в частотной области в виде единичного отсчета на
определенной позиции.
Обратите внимание, что вычисляется прямое БПФ, поскольку операции БПФ и ОБПФ равнозначны и отличаются на
константу и знак в поворачивающих множителях.
In [3]:
N, M = 32, 4
# Create freq signal
x = np.zeros((N,M))
x[0][0] = 1
x[1][1] = 1
x[3][2] = 1
x[8][3] = 1
# Calculate FFT
X = fft(x, axis=0)
# Plot results
fig = plt.figure(figsize=(14, 8), dpi=80)
for i in range(M*3):
plt.subplot(4, 3, i+1)
if i % 3 == 0:
if i % 3 == 0:
plt.title('Spectrum')
plt.stem(x[:,i//3], use_line_collection=True, basefmt='C0')
if (i-1) % 3 == 0:
plt.title('Real Part (cos)')
plt.plot(np.real(X[:,i//3]), '-o')
if (i-2) % 3 == 0:
plt.title('Imag Part (sin)')
plt.plot(np.imag(X[:,i//3]), '-o')
plt.xlim([-0.5, N-0.5])
plt.xlabel('samples')
plt.grid()
plt.tight_layout()
Спектр суммы гармонических сигналов
Покажем, как выглядит спектр суммы гармонических сигналов (работает аддитивный закон: спектр суммы сигналов равен
сумме спектров сигналов).
Сигнал состоит из трех гармонических компонент.
Амплитуды гармоник: A1, A2, A3 = 5, 1, 3
Частоты гармоник: f1, f2, f3 = 2, 7, 12
In [4]:
N = 128
# Time vector
t = np.linspace(0, 1, N)
# Amplitudes and freqs
f1, f2, f3 = 2, 7, 12
A1, A2, A3 = 5, 1, 3
# Signal
x = A1 * np.cos(2*np.pi*f1*t) + A2 * np.cos(2*np.pi*f2*t) + A3 * np.cos(2*np.pi*f3*t)
# Calculate FFT
X = fft(x)
X = 2*np.abs(X) / N
# Plot results
fig = plt.figure(figsize=(12, 4), dpi=80)
# Time: signal
plt.subplot(1, 2, 1)
plt.title('Signal')
plt.title('Signal')
plt.stem(x, use_line_collection=True, basefmt='C0')
plt.xlim([0, N-1])
plt.xlabel('samples')
plt.grid()
# Freq: Spectrum
plt.subplot(1, 2, 2)
plt.title('Spectrum')
plt.stem(X, use_line_collection=True, basefmt='C0')
plt.xlim([0, N//2-1])
plt.xlabel('frequency')
plt.grid()
plt.tight_layout()
Периодическая последовательность
Посмотрим, как изменится спектральная плотность периодической последовательности x(nT) , если её повторить $M$ раз
через определенное число тактов с периодом $N$, где $M$ – количество повторений дискретной последовательности.
В качестве примера возьмем последовательность x(nT) = {1, 1, 1}, M = 4, N = 9 .
In [5]:
N = 9
M = 4
# Signal period
# Number of repeats
# Signal
x = np.zeros(N)
x[0:3] = 1
y = np.tile(x, M)
y
Out[5]:
array([1., 1., 1., 0., 0., 0., 0., 0., 0., 1., 1., 1., 0., 0., 0., 0., 0.,
0., 1., 1., 1., 0., 0., 0., 0., 0., 0., 1., 1., 1., 0., 0., 0., 0.,
0., 0.])
In [6]:
# Forward FFT
NFFT = 1024
xFFT = fft(y, NFFT)
# Magnitude spectrum
yA = np.abs(xFFT)
print('Max amplitude = sum of ones * M = {}'.format(yA.max()))
yA /= np.max(yA)
# Phase spectrum
yF = np.angle(xFFT)
# FFT for input signal
xFFT = fft(x, NFFT)
# Magnitude spectrum
xA = np.abs(xFFT)
xA = np.abs(xFFT)
xA /= np.max(xA)
# FFT for repeats
xFFT = fft(x, NFFT//N)
# Magnitude spectrum
xM = np.abs(xFFT)
xM /= np.max(xM)
xM = np.tile(xM, N)
#List of signals
xT = [y, yA]
lst_title = ['Signal', 'Spectrum', 'Phase']
# Plot results
fig = plt.figure(figsize=(12, 6), dpi=80)
for i, sig in enumerate(xT):
plt.subplot(2, 1, int(2**i))
plt.ylabel('Level')
plt.title(lst_title[i])
if i == 0:
plt.stem(sig, use_line_collection=True, basefmt='C0')
plt.xlabel('Time samples')
plt.ylim([0, 1.5])
plt.xlim([-0.5, N*M-0.5])
else:
plt.plot(sig, '-', linewidth=2.5, label='Result Spectrum y(t)')
plt.plot(xA, '--', linewidth=1.5, label='Input Spectrum x(t)')
plt.plot(xM, '-.', linewidth=1.5, label='Repeats by M = %d' % M)
plt.xlabel('Freq samples')
plt.xlim([0, NFFT-1])
plt.legend(loc='upper right')
plt.grid()
plt.tight_layout()
Max amplitude = sum of ones * M = 12.0
На нулевой частоте модуль спектра численно равен сумме количества отсчетов непериодической последовательности N =
3 . После перемножения двух спектров, получим результирующий спектр периодической последовательности. Уровень
сигнала на нулевой частоте равен сумме единичных импульсов, а т.к. последовательность периодична, это можно записать
через формулу:
$A_0 = \sum_{n=0}^{NM}x(nT)$
Таким образом, чтобы получить итоговый спектр периодической последовательности, необходимо проделать следующие
шаги:
1. Разделить интервал на N частей (период сигнала),
2. Каждую часть интервалов разбить на M частей (период повторения),
3. Найти модуль спектра множителя повторения | M(ejωT) |,
4. Найти спектр исходной последовательности | X(ejωT) |,
5. Перемножить спектры | M(ejωT) | и | X(ejωT) |, получив спектр периодической последовательности с периодом N и
числом повторений М.
Поворотные множители
Коэффициенты матрицы ДПФ (twiddle factor) или поворотные множители $W_{nk}$ можно найти по следующей формуле:
$W_{k,n} = e^{\frac{-2\pi j}{N}nk}$
Таким образом, матрица ДПФ без учета нормирующего множителя устроена так: первые строка и столбец состоят из единиц,
во второй строке стоят корни из единицы порядка n в естественном порядке, следующие строки являются
последовательными степенями второй строки. В качестве примера приведем матрицу размерностью 4х4.
In [7]:
N = 4
nk = np.array([i*j for i in range(N) for j in range(N)]).reshape(N, N)
# Twiddle
Wnk = np.round(np.exp(-2j*np.pi*nk/N), 3)
print(Wnk)
[[
[
[
[
1.+0.j 1.+0.j 1.+0.j 1.+0.j]
1.+0.j 0.-1.j -1.-0.j -0.+1.j]
1.+0.j -1.-0.j 1.+0.j -1.-0.j]
1.+0.j -0.+1.j -1.-0.j 0.-1.j]]
Построим графики реальной и мнимой части матрицы поворачивающих множителей при N = 8 .
In [8]:
N = 8
nk = np.array([i*j for i in range(N) for j in range(N)]).reshape(N, N)
# Twiddle
Wnk = np.round(np.exp(-2j*np.pi*nk/N), 3)
print(Wnk)
fig = plt.figure(figsize=(12, 4), dpi=80)
plt.subplot(1, 2, 1)
for i in range(N):
plt.plot(np.real(Wnk[i,:]), '--o', linewidth=1.15)
plt.grid(True)
plt.subplot(1, 2, 2)
for i in range(N):
plt.plot(np.imag(Wnk[i,:]), '--o', linewidth=1.15)
plt.grid(True)
plt.tight_layout()
[[ 1.
+0.j
1.
+0.j
[ 1.
+0.j
-0.707+0.707j
[ 1.
+0.j
0.
-1.j
[ 1.
+0.j
0.707+0.707j
[ 1.
+0.j
-1.
-0.j
[ 1.
+0.j
0.707-0.707j
[ 1.
+0.j
-0.
+1.j
[ 1.
+0.j
-0.707-0.707j
1.
+0.j
1.
+0.j
0.707-0.707j
-0.
+1.j
0.
-1.j
-1.
-0.j
-0.707-0.707j
0.
-1.j
-1.
-0.j
1.
+0.j
-0.707+0.707j
-0.
+1.j
-0.
+1.j
-1.
-0.j
0.707+0.707j
-0.
-1.j
1.
+0.j
1.
+0.j
1.
+0.j
]
0.
-1.j
-0.707-0.707j
0.707+0.707j]
-1.
-0.j
-0.
+1.j
-0.
+1.j
]
-0.
+1.j
0.707-0.707j
-0.707+0.707j]
1.
+0.j
-1.
-0.j
-1.
-0.j
]
0.
-1.j
0.707+0.707j
-0.707-0.707j]
-1.
-0.j
0.
-1.j
-0.
-1.j
]
-0.
+1.j
-0.707+0.707j
0.707-0.707j]]
1.
+0.j
-1.
-0.j
1.
+0.j
-1.
-0.j
1.
+0.j
-1.
-0.j
1.
+0.j
-1.
-0.j
Построим графики реальной части матрицы поворачивающих множителей при N = 16 .
In [9]:
N = 16
nk = np.array([i*j for i in range(N) for j in range(N)]).reshape(N, N)
# Twiddle
Wnk = np.round(np.exp(-2j*np.pi*nk/N), 5)
fig = plt.figure(figsize=(14, 8), dpi=80)
for i in range(N):
plt.subplot(N//4, 4, i+1)
plt.plot(np.real(Wnk[i,:]), '--o', linewidth=0.5, label='W{}'.format(i))
plt.grid(True)
plt.legend(loc='upper right')
plt.tight_layout()
Переход от ДПФ к БПФ
Преобразование Фурье лежит в основе методов свертки и проектировании цифровых корреляторов, активно применяется
при спектральном анализе, используется при работе с длинными числами. Однако до появления компьютеров ДПФ
использовалось редко, поскольку вычисление ДПФ даже для 64 отсчетов требует 4096 операции комплексного умножения и
практически столько же операций сложения, что вручную считать довольно долго и трудоемко. Для N = 1024 потребуется
около миллиона операций комплексного умножения и миллион операций комплексного умножения. Чем больше точек
вычисления (чем больше длина ДПФ), тем больше времени затрачивается на вычисления в связи с увеличением количества
операций.
Вычисление преобразования Фурье по стандартной формуле предполагает выполнение большого числа операций
сложения и умножения. Очевидно, что возникает необходимость разработать алгоритмы, которые уменьшают число
математических действий при расчёте ДПФ.
Следует заметить что, вычислять ДПФ напрямую не обязательно и можно обойтись существенно меньшим числом
операций. Рассмотрим основную идею БПФ, которая состоит в разбиении исходной N–мерной последовательности $x(n), n =
0, ... , N–1$ на части. При этом для каждой части можно вычислить ДПФ отдельно, а затем линейно просуммировать с
остальными, чтобы получить исходное преобразование. В свою очередь, эти части меньшего размера можно разбить на ещё
меньшие части, и проделать те же самые операции.
Пусть длина периодической последовательности равна $N$ , тогда для вычисления одного спектрального отсчета
потребуется $N$ операций комплексного умножения и сложения. Таким образом, общая вычислительная сложность
алгоритма ДПФ составит $N^2$ умножений и сложений. Если разделить исходную последовательность на две равные части
по $N/2$ элементов, то для выполнения вычисления преобразования по классической формуле на каждом этапе
потребуется в два раза меньше операций сложения и умножения.
При этом каждое из N/2–точечных ДПФ также можно вычислить путем замены $N/2$–точечного ДПФ на два $N/4$–точечных.
В этом случае количество операций комплексного сложения и умножения уменьшается еще в два раза. Суть данного
алгоритма ДПФ заключается в том, что можно продолжать разбиение исходной последовательности до тех пор, пока
возможно целочисленное деление последовательности на двойку. Понятно, что если длина входной последовательности $N
= 2m$, где $m$ – положительное целое число, то исходную последовательность можно разделить пополам всего m раз.
Алгоритмы БПФ, с длиной последовательности $N = 2m$, называются алгоритмы БПФ по основанию 2 (Radix-2 FFT).
Эффективность алгоритма БПФ полностью зависит от способа разбиения и объединения последовательности. Очевидно,
что делить последовательности на две части можно по-разному, однако от этого зависит, сможем ли мы при объединении
получить неискаженный спектр сигнала и чего с точки зрения вычислительных затрат и объема использования ресурсов это
будет нам стоить. Количество операций БПФ линейно зависит от длины последовательности $N$.
Сравнение эффективности
Ниже представлена таблица, показывающая сравнение эффективности алгоритмов БПФ в сравнении с ДПФ.
Эффективность алгоритма БПФ и количество выполняемых операций линейно зависит от длины последовательности N
ДПФ
БПФ
Отношение числа
комплексных сложений
Отношение числа
комплексных умножений
2
4
1
4
8
4
1.5
56
12
24
5.3
2.3
256
240
32
64
8
3.75
32
1024
992
80
160
12.8
6.2
64
4096
4032
192
384
21.3
10.5
128
16384
16256
448
896
36.6
18.1
Число операций
умножения
Число
операций
сложения
Число операций
умножения
Число
операций
сложения
2
4
2
1
4
16
12
8
64
16
N
...
...
...
...
...
...
...
4096
16777216
16773120
24576
49152
683
341
8192
67108864
67100672
53248
106496
1260
630
Из таблицы видно, что использование БПФ существенно экономит на количестве операций, причем, чем больше длина
последовательности N, тем больше экономия.
Например, для $N = 8192$ отсчётов при вычислении ДПФ потребуется 67 миллионов операций комплексного сложения и
умножения! Используя алгоритмы БПФ, можно снизить эти числа в $~1260$ и $~630$ раз соответственно!!
Алгоритмы БПФ
Существует два основных метода вычисления БПФ по основанию 2 (Radix-2): с прореживанием (или децимацией) по
частоте и по времени. Рассмотрим оба варианта.
Рассмотрим первый способ разбиения последовательности – прореживание по времени, который также называют
алгоритмом БПФ с «децимацией по времени» FFT Decimation-in-time [DIT]. Идея заключается в том, что исходная
последовательность отсчётов $x(n)$ с длиной N разбивается на две последовательности $x0(n)$ и $x1(n)$ равной длины
$N/2$.
Причем $x0(n)$ - последовательность четных отсчетов $x0(n) = x(2n), n = 0, ..., N/2 - 1$
а $x1(n)$ - последовательность нечетных отсчетов $x1(n) = x(2n+1), n = 0, ..., N/2 - 1$
Минуя математические выкладки (их можно найти в любой литературе по цифровой обработке сигналов), запишем основные
правила вычисления БПФ путём разбиения последовательности на четные и нечетные.
Алгоритм БПФ с децимацией по времени :
осуществить двоично-инверсную перестановку отсчетов входного сигнала, обеспечив разбиение исходной
последовательности;
сделать N/2 операций «Бабочка» для получения первого объединения, используя поворотные коэффициенты;
повторить операцию «Бабочка» для перехода на следующие этапы, также используя поворотные коэффициенты.
После всех вышеописанных действий получим на выходе ДПФ входной последовательности.
«Бабочка» - направленный граф, с помощью которого вычисляется пара комплексных отсчетов по предыдущим значениям.
Для БПФ с прореживанием по времени бабочка по основанию 2 записывается по формуле:
$ X = A + B\cdot W^{-k}_{N}$
$ Y = A - B\cdot W^{-k}_{N}$
В алгоритме БПФ с децимацией по времени производилось разделение исходного сигнала в соответствии с двоичноинверсной перестановкой – на четные и нечетные части. Тем самым получем первую и вторую половину спектра. В
алгоритме с прореживанием по частоте наоборот, исходный сигнал делится пополам, а на выходе получаются две
последовательности спектральных отсчетов – четная и нечетная (поэтому алгоритм и называется «прореживание по
частоте»).
Последовательность отсчётов $x(n)$ с длиной N разбивается на две последовательности $x0(n)$ и $x1(n)$ равной длины
$N/2$.
Причем $x0(n)$ - последовательность первой половины данных $x0(n) = x(n), n = 0, ..., N/2 - 1$
а $x1(n)$ - последовательность второй половины данных $x1(n) = x(n), n = N/2, ..., N - 1$
Принципиальная разница алгоритмов в том, что при прореживании по времени умножение на поворотные коэффициенты
производилось после ДПФ четной и нечетной последовательности, а при использовании децимации по частоте умножение
производится до ДПФ.
При этом вычислительная эффективность и скорость обоих алгоритмов идентична.
Алгоритм БПФ с децимацией по частоте :
сделать N/2 операций «Бабочка» для получения первого объединения, используя поворотные коэффициенты;
повторить операцию «Бабочка» для перехода на следующие этапы, также используя поворотные коэффициенты.
осуществить двоично-инверсную перестановку результирующего сигнала;
Бабочка в этом случае выглядит несколько иначе:
$ X = A + B$
$ Y = (A - B)\cdot W^{-k}_{N}$
Python библиотека БПФ
Python библиотека scipy для вычисления различных преобразований Фурье (синусное, косинусное, прямое, обратное,
многомерное, вещественное) содержит одноименный пакет fftpack. Для импорта пакета в проект необходимо выполнить
команду:
from scipy.fftpack import *
# or
from scipy.fftpack import fft, ifft, fftshift
from scipy.fftpack import fft, ifft, fftshift
Список функций из пакета fftpack:
Быстрое преобразование Фурье
Function
Description
fft(x[, n, axis, overwrite_x])
Прямое БПФ
ifft(x[, n, axis, overwrite_x])
Обратное БПФ
fft2(x[, shape, axes, overwrite_x])
Двумерное прямое БПФ
ifft2(x[, shape, axes, overwrite_x])
Двумерное обратное БПФ
fft2(x[, shape, axes, overwrite_x])
Многомерное прямое БПФ
ifft2(x[, shape, axes, overwrite_x])
Многомерное обратное БПФ
rfft(x[, n, axis, overwrite_x])
Прямое БПФ вещественного сигнала
irfft(x[, n, axis, overwrite_x])
Обратное БПФ вещественного сигнала
dct(x[, type, n, axis, norm, overwrite_x])
Прямое косинусное ПФ
idct(x[, type, n, axis, norm, overwrite_x])
Обратное косинусное ПФ
dctn(x[, type, shape, axes, norm, overwrite_x])
Многомерное прямое косинусное ПФ
idctn(x[, type, shape, axes, norm,
overwrite_x])
Многомерное обратное косинусное
БПФ
dst(x[, type, n, axis, norm, overwrite_x])
Прямое синусное ПФ
idst(x[, type, n, axis, norm, overwrite_x])
Обратное синусное ПФ
dstn(x[, type, shape, axes, norm, overwrite_x])
Многомерное прямое синусное ПФ
idstn(x[, type, shape, axes, norm,
overwrite_x])
Многомерное обратное синусное БПФ
Дифференциальные и псевдо-дифференциальные операторы
применяются к периодическим последовательностям.
Function
Description
diff(x[, order, period, _cache])
k-производная (или интеграл)
tilbert(x, h[, period, _cache])
h-Tilbert преобразование
itilbert(x, h[, period, _cache])
Обратное h-Tilbert преобразование
hilbert(x[, _cache])
Преобразование Гильберта
ihilbert(x)
Обратное преобразование Гильберта
cs_diff(x, a, b[, period,
_cache])
(a,b)-cosh/sinh псевдо-производная
sc_diff(x, a, b[, period,
_cache])
(a,b)-sinh/cosh псевдо-производная
ss_diff(x, a, b[, period,
_cache])
(a,b)-sinh/sinh псевдо-производная
cc_diff(x, a, b[, period,
_cache])
(a,b)-cosh/cosh псевдо-производная
shift(x, a[, period, _cache])
Сдвиг последовательности y(u) =
x(u+a)
Вспомогательные функции
Function
Свертка сигналов
Description
fftshift(x[, axes])
Симметричный сдвиг нулевого отсчета БПФ в
центр
ifftshift(x[, axes])
Обратный симметричный сдвиг
fftfreq(n[, d])
Возвращает частоты преобразования Фурье
rfftfreq(n[, d])
Возвращает частоты ДПФ
next_fast_len(target)
Поиск ближайшего числа 2^k для вычисления БПФ
На базе БПФ можно вычислить свертку длинных последовательностей. Этот метод применяется в условиях ограниченности
вычислительных ресурсов (например, в устройства программируемых логических интегральных схем - ПЛИС). В следующих
разделах будет подробно рассмотрена задача свертки последовательностей.
Сигналы произвольной формы
Любой сигнал произвольной формы можно представить в виде набора гармонических сигналов разных частот. Иными
словами, сигнал сложной формы во временной области имеет набор комплексных отсчетов в частотной области, которые
называются гармоники. Эти отсчеты выражают амплитуду и фазу гармонического воздействия на определенной частоте.
Чем больше набор гармоник в частотной области, тем точнее представляется сигнал сложной формы.
Например, имеется сигнал прямоугольной формы. Требуется представить его в виде суммы гармонических сигналов. На
следующем примере покажем, как влияет количество частотных комплексных отсчётов на форму сигнала во временной
области.
Создаем сигнал прямоугольной формы,
Вычисляем БПФ этого сигнала,
Задаем массив частот, из которых восстанавливается исходный сигнал,
Отображаем результат.
Создадим прямоугольный сигнал единичной амплитуды и вычислим его БПФ. Длина N = 1024 отсчета. Сигнал принимает
нулевые значения во всех точках, кроме диапазона [64 : 256] . Покажем, как выглядит форма сигнала во временной
области, если его набрать из суммы гармоник. Для наглядности приведем графики при различных значениях набора сумм 3, 10, 30, 90, 200, N/2 . Очевидно, что из трех гармоник воссоздать точную форму прямоугольного импульса не
получится. При значении 10 форма сигнала начинает стремиться к прямоугольной. При значении 30 и 90 всё ещё видны
искажения, в частности на границах резкого излома функции. При значении N/2 сигнал имеет исходную форму (воссоздается
из достаточного набора гармоник для прямоугольного импульса).
Это означает, что резкие перепады сигнала во временной области вносят вклад в верхние (высокие) частоты спектра
сигнала, а гладкие изменения сигнала - вносят вклад в нижние (низкие) частоты спектра сигнала.
In [10]:
N = 1024
# Create input signal
x = np.zeros(N)
x[64:256] = 1
# Find Forward FFT
X = fft(x, N)
# Normalized shifted spectrum
Xs = fftshift(np.abs(X))
Xs /= np.max(Xs)
# Normalized frequency
f = np.linspace(-0.5, 0.5, N, endpoint=True)
# Plot input signal in time domain
plt.figure(figsize=(14, 9), dpi=80)
plt.subplot(4, 2, 1)
plt.plot(x)
plt.title('Input signal')
plt.xlabel('Samples')
plt.ylabel('Amplitude')
plt.xlim([0, N-1])
plt.xticks(np.linspace(0, N, 9, endpoint=True))
plt.grid()
# Plot signal in freq domain
plt.subplot(4, 2, 2)
plt.stem(f, Xs, use_line_collection=True, basefmt='C0')
plt.title('Spectrum')
plt.xlabel('Frequency')
plt.ylabel('Magnitude')
plt.xlim([-1/16, 1/16])
plt.xticks(np.linspace(-1/16, 1/16, 6, endpoint=True))
plt.grid()
# Set the list - number of harmonics
l_freqs = (3, 10, 30, 90, 200, N//2)
# Plot signal with several
for i, j in enumerate(l_freqs):
plt.subplot(4, 2, i+3)
K = X.copy()
K[j:] = 0
k = np.real(ifft(K))
plt.plot(k, color='C'+str(i+1), linewidth=1.75)
plt.title(f'N of freqs = {j}')
plt.xlabel('Samples')
plt.ylabel('Amplitude')
plt.xlim([0, N-1])
plt.xticks(np.linspace(0, N, 9, endpoint=True))
plt.grid()
plt.tight_layout()
plt.savefig("fig1_gibbs.png")
Эффект Гиббса
Вносимые пульсации в области резких перепадов сигнала связаны с эффектом Гиббса. Этот эффект связан с
последовательным приближением к исходной форме в виде частичных сумм ряда Фурье. Иными словами, природа
пульсаций в восстанавливаемом сигнале напрямую связана с эффекта Гиббса. Эффект Гиббса ярко выражен при резких
нарушениях монотонности функции. На резких перепадах и скачках этот эффект максимален.
На рисунке ниже представлен график восстановления линейного сигнала с помощью частичной суммы ряда Фурье при
разных значениях количества суммарных отсчетов.
In [11]:
N = 1024
# Create input signal
x = np.zeros(N)
x[64:512] = np.linspace(0, 1, 512-64)
# Find Forward FFT
X = fft(x, N)
# Set the list - number of harmonics
l_freqs = (2, 3, 6, 10, 50, N//2)
# Plot signal with several
plt.figure(figsize=(14, 4), dpi=80)
plt.figure(figsize=(14, 4), dpi=80)
plt.title('Input signal')
plt.xlabel('Samples')
plt.ylabel('Amplitude')
plt.xlim([0, N-1])
plt.xticks(np.linspace(0, N, 9, endpoint=True))
for i, j in enumerate(l_freqs):
K = X.copy()
K[j:] = 0
k = np.real(ifft(K))
plt.plot(k, color='C'+str(i), linewidth=1.75, label='N freq = {}'.format(l_freqs[i]))
plt.grid()
plt.legend()
plt.tight_layout()
plt.savefig("fig2_gibbs.png")
Цифровая обработка сигналов - 3
Title
Digital signal processing
Author
Alexander Kapitanov
Contact
sallador@bk.ru
Project lang
Python
Packages
numpy, scipy, matplotlib
License
GNU GPL 3.0
Введение
Перед вами обучающий материал по основам цифровой обработки сигналов с использованием средств языка
программирования Python. Предполагается, что читатель имеет базовые знания из области высшей математики, а также
владеет языком Python и хотя бы поверхностно знает различные python-библиотеки - numpy/scipy, matplotlib и другие.
Для пользователей MATLAB / GNU Octave освоение материала с точки зрения программного кода не составит труда,
поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из python-библиотек.
Свертка и корреляция
В реальных задачах часто ставится вопрос о степени похожести одного процесса на другого или же о независимости одного
процесса от другого. Иными словами, требуется определить взаимосвязь между сигналами, то есть найти корреляцию.
Методы корреляции используются в широком диапазоне задач: поиск сигналов, компьютерное зрение и обработка
изображений, в задачах радиолокации для определения характеристик целей и определения расстояния до объекта. Кроме
того, с помощью корреляции производится поиск слабых сигналов в шумах.
В разделе фильтрация сигналов вводилось понятие импульсной характеристики фильтра. Напомним, что импульсной
характеристикой $h(n)$ называется реакция цепи на входное воздействие в виде функции Дирака (δ-функции). Она
отражает влияние цепи на сигнал.
В задачах прохождения сигналов через различные цифровые узлы происходит свертка сигнала с импульсной
характеристикой фильтра.
Корреляцию между двумя сигналами можно вычислить как сумму произведений пар отсчетов исследуемых сигналов.
Если взять две абсолютно независимые случайные последовательности, то их сумма произведений стремится к нулю.
Говорят, что такие сигналы обладают нулевой корреляцией. Причем, чем длиннее последовательности, тем сильнее
результат стремится к нулевому значению.
Корреляция бывает положительной и отрицательной. Положительная корреляция - большие значения одного сигнала
связаны с большими значениями другого сигнала (увеличение одной переменной взаимосвязано с увеличением другой
переменной). Отрицательную корреляцию проще всего понимать так: увеличение одной переменной связано с уменьшением
другой переменной.
Формула взаимной корреляции:
$ r_{12} = \frac{1}{N} \sum_{n=0}^{N-1}x_1(n)x_2(n)$
Нормирующий множитель $\frac{1}{N}$ применяется для исключения влияния длительности последовательностей.
В терминах функционального пространства сигналов корреляция может быть выражена как косинус угла между векторами.
Следовательно, при полном совпадении сигналов степень их связи будет принимать положительное единичное значение,
при полной противоположности сигналов - отрицательную единицу, а при полном несовпадении - нулевое значение.
In [1]:
import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import fft, ifft
%matplotlib inline
Приведем примеры сигналов и найдем корреляцию между ними
Положительная корреляция:
In [2]:
# signal x1(n)
x1 = np.array([1, 2, 3, 4, 5])
# correlation
np.correlate(x1, x1, mode='valid')
Out[2]:
array([55])
In [3]:
# signal x1(n)
x1 = np.array([1, 2, 3, 4, 5])
# correlation via sum
np.sum(x1*x1)
Out[3]:
55
Как видно, встроенная функция correlate() для совпадающих сигналов вычисляет сумму произведений, что полностью
согласуется с формулой.
Отрицательная корреляция:
In [4]:
# signal x2(n)
x2 = -1 * np.array([1, 2, 3, 4, 5])
# correlation
np.correlate(x1, x2, mode='valid')
Out[4]:
array([-55])
Разные сигналы:
In [5]:
# signal x1(n), x2(n)
x1 = np.ones(5)
# [1, 1, 1, 1, 1]
x2 = np.arange(5)
# [0, 1, 2, 3, 4]
# correlation
np.correlate(x1, x2, mode='valid')
Out[5]:
array([10.])
In [6]:
np.sum(x1*x2)
Out[6]:
10.0
# correlation as sum of products
На практике, когда два сигнала коррелируют, их взаимное расположение во времени - неизвестно. Сигналы могут иметь
одинаковую форму, но задержаны друг относительно друга. В связи с этим, для установления максимальной корреляции, её
требуется находить для нескольких задержек.
Случайные сигналы
Найдем корреляцию двух псевдослучайных процессов.
Параметр seed() задает начальное условие для случайного процесса. Если установить какое-либо число, то при вызове
любой функции случайного числа будет генерироваться предопределенный набор чисел (псевдослучайный).
С помощью метода randint() из библиотеки numpy.random зададим случайную последовательность целых чисел.
Случайные процессы с нулевой корреляцией:
In [7]:
N = 20
# No correlation. Seed for all random process
np.random.seed(1)
x1 = np.random.randint(-10, 10, N)
x2 = np.random.randint(-10, 10, N)
# correlation
r12 = np.correlate(x1, x2, mode='valid')
# plot results
plt.figure(figsize=(14, 4), dpi=80)
plt.plot(x1, '-o', linewidth=0.1, markersize=8)
plt.plot(x2, '-s', linewidth=0.1, markersize=8)
plt.xlim([-0.5, N-0.5])
plt.grid(True)
print('No correlation, r12 = {}.'.format(r12))
No correlation, r12 = [0].
Случайные процессы с ненулевой корреляцией:
In [8]:
N = 20
# Correlation
np.random.seed(1)
x1 = np.random.randint(-10, 10, N)
np.random.seed(2)
x2 = np.random.randint(-10, 10, N)
# correlation
r12 = np.correlate(x1, x2, mode='valid')
# plot results
plt.figure(figsize=(14, 4), dpi=80)
plt.plot(x1, '-o', linewidth=0.1, markersize=8)
plt.plot(x2, '-s', linewidth=0.1, markersize=8)
plt.xlim([-0.5, N-0.5])
plt.grid(True)
plt.grid(True)
print('Correlation, r12 = {}.'.format(r12))
Correlation, r12 = [-164].
Фильтрующее свойство дельта-функции в процессе вычисления корреляции позволяет найти значение сигнала в момент,
когда дельта-функция не равна 0:
In [9]:
N = 10
# delta-function
x1 = np.zeros(N)
x1[4] = 1
# random signal
np.random.seed(2)
x2 = np.random.randn(N)
# correlation
r12 = np.correlate(x1, x2, mode='valid')
# plot results
plt.figure(figsize=(14, 4), dpi=80)
plt.plot(x1, '-o', linewidth=0.1, markersize=8)
plt.plot(x2, '-s', linewidth=0.1, markersize=8)
plt.xlim([-0.5, N-0.5])
plt.grid(True)
print('Correlation, r12 = {}.'.format(r12))
Correlation, r12 = [-1.79343559].
Автокорреляционная функция
Автокорреляционная функция (АКФ) - показывает зависимость между сигналом и его копией, сдвинутой по времени.
АКФ находит применение в кодировании информации. Выбор кодирующей последовательности по параметрам длины,
частоты и формы во многом обусловлен корреляционными свойствами этой последовательности. Наилучшая кодовая
последовательность обладает наименьшим значением вероятности ложного обнаружения или срабатывания (для
последовательность обладает наименьшим значением вероятности ложного обнаружения или срабатывания (для
детектирования сигналов, для пороговых устройств) или ложной синхронизации (для передачи и приема кодовых
последовательностей).
Автокорреляционная функция помогает находить повторяющиеся участки во временной последовательности, с помощью
АКФ можно находить несущую частоту сигнала.
Поскольку АКФ есть произведение сигнала и его копии, то физический смысл АКФ - энергия сигнала. В частности, в нулевой
момент времени ( n = 0 ) АКФ равна энергии сигнала.
В numpy нет встроенной функции автокорреляции, но её несложно написать самому на базе функции correlate() .
Свойства АКФ
1.
2.
3.
4.
5.
АКФ это симметричная и четная функция.
Имеет максимум в нуле.
АКФ периодической последовательности - периодическая функция.
АКФ суммы двух некоррелированных сигналов - сумма АКФ этих сигналов.
АКФ бесконечного во времени белого шума имеет пик в нулевом значении и нули во всех остальных.
АКФ прямоугольного импульса
Пример: Автокорреляционная функция прямоугольного импульса - треугольный сигнал. Ниже будет показано, что
корреляция и свертка сигнала с самим собой даёт одинаковый результат.
In [10]:
# Auto-correlation function
def auto_corr(x):
res = np.correlate(x, x, mode='same')
return res # / np.max(res)
# Signal
x = np.concatenate([np.zeros(5), np.ones(5), np.zeros(5)])
# ACF
cfx = auto_corr(x)
xl = [x, cfx]
# Pot results
plt.figure(figsize=(14, 5), dpi=80)
for i in range(2):
plt.subplot(2, 1, i+1)
plt.stem(xl[i], linefmt='C0', markerfmt='D', use_line_collection=True)
plt.grid(True)
plt.xlim([-0.5, x.size-0.5])
Поскольку вычисление АКФ прямым методом - трудозатратная операция (большое число операций умножения и сложения),
выполняемая за $O(N^2)$, то во многих задачах встаёт вопрос о снижении качества корреляционных свойств в связи с
уменьшением длины последовательности. Однако, с помощью быстрого преобразования Фурье (БПФ) можно свести
вычислительную сложность к $O(Nlog(N)$.
С помощью теоремы Винера-Хинчина, которая связывает АКФ сигнала и его спектральную плотность мощности, можно
вычислить АКФ через двойное взятие БПФ сигнала.
$\Psi(\tau) = Re[IFFT( | FFT(x) |^2 )]$
Свертка
Свертка описывает взаимодействие сигналов между собой. Если один из сигналов - импульсная характеристика фильтра, то
свертка входной последовательности с импульсной характеристикой есть ни что иное, как реакция цепи на входное
воздействие. Иными словами, результирующий сигнал отражает прохождение сигнала через фильтр.
Как правило, выходной сигнал является запаздывающей (относительно входа) функцией. Кроме того, выходной сигнал
может быть усилен или подавлен относительно входного сигнала.
Чтобы найти импульсную характеристику цифрового фильтра, необходимо подать на его вход единичный импульс
(дельта-функцию), который равен 1 в одной точке и равен 0 во всех остальных точках
Свертка и корреляция
Связь свертки и корреляции достаточно проста: свертка эквивалентна взаимной корреляции двух последовательностей,
причем одна из последовательностей обращена во времени относительно другой. В случае с корреляцией,
последовательности должны быть одинаковой длины. В случае свертки последовательности могут иметь разную длину,
тогда этот процесс называется линейной сверткой. В случае, если длины последовательностей совпадают - это циклическая
(круговая) свертка.
Свойства свертки
1. Коммутативность:
$a*b = b*a$
Из этого выражения вытекает следующее утверждение:
$ \sum_{m=0}^{N-1}a(m)b(n-m) = \sum_{m=0}^{N-1}a(n-m)b(n)$
1. Дистрибутивность:
$a*(b+c) = a*b + a*c$
1. Ассоциативность:
$a*(b*c) = (a*b)*c = (a*c)*b$
Существует два типа свертки - линейная и циклическая (круговая).
Линейная свертка
Линейная свертка двух сигналов $a(n)$ , где $n = 0, ..., N-1$ и $b(n)$, где $n = 0, ..., M-1$ описывается уравнением:
$ s(n) = a*b = \sum_{m=0}^{n}a(m)\cdot b(n-m)$
где
$n = 0, ..., N+M-2$ ,
$N$ - длина сигнала $a(n)$ ,
$M$ - длина сигнала $b(n)$ ,
Вычисление свертки - итеративный процесс, в котором сигналы сдвигают друг относительно друга, затем перемножают и
складывают. Предполагается, что сигналы равны нулю вне заданных своих диапазонов, то есть $a(n) = 0$ при $N < n < 0$ и
$b(n) = 0$ при $M < n < 0$.
На следующем примере вычислим пошагово свертку сигналов:
a(n) = [1, 2, 3, 4], N = 4
b(n) = [3, 2, 1], M = 4
Простейший алгоритм (через циклическую свёртку):
1. Дополняем нулями слева первый сигнал до длины N+M-1.
2.
3.
4.
5.
Инвертируем во времени второй сигнал.
Дополняем нулями справа второй сигнал до длины N+M-1.
В цикле от 0 до N+M-2 сдвигаем второй сигнал вправо (или первый сигнал влево)
Вычисляем на каждом шаге цикла произведения элементов и подсчитываем сумму произведений.
Сравним полученный результат и значения, вычисленные с помощью встроенной функции convolve() с параметром
mode='full' .
In [11]:
# input parameters
N, M = 4, 3
# lists of data
a = [1, 2, 3, 4]
b = [3, 2, 1]
# signals
an = np.concatenate([np.zeros(M-1, dtype=int), a])
bn = np.concatenate([b[::-1], np.zeros(N-1, dtype=int)])
print('a(n) = ', a)
print('b(n) = ', b)
# Convolution with 'same' mode with list comprehension:
ab = np.array([np.sum(an * np.roll(bn, i)) for i in range(N+M-1)])
# simple way:
# ab = []
# for i in range(N+M-1):
#
br = np.roll(bn, i)
#
sm = np.sum(an * br)
#
ab.append(sm)
# shift second signal
# calc sum of prods
# append new value to the list
# Function convolution:
print('\na(n) * b(n) = ', ab)
# Convolution with np.convolve method:
cv = np.convolve(a,b, mode='full')
print('np.convolve = ', cv)
# Check conv method:
ab_check = np.all(ab == cv)
print(ab_check)
a(n) =
b(n) =
[1, 2, 3, 4]
[3, 2, 1]
a(n) * b(n) =
np.convolve =
True
[ 3
[ 3
8 14 20 11
8 14 20 11
4]
4]
Пошаговое объяснение линейной свёртки
Важно помнить, что второй сигнал сначала инвертируется слева направо, согласно формуле вычисления свертки!
Step 1:
a = [0, 0, 1, 2, 3, 4]
b = [1, 2, 3, 0, 0, 0]
sum of prod = [3]
Step 2:
a = [0, 0, 1, 2, 3, 4]
b = [0, 1, 2, 3, 0, 0]
sum of prod = 1*2 + 2*3 = [8]
Step 3:
a = [0, 0, 1, 2, 3, 4]
b = [0, 0, 1, 2, 3, 0]
sum of prod = 1*1 + 2*2 + 3*3 = [14]
Step 4:
a = [0, 0, 1, 2, 3, 4]
b = [0, 0, 0, 1, 2, 3]
sum of prod = 1*2 + 2*3 + 3*4 = [20]
Step 5:
a = [0, 0, 1, 2, 3, 4]
b = [3, 0, 0, 0, 1, 2]
sum of prod = 1*3 + 2*4 = [11]
Step 6:
a = [0, 0, 1, 2, 3, 4]
b = [2, 3, 0, 0, 0, 1]
sum of prod = 1*4 = [4]
Convolution seq = [3, 8, 14, 20, 11, 4]
Свёртка прямоугольного импульса
Свёртка прямоугольного импульса с самим собой вырождается в сигнал треугольной формы. Как было показано выше, для
автокорреляционной функции результат аналогичен:
In [12]:
# Signal
x = np.concatenate([np.zeros(5), np.ones(5), np.zeros(5)])
# Convolution
cv = np.convolve(x, x, mode='same')
xl = [x, cv]
# Pot results
plt.figure(figsize=(14, 5), dpi=80)
for i in range(2):
plt.subplot(2, 1, i+1)
plt.stem(xl[i], linefmt='C0', markerfmt='D', use_line_collection=True)
plt.grid(True)
plt.xlim([-0.5, x.size-0.5])
Циклическая свёртка
Циклическая (круговая) свертка отличается от линейной тем, что входные сигналы имеют одинаковую длительность $N$.
Циклическая свертка двух сигналов $a(n)$ и $b(n)$, где $n = 0, ..., N-1$ , описывается уравнением:
$ s(n) = a*b = \sum_{m=0}^{N-1}a(m)\cdot b(n-m)$
где $n = 0, ..., N-1$ , а число $N$ - длина сигнала $a(n)$ . Как видно, результат циклической свёртки имеет длину N.
На следующем примере вычислим пошагово свертку сигналов:
a(n) = [1, 2, 3, 4]
b(n) = [3, 2, 1, 0]
Алгоритм:
1. Инвертируем второй сигнал,
2. В цикле от 0 до N-1 сдвигаем второй сигнал вправо (или первый сигнал влево)
3. Вычисляем на каждом шаге цикла произведения элементов и подсчитываем сумму произведений.
Полученный результат не совпадает со встроенным методом convolve() с параметром mode='same' в связи с тем, что
для этого метода в библиотеке numpy используется дополнение нулями.
In [13]:
# Input parameters
N = 4
# Signals
an = np.array([1, 2, 3, 4], dtype=int)
bn = np.array([3, 2, 1, 0], dtype=int)
print('a(n) = ', an)
print('b(n) = ', bn)
# Convolution with list comprehension:
ab = np.array([np.sum(an * np.roll(bn[::-1], i+1)) for i in range(N)])
# simple way:
# ab = []
# for i in range(N):
#
br = np.roll(bn, i+1)
#
sm = np.sum(an * br)
#
ab.append(sm)
# shift second signal
# calc sum of prods
# append new value to the list
# Function convolution:
print('a(n) * b(n) = ', ab)
a(n) = [1 2 3 4]
b(n) = [3 2 1 0]
a(n) * b(n) = [14 12 14 20]
Пошаговое объяснение циклической свёртки
Первым шагом инвертируем сигнал b(n) и начинаем с -1 отсчета
Step 1:
a = [1, 2, 3, 4]
b = [3, 0, 1, 2]
sum of prod = 1*3 + 1*3 + 2*4 = [14]
Step 2:
a = [1, 2, 3, 4]
b = [2, 3, 0, 1]
sum of prod = 1*2 + 2*3 + 1*4 = [12]
Step 3:
a = [1, 2, 3, 4]
b = [1, 2, 3, 0]
sum of prod = 1*1 + 2*2 + 3*3 = [14]
sum of prod = 1*1 + 2*2 + 3*3 = [14]
Step 4:
a = [1, 2, 3, 4]
b = [0, 1, 2, 3]
sum of prod = 1*2 + 2*3 + 3*4 = [20]
Convolution seq = [14, 12, 14, 20]
В связи с тем, что в библиотеке numpy отсутствует встроенная функция для вычисления циклической свёртки, можно
использовать свойство преобразования Фурье.
Свертка через БПФ
Из предыдущих курсов, посвященных преобразованию Фурье, известно правило:
Свертка двух сигналов во временной области равна произведению их спектров в частотной области
$a(n) * b(n) = A(k) \cdot B(k)$
Используя это правило, можно вычислить циклическую свертку двух сигналов.
In [14]:
# Convolution with IFFT of FFT(a) * FFT(b)
def circle_conv(an, bn):
"""
Calculate circular convolution via FFTs.
Signals an & bn must have same shape.
You should import fft and ifft from scipy.fftpack.
Parameters
---------an : np.array
real 1D numpy array
bn : np.array
real 1D numpy array
"""
return np.real(ifft(fft(an) * fft(bn)))
# Input parameters
N = 4
# Signals
an = np.array([1, 2, 3, 4], dtype=int)
bn = np.array([3, 2, 1, 0], dtype=int)
# Calculate circular convolution
cv = circle_conv(an, bn)
print('circular convolution = ', cv)
# Check conv method
ab_check = np.all(ab == cv)
print(ab_check)
circular convolution =
True
[14. 12. 14. 20.]
Вычисление свёртки через БПФ имеет ряд преимуществ, одно из которых связано с количеством выполняемых операций
при вычислении.
Например, сигнал $a(n)$ имеет длину $N = 2000$, а сигнал $b(n)$ имеет длину $M = 8000$. Вычисление линейной свёртки
потребует $N*M = 16.000.000$ операций умножения и сложения.
Однако, если дополнить обе последовательности до $N_{FFT} = 8192$, то для вычисления БПФ потребуется $N\cdot log_{2}
(N) \approx 106.000$ операций комплексного умножения (или в 4 раза больше операций вещественного умножения).
Из формулы для вычисления свёртки через БПФ очевидно, что требуется три звена БПФ: два прямых БПФ для входных
сигналов и одно обратное БПФ для произведения спектров сигналов. Комплексные умножения спектров вносят
несущественный вклад (8192 комплексных умножения), поэтому результирующее оценочное значение количества операций
$3 \cdot 4 \cdot N\cdot log_{2}(N) \approx 1.280.000$
Полученное значение в 12.5 раз меньше, чем если бы пришлось вычислять линейную свёртку по формуле из определения.
Сравнение эффективности
Ниже представлена таблица сравнения эффективности быстрой свертки и свертки, вычисляемой по прямой формуле. В
таблице сравнивается число действительных умножений, требуемых для вычисления свертки.
Как видно, для длин БПФ до 64, быстрая свёртка проигрывает у прямого метода. Однако, при увеличении длины БПФ
результаты меняются в обратную сторону - быстрая свертка начинает выигрывать у прямого метода. Причем, чем больше
длина БПФ, тем лучше выигрыш.
N
Прямой
Быстрая свертка Отношение
метод
8
64
448
0.14
16
256
1088
0.24
32
1K
2560
0.4
64
4K
5888
0.7
128
16K
13312
1.23
...
...
...
...
2K
4M
311296
13.5
Список функций из пакета signal:
Ниже приведен список основных функций из пакета scipy по тематике свертки и корреляции.
Свертка и корреляция
Function
Description
convolve(in1, in2[, mode,
method])
Свертка двух N-мерных массивов
correlate(in1, in2[, mode,
method])
Кросс-корреляция двух N-мерных массивов
fftconvolve(in1, in2[, mode,
axes])
Свертка двух N-мерных массивов через БПФ
convolve2d(in1, in2[, mode,
boundary, fillvalue])
Свертка двух 2-мерных массивов
correlate2d(in1, in2[, mode,
boundary, ...])
Корреляция двух 2-мерных массивов
sepfir2d(input, hrow, hcol)
Свертка массива рангом 2 с характеристикой фильтра ранга 1. Функция может использоваться для
поиска изображения по его B-сплайновому представлению.
choose_conv_method(in1, in2[,
mode, measure])
In [15]:
from scipy import signal
# Signal
sig = np.repeat([0., 1., 0.], 200)
# Window
win = signal.kaiser(32, beta=11)
# Filter by using convolve
fil = signal.convolve(sig, win, mode='same') / np.sum(win)
# list of frequencies
f_list = [sig, win, fil]
t_list = ['Signal', 'Window', 'Convolve']
# Plot
plt.figure(figsize=(14, 6), dpi=80)
for i in range(3):
Поиск наибыстрейшего метода корреляции или свертки
for i in range(3):
plt.subplot(3, 1, i+1)
plt.plot(f_list[i], '-', linewidth=2.0)
plt.title(t_list[i])
plt.xlabel('Samples')
plt.ylabel('Amplitude')
plt.xlim([0, f_list[i].size-1])
plt.grid()
plt.tight_layout()
Цифровая обработка сигналов - 4
Title
Digital signal processing
Author
Alexander Kapitanov
Contact
sallador@bk.ru
Project lang
Python
Packages
numpy, scipy, matplotlib
License
GNU GPL 3.0
Введение
Перед вами обучающий материал по основам цифровой обработки сигналов с использованием средств языка
программирования Python. Предполагается, что читатель имеет базовые знания из области высшей математики, а также
владеет языком Python и хотя бы поверхностно знает различные python-библиотеки - numpy/scipy, matplotlib и другие.
Для пользователей MATLAB / GNU Octave освоение материала с точки зрения программного кода не составит труда,
поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из python-библиотек.
Сигналы
В предыдущих частях мы узнали, что сигнал - это физический процесс, параметры которого изменяются в соответствии с
передаваемым сообщением. Сигналы бывают – случайные и детерминированные.
Случайным сигналом называют функцию времени, значения которой заранее неизвестны и могут быть предсказаны лишь с
некоторой вероятностью. К основным характеристикам случайных сигналов относятся:
закон распределения (относительное время пребывания значения сигнала в определенном интервале),
спектральное распределение мощности.
Случайные сигналы делятся на два класса: 1) шумы - беспорядочные колебания, состоящие из набора разных частот и
амплитуд, 2) сигналы, несущие информацию, для обработки которых требуется прибегать к вероятностным методам.
Случайные сигналы характеризуются плотностью распределения вероятностей. Плотность вероятности это один из
способов задания распределения случайных величин. Плотность вероятности - неотрицательная функция при любых
значениях дискретного сигнала. Для аналоговых случайных сигналов интеграл от функции сигнала во всем диапазоне
значений стремится к единице. Для дискретных случайных величин не существует функции плотности распределения
вероятностей, т.к. дискретная случайная величина не является непрерывной функцией. Однако, математический аппарат
позволяет вычислять приближенные значения функции.
Простые примеры дискретных случайных величин:
количество выпавших орлов и количество выпавших решек при броске монеты счетное число N раз,
число попаданий в мишень при ограниченном числе выстрелов.
погрешности измерений приборов
Случайные сигналы
Плотность вероятности случайного сигнала позволяет определить математические моменты разного порядка:
Математическое ожидание: среднее значение последовательности случайных величин
1
m=
N
N−1
∑n =0 x(n)
Под математическим ожиданием в теории сигналов зачастую понимают смещение сигнала по уровню относительно нуля
(постоянная составляющая).
В python для вычисления математического ожидания используется метод mean()
Дисперсия: среднее значение квадратов разностей между значениями последовательности и её средним значением
1
σ2 =
N−1
N−1
∑n =0 | x(n) − m | 2
В литературе часто используется термин среднеквадратическое отклонение. Эта величина равна квадратному корню из
дисперсии сигнала.
В python для вычисления дисперсии используется метод - var() , а для поиска среднеквадратического отклонения
используется метод - std() .
In [1]:
import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import fft, rfft
%matplotlib inline
Случайный дискретный сигнал при N = 100000 отсчётов и его плотность вероятности:
In [2]:
N = 100000
# Random signal
m, s = 0, 10
np.random.seed(2)
sig = np.random.normal(m, s, N)
# Create hist for PDF
hist, _ = np.histogram(sig, bins=list(range(0, 256)))
# Plot figure
fig = plt.figure(1, figsize=(14, 5), dpi=80)
plt.subplot(1, 2, 1)
plt.title('Random signal')
plt.xlabel('Samples')
plt.ylabel('Amplitude')
plt.plot(sig, color='C0')
plt.xlim([0, N-1])
plt.grid()
plt.subplot(1, 2, 2)
plt.title('Probability density function')
plt.xlabel('Value')
plt.ylabel('Level')
plt.xlim([-4*s, 4*s])
plt.hist(sig, bins=list(range(-s*3, s*3)), color='C1', label=r'$\mu = %d, \sigma$ = %d' % (m, s))
plt.grid()
plt.legend(loc='upper left')
plt.tight_layout()
print('Mean of the signal:', np.mean(sig))
print('Std. of the signal:', np.std(sig))
Mean of the signal: -0.032692104037689
Std. of the signal: 10.020365002664889
Нормальное распределение
Согласно центральной предельной теореме, сумма большого числа слабо зависимых случайных величин имеет
распределение близкое к нормальному. При этом, случайные величины распределены в рамках определенного масштаба,
то есть ни одно из значений не вносит существенного вклада в конечную сумму.
Нормальное распределение (распределение Гаусса) - распределение вероятностей, которое задаётся функцией:
1
f(x) =
σ√2π
( x − μ )2
2σ2
e−
где μ - математическое ожидание (среднее значение случайного процесса), а σ - среднеквадратическое отклонение.
Нормальное распределение считается стандартным, если μ = 0, σ = 1.
Правило "трех сигм" 3σ
Правило трех сигм гласит, что с вероятностью P = 0.997 значения нормально распределенной последовательности лежат в
интервале утроенного значения среднеквадратического отклонения. Иными словами, практически все значения случайного
процесса лежат в интервале трех сигм, то есть в диапазоне (x − 3σ, x + 3σ).
Ниже представлены графики плотности вероятности и функции распределения нормального закона распределения при
различных параметрах математического ожидания и дисперсии.
Для построения графиков используется метод norm(mu, sigma) из пакета numpy.stats , а не функция randn() из
пакета numpy.random . Это связано с тем, что у norm() возвращает объект, у которого есть методы PDF - плотность
вероятности и CDF - функции распределения случайной величины.
In [3]:
from scipy.stats import norm
# Gaussian parameters
mu = [0, 0, -1, -3, -4]
sg = [0.2, 1, 1, 0.5, 0.3]
# Create Normal distributions
pxn = [norm(mu[i], sg[i]) for i in range(5)]
tt = np.linspace(-5, 5, N)
# Plot PDF and CDF
fig = plt.figure(1, figsize=(14, 5), dpi=80)
plt.subplot(1,2,1)
plt.title('Probability density function')
for i in range(5):
plt.plot(tt, pxn[i].pdf(tt), color='C'+str(i), markersize=2, label='$\mu$ = %d, $\sigma^2$ = %0
.2f' % (mu[i], sg[i]))
plt.legend(loc='upper right')
plt.xlim([-5, 5])
plt.grid(True)
plt.subplot(1,2,2)
plt.title('Cumulative distribution function')
for i in range(5):
plt.plot(tt, pxn[i].cdf(tt), color='C'+str(i), markersize=2, label='$\mu$ = %d, $\sigma^2$ = %0
.2f' % (mu[i], sg[i]))
plt.legend(loc='lower right')
plt.xlim([-5, 5])
plt.grid(True)
Длина случайного процесса
На основании центральной предельной теоремы, чем больше длительность случайного процесса, тем сильнее он похож на
нормальное (Гауссовское) распределение. Можно показать, что при увеличении длины сигнала, функция плотности
вероятности стремится к функции нормального распределения.
Зададим длину случайной последовательности N = 100, 1000, 10000, 100000 отсчётов. На приведенных ниже графиках
показано, как длина случайного процесса влияет на форму графика плотности вероятности.
In [4]:
N = 10 ** np.arange(2,6)
# Set random seed
np.random.seed(1)
plt.figure(figsize=(12, 8), dpi=80)
for i in range(len(N)):
# create random signal
dat = np.random.normal(size=N[i])
# hist and bins
hist, bins = np.histogram(dat, np.linspace(-5, 5, 30))
# probability density function
pdf = norm.pdf(bins)
plt.subplot(len(N), 2, 2*i+1)
if i == 0:
plt.title('Random signal')
plt.plot(dat)
plt.xlim([0, dat.size])
plt.grid(True)
plt.subplot(len(N), 2, 2*i+2)
if i == 0:
plt.title('Probability density function')
plt.plot(bins[:-1], hist, color='C1', label='N = 10^{}'.format(int(np.log10(N[i]))))
plt.xlim([-4, 4])
plt.legend(loc='upper right')
plt.grid(True)
plt.tight_layout()
Python библиотека Random
Python библиотека numpy содержит пакет random, который содержит набор функций математической статистики. Для
импорта пакета в проект необходимо выполнить команду:
from numpy.random import *
# or
import numpy as np
Кроме того, в библиотеке scipy содержится пакет *stats, который дополняет (и частично переопределяет) функционал пакета
random. Приведем список основных функций из пакета random:
Function
Description
rand(d0, d1, ..., dn)
Равномерное распределение (возвращает N-мерный массив)
randn(d0, d1, ..., dn)
Стандартное нормальное распределение (возвращает N-мерный массив)
randint(low[, high, size,
dtype])
Массив целочисленных значений в заданном диапазоне
random([size])
Равномерное распределение в интервале [0.0, 1.0)
shuffle(x)
Перестановка элементов последовательности "на лету"
permutation(x)
Перестановка элементов массива или возврат их индексов
normal([loc, scale, size])
Массив случайных чисел, распределенных по нормальному закону
pareto(a[, size])
Массив случайных чисел, распределенных по закону Парето
poisson([lam, size])
Массив случайных чисел, распределенных по закону Пуассона
rayleigh([scale, size])
Массив случайных чисел, распределенных по Рэлеевскому закону
seed([seed])
Инициализация псевдослучайной величины
В задачах цифровой обработки сигналов случайные процессы играют важную роль. С помощью случайных величин можно
моделировать воздействие реальной среды на прохождение сигнала от источника к приёмнику данных. Зачастую, при
прохождении сигнала через какое-то шумящее звено, к сигналу добавляется так называемый белый шум. Как правило,
спектральная плотность такого шума равномерно (одинаково) распределена на всех частотах, а значения шума во
временной области распределены нормально (Гауссовский закон распределения). Поскольку белый шум физически
добавляется к амплитудам сигнала в выбранные отсчеты времени, он называется аддитивный. Таким образом, основной
источник шумов носит название аддитивный белый гауссовский шум (AWGN - Additive white Gaussian noise).
Стоит отметить, что термин белый связан с тем, что спектральные составляющие равномерно распределены по всему
диапазону частот. Изучение особенностей шумов выходит за рамки этого материала, но в последующих лекциях
планируется вернуться к вопросам влияния шумов на протекающие процессы в устройствах, в частности в цифровых.
Поскольку частотные значения распределены равномерно, автокорреляционная функция (АКФ) белого шума в идеале
стремится к дельта-функции.
Приведем график белого шума во временной области, а также построим его АКФ. В качестве генератора белого шума
воспользуемся функцией randn() из пакета random
In [5]:
# Auto-correlation function
def auto_corr(x):
res = np.correlate(x, x, mode='same')
return res / np.max(res)
N = 1000
# Random signal
np.random.seed(2)
dat = np.random.randn(N)
dat = np.random.randn(N)
# ACF: Auto-correlation
cfx = auto_corr(dat)
plt.figure(figsize=(14, 4), dpi=80)
plt.subplot(1, 2, 1)
plt.title('Random signal')
plt.plot(dat)
plt.xlim([0, dat.size])
plt.grid(True)
plt.subplot(1, 2, 2)
plt.title('Auto-correlation')
plt.plot(np.linspace(-N//2, N//2, N), cfx)
plt.xlim([-N//2, N//2])
plt.grid(True)
plt.tight_layout()
Цифровая обработка сигналов - 5
Title
Digital signal processing
Author
Alexander Kapitanov
Contact
sallador@bk.ru
Project lang
Python
Packages
numpy, scipy, matplotlib
License
GNU GPL 3.0
Введение
Перед вами обучающий материал по основам цифровой обработки сигналов с использованием средств языка
программирования Python. Предполагается, что читатель имеет базовые знания из области высшей математики, а также
владеет языком Python и хотя бы поверхностно знает различные python-библиотеки - numpy/scipy, matplotlib и другие.
Для пользователей MATLAB / GNU Octave освоение материала с точки зрения программного кода не составит труда,
поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из python-библиотек.
Сигналы
In [1]:
import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import fft, rfft, fftshift
%matplotlib inline
Детерминированные сигналы
В мире существует множество сигналов различной формы, однако в задачах цифровой и аналоговой обработки часто
используются известные сигналы - гармонической формы, модулированные (по амплитуде, частоте или фазе). Как известно,
сигнал любой формы можно представить как совокупность гармонических сигналов разных частот и амплитуд (то есть набор
спектральных отсчетов). Можно сказать, что чем сложнее сигнал - тем больше спектральных отсчетов требуется для его
представления. В частности, для представления сигналов с резкими изменениями формы требуются высокие частоты
спектра, а для "гладких" сигналов и медленно меняющихся процессов высокие частоты не требуются и не вносят вклад в
результирующий сигнал (и его спектр).
Гармонический сигнал
Гармонический сигнал задается уравнением:
$s(t) = A \cdot cos(2\pi ft +\phi)$,
где A – амплитуда колебания, f - частота сигнала, φ – начальная фаза.
Комплексная запись такого сигнала:
$s = A \cdot e^{j(2\pi ft +\phi)}$,
где j - комплексная единица. Часто выражается как $j = \sqrt-1$
Ниже представлен график гармонического сигнала при различных параметрах значения частоты. Амплитуда = 1, начальная
фаза = 0 (константы).
In [2]:
n = 100
t = np.linspace(0, 1, n, endpoint=True)
# list of frequencies
f_list = np.array([1, 2, 3, 5, 8, 10, 15, 20, 30])
plt.figure(figsize=(12, 6), dpi=80)
for i, freq in enumerate(f_list):
plt.subplot(3, 3, i+1)
plt.plot(t, np.sin(2*np.pi*freq*t))
plt.title(f'Frequency = {freq}')
plt.xlabel('Samples')
plt.ylabel('Amplitude')
plt.xlim([0, 1])
plt.xticks(np.linspace(0, 1, 11, endpoint=True))
plt.grid()
plt.tight_layout()
Модуляция
Несмотря на то, что модуляция присуща аналоговым колебаниям, необходимо понимать, какими способами можно
передавать информационные сообщения. Для цифровых сигналов модуляция дискретными колебаниями называется
манипуляция и также будет рассмотрена в этом разделе.
Модуляцией называется процесс изменения одного или нескольких параметров сигнала. Модулируемый сигнал называется
"несущим" (на частоте этого сигнала передается модулируемое сообщение). Информационный сигнал называется
модулирующим. Как правило, модулирующий сигнал - низкочастотный, а несущий сигнал - высокочастотный. В процессе
модуляции несущего сигнала спектр модулирующего сигнала переносится в область несущей частоты. Гармонические
сигналы можно модулировать во времени по амплитуде, частоте и фазе.
Передача электромагнитного поля в пространстве выполняется с помощью антенн, размер которых зависит от длины волны
$\lambda$, низкочастотные информационные сигналы во многих случаях просто физически невозможно передать от
источника к получателю (требуются антенны огромных размеров). В связи с этим применяются методы модуляции
высокочастотных несущих колебаний.
Амплитудная модуляция
Амплитудная модуляция - широко известный способ изменения формы сигнала по параметру амплитуды. Из названия
очевидно, что амплитуда такого сигнала изменяется во времени. Закон изменения амплитуды - произвольный, на практике
часто используется модуляция гармоническим колебанием.
Формула простейшего гармонического АМ-сигнала:
$s(t) = A_c \cdot (1 + m \cdot cos(\omega_mt +\phi)) \cdot cos(\omega_сt)$,
где
$A_{c}$ – амплитуда несущего колебания,
$\omega_{c}$ – частота несущего сигнала,
$\omega_{m}$ – частота модулирующего (информационного) сигнала,
$\phi$ – начальная фаза модулирующего сигнала,
m - коэффициент модуляции.
m - коэффициент модуляции.
Тогда, радиосигнал состоит из несущего колебания и двух боковых полос. Из названия, очевидно, что несущая частота - та,
на которой распространяется сигнал. Как правило, это высокая частота относительно модулирующей частоты.
Модулирующая частота, в свою очередь, низкочастотная. Это такая частота, на которой передается информационное
сообщение.
Для синусоидального сигнала, использованного в качестве примера боковые полосы представляют собой синусоидальные
сигналы и их частоты равны $\omega_{c}+\omega_{m}$ и $\omega_{c}-\omega_{m}$. Спектр АМ-сигнала всегда симметричен
относительно центральной (несущей) частоты.
Важно понимать, что центральная частота не несет полезной информации, хоть и называется "несущая". В это понятие
вкладывается значение частоты, относительно которого располагаются информационные (модулирующие) частоты сигнала.
Создадим функцию АМ-сигнала:
In [3]:
def signal_am(amp=1.0, km=0.25, fc=10.0, fs=2.0, period=100):
"""
Create Amplitude modulation (AM) signal
Parameters
---------amp : float
Signal magnitude
km : float
Modulation coeff: amplitude sensitivity 0 <= km < 1
fc : float
Carrier frequency
fs : float
Signal frequency
period : integer
Number of points for signal (same as period)
"""
tt = 2.0 * np.pi * np.linspace(0, 1, period)
return amp * (1 + km * np.cos(fs * tt)) * np.cos(fc * tt)
На приведенных ниже графиках показано, как меняется форма и спектр АМ-сигнала при изменении параметра несущей
частоты $f_c$:
Как видно, спектр АМ-сигнала состоит из трех компонент: центральная - несущая, и две боковые - модулирующие. При
изменении несущей частоты происходит смещение всего АМ-сигнала по частоте.
In [4]:
N = 1024
# Create AM-signal
fs = 15
fc = [20, 45, 60]
# Modulation frequency
# Carrier frequency
sig = [signal_am(amp=1.0, km=0.45, fc=i, fs=fs, period=N) for i in fc]
# Calculate FFT
sft = np.abs(rfft(sig, axis=1)) / N / 0.5
plt.figure(figsize=(12, 6), dpi=80)
for i, freq in enumerate(fc):
plt.subplot(len(fc), 2, 2*i+1)
if i == 0:
plt.title('AM-signal')
plt.plot(sig[i])
plt.xlim([0, N-1])
plt.grid(True)
plt.subplot(len(fc), 2, 2*i+2)
if i == 0:
plt.title('Spectrum')
plt.plot(sft[i])
plt.xlim([0, N//2-1])
plt.grid(True)
plt.tight_layout()
На приведенных ниже графиках показано, как меняется форма и спектр АМ-сигнала при изменении параметра частоты
модулирующего колебания $f_s$:
Как видно, при изменении модулирующей частоты, спектр не сдвигается, но изменяется расстояние между центральной
(несущей) частотой и боковыми (модулирующими) частотами.
Ширина спектра АМ сигнала равна удвоенной частоте модулирующего сигнала.
In [5]:
N = 1024
# Create AM-signal
fs = [5, 12, 23]
fс = 60
# Modulation frequency
# Carrier frequency
sig = [signal_am(amp=1.0, km=0.45, fc=fс, fs=i, period=N) for i in fs]
# Calculate FFT
sft = np.abs(rfft(sig, axis=1)) / N / 0.5
plt.figure(figsize=(12, 6), dpi=80)
for i, freq in enumerate(fs):
plt.subplot(len(fc), 2, 2*i+1)
if i == 0:
plt.title('AM-signal')
plt.plot(sig[i])
plt.xlim([0, N-1])
plt.grid(True)
plt.subplot(len(fs), 2, 2*i+2)
if i == 0:
plt.title('Spectrum')
plt.plot(sft[i])
plt.xlim([0, N//2-1])
plt.grid(True)
plt.tight_layout()
Наконец, посмотрим, как меняется форма и спектр АМ-сигнала при изменении параметра коэффициента модуляции
$k_m$:
Как видно, при изменении коэффициента модуляции, спектр сигнала остается на месте. Меняется только уровень боковых
составляющих. Заметим, что при $k_m > 1$ возникает так называемая избыточная модуляция (перемодуляция).
Максимальное значение коэффициента модуляции, при котором не возникает перемодуляции АМ-сигнала $k_m = 1$.
Амплитуда центральной гармоники равна амплитуде несущего колебания: $A_c = A_o$.
Амплитуда боковых составляющих равна $A_m = \frac{A_o\cdot m}{2}$
In [6]:
N = 1024
# Create AM-signal
fs = 6
fс = 40
km = [0.35, 0.85, 5]
# Modulation frequency
# Carrier frequency
# modulation coeff.
sig = [signal_am(amp=1.0, km=i, fc=fс, fs=fs, period=N) for i in km]
# Calculate FFT
sft = np.abs(rfft(sig, axis=1)) / N / 0.5
plt.figure(figsize=(12, 6), dpi=80)
for i, freq in enumerate(km):
plt.subplot(len(km), 2, 2*i+1)
if i == 0:
plt.title('AM-signal')
plt.plot(sig[i])
plt.xlim([0, N-1])
plt.grid(True)
plt.subplot(len(km), 2, 2*i+2)
if i == 0:
plt.title('Spectrum')
plt.plot(sft[i])
plt.xlim([0, N//2-1])
plt.grid(True)
plt.tight_layout()
Среди класса сигналов с амплитудной модуляцией есть ряд сигналов, которые лучше используют энергетические
характеристики сигнала. Например, сигналы с подавленной несущей (балансная модуляция) относятся к классу АМсигналов, и позволяют производить передачу сообщений более экономно в плане энергетических спектральных
характеристик. Также есть амплитудная модуляция с одной боковой полосой (single-sideband modulation, SSB), нашедшая
применение в профессиональной и любительской радиосвязи. В свою очередь, модуляция с одной боковой полосой
разделяется на модуляцию с верхней (upper sideband, USB) и нижней боковой полосой (lower sideband, LSB).
Угловая модуляция
Под термином угловая модуляция понимается модуляция по фазе или по частоте (математически можно представить, что
изменяется "угол" тригонометрической функции). Таким образом, сигналы с угловой модуляцией делятся на частотномодулированные (ЧМ) сигналы и фазо-модулированные (ФМ) сигналы.
При фазовой модуляции значение угла фазы изменяется пропорционально информационному сообщению, при частотной
модуляции информационный сигнал управляет частотой несущего колебания. В обоих случаях амплитуда сигнала остается
неизменной.
Сигналы с угловой модуляцией применяются в музыкальных синтезаторах, в телевещании для передачи звука и сигнала
цветности, а также для качественной передачи звуковых сообщений (например, радиовещание в УКВ диапазоне). Высокое
качество в сравнении с АМ-сигналами достигается за счет лучшего использования частотного диапазона передаваемого
сообщения. Иными словами, в полосе сигнала укладывается больше информации, чем в сигналах с АМ-модуляцией. Кроме
того, информационное сообщение сигналов с угловой модуляцией менее подвержено серьёзному влиянию окружающей
среды при передаче, поскольку информация содержится не в амплитуде. Очевидно, что в процессе распространения сигнал
чаще претерпевает изменения амплитуды, чем изменения фазы или частоты.
Формула сигнала с угловой модуляцией:
$s(t) = A \cdot cos(2\pi f_c t + k u_{m}(t)) $
В случае модуляции гармоническим колебанием:
$s(t) = A_c \cdot cos(2\pi f_c t + \frac{A_{m} f_{\Delta}}{f_{m}} sin(2\pi f_s t)) $,
где
$A_{c}$ – амплитуда несущего колебания,
$A_{m}$ – амплитуда модулирующего колебания,
$f_{c}$ – частота несущего сигнала,
$f_{m}$ – частота модулирующего (информационного) сигнала,
$f_{\Delta}$ – девиация частоты.
Отношение девиации частоты к частоте модулирующего колебания называют индексом частотной модуляции. Как и в
случае с АМ-колебанием, модулирующая частота - низкочастотная относительно частоты несущей.
Создадим упрощенную python-функцию ЧМ-сигнала:
$A_{mp}$ – амплитуда колебания,
$f_{c}$ – частота несущего сигнала,
$f_{m}$ – частота модулирующего сигнала,
$k_{d}$ – девиация частоты.
In [7]:
def signal_fm(amp=1.0, kd=0.25, fc=10.0, fs=2.0, period=100):
"""
Create Frequency modulation (FM) signal
Parameters
---------amp : float
Signal magnitude
kd : float
Frequency deviation, kd < period/4,
Frequency deviation, kd < period/4,
e.g. fc = 0, fs = 1, kd = 16
fc : float
Carrier frequency
fs : float
Signal frequency
period : integer
Number of points for signal (same as period)
"""
tt = 2.0 * np.pi * np.linspace(0, 1, period)
return amp * np.cos(fc * tt + kd/fs * np.sin(fs * tt))
Построим сигналы с частотной модуляцией в зависимости от значения девиации частоты:
In [8]:
N = 1024
fs = 5
fс = 65
kd = [3, 23, 40]
# Modulation frequency
# Carrier frequency
# modulation coeff.
sig = [signal_fm(amp=1.0, kd=i, fc=fс, fs=fs, period=N) for i in kd]
# Calculate FFT
sft = np.abs(fft(sig, axis=1))
plt.figure(figsize=(12, 6), dpi=80)
for i, freq in enumerate(kd):
plt.subplot(len(kd), 2, 2*i+1)
if i == 0:
plt.title('FM-signal')
plt.plot(sig[i])
plt.xlim([0, N//2-1])
plt.grid(True)
plt.subplot(len(kd), 2, 2*i+2)
if i == 0:
plt.title('Spectrum')
plt.plot(sft[i])
plt.xlim([0, N//2-1])
plt.grid(True)
plt.tight_layout()
Модулирующий и частотно-модулированный сигналы
In [9]:
N = 512
sig = signal_fm(amp=1.0, kd=15, fc=40, fs=4, period=N)
sig = signal_fm(amp=1.0, kd=15, fc=40, fs=4, period=N)
smd = np.sin(4 * 2.0 * np.pi * np.linspace(0, 1, N))
plt.figure(figsize=(12, 6), dpi=80)
plt.subplot(2, 1, 1)
plt.title('Modulation signal')
plt.plot(smd)
plt.xlim([0, N//2-1])
plt.grid(True)
plt.subplot(2, 1, 2)
plt.title('FM-signal')
plt.plot(sig)
plt.xlim([0, N//2-1])
plt.grid(True)
Как видно, чем больше девиация по частоте, тем шире спектр сигнала с угловой модуляцией.
Линейная частотная модуляция
Сигналы с линейной частотной модуляцией (ЛЧМ) сигналы - это класс сигналов с частотной модуляцией, при которой
частота несущего сигнала изменяется по линейному закону.
В задачах радиолокации часто требуется получить заданную разрешающую способность по дальности, определяемую как
минимальное расстояние между двумя целями, при которой дальность до каждой из целей определяется раздельно. Эта
величина обратно пропорциональна ширине спектра сигнала. Следовательно необходимо увеличивать ширину спектра для
уменьшения значения разрешающей способности.
Увеличение ширины спектра сигнала можно достичь с помощью уменьшения длительности сигнала. Но это в свою очередь
приводит к уменьшению энергии сигнала и дальности обнаружения. Компромиссное решение - использование сигналов
сложной формы, в частности - ЛЧМ-сигналов.
Функция изменения частоты линейна:
$ f(t) = f_{0} + k t $
где:
$ f_{0} = (F_{max} + F_{min}) / 2 $ - центральное значение несущей частоты.
$ k = (F_{max}-F_{min}) / T_{c} $ - коэффициент модуляции
$ T_c $ - длительность сигнала
Основное применение ЛЧМ-сигналов - задачи радиолокации. Широкополосные ЛЧМ сигналы позволяют обеспечить
высокую разрешающую способность по дальности без уменьшения длительности посылаемых (зондируемых) импульсов.
Основное понятие ЛЧМ сигнала - это база сигнала, которая характеризуется произведением ширины спектра и длительности
импульса сигнала.
импульса сигнала.
$ \beta = \Delta f \cdot \tau $
Если база ЛЧМ сигнала $ \beta >> 1 $, то его спектр стремится к прямоугольному виду, а фазовый спектр имеет
квадратичную зависимость от частоты. Известно, что при прохождении через согласованный фильтр происходит сжатие
ЛЧМ-сигнала. Это в свою очередь порождает узкий корреляционный пик большой амплитуды.
Для сжатия ЛЧМ сигналов часто применяется операция быстрой свёртки, которая строится на базовых функциональных
блоках цифровой обработки. Это ядра быстрого преобразования Фурье (БПФ), комплексные перемножители и блоки памяти,
содержащие набор коэффициентов опорной функции.
Как видно, базовые операции цифровой обработки применимы и к задачам радиолокации.
ЛЧМ сигнал опишем формулой:
$ s(t) = A cos(2\pi f_{0}t + \pi\beta t^{2}) $
где
$ A $ - амплитуда сигнала.
$ f_{0} $ - начальное значение частоты,
$ \beta $ - коэффициент ЛЧМ-модуляции,
Соответствующая функция на python:
In [10]:
def signal_chirp(amp=1.0, freq=0.0, beta=0.25, period=100, **kwargs):
"""
Create Chirp signal
Parameters
---------amp : float
Signal magnitude
beta : float
Modulation bandwidth: beta < N for complex, beta < 0.5N for real
freq : float or int
Linear frequency of signal
period : integer
Number of points for signal (same as period)
kwargs : bool
Complex signal if is_complex = True
Modulated by half-sine wave if is_modsine = True
"""
is_complex = kwargs.get('is_complex', False)
is_modsine = kwargs.get('is_modsine', False)
t = np.linspace(0, 1, period)
tt = np.pi * (freq * t + beta * t ** 2)
if is_complex is True:
res = amp * (np.cos(tt) + 1j * np.sin(tt))
else:
res = amp * np.cos(tt)
if is_modsine is True:
return res * np.sin(np.pi * t)
return res
Построим график ЛЧМ-сигнала для разных значений параметра $\beta$. Как видно, при увеличении параметра, расширяется
спектр сигнала.
In [11]:
N = 1024
beta = [25, 49, 157]
schirp = [signal_chirp(amp=1, freq=10, beta=i, period=N) for i in beta]
# Calculate FFT
sft = np.abs(fft(schirp, axis=1))
plt.figure(figsize=(12, 6), dpi=80)
plt.figure(figsize=(12, 6), dpi=80)
for i, freq in enumerate(kd):
plt.subplot(len(kd), 2, 2*i+1)
if i == 0:
plt.title('Chirp')
plt.plot(schirp[i])
plt.xlim([0, N-1])
plt.grid(True)
plt.subplot(len(kd), 2, 2*i+2)
if i == 0:
plt.title('Spectrum')
plt.plot(sft[i])
plt.xlim([0, N//2-1])
plt.grid(True)
plt.tight_layout()
Комплексный ЛЧМ-сигнал
Зачастую ЛЧМ-импульсы дополнительно модулируются синусоидальной огибающей для достижения лучших спектральных
характеристик. Также можно использовать комплексный ЛЧМ-сигнал.
In [12]:
N = 2048
beta = 88
schirp = signal_chirp(amp=1, freq=0, beta=beta, period=N, is_complex=True)
# Calculate FFT
sft = np.abs(fftshift(fft(schirp)))
plt.figure(figsize=(12, 4), dpi=80)
plt.subplot(1, 2, 1)
plt.title('Chirp')
plt.plot(np.real(schirp))
plt.plot(np.imag(schirp))
plt.plot(np.linspace(0, 1, N//2), '--', linewidth='2.5')
plt.xlim([0, N//2])
plt.grid(True)
plt.subplot(1, 2, 2)
plt.title('Spectrum')
plt.plot(sft)
plt.xlim([N//2-beta, N//2+2*beta])
plt.grid(True)
plt.tight_layout()
Манипуляция
В теории передачи дискретных сообщений процесс преобразования битового потока в последовательность элементов
сигнала называется цифровой модуляцией или манипуляцией. Иными словами, для дискретных (цифровых) систем процесс
модуляции сигналов называется манипуляцией. Как и в случае с аналоговыми сигналами, цифровые гармонические
последовательности могут быть манипулированы по амплитуде, фазе и частоте.
При низкочастотной модуляции (baseband modulation) эти сигналы имеют вид импульсов заданной формы. Для полосовой
модуляции (bandpass modulation) импульсы заданной формы модулируют синусоиду, называемую несущей (carrier
frequency).
Виды манипуляций:
Амплитудная (и квадратурная амплитудная) манипуляция (АМн и КАМ),
Частотная манипуляция (ЧМн),
Фазовая манипуляция (ФМн).
Амплитудная манипуляция (Amplitude-shift keying, ASK) - преобразование сигнала, при котором скачкообразно меняется
амплитуда несущего колебания. Наиболее распространена квадратурная амплитудная манипуляция высоких порядков
(Quadrature amplitude modulation, QAM).
Частотная манипуляция (Frequency-shift keying, FSK) - преобразование сигнала, при котором скачкообразно меняется
частота несущего сигнала в зависимости от значения цифрового сообщения.
Фазовая манипуляция (Phase-shift keying, PSK) - процесс преобразования сигнала, при котором скачкообразно изменяется
фаза несущего колебания. Существует большой класс сигналов с фазовой манипуляцией: двоичная (BPSK, QPSK, 8-PSK и
т.д.)
Амплитудная манипуляция
При квадратурной амплитудной манипуляции изменяется амплитуда и фаза сигнала. Это позволяет увеличить количество
передаваемой информации. ДЛя представления манипулированных сигналов вводится понятие сигнального созвездия
(constellation diagram). Оно представляет все возможные значения комплексной амплитуды манипулированного сигнала в
виде точек на комплексной плоскости.
В идеале импульсы амплитудной манипуляции - прямоугольные, но на практике используются более гладкие импульсы в
связи с тем, что для обеспечения строго прямоугольных модулирующих импульсов требуется недопустимо широкая полоса
спектра сигнала.
Для обеспечения высокой скорости передачи и качественного уровня достоверности приёма использование сигналов только
с амплитудной модуляцией - недостаточно. В связи с этим, на практике стали широко применяться сигналы с модуляцией по
нескольким параметрам. Наиболее широкое распространение получили сигналы с амплитудно-фазовой манипуляцией,
которые также квадратурным амплитудно-модулированными сигналами (КАМ). Они получаются путём комбинирования
методов амплитудной и фазовой манипуляции, что позволяет увеличить количество передаваемых бит в одном символе, и
повысить помехоустойчивость по сравнению с использованием только АМн или ФМн колебаний.
Ниже приведен пример простейшей амплитудной манипуляции гармонического сигнала. Последовательность символов
задана с помощью генератора случайных чисел нулей и единиц.
In [13]:
N = 64
# Random array of ones and zeros
# Random array of ones and zeros
np.random.seed(6)
mod_rnd = np.random.randint(0, 2, 40)
# Repeat number of ones and zeros
mod_ask = np.repeat(mod_rnd, repeats=N)
# ASK signal
M = mod_ask.size
sig_ask = mod_ask * np.sin(64 * 2.0 * np.pi * np.linspace(0, 1, M))
# PLot results
plt.figure(figsize=(12, 6), dpi=80)
plt.subplot(2, 1, 1)
plt.title('Digital signal')
plt.plot(mod_ask, color='C0', linewidth=2.0)
plt.xlim([0, M-1])
plt.grid(True)
plt.subplot(2, 1, 2)
plt.title('ASK-signal')
plt.plot(mod_ask, '--', color='C0', linewidth=2.0)
plt.plot(sig_ask, '-', color='C1', linewidth=2.0)
plt.xlim([0, M-1])
plt.grid(True)
plt.tight_layout()
Частотная манипуляция
Для ЧМн сигналов варьируемым параметром выступает частота, причем амплитуда и начальная фаза остаются
неизменными. Логическим уровням '0' и '1' ставятся в соответствие два значения частоты. Их выбирают из условия
ортогональности на интервале длительности сигнала T.
Принцип формирования ЧМн сигналов достаточно прост. Есть несколько генераторов, формирующих колебания на разных
частотах. Модулирующий цифровой сигнал переключает мультиплексор выбора сигнала с одного из генераторов. Таким
образом, формируется посылка в виде сигналов разных частот. Например, для двоичной частотной манипуляции
используется две частоты. Две позиции кодируются однобитовым числом: "0" соответствует частоте с первого генератора,
"1" - частоте со второго генератора.
In [14]:
N = 200
# Random array of ones and zeros
np.random.seed(1)
mod_rnd = np.random.randint(0, 2, 20)
# Repeat number of ones and zeros
mod_fsk = np.repeat(mod_rnd, repeats=N)
# FSK signal
M = mod_fsk.size
M = mod_fsk.size
mod_frq = np.zeros(M)
# Set freq 'bits' (0, 1)
mod_frq[mod_fsk == 0] = 10
mod_frq[mod_fsk == 1] = 50
sig_fsk = np.sin(mod_frq *
2.0 * np.pi * np.linspace(0, 1, M))
# PLot results
plt.figure(figsize=(12, 6), dpi=80)
plt.subplot(2, 1, 1)
plt.title('Digital signal')
plt.plot(mod_fsk, color='C0', linewidth=2.0)
plt.xlim([0, M-1])
plt.grid(True)
plt.subplot(2, 1, 2)
plt.title('FSK-signal')
plt.plot(mod_fsk, '--', color='C0', linewidth=2.0)
plt.plot(sig_fsk, '-', color='C1', linewidth=2.0)
plt.xlim([0, M-1])
plt.grid(True)
plt.tight_layout()
Фазовая манипуляция
Для таких сигналов информационным параметром выступает фаза, причем для упрощения реализации цифровых систем
значению логической '1' соответствует нулевая начальная фаза, а '0' – противоположное значение $\pi$ (для двухбитовой
фазовой манипуляции). Передача логических уровней выполняется на одной несущей частоте. В литературе такие ФМн
колебания часто называют ФМ-2 сигналами (BPSK, Binary phase-shift keying), где 2 означает количество вариаций фазы.
Следует отметить, что ФМ-2 сигналы не позволяют получить высокие скорости передачи информации по каналу связи с
ограниченной полосой, но являются наиболее помехоустойчивыми к шумам. Простейший ФМ-2 сигнал не нашел
практического применения из-за слишком широкой полосы и возможного случайного скачка фазы на $\pi$, что называется
"режим обратной работы".
In [15]:
N = 200
# Random array of ones and zeros
np.random.seed(1)
mod_rnd = np.random.randint(0, 2, 25)
# Repeat number of ones and zeros
mod_psk = np.repeat(mod_rnd, repeats=N)
# PSK signal
M = mod_psk.size
sig_psk = np.sin(25 * 2.0 * np.pi * np.linspace(0, 1, M) + np.pi * mod_psk)
# PLot results
plt.figure(figsize=(12, 6), dpi=80)
plt.subplot(2, 1, 1)
plt.title('Digital signal')
plt.plot(mod_psk, color='C0', linewidth=2.0)
plt.xlim([0, M-1])
plt.grid(True)
plt.subplot(2, 1, 2)
plt.title('PSK-signal')
plt.plot(mod_psk, '--', color='C0', linewidth=1.5)
plt.plot(sig_psk, '-', color='C1', linewidth=2.0)
plt.xlim([0, M-1])
plt.grid(True)
plt.tight_layout()
Основной недостаток сигналов с однобитовой манипуляцией - нерациональное распределение энергии в частотном
диапазоне. Из-за скачкообразного изменения варьируемых параметров на границах переходов символов, большая часть
энергии содержится за пределами главного лепестка спектра, что приводит к внеполосному излучению.
Чтобы избежать этого, стали применяться сигналы с непрерывной фазой (СНФ). Существует три основных метода, с
помощью которых строятся сигналы с относительно плавным изменением параметров сигнала на границах перехода:
амплитудный, фазовый и комбинация из двух предыдущих – амплитудно-фазовый. Амплитудный метод позволяет
уменьшить резкое изменение уровня сигнала в момент скачка фазы колебания до нуля. Фазовый метод исключает прыжки
фазы, при которых наиболее вероятна ситуация ложного перехода. Амплитудно-фазовый метод сочетает в себе свойства
двух предыдущих, причем амплитудный метод ограничивает логические уровни, сглаживая шумы, а фазовый предназначен
для подавления боковых лепестков спектра.
Детальное исследование представленных выше сигналов, а также рассмотрение более сложных сигналов и видов
модуляции и манипуляции выходит за рамки этого курса.
Цифровая обработка сигналов - 6
Title
Digital signal processing
Author
Alexander Kapitanov
Contact
sallador@bk.ru
Project lang
Python
Packages
numpy, scipy, matplotlib
License
GNU GPL 3.0
Введение
Перед вами обучающий материал по основам цифровой обработки сигналов с использованием средств языка
программирования Python. Предполагается, что читатель имеет базовые знания из области высшей математики, а также
владеет языком Python и хотя бы поверхностно знает различные python-библиотеки - numpy/scipy, matplotlib и другие.
Для пользователей MATLAB / GNU Octave освоение материала с точки зрения программного кода не составит труда,
поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из python-библиотек.
Сигналы и фильтры
В предыдущих разделах мы ввели понятие сигнала, спектра, Z-формы. В процессе прохождения сигнала от источника до
получателя, последовательность данных претерпевает изменения и преобразования. Эти преобразования обусловлены
прохождением сигнала через различные вычислительные устройства, реализующие ту или иную математическую задачу. В
задачах цифровой обработки сигналов данные проходят через цифровые цепи, которые называются фильтрами.
Цифровые фильтры, как и аналоговые, обладают различными характеристиками. Как правило, эти характеристики
выражаются в частотном представлении - амплитудно-частотная и фазо-частотная характеристики фильтра. Цифровые
фильтры используются в основном для улучшения качества сигнала - для выделения сигнала из последовательности
данных, либо для ухудшения нежелательных сигналов - для подавления определенных сигналов в приходящих
последовательностях отсчетов.
На сегодняшний день цифровые фильтры применяются практически везде, где требуется обработка сигналов. Даже
примитивные математические операции (умножение и сложение) можно представить в виде цифрового фильтра.
Следовательно, всё устройства, которые нас окружают (компьютеры, телефоны, телевизоры, и т.д.) содержат ряд тех или
иных цифровых фильтров. Например, в телевизорах используются фильтры для преобразования выводимого изображения.
Настройка яркости - по сути фильтрация изображения.
Таким образом, цифровые фильтры применяются в широком спектре задач обработки сигналов: спектральный анализ,
обработка аудио- и видео-данных, обработка речи, движения и т.д. Применительно к задачам ЦОС, фильтр - это некоторая
математическая система, которая изменяет форму входного сигнала (амплитуду, фазу, частоту).
Преимущества цифровых фильтров:
Возможность получения характеристик, которые невозможно получить аналоговыми методами (например, точную
линейную ФЧХ).
Цифровые фильтры стабильнее к внешним изменениями среды (температура, влажность, давление). Следовательно,
цифровые фильтры не требуют постоянной калибровки.
Простота перестройки частоты обработки сигнала.
В зависимости от скорости обработки и частоты сигнала, один фильтр может одновременно обрабатывать данные с
нескольких каналов.
Данные до и после фильтра можно сохранить на любой носитель. Аналоговые сигналы записать сложнее (в любом
случае требуется перевод в цифровую форму и обратно).
Низкая потребляемая мощность и низкая стоимость относительно аналоговых фильтров.
Повышенная точность вычисления (современные цифровые устройства не ограничены в точности вычисления).
Простота проектирования фильтров со сложными частотными характеристиками.
В задачах биомедицины применение аналоговых фильтров на очень низких частотах затруднительно, в отличие от
цифровых фильтров.
Недостатки цифровых фильтров
Ограниченная разрядность. В процессе вычисления в цифровых фильтрах с конечной разрядностью накапливаются
шумы квантования, шумы округления. Одна из типовых задач ЦОС - выбор подходящей разрядность фильтра.
Ограничение скорости обработки. Как правило, аналоговые фильтры способны обрабатывать данные на очень
больших частотах. Цифровые фильтры ограничены частотой дискретизации.
Аппаратное обеспечение. Поскольку реальные сигналы в природе - непрерывные, для их обработки используются
АЦП и ЦАП. От характеристик этих устройств также зависит качество получаемых цифровых (аналоговых) сигналов.
Сигналы и фильтры в зависимости способа представления характеризуются разными функциями:
Сигнал
Фильтр
отсчеты x(n)
импульсная характеристика h(n)
z-форма X(z)
передаточная функция H(z)
спектральная плотность X(ejϕ)
частотная характеристика H(ejϕ)
модуль спектра | X(ejϕ) |
АЧХ | H(ejϕ) |
аргумент спектра arg(X(ejϕ))
ФЧХ arg(H(ejϕ))
Импульсной характеристикой h(n) называется реакция цепи на входное воздействие в виде функции Дирака (δ-функции).
Она отражает влияние цепи на сигнал. В цифровых устройствах импульсная характеристика может быть конечной или
бесконечной. Следовательно, существует два класса цифровых фильтров - с конечной импульсной характеристикой и с
бесконечной импульсной характеристикой.
Цифровые фильтры описываются разностным уравнением:
1
y(k) =
a0
N
M
⋅ (∑k =0 bkx(n − k) − ∑k =0 aky(n − k))
В этой формуле y(k) - выходное воздействие или отсчеты на выходе цифрового фильтра. x(k) - входной сигнал. ak и bk множители (коэффициенты) цифровых звеньев на входе и выходе. Эти множители также называются коэффициентами
числителя и знаменателя передаточной характеристики фильтра.
Передаточная характеристика фильтра имеет следующий вид:
b 0 +b 1 z − 1 + . . . +b Nz − N
B ( z)
H(z) =
A ( z)
=
1 +a 1 z − 1 + . . . +a Mz − M
где N и M - количество линий задержки для входного и выходного сигналов. В общем виде это формула БИХ-фильтра. Если
знаменатель равен единице, то формула соответствует выражению для КИХ-фильтра (цифровой фильтр без обратной
связи).
По реализации цифрового фильтра различают два метода: аппаратный и программный. Аппаратные фильтры реализуются
на ПЛИС или специализированных сигнальных процессорах. Программные фильтры реализуются с помощью программ,
выполняемых процессором или микроконтроллером.
Фильтры могут быть рекурсивными, когда выходной отсчет зависит от предыдущих выходных и от входного, т.е. в схеме
присутствует обратная связь, или нерекурсивными, когда выходной отсчет зависит только от входных отсчетов.
БИХ и КИХ фильтры
КИХ фильтр (англ. FIR — «finite impulse response») - это цифровой фильтр с конечной импульсной характеристикой.
Импульсная характеристика такого фильтра ограничена во времени, то есть имеет счётное число коэффициентов. Начиная
с определенного момента времени она становится равной нулю. Если на вход КИХ-фильтра подать единичный импульс, на
выходе фильтра будет конечное число отсчетов. Как правило, ФЧХ фильтра с конечной импульсной характеристикой линейна
В общем случае, КИХ-фильтры реализуются без обратных связей, то есть они нерекурсивные. Однако, с помощью
математических преобразований можно привести фильтр к рекурсивной форме.
Разностное уравнение КИХ-фильтра:
N−1
y(n) = ∑k =0 h(k)x(n − k)
где
y(n) - выходной дискретный сигнал (сумма взвешенных входных импульсов),
x(n) - входной дискретный сигнал (последовательность отсчётов),
h(n) - коэффициенты импульсной характеристики фильтра,
N - длина (порядок) фильтра.
Передаточная характеристика КИХ-фильтра:
N−1
H(z) = ∑k =0 h(k)z −k
Напомним, что операция z −k - задержка последовательности на k-отсчетов.
БИХ фильтр (англ. IIR — «infinite impulse response») - это цифровой фильтр с бесконечной во времени импульсной
характеристикой, то есть имеет очень большое или бесконечное число коэффициентов. БИХ фильтры также называют
рекурсивными в связи с тем, что при их реализации используются обратные связи (сигнал с выхода фильтра через
элементы задержки поступает на фильтр и вносит изменения сам в себя). Передаточная функция БИХ-фильтра имеет
дробно-рациональный вид. Основные известные БИХ-фильтры: фильтр Чебышева, Баттерворта, Калмана, Бесселя и т.д.
Разностное уравнение БИХ-фильтра:
N
M
y(n) = ∑k =0 bkx(n − k) − ∑k =0 aky(n − k)
или
y(n) = b0 x(n) + b1 x(n − 1) + bMx(n − M) + . . . − a1 y(n − 1) − a2 y(n − 2) − . . . − aNy(n − N)
Как видно, выходной сигнал за счет обратных связей влияет сам на себя.
Передаточная характеристика БИХ-фильтра:
b 0 +b 1 z − 1 + . . . +b Nz − N
B ( z)
H(z) =
A ( z)
=
1 +a 1 z − 1 + . . . +a Mz − M
В отличие от КИХ фильтров, БИХ фильтры не всегда являются устойчивыми. Для устойчивости цифрового БИХ фильтра
требуется, чтобы все полюса передаточной характеристики по модулю были строго меньше единицы (то есть лежали внутри
единичной окружности на z-плоскости).
Порядок фильтра – максимальная степень в выражении передаточной функции H(z).
Передаточная функция может быть реализована при помощи различных структурных схем. Наиболее распространены
последовательные и параллельные структурные схемы. Если передаточную дробно-рациональную функцию рекурсивного
фильтра представить в виде произведения передаточных функций первого и второго порядка, то структурная схема будет
последовательной. Если передаточную функцию рекурсивного фильтра представить в виде суммы передаточных функций
первого и второго порядка, то структурная схема будет параллельной.
Каноническая и прямая схема
Структурную схему цифрового фильтра можно представить в прямой и канонической форме. Цифровые фильтры могут быть
реализованы с использованием трех цифровых элементов: умножитель, сумматор и блок задержки. Очевидно, что
умножители требуются для умножения отсчётов на коэффициенты ak и ak, а сумматор объединяет полученные результаты.
Структурная схема нерекурсивного КИХ-фильтра, согласно уравнению:
Количество линий задержки всегда на единицу меньше, чем число коэффициентов или порядок фильтра. Импульсная
характеристика КИХ фильтра совпадает с набором коэффициентов этого фильтра.
Структурная схема БИХ-фильтра выглядит несколько сложнее из-за наличия обратных связей:
Количество линий задержки БИХ фильтра равно N + M.
Структурная схема в каноническом виде минимизирует количество линий задержки, поскольку использует общие линии
задержки. Входной сумматор - с обратными связями. Выходной сумматор - обобщает результат. Преобразование от одной
формы к другой достаточно просто и тривиально
Выбор фильтра
Перед разработчиками цифровых устройств часто встает задача выбора типа фильтра. Выбор между КИХ и БИХ фильтрами
производится по следующим критериям:
Фазовая характеристика БИХ фильтра - нелинейна. КИХ фильтры могут иметь строго линейную фазовую
характеристику. Это означает, что такой фильтр не вносит искажений в форму сигнала.
КИХ фильтры - устойчивы, т.к. реализуются по нерекурсивной форме. БИХ фильтры могут быть неустойчивыми.
В реальных задачах стоит вопрос о выборе разрядности данных (округление, квантование). Эти процессы вносят
меньший вклад в устройства без обратных связей, то есть в КИХ фильтры.
Реализация АЧХ сложной формы или максимально прямоугольной формы потребует значительного числа
коэффициентов КИХ фильтра. БИХ фильтры с этой задачей справляются лучше.
коэффициентов КИХ фильтра. БИХ фильтры с этой задачей справляются лучше.
У КИХ фильтров, как правило, нет эквивалентных аналоговых фильтров.
КИХ фильтры позволяют легко получать требуемые характеристики (уровень затухания, неравномерности в полосе
пропускания, частота среза и т.д.)
БИХ фильтры существенно экономнее по количеству операций умножения, сложения и количеству линий задержки.
Пример
Пусть есть фильтр, который описывается следующей передаточной функцией:
b 0 +b 1 z − 1 +b 2 z − 2
H(z) =
1 +a 1 z − 1 +a 2 z − 2
,
где
N = 2, M = 2
bi = {0.1, − 0.6, 0.5}
ai = {1, 0.7, − 0.2}
Количество разностных уравнений для конкретного фильтра равно числу сумматоров в схеме. Зная разностное уравнение
можно найти импульсную характеристику фильтра: на вход подается единичный импульс (начальные условия нулевые)
Найдем импульсную характеристику средствами Python. С помощью функции lfilter(b, a, x) моделируется процесс
прохождения сигнала x через цифровой фильтр, с коэффициентами передаточной характеристики a и b .
In [1]:
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import lfilter, freqz, butter, firls, remez, firwin, firwin2, group_delay
from scipy.fftpack import fft, fftshift
%matplotlib inline
In [2]:
N = 128
# Delta-function
x = np.ones(N)
x[0] = 1
#
#
b
a
Input signal:
h(z) = [b0 + b1*z^(-1) + b2*z^(-2)] / a0 + a1*z^(-1) + a2*z^(-2)
= [0.1, -0.6, 0.5]
= [1, 0.7, -0.2]
y1 = lfilter(b, a, x)
plt.figure(figsize=(12, 4), dpi=80)
plt.title('Impulse responce')
plt.stem(y1, use_line_collection=True, basefmt='C0')
plt.xlim([-0.5, N-0.5])
plt.grid(True)
Если фильтр устойчив, то отсчеты y(n) уменьшаются по величине со временем .
Как видно на предыдущем графике - рассчитанный БИХ-фильтр - устойчив.
БИХ-фильтры (SCIPY / MATLAB)
Ниже представлен список основных функций БИХ-фильтров для реализации в python с помощью пакета сигналов scipy.signal . Большинство функций имеют аналогичные MATLAB-прототипы.
Function
Description
iirdesign(wp, ws, gpass,
gstop[, analog, ...])
Функция для полного расчёта цифрового фильтра. Возвращает коэффициенты a, b , нули и
полюсы и т.д.
iirfilter(N, Wn[, rp, rs,
btype, analog, ...])
Реализация БИХ-фильтра выбранного типа и N-порядка. Возвращает коэффициенты a, b , нули и
полюсы и т.д.
butter(N, Wn[, btype, analog,
output, fs])
Фильтр Баттерворта. Реализует фильтр N-порядка и возвращает коэффициенты фильтра.
buttord(wp, ws, gpass, gstop[,
analog, fs])
Возвращает минимальный порядок, требуемый для реализации фильтра
cheby1(N, rp, Wn[, btype,
analog, output, fs])
Фильтр Чебышева 1 типа. Реализует фильтр N-порядка и возвращает коэффициенты фильтра.
cheb1ord(wp, ws, gpass, gstop[,
analog, fs])
Возвращает минимальный порядок, требуемый для реализации фильтра
cheby2(N, rs, Wn[, btype,
analog, output, fs])
Фильтр Чебышева 2 типа. Реализует фильтр N-порядка и возвращает коэффициенты фильтра.
cheb2ord(wp, ws, gpass, gstop[,
analog, fs])
Возвращает минимальный порядок, требуемый для реализации фильтра
ellip(N, rp, rs, Wn[, btype,
analog, output, fs])
Эллиптический БИХ-фильтр (Кауэра)
ellipord(wp, ws, gpass, gstop[,
analog, fs])
Возвращает минимальный порядок, требуемый для реализации фильтра от значений входных
аргументов
bessel(N, Wn[, btype, analog,
output, norm, fs])
БИХ-фильтр Бесселя.
iirnotch(w0, Q[, fs])
Заграждающий фильтр. Возвращает коэффициенты a, b . Входные аргументы - частота сигнала,
добротность и частота среза
iirpeak(w0, Q[, fs])
Полосовой фильтр. Функция возвращает коэффициенты a, b фильтра второго порядка. Входные
аргументы - частота сигнала, добротность и частота среза
Фильтр Баттерворта
Пример реализации фильтра Баттерворта 3 порядка. Покажем, как зашумленный сигнал проходит через такой фильтр:
In [3]:
# Create input signal
t = 2 * np.pi * np.linspace(-1, 1, 500)
x = np.sin(0.25*t*t)+ 0.95*np.sin(2.0*t)
# Add some white noise
np.random.seed(1)
xn = x + np.random.randn(len(t))
# 3-order lowpass butterworth filter
b, a = butter(3, 0.2)
z = lfilter(b, a, xn)
wn = [0.01, 0.05, 0.1, 0.2]
# Calculate IIR filter
zz = np.zeros((t.size, 4))
for i in range(4):
b, a = butter(3, wn[i])
zz[:, i] = lfilter(b, a, xn)
# Plot results
plt.figure(figsize=(16, 8), dpi=80)
for i in range(4):
for i in range(4):
plt.subplot(2, 2, i+1)
plt.plot(t, xn, 'C0--', linewidth=1.5)
plt.plot(t, zz[:,i], 'C1', linewidth=2.5)
plt.xlim([-2 * np.pi, 2 * np.pi])
plt.grid(True)
plt.legend(('Signal', 'Filtered, wn = {}'.format(wn[i])), loc='lower left')
Рекурсивные КИХ фильтры
Как было сказано ранее, КИХ фильтры в основном строятся по нерекурсивной форме, однако есть способы приведения
фильтров к рекурсивному виду.
Рассмотрим следующий пример. Запишем передаточную характеристику фильтра:
H(z) = 1 + z −1 + z −2 + z −3 ,
Домножим передаточную функцию на
1 −z − 1
( 1 −z − 1
.
Пропустим математические выкладки (при желании, это можно сделать самостоятельно ввиду тривиальности
рассматриваемой задачи) и запишем результат:
1 +z − 3
H(z) =
1 −z − 1
Структурная схема такого фильтра представлена на следующем рисунке. Она состоит из двух цепей: звено без обратной
связи - дифференцирующее, а звено с обратной связью - интегрирующее (сумматор с обратной связью).
Покажем, что сигнал, прошедший через рекурсивный КИХ-фильтр, имеет аналогичные характеристики.
In [4]:
N = 25
# Delta-function
x = np.zeros(N)
x[0] = 1
#
M
#
#
b
a
Filter order - M
= 16
Input signal
h(z) = 1 + z^(-1) + ... + z^(-9)
= np.ones(M-1)
= [1]
y1 = lfilter(b, a, x)
y1 = lfilter(b, a, x)
# Change to recursive form
b = np.zeros(M)
b[0] = 1
b[M-1] = -1
a = [1, -1]
y2 = lfilter(b, a, x)
# Check the difference
np.all(y1 == y2)
Out[4]:
True
In [5]:
plt.figure(figsize=(12, 3), dpi=80)
plt.stem(y2, use_line_collection=True, basefmt='C0')
plt.xlim([-0.5, N-0.5])
plt.xlabel('Samples')
plt.suptitle('Filtered signal')
plt.grid(True)
Как видно из графика, импульсная характеристика рекурсивного фильтра равна вектору единиц. Причем, длина вектора
равна длине фильтра.
Однородные КИХ фильтры
Такие КИХ фильтры называются однородными. Для реализации этих фильтров не требуется операция умножения,
следовательно фильтр работает достаточно быстро и довольно хорошо реализуется на ПЛИС.
Недостатком таких фильтров является большой уровень боковых лепестков. Боковые лепестки АЧХ подавляются путем
каскадирования фильтров, при этом положение нулей не меняется, а меняется только соотношение уровней главного и
бокового лепестков, относительный уровень боковых лепестков уменьшается при перемножении АЧХ.
Второй недостаток однородных фильтров – непрямоугольная форма АЧХ. Чтобы сделать ее более прямоугольной,
используют корректирующий КИХ-фильтр, таким образом форма главного лепестка становится более прямоугольной, но
увеличивается уровень боковых лепестков.
В разделе, связанном с децимацией и интерполяцией сигналов мы подробнее рассмотрим эти фильтры.
С помощью функции freqz можно найти частотную характеристику фильтра.
In [6]:
N = 512
f = np.linspace(0, 1, N, endpoint=True)
b = [1, 1, 1]
plt.figure(figsize=(14, 4), dpi=80)
plt.subplot(1, 2, 1)
for i in range(4):
_, h = freqz(b, N)
_, h = freqz(b, N)
h = np.abs(h)
plt.plot(f, h/np.max(h))
plt.xlim([0, 1])
plt.grid(True)
b.append(1)
plt.xlabel('Normalized Freq')
plt.title('CIC freq responce')
plt.tight_layout()
КИХ фильтры с линейной ФЧХ
Самая важная особенность КИХ фильтров заключается в возможности получения точной линейной фазовой
характеристики.
Почему это важно? Сигнал при прохождении через фильтр подвергается различным преобразованиям. В частности,
изменяются амплитуда и фаза сигнала в зависимости от частотной характеристики фильтра (амплитудной, АЧХ и фазовой,
ФЧХ). Для многочастотных сигналов недопустимо, чтобы при прохождении цифровых узлов обработки, фаза сигнала
искажалась. Причем, если АЧХ в полосе пропускания сделать практически постоянной не составляет труда, то с ФЧХ
возникают проблемы.
Для оценки искажений фазы удобно ввести понятия фазовой и групповой задержек.
Фазовая задержка — это величина задержки для каждой из частотных компонент сигнала. Определяется как угол сдвига
фазы, деленный на частоту.
τϕ = − θ(ω)/ω
Групповая задержка — это средняя временная задержка всего многочастотного сигнала. Определяется как производная
фазы по частоте.
τg = − dθ(ω)/ω
Из формулы для групповой задержки очевидно условие линейности ФЧХ фильтра. Правило:
Если ФЧХ — линейна, то групповая задержка после взятия производной равна константе
Иными словами групповая задержка постоянна для всех частотных компонент. Таким образом, линейность фазовой
характеристики — одна из важнейших особенностей КИХ-фильтров.
Симметрия импульсной характеристики
Для обеспечения линейности ФЧХ необходимо выполнение условия симметрии импульсной характеристики (или
коэффициентов) фильтра. Проще говоря, КИХ фильтр с линейной ФЧХ — симметричен. Существует 4 типа фильтров,
отличающихся четностью порядка фильтра N и типом симметрии:
положительная симметрия, четный порядок,
отрицательная симметрия, четный порядок,
положительная симметрия, нечетный порядок,
отрицательная симметрия, нечетный порядок.
π
Например, для фильтров с отрицательной симметрией можно получить сдвиг фазы на . Такие фильтры используются для
Например, для фильтров с отрицательной симметрией можно получить сдвиг фазы на 2 . Такие фильтры используются для
проектирования дифференциаторов и преобразования Гильберта.
Огибающая импульсной характеристики КИХ фильтра строится по закону ~sin(x)/x независимо от типа фильтра (низких
частот, верхних частот, дифференциатор, полосовой или режекторный фильтр). Для решения практических задач не
приходится задумываться о том, какого типа фильтр выбран.
Проектирование КИХ фильтров
Под «расчетом FIR фильтра» в большинстве случаев понимают поиск его коэффициентов по значениям частотной
характеристики.
При создании нового цифрового КИХ фильтра инженер проходит через определенные стадии разработки:
Спецификация фильтра. Задается тип фильтра (ФНЧ, ФВЧ, полосовой, режекторный), количество коэффициентов N,
требуемая частотная характеристика, с допусками на нелинейность в полосе затухания и полосе пропускания и т. д.
Вычисление коэффициентов. Любыми доступными способами и средствами вычисляются коэффициенты фильтра,
удовлетворяющие спецификации из предыдущего пункта.
Анализ следствий конечной разрядности. На этом этапе оценивается влияние эффектов квантования на
коэффициенты фильтра, промежуточные и выходные данные.
Реализация. На этой стадии происходит разработка фильтра аппаратными или программными средствами: на
доступном языке программирования или на базе ПЛИС или специальных сигнальных процессоррах.
Этапы разработки могут быть несколько иными, но суть проектирования цифрового КИХ фильтра всегда остается та же.
Спецификация фильтра
На этой стадии инженер производит поиск компромиссных решений для реализации требуемого КИХ фильтра с нужными
параметрами. Их немного, но часто приходится жертвовать одним параметром для достижения требуемых значений по
другим величинам.
A pass — неравномерность в полосе пропускания,
A stop — уровень затухания в полосе подавления,
F pass — граничная частота полосы пропускания,
F stop — граничная частота полосы затухания,
N — порядок фильтра (количество коэффициентов фильтра).
На практике, параметры A pass и A stop задают в децибелах (дБ), а расстояние между F pass и F stop выражает ширину полосы
перехода фильтра. Логично, что значение A pass должно быть как можно меньше, A stop как можно больше, а отношение
F pass /F stop в идеале стремится к единице (идеально прямоугольная АЧХ).
Количество коэффициентов не зря вносится в спецификацию фильтра. Как будет показано далее, от порядка фильтра N и
разрядности коэффициентов зависят параметры частотной характеристики фильтра.
Вычисление коэффициентов фильтра
Существует множество методов расчета коэффициентов фильтра — метод взвешивания оконными функциями, метод
частотной выборки, различные оптимальные (по Чебышеву) методы с применением алгоритма Ремеза и т.д. Все методы
уникальны по своим особенностям и дают те или иные результаты. Для метода оконного взвешивания негативным
проявлением становится эффект Гиббса, вносящий неравномерность и выбросы в частотную характеристику фильтра
между рассчитанными точками функции. Бороться с ним можно бесконечно и безрезультатно, но на практике вводят допуски
по неравномерностям в полосе пропускания и полосе подавления.
Основным методом расчета коэффициентов для многих фильтров является модифицированный алгоритм Ремеза —
«Parks-McClellan algorithm». Это косвенный итерационный метод для нахождения оптимальных значений с Чебышевской
характеристикой фильтра. Особенность метода заключается в минимизации ошибки в полосе затухания и полосе
пропускания путем Чебышевской аппроксимации импульсной характеристики.
Вполне логично, что чем больше количество коэффициентов, тем меньше неравномерность АЧХ и тем она прямоугольнее.
От выбора метода зависит конечный результат, но все они сводятся к одним и тем же целям — минимизации выбросов в
полосе пропускания и увеличении «прямоугольности» АЧХ (при сохранении условия линейности ФЧХ).
Анализ следствий конечной разрядности
Разрядность коэффициентов — главный фактор, от которого зависит вид частотной характеристики. На примере
современных программируемых логических интегральных схемах (ПЛИ) разрядность коэффициентов может быть выбрана
любой, но реальные значения лежат пределах от 16 до 27 битов в связи с особенностью реализации вычислительных блоков
(DSP48).
Для высоких порядков фильтра часто требуется обеспечить большой динамический диапазон разрядной сетки, но если
этого не удается сделать, рано или поздно начинают проявляться ошибки квантования. Из-за ограниченной разрядности
коэффициентов модифицируется частотная характеристика, а в некоторых случаях она искажается настолько сильно, что
приходится жертвовать параметрами из частотной спецификации для достижения приемлемого результата. Так или иначе,
разрядность представления коэффициентов прямо влияет на максимально возможное затухание A stop . Поэтому при
использовании слишком ограниченной разрядной сетки коэффициентов, порой невозможно достичь желаемого подавления
даже при огромных порядках фильтра!
Реализация
С помощью современных библиотек на разных языках программирования (С++, Python, MATLAB, и т.д.) программная
реализация КИХ фильтров не составляет труда. Однако, аппаратная реализация на микроконтроллерах или ПЛИС - сложная
и нетривиальная задача.
Для реализации простейших КИХ фильтров требуются операции задержки, умножения на коэффициенты и сложение
результатов произведения. Основной узел, с помощью которого реализуется КИХ фильтр на ПЛИС — целочисленный DSP
блок. В этом блоке происходят все математические операции — перемножение входных отсчетов с коэффициентами
фильтров, задержка входного сигнала, суммирование данных. Современные узлы DSP содержат предварительный
сумматор, поэтому даже операции суммирования для фильтров с симметричной ИХ можно делать внутри этого узла.
Помимо DSP блока, фильтру нужна память для хранения коэффициентов и реализации звена задержки. Как правило, этих
ресурсов у ПЛИС более чем достаточно.
Расчет КИХ фильтров на Python
Программная реализация КИХ фильтра - поиск коэффициентов импульсной характеристики.
Расчёт КИХ фильтров производится с помощью некоторых функций из пакета scipy.signal . Перечислим все методы
проектирования КИХ фильтров и подробно расмотрим каждый из них.
Function
Description
firls(numtaps, bands, desired[,
weight, nyq, fs])
Расчет КИХ-фильтра с помощью метода наименьших квадратов
firwin(numtaps, cutoff[, width,
window, ...])
Реализация КИХ-фильтра N-порядка с применением оконной функции. Задается частота
среза.
firwin2(numtaps, freq, gain[, nfreqs,
...])
Расчет фильтра с применением оконной функции. Задается набор нормированных частот и
амплитуд на этих частотах
remez(numtaps, bands, desired[,
weight, Hz, ...])
Расчет оптимального фильтра с помощью алгоритма Ремеза
group_delay(system[, w, whole, fs])
Вспомогательная функция для расчета групповой задержки. Входные параметры - массив
коэффициентов a, b
get_window(window, Nx, fftbins=True)
[source]
Возвращает коэффициенты оконной функции требуемой длины
Расчет КИХ-фильтра с помощью метода наименьших квадратов
С помощью метода наименьших квадратов эта функция рассчитывает коэффициенты фильтра, который имеет наилучшее
приближение к требуемой частотной характеристике. Математически в процессе поиска коэффициентов интеграл от
взвешенной среднеквадратичной ошибки в пределах полосы пропускания сводится к минимуму.
Метод firls возвращает коэффициенты КИХ фильтра. Входные аргументы функции:
numtaps - порядок фильтра,
bands - монотонная неубывающая последовательность частот. Все элементы должны быть неотрицательными и
меньше или равными частоте Найквиста, заданной параметром nyq .
desired - последовательность амплитуд, содержащая требуемое усиление и ослабление на заданных значениях
частот из bands .
weight - относительный "вес" полос пропускания и подавления. Задает компромисс качества в этих полосах.
nyq или fs - частота Найквиста. Если значение не задано, по умолчанию равно единице.
Расчет КИХ-фильтра с помощью алгоритма Ремеза:
Метод remez возвращает коэффициенты КИХ фильтра. Входные аргументы идентичны предыдущему методу:
Метод remez возвращает коэффициенты КИХ фильтра. Входные аргументы идентичны предыдущему методу:
numtaps - порядок фильтра,
bands - монотонная неубывающая последовательность частот. Все элементы должны быть неотрицательными и
меньше или равными частоте Найквиста, заданной параметром nyq .
desired - последовательность амплитуд, содержащая требуемое усиление и ослабление на заданных значениях
частот из bands .
weight - относительный "вес" полос пропускания и подавления. Задает компромисс качества в этих полосах.
Hz или fs - частота Найквиста. Если значение не задано, по умолчанию равно единице.
Расчет КИХ-фильтра оконным методом:
Методы firwin и firwin2 возвращают коэффициенты КИХ фильтра.
Метод firwin
numtaps - порядок фильтра,
cutoff - частота среза относительно частоты дискретизации fs .
width - если задано значение, то показывает ширину перехода от полосы пропускания до полосы подавления.
window - оконная функция. Применяется в совокупности с методом get_window или напрямую задается название
окна.
fs - частота дискретизации или частота Найквиста. Если значение не задано, по умолчанию равно единице.
Метод firwin2
numtaps - порядок фильтра,
freq - монотонная неубывающая последовательность частот. Все элементы должны быть неотрицательными и
меньше или равными частоте Найквиста, заданной параметром fs .
gain - последовательность амплитуд, содержащая требуемое усиление и ослабление на заданных значениях частот
из freq .
window - оконная функция. Применяется в совокупности с методом get_window или напрямую задается название
окна.
fs - частота дискретизации или частота Найквиста. Если значение не задано, по умолчанию равно единице.
Оконная функция
Оконным функциям и их особенностям посвящен отдельный раздел, однако перечислим наиболее используемые оконные
функции в практических задачах: Кайзера, Гаусса, Блэкмана-Харриса, окно с плоской вершиной, Хэмминга, Ханна и т.д..
Для выбора оконной функции применяется метод get_window . Входные аргументы - название окна и длина импульсной
характеристики.
Функция возвращает одномерный массив коэффициентов - значений импульсной характеристики. Эти коэффициенты путем
операции свёртки "накладываются" на импульсную характеристику КИХ фильтра.
Групповая задержка
Это вспомогательная функция для расчета групповой задержки цифровых фильтров. Входные параметры - массив
коэффициентов a, b . Метод возвращает набор частот и соответствующий массив групповых задержек по этим частотам.
Примеры
Первый пример - использование функции firwin2 . Зададим массив нормированных частот от 0 до 1. Зададим усиление
на выбранных частотах, а также порядок фильтра. Построим импульсную характеристику.
In [7]:
N = 100
# List of freqs
lst_freqs = np.linspace(0, 1, N)
# List of gains
lst_gain = np.zeros(N)
lst_gain[0:20] = 1
# FIR filter taps
NFIR = 64
NFIR = 64
taps = firwin2(NFIR, lst_freqs, lst_gain)
plt.figure(figsize=(12, 6), dpi=80)
plt.title('Impulse responce')
plt.stem(taps, use_line_collection=True, basefmt='C0')
plt.xlim([0, NFIR-1])
plt.xlabel('Samples')
plt.grid(True)
Построим АЧХ полосового фильтра и фильтра нижних частот с помощью трех методов: firls(), remez(), firwin2() .
In [8]:
# Input parameters
fs = 10
N = 117
desired = (0, 0, 1, 1, 0, 0)
bands = (0, 1, 2, 4, 4.5, 5)
# FIR filters
fir_firls = firls(N, bands, desired, fs=fs)
fir_remez = remez(N, bands, desired[::2], fs=fs)
fir_firwin2 = firwin2(N, bands, desired, fs=fs)
# PLot results and calculate FFTs
plt.figure(figsize=(12, 5), dpi=80)
plt.title('Frequency responce')
for fir in (fir_firls, fir_remez, fir_firwin2):
freq, resp = freqz(fir)
resp = np.abs(resp)
resp /= np.max(resp) + 10**(-15)
plt.plot(freq, 20*np.log10(resp))
plt.xlim([0, np.pi])
plt.ylim([-180, 5])
plt.legend(['firls', 'remez', 'firwin2'], loc ='upper left')
plt.grid(True)
КИХ фильтр Кайзера
Покажем прохождение зашумленного гармонического сигнала через КИХ фильтр. Также добавим к этому сигналу несколько
высокочастотных гармонических сигналов разной амплитуды.
Как видно, зашумленный сигнал во временной области не поддается никакому анализу. Пропустив такой сигнал через КИХ
фильтр с заранее подобранной частотой среза, можно выделить интересуемый сигнал из помех.
Следует отметить, что все сигналы и шумы, попавшие в полосу пропускания фильтра - остаются и вносят вклад в
качественные характеристики результирующего сигнала.
In [9]:
N = 1024
# Create input signal
t = np.linspace(0, 1, N, endpoint=True)
x = 3*np.cos(2*np.pi*20*t) + 210*np.sin(2*np.pi*117*t) + 100*np.sin(2*np.pi*184*t) + 380*np.sin(2*np
.pi*281*t)
# Add some white noise
np.random.seed(1)
xn = x + 5*np.random.randn(N)
# Kaiser FIR filter
taps = 160
h = firwin(taps, 0.1, window=('kaiser', 9))
y = lfilter(h, 1, xn)
# List of input signals
lst_sig = [xn, h, y]
sig_titles = ['Noisy signal', 'FIR impulse responce', 'Filtered signal']
fft_titles = ['Input spectrum', 'FIR filter', 'Result']
plt.figure(figsize=(12, 8), dpi=80)
for i in range(3):
# Calculate FFTs
clc_fft = np.abs(fft(lst_sig[i], N))
clc_fft = 20*np.log10(10e-11+clc_fft/np.max(clc_fft))
# Plot signals
plt.subplot(3, 2, 2*i+1)
plt.plot(lst_sig[i], color='C'+str(i))
plt.title(sig_titles[i])
if (i == 2):
plt.ylim([-5, 5])
plt.xlim([taps, lst_sig[i].size//2-1])
else:
plt.xlim([0, lst_sig[i].size-1])
plt.grid(True)
plt.subplot(3, 2, 2*(i+1))
plt.plot(clc_fft, color='C'+str(i))
plt.title(fft_titles[i])
plt.xlim([0, N//2-1])
plt.grid(True)
plt.tight_layout()
На представленном выше рисунке видно, что выходной отфильтрованный сигнал с небольшими искажениями похож на
гармонический сигнал, который требовалось получить. К сожалению, добиться идеальной формы гармонического колебания
с помощью фильтрации КИХ или БИХ фильтрами - невозможно, поскольку основная задача фильтра - отсечение ненужных
спектральных компонент. Для улучшения качества фильтруемого сигнала применяются другие методы цифровой обработки
сигналов (спектральные и корреляционные).
На этом заканчивается раздел,посвященный цифровой фильтрации. В следующих разделах будут подробно описаны
оконные функции, задачи многоскоростной обработки сигналов - децимации и интерполяции, расчёт фильтра-корректора и
т.д.
Цифровая обработка сигналов - 7
Title
Digital signal processing
Author
Alexander Kapitanov
Contact
sallador@bk.ru
Project lang
Python
Packages
numpy, scipy, matplotlib
License
GNU GPL 3.0
Введение
Перед вами обучающий материал по основам цифровой обработки сигналов с использованием средств языка
программирования Python. Предполагается, что читатель имеет базовые знания из области высшей математики, а также
владеет языком Python и хотя бы поверхностно знает различные python-библиотеки - numpy/scipy, matplotlib и другие.
Для пользователей MATLAB / GNU Octave освоение материала с точки зрения программного кода не составит труда,
поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из python-библиотек.
Оконные функции
Для аналоговых сигналов или для бесконечного по времени дискретного сигнала синусоидальной формы его спектр — это
дельта-функция на частоте этого сигнала. На практике спектр реального ограниченного по времени гармонического сигнала
эквивалентен функции ~$\frac{sin(x)}{x} = sinc(x)$, а ширина главного лепестка зависит от длительности интервала анализа
сигнала $Т$. Ограничение по времени есть ни что иное как умножение сигнала на прямоугольную огибающую.
Из предыдущих лекций мы узнали, что умножение сигналов во временной области есть свертка их спектров в частотной (и
наоборот: свертка сигналов во временной области есть произведение их спектров). В связи с этим спектр ограниченного
прямоугольной огибающей гармонического сигнала эквивалентен ~$sinc(x)$. Это также связано с тем, что мы не можем
интегрировать сигнал на бесконечном интервале времени, а преобразование Фурье в дискретной форме, выраженное через
конечную сумму — ограничено по числу отсчетов.
Как правило, длина БПФ в современных устройствах цифровой обработки принимает значения $N_{FFT}$ от 8 до нескольких
миллионов точек. Ограничивая сигнал на интервале $N$, мы тем самым накладываем «окно» прямоугольной формы,
длительностью $N$ отсчётов. Следовательно, результирующий спектр — есть спектр перемноженного гармонического
сигнала и прямоугольной огибающей.
Перейдем к примеру. Построим спектр короткого гармонического сигнала при следующих параметрах: длина сигнала
$N=256$, длина БПФ - $N_{FFT}=2048$ . Для наглядности график спектра представим в логарифмическом масштабе.
In [1]:
import numpy as np
import matplotlib.pyplot as plt
from scipy.fftpack import fft, ifft, fftshift
import scipy.signal as sig
%matplotlib inline
In [2]:
# Input parameters
N = 256
NFFT = 2048
# Input signal (long: N >> NFFT)
tt = np.linspace(0, 1, N, endpoint=True)
xx = np.cos(2*np.pi*32*tt)
# Calculate FFT
sft = np.abs(fft(xx, NFFT))
slg = 20*np.log10(sft / np.max(sft))
plt.figure(figsize=(12, 6), dpi=80)
plt.subplot(2,1,1)
plt.title('Periodic signal, N = {}'.format(N))
plt.title('Periodic signal, N = {}'.format(N))
plt.xlabel('time samples')
plt.ylabel('Magnitude')
plt.plot(xx)
plt.xlim([0, N-1])
plt.grid(True)
plt.subplot(2,1,2)
plt.title('Spectrum, NFFT = {}'.format(NFFT))
plt.xlabel('freq samples')
plt.ylabel('level [dB]')
plt.plot(slg)
plt.xlim([0, NFFT//2])
plt.ylim([-40, 0])
plt.grid(True)
plt.tight_layout()
Как видно, спектр короткого гармонического сигнала в реальной жизни не эквивалентен дельта-функции, а похож на свертку
спектров прямоугольного сигнала и гармонического сигнала. На графике показана первая половина частотной области.
Итоговый сигнал - симметричен относительно половины частоты дискретизации или параметра $N_{FFT}/2$.
Напомним, что спектр прямоугольного сигнала эквивалентен выражению ~$\frac{sin(x)}{x} = sinc(x)$. То есть на частоте
сигнала на дельта-функцию как бы "накладывается спектр прямоугольного окна. При увеличении длительности
гармонического сигнала во временной области, его спектр стремится к дельта-функции на частоте этого сигнала, а влияние
прямоугольного окна снижается.
То есть, ограничение сигнала во времени приводит к наложению «окна» прямоугольной формы. На приведенном ниже
примере длительность сигнала существенно увеличена ( $N = 65536$. Как видно, спектр такого сигнала стремится к дельтафункции.
In [3]:
# Input parameters
N = 65536
# Input signal (long: N >> NFFT)
tt = np.linspace(0, 1, N, endpoint=True)
xx = np.cos(2*np.pi*32*tt)
# Calculate FFT
sft = np.abs(fft(xx, N))
slg = 20*np.log10(sft / np.max(sft))
plt.figure(figsize=(12, 6), dpi=80)
plt.subplot(2,1,1)
plt.title('Periodic signal, N = {}'.format(N))
plt.xlabel('time samples')
plt.ylabel('Magnitude')
plt.plot(xx)
plt.plot(xx)
plt.xlim([0, N-1])
plt.grid(True)
plt.subplot(2,1,2)
plt.title('Spectrum, NFFT = {}'.format(N))
plt.xlabel('freq samples')
plt.ylabel('level [dB]')
plt.plot(slg)
plt.xlim([0, N//256])
plt.ylim([-60, 0])
plt.grid(True)
plt.tight_layout()
К сожалению, в реальной жизни и на практике использование бесконечных сигналов - невозможно и трудозатратно:
Очень длинные сигналы требуют больших объемов памяти для хранения значений.
Длинные сигналы содержат больше энергии нежели короткие сигналы при прочих равных условиях, что в свою очередь
затрудняет передачу и приём таких сигналов.
Длинные сигналы требуют больше вычислительных ресурсов для их обработки (свёртка, фильтрация, преобразование
Фурье).
Длинные импульсы подвержены бОльшим искажениям, чем короткие в связи с повышенной длительностью
распространения в физической среде.
При умножении сигнала на прямоугольное окно (усечение длинной последовательности до реального сигнала) происходит
так называемый эффект "растекания спектра" или "размытия" спектра. Главная проблема размытия спектра связана с тем,
что боковые лепестки более сильного сигнала могут скрыть в себе слабые сигналы. Ниже будет показано, как с помощью
оконных функций снизить влияние растекания спектра.
Оконные функции
В задачах цифровой обработки сигналов придуманы окна различной формы, которые при наложении на сигнал во
временной области, позволяют качественно улучшить его спектральные характеристики. Большое количество всевозможных
окон обусловлено в первую очередь одной из главных особенностей любого оконного наложения. Эта особенность
выражается во взаимосвязи уровня боковых лепестков и ширины центрального лепестка.
Правило: чем сильнее подавление боковых лепестков спектра, тем шире главный лепесток спектра, и наоборот
Представим себе сигнал, который разбивается на несколько последовательностей, каждая из которых обрабатывается
независимо, а затем сшивается в единый сигнал. При вычислении БПФ происходит наложение прямоугольного окна.
Следовательно, последующее восстановление формы сигнала приведет к нежелательным эффектам, которые выражены в
искажении формы сигнала на стыках (всплески сигнала). Для того, чтобы сгладить эти всплески можно применить оконную
фильтрацию.
Одно из применений оконных функций: обнаружение слабых сигналов на фоне более сильных путём подавления уровня
боковых лепестков. Основные оконные функции в задачах ЦОС — треугольное, синусоидальное, окно Ланцоша, Ханна,
Хэмминга, Блэкмана, Харриса, Блэкмана-Харриса, окно с плоской вершиной, окно Наталла, Гаусса, Кайзера и
Хэмминга, Блэкмана, Харриса, Блэкмана-Харриса, окно с плоской вершиной, окно Наталла, Гаусса, Кайзера и
множество других. Большая часть из них выражена через конечный ряд путём суммирования гармонических сигналов с
определенными весовыми коэффициентами. Такие сигналы отлично реализуются на практике на любых аппаратных
устройствах (программируемые логические схемы или сигнальные процессоры).
Окна сложной формы рассчитываются путём взятия экспоненты (окно Гаусса) или модифицированной функции Бесселя
(окно Кайзера). Такие оконные функции сложнее реализуются в интегральных микросхемах (для вычисления функций
экспоненты или функции Бесселя требуется таблица кодировки одного значения в другое).
Коэффициент подавления
Очевидно, что при умножении сигнала на оконную функцию происходит изменение амплитуды результирующего колебания.
В задачах ЦОС вводится понятие коэффициента ослабления, который характеризует подавление сигнала в процессе
оконной фильтрации в сравнении с прямоугольным окном. Формула для вычисления коэффициента ослабления:
$ \beta = \frac{A_{w}}{A_{r}} \cdot \frac{1}{N} \sum_{n=0}^{N-1}w(n)$ ,
где:
$A_{w}$ - уровень постоянной составляющей оконной функции,
$A_{r}$ - уровень постоянной составляющей прямоугольного окна,
$w(n)$ - отсчеты оконной функции,
$N$ - длина оконной функции.
С помощью python предварительно определим функцию, которая отображает оконные функции:
In [4]:
def dft_win(w):
"""
Plot window function and spectrum of the window
Parameters
---------w : np.array
input window vector
"""
# Find length of window
N = len(w)
# FFT size
NFFT = 2**12
# Calculate FFT
W = fftshift(fft(w, NFFT))
# Find max and add minimum floating-point value (except divide-by-zero)
W = W / np.amax(W) + np.nextafter(0,1)
tt = np.linspace(-1, 1, NFFT)
# plot window function and its spectrum
fig = plt.figure(figsize=(12, 6), dpi=80)
plt.subplot(2,1,1)
plt.stem(w, use_line_collection=True, basefmt='C0')
plt.title('Window fucntion')
plt.xlabel('Samples')
plt.ylabel(r'$w[k]$')
plt.xlim([0, N-1])
plt.grid(True)
plt.subplot(2,1,2)
plt.plot(tt, 20*np.log10(np.abs(W)))
plt.title('Spectrum')
plt.xlabel('Frequency')
plt.ylabel('Level in dB')
plt.axis([-1, 1, -120, 2])
plt.grid(True)
plt.tight_layout()
Основные оконные функции
Ниже приведены выражения для основных оконных функций. Длительность оконной функции - $N$ , $w(n)$ - отсчеты
оконной функции. В Python библиотеке scipy в пакете signal доступны все широко известные окна. Их вызов
оконной функции. В Python библиотеке scipy в пакете signal доступны все широко известные окна. Их вызов
достаточно прост. Далее в виде таблицы и графиков будет показана сравнительная эффективность различных окон.
Правило: сумма модулей коэффициентов оконной функции равна единице!
Прямоугольное окно
$w(n) = 1$
Самое простое окно, обладает наихудшими характеристиками и получается автоматически при усечении
последовательности до $N$ отсчетов. Максимальный уровень боковых лепестков (УБЛ) частотной характеристики
прямоугольного окна: -13 дБ.
Python: signal.boxcar(M)
In [5]:
N = 64
dft_win(np.ones(N))
Треугольное окно
Также известно как окно Бартлета.
$w(n) = 1 - \frac{n - N / 2}{L / 2}$
где
$L = N, N+1, N+2 $
Максимальный уровень боковых лепестков: -26 дБ.
Python: signal.triang(M) или bartlett(M)
In [6]:
N = 64
dft_win(sig.triang(N))
Синус
$w(n) = sin(\frac{\pi\cdot n}{N-1})$
Простое с точки зрения программной и аппаратной реализации окно. Максимальный уровень боковых лепестков
синусоидального окна: -23 дБ.
Python: signal.cosine(M)
In [7]:
N = 64
dft_win(sig.cosine(N))
Окно Ханна (Хеннинга)
$w(n) = 0.5 \cdot [1 - cos(\frac{2\pi n}{N-1})]$
Также это окно называют окном Блэкмана-Харриса второго порядка. Максимальный уровень боковых лепестков
синусоидального окна: -31.5 дБ.
Python: signal.hann(M) и signal.hanning(M)
In [8]:
N = 64
dft_win(sig.hann(N))
Окно Хемминга
$w(n) = 0.53836 - 0.46164 \cdot cos(\frac{2\pi n}{N-1})$
Максимальный уровень боковых лепестков: -42 дБ.
Python: signal.hamming(M)
In [9]:
N = 64
dft_win(sig.hamming(N))
Окно Блэкмана
$w(n) = a_0 - a_1 \cdot cos(\frac{2\pi n}{N-1}) + a_2 \cdot cos(\frac{4\pi n}{N-1}) $
где
$a_0 = \frac{1-\alpha}{2}; a_1 = 0.5 ; a_2 = 0.5\cdot\alpha $
При $\alpha = 0.16$ максимальный уровень боковых лепестков: -58 дБ.
Python: signal.blackman(M)
In [10]:
N = 64
dft_win(sig.blackman(N))
Окно Блэкмана-Харриса
Задается суммой четырех слагаемых (то есть окно четвертого порядка).
$w(n) = a_0 - a_1 \cdot cos(\frac{2\pi n}{N-1}) + a_2 \cdot cos(\frac{4\pi n}{N-1}) - a_3 \cdot cos(\frac{6\pi n}{N-1}) $
где
$a_0 = 0.35875, a_1 = 0.48829, a_2 = 0.14128, a_3 = 0.01168 $
Максимальный уровень боковых лепестков: -92 дБ.
Python: signal.blackmanharris(M)
In [11]:
N = 64
dft_win(sig.blackmanharris(N))
Окно Блэкмана-Наталла
Формула аналогична окну Блэкмана-Харриса. Различие лишь в коэффициентах. Задается суммой четырех слагаемых.
$w(n) = a_0 - a_1 \cdot cos(\frac{2\pi n}{N-1}) + a_2 \cdot cos(\frac{4\pi n}{N-1}) - a_3 \cdot cos(\frac{6\pi n}{N-1}) $
где
$a_0 = 0.3635819, a_1 = 0.4891775, a_2 = 0.1365995, a_3 = 0.0106411 $
Максимальный уровень боковых лепестков: -93 дБ.
Python: signal.nuttall(M)
In [12]:
N = 64
dft_win(sig.nuttall(N))
Окно с плоской вершиной
Окно с плоской вершиной (Flat-top window).
$w(n) = a_0 - a_1 \cdot cos(\frac{2\pi n}{N-1}) + a_2 \cdot cos(\frac{4\pi n}{N-1}) - a_3 \cdot cos(\frac{6\pi n}{N-1}) + a_4 \cdot
cos(\frac{8\pi n}{N-1}) $
где
$a_0 = 0.21556895, $
$a_1 = 0.41663158, $
$a_2 = 0.277263158, $
$a_3 = 0.083578947, $
$a_4 = 0.0069474 $
Максимальный уровень боковых лепестков: -70 дБ.
Python: signal.flattop(M)
In [13]:
N = 64
dft_win(sig.flattop(N))
Окно Кайзера
Окно Кайзера. Варьируется с помощью параметра $\beta$, который определяет уровень затухания и крутизну спада
частотной характеристики. Окно Кайзера - своего рода универсальное окно, с помощью которого можно выбирать те или
иные параметры фильтрации для широкого класса задач.
$w(n) = \frac{|I_{0} \sqrt{1 - (\frac{2n-N+1}{N-1})^2} |}{|I_{0}(\beta)|}$
где
$I_{0}$ - модифицированная функция Бесселя первого рода нулевого порядка.
$\beta $ - коэффициент, который определяет долю энергии, сосредоточенной в главном лепестке спектра оконной
функции.
Чем больше $\beta$, тем больше доля энергии внутри главного лепестка, и тем шире главный лепесток. Следовательно, тем
меньше уровень боковых лепестков (лучше подавление в задачах фильтрации). На практике функция Кайзера в аппаратной
части практически не реализуется, но применяется программно (расчет коэффициентов КИХ-фильтра). В реальных задачах
используются значения $\beta$ от 5 до 11.
Python: signal.kaiser(M, beta)
In [14]:
N = 64
dft_win(sig.kaiser(N, beta=4))
In [15]:
N = 64
dft_win(sig.kaiser(N, beta=10))
Окно Гаусса
Окно Гаусса задается экспоненциальной функцией и варьируется параметром дисперсии (среднеквадратического
отклонения).
$w(n) = e^{-\frac{1}{2}(\frac{n}{\sigma})^{2}}$
Частотные свойства окна зависят от параметра $\sigma$.
Чем больше $\sigma$, тем уже главный лепесток, но выше уровень боковых лепестков (хуже подавление).
На практике окно Гаусса в аппаратной части практически не реализуется, но применяется программно, например в задачах
расчета коэффициентов КИХ-фильтра.
Python: signal.gaussian(M, std)
In [16]:
N = 64
dft_win(sig.gaussian(N, std=16))
In [17]:
N = 64
dft_win(sig.gaussian(N, std=8))
Мы рассмотрели основные оконные функции.
Оконные функции numpy
В python пакете numpy набор оконных функций ограничен.
bartlett(M) - треугольная функция,
blackman(M) - функция Блэкмана,
hamming(M) - окно Хэмминга,
hanning(M) - окно Хэннинга или Ханна,
kaiser(M, beta) - окно Кайзера.
В отличие от numpy пакет scipy расширяет возможности оконной фильтрации, и как было видно в примерах выше дополняет функционал. Приведем список основных функций из пакета scipy.signal
Оконные функции scipy
Function
Description
Side-Lobe Level
boxcar(M[, sym])
Прямоугольное окно
13
triang(M[, sym])
Треугольное окно
26
bartlett(M[, sym])
Треугольное окно (Бартлета)
26
cosine(M[, sym])
Косинусное окно
23
hann(M[, sym])
Окно Ханна (Хеннинга)
31.5
hanning(M[, sym])
Окно Хеннинга (Ханна)
31.5
hamming(M[, sym])
Окно Хемминга
42
blackman(M[, sym])
Окно Блэкмана
58
blackmanharris(M[, sym])
Функция Блэкмана-Харриса
92
nuttall(M[, sym])
Окно Наттала
93
Окно Наттала
nuttall(M[, sym])
Function
flattop(M[, sym])
kaiser(M, beta[, sym])
Функция Кайзера (параметр - $\beta$)
$f(\beta)$
gaussian(M, std[, sym])
Функция Гаусса (параметр - $\sigma$)
$f(\sigma)$
Основные оконные функции
In [18]:
N = 64
# All windows
ww = np.zeros((N, 9))
ww[:,0]
ww[:,1]
ww[:,2]
ww[:,3]
ww[:,4]
ww[:,5]
ww[:,6]
ww[:,7]
ww[:,8]
=
=
=
=
=
=
=
=
=
93
Description Side-Lobe Level
Окно с плоской вершиной
70
np.ones(N)
sig.triang(N)
sig.hann(N)
sig.hamming(N)
sig.blackman(N)
sig.blackmanharris(N)
sig.nuttall(N)
sig.flattop(N)
sig.kaiser(N, beta=8)
lst_titles = ['Rectangular', 'Bartlett', 'Hann (Hanning)',
'Hamming', 'Blackman', 'Blackmann-Harris 4-term',
'Nuttall', 'Flat-top window', 'Kaiser (w/ beta)'
]
# Plot window function and its spectrum
fig = plt.figure(figsize=(14, 8), dpi=80)
for i in range(9):
plt.subplot(3, 3, i+1)
plt.stem(ww[:,i], use_line_collection=True, basefmt='C0')
plt.title(lst_titles[i])
plt.xlabel('Samples')
plt.ylabel(r'$w[k]$')
plt.xlim([0, N-1])
plt.grid(True)
plt.tight_layout()
Спектры основных оконных функций
In [19]:
NFFT = 2**12
# Calculate FFT
WW = fft(ww, NFFT, axis=0)
WW = WW / np.amax(WW, axis=0) + np.nextafter(0,1)
tt = np.linspace(-1, 1, NFFT)
# Plot window function and its spectrum
fig2 = plt.figure(figsize=(14, 8), dpi=80)
for i in range(9):
plt.subplot(3, 3, i+1)
plt.plot(tt, 20*np.log10(np.abs(fftshift(WW[:,i]))))
plt.title(lst_titles[i])
plt.xlabel('Frequency')
plt.ylabel('Level in dB')
plt.axis([-1, 1, -120, 2])
plt.grid(True)
plt.tight_layout()
Поиск слабых сигналов
Ранее было сказано, что с помощью оконной фильтрации возможно выделение слабых сигналов на фоне более сильных.
Докажем это, построив график суммы двух гармонических сигналов, расположенных близко друг к другу по частоте и
существенно отличающихся по амплитуде.
На следующем графике приведен спектр без оконной фильтрации (окно - прямоугольное) и с фильтрацией входного сигнала
окном Кайзера с заданным параметром $beta = 7$
In [20]:
# Input parameters
N = 128
NFFT = 2048
# Input signal (long: N >> NFFT)
tt = np.linspace(0, 1, N, endpoint=True)
xx = 100*np.cos(2*np.pi*32*tt)+np.cos(2*np.pi*40*tt)
# Window (Kaiser)
wn = sig.kaiser(N, beta=7)
yy = xx*wn
# Calculate FFT 1
sft = np.abs(fft(xx, NFFT))
sft = np.abs(fft(xx, NFFT))
slg = 20*np.log10(sft / np.max(sft))
# Calculate FFT 2
yft = np.abs(fft(yy, NFFT))
ylg = 20*np.log10(yft / np.max(yft))
lst_ffts = [slg, ylg]
lst_wins = ['No window', 'Kaiser window']
plt.figure(figsize=(12, 5), dpi=80)
for i in range(2):
plt.subplot(1,2,i+1)
plt.title(lst_wins[i])
plt.xlabel('freq samples')
plt.ylabel('level [dB]')
plt.plot(lst_ffts[i])
plt.xlim([0, NFFT//2])
plt.ylim([-80, 0])
plt.grid(True)
plt.tight_layout()
Как видно на предыдущем рисунке, без оконной функции практически невозможно различить слабый сигнал на фоне
сильного. Однако, применяя оконную функцию с хорошими свойствами подавления, удается детектировать слабый сигнал
на фоне сильного!
Цифровая обработка сигналов - 8
Title
Digital signal processing
Author
Alexander Kapitanov
Contact
sallador@bk.ru
Project lang
Python
Packages
numpy, scipy, matplotlib
License
GNU GPL 3.0
Введение
Перед вами обучающий материал по основам цифровой обработки сигналов с использованием средств языка
программирования Python. Предполагается, что читатель имеет базовые знания из области высшей математики, а также
владеет языком Python и хотя бы поверхностно знает различные python-библиотеки - numpy/scipy, matplotlib и другие.
Для пользователей MATLAB / GNU Octave освоение материала с точки зрения программного кода не составит труда,
поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из python-библиотек.
Многоскоростная обработка сигналов
В предыдущих разделах мы изучили цифровые фильтры - с конечной импульсной характеристикой (КИХ) и с бесконечной
импульсной характеристикой (БИХ). Многоскоростная обработка сигналов (multirate processing) предполагает, что в процессе
линейного преобразования цифровых сигналов возможно изменение частоты дискретизации в сторону уменьшения или
увеличения, либо в дробное число раз. Это приводит к более эффективной обработке сигналов, так как открывается
возможность использования минимально допустимых частот дискретизации и, как следствие, значительного уменьшения
требуемой вычислительной производительности проектируемой цифровой системы. Для преобразования частоты
дискретизации в дробное число раз необходимо использовать каскады повышения и понижения частоты дискретизации
совместно.
Основными составными элементами системы многоскоростной ЦОС являются компрессоры и экспандеры частоты
дискретизации, понижающие и соответственно повышающие частоту дискретизации преобразуемых цифровых
последовательностей. При этом, если понижение частоты дискретизации в R раз (R – целое число) с помощью компрессора
сводится к тому, что в выходном сигнале сохраняются только отсчеты с номерами, кратными R, то повышение частоты
дискретизации в R раз с помощью экспандера предполагает размещение (R-1) нулей между каждой парой соседних
отсчетов входного сигнала.
Децимация (прореживание) – понижение частоты дискретизации. Понижение частоты дискретизации получается путем
сохранения одного отсчета входной последовательности и удалением R-1 отсчетов последовательности сигнала, что
выражается следующей формулой:
y[n] = x[nR]
Простая компрессия цифровых последовательностей приводит к наложению периодических составляющих спектра
«прореженного» сигнала вследствие эффекта отражения (ухудшаются спектральные характеристики выходного сигнала).
Следовательно, понижение частоты дискретизации требует подключения низкочастотного фильтра (ФНЧ). Таким образом,
структурная схема фильтра дециматора получается путем каскадного соединения ФНЧ и компрессора. Тогда, формула,
связывающая входной и выходной сигналы, преобразуется к виду:
N−1
y[n] = ∑k =0 x[nR − k] ⋅ h[k] ,
где
h[k] - отсчёты фильтра с конечной импульсной характеристикой,
x[nR − k] - прореженный входной сигнал,
Выходной сигнал фильтра дециматора сохраняет только каждый R-й отсчет. Следовательно, для класса фильтров с
конечной импульсной характеристикой (КИХ-фильтров), когда пределы суммирования принимают конечные значения,
потенциально возможно уменьшение приведенных вычислительных затрат в R раз. Это выражается в уменьшении скорости
обработки или в уменьшении количества затрачиваемых логических ресурсов, если рассматривать микросхемы ПЛИС.
Интерполяция – повышение частоты дискретизации. Операция увеличения частоты дискретизации задается введением R-1
нулевых отсчетов во входную последовательность и выражается формулой:
y[n] =
{
x[n/R], n = 0, L, 2L, . . .
0, n ≠ 0, L, 2L, . . .
Поскольку размещение нулей эквивалентно сжатию в R раз и периодическому продолжению спектра входного сигнала, то
при повышении частоты дискретизации требуется также подключение ФНЧ. Таким образом, структурная схема фильтра
интерполятора получается путем каскадного соединения экспандера и ФНЧ, а формула для выходного сигнала
преобразуется к виду:
N−1
y[n] = ∑k =0 x[nR − k] ⋅ h[k] ,
где
h[k] - отсчёты фильтра с конечной импульсной характеристикой,
x[nR − k] - входной сигнал, со вставкой нулей между отсчётами.
Выходной сигнал фильтра-интерполятора использует «прореженную» в R раз входную последовательность. Следовательно,
вычислительные затраты и память КИХ-фильтра потенциально уменьшаются в R раз.
CIC фильтры
В предыдущем разделе рассматривался класс однородных КИХ-фильтров. С их помощью возможно проектировать
фильтры для изменения частоты дискретизации. Для реализации этих фильтров не требуется операция умножения,
следовательно фильтр работает достаточно быстро и довольно хорошо реализуется на таких устройствах, как ПЛИС.
Недостатком таких фильтров является большой уровень боковых лепестков. Боковые лепестки АЧХ подавляются путем
каскадирования фильтров, при этом положение нулей не меняется, а меняется только соотношение уровней главного и
бокового лепестков, относительный уровень боковых лепестков уменьшается при перемножении АЧХ.
Второй недостаток однородных фильтров – непрямоугольная форма АЧХ. Чтобы сделать ее более прямоугольной,
используют корректирующий КИХ-фильтр, таким образом форма главного лепестка становится более прямоугольной, но
увеличивается уровень боковых лепестков.
Однородные фильтры, образуя каскад интегратора и дифференцирующего звена, называются интегрально-гребенчатыми
фильтрами (CIC, Cascaded integrator–comb). Далее по тексту будем использовать эту терминологию.
CIC фильтр состоит из двух базовых звеньев: интегратор и гребенчатый фильтр (дифференциатор). Интегрирующее звено
(int) представляет собой обычный БИХ-фильтр первого порядка, выполненный как самый простой аккумулятор. Гребенчатый
фильтр (comb) является КИХ-фильтром первого порядка. На следующем рисунке представлены схемы интегратора и
дифференцирующего звена:
Между интегратором и гребенчатым фильтром часто ставится узел повышения или понижения частоты дискретизации в
целое число раз — R.
В случае понижения частоты дискретизации из входной последовательности выбирается каждый R-отсчет, образуя
прореженную выходную последовательность.
В случае повышения частоты дискретизации между отсчетами входной последовательности просто вставляются нули,
которые затем сглаживаются в интегрирующей секции, образуя последовательность на увеличенной частоте
дискретизации.
Формулы для передаточной и амплитудно-частотной характеристик фильтра:
Передаточная характеристика
1 −z − RM
H(z) =
RM−1
(∑k =0 z −k)N
=[
1 −z − 1 N
]
Формула АЧХ
sin ( πRMf)
‖H(f)‖ = [
sin ( πf)
]N
CIC фильтр-дециматор
Если CIC-фильтр используется для понижения частоты дискретизации, то он называется дециматором. В таком случае
первым звеном идет интегратор, затем происходит понижение частоты дискретизации и, наконец, идет звено
дифференцирующего фильтра.
CIC фильтр-интерполятор
Если CIC-фильтр используется для повышения частоты дискретизации, то он называется интерполятором. В таком случае
дифференцирующее звено стоит на первом месте, затем происходит повышение частоты дискретизации и, наконец, идет
звено интегрирующего фильтра.
Каскадное соединение интегратора и гребенчатого фильтра без операций децимации и интерполяции называется
фильтром «скользящего среднего». Уровень первого бокового лепестка такого фильтра составляет всего -13 дБ, что
достаточно мало для серьезных задач ЦОС. В большинстве практических задач параметр M = 1. Ниже по тексту будет
представлена реализация фильтров именно с этим значением параметра.
В силу линейности математических операций, происходящих в CIC фильтре возможно каскадное соединение нескольких
фильтров подряд. Это дает пропорциональное уменьшение уровня боковых лепестков, но также увеличивает "завал"
главного лепестка амплитудно-частотной характеристики. Таким образом, при N-каскадном соединении однотипных CIC
фильтров происходит перемножение идентичных передаточных характеристик. Как правило, секции интеграторов и
гребенчатых фильтров объединяются вместе по типу. Например, сначала последовательно ставится N секций однотипных
интеграторов, затем N секций однотипных дифференцирующих фильтров. На следующем рисунке изображен CIC фильтрдециматор третьего порядка N = 3.
На следующем рисунке приведена АЧХ фильтра первого порядка N = 1 при различных параметрах коэффициента
децимации R:
In [1]:
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import freqz
from scipy.fftpack import fft
%matplotlib inline
# Import numpy
# Import matplotlib
In [2]:
N = 2**15
f = np.linspace(0, 0.5, N, endpoint=True)
# Create CIC filter as recursive FIR
b = [1, 1, 1]
# Plot results
plt.figure(figsize=(10, 4), dpi=80)
for i in range(4):
_, h = freqz(b, 1, worN=N)
h = np.abs(h)
plt.plot(f, 20*np.log10(h/np.max(h)+10e-12), label=f'R = {len(b)}')
plt.xlim([0, 0.5])
plt.ylim([-30, 0])
plt.grid(True)
b.append(1)
plt.legend(loc='upper right')
plt.xlabel('Normalized Freq')
plt.title('CIC frequency responce')
plt.tight_layout()
In [3]:
b = [1, 1]
# Plot results
plt.figure(figsize=(10, 6), dpi=100)
for i in range(9):
_, h = freqz(b, 1, worN=N)
h = np.abs(h)
plt.subplot(3, 3, i+1)
plt.plot(f, 20*np.log10(h/np.max(h)+10e-12), label=f'R = {len(b)}', color='C'+str(i))
plt.xlim([0, 0.5])
plt.ylim([-30, 0])
plt.grid(True)
b.append(1)
plt.legend(loc='upper right')
plt.tight_layout()
АЧХ CIC фильтра полностью эквивалентна частотной характеристике FIR фильтра с прямоугольной импульсной
характеристикой (ИХ). Как видно из предыдущего примера, коэффициенты числителя - массив единиц, а коэффициент
знаменателя также равен единице.
Общая ИХ фильтра определяется как свертка всех импульсных характеристик каскадов связки интегратора и гребенчатого
фильтра. С ростом порядка CIC фильтра, его ИХ интегрируется соответствующее число раз. Таким образом, для CIC
фильтра первого порядка ИХ – прямоугольник, для фильтра второго порядка ИХ – равнобедренный треугольник, для
третьего порядка ИХ – парабола и т.д.
Python реализация CIC фильтра
К сожалению, на сегодняшний день в Python пакетах для математических вычислений numpy/scipy отсутствует ряд операций
цифровой обработки сигналов. В частности, отсутствует реализация CIC фильтров, осуществляющих задачи децимации и
интерполяции. В связи с этим, разработан класс CicFilter , который принимает входную последовательность и содержит
два метода:
decimator(r, n) - фильтр-дециматор,
interpolator(r, n) - фильтр-интерполятор.
где r - коэффициент децимации или интерполяции, n - порядок фильтра, (параметр m = 1 всегда).
In [4]:
class CicFilter:
"""
Cascaded Integrator-Comb (CIC) filter is an optimized class of
finite impulse response (FIR) filter.
CIC filter combines an interpolator or decimator, so it has some
parameters:
R - decimation or interpolation ratio,
N - number of stages in filter (or filter order)
M - number of samples per stage (1 or 2)*
* for this realisation of CIC filter just leave M = 1.
CIC filter is used in multi-rate processing. In hardware
applications CIC filter doesn't need multipliers, just only
adders / subtractors and delay lines.
Equation for 1st order CIC filter:
y[n] = x[n] - x[n-RM] + y[n-1].
Parameters
---------x : np.array
input signal
"""
def __init__(self, x):
self.x = x
def decimator(self, r, n):
"""
CIC decimator: Integrator + Decimator + Comb
Parameters
---------r : int
decimation rate
n : int
filter order
"""
# integrator
y = self.x[:]
for i in range(n):
y = np.cumsum(y)
# decimator
y = y[::r]
# comb stage
return np.diff(y, n=n, prepend=np.zeros(n))
def interpolator(self, r, n, mode=False):
"""
CIC inteprolator: Comb + Decimator + Integrator
Parameters
---------r : int
interpolation rate
n : int
filter order
mode : bool
False - zero padding, True - value padding.
"""
# comb stage
y = np.diff(self.x, n=n,
prepend=np.zeros(n), append=np.zeros(n))
# interpolation
if mode:
y = np.repeat(y, r)
else:
else:
y = np.array([i if j == 0 else 0 for i in y for j in range(r)])
# integrator
for i in range(n):
y = np.cumsum(y)
if mode:
return y[1:1 - n * r]
else:
return y[r - 1:-n * r + r - 1]
Проведем тестирование разработанного класса CicFilter . Для это создадим вспомогательную функцию для построения
графиков.
In [5]:
def plot_filter(r=None, n=None, samples=100, mode=None):
# Create signal
tt = np.linspace(0, 1, samples)
np.random.seed(1)
if mode == 'Decimator':
x = 1.5 * np.sin(4 * np.pi * tt) + 1.7 * np.sin(8.3 * np.pi * tt)
x += 0.9*np.random.randn(samples)
if mode == 'Interpolator':
x = np.sin(1.7 * np.pi * tt) + 1.7 * np.sin(5.3 * np.pi * tt)
x += 0.3*np.random.randn(samples)
# Apply filter
clf = CicFilter(x)
if mode == 'Decimator':
zz = [clf.decimator(i, j) for i, j in zip(r, n)]
if mode == 'Interpolator':
zz = [clf.interpolator(i, j, mode=True) for i, j in zip(r, n)]
# Plot figure
plt.figure(figsize=(12, 8), dpi=80)
# plt.title(mode)
plt.subplot(4, 2, 1)
plt.title('Change N:')
plt.plot(x, '-', color='C0', label='Signal')
plt.xlim([0, samples-1])
plt.legend(loc='upper right')
plt.grid(True)
for j in range(len(r)):
plt.subplot(4, 2, 2+j)
if j == 0:
plt.title('Change R:')
plt.stem(zz[j],
use_line_collection=True,
linefmt='C2',
basefmt='C0',
label=f'R = {r[j]}, N = {n[j]}'
)
plt.grid(True)
plt.legend(loc='upper right')
plt.tight_layout(True)
Python CIC фильтр-дециматор
In [6]:
# Number os samples
N = 500
# Filter parameters (length of lists should be same):
flt_r = [3, 6, 4, 6, 8, 6, 15]
flt_n = [4, 1, 4, 2, 4, 8, 4]
plot_filter(r=flt_r, n=flt_n, samples=N, mode='Decimator')
plot_filter(r=flt_r, n=flt_n, samples=N, mode='Decimator')
Python CIC фильтр-интерполятор
In [7]:
# Number os samples
N = 30
# Filter parameters (length of lists should be same):
flt_r = [2, 3, 3, 3, 5, 3, 7]
flt_n = [3, 1, 3, 2, 3, 6, 3]
plot_filter(r=flt_r, n=flt_n, samples=N, mode='Interpolator')
Рост разрядности данных
К несчастью, увеличение величины задержки M в гребенчатой структуре и увеличение порядка фильтра N приводят к росту
коэффициента передачи. Это в свою очередь приводит к увеличению разрядности на выходе фильтра. В задачах ЦОС, где
применяются CIC фильтры с целочисленной арифметикой нужно всегда об этом помнить и следить, чтобы передаваемые
сигналы не выходили за используемую разрядную сетку. К примеру, негативный эффект роста разрядности проявляется в
значительном увеличении используемых ресурсов ПЛИС. Также следует отметить, что сумматор в цепи интегратора должен
быть без переполнения.
Интерполятор: использование ограниченной точности не влияет на внутреннюю разрядность регистров, масштабируется
только последний выходной каскад. Существенный рост разрядности данных происходит в секциях интеграторов.
B OUT = ceil[Nlog2 (RM) + B IN]
Дециматор: CIC фильтр-дециматор очень чувствителен к параметрам M, R и N, от которых зависит разрядность
промежуточных и выходных данных. И дифференцирующее звено, и интегратор влияют на конечную разрядность выходного
сигнала.
( RM) N
B OUT = ceil[log2 (
R
) + B IN]
В этих формулах:
B IN — разрядность входных данных,
B OUT — разрядность выходных данных,
R — коэффициент дискретизации,
M — параметр задержки,
N — порядок фильтра (количество каскадов).
ceil - математическая операция округления в сторону большего значения.
Python Resampling
Программная реализация методов децимации и интерполяции .
Применение дециматоров и интерполяторов производится с помощью некоторых функций из пакета scipy.signal .
Перечислим основные функции:
Function
Description
decimate(x, q[, n, ftype, axis,
zero_phase])
Децимация сигнала с применением сглаживающего фильтра ФНЧ
resample(x, num[, t, axis, window])
Изменение количества отсчетов сигнала x на q (методом Фурье)
upfirdn(h, x[, up, down, axis])
Трехступенчатая обработка: Интерполяция, фильтрация (КИХ), децимация
resample_poly(x, up, down[, axis, window])
Изменение количества отсчетов сигнала с использованием полифазного
фильтра
Децимация
Метод decimate позволяет децимировать сигнал с применением сглаживающего фильтра нижних частот:
x - входной сигнал (одномерный или многомерный вектор данных
q - целочисленный коэффициент децимации
n - целочисленный порядок фильтра, по умолчанию равен 8 для БИХ-фильтров и 20 для КИХ-фильтров
ftype - выбор фильтра: БИХ - iir или КИХ - fir
axis - ось, вдоль которой производится децимация (для многомерных массивов)
zero_phase - нулевой сдвиг фазы. Предотвращает сдвиг фазы при прохождении сигнала через фильтр. По
умолчанию True
Для коэффициента децимации q > 13 необходимо использовать каскадное соединение дециматоров (многократный
Для коэффициента децимации q > 13 необходимо использовать каскадное соединение дециматоров (многократный
вызов метода decimate() .
In [8]:
from scipy.signal import decimate
# Input signal
N = 500
tt = np.linspace(0, 1, N)
x = 1.5 * np.sin(4 * np.pi * tt) + 1.9 * np.sin(11.3 * np.pi * tt) + 0.2 * np.random.randn(N)
# Decimation
y = decimate(x, q=8, n=8)
ty = np.linspace(0, 1, y.size)
# Plot figure
plt.figure(figsize=(12, 3), dpi=80)
plt.title('Python Decimate method')
plt.plot(x, '-', color='C1', label='Signal')
plt.stem(np.linspace(0, N, y.size), y, use_line_collection=True, linefmt='C2', basefmt='C0', label=
'Decimate')
plt.xlim([0, N-1])
plt.legend(loc='upper right')
plt.grid(True)
Ресемплинг
Метод resample позволяет изменить частоту дискретизации в дробное число раз
x - входной сигнал (одномерный или многомерный вектор данных)
num - количество отсчетов в выходном сигнале
t - массив временных меток для выходного сигнала
axis - ось, вдоль которой производится децимация (для многомерных массивов)
window - оконная функция, применяемая в методе Фурье при расчете выходного массива
Децимация и интерполяция с помощью resample
In [9]:
from scipy.signal import resample
# Input signal
N = 500
tt = np.linspace(0, 1, N)
np.random.seed(1)
x = 1.9 * np.sin(10.3 * np.pi * tt ** tt) + 0.2 * np.random.randn(N)
y = resample(x, num=50, window='blackmanharris')
ty = np.linspace(0, 1, y.size)
# Plot figure
plt.figure(figsize=(14, 4), dpi=80)
plt.subplot(1, 2, 1)
plt.title('Python resample (1)')
plt.plot(x, '-', color='C1', label='Signal')
plt.stem(np.linspace(0, N, y.size), y, use_line_collection=True, linefmt='C2', basefmt='C0', label=
'Decimate')
'Decimate')
plt.xlim([0, N-1])
plt.legend(loc='upper right')
plt.grid(True)
# Input signal
N = 10
tt = np.linspace(0, 1, N)
x = np.sin(1.5 * np.pi * tt)
y = resample(x, num=40, window='blackmanharris')
ty = np.linspace(0, 1, y.size)
# Plot figure
plt.subplot(1, 2, 2)
plt.title('Python resample (2)')
plt.plot(x, '-o', color='C1', label='Signal')
plt.stem(np.linspace(0, N, y.size), y, use_line_collection=True, linefmt='C2', basefmt='C0', label=
'Interpolate')
plt.xlim([0, N-1])
plt.legend(loc='upper right')
plt.grid(True)
Метод upfirdn производит обработку в три стадии: интерполяция, фильтрация (КИХ), децимация сигнала.
h - коэффициенты КИХ-фильтра
x - входной сигнал (одномерный или многомерный вектор данных)
up - коэффициент интерполяции
down - коэффициент децимации
axis - ось, вдоль которой производится децимация (для многомерных массивов)
Метод resample_poly изменяет количество отсчетов входного сигнала с использованием полифазного фильтра
x - входной сигнал (одномерный или многомерный вектор данных)
up - коэффициент интерполяции
down - коэффициент децимации
axis - ось, вдоль которой производится децимация (для многомерных массивов)
window - оконная функция
Фильтр скользящего среднего
Фильтр скользящего среднего (Moving average filter, MAF) - разновидность КИХ-фильтров (в некоторых случаях БИХфильтров). Отличительной особенностью фильтра скользящего среднего является равенство единице суммы
коэффициентов.
N−1
∑k =0 bk = 1
Как было сказано в предыдущих разделах, КИХ фильтры можно привести к рекурсивному виду. Рассмотрим следующий
пример. Запишем передаточную характеристику фильтра:
H(z) = 1 + z −1 + z −2 + z −3 ,
Домножим передаточную функцию на
1 −z − 1
( 1 −z − 1
.
Пропустим математические выкладки (при желании, это можно сделать самостоятельно ввиду тривиальности
рассматриваемой задачи) и запишем результат:
1 +z − 3
H(z) =
1 −z − 1
Структурная схема такого фильтра представлена на следующем рисунке. Она состоит из двух цепей: звено без обратной
связи - дифференцирующее, а звено с обратной связью - интегрирующее (сумматор с обратной связью).
FIR Recursive
Python реализация
Таким образом, фильтр скользящего среднего можно реализовать с помощью прямого КИХ-фильтра, либо с помощью
рекурсивной формы. Параметр M - величина задержки в дифференцирующем звене. Кроме того, фильтр скользящего
среднего можно реализовать с помощью операции свертки сигналов (что по сути эквиваленто реализации с помощью КИХфильтра в прямой форме). В качестве ядра свертки выступает массив единиц. Ниже представлено несколько реализаций
фильтра скользящего среднего на Python
In [10]:
class MafFilter:
"""
Moving average filter:
M - moving-average step (delay in comb stage)
Parameters
---------x : np.array
input 1-D signal
"""
def __init__(self, x):
self.x = x
def maf_conv(self, m=2):
"""
Calculate moving average filter via convolution
Parameters
---------m : int
moving average step
"""
coe = np.ones(m) / m
return np.convolve(self.x, coe, mode='same')
def maf_fir(self, m=2):
"""
Calculate moving average filter as FIR
Parameters
---------m : int
moving average step
"""
return lfilter(np.ones(M-1), 1, self.x)
def maf_iir(self, m=2):
"""
Calculate moving average filter as FIR
Parameters
---------m : int
moving average step
"""
# Change to recursive form
a = [1, -1]
b = np.zeros(M)
b = np.zeros(M)
b[0], b[-1] = a
return lfilter(b, a, self.x)
Пример фильтрации
На следующем примере можно видеть "сглаживающий" эффект фильтра скользящего среднего. Чем выше порядок фильтра
- тем лучше проявляется эффект сглаживания.
In [11]:
N = 300
M = (2, 5, 20)
# Number of samples
# Moving average step
LM = len(M)
# Size of M
# Input signal w/ noise:
sig = np.concatenate(
(
np.zeros(int(N/2)),
np.ones(int(N/4)) * 7,
np.zeros(int(N/2)))
)
lns = sig.size
# Size of signal
# Add some noise and peaks
np.random.seed(2)
sig += np.random.randn(lns)
rnd = np.random.randint(0, lns, 15)
sig[rnd] = 15
# Add Gaussian noise
# Add random numbers for index
# Add peaks
# Calculate Moving Average filter:
filt = MafFilter(sig)
res = np.zeros((lns, LM))
for i in range(LM):
res[:, i] = filt.maf_conv(m=M[i])
# Calculate Frequency responce:
hfq = np.zeros((lns, LM))
for j in range(LM):
for i in range(lns):
if i == 0:
hfq[i, j] = 1
else:
hfq[i, j] = np.abs(np.sin(np.pi * M[j] * i / 2 / lns) / M[j] /
np.sin(np.pi * i / 2 / lns))
# Calculate spectrum of input signal:
fft_sig = np.abs(fft(sig))
fft_sig /= np.max(fft_sig)
# Calculate spectrum of output signal:
fft_out = np.zeros((lns, LM))
for i in range(LM):
fft_out[:, i] = np.abs(fft(res[:, i]))
fft_out[:, i] /= np.max(fft_out[:, i])
# Plot results:
plt.figure(figsize=(12, 6), dpi=120)
plt.subplot(3, 2, 1)
plt.plot(sig, linewidth=1.25)
plt.title('Input signal')
plt.grid()
plt.xlim([0, lns-1])
plt.subplot(3, 2, 3)
for i in range(LM):
plt.plot(hfq[:, i], linewidth=1.25, label="M=%d" % M[i])
plt.title('MA filter responce')
plt.grid()
plt.legend(loc=1)
plt.xlim([0, lns-1])
plt.subplot(3, 2, 5)
for i in range(LM):
plt.plot(res[:, i], linewidth=1.0, label="M=%d" % M[i])
plt.title('Output signal')
plt.grid()
plt.legend(loc=2)
plt.xlim([0, N-1])
for i in range(LM):
plt.subplot(3, 2, 2*i+2)
plt.plot(sig, '-', linewidth=0.5)
plt.plot(res[:, i], linewidth=1.5)
plt.title('Moving average, M = %d' % M[i])
plt.grid()
plt.xlim([0, lns-1])
plt.tight_layout()
Цифровая обработка сигналов - 9
Title
Digital signal processing
Authors
Vladimir Fadeev, Zlata
Fadeeva
Contact
vladimir_fadeev1993@mail.ru
Project lang
Python
Packages
numpy, scipy, matplotlib
License
GNU GPL 3.0
Введение
Перед вами обучающий материал по основам цифровой обработки сигналов с использованием средств языка
программирования Python. Предполагается, что читатель имеет базовые знания из области высшей математики, а также
владеет языком Python и хотя бы поверхностно знает различные python-библиотеки - numpy/scipy, matplotlib и другие.
Для пользователей MATLAB / GNU Octave освоение материала с точки зрения программного кода не составит труда,
поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из python-библиотек.
Непараметрические методы спектрального анализа
Нередко перед исследователями встаёт вопрос анализа характеристик сигнала, процесса или явления.
Одним из инструментов по определению таких характеристик является спектральный анализ.
Методы спектрального анализа можно разделить на две большие группы:
1. параметричесие методы;
2. непараметрические методы.
Для применения параметрических методов требуется априорное знание о параметрах исследуемого объекта, в случае
непараметрических методов - не требуется. Именно о последних и пойдет речь в данном семинаре.
Допущение: Будут рассматриваться стационарные в широком смысле (WSS - wide-sense stationary)
случайные процессы.
Спектр мощности для случайного в широком смысле процесса x(n) (где n - номер временного отсчета) представляет из
себя ничто иное, как преобразование Фурье автокорреляционной функции данного процесса [1, 393]:
Px (ejω ) =
∞
∑ rx (k)ejkω
−∞
(1)
где ω - это циклическая частота, а k - номер частотного отсчета (индекс частоты).
На конечном интервале автокорреляционная функция примет вид:
r^(k) =
1
N
N−1
∑ x(n + k)x∗ (n)
n=0
(2)
где N - длина последовательности временных отсчетов.
Метод периодограмм
Метод периодограмм
Одним из самых простых и популярных представителей группы непараметрических методов является метод периодограмм,
предложенный Артуром Шустером ещё в конце XIX века. Рассмотрим математическое описание данного метода.
Для начала, в качестве ограничения зададим условие, непозволяющее нашему сигналу
интервала:
x(n) выходить за пределы
xN (n)
=
x(n), 0 ≤ n ≤ N
{
0,
otherwise
(3)
Следовательно, xN (n) - это результат перемножения сигнала с оконной функцией прямоугольного вида:
xN (n)
= ωR (n)x(n)
(4)
Приняв во внимание формулу (3), переопределим формулу (2) через свертку:
r^(k)
1
=
xN (k)
N
∗ xN (−k)
(5)
Тогда преобразование Фурье автокорреляционной функции даст следующий результат:
P^Per (ejω )
=
1
∗ (ejω )
XN (ejω )XN
N
1
∣∣XN (ejω )∣∣ 2
=
N
(6)
Следовательно, периодограмма пропорциональна квадрату амплитуды преобразованию Фурье дискретного времени (DTFT discrete-time Fourier transform), а значит вполне может быть вычислена через алгоритм БПФ (FFT) на этапе программной
реализации.
В python метод периодограмм реализован в рамках библиотеки scipy.signals в виде метода periodogram.
Возвратимся к формуле (4). Было отмечено, что периодограмма пропорциональна результату перемножения сигнала с
оконной функцией ω(n), при условии, что данная функцию является прямоугольной. Однако, нужно отметить, что оконная
функция может быть и других форм.
В методе periodogram библиотеки scipy форма окна определяется параметром window (полный список
доступных форм можно посмотреть по данной ссылке).
Периодограмма с использованием непрямоугольного окна часто называется модифицированной:
P^M (ejω )
∣2
1 ∣ ∞
−jnω
=
∣ ∑ x(n)ω(n)e
∣
NU ∣n=−∞
∣
(7)
где N - это длина окна, а
U - это константа [1, с. 410]:
1 N−1
U=
∑ |ω(n)|2
N n=0
(8)
которая показывает асимптотическую несмещенность (unbiased) модифицированной периодограммы.
которая показывает асимптотическую несмещенность (unbiased) модифицированной периодограммы.
Методы Бартлетта и Уэлча
Рассмотрим более последовательные оценки мощностных спектров. Предпосылкой является наблюдение, что, при
увеличении длины последовательности N до бесконечности, математическое ожидание периодограммы стремится к
Px (ejω ):
lim E{P^Per (ejω )
N→∞
} = Px (ejω )
(9)
Соответственно, если мы найдём последовательную оценку мат. ожидания E{P^Per (ejω )}, то оценка Px (ejω ) так же будет
последовательной. Для этого можно применить классическое усреднение по некоторой выбоке реализаций.
Конечно, в реальных системах более реалистичным является случай, когда вместо сбора достаточного количества
реализаций процесса, мы исследуем сигнал достаточной длины, который разбивается на последовательности (sequences),
а уже те, в свою очередь, используются для усреднения (рис.1).
Рис. 1. Разбиение
x(n) на неперекрывающиеся последовательности [1, c. 413].
В литературе такой подход называется методом Бартлетта [2, c. 332]:
1
P^B (ejω ) =
N
K−1 ∣L−1
∑ ∣∣∑ x(n
i=0 ∣ n=0
∣2
∣
∣
−jnω ∣
+ iL)e
(10)
где K - это количество неперекрывающихся ( non-overlapping) последовательностей длинной
говоря, перед нами формула усреднения периодограмм.
L каждая, а N = KL. Иначе
Однако, и это ещё не всё. В 1967 году Ф.Д. Уэлч предлагает метод, который позже будет носить его же имя [2, c.333][3].
Подразумеваются следующие отличия от метода Бартлетта:
1) разбиение сигнала в том числе на пересекающиеся (overlapping) последовательности;
2) применение не только прямоугольных оконных функций (модифицированных периодограмм).
В python метод Уэлча реализован в рамках библиотеки scipy.signals в виде метода welch.
Применение непрямоугольных окон позволяет достичь больших степеней свободы в вопросах перекрытия (overlapping) [4].
При этом, используя перекрывающиеся последовательности, мы повышаем общее количество фрагметов сигнала. Как
следствие, периодограмма Уэлча будет менее осциллирующей (изрезанной), чем периодограмма Бартлетта [2, c.333].
Взаимосвязь между программными реализациями методов
Можно отметить следующую тенденции: метод Уэлча является общим случаем для методов Бартлетта и
модифицированной периодограммы, а значит и для самого метода периодограмм. Именно это наблюдение легло в основу
архитектуры методов в рамках реализации их на Python в рамках библиотеки scipy.
Моделирование
In [1]:
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
%matplotlib inline
В качестве примера рассмотрим гармонический сигнал следующего вида:
In [2]:
w_1 = 40 # frequency of the 1st component of the signal (Hz)
w_2 = 60 # frequency of the 2nd component of the signal (Hz)
a = 0.5 # magnitude of the 1st component of the signal
b = 1.0 # magnitude of the 2nd component of the signal
Зададим временной интервал:
In [3]:
Nsub = 10 # number of subsequences
t = np.array([i for i in range(1,301*Nsub)])/1000 # time samples (s)
fs = 1 / (t[1]-t[0]) # sampling frequency (Hz)
Nfft = int(3e3)
Моделируем сигнал:
In [4]:
x = a*np.cos(2*np.pi*w_1*t) + b*np.sin(2*np.pi*w_2*t) # considered signal
f = fs*np.array([i for i in range(int(len(x)))]) / len(x) # frequencies
In [5]:
# Plot results
plt.subplots(1, 1, figsize=(12, 4), dpi=75)
plt.plot(t[:200], x[:200])
plt.ylabel('Signal magnitudes')
plt.xlabel('Time (s)')
plt.title('Signal')
plt.xlim([0, 0.2])
plt.grid(True)
plt.tick_params(axis ='x', rotation = 45)
plt.tight_layout()
Построим частотный спектр амплитуд ДПФ:
In [6]:
FFT = np.fft.fft(x, n=Nfft) # Fast Fourier Transform
amps = np.abs(FFT) / (len(FFT) / 2) # magnitudes of FFT
l = int(len(f)/4)
plt.subplots(1, 1, figsize=(12, 4), dpi=80)
plt.stem(f[:l], amps[:l], use_line_collection=True)
plt.ylabel('FFT magnitudes')
plt.xlabel('Frequencies (Hz)')
plt.title('Signal')
plt.grid(True)
plt.xticks(np.arange(0, f[l], 10))
plt.yticks(np.arange(0, max(amps)+0.1, .1))
plt.tick_params(axis ='x', rotation = 45)
plt.xlim([0, 240])
plt.tight_layout()
Моделируем аддитивный шум:
In [7]:
np.random.seed(42)
n = 2*np.random.randn(len(t)) # white Gaussian noise
FFT = np.fft.fft(n, n=Nfft)
amps = np.abs(FFT) / (len(FFT) / 2)
plt.subplots(1, 1, figsize=(12, 4), dpi=80)
plt.stem(f[:len(amps)], amps, use_line_collection=True)
plt.ylabel('FFT magnitudes')
plt.xlabel('Frequencies (Hz)')
plt.title('Noise')
plt.yticks(np.arange(0, max(amps), .1))
plt.xlim([0, 1000])
plt.grid(True)
plt.tight_layout()
Добавляем шум к исходному сигналу:
In [8]:
y = x + n # signal + noise
In [9]:
plt.subplots(1, 1, figsize=(11, 4), dpi=75)
plt.plot(t[:200], y[:200])
plt.ylabel('Noised signal magnitudes')
plt.xlabel('Time (s)')
plt.title('Signal + noise')
plt.xlim([0, 0.2])
plt.tick_params(axis ='x', rotation = 45)
plt.grid(True)
plt.tight_layout()
Попробуем проанализировать данный сигнал с помощью методов периодограмм и модифицированных периодограмм.
In [10]:
windows = ['hamming', None]
plt.subplots(1, 1, figsize=(11, 4), dpi=100)
for window in windows:
if window == None:
label = 'rectangular'
else:
label = window
f, Pxx_den = signal.periodogram(y, fs=fs, scaling='spectrum', nfft=Nfft, window=window)
plt.semilogy(f[1:], Pxx_den[1:], label=label)
plt.ylabel('Spectrum')
plt.xlabel('Frequencies (Hz)')
plt.title('Periodogram')
plt.xticks(np.arange(0, max(f), 10))
plt.tick_params(axis ='x', rotation = 70)
plt.legend(loc='best')
plt.grid(True)
plt.tight_layout()
Две составляющие полезного сигнала, конечно, различимы, но при больших шумовых амплитудах методы могут и не
справится.
Попробуем применить метод Бартлетта для того же сигнала:
In [11]:
windows = ['bartlett','hamming','blackman']
plt.subplots(1, 1, figsize=(11, 4), dpi=100)
for window in windows:
if window == 'bartlett':
label = 'rectangular'
else:
label = window
f, Pxx_den = signal.welch(y, fs=fs, nperseg = len(x)/Nsub, noverlap=0, scaling='spectrum', nfft
=Nfft, window=window)
plt.semilogy(f, Pxx_den, label=label)
plt.legend()
plt.ylabel('Spectrum')
plt.xlabel('Frequencies (Hz)')
plt.title('Bartlett')
plt.xticks(np.arange(0, max(f), 10))
plt.tick_params(axis ='x', rotation = 70)
plt.legend(loc='best')
plt.grid(True)
plt.tight_layout()
Отмечаем лучшую различимость составляющих полезного сигнала в случае разбиения на последовательности.
Литература
1. Hayes M. H. Statistical digital signal processing and modeling. – John Wiley & Sons, 2009.
2. Солонина А. И. Цифровая обработка сигналов. Моделирование в MATLAB. – БХВ-Петербург, 2013.
3. "Digital Signal Processing: The Welch Method" by Prof. Dr.-Ing. Sascha Spors. URL: https://dspnbsphinx.readthedocs.io/en/nbsphinx-experiment/spectral_estimation_random_signals/welch_method.html
4. Solomon, Jr, O M. PSD computations using Welch's method. [Power Spectral Density (PSD)]. United States: N. p., 1991. Web.
4. Solomon, Jr, O M. PSD computations using Welch's method. [Power Spectral Density (PSD)]. United States: N. p., 1991. Web.
doi:10.2172/5688766. - p.38.
Цифровая обработка сигналов - 10
Title
Digital signal processing
Author
Alexander Kapitanov
Contact
sallador@bk.ru
Project lang
Python
Packages
numpy, scipy, matplotlib
License
GNU GPL 3.0
Введение
Перед вами обучающий материал по основам цифровой обработки сигналов с использованием средств языка
программирования Python. Предполагается, что читатель имеет базовые знания из области высшей математики, а также
владеет языком Python и хотя бы поверхностно знает различные python-библиотеки - numpy/scipy, matplotlib и другие.
Для пользователей MATLAB / GNU Octave освоение материала с точки зрения программного кода не составит труда,
поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из python-библиотек.
Усреднение по частоте и по времени
Этот раздел посвящен ещё одной важной теме, в которой разработчики часто путаются при создании приложений цифровой
обработки сигналов. Посмотрим, как меняется спектр сигнала при его накоплении по времени и по частоте. Для этого
зададим входное гармоническое воздействие:
$s(t) = A \cdot cos(\frac{2\pi\cdot t}{T})$,
и добавим к нему аддитивный белый Гауссовский шум (нормальное распределение) AWGN :
Функция плотности вероятности: $f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{- \frac{(x-\mu)^2}{2\sigma^2}}$
где $\mu$ - математическое ожидание (среднее значение случайного процесса), а $\sigma$ - среднеквадратическое
отклонение.
Таким образом, входной сигнал:
$s(t) = A \cdot cos(\frac{2\pi\cdot t}{T}) + N(\mu,\sigma)$.
In [1]:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings("ignore", message="numpy.dtype size changed")
warnings.filterwarnings("ignore", message="numpy.ufunc size changed")
from scipy.fftpack import fft, fftshift
from scipy.signal.windows import kaiser, flattop
# Matplotlib default params
plt.rcParams['axes.facecolor'] = 'white'
plt.rcParams['axes.edgecolor'] = 'white'
plt.rcParams['axes.grid'] = True
plt.rcParams['grid.alpha'] = 1
# plt.rcParams['legend.loc'] = 'best'
Для удобства анализа напишем функцию signals_compare , цель которой - построение графиков спектра от входного
зашумленного сигнала при различных частотах freq .
Параметр l задает количество усреднений по частоте и времени.
Основной цикл: На вход системы поступает сигнал длины n*l , где l - количество усреднений, n - длина БПФ.
1. Вычисляем БПФ сигнала длиной n ,
2. Вычисляем сумму сигналов длиной n по l разбиений (усреднений), от полученной суммы вычисляем БПФ,
3. Вычисляем l БПФ от сигналов длины n , а затем полученные результаты усредняем.
Примечания:
Очевидно, что суммирование серий БПФ должно производиться после взятия операции модуля, т.к. при сложении
компонент с различной фазой возможна потеря информации (сигнала).
Параметры частот подбираются специальным образом с целью показать существующие нюансы.
Длина БПФ во всех случаях задана постоянной и равна N = 512 отсчётов.
Для удобства анализа рассматриваются нормированные спектры в логарифмическом масштабе.
Таким образом, посмотрим на спектральные составляющие во всех трех случаях:
In [2]:
def freqtime_compare(freq=201, suptitle='', l=1):
n = 512
m = n*l
# Add AWGN
np.random.seed(42)
awgn = np.random.normal(0, 9*1e-2, m)
# Input signal
t = np.linspace(0, 1, m)
x = np.cos(2*np.pi*freq*t) + awgn
x1 = x.reshape(l, n)
x2 = x.reshape(l, n).sum(0)
# FFT
Xx = np.abs(fft(x[:n], n))[:n//2]
X1 = (np.abs(fft(x1, n))).sum(axis=0)[:n//2]
X2 = np.abs(fft(x2, n))[:n//2]
Xxlog = 20*np.log10(Xx / Xx.max())
X1log = 20*np.log10(X1 / X1.max())
X2log = 20*np.log10(X2 / X2.max())
fn = np.linspace(0, 0.5, n//2)
# Plot
plt.figure(figsize=(14, 2), dpi=120)
plt.suptitle(suptitle)
plt.subplot(1, 3, 1)
plt.plot(fn, Xxlog, color='C0', label=f'N={n}')
plt.ylim([-60, 0])
plt.legend(loc='upper right')
plt.subplot(1, 3, 2)
plt.plot(fn, X1log, color='C2', label='Avg (freq)')
plt.ylim([-60, 0])
plt.legend(loc='upper right')
plt.subplot(1, 3, 3)
plt.plot(fn, X2log, color='C3', label='Avg (time)')
plt.ylim([-60, 0])
plt.legend(loc='upper right')
Число усреднений: 1
При отсутствии усреднения по частоте или времени графики спектров полностью совпадают с модулем БПФ исходного
сигнала.
Левый график: БПФ сигнала длины N
Средний график: БПФ усредненного по частоте сигнала,
Правый график: БПФ усредненного по времени сигнала.
In [3]:
freqtime_compare(freq=121*1, l=1, suptitle='NumAverage = 1')
freqtime_compare(freq=121*1, l=1, suptitle='NumAverage = 1')
Число усреднений: 15 и 150, частота сигнала кратна числу усреднений
Увеличивая число усреднений, начинают изменяться спектры при накоплении сигналов в частотной и временной областях. В
частном случае, когда частота сигнала кратна числу усреднений, имеем следующее:
Усреднение по частоте
Спектр не меняет своего амплитудного значения на частоте сигнала,
На остальных частотах происходит усреднение некореллированного белого шума
Снижается уровень шумовых выбросов,
Уровень шума выходит на определенный уровень,
Если число усреднений стремится к бесконечности - спектр шума спрямляется в постоянную величину.
Усреднение по времени
Отношение сигнал шум (Signal noise ratio, SNR) увеличивается пропорционально увеличению усреднений,
Уровень шума уменьшается.
In [4]:
l_avg = 15
freqtime_compare(freq=121*l_avg, l=l_avg, suptitle=f'NumAverage = {l_avg}')
In [5]:
l_avg = 150
freqtime_compare(freq=121*l_avg, l=l_avg, suptitle=f'NumAverage = {l_avg}')
Число усреднений: 15, частота сигнала не кратна числу усреднений
Увеличивая число усреднений, начинают изменяться спектры при накоплении сигналов в частотной и временной областях. В
случае, когда частота сигнала не кратна длине БПФ, усреднение по времени даёт совершенно противоположные
результаты.
Усреднение по частоте
Те же свойства, что и ранее.
Те же свойства, что и ранее.
Усреднение по времени
Уровень шума существенно возрастает,
Выбросы шума по-прежнему не сглаживаются.
In [6]:
freqtime_compare(freq=1210, l=15, suptitle='Break input phases')
Как видно, усреднение по времени приводит к разным результатам в зависимости от кратности частоты сигнала длине БПФ.
Для того, чтобы понять различия в результатах, посмотрим на зашумленный сигнал во временной области в обоих случаях.
In [7]:
def time_compare(freq=201, l=1):
n = 512
m = n*l
np.random.seed(42)
x = np.cos(2*np.pi*freq*np.linspace(0, 1, m)) + np.random.normal(0, 9*1e-1, m)
y = x.reshape(l, n).sum(axis=0) / l
plt.figure(figsize=(9, 3), dpi=80)
plt.plot(y, color='C'+str(l), label=f'Averages = {l}')
plt.legend(loc='upper left')
plt.xlim([0, n])
plt.tight_layout()
Вариант 1: Начальные фазы усредняемых сигналов совпадают
In [8]:
time_compare(freq=512, l=64)
Вариант 2: Начальные фазы усредняемых сигналов различаются
In [9]:
time_compare(freq=512, l=65)
Из представленных выше графиков видно, что если фазы суммируемых компонент совпадают - форма сигнала сохраняется.
В противном случае, форма сигнала представляет собой шумоподобный случайный процесс.
Таким образом, пользоваться усреднением по времени в общем случае - нельзя. Исключение составляют системы, в
которых начальные фазы сигналов, из которых складывается результирующий сигнал, одинаковы. Очевидно, что это
частный случай, который практически невозможен на практике в реальных системах цифровой обработки.
Для усреднения модулей спектральных отсчетов по частоте зависимости от начальной фазы нет, поэтому результирующий
спектр сглаживается при увеличении числа усреднений. На следующем графике изображены амплитудные спектры всех
компонент, а также результирующий спектр, равный сумме всех спектральных выборок.
In [10]:
def freq_only(l=32, n=512):
# Initial Parameters
m = l*n
freq = l*(n/4 - 1.5374)
# Input signal
np.random.seed(42)
x = np.cos(2*np.pi*freq*np.linspace(0, 1, m)) + np.random.normal(0, 4*1e-1, m)
x = x.reshape(l, n)
y1 = np.abs(fft(x, n))
y2 = y1.sum(axis=0)
y1log = 20*np.log10(y1.T / y1.max(axis=1))
y2log = 20*np.log10(y2 / y2.max())
plt.figure(figsize=(14, 4), dpi=120)
plt.subplot(1, 2, 1)
plt.plot(y1log[:n//2,:6], linewidth=1.25)
plt.ylim([-30, 0])
plt.xlim([n//4-n//8, n//4+n//8])
plt.subplot(1, 2, 2)
plt.plot(y2log[:n//2], label='Spectrum (average)')
plt.ylim([-30, 0])
plt.xlim([n//4-n//8, n//4+n//8])
plt.legend()
plt.tight_layout()
freq_only(n=1024)
Полифазное быстрое преобразование Фурье
В связи с тем, что в некоторых случаях при усреднении сигнала по времени, мы получали выигрыш в отношении сигнал-шум,
попробуем использовать это для получения лучших частотных характеристик сигнала.
Под полифазным БПФ понимается следующий алгоритм цифровой обработки сигналов:
на вход системы поступает L сигналов по N отсчётов (полная длина выборки M = L*N )*
на выборку длины M накладывается оконная функция,
выборки длиной N суммируются по отсчётам,
от результирующей выборки вычисляется БПФ.
* - на следующем шаге наложение оконной функции может отсутствовать.
Входной сигнал $x(k), k = 0, ..., M-1$ длительностью $M$ умножается на оконную функцию $w(k), k = 0, ..., M-1$. Затем $x(k)$
сигнал разбивается на $L$ компонент по $N$ отсчётов, которые складываются друг с другом, образуя суммарный сигнал
$y(k), k = 0, ..., N-1$. От полученного сигнала вычисляется преобразование Фурье.
Посмотрим, как выглядит спектр полифазного БПФ при небольшой длине выборки N . Зададим:
N - длина исходного сигнала,
M - длина слагаемых для полифазной схемы,
L - количество разбиений.
Входной сигнал - сумма двух гармонических воздействий с разными частотами f1 и f2 . Шумы отсутствуют. Оконная
функция не применяется. Построим графики модулей спектров для исходного сигнала и сигнала, полученного в результате
разбиений на L компонент и дальнейшего суммирования во временной области.
In [11]:
# Number of samples: N
# Number of parts: L
# Total length of signal: M
N, L = 16, 3
M = N*L
# Input signal
t = np.linspace(0, 1, M)
f1, f2 = L, 4*L
x = np.cos(2*np.pi*f1*t) + np.cos(2*np.pi*f2*t)
y = x.reshape(L, N).sum(0)
# FFT - M size
XM = np.abs(fft(x, M))[:M//2]
XM /= XM.max()
# FFT - N size
XN = np.abs(fft(y, N))[:N//2]
XN /= XN.max()
# Interpolated spectrum
XZ = np.zeros(M//2)
#XZ[::L] = XM[::L]
XZ[::L] = XN
На следующем графике представлено два сигнала во временной и частотной областях:
исходный сигнал длины N ,
суммарный сигнал длины M , полученный в результате суммы выборок L .
Как видно, спектры сигналов практически идентичны.
In [12]:
plt.figure(figsize=(12, 5), dpi=120)
plt.subplot(2, 2, 1)
plt.plot(x, '-o', markersize=6, color='C0', label='Input signal')
plt.legend(loc='upper right')
plt.subplot(2, 2, 2)
plt.plot(y, '-*', markersize=6, color='C1', label='Decimated signal')
plt.legend(loc='upper right')
plt.subplot(2, 2, 3)
plt.subplot(2, 2, 3)
plt.stem(XM, use_line_collection=True, linefmt='C2', basefmt='C2', label='Spectrum (signal)')
plt.legend(loc='upper right')
plt.subplot(2, 2, 4)
plt.stem(XZ, use_line_collection=True, linefmt='C3', basefmt='C3', label='Spectrum (decimated)')
plt.legend(loc='upper right')
plt.tight_layout()
Спектр полифазного БПФ полностью эквивалентен (в пределах погрешностей вычислений) спектру БПФ всей
последовательности, децимированной по количеству выборок, реализующих полифазный алгоритм. Иными словами, спектр
полифазного БПФ равен прореженному спектру исходной последовательности. Следующий рисунок отображает это
утверждение.
In [13]:
plt.figure(figsize=(12, 3), dpi=120)
plt.subplot(1, 3, 1)
plt.stem(XN,
use_line_collection=True,
label='Polyphase'
)
plt.legend(loc='upper right')
plt.subplot(1, 3, 2)
plt.stem(XM[::L],
use_line_collection=True,
label='Decimated'
)
plt.legend(loc='upper right')
plt.subplot(1, 3, 3)
plt.stem(XN-XM[::L],
use_line_collection=True,
label='Difference'
)
plt.ylim(1e-16*np.array([-2, 2]))
plt.legend(loc='upper right')
plt.tight_layout()
Потеря сигнала
Факт идентичности спектров может навести на мысль использовать БПФ меньшей длины. В частности, это актуально для
высоконагруженных приложений, где критично время вычисления или не достаточно ресурсов для вычисления БПФ
больших длин. Но так ли это на самом деле и всегда ли применима эта схема?
Посмотрим, что будет, если частоту одного из сигналов сдвинуть на 1 отсчёт (в понятиях спектральных компонент БПФ). В
этом случае частота становится не кратной длине разбиений.
In [14]:
# Input signal
N, L = 16, 5
M = N*L
t = np.linspace(0, 1, M)
f1, f2 = L+1, 4*L
x = np.cos(2*np.pi*f1*t) + np.cos(2*np.pi*f2*t)
y = x.reshape(L, N).sum(0)
# FFT
XM = np.abs(fft(x, M))[:M//2]
XN = np.abs(fft(y, N))[:N//2]
XM /= XM.max()
XN /= XN.max()
# Interpolated spectrum
XZ = np.zeros(M//2)
#XZ[::L] = XM[::L]
XZ[::L] = XN
plt.figure(figsize=(12, 5), dpi=120)
plt.subplot(2, 2, 1)
plt.plot(x, '-o', markersize=6, color='C0', label='Input signal')
plt.legend(loc='upper right')
plt.subplot(2, 2, 2)
plt.plot(y, '-*', markersize=6, color='C1', label='Decimated signal')
plt.legend(loc='upper right')
plt.subplot(2, 2, 3)
plt.stem(XM, use_line_collection=True, linefmt='C2', basefmt='C2', label='Spectrum (signal)')
plt.legend(loc='upper right')
plt.subplot(2, 2, 4)
plt.stem(XZ, use_line_collection=True, linefmt='C3', basefmt='C3', label='Spectrum (decimated)')
plt.legend(loc='upper right')
plt.tight_layout()
Как видно из следующего графика, сигнал на частоте f1 пропал из спектра полифазного БПФ. Известно, что спектр
полифазного БПФ равен децимированному спектру исходного сигнала. Следовательно, в результате децимации по частоте
эта спектральная компонента не вошла в рассматриваемую выборку (отсчеты берутся кратно L ).
Ранее мы выяснили, что при несовпадении начальных фаз выборок, формирующих суммарный сигнал, характеристики
такого сигнала ухудшаются. Форма сигнала меняется, а уровень спектральной компоненты существенно уменьшается в
связи с тем, что амплитуда суммарного сигнала падает.
В качестве доказательства построим графики сигналов на частотах f1 и f2 во временной области до суммирования и
после.
In [15]:
plt.figure(figsize=(12, 5), dpi=80)
plt.subplot(2, 2, 1)
plt.plot(np.cos(2*np.pi*f1*t), '-*', markersize=4, color='C0', label='Freq1')
for i in range(1, L):
plt.axvline(i*N, color='C4', linewidth=1.5)
plt.legend(loc='upper right')
plt.subplot(2, 2, 2)
plt.plot(np.cos(2*np.pi*f2*t), '-o', markersize=4, color='C2', label='Freq2')
plt.legend(loc='upper right')
plt.subplot(2, 2, 3)
plt.plot(np.cos(2*np.pi*f1*t).reshape(L, N).sum(0) / L, '-*', markersize=4, color='C0', label='Freq1
')
plt.ylim([-1, 1])
plt.subplot(2, 2, 4)
plt.plot(np.cos(2*np.pi*f2*t).reshape(L, N).sum(0) / L, '-o', markersize=4, color='C2', label='Freq2
')
plt.ylim([-1, 1])
plt.tight_layout()
Оконные функции
Ранее мы выяснили, что спектр полифазного сигнала (полифазного БПФ) эквивалентен разреженному спектру всей
последовательности (коэффициент децимации равен L ). При использовании сигналов, частота которых не кратна L в
результирующем спектре теряется информация. Дабы избежать потери сигнала, попробуем использовать оконную функцию,
которая "размазывает" спектр сигнала по частоте.
Для этих целей попробуем применить оконную функцию с плоской вершиной flattop window .
In [16]:
# Window function: flattop
Nfft = 64
win_freq = np.linspace(-1, 1, Nfft)
win_flat = flattop(Nfft) # from scipy
win_ffts = fftshift(np.abs(fft(win_flat, Nfft)))
win_ffts = win_ffts / np.amax(win_ffts, axis=0) + np.nextafter(0,1)
win_logs = 20*np.log10(win_ffts)
# Plot results
# Plot results
plt.figure(figsize=(12, 3), dpi=120)
plt.subplot(1, 2, 1)
plt.plot(win_flat, '-o', markersize=4, label='Window function')
plt.legend(loc='upper right')
plt.xlim([0, Nfft-1])
plt.subplot(1, 2, 2)
plt.plot(win_freq, win_logs,'-*', markersize=4, color='C3', label='Spectrum')
plt.xlim([-20/Nfft, 20/Nfft])
plt.ylim([-90, 0])
plt.legend(loc='upper left')
plt.tight_layout()
Умножим полный сигнал длительностью N на оконную функцию. Затем разобьём этот сигнал на L выборок по N
отсчётов. От суммы полученных выборок вычислим БПФ длиной M .
После умножения исходного сигнала на оконную функцию результирующие спектральные компоненты расширяются. В
идеале необходимо подобрать такое "расширение", чтобы не потерялся ни один спектральный отсчёт.
In [17]:
N, L = 16, 5
M = N*L
# Input signal + Window Function
#wn = kaiser(M, beta=13)
wn = flattop(M)
t = np.linspace(0, 1, M)
f1, f2 = 2*L-1, 4*L-1
x = np.cos(2*np.pi*f1*t) + np.cos(2*np.pi*f2*t)
x *= wn
y = x.reshape(L, N).sum(0)
# FFT - M size
XM = np.abs(fft(x, M))[:M//2]
XM /= XM.max()
# FFT - N size
XN = np.abs(fft(y, N))[:N//2]
XN /= XN.max()
# Interpolated spectrum
XZ = np.zeros(M//2)
#XZ[::L] = XM[::L]
XZ[::L] = XN
plt.figure(figsize=(12, 5), dpi=120)
plt.subplot(2, 2, 1)
plt.plot(x, '-o', markersize=6, color='C0', label='Input signal')
plt.legend(loc='upper right')
plt.subplot(2, 2, 2)
plt.plot(y, '-*', markersize=6, color='C1', label='Decimated signal')
plt.legend(loc='upper right')
plt.subplot(2, 2, 3)
plt.stem(XM, use_line_collection=True, linefmt='C2', basefmt='C2', label='Spectrum (signal)')
plt.legend(loc='upper right')
plt.subplot(2, 2, 4)
plt.stem(XZ, use_line_collection=True, linefmt='C3', basefmt='C3', label='Spectrum (decimated)')
plt.legend(loc='upper right')
plt.tight_layout()
plt.tight_layout()
Как видно, применение оконной функции позволило не потерять информацию по частотам f1 и f2 , несмотря на то, что
обе не кратны количеству разбиений L .
Примеры полифазного БПФ
Ниже приведены различные комбинации выполнения усреднения по времени с последующим вычислением БПФ.
Рассмотрим основные особенности.
In [18]:
def calculate_ffts(f1, f2, n, step, beta=7, use_win=False):
# Time vector
m = n*step
t = np.linspace(0, 1, m)
# Add AWGN
np.random.seed(42)
awgn = np.random.normal(0, 2*1e-3, m)
# Signal, window function, polyphase FFTs
wn = kaiser(m, beta=beta)
x = np.cos(2*np.pi*f1*t) + np.cos(2*np.pi*f2*t) + awgn
y = (x * wn).reshape(step, n).sum(0)
if use_win:
x *= wn
# FFT - M size
XW = np.abs(fft(x, n))[:n//2]
XW /= XW.max()
# FFT - N size
XN = np.abs(fft(y, n))[:n//2]
XN /= XN.max()
# Log spectrum
XWlog = 20*np.log10(XW / XW.max())
XNlog = 20*np.log10(XN / XN.max())
return XWlog, XNlog
nfft, step = 2048, 4
Xw = np.zeros([6, nfft//2])
Xn = np.zeros([6, nfft//2])
Xw[0],
Xw[1],
Xw[2],
Xw[3],
Xw[4],
Xw[5],
Xn[0]
Xn[1]
Xn[2]
Xn[3]
Xn[4]
Xn[5]
=
=
=
=
=
=
calculate_ffts(182,
calculate_ffts(184,
calculate_ffts(184,
calculate_ffts(184,
calculate_ffts(184,
calculate_ffts(185,
312,
312,
312,
192,
200,
191,
xs_titles = ['Loss signal at 1st freq',
'Determine both freqs',
nfft,
nfft,
nfft,
nfft,
nfft,
nfft,
step,
step)
step,
step,
step,
step)
use_win=True)
beta=150)
beta=300)
beta=1)
'Determine both freqs',
'Change window function',
'Bad window function',
'No window function',
'Improve freq resolution',
]
Будем рассматривать сумму двух гармонических сигналов с добавлением белого шума. Перед вычислением полифазного
БПФ всегда накладывается оконная функция Кайзера с переменным параметром beta , но для сравнения наложение окна
на исходный сигнал может отсутствовать. Для удобства построения графиков написана специальная функция, принимающая
на вход следующие параметры:
f1 , f2 - частоты гармонических колебаний,
nfft - длина БПФ,
step - количество усреднений (эквивалентно параметру l ),
use_win - использование оконной функции Кайзера (True/False)
beta - параметр оконной функции Кайзера.
Параметры: длина БПФ nfft = 2048 и количество усреднений step = 4 не меняются.
Результаты:
1. f1 = 182 , f2 = 312 - потеря сигнала на первой частоте (некратной разбиению) в связи с неправильным выбором
оконной функции (спектр не расширяется, начальные фазы суммируемых компонент - различны),
2. f1 = 184 , f2 = 312 - улучшение отношения сигнал-шум в связи с точным попаданием частот (начальные фазы
суммируемых компонент одинаковы, искажение сигнала не происходит, уровень не падает),
3. f1 = 184 , f2 = 312 , beta=150 - при увеличении параметра beta происходит расширение спектральных
компонент, что может привести к неразличимости сигналов (см. далее),
4. f1 = 184 , f2 = 192 , beta=300 - из-за неверного выбора параметра оконной функции произошло наложение двух
стоящих рядом гармоник. В этом случае при полифазной обработке невозможно различить два сигнала.
5. f1 = 184 , f2 = 192 , beta=1 - отсутствие оконной фильтрации ожидаемо приводит к совпадению спектра
исходного сигнала и спектра сигнала при полифазной обработке.
6. f1 = 185 , f2 = 191 - сигналы сдвинуты ещё ближе друг к другу. В случае полифазной обработки с правильно
выбранным параметром оконной функции возможно получить различимость двух гармоник, однако в исходном спектре
эти гармоники сливаются в одну.
In [19]:
plt.figure(figsize=(14, 8), dpi=120)
for i in range(6):
plt.subplot(3, 2, i+1)
plt.title(xs_titles[i])
plt.plot(Xw[i], '--', linewidth=2, label='Spectrum')
plt.plot(Xn[i], label='Polyphase', linewidth=2, color='C'+str(1+i))
plt.xlim([16, 140])
plt.ylim([-110, 0])
plt.xlabel('Freq (Hz)')
plt.legend(loc='upper right')
plt.tight_layout()
Выводы
Физическая природа улучшения характеристик сигналов при их усреднении выражена в увеличении времени наблюдения
за процессом. Чем дольше мы наблюдаем за физическим явлением, тем больше информации о нем мы можем дать. На
основании этого можно сделать ряд выводов, которые помогут лучше понять возможности использования тех или иных
алгоритмов усреднения сигналов.
Использование усреднения по частоте позволяет получить качественное представление модуля спектра сигнала,
уменьшив шумовые выбросы.
Детерминированные сигналы не меняют своего уровня по амплитуде, а случайные шумовые компоненты сглаживаются
в процессе усреднения.
Использование усреднения по времени приводит к разным результатам и в общем случае должно использоваться с
большой осторожностью:
спектр полифазного БПФ совпадает с разреженным спектром исходной (длинной) последовательности,
при несовпадении начальных фаз гармонических сигналов, участвующих в суммировании, происходит искажение
результирующего сигнала. Это отражается на форме сигнала во временной области, а также на уровне сигнала,
при совпадении начальных фаз гармонических сигналов возможно получить лучшие показатели отношения сигналшум и визуально получить лучшую разрешающую способность,
для качественного использования полифазного БПФ рекомендуется использовать оконные функции с правильно
подобранными параметрами, влияющими на ширину спектра сигнала.
In [20]:
def signals_compare(freq=280, suptitle=''):
N, L = 512, 64
M = N*L
# Input signal
np.random.seed(42)
x1 = np.cos(2*np.pi*freq*np.linspace(0, 1, M)) + np.random.normal(0, 5*1e-3, M)
x2 = np.copy(x1[:N])
x3 = x1.reshape(L, N).sum(0)
# FFT - M size
XM = np.abs(fft(x1, M))[:M//2]
XN = np.abs(fft(x2, N))[:N//2]
XS = np.abs(fft(x3, N))[:N//2]
XNlog = 20*np.log10(XN / XN.max())
XMlog = 20*np.log10(XM / XM.max())
XSlog = 20*np.log10(XS / XS.max())
fn = np.linspace(0, 0.5, N//2)
fm = np.linspace(0, 0.5, M//2)
plt.figure(figsize=(12, 3), dpi=80)
plt.suptitle(suptitle)
plt.subplot(1, 3, 1)
plt.plot(fn, XNlog, color='C2', label=f'NFFT = {N}')
plt.ylim([-110, 0])
plt.legend(loc='upper right')
plt.subplot(1, 3, 2)
plt.plot(fn, XSlog, color='C4', label=f'NFFT = {N} + Sum')
plt.ylim([-110, 0])
plt.legend(loc='upper right')
plt.subplot(1, 3, 3)
plt.plot(fm, XMlog, color='C3', label=f'NFFT = {M}')
plt.ylim([-110, 0])
plt.legend(loc='upper right')
plt.tight_layout()
signals_compare(freq=256, suptitle='Equal start phases')
signals_compare(freq=258, suptitle='Not equal start phases')