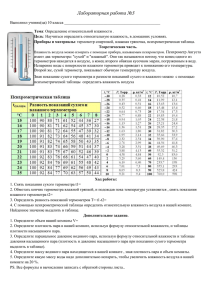
1.3.Зависят ли коэффициенты преобразования медного и платинового термометров сопротивления от температуры, если известно, что сопротивления связаны с температурой выражениями Rt – Ro(l+at) для медного термометра, Ri=Ro(l+At+BR) для платинового термометра. Решение: Коэффициент чувствительность преобразования – это S подобен характеристика чувствительности, измерительного прибора, но а коэффициент преобразования – характеристика измерительного преобразователя. Входным сигналом термометра является температура, а выходным сигналом – электрическое сопротивление термометра. Коэффициент преобразования для медного термометра SM = dRldt = Raα; для платинового термометра Sn = dR/dt = Ro (А + B). Следовательно, для медного термометра коэффициент преобразования не зависит от температуры, а для платинового – изменяется с изменением температуры. 1.4. При проверке автоматического потенциометра со шкалой 0 – 500 °C для градуировки типа К (никельхром – никельалюминий, хромель-алюмель) выяснилось, что стрелка и перо прибора смещены относительно нулевой отметки на 10 °C в сторону завышения. Как должна быть учтена эта систематическая погрешность измерения температуры при обработке диаграммной бумаги, например, на отметке 430 °C? Решение: Для учета систематической погрешности все результаты, считанные с диаграммной бумаги в градусах, необходимо перевести по градуировочным таблицам [1] в милливольты, прибавить поправку в милливольтах, а затем результат снова перевести в градусы. Смещение стрелки и пера от 0 до 10 °C соответствует для градуировки ХК изменению термо-ЭДС на 0,65 мВ. По диаграммной бумаге отсчитано 430 °C, термо-ЭДС для 430 °C градуировки ХК - составляет 34,12 мВ, с учетом поправки 34,12+(-0,65) = 33,47 мВ. Определяем значение температуры t = 422,75 °C. 1.5. При испытании измерительной системы дифманометр – вторичный прибор в нормальных условиях эксплуатации прибор устанавливался в конечной точке шкалы при следующих значениях перепада давления ∆рi на входе в дифманометр: i 1 2 3 4 5 6 7 8 ∆рi,кПа 84,15 84,06 83,80 89,94 83,94 84,10 84,02 84,03 Затем было изменено напряжение питания измерительной системы на +10% Ụом. При этом прибор устанавливался в конечной точке шкалы при следующих значениях перепада давления ∆рi на входе: i 1 2 3 4 5 6 7 8 ∆рi,кПа 83,85 83,73 83,82 83,76 83,84 83,82 83,83 83,75 Оцените погрешность показаний измерительной системы, вызванную отклонением напряжения питания. Как называется эта погрешность? Решение: Определим оценку наиболее вероятного значения перепада давления, соответствующего конечной точке шкалы прибора, при нормальных условиях [формула (1.3)]: ∆𝜌̃ = 84.15+84.06+83.80+83.90+83.94+84.10+84.02+84.03 8 = 672 8 = 84 кПа. Найдем оценку наиболее вероятного значения перепада давления при напряжении питания, составляющем 110 % UHом. ∆𝜌̃∗ = 83.85+83.73+83.82+83.76+83.84+83.82+83.82+83.83+83.75 8 = 640.4 8 = 83.8 кПа. Таким образом, можно найти оценку наиболее вероятного значения погрешности в конечной точке шкалы, вызванной изменением напряжения питания измерительной системы: ∆̃= ∆𝜌̃∗ − ∆𝜌̃ = 83,8 – 84 = -0,2 кПа. Эта погрешность называется дополнительной, так как она вызвана отклонением одной из влияющих величин (напряжения питания) от нормального значения. 1.6.Определите абсолютное и относительное изменение показаний газового манометрического термометра, вызванное изменением' барометрического давления от 100,45 до 96,45 кПа. Шкала прибора 0– 100 °C, что соответствует изменению давления от 0,67 до 0,92 МПа. Прибор показывает температуру 80 °C. Шкала прибора равномерная. Решение: Изменение барометрического давления составляет 4 кПа. Так как измерительные приборы манометрических термометров измеряют избыточное давление, то показания прибора будут завышены на 4 кПа. Шкала газового термометра равномерная, и по давлению диапазон шкалы составляет 250 кПа. Таким образом, показания термометра будут завышены на 100˖ 4 250 = 1,6 °C. Абсолютная погрешность на отметке 80 °C 𝛿= +1.6 80 ˖100=+2% 1.7.Для технического манометра класса 1,5 нормальная температура окружающей среды 20±5°С, рабочая температура +5/+ 50 °C. Одинаковыми ли погрешностями будут характеризоваться показания прибора при температуре окружающей среды 1=24, 1=10 и 1=55 °C при условии, что остальные влияющие величины имеют нормальные значения? Решение: При температуре 24 °C будет иметь место основная погрешность, так как нормальные условия работы прибора 20±5°С. При температуре 10 °C кроме основной погрешности будет иметь место дополнительное изменение показаний прибора от изменения температуры. Погрешность при температуре 55 °C не нормируется, так как она выходит за пределы рабочей области температур. 1.8. Одинаков ли предел допускаемой относительной погрешности измерения во всех -точках шкалы автоматического потенциометра? Решение: Нет. Для всех точек шкалы одинаков предел допускаемой абсолютной погрешности ∆0, определяемый классом точности средств измерений и диапазоном измерения. Предел допускаемой относительной погрешности 𝛿0 =∆0/𝑥𝑖 зависит от отметки шкалы хi. Чем меньше показания прибора по шкале, тем больше относительная погрешность. Поэтому диапазон измерения прибора нужно выбирать таким образом, чтобы измеряемая величина находилась в конце шкалы. 1.9. Было проведено однократное измерение термо-ЭДС автоматическим потенциометром класса 0,5 градуировки ХК со шкалой 200'– 600 °C. Указатель стоит на отметке 550 °C. Оцените, максимальную относительную погрешность измерения термоЭДС потенциометром на отметке 550 °C. Зависит ли относительная погрешность от показаний прибора? Условия работы нормальные. Решение: Если кроме класса потенциометра нет никаких других метрологических характеристик, то можно оценить только пределы допускаемой погрешности. Предел допускаемой погрешности в нашем случае определяется через класс К и диапазон измерения хк-хн потенциометра: 𝑥𝑘− 𝑥𝐻 ∆0 = −𝐾 100 Для потенциометров погрешность выражается в милливольтах [2]: хк = E (600°C, 0°С) = 49,11 мВ; хн = Е (200 °C, 0 °C) = 14,59 мВ; 49,11 − 14,59 − 0,5 = 0,1726 мВ. 100 Предел относительной погрешности на отметке 550 °C * ∆0 = 𝛿0 = ∆0 0.1726 100 = 100 = 0.386% 𝐸(550 °C, 0°C) 44.71 Предел допускаемой абсолютной погрешности одинаков для всех отметок шкалы, тогда как предел относительной погрешности увеличивается к началу шкалы. Например, на отметке 300 °C. 𝛿0 = 0.1726 22.88 100 = 0.754 % Поэтому диапазон измерения прибора нужно выбирать таким образом, чтобы измеряемая величина находилась в конечной части шкалы. 1.10 При градуировке расходомера в конечной точке шкалы объемным методом были получены следующие значения времени наполнения бака τ: i 1 2 3 4 5 6 7 8 9 τi, c 97.5 94.8 94.7 95.2 94.9 95.3 91.1 95.2 95.3 Предполагается, что эти значения времени распределены по закону Стьюдента. Объем бака V=507±0,1 л. Каким образом оценить значение расхода в конечной точке шкалы расходомера и как определить погрешность этой оценки, если систематическая погрешность измерения времени отсутствует? Решение: Найдем оценку наиболее вероятного значения времени наполнения бака [формула (1.3)] 𝜏= 94.5 + 94.8 + 94.7 + 95.2 + 94.9 + 95.3 + 95.1 + 95.2 + 95.3 = 95 𝑐. 9 Половина ширины доверительного интервала 𝜀𝑝 для распределения Стьюдента определяется по формуле (1.7) 0.0825 𝜀𝑝 = 3.36√ = 0.32 𝑐 9 Расход определяется по формуле Q -V/x. Измерения объема V и времени т являются взаимонезависимыми, поэтому погрешность градуировки расходомера вычисляется как результат косвенного измерения по формуле (1.1). ∆= ±√( 𝜕𝑄 𝜕𝑉 ∆𝑉)2 + ( 𝜕𝑄 𝜕𝜏 0.1 507 95 95 ∆𝜏)2 =±√( )2 + ( 0.32)2 = ±0.018 л/с. 1.11. Сопротивление термометра градуировки 10 П измеряется потенциометрическим методом. Оцените погрешность измерения температуры термопреобразователя сопротивления, если известно, что допустимое отклонение от градуировочных значений не должно превышать 0,3 °C. Термопреобразователь II класса, измеряемая температура t = 100 °C. Сопротивление образцовой катушки составляет Rк=10±0,01 Ом. Измерение падения напряжения осуществляется лабораторным потенциометром типа ПП-63 класса 0,05. Допустимое значение его основной погрешности, мВ, не превышает: ∆е ≤ ± (5˖10–4 U + 0,5 Uр), где U – показание потенциометра, мВ; Uр –цена деления шкалы реохорда, мВ. Значение тока, протекающего через сопротивление, равно 3 мА. Решение: Сопротивление термопреобразователя Rt=Rk(Ut/Uk).Падение напряжения на образцовой катушке Uk =10˖3 = 30 мВ. Сопротивление термопреобразователя при 1=100 °C (табл. П.18) Р100= 13,9113 Ом. Падение напряжения на термопреобразователе Ut= 13,9113˖3=41,73 мВ. Оценим предел допускаемой погрешности определения сопротивления термопреобразователя по формуле (1.1) ∆Rt/Rt ≤ √(∆𝑅𝑘 /𝑅𝑘 )2 +(∆𝑈𝑡 /𝑈𝑡 )2 + (∆𝑈𝑘 /𝑈𝑘 )2 Тогда ∆𝑅𝑘 /𝑅𝑘 <0,01/10 = 0,001 (по условию). ∆𝑈𝑡 подсчитывается по формуле ∆𝑈𝑡 = ± (5˖10-4 ˖41,73 + 0,5˖0,05) = ±0,0459 мВ; Отношение ∆𝑈𝑡 /𝑈𝑡 <± 0,0011, или ±0,11%. Величина ∆𝑈𝑘 <± (5˖10-4 -30 + 0,5˖0,05) = ±0,04 мВ. Отношение ∆𝑈𝑘 /𝑈𝑘 <±0,0013, или ±0,13%. Значение ∆𝑅𝑘 /𝑅𝑘 ≤± откуда ∆Rt<0.00274 Ом. √(0,001)2 + (0,0011)2 + (0,0013)2 =0,00197, Точность измерения сопротивления достаточно высока, однако изменение сопротивления термопреобразователя при изменении температуры от 0 до 100 °C также невелико и составляет 3,9113 Ом, поэтому относительная погрешность измерения' сопротивления уже составляет 𝛿 = ∆𝑅𝑡 (𝑅100 − 𝑅0 )100=0,0274/3,9113˖100=0,7%, что соответствует ∆tR≤0.712 °C Оценим предел допускаемой суммарной погрешности определениятемпературы с учетом погрешности термопреобразователя ∆tT=0,3°C (по условию) ∆𝑡Σ ≤ √∆𝑡𝑇2 + ∆𝑡𝑅2 = √0.32 + 0.7122 = ±0.773°C Таким образом, суммарная погрешность измерения температуры ∆𝑡Σ ≤ ±0.773°C 1.12 Каким образом оценить погрешность измерения температуры, если известно, что для медного термометра сопротивления R*0 =49,95 Ом и α*=4,25˖10-3 К-1. Градуировочные таблицы составлены для R0=50 Ом и α=4,28˖10-3 К-1. Решение: Погрешность, возникающая в результате того, что 𝑅0∗ =49,95 Ом и α*=4,25˖10-3К-1, будет систематической. Температура, определенная по градуировочным таблицам, t*=(𝑅𝑡∗ − 𝑅0 )/ 𝑅0 𝛼 Действительная температура 𝑡 = (𝑅𝑡∗ − 𝑅0∗ )/(𝑅0∗ 𝛼 ∗ ) Поправка к показаниям, определенным по градуировочным таблицам, 𝑅𝑡∗ −𝑅0∗ t-t*= 𝑅0∗ 𝛼 ∗ − 𝑅𝑡∗ −𝑅0 𝑅0 𝛼 . Для 𝑅𝑡∗ = 71.4 Ом и 𝑡 ∗ = 100 °C 𝑡 = 100 + 71.40 − 49.95 71.40 − 50.00 − = 101.04 °C 49.95 ∗ 4.25 ∗ 10−3 50.00 ∗ 4.28 ∗ 10−3 Погрешность имеет постоянный знак, и поэтому мы ее учитываем, введя поправку в измеренное значение температуры. В предыдущей задаче можно было определить интервал, в котором находится действительная температура, но вводить поправку было нельзя, поскольку знак и значение погрещности были неизвестны. 2.11.Будет ли изменяться термо-ЭДС термоэлектрического термометра типа ХК при изменении температуры рабочего конца, но при сохранении разности температур рабочего конца и свободных концов, например Е (300, 50 °C) и Е (600, 350°C)? Решение: При одинаковой разности температур рабочего и свободных концов термо-ЭДС, развиваемая термоэлектрическим термометром, будет одинаковой, если характеристика термометра линейная. Характеристика термоэлектрического термометра типа ТХК нелинейна, в силу чего и термоЭДС будут различными. Это легко пояснить с помощью табл. П.9 или рис.1: Е (300 °C, 50 °C) = Е (300 °C, О °C) - Е (50 °C, О °C) = 22,88-3,35= 19,53 мВ; Е (600 °C, 350 °C) = 21,97 мВ. 2.12. На рис. 2.1 изображена характеристика термоэлектрического термометра при температуре свободных концов, равной 0 °C. Как изменится его характеристика, если температура свободных концов увеличится? Решение: Термо-ЭДС, развиваемая термоэлектрическим термометром, уменьшится на E(t0, 0). Это соответствует смещению всей его характеристики вниз по оси Е на E(t0, 0) (рис. 2). Рис.2 2.13. Характеристика термоэлектрического термометра представлена на рис. 2.2, а. Какая зависимость из изображенных на рис 2.2, б будет характеризовать коэффициент преобразования термометра? Изменится ли его коэффициент преобразования при изменении температуры свободных концов? Решение: Коэффициент преобразования термоэлектрического термометра S=dE/dt изменяется в зависимости от температуры, так как E =f(t) нелинейна. Очевидно, что в начале характеристики с увеличением температуры рабочего конца коэффициент преобразования растет, а затем вследствие выравнивания темпа роста постоянному термо-ЭДС коэффициент преобразования значению. Следовательно, зависимость стремится к коэффициента преобразования от температуры будет соответствовать штриховой линии на рис. 2. Как следует из решения 2.12, при изменении 4 характеристика термоэлектрического термометра смещается так, что изменение t0 не вызовет изменения зависимости коэффициента преобразования от температуры. 2.14. В печь для поверки помещено несколько термоэлектрических термометров, о которых известно, что они стандартные, но их тип неизвестен. Свободные концы термометров помещены в термостат, температура в котором поддерживается постоянной, но ее значение также неизвестно. Можно ли определить тип термоэлектрических термометров, если температура в печи известна и может изменяться в интервале от 300 до 600 °C, а термо-ЭДС измеряется лабораторным потенциометром? Решение: Градуировку стандартных термоэлектрических термометров определить можно. Для этого следует измерить термо-ЭДС. По этим значениям нужно определить средний коэффициент преобразования исследуемых термометров на данном температурном интрвале и сравнить с коэффициентами преобразования стандартных термоэлектрических термометров по табличным данным на том же интервале температур. 2.15. На рис. 2.3 даны схемы измерения температуры поверхности медной пластины. В случае а электроды термоэлектрического термометра сварены вместе и затем приварены к пластине, в случае б каждый из электродов приваривался к пластине отдельно и между электродами нет непосредственного контакта. Учитывая большую теплопроводность меди и полагая плохой теплообмен пластины с окружающей средой, можно считать, что температура медной пластины во всех точках подсоединения к ней термоэлектродов одинакова. Будет ли термо-ЭДС обоих термометров одинакова при одинаковой температуре свободных концов? Решение: Термо-ЭДС, развиваемая обеими термоэлектрическими термометрами, будет одинакова. Из основных положений теории термоэлектрических термометров известно, что включение третьего проводника в цепь термометра не изменяет термо-ЭДС, если температура мест подсоединения этого проводника одинакова. 2.16. Введите поправку в показания термоэлектрического термометра и определите температуру рабочего конца, если известно, что термо-ЭДС термометра типа S (платинородий–платиновый) равна 3,75 мВ, а температура свободных концов 32 °C. Решение: Определим по табл. П.12, Е (32 °C, 0 °C) =0,185 мВ. Определяем термо-ЭДС термометра с учетом поправки Е (t, 0) = Е (t °C, 32 °C) + Е (32 °C, 0 °C) = 3,75 + 0,185 = 3,935 мВ. По табл. П.12 определяем соответствующую температуру t=469,7 °C. 2.17.Термоэлектрический термометр типа S (платинородий–платиновый) подсоединен к измерительному прибору ИП медными проводами (рис. 2.4). Изменится ли термо-ЭДС, если вместо медных проводов подсоединение будет осуществлено алюминиевыми проводами? Значения температур концов термометра остались прежними. Решение: В соответствии с теоремой о третьем проводнике термо-ЭДС термоэлектрического термометра не зависит от материала проводника, подключенного к свободным концам, если температура свободных концов одинакова. 2.18.Термоэлектрический термометр типа S (платинородий–платиновый) подключен к измерительному прибору медными проводами. Температура рабочего конца 700, свободных концов 20 °C. Изменится ли термо-ЭДС, если температура места подключения медного провода к платинородиевому термоэлектроду увеличилась до 100 °C, а температура места подключения медного провода к платиновому термоэлектроду осталась равной 20 °C. Градуировочная характеристика термоэлектрического термометра типа S приведена в табл. П.12. Термо-ЭДС пары платинородий–медь при температурах спаев 100 и 20 °C Е (100 °C, 20°С)= –0,077 мВ. Решение: Термо-ЭДС Е", действующая в цепи, изменится на Е' Е" = E(700°С, 20°C) – Е'(100 °C, 20°С) = 6,274 - 0,113 + 0,077 = 6,238 мВ. 2.19. Подключение термоэлектрического термометра к измерительному прибору осуществляется удлиняющими термоэлектродными проводами (рис. 2.5). Обязательным ли является требование равенства температур мест соединения t1и t2? Решение: Температуры t1 и t2 могут быть различными, если удлиняющие термоэлектродные провода электродам. этим Под термоэлектроидентичны подразумевается соответствующим отсутствие термо-ЭДС в термоэлектрическом термометре, составленном из электрода термометра и соответствующего удлиняющего термоэлектродного провода: EAC(t, t0)=0; EBD(t, t0)=0; В общем случае удлиняющие провода не термоэлектроидентичны электродам термометра, поэтому для. исключения возникновения паразитной термо-ЭДС в цепи прибора должны быть выполнены следующие условия: 1) термо-ЭДС, развиваемая термометром и удлиняющими проводами, в интервале температур 0—100 °C, должна быть одинаковой; 2) подключение удлиняющих проводов к термометру должно осуществляться с соблюдением полярности; 3) места соединения удлиняющих проводов с электродами термометра должны иметь одинаковую температуру. 2.20. На рис. 2.6 представлены характеристики различных термоэлектрических термометров. Укажите, какие из них можно подключить к измерительному прибору без удлиняющих термоэлектродных проводов обычными медными и при этом не будет возникать искажение термо-ЭДС. Решение: Термоэлектрический термометр 3 (см. рис. 2.6) на большом интервале температур не развивает никакой термо-ЭДС, поэтому он может подключаться к измерительному прибор медными проводами. Термометр 4 на этом же интервале температур развивает незначительную термо-ЭДС, он тоже-может подключаться без удлиняющих термоэлектродных проводов, если возникающие при этом погрешности укладываются в допустимые значения. Все остальные типы термометров должны подключаться к измерительному прибору с помощью удлиняющих термоэлектродных проводов.