ПРОВЕРКА СУЩЕСТВОВАНИЯ ТРЕНДА ВО ВРЕМЕННОМ РЯДУ

СОДЕРЖАНИЕ
1. ВВЕДЕНИЕ .......................................................................................................... 3
2. ОСНОВНЫЕ КОМПОНЕНТЫ ВРЕМЕННОГО РЯДА .................................. 6
3. ПРОВЕРКА СУЩЕСТВОВАНИЯ ТРЕНДА ВО ВРЕМЕННОМ РЯДУ....... 7
3.1. МЕТОД ПРОВЕРКИ РАЗНОСТИ СРЕДНИХ УРОВНЕЙ .................... 7
3.2. МЕТОД ФОРСТЕРА - СТЬЮАРТА ........................................................ 8
4. МЕТОД ЧОУ ПРОВЕРКИ СТАБИЛЬНОСТИ ТЕНДЕНЦИИ ..................... 12
5. ЗАКЛЮЧЕНИЕ ................................................................................................. 16
6. СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ ............. 17
2
1. ВВЕДЕНИЕ
В каждой сфере экономики встречаются явления, которые интересно и
важно изучать в их развитии, т.к. они изменяются во времени. С течением
времени изменяются цены, экономические условия, режим протекания того
или иного производственного процесса. Совокупность измерений подобного
рода показателей в течение некоторого периода времени и представляет
временной ряд.
Цели анализа временных рядов могут быть различными. Можно,
например, стремиться предсказать будущее на основании знаний прошлого,
пытаться выяснить механизм, лежащий в основе процесса, и управлять им.
Необходимо уметь освобождать временной ряд от компонент, которые
затемняют его динамику. Часто требуется сжато представлять характерные
особенности ряда.
Временным рядом называют последовательность наблюдений, обычно
упорядоченную во времени, хотя возможно упорядочение и по какому-либо
другому параметру. Основной чертой, выделяющей анализ временных рядов
среди других видов статистического анализа, является существенность
порядка, в котором производятся наблюдения.
Различают два вида временных рядов. Измерение некоторых величин
(температуры, напряжения и т.д.) производится непрерывно, по крайней мере
теоретически. При этом наблюдения можно фиксировать в виде графика. Но
даже в том случае, когда изучаемые величины регистрируются непрерывно,
практически при их обработке используются только те значения, которые
соответствуют дискретному множеству моментов времени. Следовательно,
если время измеряется непрерывно, временной ряд называется непрерывным,
если же время фиксируется дискретно, т.е. через фиксированный интервал
времени, то временной ряд дискретен.
Дискретные временные ряды получаются двумя способами:
3
– выборкой из непрерывных временных рядов через регулярные
промежутки
времени
(например,
численность
населения,
величина
собственного капитала фирмы, объем денежной массы, курс акции), — такие
временные ряды называются моментными;
– накоплением переменной в течение некоторого периода времени
(например, объем производства какого-либо вида продукции, количество
осадков, объем импорта), — в этом случае временные ряды называются
интервальными.
В эконометрии принято моделировать временной ряд как случайный
процесс, называемый также стохастическим процессом, под которым
понимается статистическое явление, развивающееся во времени согласно
законам теории вероятностей. Случайный процесс — это случайная
последовательность. Обычно предполагают, что эта последовательность идет
от минус до плюс бесконечности: {Xt}t=−∞, ..., +∞. Временной ряд— это лишь
одна частная реализация такого теоретического стохастического процесса:
x={xt}t=1, ..., T = (x1, ..., xT )', где T — длина временного ряда. Временной ряд x =
(x1, ..., xT )' также часто неформально называют выборкой. Обычно стоит
задача по данному ряду сделать какие-то заключения о свойствах лежащего в
его основе случайного процесса, оценить параметры, сделать прогнозы и т.п.
В литературе по временным рядам существует некоторая неоднозначность, и
иногда временным рядом называют сам случайный процесс {Xt}t=−∞, ..., +∞, либо
его отрезок {xt}t=1, ..., T, а иногда статистическую модель, которая порождает
данный случайный процесс.
Возможные значения временного ряда в данный момент времени t
описываются с помощью случайной величины xt и связанного с ней
распределения вероятностей p(xt). Тогда наблюдаемое значение xt временного
ряда в момент t рассматривается как одно из множества значений, которые
могла бы принять случайная величина xt в этот момент времени. Следует
отметить,
однако, что,
как
правило,
4
наблюдения
временного
ряда
взаимосвязаны, и для корректного его описания следует рассматривать
совместную вероятность p(x1, ..., xT ). [1]
5
2. ОСНОВНЫЕ КОМПОНЕНТЫ ВРЕМЕННОГО РЯДА
Компоненты временного ряда - факторы, влияющие на уровни временного ряда. Обычно выделяют четыре базовые компоненты временного ряда:
трендовую, циклическую, сезонную и нерегулярную (или случайную). Анализ
временных рядов путём разложения их на перечисленные компоненты называется декомпозицией.
Трендовая компонента отражает долговременную тенденцию. Для
её построения используют метод аналитического выравнивания, который
заключается
в подборе
функции,
наилучшим
образом
описывающей
зависимость уровней временного ряда от времени. Параметры функции
определяются на основе метода наименьших квадратов (МНК). Наиболее
часто используют линейную, экспоненциальную, логарифмическую и полиномиальную функции.
Циклическая компонента отражает циклические изменения уровней
временного ряда для периодов св. 1 года. Циклическая компонента связана
с циклами деловой активности; её периодичность составляет от 2 до 10 лет.
Циклическую компоненту сложно идентифицировать, если анализировать
данные за непродолжительный, относительно цикла, период времени. В этом
случае циклическую компоненту невозможно отделить от трендовой.
Сезонная компонента отражает периодические изменения уровней
временного ряда внутри года и может отражать квартальные, месячные или
недельные циклы. Сезонная компонента может быть измерена с помощью
индексов сезонности; наиболее часто используют месячные индексы.
Нерегулярная компонента отражает нерегулярные флуктуации (от лат.
fluctuatio – колебание) уровней временного ряда, которые невозможно
предсказать,
является
следствием
однократных,
событий, влияющих на уровни ряда.[2]
6
а не систематических
3. ПРОВЕРКА СУЩЕСТВОВАНИЯ ТРЕНДА ВО ВРЕМЕННОМ
РЯДУ
Проверка существования тренда во временном ряду осуществляется
несколькими методами. Рассмотрим два самых известных из них.
3.1. Метод проверки разности средних уровней
Реализация метода проверки разности средних уровней состоит из
четырех этапов.
На первом этапе исходный временной ряд у1, у2, у3, ... уn разбивается
на две примерно равные по числу уровней части: в первой части n1 первых
уровней исходного ряда, во второй - п2 остальных уровней (n1 + n2 = n).
На втором этапе для каждой из этих частей вычисляются средние
значения и дисперсии:
y̅1 =
σ12
=
∑n1
t=1 yt
y̅2 =
n1
∑n1
̅1 )
t=1(yt −y
Третий
2
σ22
n1 −1
этап заключается
в
=
∑n1
t=n1 +1 yt
n2
∑n1
̅2 )
t=n1 +1(yt −y
проверке
2
n2 −1
равенства
(однородности)
дисперсий обеих частей ряда с помощью F-критерия Фишера, которая
основана на сравнении расчетного значения этого критерия:
σ12
, если σ12 > σ22
σ22
F=
σ22
2
2
2 , если σ1 < σ2
σ
{ 1
}
с
табличным
(критическим)
значением
критерия
Фишера Fα с
заданным уровнем значимости (уровнем ошибки) α. В качестве α чаще всего
берут значения ОД (10%-ная ошибка), 0,05 (5%-ная ошибка), 0,01 (1%-ная
ошибка). Величина 1 - α называется доверительной вероятностью.
Если расчетное значение F меньше табличного Fα, то гипотеза о
равенстве дисперсий принимается и переходят к четвертому этапу.
Если F больше или равно Fα, гипотеза о равенстве дисперсий отклоняется и
7
делается вывод, что данный метод для определения наличия тренда ответа не
дает.
На четвертом этапе проверяется гипотеза об отсутствии тренда с
использованием t-критерия Стьюдента. Для этого определяется расчетное
значение критерия Стьюдента по формуле
t=
|y̅1 − y̅2 |
1
1
σ√n + n
1
2
где σ - среднеквадратическое отклонение разности средних:
(n1 − 1)σ12 + (n2 − 1)σ22
σ=√
n1 + n2 − 2
Если расчетное значение t меньше табличного значения статистики
Стьюдента ta с заданным уровнем значимости а, гипотеза принимается, т.е.
тренда нет, в противном случае тренд есть. Заметим, что в данном случае
табличное значение ta берется для числа степеней свободы, равного n1 + n2 −
2 при этом данный метод применим только для рядов с монотонной
тенденцией.[3]
3.2. Метод Форстера – Стьюарта
Этот метод обладает большими возможностями и даст более надежные
результаты по сравнению с предыдущим. Кроме тренда самого ряда (как
говорят, тренда в среднем), он позволяет установить наличие тренда
дисперсии временного ряда: если тренда дисперсии нет, то разброс уровней
ряда постоянен; если дисперсия увеличивается, то ряд "раскачивается" и т.д.
Реализация метода также содержит четыре этапа.
На первом этапе производится сравнение каждого уровня исходного
временного ряда, начиная со второго уровня, со всеми предыдущими, при этом
определяются две числовые последовательности:
1, если yt больше всех предыдущих уровней
kt = {
}
0 − в противном случае
1, если yt меньше всех предыдущих уровней
lt = {
}
0 − в противном случае
8
t = 2,3,…, n.
На втором этапе вычисляются величины S и d:
n
n
s = ∑(k t + lt )
d = ∑(k t − lt )
t=2
Нетрудно
t=2
заметить,
что
величина s, характеризующая
изменение
временного ряда, принимает значения от (- n - 1) (ряд монотонно убывает) до
(n - 1) (ряд монотонно возрастает). Величина d характеризует изменение
дисперсии уровней временного ряда и изменяется от 0 (все уровни ряда равны)
до (n - 1) (ряд монотонный или с чередованием подъемов и падений уровней).
Третий этап заключается в проверке гипотез: можно ли считать
случайными:
1) отклонение величины d от величины m - математического ожидания
величины d для ряда, в котором уровни расположены случайным образом;
2) отклонение величины s от нуля.
Эта проверка проводится с использованием расчетных значений tкритерия Стьюдента для дисперсии и для средней:
ts =
td =
|s−μ|
σ1
|d−0|
σ2
σ1 = √2 ln n − 3,4253
σ2 = √2 ln n − 0,8456
Для удобства имеются табулированные значения величин μ, σ1, и σ2;
где μ - математическое ожидание величины d, определенной для ряда, в
котором уровни расположены случайным образом;
σ1 - среднеквадратическое отклонение для величины d;
σ2 - среднеквадратическое отклонение для величины s.
На четвертом
табличным
этапе расчетные
значением t-критерия
значения ts и td сравниваются
Стьюдента
с
заданным
с
уровнем
значимости tα. Если расчетное значение меньше табличного, то гипотеза об
отсутствии соответствующего тренда принимается; в противном случае тренд
есть. Например, если tα больше табличного значения ta, a td меньше ta, то для
9
данного временного ряда имеется тренд в среднем, а тренда дисперсии
уровней ряда нет.[3]
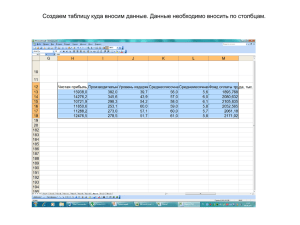
Пример.
Имеется временной ряд yt, содержащий данные об объеме перевозок
грузов железнодорожным транспортом, млн.тонн.
1 шаг. Составить последовательности kt и lt, рассчитать их сумму и
разность, подсчитать итоговые суммы S и d.
Таблица 1. Последовательности kt и lt, их сумма и разность.
2 шаг. Рассчитать стандартные отклонения и t-статистики для
последовательностей.
Таблица 2. Стандартные отклонения и t-статистики
для последовательностей kt и lt..
10
3 шаг. Сравнить значения t-статистик. ts и td больше критического
значения, что подтверждает гипотезу о наличии тренда.[4]
11
4. МЕТОД ЧОУ ПРОВЕРКИ СТАБИЛЬНОСТИ ТЕНДЕНЦИИ
Тест на равенство коэффициентов регрессии в двух выборках называют
тестом Чоу. Нулевая гипотеза проверяется с помощью F-статистики для
гипотезы о том, что коэффициенты при всех добавленных переменных равны
нулю.
Рассмотрим
модель
включающую т параметров.
множественной
МНК-оценки
параметров
регрессии,
получим
по
выборочным данным объемом п.
Обозначим S0 = ∑ni=1 e2i — сумма квадратов остатков для общего
уравнения регрессии (полученного по выборке объемом п). Есть основание
предполагать, что целесообразно общую выборку разбить на две частные
выборки объемами n1 и n2, где n1 + n2 = n оценить для каждой из них
n
n
1
2
уравнение регрессии. Обозначим S1 = ∑i=1
e2i1 , S2 = ∑i=n
e2 — суммы
1 +1 i2
квадратов остатков по первой и второй регрессиям соответственно.
Равенство S0 = S1 + S2 возможно только в случае совпадения оценок
параметров всех трех регрессий. Чем сильнее различие в поведении Y для
двух
частных
регрессий,
сумму S1 + S2. Разность S0
тем
больше S0 будет
превосходить
- (S1 + S2) является показателем улучшения
качества модели при разбиении объема выборки на две части. При вычислении
величины S0 число степеней свободы равно n- m - 1. При вычислении суммы
(S1 + S2) число степеней свободы равно n - 2m - 2, так как оцениваются
параметры двух регрессий.
Общую выборку целесообразно разбивать на две части только в том
случае, если уменьшение дисперсии будет значимо больше оставшейся
необъясненной дисперсии при использовании двух регрессий. Анализ
выполняется при помощи стандартной процедуры сравнения дисперсий на
основе F-статистики. В данном случае она имеет вид:
F(α; m + 1; n − 2(m + 1)) =
S0 − (S1 + S2 ) n − 2(m + 1)
∗
S1 + S2
m+1
12
Полученная статистика подчиняется F-распределению Фишера с т + 1
и п - 2т - 2 степенями свободы. Если уменьшение дисперсии статистически не
отличается от необъясненной дисперсии, т.е. вычисленное значение Fстатистики F< Fкр, то нет оснований для разбиения выборки на две части. В
противном случае это может привести к улучшению качества модели.
Замечание. Тест Чоу вполне достаточен для определения структурных
изменений в выборочных данных. Однако более информативным является
использование фиктивных переменных, так как их анализ позволяет не только
установить наличие или отсутствие структурных изменений, но и оценить
степень влияния как фиктивных, так и количественных регрессоров на
эндогенную переменную, оценить качество регрессии в целом.
Пример №1.
По данным табл. 3 оценим регрессию D = b0+ b1Р + ε:
а) по всем данным;
б) по данным за 1995—1997 гг.;
в) по данным за 1998—2003 гг.
Проверим данные на отсутствие структурного сдвига при помощи теста
Чоу.
Решение. Оценку модели для всех трех случаев выполним при помощи
инструмента «Регрессия». Результаты оценивания представлены в табл. 3.
Таблица 3.
Параметр Регрессия по
всем данным
Регрессия по данным
за 1995-1997 гг.
Регрессия по данным
за 1998-2003 гг.
n
9
3
6
b0
1349,46
5930,12
32,42
b1
11,93
-9,95
-0,14
𝑺𝒃𝟎
1336,995
170,059
0,952
𝑺𝒃𝟏
24,256
2,210
0,023
R2
0,033
0,953
0,896
13
F
0,242
20,277
34,606
S
2838,393
207,517
1,465
S0
56 395 324
43 063,63
8,58
Как следует из табл. 3, качество частных регрессий достаточно высокое,
в то время как регрессия по всем данным низкого качества. Рассчитаем тест
Чоу:
F=
S0 − (S1 + S2 ) n − 2(m + 1) 56 395 324 − (43 063,63 + 8,58)
∗
=
S1 + S2
m+1
43 063,63 + 8,58
= 3270,8
Табличное значение F-статистики для доверительной вероятности 0,95
F(0,95;2;5) = 5,8. Следовательно, нулевая гипотеза об отсутствии структурного
сдвига в выборочных данных отвергается.[5]
Пример №2.
В таблице 4 представлены данные об объёмах внутренних инвестиций у
и валового внутреннего продукта США х за 1939-1954 гг.
Таблица 4.
Год
у
Х
Год
у
х
1939
9,3
90,8
1947
34,0
232,8
1940
13,1
100,0
1948
45,9
259,1
1941
17,9
124,9
1949
35,5
258,0
1942
9,9
158,3
1950
53,8
286,2
1943
5,8
192,0
1951
59,2
330,2
1944
7,2
210,5
1952
52,1
347,2
1945
10,6
212,3
1953
53,3
366,1
1946
30,7
209,3
1954
52,7
366,3
Решение. На основании графического анализа (рис.1) можно заключить,
что для исследуемых данных, за исключением военных лет (1942-1945 гг.)
прослеживается линейная зависимость. Данные военного периода не
14
соответствуют общей тенденции. Это даёт основания для проверки гипотезы
относительно достоверности различия между моделями, охватывающими два
временных интервала.
Рис.1. Зависимость ВВП от инвестиций
Оценивание регрессии по времени для всех наблюдений уt(р) дало
следующие результаты соответственно:
yt( p )  12,084  0,19 xt   t , R 2  0,78; yt( 2)  3,32  0,17 xt   t , R 2  0,92
0, 03
0, 015
Соответствующие суммы квадратов остатков равны: S0=1272,26;
S1=258,3; S2=4,042. Применяя к исходной модели тест Чоу, получаем
значение F-статистики 23,01, что позволяет сделать вывод о достоверном
различии моделей в военное и мирное время. [6]
15
5. ЗАКЛЮЧЕНИЕ
Экономические процессы разворачиваются во времени и их можно
представить
системой
количественных
и
качественных
показателей,
зависящих от времени. В этой связи, при прогнозировании экономических
явлений особое внимание уделяется изучению временных рядов.
Временными рядами, например, будут серия ежедневных наблюдений в
течение некоторого периода за ценами товара при закрытии торгов на бирже,
дневные объемы выпуска товара, месячные показатели инфляции или индекса
потребительских цен, ежеквартальные оценки валового национального
продукта (принятые в США) или средних зарплат (принятые в России для
ежеквартального индексирования пенсий), ежегодные данные об объеме,
выручке и прибыли компании.
Временные ряды, естественно, не ограничиваются исключительно
экономическими величинами; известно их использование при анализе
процессов в энергосистемах, атомной промышленности, химических и
нефтехимических производствах, причем в этом случае часто используются
более мелкие дискретности времени, чем в экономике - минуты и даже
секунды при обработке данных о быстропротекающих процессах в атомной
энергетике или при исследовании переходных процессов в химической
кинетике.
Анализ временных рядов применялся при слежении за подводными
лодками «вероятного противника» в 70-80-е годы, и при обработке данных
наблюдений в системах ПВО, и при прогнозах проходимости радиосигналов в
атмосфере и ионосфере, и при моделировании транспортных потоков на
автотрассах. [7]
16
6. СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ И
ЛИТЕРАТУРЫ
1. Суслов В.И., Ибрагимов Н.М., Талышева Л.П., Цыплаков А.А.
Эконометрия. - Новосибирск: Издательство СО РАН, 2005. - 744 с.
Электронная версия (2005); https://booksee.org/book/482499
2. Козарезова Л. О. КОМПОНЕНТЫ ВРЕМЕННОГО РЯДА // Большая
российская
энциклопедия.
Электронная
версия
(2016);
https://bigenc.ru/economics/text/2087489
3. Гармаш, А. Н. Экономико-математические методы и прикладные
модели : учебник для бакалавриата и магистратуры / А. Н. Гармаш,
И. В. Орлова, В. В. Федосеев ; под редакцией В. В. Федосеева. — 4-е
изд., перераб. и доп. — Москва : Издательство Юрайт, 2019. — 328 с. —
(Бакалавр и магистр. Академический курс). Электронная версия (2019):
https://urait.ru/viewer/ekonomiko-matematicheskie-metody-i-prikladnyemodeli-406453#page/1
4. Предварительный анализ временных рядов [Электронный ресурс]:
Учеб. пособие/ T.И. Белых, А.В. Бурдуковская. – Иркутск: Изд-во БГУ,
2018. – 105 с. – Режим доступа: lib-catalog@bgu.ru.
5. Галочкин, В. Т. Эконометрика : учебник и практикум для бакалавриата
и специалитета / В. Т. Галочкин. — Москва : Издательство Юрайт, 2019.
— 288 с. Электронная версия (2019) : https://urait.ru/viewer/ekonometrika431440#page/1
6. Учебно-методическое пособие. — Эконометрика: практикум для студ.
спец. «Информационные системы и технологии в экономике» всех форм
обуч. / С.А.Поттосина, А.Э.Алёхина. - Минск: БГУИР, 2013. — 98 с.
https://libeldoc.bsuir.by/bitstream/123456789/394/2/Ekonometrika.pdf
7. Лазарев А., Мешкова Л. Эконометрика - Временные ряды и
прогнозирование. Учебное пособие. Издательство Международного
17
Информационного
Нобелевского
Центра,
http://forex.kbpauk.ru/showflat.php/Cat/0/Number/43804/Main/43804
18
2002.