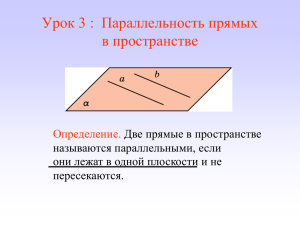
Параллельность прямых в пространстве Напомним, что две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются:. Как известно из курса планиметрии, через точку M, не лежащую на прямой a, в плоскости можно провести единственную прямую ba. Докажем, что и в пространстве через точку M a проходит единственная прямая ba: Теорема о существовании и единственности прямой, параллельной данной: Через точку, не лежащую на данной прямой, можно провести единственную прямую, параллельную данной. Дано: a; M a. Доказать: ! ba: M b. Рисунок 26 Докажем теперь вспомогательную теорему – лемму о пересечении плоскости параллельными прямыми: Лемма о пересечении плоскости параллельными прямыми: Если одна из двух параллельных прямых пересекает плоскость, то вторая прямая также пересекает эту плоскость. Дано: ab; a = ! A. Доказать: b = ! B. Рисунок 27 Пользуясь доказанной леммой, докажем теорему о параллельности трех прямых: Теорема о параллельности трех прямых (свойство транзитивности параллельности прямых): Две прямые, параллельные третьей прямой, параллельны между собой. Дано: ac; bc. Доказать: ab. Рисунок 28