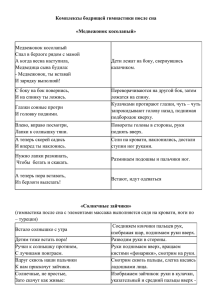
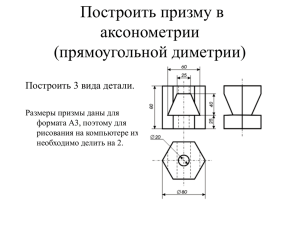
Y=||𝒙| − 𝟏| 1. Строим y= x 2. Строим Y=|𝒙| y>0-модуль, то поднимаем вверх зеркально относительно оси Х все что лежит при отрицательных Y Или если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю 3. Сдвиг вдоль y на -1 , Y=|𝒙| − 𝟏 4. Y=||𝒙| − 𝟏| y>0-модуль, поднимаем вверх зеркально относительно оси Х все что лежит при отрицательных Y Или если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю Y=||𝒙 − 𝟏| − 𝟏| 1.Y=|𝒙 − 𝟏| 2.Y=|𝒙 − 𝟏| -1 3.Y=||𝒙 − 𝟏| − 𝟏| 𝑦=||𝒙𝟐 − 𝟐| − 𝟐| 1. Строим подмудульное 𝑦=𝒙𝟐 − 𝟐 2. Строим 𝑦=|𝒙𝟐 − 𝟐| y>0-модуль, то поднимаем вверх зеркально относительно оси Х все что лежит при отрицательных Y Или если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю 3. Строим 𝑦=|𝒙𝟐 − 𝟐| -2 – сдвиг вниз на 2 4. Строим 𝑦=||𝒙𝟐 − 𝟐| − 𝟐| y>0-модуль, то поднимаем вверх зеркально относительно оси Х все что лежит при отрицательных Y Или если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю Т.к по условию y>0-модуль, y>0-модуль, то поднимаем вверх зеркально относительно оси Х все что лежит при отрицательных Y Или если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю (отражение по вертикали вдоль Y) Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем. Если модуль навешен только на аргументе Х , то отражаем относительно оси «y» положительный х (отражение по горизонтали, вдоль Х) y>0-модуль, то поднимаем вверх зеркально относительно оси Х все что лежит при отрицательных Y или если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю Здесь точкой перемены знака подмодульного выражения является х=4. Тогда на интервале (-∞; 4] функция выглядит так: А на интервале [4; ∞) так: Точка вершин парабол (2;-12) вниз ветви, и точка вершины параболы (6, -20), ветви вверх. В итоге имеем: Точки перемен знака подмодульных выражений – 4 и (-2). Точки эти (они выколоты) разбивают числовую прямую на три интервала, на которых данная функция будет выглядеть: На первом интервале (-∞; -2): На втором интервале (-2;4): На третьем интервале (4;∞): Начнем построение с “базовой” для этого графика функции она выглядит так: Далее добавим знак модуля под корень: , Модуль навешен на аргумент, поэтому отражаем все что в положиельных Теперь опустим этот график вниз на 4 единицы по оси у: “Отзеркалим” все, что ниже оси х, вверх, и не забудем поделить все ординаты на 2: