ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ
Кафедра вычислительной техники
МЕТОДЫ И СРЕДСТВА
ЗАЩИТЫ КОМПЬЮТЕРНОЙ
ИНФОРМАЦИИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ
ЛАБОРАТОРНЫХ РАБОТ
Укрупненная группа направлений и
специальностей
230000 «Информатика и вычислительная техника»
Направление подготовки:
230100 «Информатика и вычислительная техника»
Специальность:
230101 «Вычислительные машины, комплексы,
системы и сети»
Разработал: доцент кафедры ВТ Глухих В.И.
Иркутск 2007
Основным инструментом защиты информации являет шифрование
данных. Сами алгоритмы шифрования, будучи относительно простыми,
легко реализуются даже на простейших ЭВМ, вычислительные ресурсы
которых, оказываются избыточными. Однако, задача вскрытия криптографических ключей методами прямого перебора наталкивается на
непреодолимые трудности как в вследствие отсутствия эффективных
алгоритмов вычислений, так и недостаточности вычислительных ресурсов даже самых совершенных суперЭВМ. Собственно эти трудности и
являются гарантией эффективности современных методов защиты информации. Расчетное время вскрытия криптографических ключей является количественной мерой защищенности информации.
Постоянные атаки на криптографические системы защиты информации, как со стороны законных владельцев (криптотестирование), так
и со стороны их оппонентов (криптоанализ) преследуют противоположные цели, но ведут, в конечном счете, к непрерывному совершенствованию средств и методов защиты информации.
Возможно, задачи вскрытия ключей и будут решены с появлением
квантовых компьютеров, но до тех пор наиболее перспективным
направлением криптоанализа и криптотестирования является использование параллельных узкоспециализированных высокопроизводительных вычислителей – микропроцессоров и микроконтроллеров.
Рядом ведущих производителей микроэлектроники (фирмы Altera,
Xilinx, Actel, Lattice и др.) созданы Программируемые Логические Интегральные Схемы (ПЛИС), имеющие в своем составе миллионы логических элементов, модули сверхбыстрой памяти, сигнальные процессоры и др., с тактовыми частотами работы в несколько ГГц. ПЛИС могут
быть как энергонезависимыми, так и перепрограммируемыми в системе.
Такие ПЛИС лежат в основе аппаратной части современных криптографических лабораторий, используемых для прикладных, учебных и
научных целей.
Поскольку, одним из общих требований, предъявляемых к средствам защиты информации, является возможность их реализации как
программными, так и аппаратными средствами, в лабораторном практикуме предполагается выполнение всех заданий:
программно с использованием любых алгоритмических языков высокого уровня,
аппаратно, путем разработки проекта на языке описания аппаратуры
(AHDL, VHDL и др.) и их реализации на ПЛИС.
Выполнение задания каждой лабораторной работы должно включать:
2
Теоретическая проработка алгоритма (пособие, литература, интернет).
Моделирование работы алгоритма.
Программирование на языке высокого уровня для реализации на
ЭВМ.
Программирование на ассемблере для реализации на микроконтроллере.
Программирование на языке описания аппаратуры для реализации на ПЛИС.
Лабораторная работа 1. Кодер Хемминга
Помехоустойчивое кодирование основано на использовании избыточных кодов, в которых каждое кодовое слово длиной n символов имеет k информационных разрядов и m проверочных: n k m . Кодер избыточного кода преобразует разряды информационного слова
в
разряды
кодового
слова
{ak , ak 1 ,..., a2 , a1}
{bk m ,..., bk 1 , ak , ak 1 ,..., a2 , a1} {zn , zn1 ,..., z2 , z1} .
Задачей помехоустойчивого кодирования является обнаруживать в
искаженном кодовом слове ошибки кратностью g î и, в случае обнаружения, исправлять ошибки кратностью gè (самокорректирующееся кодирование).
Из n символов может быть построено 2 n комбинаций возможных
слов, 2 k из которых разрешенные, а все остальные – запрещенные. Разрешенные кодовые комбинации выбираются так, чтобы они отличались
друг от друга как можно большим числом символов, т.е. кодовое расстояние d между ними было максимальным. Если минимальное кодовое расстояние для всех пар разрешенных кодовых комбинаций – dmin ,
то такой код может обнаруживать go dmin 1 и исправлять gu (dmin 1) / 2
ошибок.
Простейшим самокорректирующимся кодом является двоичный
код Хемминга, для которого n k m 2m 1 , dmin 3 . Проверочные разa j по формуле:
ряды bk j вычисляются из информационных
bk j a j a1 a 2 a3 ... ak , где j 1, 2,...k . Знак означает суммирование «по модулю 2».
Если все проверочные суммы или синдромы (S):
S1 z1 z3 z5 z7 ...
S2 z2 z3 z6 z7 ...
S3 z4 z5 z6 z7 ...
3
(1)
равны нулю, то среди кодовых разрядов {z} нет ошибок, иначе число,
разрядами которого являются проверочные суммы (синдромы), указывает на номер позиции, в которой находится ошибка. Это свойство позволяет сделать для кода Хемминга декодирующее устройство очень
простым.
Коэффициенты проверочных сумм, сведенные в матрицу, образуют
проверочную матрицу кода:
1 0 1 0 1 0 1 ...
(2)
H 0 1 1 0 0 1 1 ...
0 0 0 1 1 1 1 ...
Умножение кодового вектора z , координатами которого являются раз-
ряды кодового слова, на транспонированную проверочную матрицу
H T дает вектор синдрома S :
z H T ST
(3)
Анализ синдрома позволяет обнаруживать наличие ошибок в кодовой
комбинации и, возможно, исправлять их.
Кодирование, т.е. преобразование информационных разрядов в
разряды кодовой комбинации, осуществляется путем умножения информационного вектора на порождающую или образующую матрицу
G:
a G zT
(4)
Порождающая матрица G связана с проверочной матрицей H соотношением:
G HT 0
(5)
Соотношение (5) позволяет вычислять порождающую матрицу по известной проверочной матрице.
Матричное представление кодов удобно при программном методе
реализации кодирования. Для аппаратной реализации кодирования используют полиноминальное представление кода, когда кодовой комби{ z}
нации
ставится
в
соответствие
полином
0
2
3
n2
n 1
z ( x) d1 x d 2 x d3 x d 4 x ... d n 1 x d n x . Образующей матрице G соответствует образующий полином g ( x ) , а проверочной матрице – проверочный полином h( x) .
ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
1. Построить кодер и декодер кода Хемминга, заданный образующим многочленом, табл.8.1. Значения параметров n и m выбрать самостоятельно.
2. Собрать схему на рис.8.1 и эксперименгтально оценить корректирующую способногсть кода go, gu.
4
Таблица 8.1. Образующие многочлены кода Хемминга
1
2
3
g ( x) x 3 x 2 1
4
5
6
g ( x) x 3 x 1
g ( x) x 4 x 3 1
g ( x) x 4 x 1
g ( x) x 5 x 2 1
g ( x) x 5 x 3 1
Логический элемент «исключающее ИЛИ» или выполняет роль
управляемого инвертор: когда y j 0 сигнал в линии повторяется (нет
ошибки); когда y j 1 сигнал в линии инвертируется (ошибка вносится).
Так y(1000000…) вносит ошибку в старший разряд кодового слов z;
y(00000…) – не вносит ошибок; y(1111111…) - искажает все разряды z.
Лабораторная работа 2. Генератор псевдослучайных чисел
Случайными называются последовательности, зная предшествующие значения которых невозможно достоверно предсказать значения
последующих. Истинно случайные последовательности формируются
на основании шумовых характеристик некоторых физических процессов (шумовые диоды, распад радиоактивных веществ и др.). Псевдослучайными последовательностями (ПСП) называют такие случайные последовательности, значения которых периодически повторяются. Если
период повторения велик и превосходит ресурсы памяти Системы, то
такая Система не может отличить истинно случайную последовательность от псевдослучайной. Достоинством ПСП является воспроизводимость результатов. В большинстве случаев криптографические ключи
формируются с помощью ПСП. Сеансовые или одноразовые ключи
должны быть случайными.
Ниже рассмотрены наиболее распространенные методы формирования псевдослучайных последовательностей (ПСП).
1. Конгруэнтные генераторы.
1.1. Линейные и мультипликативные конгруэнтные генераторы.
Линейным конгруэнтным генератором (ЛКГ) с параметрами
( x0 , a, c, N ) называется программный генератор РРСП, порождающий
псевдослучайную последовательность x1 , x2 ,... A, A {0,1,..., N 1} с помощью рекуррентного соотношения:
xt 1 (axt c) mod N , t 0,1...
(1)
5
Параметры этого генератора (1) имеют следующий смысл: x0 A –
начальное, или стартовое, значение; a A \{0} – ненулевой множитель;
c A – приращение; N – модуль, равный мощности алфавита A.
Если приращение c 0 , то генератор (1) называется мультипликативным конгруэнтным генератором (МКГ), а если c 0 , то смешанным
конгруэнтным генератором (СКГ).
Перечислим свойства псевдослучайной последовательности, порождаемой ЛКГ:
1. Для общего члена последовательности (1) справедлива формула:
at 1
x1 at x0
c mod N , t 1 .
a 1
2. Найдется номер A , начиная с которого последовательность (1)
«зацикливается» с периодом T N
3. Для любого k 2 подпоследовательность x0 , xk , x2k ,... A получен-
ная из псевдослучайной последовательности (1) удалением всех членов, не кратных k , оказывается псевдослучайной последовательностью, порожденной ЛКГ (1), с параметрами ( x0 , a, c, N ) , где
a a k mod N , c
c(a k 1)
mod N .
a 1
4. Псевдослучайная последовательность (1), порождаемая ЛКГ, достигает максимального значения периода Tmax N тогда и только тогда,
когда выполнены следующие три условия:
a) c, N – взаимно простые, т.е. НОД(c,N)=1;
b) число b a 1 кратно p для любого простого числа p N , являющегося делителем N ;
c) число b кратно 4, если N кратно 4.
5. Для МКГ, если x0 , N – взаимно простые ( a – первообразный элемент по модулю N , а ( N ) – максимально возможный порядок по модулю N ), то псевдослучайная последовательность имеет максимальный период Tmax .
6. Для МКГ, если N 10q , q 5 и x0 не кратно 2 или 5, то
Tmax 5 10q 1
N
тогда и только тогда, когда вычет принимает a mod 200
20
одно из следующих значений:
3, 11,13, 19, 21,27, 29, 37, 53, 59, 61, 67, 69, 77, 83, 91, 109, 117, 123,
131, 133, 139, 141, 147, 163, 171, 173, 179, 181, 187, 189, 197.
6
7. Для МКГ, если N 2q , q 4 , то максимально возможное значение
N
псевдослучайной последовательности достига4
ется, если x0 1 – нечетно и вычет a mod 8 {3,5} .
периода Tmax 2q 2
8. «Слабость» ЛКГ и МКГ заключается в том, что если рассматривать последовательные биграммы ( z1(t ) , z2(t ) ) : z1(t ) xt , z2(t ) xt 1 , то точки
z t ( z1(t ) , z2 (t ) ), t 1, 2... на плоскости R2 будут лежать на прямых из семейства z2 az1 c kN , k 0,1...
1.2. Нелинейные конгруэнтные генераторы.
Восьмое свойство линейного и мультипликативного конгруэнтных
генераторов псевдослучайных последовательностей представляет «слабость» этих генераторов и может активно использоваться для построения криптоатак в целях оценки параметров a, c, x0 . Для устранения этого
недостатка 0xca,,используют нелинейные конгруэнтные генераторы
псевдослучайных последовательностей. Наибольшее распространение
получили три подхода, описание которых приводится ниже.
1.2.1. Квадратичные конгруэнтные генераторы.
Этот алгоритм генерации псевдослучайной последовательности
x A {0,1,..., N 1} определяется квадратичным рекуррентным соотношением:
xt 1 (dxt2 axt c) mod N , t 0,1...
(2)
где x0 , a, c, d A – параметры генератора. Выбор этих параметров осуществляется на основе следующих свойств последовательности:
1. Квадратичная конгруэнтная последовательность (2) имеет
наибольший период Tmax N тогда и только тогда, когда выполнены
следующие условия:
a) c, N – взаимно простые числа;
b) d , a 1 – кратны p , где p — любой нечетный простой делитель
N;
c) d – четное число, причем
(a 1) mod 4, если N кратно 4
d
(a 1) mod 2, если N кратно 2
d) Если N кратно 9, то либо d mod9 0 , либо d mod9 1 и
cd mod9 6 .
e) Если N 2q , q 2 то наибольший период Tmax 2q тогда и только
тогда, когда c – нечетно, d – четно, a – нечетное число, удовлетворяющее соотношению: a (d 1) mod 4 .
1.2.2. Генератор Эйхенауэра – Лена с обращением.
7
Псевдослучайная нелинейная конгруэнтная последовательность
Эйхенауэра – Лена с обращением определяется следующим нелинейным рекуррентным соотношением:
(ax 1 c) mod N , если x t 1
xt 1 t
если x t 0
c,
1
где x – обратный к xt элемент по модулю N , т.е. xt xt1 1(mod N ) ;
(3)
x0 , a, c A – параметры генератора.
1. Если N 2q , a,x 0 – нечетны, c — четно, то генератор (3) имеет
максимально возможный период Tmax 2q 1 тогда и только тогда, когда
a 1(mod 4), c 2(mod4) .
1.2.3. Конгруэнтный генератор, использующий умножение с
переносом.
При этом нелинейная конгруэнтная псевдослучайная последовательность определяется рекуррентным соотношением:
xt 1 (axt ct ) mod N
(4)
где, в отличие от (2), «приращение» ct c( xt 1 , xt 2 ,..., x0 ) изменяется во
времени и зависит от указанных аргументов нелинейно:
ax c
ct наибольшее целое, меньшее или равное числу в скобках: t 1 t 1
N
(5)
Параметрами нелинейного конгруэнтного генератора (4), (5) являются x0 , c0 , a, N .
2. Рекуренты в конечном поле
Обобщением мультипликативной конгруэнтной последовательности является линейная рекуррентная последовательность порядка над
конечным полем GF ( p k ) :
xt 1 (a1 xt a2 xt 1 ... ak xt k 1 ) mod p
(6)
где a1 ,..., ak A {0,1,..., p 1}– коэффициенты рекурренты, а x0 ,..., x k 1 A –
начальные значения рекурренты.
Параметры генератора псевдослучайной последовательности (6):
p, k , a1 ,..., a k 1 . Начальные значения выбираются x0 ,..., x k 1 A произвольно так, чтобы не обращались в ноль одновременно. Коэффициенты рекурренты a1 ,..., ak A выбираются таким образом, чтобы порождающий
полином
f ( x) x k a1 x k 1 ... ak 1 x ak
(7)
являлся примитивным многочленом по модулю p , т.е. многочлен (5)
имел корень x , являющийся первообразным элементом поля GF ( p k ) .
8
При таком выборе параметров достигается максимально возможный
период Tmax p k 1 псевдослучайной последовательности (6).
3. Последовательности, порождаемые регистрами сдвига с обратной связью.
Линейным регистром сдвига с обратной связью (Linear Feedback
Shift Register, LFSR) называется логическое устройство, схема которого
изображена на рис. 8.1.
LFSR состоит из n ячеек памяти, двоичные состояния которых в
момент
времени
характеризуются
значениями
t 0,1,...
S0 (t ), S1 (t ),..., Sn1 (t ) A {0,1} . Выходы ячеек памяти связаны не только последовательно друг с другом, но и с сумматорами в соответствии с
коэффициентами передачи a0 , a1 ,..., an1 A : если ai 1 , то значение Si (t ) iой ячейки передается на один из входов i-го сумматора; если же ai 0 ,
то такая передача отсутствует. Состояние LFSR в текущий момент времени t задается двоичным n - вектор-столбцом S (t ) (Sn1 (t ),..., S0 (t )) ' .
Содержание ячеек LFSR с течением времени изменяется следующим образом, определяя тем самым динамику состояний LFSR:
Si 1 (t ),
Si (t 1) n 1
a j S j (t ),
j 0
если i 0, n 2
(8)
если i=n-1
Текущие значения нулевой ячейки регистра используются в качестве элементов порождаемой LFSR двоичной псевдослучайной после...
an-1
an-2
an-3
a1
a0
St
...
Serial OUT
Sn-1
Sn-2
Sn-3
S1
S0
Parallel OUT
Рис.8.1. Блок-схема LFSR.
довательности s y S0 (t ) .
Модель (8) является частным случаем модели (7) линейной рекурренты над полем GF (2n ) , поэтому коэффициенты {ai } выбираются со9
гласно методике, приведенной в предыдущем пункте. То есть многочлен, по которому строится LFSR, должен быть примитивным по «модулю 2». Степень многочлена является длиной сдвигового регистра.
Примитивный (базовый) многочлен степени n по «модулю 2» – это неприводимый многочлен, который является делителем x2 1 1 , но не является делителем x d 1 для всех d , являющихся делителями 2n 1 . Неприводимый многочлен степени n нельзя представить в виде умножения
многочленов кроме него самого и единичного.
4. Генераторы Фибонначи. Общий вид рекуррентного соотношения, определяющего генератор Фибоначчи, задается уравнением
(9)
xt xt r xt s , t=r,r+1,r+2,...
где r , s N (r s) – параметры генератора; элемент xt Vk представляет
собой двоичный k -вектор и действие выполняется побитно.
5. Криптостойкие генераторы на основе односторонних функций.
Для повышения стойкости алгоритмов генерации псевдослучайных последовательностей к криптоанализу в последнее время предлагается синтезировать алгоритмы на основе известных в криптографии
односторонних функций. Характерное свойство односторонних (oneway) функций состоит в том, что для вычисления значения функции по
заданному значению аргумента существует полиномиально сложный
алгоритм, в то время как для вычисления аргумента по заданному значению функции полиномиально сложного алгоритма не существует
(или он не известен). Доказательство свойства односторонности функции является трудной математической задачей, поэтому в настоящее
время в криптосистемах часто используются «кандидаты в односторонние функции», для которых показано лишь, что в настоящее время
не известны полиномиально сложные алгоритмы вычисления обратной
функции. Примерами таких «кандидатов» являются некоторые известные криптоалгоритмы (например, DES) и хэш-функции (например,
SHA-1).
Генераторы, основанные на математическом аппарате односторонних функций: ANSI X9.17, FIPS-186, Yarrow-160.
6. Криптостойкие генераторы, основанные на проблемах теории чисел.
Стойкость данных генераторов псевдослучайных последовательностей основывается на неразрешимости с полиномиальной сложностью (на данный момент) некоторых известных проблем теории чисел:
факторизации больших чисел и дискретного логарифмирования.
n
10
Примерами, генераторов основанных на данных проблемах являются: RSA-алгоритм генерации псевдослучайных последовательностей,
модификация Микали-Шнорра RSA-алгоритм генерации псевдослучайных последовательностей, BBS (Blum–Blum–Shub) – алгоритм генерации псевдослучайных последовательностей.
7. Комбинирование алгоритмов генерации методом Макларена – Марсальи.
Пусть имеется два простейших генератора псевдослучайных последовательностей: G1 и G2 . Генератор G1 порождает «элементарную»
последовательность
над
алфавитом
мощности
N:
x0 , x1 ,... A( N ) {0,1,..., N 1} , а генератор G2 – над алфавитом K:
y0 , y1 ,... A( K ) {0,1,..., K 1} .
Пусть имеется вспомогательная таблица T {T (0), T (1),..., T ( K 1)} , из
K целых чисел (память из K ячеек).
Метод Макларена – Марсальи комбинирования последовательностей {xi }, {yi } для получения выходной псевдослучайной последовательности {zk } состоит в следующем. Сначала T - таблица заполняется
K первыми членами последовательности {xi } . Элементы выходной последовательности
вычисляются
следующим
образом:
s yk , z k T (s), T(s) x K k , k=0,1,...
Метод комбинирования Макларена – Марсальи позволяет ослабить зависимость между членами {zk } и увеличить период псевдослучайной последовательности.
8. Комбинирование LFSR-генераторов.
LFSR-генераторы часто используются в качестве генераторов элементарных псевдослучайных последовательностей и применяются для
комбинирования генераторов. Отметим, что LFSR-генераторы можно
использовать в качестве G1 , G2 в генераторе Макларена–Марсальи.
Например, одним из способов комбинирования LFSR-генераторов является полиномиальное комбинирование элементарных последовательностей. Общая модель комбинирования LFSR-генераторов представлена на рис. 8.2.
Здесь функция общего полиномиального вида:
y F ( x) a0 ai xi aij xi x j ... a12...M x1 x2 ...xM mod 2.
1i M
1 j M
11
LFSR1-генератор
X1t
LFSR2-генератор
X2t
1t
F
Yt
...
LFSRM-генератор
XMt
Рис.8.2. Общая модель комбинирования LFSR-генераторов.
ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
1. Построить LFSR-генератор, заданный образующим многочленом,
табл.8.2.
2. Использую статистическое тестирование, проверить гипотезу о
том, что сгенерированная последовательность действительно имеет
равномерное распределение.
Таблица 8.2. Образующие многочлены ПСП
1
2
3
4
5
6
7
g ( x) x8 x 4 x 3 x 2 1
8
9
10
11
12
13
14
g ( x) x 9 x 4 1
g ( x) x10 x3 1
g ( x) x11 x 2 1
g ( x) x12 x6 x 4 x 1
g ( x) x13 x 4 x3 x 1
g ( x) x14 x5 x3 x 1
g ( x) x15 x 1
g ( x) x16 x5 x3 x 2 x 1
g ( x) x17 x5 1
g ( x) x17 x5 1
g ( x) x17 x6 1
g ( x) x18 x7 1
g ( x) x19 x5 x 2 x 1
Лабораторная работа 3. Контроллер DES
Алгоритм шифрования DES относится к блочным алгоритмам
шифрования, в которых файл разбивается на блоки длиной 64 бит и к
каждому блоку применяется одна и та же процедура преобразования открытого текста в закрытый шифротекст. Алгоритм шифрования подробно разобран в четвертой части Пособия
Алгоритм шифрования DES в базовом режиме использования
(электронная кодовая книга ECB (Electronic Code Book)) имеет три основных недостатка:
1. Относительно короткий ключ 64 бита, позволяет пытаться выполнить криптоанализ путем прямого перебора возможных комбинаций с
12
применение современных средств вычислительной техники и методов
распараллеливания вычислений.
2. Шифрование одинаковых, сравнительно коротких, блоков открытого текста дает одинаковые шифроблоки. Это позволяет пытаться отгадать содержание открытых блоков, например: пробелы, даты и др.
Угадывание открытого блока и знание шифроблока позволяет вычислить ключ шифрования.
3. Одним из общих требований к алгоритмам шифрования является
равенство длин открытого текста и шифротекста. Однако, длина открытого текста не всегда бывает кратна длине 64 бит и последний блок оказывается неполным.
Проблема «коротких ключей» может быть решена многократным
повторным шифрованием с использованием нескольких ключей шифрования. Остальные проблемы успешно решаются применением нескольких режимов использования DES:
сцепление блоков шифра CBC (Cipher Block Chaining);
обратная связь по шифротексту CFB (Cipher Feed Back);
обратная связь по выходу OFB (Output Feed Back).
ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
1. Построить блочный шифратор/дешифратор для варианта из
табд.8.3.
2. Выполнить шифрование заданного файла аппаратным методом
3. Выполнить дешифрование шифротекста программным методом.
4. Использую статистическое тестирование, проверить гипотезу о
том, что распределение символов шифротекста имеет равномерное распределение.
Таблица 8.3. Режимы использования DES
1
2
3
4
5
6
Шифратор/дешифратор DES в базовом режиме электронная кодовая книга ECB (Electronic Code Book)
Тройное шифрование/дешифрование DES с двумя ключами
Тройное шифрование/дешифрование DES с двумя ключами и промежуточным дешифрованием на смежном ключе
Шифратор/дешифратор DES в режиме сцепление блоков шифра
CBC (Cipher Block Chaining)
Шифратор/дешифратор DES в режиме обратная связь по шифротексту CFB (Cipher Feed Back)
Шифратор/дешифратор DES в режиме обратная связь по выходу
OFB (Output Feed Back)
13
Лабораторная работа 4. Контроллер квитанции CRC
Квитирование передаваемых данных является альтернативой помехоустойчивому кодированию, когда данные неуникальные и могут быть
возобновлены передающей стороной. При квитировании, данные передаются наиболее экономичным способом и сопровождаются специальной структурой, по которой можно судить о целостности полученного
файла. Если на приемной стороне анализ квитанции позволил сделать
заключение об искажении полученного файла, то делается запрос на повторную передачу данных. Квитанция, которая часто называют контрольной суммой, не обладает криптостойкостью и предназначена для
защиты передаваемых данных от непредумышленных искажений.
Требования к квитанции, её свойства и алгоритмы формирования
подробно изложены во второй части Пособия.
ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
1. Построить контроллер контрольной суммы CRC для варианта из
табл.2.1.
2. Сформировать квитанцию для заданного файла программно табличным методом (таблицу сформировать программно).
3. Выполнить проверку квитанции для заданного файла аппаратным
методом.
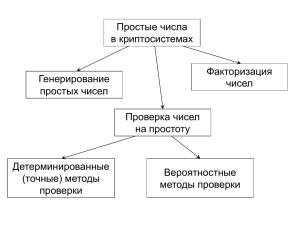
Лабораторная работа 5. Генератор ассиметричных ключей
Для ассиметричных систем шифрования ключи должны быть не
только случайными, но и простыми, т.е. должны делиться только на 1
или на самих себя.
Здесь возможно два подхода:
1. Сгенерировать случайное число и проверить, является ли оно
простым или нет.
2. С помощью специальных алгоритмов сразу строить случайное
простое число.
Наиболее простым в реализации представляется первый подход,
Здесь в свою очередь самым очевидным способом проверки простоты
числа N является проверка на делимость.
В настоящее время известно достаточно большое число эффективных способов проверки больших чисел на простоту.
1. Метод пробных делений
Если n – составное, то n a b , где 1 a b причем a b . Поэтому
для d 2, n мы проверяем, делится ли n на d ? Если делитель числа n
не будет найден, то n – простое. В противном случае будет найден минимальный простой делитель числа n , т.е. мы да же разложим n на два
14
множителя. Сложность метода составляет O( n ) арифметических операций с целыми числами.
Возможны модификации этого метода. Например, мы можем
проверить, делится ли n на 2 и на 3 , и если нет, то перебираем далее
только числа d вида 1 6 j,5 6 j, j 1, 2,... .
3. Решето Эратосфена
4. Если мы хотим составить таблицу всех простых чисел среди чисел
2,3,..., n то нужно сначала вычеркнуть все числа, делящиеся на 2, кроме
2. Затем взять число 3 и вычеркнуть все последующие числа, делящиеся
на 3 . Затем взять следующее не вычеркнутое число (т. е. 5) и вычеркнуть все последующие делящиеся на него числа, и так далее. В итоге
останутся лишь простые числа.
Для реализации метода нужен большой объем памяти ЭВМ, однако
для составления таблиц простых чисел он является наилучшим.
Всего требуется O(log3 n) арифметических операций.
3. Критерий Вильсона
Теорема 1
Для любого n следующие условия эквивалентны:
1. n - простое;
2. (n 1)! 1(mod n)
Данный критерий иногда бывает удобен в доказательствах, но
применять его для проверки простоты невозможно ввиду большой трудоемкости.
4. Тест на основе малой теоремы Ферма
Малая теорема Ферма утверждает, что если n – простое, то для
a a, n 1 имеет место сравнение:
(1)
a n1 1(mod n)
Обратное утверждение неверно.
Из этой теоремы следует, что если (1) не выполнилось хотя бы для
одного числа а в интервале 2; n 1 , то n – составное. Поэтому можно
предложить следующий вероятностный тест простоты:
1. Выбираем случайное число из интервала 1; n 1 и проверяем с
помощью алгоритма Евклида условие НОД (a, n) 1 .
2. Проверяем выполнимость сравнения a n1 1(mod n) .
3. Если сравнение (1) не выполнено, то ответ n – составное
4. Если сравнение (1) выполнено, то ответ неизвестен, но можно
повторить тест еще раз.
Если выполняется сравнение (1), то говорят, что число n является
nпсевдопростым по основанию a . Заметим, что существует бесконечно
15
много пар чисел (a, n) , где n – составное и псевдопростое по основанию
a . Например, при (a, n) (2,341) получаем 2340 (210 )34 1(mod 341) , хотя
341 11 31 .
Особый случай составляют составные числа, для которых условие
сравнения выполняется при всех основаниях. Они называются псевдопростыми числами, или числами Кармайкла.
Таким образом, при применении описанного выше теста может
возникнуть три ситуации:
число n простое и тест всегда говорит «не известно»;
число n составное и не является числом Кармайкла; тогда с nвероятностью успеха не меньше 1/ 2 тест дает ответ « n – составное»;
число n составное и является числом Кармайкла, тогда тест nвсегда дает ответ «не известно».
Числа Кармайкла являются достаточно редкими. Так, имеется всего
2163 чисел Кармайкла не превосходящих 25 109 . До 105 числами Кармайкла являются только следующие 16 чисел: 561, 1105, 1729, 2465,
2821, 6601, 8911, 10585, 15841, 29341, 41041, 46657, 52633, 62745, 63973
и 75361. Проверка того, является ли заданное число числом Кармайкла,
требует нахождения разложения числа на простые сомножители, т. е.
факторизации числа. Поскольку задача факторизации чисел является
более сложной, чем задача проверки простоты, то предварительная отбраковка чисел Кармайкла не представляется возможной. Поэтому в
приведенном выше тесте простые числа и числа Кармайкла полностью
неразличимы.
5. Тест Соловея – Штрассена
Теорема 2.
Для любого нечетного n следующие условия эквивалентны:
1. n - простое;
2. Множество:
a
a ( n 1)/2 (mod n)
n
(2)
a
где – символ Лежандра.
n
Р. Соловей и В.Штрассен предложили следующий вероятностный
тест для проверки простоты чисел:
1. Выбираем случайное число a из интервала 1; n 1 и проверяем с
помощью алгоритма Евклида условие НОД(a, n) 1
2. Если оно не выполняется, то n – составное.
3. Проверяем выполнимость сравнения (2).
4. Если оно не выполняется, то n – составное.
16
5. Если сравнение выполнено, то ответ неизвестен (и тест можно по-
вторить еще раз).
Сложность данного теста, как и теста на основе малой теоремы
Ферма, оценивается величиной O(log3 n) .
Данный тест полностью аналогичен тесту на основе малой теоремы
Ферма, однако, он обладает решающим преимуществом – при его использовании возникает только две ситуации:
число n простое и тест всегда говорит «не известно»;
число n составное и тест с вероятностью успеха не меньше
1/ 2 дает ответ « n – составное».
После повторения теста k раз вероятность неотбраковки составного числа не превосходит 1 / 2 k .
6. Тест Леманна
Далее приведена последовательность действий при проверке простоты числа n :
1. Выбрать случайно число a , меньшее n .
2. Вычислить t a ( p 1)/2 mod n .
3. Если t 1 (или или), то n не является простым.
4. Если t 1 (или или), то вероятность того, что число n не является простым, не больше 1/ 2 .
Повторите эту проверку k раз. Если результат вычислений равен 1
или -1, но не всегда равен 1, то n является простым числом с вероятностью ошибки 1 / 2 k .
7. Тест Рабина – Миллера
Пусть n – нечетное и n 1 2t t , t – нечетное. Если число n является
простым, то при всех a 2 выполняется сравнение a n1 1(mod n) . Поэтому, рассматривая элементы at , a2t ,..., a2 t можно заметить, что либо среди
них найдется равный 1(mod n) , либо at 1(mod n) .
На этом замечании основан следующий вероятностный тест простоты:
1. Выбираем случайное число a из интервала 1; n 1 и проверяем с
помощью алгоритма Евклида условие НОД(a,n)=1.
2. Если оно не выполняется, то ответ « n – составное».
3. Вычисляем a t mod n .
4. Если at 1(mod n) , то переходим к шагу 1.
5. Вычисляем at mod n, a2t mod n,..., a2 t mod n до тех пор, пока не появится 1 .
6. Если ни одно из этих чисел не равно 1 , то ответ « n −составное»;
s1
s1
17
7. Если мы достигли n , то ответ неизвестен (и тест можно повторить
еще раз).
Арифметическая сложность данного теста, очевидно, составляет
O ( s n) . После повторения данного теста k раз вероятность неотбраковки составного числа не превосходит 1 / 4 k .
Тест Рабина – Миллера всегда сильнее теста Соловея – Штрассена.
Точнее, если при фиксированном n число a проходит тест Рабина –
Миллера и не показывает, что n составное, то оно проходит тест Соловея – Штрассена с тем же результатом.
8. Полиномиальный тест распознавания простоты. Данный алгоритм основан на следующем критерии простоты.
Теорема 3.
Пусть числа a, n взаимно просты. Тогда n – простое в том и только
в том случае, когда выполнено сравнение:
(3)
( x a)n ( x n a)(mod n)
Приведем сам алгоритм.
Вход: целое n 1 .
1. Если число n имеет вид a b , то ответ « n – составное».
2.
3.
4.
5.
r 2
Цикл пока r n :
Если НОД(r,n)≠1, то ответ « n – составное».
Если r – простое, то вычислить q – наибольший простой делитель r 1 ; если (q 4 r log2 n) и n( r 1)/ q 1(mod r ) , то выйти из цикла.
6. r r 1 .
7. Завершить цикл.
8. Если r n , то ответ « n – составное».
9. Если n 1 2 r log n , то a 1, n 1 проверить выполнение усло2
вия: Í Î Ä (a, n) 1 .
10. Если n 1 2 r log 2 n , то a 1, 2 r log 2 n проверить выполнение
условия: ( x a)n ( xn a)(mod xr 1) .
11. Если на шаге 9-10 нарушились равенства, то ответ « n – составное».
12. Если мы дошли до этого шага, то ответ « n – простое».
9. Метод Михалеску.
Данный метод является алгоритмом генерации доказуемо простых
чисел.
Алгоритм генерации доказуемо простых m -разрядных чисел состоит в следующем. Пусть B 0 – целое число и s, c 0 – действительные константы.
18
1. Если m B , то алгоритм возвращает случайное простое число с m
двоичными разрядами (порожденное с помощью пробных делений).
2. Строим с помощью рекурсии целое число F из интервала
2em F 2cem , факторизация которого полностью известна, где e
можно положить 1/ 2 или 1/ 3 в зависимости от применяемого достаточного условия простоты.
3. Выбираем случайное число t (2m2 / F , 2m1 / F sm) .
4. Ищем простое число в арифметической прогрессии
P {n n0 ia : n0 ta 1, a 2F , i 0, s} .
Тест простоты, применяемый на шаге 4, выполняется в два этапа.
Этап 1. Пробные деления на простые числа, не превосходящие A,
где A
– заданная верхняя граница.
Этап 2. Проверка простоты с помощью теста Рабина—Миллера.
ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
Реализовать приложение, позволяющее генерировать простое число по следующей схеме (с использованием, например, теста Рабина –
Миллера):
1. Сгенерируйте случайное p - битовое число n .
2. Установите старший и младший биты равными 1. (Старший бит
гарантирует требуемую длину простого числа, а младший бит
обеспечивает его нечетность.)
3. Убедитесь, что n не делится на небольшие простые числа: 3, 5, 7,
11, и т.д. Во многих реализациях проверяется делимость n на все
простые числа, меньшие 256. Наиболее эффективной является
проверка на делимость для всех простых чисел, меньших 2000.
4. Выполните один тест Рабина – Миллера проверки простоты числа
для некоторого случайного a . Если n проходит тест, сгенерируйте другое случайное a и повторите проверку. Выбирайте небольшие a значения для ускорения вычислений. Выполните пять тестов. (Одного может показаться достаточным, но выполните
пять.) Если n не проходит одной из проверок, сгенерируйте другое n и попробуйте снова.
5. Вместо теста Рабина-Миллера использовать тест, заданный в варианте из табл.8.4.
19
Таблица 8.4. Способы проверки простых чисел на «простоту»
1
2
3
4
Решето Эратосфена
Тест Леманна
Метод Михалеску
Тест Соловея – Штрассена
5 Тест Рабина – Миллера
Полиномиальный тест простоты.
Тест Рабина – Миллера
Метод пробных делений
Критерий Вильсона+Решето Эратосфена
10 Метод Михалеску
6
7
8
9
Все простые числа, не превосходящие 256 перечислены ниже:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79,
83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163,
167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241,
251.
Можно не генерировать n случайным образом каждый раз, но последовательно перебирать числа, начиная со случайно выбранного,
необходимо до тех пор, пока не будет найдено простое число.
Этап (3) не является обязательным. Проверка, что случайное нечетное не делится на 3, 5 и 7 отсекает 54 процента нечетных чисел еще
до этапа (4). Проверка делимости на все простые числа, меньшие 100,
убирает 76 процентов нечетных чисел, проверка делимости на все простые числа, меньшие 256, убирает 80 процентов нечетных чисел. В общем случае, доля нечетных кандидатов, которые не делятся ни на одно
простое число, меньшее z , равна 1.12 / ln z .
Лабораторная работа 6. Контроллер хеш-функций
Хеш-функция предназначена для сжатия подписываемого документа М до нескольких десятков или сотен бит. Хеш-функция h(-) принимает в качестве аргумента сообщение (документ) М произвольной
длины и возвращает хеш-значение h( M ) H фиксированной длины.
Обычно хешированная информация является сжатым двоичным представлением основного сообщения произвольной длины. Следует отметить, что значение хеш-функции h(M ) сложным образом зависит от документа М и не позволяет восстановить сам документ М .
Хеш-функция должна удовлетворять целому ряду условий:
1. Хеш-функция должна быть чувствительна к всевозможным изменениям в тексте М , таким как вставки, выбросы, перестановки и т.п.;
2. Хеш-функция должна обладать свойством необратимости, то есть
задача подбора документа M 1 , который обладал бы требуемым значением хеш-функции, должна быть вычислительно неразрешима;
20
3. Вероятность того, что значения хеш-функции двух различных до-
кументов (вне зависимости от их длин) совпадут, должна быть ничтожно мала.
Большинство хеш-функции строится на основе однонаправленной
функции f () , которая образует выходное значение длиной n при задании двух входных значений длиной n . Этими входами являются блок
исходного текста M и хеш-значение Hi 1 предыдущего блока текста,
рис.8.3:
Hi f (M i , Hi 1 )
64 бит
Вектор
инициализации
M0
64 бит
M1
Mi
H(i-1)
H
128 бит
...
128 бит
ML-1
H(i)
...
H
128 бит
128 бит
Хеш-значение
H
128 бит
128 бит
Рис.8.3. Схема хеширования данных.
Хеш-значение вычисляемое при вводе последнего блока текста,
становится хеш-значением всего сообщения M .
В результате однонаправленная хеш-функция всегда формирует
выход фиксированной длины n (независимо от длины входного текста).
Однонаправленную хеш-функцию можно построить, используя
симметричный блочный алгоритм. Наиболее очевидный подход состоит
в том, чтобы шифровать сообщение M посредством блочного алгоритма
в режиме СВС или СFВ с помощью фиксированного ключа и некоторого вектора инициализации, Последний блок шифротекста можно рассматривать в качестве хеш-значения сообщения M . При таком подходе
не всегда возможно построить безопасную однонаправленную хешфункцию, но всегда можно получить код аутентификации сообщения
MAC (Message Authentication Code).
Более безопасный вариант хеш-функции можно получить, используя блок сообщения в качестве ключа, предыдущее хеш-значение в качестве входа, а текущее хеш-значение в качестве выхода. Реальные хешфункции проектируются еще более сложными. Длина блока обычно
определяется длиной ключа, а длина хеш-значения совпадает с длиной
блока. Поскольку большинство блочных алгоритмов являются 64битовыми, некоторые схемы хеширования проектируют так, чтобы хешзначение имело длину, равную двойной длине блока.
21
ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
1. Построить на ПЛИС или микроконтроллере устройство для формирования хеш-функции (ХЕШ-контроллер) для варианта из табл.8.5.
2. Сформировать хеш-значение для заданного файла программным
методом.
3. Выполнить проверку хеш-значения для заданного файла аппаратным методом.
Таблица 8.5. Часто используемые хеш-функции
1
2
3
4
5
MD4
ГОСТ 34.11.94
MAC
SHA-256
DES-CFB
6
7
8
9
10
MD5
DES-CBC
SHA-1
SHA-384
SHA-512
Лабораторная работа 7. Контроллер RSA
Эффективными системами криптографической защиты данных являются асимметричные криптосистемы, называемые также криптосистемами с открытым ключом. В таких системах для зашифрования данных используется один ключ, а для расшифрования другой ключ (отсюда и название – ассиметричные). Первый ключ является открытым и
может быть опубликован для шифрования своей информации любым
пользователем сети. Получатель зашифрованной информации для расшифровки данных использует второй ключ, являющийся секретным.
При этом должно соблюдаться следующее условие: секретный ключ не
может быть определен из опубликованного открытого ключа.
Криптографические системы с открытым ключом используют необратимые или односторонние функции, обладающие важным свойством: при заданном значении x относительно просто вычислить значение f ( x) , однако, если y f ( x) , то нет простого пути для вычисления
значения x , то есть очень трудно рассчитать значение обратной функции x f 1 ( y) .
В настоящее время широко используется метод криптографической
защиты данных с открытым ключом RSA, получившим название по
начальным буквам фамилий его изобретателей (Rivest, Shamir,
Adleman). На основе метода RSA разработаны алгоритмы шифрования,
успешно применяемые для защиты информации. Он обладает высокой
криптостойкостью и может быть реализован при использовании относительно несложных программных и аппаратных средств. Данный метод
позволил решить проблему обеспечения персональных подписей в
22
условиях безбумажной передачи и обработки данных. Описание схем
формирования шифротекста в алгоритмах типа RSA приведено в различной литературе.
Использование метода RSA для криптографической защиты информации может быть пояснено с помощью структурной схемы, представленной на рисунке.
Функционирование криптосистемы на основе метода RSA предполагает формирование открытого и секретного ключей, рис.8.4.
k ( p 1) (q 1)
Выбор из ПСП
простых чисел p и q
n pq
Выбор из ПСП числа d
взаимно простого с k
Вычисление
(e d ) mod k 1
{n, d }
{n, e}
Ключ расшифрования Ключ шифрования
(открытый)
(секретный)
Рис.8.4. Схема формирования асимметричных ключей
С этой целью необходимо выполнить следующие математические операции:
1. Выбираем два больших простых числа p и q , понимая под простыми числами такие числа, которые делятся на само себя и число
1.
2. Определяем произведение n p q .
3. Вычисляем число k ( p 1)(q 1) .
4. Выбираем большое случайное число d , взаимно простое с числом
k (взаимно простое число — это число, которое не имеет ни одного общего делителя, кроме числа 1)
5. Определяем число e , для которого истинным является соотношение
(e d ) mod k 1
6. Принимаем в качестве открытого ключа пару чисел {е, n}.
7. Принимаем в качестве секретного ключа пару чисел {d, n}.
Для зашифровки передаваемых данных с помощью открытого
ключа {е, n} необходимо выполнить операции:
23
● Разбить шифруемый текст на блоки, каждый из которых может
быть представлен в виде чисел M (i) 0,1,..., n 1 .
● Зашифровать текст в виде последовательности чисел M (i) с помощью открытого ключа {e, n} по формуле
C (i) (M (i)e ) mod n
● Расшифрование шифротекста, представленного в виде последовательности чисел C (i ) , производится с помощью секретного ключа
{d, n} при выполнении следующих вычислений:
M(i) = (C(i)d) mod n
В результате получаем последовательность чисел M(i), представляющих исходные данные. На практике при использовании метода RSA
длина р и q составляет 100 и более десятичных знаков, что обеспечивает
высокую криптостойкость шифротекста.
ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ
1. Сформировать ключи асимметричного шифрования и расшифрования длиной 64 двоичных разряда.
2. Зашифровать заданный файл по алгоритму RSA, реализованному
программно, схема на рис.8.5.
3. Расшифровать зашифрованный текст с помощью дешифрующего
устройства, реализованного аппаратно на ПЛИС или микроконтроллере
Открытый
текст:
M(0)
а)
шифрование
M(2)
...
( M (0)e ) mod n
Шифротекст: C(0)
b)
расшифрование
Открытый
текст:
M(1)
C(1)
...
C(2)
...
(C (0)d ) mod n
M(0)
M(1)
...
...
M(2)
M(i)
...
M(n-1)
( M (i)e ) mod n
C(i)
...
C(n-1)
24
C(n)
(C (i)d ) mod n
M(i)
...
M(n-1)
Рис.8.5. Схема асимметричного шифрования а) и расшифрования b).
(контроллер RSA).
M(n)
M(n)
ЛИТЕРАТУРА
Аршинов М. Н., Садовский Л. Е. Коды и математика (рассказы
о кодировании). - М.: Наука, 1983. – 144 с.
2.
Баричев С.Г., Гончаров В.В., Серов Р.Е. Основы современной
криптографии. Учебное пособие. - М.: Горячая линия – Телеком, 2001. –
120 с.
3.
Безопасность сети на основе Windows 2000. Учебный курс
MCSE. - М.: ИТД Русская Редакция. 2001. – 912 с.
4.
Белов Е.Б., Лось В.П., Мещеряков Р.В., Шелупанов А.А. Основы информационной безопасности. Учебное пособие для вузов. - М.:
Горячая линия – Телеком, 2006. – 544 с.
5.
Бернет С., Пэйн С. Криптография. Официальное руководство
RSA Security. - М.: Бином-Пресс, 2002. - 384 с.
6.
Галатенко В.А. Стандарты информационной безопасности.
Курс лекций. – М.: ИНТУИТ. РУ, 2004. – 328 с.
7.
Галатенко В.А. Основы информационной безопасности. Курс
лекций. – М.: ИНТУИТ. РУ, 2006. – 205 с.
8.
Галицкий А.В., Рябко С.Д., Шаньгин В.Ф. Защита информации
в сети – анализ технологий и синтез решений. – М.: ДМК Пресс, 2004. –
616 с.
9.
Голдовский И. Безопасность платежей в Интернете. - СПб.:
Питер, 2001. – 240 с.
10. Государственная тайна и ее защита. Собрание законодательных и нормативных правовых актов. - М.: «Ось-89», 2004. - 160 с.
11. ГОСТ 28147-89. Система обработки информации. Защита
криптографическая. Алгоритм криптографического преобразования. М.: Госстандарт СССР, 1989.
12. ГОСТ Р 34.10-2001. Информационная технология. Криптографическая защита информации. Процессы формирования и проверки
электронной цифровой подписи.
13. ГОСТ Р 34.10-94. Информационная технология. Криптографическая защита информации. Процедуры выработки и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма. - М.: Госстандарт России, 1994.
14. ГОСТ Р 34.11-94. Информационная технология. Криптографическая защита информации. Функция хэширования. - М.: Госстандарт
России, 1994.
15. ГОСТ Р ИСО/МЭК 15408-1-2002. Информационная технология. Методы и средства обеспечения безопасности. Критерии оценки
1.
25
безопасности информационных технологий. Часть 1. Введение и общая
модель. - М.: ИПК «Издательство стандартов», 2002.
26