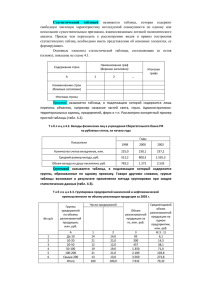
Цель работы: ознакомиться с основными статистическими понятиями, используемыми в гидрологии, и получить общую подготовку для выполнения последующих работ. Основные задачи: 1) на основе элементарных методов преобразования исходных данных и их наглядного представления произвести анализ рассматриваемых процессов по имеющим рядам наблюдений; 2) выявить, в первом приближении, особенности данных и внутренне закономерности представленных ими рассматриваемых процессов. Исходные данные: два временных ряда данных о среднегодовом и максимальном стоке за совместный период наблюдений, продолжительностью 40 лет. Ход работы: Был проведен разведочный анализ рядов среднегодовых и максимальных расходов р. Адагум у г. Крымск за период с 1965 по 2011 г. Исходные данные: Таблица 1. Среднегодовые расходы р.Адагум – г.Крымск. Год 1965 1966 1967 1968 1969 1970 1971 1972 1973 1974 Средний 3.44 3.25 4.02 3.91 1 2.64 2.43 1.09 2.35 1.62 Год 1975 1976 1977 1978 1979 1980 1981 1982 1983 1985 Средний 3.26 3.18 1.97 2.33 2.09 2.89 4.3 2.07 2.44 2.5 Год 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 Средний 2.64 2.99 3.04 3.15 2.56 2.12 4.11 1.88 1.79 6.22 Год 1996 1997 1998 1999 2000 2007 2008 2009 2010 2011 Средний 2.98 5.16 6.82 2.59 3.88 2.01 1.74 2.5 3.55 3.03 Таблица 2. Максимальные расходы р.Адагум – г.Крымск. Год 1965 1966 1967 1968 1969 1970 1971 1972 1973 1974 Средний 507 97.8 148 65.4 14.0 57.1 56.5 23.8 77.3 33.3 Год 1975 1976 1977 1978 1979 1980 1981 1982 1983 1985 Средний 103 312 122 82.0 110 38.6 185 68.1 237 94.4 Год 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 Средний 105 63.4 99.4 142 69.9 18.6 112 15 71 355 Год 1996 1997 1998 1999 2000 2007 2008 2009 2010 2011 Средний 55.3 66.7 416 78.7 555 129 99.6 166 736 520 Были построены графики изменений рассматриваемых процессов во времени гидрографов (Рис.1). 800 700 РАСХОД, М3/С 600 500 400 300 200 100 1993 1991 1972 1974 1980 1996 1971 1970 1987 1968 1997 1982 1990 1994 1973 1999 1978 1985 1966 1988 2008 1975 1986 1979 1992 1977 2007 1989 1967 2009 1981 1983 1976 1995 1998 1965 2011 2000 2010 0 ГОДЫ Средний Максимальный Рисунок 1. Гидрограф значений максимальных и среднегодовых расходов р. Адагум - г. Крымск. Были рассчитаны значения статистических совокупностей и координат эмпирических функций распределения и обеспеченности по исходным рядам стока; построены гистограммы, эмпирические функции распределения и обеспеченности. Расчет значений статистической совокупности для каждого исходного ряда производился в таблице 3. Для этого амплитуда исходного ряда разбивается на равные интервалы. В данном случае количество интервалов для обоих рассматриваемых рядов стока было принято равным 6 при длине интервалов 5,82 для ряда среднегодовых расходов и 722 для ряда максимальных расходов. Границы интервалов заносились в первую строку статистических совокупностей (таблица 3). Затем по исходным рядам подсчитывалось число значений стока в каждом интервале m, которые приводятся во второй строке таблицы 3. В третью строку статистических совокупностей заносились частоты р, определённые по формуле 𝑝 = 𝑚/𝑛. Таблица 3. Статистическая совокупность ряда годовых расходов р. Адагум - г. Крымск. Значение Параметры Интервал Число значений, m Частота, p Интервал Число значений, m Частота, p Среднегодовые расходы 1--2 2--3 3--4 7 0.18 17 0.43 14--134 134--254 254--374 28 0.70 5 0.13 2 0.05 4--5 5--6 6--7 1 0.03 2 0.05 374--494 494--614 614--737 1 0.03 3 0.08 1 0.03 10 3 0.25 0.08 Максимальные расходы Расчет координат эмпирической функции обеспеченности и функции распределения по первому и второму рядам производился в таблице 4. В первой строке указывались нижние границы интервалов статистических совокупностей. Во второй строке приводилось число случаев, когда значения расходов ниже соответствующей нижней границы интервала – К1, в третьей строке – когда значения расходов равны или выше нижней границы интервала – К2. В четвертой и пятой строках указывались значения ординат функции распределения F(х) и кривой обеспеченности Р(х). Таблица 4. Расчет эмпирических функций распределения и обеспеченности ряда расходов (р. Адагум - г. Крымск). Значение Параметр Нижняя граница интервала K1 K2 F(x) P(x) Параметр Нижняя граница интервала K1 K2 F(x) P(x) Среднегодовые расходы 1 0 40 0.00 1.00 2 7 33 0.18 0.83 14 0 40 0 1 134 28 12 0.70 0.30 3 4 5 24 34 37 16 6 3 0.60 0.85 0.93 0.40 0.15 0.08 Максимальные расходы 254 33 7 0.83 0.18 374 35 5 0.88 0.13 494 36 4 0.90 0.10 6 38 2 0.95 0.05 7 40 0 1.00 0.00 614 39 1 0.98 0.03 737 40 0 1.00 0.00 Построение в одних координатных осях гистограммы, эмпирических функций распределения и эмпирических функций обеспеченности отдельно для первого (рис. 2) и второго (рис.3.) рядов производилось по данным табл. 3 и табл.4. На рисунках по оси абсцисс откладывались значения нижней границы интервалов, а по оси ординат – для эмпирической функции распределения – К1 и для ординаты эмпирической функции обеспеченности – К2. 1,2 1 P(x) 0,8 0,6 0,4 0,2 0 1 2 3 4 5 6 7 Q, м3/c Частота, p F(x) P(x) Рисунок 2. Гистограмма, кривые функций распределения и обеспеченности среднегодовых расходов воды (р. Адагум - г. Крымск). 1,2 1 P(x) 0,8 0,6 0,4 0,2 0 14 134 254 374 494 614 737 Q, м3/с Частота, p F(x) P(x) Рисунок 3. Гистограмма, кривые функций распределения и обеспеченности максимальных расходов воды (р. Адагум - г. Крымск). Была проведена оценка числовых характеристик. Были определены по обоим рядам оценок моды и медианы. В данном случае, для ряда среднегодовых расходов мода равна 2,64, для ряда максимального стока -моды выявлено не было. Медиана составляет соответственно 2,64 и 98,6. Так как в данном случае все члены исходных рядов положительны, то расчет других числовых характеристик производился по таблице 5. В данной таблице в первой колонке указывался порядковый номер членов ряда, во второй – год наблюдения, в третьей – значения среднегодовых расходов, в четвертой – значения средних годовых расходов в 𝑥 убывающем порядке, в пятой – модульные коэффициенты (𝑘𝑖 = 𝑚𝑖 ), в шестой – отклонения 𝑖 модульных коэффициентов от единицы, в седьмой и восьмой – отклонения от единицы в квадрате и кубе, в девятой – значения эмпирической обеспеченности, рассчитанные по 𝑚 формуле 𝑃̂ = 𝑛𝑙𝑖 . В нижней строке таблицы представлены суммы расходов, модульных коэффициентов, отклонений модульных коэффициентов от единицы и суммы квадратов и кубов отклонений от единицы. Таблица 5. Расчет статистических характеристик ряда максимальных расходов (р. Адагум - г. Крымск). № п/п 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 Год 1965 1966 1967 1968 1969 1970 1971 1972 1973 1974 1975 1976 1977 1978 1979 1980 1981 1982 1983 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 Qср 3.44 3.25 4.02 3.91 1 2.64 2.43 1.09 2.35 1.62 3.26 3.18 1.97 2.33 2.09 2.89 4.3 2.07 2.44 2.5 2.64 2.99 3.04 3.15 2.56 2.12 4.11 1.88 1.79 6.22 2.98 5.16 Qср ранж 6.82 6.22 5.16 4.3 4.11 4.02 3.91 3.88 3.55 3.44 3.26 3.25 3.18 3.15 3.04 3.03 2.99 2.98 2.89 2.64 2.64 2.59 2.56 2.5 2.5 2.44 2.43 2.35 2.33 2.12 2.09 2.07 Ki 2.32 2.12 1.76 1.46 1.40 1.37 1.33 1.32 1.21 1.17 1.11 1.11 1.08 1.07 1.03 1.03 1.02 1.01 0.98 0.90 0.90 0.88 0.87 0.85 0.85 0.83 0.83 0.80 0.79 0.72 0.71 0.70 K(i-1) 1.32 1.12 0.76 0.46 0.40 0.37 0.33 0.32 0.21 0.17 0.11 0.11 0.08 0.07 0.03 0.03 0.02 0.01 -0.02 -0.10 -0.10 -0.12 -0.13 -0.15 -0.15 -0.17 -0.17 -0.20 -0.21 -0.28 -0.29 -0.30 K(i-1)2 1.745 1.247 0.572 0.215 0.159 0.135 0.109 0.103 0.043 0.029 0.012 0.011 0.007 0.005 0.001 0.001 0.000 0.000 0.000 0.010 0.010 0.014 0.017 0.022 0.022 0.029 0.030 0.040 0.043 0.078 0.083 0.087 (Ki-1)3 2.305 1.393 0.432 0.099 0.063 0.050 0.036 0.033 0.009 0.005 0.001 0.001 0.001 0.000 0.000 0.000 0.000 0.000 0.000 -0.001 -0.001 -0.002 -0.002 -0.003 -0.003 -0.005 -0.005 -0.008 -0.009 -0.022 -0.024 -0.026 Pm 2 5 7 10 12 15 17 20 22 24 27 29 32 34 37 39 41 44 46 49 51 54 56 59 61 63 66 68 71 73 76 78 33 34 35 36 37 38 39 40 1998 1999 2000 2007 2008 2009 2010 2011 6.82 2.59 3.88 2.01 1.74 2.5 3.55 3.03 117.54 2.01 1.97 1.88 1.79 1.74 1.62 1.09 1 117.54 0.68 0.67 0.64 0.61 0.59 0.55 0.37 0.34 40 -0.32 -0.33 -0.36 -0.39 -0.41 -0.45 -0.63 -0.66 0 0.100 0.109 0.130 0.153 0.166 0.201 0.396 0.435 6.570416 -0.032 -0.036 -0.047 -0.060 -0.068 -0.090 -0.249 -0.287 3.449626 80 83 85 88 90 93 95 98 По перечисленным суммам рассчитывались 𝑚 ̂𝑥 , 𝜎𝑥 , Cv и Сs. По данным расчетов таблицы 5, получаем: 𝑚 ̂𝑥 = ∑𝑛 𝑖=1 𝑥𝑖 𝑛 σx = √ = 117,54 40 ̂ ∑n i=1(xi −mx )2 (n−1) = 2,94 =1.21 2 ∑N i=1(ki −1) σ Cv =mx = √ x N = 0,4 3 3 Сs =∑N i=1(k i − 1) /N/Cv = 1.26 Аналогично проводился расчет статистических характеристик ряда максимальных расходов (табл. 6). Таблица 6. Расчет статистических характеристик ряда максимальных расходов (р. Адагум - г. Крымск). № п/п 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 Год 1965 1966 1967 1968 1969 1970 1971 1972 1973 1974 1975 1976 1977 1978 1979 1980 1981 1982 1983 1985 1986 Qмакс. 507 97.8 148 65.4 14 57.1 56.5 23.8 77.3 33.3 103 312 122 82 110 38.6 185 68.1 237 94.4 105 Qмакс. ранж 736 555 520 507 416 355 312 237 185 166 148 142 129 122 112 110 105 103 99.6 99.4 97.8 Ki 4.67 3.52 3.30 3.22 2.64 2.25 1.98 1.50 1.17 1.05 0.94 0.90 0.82 0.77 0.71 0.70 0.67 0.65 0.63 0.63 0.62 K(i-1) 3.67 2.52 2.30 2.22 1.64 1.25 0.98 0.50 0.17 0.05 -0.06 -0.10 -0.18 -0.23 -0.29 -0.30 -0.33 -0.35 -0.37 -0.37 -0.38 K(i-1)2 13.46 6.35 5.28 4.91 2.69 1.57 0.96 0.25 0.03 0.00 0.00 0.01 0.03 0.05 0.08 0.09 0.11 0.12 0.14 0.14 0.14 (Ki-1)3 49.38 16.01 12.14 10.88 4.40 1.96 0.94 0.13 0.01 0.00 0.00 0.00 -0.01 -0.01 -0.02 -0.03 -0.04 -0.04 -0.05 -0.05 -0.05 Pm 2 5 7 10 12 15 17 20 22 24 27 29 32 34 37 39 41 44 46 49 51 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2007 2008 2009 2010 2011 63.4 99.4 142 69.9 18.6 112 15 71 355 55.3 66.7 416 78.7 555 129 99.6 166 736 520 6305.9 94.4 82 78.7 77.3 71 69.9 68.1 66.7 65.4 63.4 57.1 56.5 55.3 38.6 33.3 23.8 18.6 15 14 6305.9 0.60 0.52 0.50 0.49 0.45 0.44 0.43 0.42 0.41 0.40 0.36 0.36 0.35 0.24 0.21 0.15 0.12 0.10 0.09 40 -0.40 -0.48 -0.50 -0.51 -0.55 -0.56 -0.57 -0.58 -0.59 -0.60 -0.64 -0.64 -0.65 -0.76 -0.79 -0.85 -0.88 -0.90 -0.91 0 0.16 -0.06 0.23 -0.11 0.25 -0.13 0.26 -0.13 0.30 -0.17 0.31 -0.17 0.32 -0.18 0.33 -0.19 0.34 -0.20 0.36 -0.21 0.41 -0.26 0.41 -0.26 0.42 -0.27 0.57 -0.43 0.62 -0.49 0.72 -0.61 0.78 -0.69 0.82 -0.74 0.83 -0.76 44.87352 89.46958 54 56 59 61 63 66 68 71 73 76 78 80 83 85 88 90 93 95 98 По перечисленным суммам рассчитывались 𝑚 ̂𝑥 , 𝜎𝑥 , Cv и Сs. По данным расчетов табл.6, получаем: 𝑚 ̂𝑥 = ∑𝑛 𝑖=1 𝑥𝑖 = 𝑛 σx = √ 6305.9 40 ̂ ∑n i=1(xi −mx ) (n−1) = 158 = 169 2 ∑N i=1(ki −1) σ Cv=mx = √ x N = 1.07 3 3 Сs =∑N i=1(k i − 1) /N/Cv = 1.85 Затем, была составлена сводная таблица оценок основных числовых характеристик (Табл.7). Таблица 7. Числовые характеристики среднегодовых и максимальных расходов (р. Адагум - г. Крымск). Название ряда Qср Qмакс mx 2.94 158 M 2.64 314 Me 2.64 98.6 Оценки 𝜎𝑥 1.21 169 Dx 1.45 28595.7 Cv 0.41 1.07 Cs 1.26 1.85 2 Примечание: 𝐷𝑥 = ∑𝑁 𝑖=1(𝑥𝑖 − 𝑚𝑥 ) /𝑁 Была произведена оценка абсолютных и относительных погрешностей расчета числовых характеристик по имеющимся рядам данных и затем была составлена сводная таблица абсолютных и относительных погрешностей (табл.8). Расчет проводился по следующим формулам: средняя квадратичекая погрешность оценка математического ожидания ̂𝑚(𝑥) = σ ̂𝑥 σ ; √𝑛 ̂̂𝑥 𝐷 средняя квадратическая погрешность оценки дисперсии σ̂𝐷(𝑥) = средняя квадратическая погрешность определения коэффициента вариации √𝑛 ̂ 2; √2 + 1,5𝐶𝑣 ̂ 2 /√2𝑛; ̂𝐶𝑣 σ ̂ = 𝐶𝑣 √1 + 𝐶𝑣 средняя квадратическая погрешность коэффициента асимметрии 6 ̂С𝑠 = √( ) (1 + 6𝐶𝑣 2 + 5𝐶𝑣 4 )𝐶𝑠. σ 𝑛 Таблица 8. Абсолютные и относительные погрешности оценок числовых характеристик среднегодовых (Qср) и максимальных (Qмакс) расходов (р. Адагум - г. Крымск). Числовые Qср Qмакс характеристики Оценка ∆, % Оценка ∆, % σ σ 2.94 0.16 5.31 158 21.82 13.81 𝑚 ̂𝑥 𝐷̂ 1.45 0.39 27.09 28595.76 9882.72 34.56 𝑥 Cv 0.41 0.04 9.87 1.09 0.14 13.21 ̂С𝑠 1.27 0.59 46.37 1.85 2.25 121.47