курсовой проект по дисциплине: “Конструирование и расчет вагонов ”

Федеральное агентство железнодорожного транспорта
Уральский государственный университет путей сообщения
Кафедра «Вагоны»
ВАГОН-ХОППЕР
ДЛЯ ПЕРЕВОЗКИ ЗЕРНА
Пояснительная записка к курсовому проекту
По дисциплине: “Конструирование и расчет вагонов ”
Проверил:
Разработал:
ассистент
Студент группы В-422
Колясов К.М.
Шевнин Н.Я.
Екатеринбург
2005г
РЕФЕРАТ
В записке 54 стр., 28 рис., 1 табл., 5 исп. источников.
ВАГОН–ХОППЕР КОЛЕСНЫЕ ПАРЫ, БАЗА ВАГОНА, БАЗА ТЕЛЕЖКИ,
КУЗОВ ВАГОНА, БУКСА, РАМА ТЕЛЕЖКИ, ГАБАРИТ, СКОЛЬЗУНЫ,
АВТОСЦЕПКА.
В проекте определены основные размеры вагона, произведено вписывание вагона
в габарит, описана конструкция вагона, произведен расчет рессорного подвешивания, расчет на прочность рамы вагона от продольной нагрузки в программном
комплексе.
190302 16 КП 156 ПЗ
Изм Лист
№ документа
Разраб.
Рук.
Н.контр.
Утв
Шевнин
Колясов
Подпись
Дата
4-х осный крытый вагон
хоппер для перевозки
зерна
Лит.
У
Лист
3
Листов
54
Кафедра «Вагоны»
УрГУПС
СОДЕРЖАНИЕ
Введение……………………………………………………………………4
1 Назначение и роль проектируемого вагона в системе грузооборота
железных дорог………………………………………………………………….5
2 Формулировка основных моментов технических требований на
проектируемый вагон…………………..…….………...………………7
3 Расчет линейных размеров и определение основных параметров вагона…..8
4 Уточнение параметров вагона по результатам вписывания в габарит…….11
5 Проектирование основных узлов кузова вагона…………………………….18
5.1 Конструкция рамы вагона…………………………………………………..20
5.2 Устройство боковых стен вагона…………………………………….…….22
5.3 Устройство торцевых стен вагона………………………………………….23
5.4 Крыша вагона …………………………………………………..…………..23
5.5 Наружное оборудование вагона ………………………………..………….24
6 Расчет характеристик рессорного подвешивания…………………….…….25
7 Определение требуемого коэффициента относительного трения фрикционного гасителя колебаний из условия плавности хода вагона по неровности 4
вида………………………………………………………………………………28
8 Проектирование гасителя колебаний исходя из требуемого значения коэффициента относительного трения …………………………………………..…40
9 Определение усилий, действующих на колесную пару в кривой пути и проверка запаса устойчивости колесной пары………………………………...…..45
10 Расчет на прочность рамы вагона на продольные нагрузки 3 режим…….52
Список использованных источников………………………………………..…54
Лист
Изм. Лист
№ докум.
Подпись Дата
ВВЕДЕНИЕ
Саморазгружающиеся вагоны типа хоппер предназначены для перевозки сыпучих грузов. Основной особенностью конструкции таких вагонов является кузов,
выполненный в нижней части по форме бункера и имеющий вертикальные боковые и наклонные торцевые стены, по которым груз сползает к разгрузочным люкам бункера. По устройству бункеров и расположению разгрузочных люков хопперы могут обеспечивать выгрузку грузов между рельсами или на стороны от
рельсовой колеи.
Хопперы строят крытыми - для перевозки грузов, нуждающихся в защите от
атмосферных осадков (цемента, зерна, минеральных удобрений, сахара и др.), или
открытыми (полувагоны - хопперы) - для перевозки угля, торфа, руды, кокса, и
др. Первые применяются на магистральных железных дорогах, вторые - на железнодорожных путях промышленного транспорта. Все виды хопперов, как правило,
строят четырехосными с типовыми ходовыми частями, тормозными, автосцепными и др. устройствами.
Применение хопперов - зерновозов позволяет устранить следующие недостатки, свойственные существующему способу перевозки зерна в крытых универсальных вагонах: трудности в осуществлении механизированной разгрузки, необходимость выполнения значительных подготовительных работ по очистке, промывке и дезинфекции кузова, большие затраты ручного труда и простои вагонов
при разгрузке зерна.
Лист
Изм. Лист
№ докум.
Подпись Дата
1 НАЗНАЧЕНИЕ И РОЛЬ ПРОЕКТИРОВАННОГО ВАГОНА В
СИСТЕМЕ ГРУЗООБОРОТА ЖЕЛЕЗНЫХ ДОРОГ
Саморазгружающиеся вагоны типа хоппер предназначены для перевозки сыпучих грузов. Основной особенностью конструкции таких вагонов является кузов,
выполненный в нижней части по форме бункера и имеющий вертикальные боковые и наклонные торцевые стены, по которым груз сползает к разгрузочным люкам бункера. По устройству бункеров и расположению разгрузочных люков хопперы могут обеспечивать выгрузку грузов между рельсами или на стороны от
рельсовой колеи.
Хопперы строят крытыми - для перевозки грузов, нуждающихся в защите от
атмосферных осадков (цемента, зерна, минеральных удобрений, сахара и др.), или
открытыми (полувагоны - хопперы) - для перевозки угля, торфа, руды, кокса, и
др. Первые применяются на магистральных железных дорогах, вторые - на железнодорожных путях промышленного транспорта. Все виды хопперов, как правило,
строят четырехосными с типовыми ходовыми частями, тормозными, автосцепными и др. устройствами.
Применение хопперов - зерновозов позволяет устранить следующие недостатки, свойственные существующему способу перевозки зерна крытых универсальных вагонах: трудности в осуществлении механизированной разгрузки, необходимость выполнения значительных подготовительных работ по очистке, промывке и дезинфекции кузова, большие затраты ручного труда и простои вагонов
при разгрузке зерна.
Для всемерного повышения эффективности общественного производства,
роста производительности труда и лучшего использования основных средств
важное значение имеют технико-экономические исследования в области вагоностроения и вагонного хозяйства.
Лист
Изм. Лист
№ докум.
Подпись Дата
От правильности выбора типов и параметров грузовых вагонов зависит рациональное расходование крупных материальных ценностей, производительность
труда на железнодорожном транспорте.
При выборе типов вагонов особенно важными факторами являются объем и
состав грузооборота.
Основными параметрами вагона, характеризующими его эффективность, являются: тара вагона; грузоподъемность; объем котла; количество осей.
1
5
1850
6
2
4
15300
3
5
11130
1428
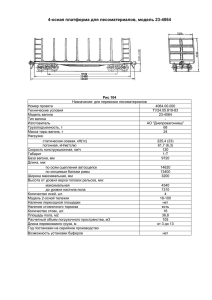
Рисунок 1–Основные размеры вагона-хоппера.
Вагон-хоппер (рис.1) состоит из: рамы 1, ходовых частей 2, ударно-тяговых
приборов 3, тормозного оборудования 4, устройств загрузки 5, устройств
выгрузки 6
Лист
Изм. Лист
№ докум.
Подпись Дата
2 ФОРМУЛИРОВКА ОСНОВНЫХ МОМЕНТОВ ТЕХНИЧЕСКИХ
ТРЕБОВАНИЙ НА ПРОЕКТИРУЕМЫЙ ВАГОН
Требования к грузовым вагонам определены государственными стандартами. Они
охватывают: общие требования, требования к материалам, надежности, безопасности работы обслуживающего персонала, маркировке и транспортированию, а
также гарантийные обязательства завода–изготовителя.
Общие требования регламентируют:
 Кинематичски словия эксплуатации;
 Параметры и размеры вагона;
 Габарит (0–Т);
 Прочность элементов вагона;
 Параметры наиболее ответственных узлов(тележек, автосцепки, тормоза и
др.);
 Конструкцию кузова;
 Грузоподъемность (70);
 Нагрузку от колесной пары на ось (23,25 тс);
 Нагрузку на погонный метр (6,25 тс/м);
 Конструктивную скорость (120 км/ч).
По надежности требования определяются установленным сроком службы вагона до списания и сроком эксплуатации до первых деповского и капитального
ремонтов.
Требования безопасности предусматривают оснащение вагонов лестницами,
подножками, кронштейнами для постановки домкратов, а также нанесение знаков
безопасности и предостерегающих надписей.
Гарантийные обязательства завода–изготовителя устанавливаются сроками
ответственности завода за качество изготовления вагона при соблюдении существующих и перспективных условий эксплуатации и ремонта вагонов.
Лист
Изм. Лист
№ докум.
Подпись Дата
3 РАСЧЕТ ЛИНЕЙНЫХ РАЗМЕРОВ И ОПРЕДЕЛЕНИЕ ОСНОВНЫХ
ПАРАМЕТРОВ ВАГОНА
Принимаем, что проектируемый вагон должен базироваться на вагоне аналоге, предшествующей конструкции. Вагон будет изготавливаться из аналогичных материалов и по той же технологии. В таком случае максимальный вес брутто вагона можно определить по зависимости:
РБР   р0  п ,
(1)
где  р0   допускаемая осевая нагрузка, определяемая мощностью верхнего строения пути.
При  р0   23,25 тс ось , имеем:
РБР  23,25  4  93 тс.
Вес брутто вагона складывается из веса тары (Т) вагона и его грузоподъемности.
Тара вагона высчитаем по формуле:
Т  КТ  Р. ,
(2)
Где: КТ – коэффициент тары (примем равным 0,307);
Р – грузоподъемность вагона (из задания равна 70 т).
Т  0,307  70  21,49тс.
По роду перевозимого груза определяется величина удельного объема кузова. Род перевозимого груза характеризуется удельным весом (i, Н/м3. В таком
случае удельный объем каждого рода груза будет равен:
i
УД

1
i


, м3 / Н . Эти за-
висимости справедливы для вагонов предназначенных для перевозки одного рода
груза. Если в вагоне перевозится широкая номенклатура грузов (5 – 10 наименований), в таком случае:
УД
 a

a
i
i УД
,
(3)
i
Лист
Изм. Лист
№ докум.
Подпись Дата
где ai – доля перевозимого груза в общем грузообороте вагона за год.
За предыдущий год вагон сделал 100 рейсов зерном (  1  0,75 т / м 3 ), и 50 рейсов с
мукой (  2  0,6 т / м 3 ).
1
УД

1
1
1
1
2
 1,3 м 3 / т ;
УД


 1,6 м 3 / т .
 2 0,6
 i 0,75
100  1,3  50  1,6
Тогда УД 
 1,4 м 3 / т .
150
Зная удельный объем УД и грузоподъемность вагона Р можно определить

геометрический объем кузова V по формуле:
V  УД  Р ;
V  1,4  71,145  100 м 3
Конструктивной особенностью кузовов типа хоппер является то, что
наружная длина кузова равна базе вагона (рисунок 2):
2 LK  2l 
V
,
VУД
(4)
где VУД  погонный объем конструкции кузова типа хоппер, приходящийся
на один метр его длины. Принимаем: для зерна 8,9 м3/метр длины.
Рисунок 2 – Линейные размеры вагона типа хоппер
Лист
Изм. Лист
№ докум.
Подпись Дата
По расчету:
2 Lн  100  8,9  11,23 м,
Длина рамы вагона будет равна:
2LР  2l  2  nK ,
(5)
где nK  минимальная длина консоли (рисунок 2);
2l – база тележки;
DГ – диаметр колеса по гребню;
 = 0,1метра – конструктивный зазор.
По расчету:
2LР  11,23  2 1,4281  14,0862 м,
Минимальная длина консоли вагона для типовой тележки будет равна:
nK 
nK 
2l DГ

,
2
2
(6)
1,85 1006

 0,1  1,4281м,
2
2
Длина вагона по осям сцепления определяется по формуле:
2LОС  2LР  2  aА ,
(7)
где аА - вылет автосцепки, т.е. расстояние от оси сцепления до концевой балки.
Размер вылета автосцепки определяется согласно ГОСТ 3475–81.
По расчету:
2LОС  14086,2  2  350  14786,2 м
Лист
Изм. Лист
№ докум.
Подпись Дата
4 УТОЧНЕНИЕ ПАРАМЕТРОВ ВАГОНА ПО РЕЗУЛЬТАТАМ
ВПИСЫВАНИЯ В ГАБАРИТ
Одним из главных условий безопасности движения локомотивов, вагонов и
другого подвижного состава является предупреждение их соприкосновения со
стационарными сооружениями, расположенными вблизи железнодорожного пути,
или с подвижным составом находящемся на соседнем пути. Поэтому стационарные сооружения должны располагаться на определенном расстоянии от пути, а
подвижной состав – иметь ограниченное поперечное очертание.
Таким образом, получаются два контура: контур, ограничивающий меньшие
допускаемые размеры приближения строения и путевых устройств к оси пути –
габарит приближения строений; и контур, ограничивающий наибольшие допускаемые размеры поперечного сечения подвижного состава – габарит подвижного
состава.
Пространство между габаритами обеспечивает безопасные смещения подвижного состава и погруженных на нем грузов, которые возникают при движении, а также обусловленные допустимыми отклонениями элементов пути.
Габариты подвижного состава являются исходными очертаниями для определения по ним расчетом (вписыванием) допустимых строительных размеров вагона.
При вписывании вагона в эксплуатационный габарит подвижного состава
производят уменьшение горизонтальных размеров этого габарита на величину зазоров и износов ходовых частей, исчисляемых в горизонтальном направлении, и
выносов частей вагона в кривых, а вертикальных размеров – на величину статического прогиба рессорного подвешивания и измеряемых в вертикальном направлении износов ходовых частей вагона.
Лист
Изм. Лист
№ докум.
Подпись Дата
Размеры цистерны уточняем путем проверки на вписывание в габарит 0 –Т
(ГОСТ 9238 – 83).
1160 1160
1400
450
1400
1600
4700
3850
1700
50
1700
Уровень верха головок
рельсов
2600
3400
430
500
1600
50
Рисунок 3 – Габарит подвижного состава 0 – Т
Горизонтальные размеры:
Максимально допускаемая ширина вагона 2 B , в рассматриваемом сечении
на некоторой высоте H от уровня головки рельса определяется по формуле:
2 Bi  2  B0  Ei ,
(8)
где B0  полуширина соответствующего габарита подвижного состава на
той же высоте, мм;
Ei  ограничения полуширины вагона для различных сечений, мм.
Для направляющих (по пятнику) поперечных сечений ограничение определяют по формуле:
Eо  (S к  d Г )  q  W  [k1  k 3 ]   , ,
(9)
Для поперечных сечений вагона, расположенных между его направляющими сечениями:
EВ  (S к  d Г )  q  w  [k 2 (2l  n)  n  k1  k 3 ]   ,
(10)
Для поперечных сечений вагона, расположенных снаружи (по консоли) его
направляющих сечений:
Лист
Изм. Лист
№ докум.
Подпись Дата
E Н  ( S к  d Г )  q  W  
2l  2n
 [k 2 (2l  n)  n  k1  k 3 ]   ,
2l
(11)
где 2Sк  максимальная ширина колеи в кривой расчетного радиуса, мм;
2d Г  минимальное расстояние между наружными гранями предельно из-
ношенных гребней колесной пары, мм;
q  суммарное наибольшее поперечное перемещение в направляющем сечении в одну сторону из центрального положения рамы тележки относительно колесной пары, мм;
w  то же, но кузова относительно рамы тележки вследствие зазоров при
максимальных износах, мм;
2l  расстояние между направляющими сечениями вагона (база вагона), м;
n  расстояние от рассматриваемого поперечного сечения вагона до
его
ближайшего направляющего сечения, м;
k
величина, на которую допускается выход вагона, проектируемого по
габаритам 0-ВМ (01-Т), 02-ВМ (02-Т), 03-ВМ (03-Т) и для нижней зоны 1-ВМ (0-Т) за очертание этих габаритов в кривой R= 250 м, мм;
k1  величина дополнительного поперечного смещения в кривой расчетного радиуса ( R = 250 м – для габаритов 0-ВМ (01-Т), 02-ВМ (02-Т), 03ВМ (03-Т) и нижней зоны 1-ВМ (0-Т); R = 200 м – для габаритов Т, 1Т и верхней зоны 1-ВМ (0-Т), мм;
k 2  коэффициент, зависящий от величины расчетного радиуса кривой ( R
= 200 м – для габаритов Т, 1-Т и верней зоны 1-ВМ (0-Т), мм;
k3  уширение габарита приближения строений в расчетной кривой (k3=180
мм для габаритов Т, 1-Т и верней зоны 1-ВМ (0-Т).
Лист
Изм. Лист
№ докум.
Подпись Дата
Числовые значения максимального бокового смещения (разбег) предельно
изношенной колесной пары S k  d Г  для вагонов колей 1520 мм в кривой расчетного радиуса определяют:


2 S K  L  2   ГMIN
S K  d Г  
,
2
(12)
где L  минимально допустимое расстояние между внутренними гранями
ободов колес колесной пары, мм;
 ГMIN  минимальная толщина гребня колеса, мм.
S K
 dГ  
1541  1437  2  25
 27 мм
2
q  eп  e р
(13)
где eп  смещение по пятнику, мм;
e р  смещение по ширине рамы, мм
q  11  6  17 мм
W  10 мм
Таблица 1– Значения коэффициентов, входящих в формулы определения
смещений
Коэффициенты
K
k1
k2
k3
Габарит
0–Т
0
2 ,5  lT2
2,5
180
Для вагона с габаритом 0-Т величина в квадратных скобках ограничения
полуширины вагона для его поперечных сечений, расположенных снаружи (по
консоли) его направляющих сечений Ен получается отрицательной, её не учитываем, т.е. принимаем равной нулю. При этом расчет ограничений производим из
условия вписывания в габарит на прямом участке пути по формуле:
Лист
Изм. Лист
№ докум.
Подпись Дата
E НП  ( S П  d Г )  q  w
2l  2  n
2l
(14)
где Е0П , ЕВП , ЕНП  ограничения полуширины соответствующих сечений в прямой,
мм;
S П  максимальная ширина колеи в прямой, мм.
Е0  (27)  17  10[2.5 * 9.25 2 ]  0  88 мм
Е в  (27) 17 10[2.5(11.13  2.8) * 2.8  214 180]  0  146.3мм
11.13  2  2.8
 [2.5(11.13  2.8) * 2.8  214  180]  0  254.7 мм
11.13
11.13  2  2.8
E H   1541  1486  10  17 
 123 мм
11.13
E H   27   10  17 
2В0  2  1700  88  3224мм
2ВВ  2  1700  146,3  3107,4 мм
3154
3224
3107
3400
123
88
66,17
2ВН  2  1700  123  3154 мм
5615
7393
Рисунок 4– Горизонтальная габаритная рамка
Из габаритной рамки видно, что вагон-хоппер зерновоз шириной 3224 мм
вписывается в принятый для него габарит 0 – Т.
Лист
Изм. Лист
№ докум.
Подпись Дата
Рисунок 5 Положение колесной пары в колее
Вертикальные размеры:
Для получения наименьшего допустимого возвышения кузова и укрепленных на нем частей над уровнем головки рельса необходимо к размерам по высоте
H Гi прибавить величину возможного в эксплуатации понижения этих частей.
i
H MIN
 H Гi  H

,
(15)
где: – H  , сумма ниже указанных величин, (hi =110 мм);
Н1 – понижение буксы (55мм);
Н2 – рамы тележки (55мм).
H Гi – размер по высоте соответствующей рамки, (430 мм).
По расчету:
hmin  430  110  540 мм

уменьшение толщины обода колеса в результате обточек его при ре-
монтах, проката и наличия местных выбоин на поверхности катания. Итоговая величина этого понижения определяется как разность между проектной толщиной
обода нового колеса и допустимой в эксплуатации наименьшей толщиной обода
Лист
Изм. Лист
№ докум.
Подпись Дата
колеса;

уменьшение радиуса колесного центра, допускаемого правилами пе-
реформирования колесных пар (для цельнокатанных колес его принимают равным нулю);

понижение за счет износов опорных поверхностей, жестко опираю-
щихся непосредственно на буксы частей (боковые рамы тележек, балансиры и
т.п.);

равномерной статической осадки надбуксового подвешивания не эки-
пированного подвижного состава вследствие старения пружин;

равномерного прогиба надбуксового подвешивания от расчетной
нагрузки;

равномерной статической осадки рессорных комплектов центрально-
го подвешивания у порожнего подвижного состава вследствие старения пружин и
рессор;

равномерного прогиба центрального подвешивания от расчетной
нагрузки.

износа по толщине пятника и подпятника (или скользунов при опира-
Ось пути
1700
1440
1380
960
871,5
55718,5
540
115
540
110
нии кузова на скользуны) и элементов подвески.
Уровень верха головок
рельсов
Рисунок 6 – Понижение габарита 0-Т и линия понижения
Лист
Изм. Лист
№ докум.
Подпись Дата
5 ПРОЕКТИРОВАНИЕ ОСНОВНЫХ УЗЛОВ КУЗОВА ВАГОНА
5.1 Конструкция рамы и кузова
Рама является главным несущим элементом, она рассчитывается на восприятие всех действующих на кузов вертикальных и продольных нагрузок. В крытых
вагонах элементы рамы соединяются с несущими элементами боковых стен в
единую
несущую
систему,
так
достигается
наибольшая
жесткость.
Рисунок. 7.– Рама крытого вагона-хоппера для зерна модели 19-752
Рама специализированного крытого вагона-хоппера для зерна модели 19-752
изготовлена из стали 09Г2Д. Рама (рис. 7) состоит из хребтовой 3, двух боковых 2,
двух концевых 5, двух шкворневых 1 и двух средних 4 балок. Хребтовая балка сваЛист
Изм. Лист
№ докум.
Подпись Дата
рена из двух Z-образных профилей №31, перекрытых в средней части коньком 8 (4
мм) для лучшего ссыпания груза. В консольной части хребтовая балка усилена розеткой 7 и упорами автосцепки. Боковые балки выполнены из уголка 125x80x10 мм.
Концевые балки сварены Г-образной формы поперечного сечения из листов толщиной 4 мм. Для безопасной работы составителя на концевой балке установлены
поручни 6. Шкворневые балки коробчатого сечения состоят: из двух вертикальных 12 (6мм) и двух горизонтальных 13 листов (10мм). На нижнем горизонтальном листе балки укреплены скользуны 10 и пятник 11. Для обеспечения прочности опорного угла и повышения жесткости сопряжения шкворневой и хребтовой
балок между ними установлена надпятниковая коробка 9. Средние поперечные
балки состоят из вертикального 14 (6мм) и нижнего наклонного 15 (8мм) листов.
Рисунок. 8.– Поперечное сечение кузова вагона-хоппера для зерна модели 19-752
5.2 Конструкция боковых стен вагона
Лист
Изм. Лист
№ докум.
Подпись Дата
Боковые степы (рис. 8) выполнены из гофрированных металлических листов 6
толщиной 3 мм, подкрепленных для жесткости десятью стойками 5, верхней 4 и
нижней 7 обвязками. Стойки изготовлены из двутавра № 10, верхняя обвязка 4
— из гнутого специального профиля толщиной 6 мм, а нижняя—из прокатного
уголка 125x80x10 мм. Для большей жесткости каждая стена связана с рамой
двумя наклонными швеллерами № 14. Буйкера 9 сварены из листов толщиной 5
мм в форме усеченной пирамиды и имеют разгрузочные крышки 10 люков с
резиновыми уплотнениями. Каждые два противоположные бункера снабжены
одним рычажным механизмом разгрузки с приводным штурвалом 8. Механизм
разгрузки обеспечивает попарное открывание и закрывание крышек люков
бункеров, а также позволяет дозировать высыпание зерна или прекращать выгрузку в любой момент времени. Он состоит из винтового привода со штурвалом, укрепленного на кронштейне, и системы шарнирно связанных между
собой рычагов и тяг с распорками, соединенными попарно с крышками разгрузочных люков. Закрытие крышек обеспечивается переходом осей распорок за
«мертвую» точку, что предохраняет крышки от самопроизвольного открывания. Для более полной выгрузки вагона предусмотрена возможность установки
на бункерах вибраторов. Наклонные торцовые стены кузова 12 располагаются
под углом 55° к плоскости рамы. Они сварены из верхнего и нижнего листов
толщиной 4 мм и двух боковых обвязок уголкового профиля сечением 60x60x6
мм. Верхний лист имеет отбортовку, которая выполняет роль верхней обвязки.
В нижней части сделана фигурная подштамповка, которая, соединяясь с
наклонным листом стены, образует поперечную балку коробчатого сечения.
Нижний лист обшивки усилен двумя продольными 15 и одним поперечным 13
поясами и подкосами 11. Для придания консольным частям кузова достаточной прочности и жесткости каждая торцовая стена усилена двумя стойкамираскосами 14 и 16 из швеллера № 14.
Лист
Изм. Лист
№ докум.
Подпись Дата
5.3 Конструкция торцевых стен вагона.
Наклонные торцовые стены кузова 12 располагаются под углом 55° к плоскости рамы. Они сварены из верхнего и нижнего листов толщиной 4 мм и двух
боковых обвязок уголкового профиля сечением 60x60x6 мм. Верхний лист имеет
отбортовку, которая выполняет роль верхней обвязки. В нижней части сделана
фигурная подштамповка, которая, соединяясь с наклонным листом стены, образует поперечную балку коробчатого сечения. Нижний лист обшивки усилен
двумя продольными 15 и одним поперечным 13 поясами и подкосами 11. Для
придания консольным частям кузова достаточной прочности и жесткости
каждая торцовая стена усилена двумя стойками-раскосами 14 и 16 из швеллера № 14.
5.4 Конструкция крыши вагона.
Крыша кузова предназначена для защиты грузов от внешних воздействий и
для усиления жесткости кузова.
Крыша кузова сварная и состоит из листовой гофрированной обшивки 1
толщиной 3мм в середине и 1,8 по бокам, подкрепленной двенадцатью дугами 3,
выполненными из уголка 75Х50Х5 мм. На крыше расположены четыре загрузочных люка щелевого типа. С торцевыми стенами крыша связана фрамугами 17, а с
боковыми - непосредственно приваркой к верхней обвязке 4 стены. Для доступа
на крышу и внутрь вагона имеются лестницы, а по всей длине крыши- трап 2.
Все несущие элементы кузова выполнены из низколегированной стали
09Г2Д, а обшивка – из стали 10ХНДП-2.
5.5 Наружное оборудование вагона.
Лист
Изм. Лист
№ докум.
Подпись Дата
Нижнею часть кузова замыкают шесть бункеров с разгрузочными люками.
Штампованные крышки люков имеют уплотнительные прокладки из резины, сохраняющей упругие свойства в интервале температур от -50 до + 100 С. Каждые
два противоположные бункеры снабжены одним рычажным механизмом разгрузки с приводным штурвалом. Механизм разгрузки обеспечивает по парное открывание и закрывание крышек бункеров, а также позволяет дозировать высыпание
зерна из вагона и прекращать выгрузку в любой момент времени. Состоит механизм из винтового привода со штурвалом, укрепленного на кронштейне, и системы шарнирно связанных между рычагов и тяг с распорками, соединенными попарно с крышками разгрузочных люков, закрытие крышек обеспечивается переходом осей распорок за «мертвую точку» на 20мм, что предохраняет крышки от
самопроизвольного открывания.
На бункерах со стороны установки штурвалов механизма разгрузки установлены специальные скобы для крепления вибраторов, с помощью которых удаляется остающееся в кузове зерно.
6 РАСЧЕТ ХАРАКТЕРИСТИК РЕССОРНОГО ПОДВЕШИВАНИЯ
Грузоподъемность вагона (Р) 70 тс (700 кН); тара вагона (Т) 22тс (220 кН);
ходовые части: две двухосные тележки, каждая из которых имеет одинарное рессорное подвешивание, расположенное в центральном проеме. Размеры центрального проема накладывают ограничения на высоту и диаметр пружин и на их количество в комплекте. Прогиб рессорного подвешивания ( fСТ ) 48,5 мм (0,0485 м),
коэффициент запаса прогиба ( kЗП ) 2,0, материал пружины 60С2 для которого:
   750 мПа  750 106 Н / м2
G= 8 10 4 мПа  8 1010 Н / м 2
Принять, что проектируемый рессорный комплект аналогичен комплекту
тележки модели 18-100 (рисунок 6.1). Рессорное подвешивание тележки включает
два рессорных комплекта, состоящие из набора двухрядных пружин и двух фрикционных клиньев гасителя колебаний. Фрикционные клинья располагаются в
гнездах надрессорной балки и своими наклонными поверхностями взаимодействуют с наклонными поверхностями надрессорной балки, а вертикальными поверхностями с фрикционными планками, укрепленными на боковой раме. Количество двухрядных пружин в одном рессорном комплекте зависит от грузоподъемности вагона и может быть пять, шесть или семь штук (обеспечить прогиб не
менее 50 мм).
 Расчет однорядной пружины
1.1 Статическая нагрузка на одну пружину равна:
РСТ 
( Р  Т )  п  РТЕЛ  п  РЧ
,
п  п1  п2
(16)
где РТЕЛ  вес тележки, 4,8 тс (48 кН).
РЧ  вес частей тележки, находящиеся над пружинами, 0,443 тс (4,43 кН).
п, п1 , п2  число тележек под вагоном, число рессорных комплектов в тележке
и число пружин в комплекте соответственно.
Лист
Изм. Лист
№ докум.
Подпись Дата
РСТ 
(70  22)  2  4,8  2  0,443
 2,9745 тс (29,745 кН )
227
1.2 Эквивалентная жесткость пружины:
СЭКВ 
С ЭКВ 
РСТ
f СТ
(17)
2,5995
 61,33 тс / м (613,3 кН / м)
0,0485
1.3 Максимальная нагрузка воспринимаемая пружиной равна:
РMAX  k ЗП  РСТ
(18)
РMAX  1,9  2,9745  5,65155 тс (56,51 кН )
1.4 Максимальный прогиб пружины соответствующий максимальной
нагрузке:
f СТ  k ЗП  f СТ
(19)
f СТ  1,9  0,0485  0,09215 м (92,15 мм)
1 – фрикционный клин; 2 – двухрядная пружина
Рисунок 9 – Рессорный комплект грузовой тележки мод. 18-100
1.5 Определение диаметра прутка пружины.
Из прочностного расчета пружин известно, что
 MAX 
где m 
8  РMAX  m
D
 индекс пружины.
d
 d
2
   ,
(20)
(21)
Лист
Изм. Лист
№ докум.
Подпись Дата
Для вагонных пружин m  3 . Для первого расчета принимаем m  5,5 .
D  средний диаметр пружины.
d  диаметр прутка пружины.

коэффициент, учитывающий кривизну витков пружины:
  1
  1
1,25 0,875 1

 3
m
m2
m
(22)
1,25 0,875
1

 3  1,262
2
5,5
5,5
5,5
Из (1.3) имеем:
d
8  56515  5,5
 1,262  0,036 м  36 мм
3,14  750  10 6
1.6 Средний диаметр пружины из (1,4) равен:
D  m d
(23)
D  5,5  34  196 мм
1.7 Число рабочих витков вычислим как:
nР 
nР 
f MAX  G  d
8  PMAX  m 3
(24)
0,09215  8  1010  0,036
 3,528
8  56515  5,53
1.8 Высота пружины в сжатом и свободном состоянии:
hСЖ  (nР  1)  d
(25)
hСЖ  (3,528  1)  36  163 мм
hСВ  hСЖ  f MAX
(26)
hСВ  163  92,15  256 мм
Вывод: Сравнивая параметры пружины: средний диаметр(D=196мм), диаметр прутка(d=36 мм) и высота в свободном состоянии(hсв=256 мм) с возможными размерами пружин рессорного комплекта (D=170мм, d=30 мм и hсв=249 мм)
видим, что данная пружина не подходит. Поэтому однорядную пружину заменим
двухрядной.
Лист
Изм. Лист
№ докум.
Подпись Дата
 Расчет двухрядной пружины
Однорядную эквивалентную пружину заменяем на двухрядную из следующего условия (рис 10):
Рисунок 10– Соотношение размеров двухрядной пружины
2.1 Для нашего случая (m=5,5) имеем:
d1  0,82  d  0,4  0,82  36  0,4  29,92 мм  30 мм
d 2  0,566  d  0,6  0,566  36  0,6  19,776 мм  20 мм
В данном случае диаметры прутков округляются до ближайших значений
по ГОСТ.
2.2 Распределение нагрузки между пружинами:
Р1  0,675  (1 
Р1  0,675  (1 
Р2  0,325  (1 
Р2  0,325  (1 
1,1
)Р
d
(27)
1,1
)  2,9745  2,069 тс (20,69 кН )
36
2,2
)Р
d
(28)
2,2
)  2,9745  0,9076 тс (9,076 кН )
36
2.3 Жесткость пружин:
С1 
Р1
2,069

 42,66 тс / м (426,6 кН / м)
f СТ 0,0485
С2 
Р2
0,9076

 18,71 тс / м (187,1 кН / м)
f СТ 0,0485
Лист
Изм. Лист
№ докум.
Подпись Дата
Суммарная жесткость двух параллельно стоящих пружин будет равна:
С  С1  С2  42,66  18,71  61,37 тс / м (613,7 кН / м)
Ошибка вычислений:

С ЭКВ  С
61,33  61,37
 100% 
 100%  0,651%
С ЭКВ
61,33
2.4 Средние диаметры пружин:
D1  d1  m  30  5,5  165 мм
D2  d 2  m  20  5,5  110 мм
2.5 Число рабочих витков пружин:
n1Р  n Р 
D
198
 3,528 
 4,23
D1
165
n2 Р  n Р 
D
198
 3,528 
 6,35
D2
110
2.6 Высота пружин в сжатом состоянии:
h1СЖ  (n1Р  1)  d1  (4,23  1)  30  157 мм
h2СЖ  (n2 Р  1)  d 2  (6,35  1)  20  147 мм
Выравнивание высот пружин производится путем увеличения числа рабочих витков из условия: n2 Р  d 2  d 2  157 мм; n2 Р 
157  20
 6,845 ;
20
тогда h1СВ  h2СВ .
2.7 Высота пружин в свободном состоянии:
h1СВ  h2CВ  h1СЖ  f MAX  157  92,15  249,05 мм
2.8 Полное число витков:
n1П  n1Р  1,5  4,23  1,5  5,73
n2 П  n2 Р  1,5  6,35  1,5  8,345
2.9 Длина заготовок (рисунок 6.3):
L1    D1  n1П  3,14 165  5,73  2969 мм
L2    D2  n2 П  3,14 110  8,345  2882 мм
Лист
Изм. Лист
№ докум.
Подпись Дата
Рисунок 11 – Геометрические размеры пружины
Опорные поверхности пружин выполняют плоскими и перпендикулярными
оси пружины. Для этого концы заготовки пружины оттягивают на длине не менее
2/3 длины витка, чем достигается постепенный переход от круглого сечения к
прямоугольному.
Лист
Изм. Лист
№ докум.
Подпись Дата
7 ОПРЕДЕЛЕНИЕ ПОТРЕБНОЙ ВЕЛИЧИНЫ КОЭФФИЦИЕНТА
ОТНОСИТЕЛЬНОГО ТРЕНИЯ ИЗ УСЛОВИЯ ДВИЖЕНИЯ ВАГОНА ПО
НЕРОВНОСТИ
1. Предварительные и необходимые теоретические замечания
Вагон представляет собой сложную механическую систему, состоящую из
набора масс соединенных между собой упруго-фрикционными связями. Для того,
чтобы описать движение (колебания) механической системы можно воспользоваться двумя способами:
1. Принцип Даламбера (Д Аламбера).
2. Уравнение Лагранжа второго рода.
1.1 Принцип
Даламбера. Рассмотрим плоскую механическую систему вынужденных колебаний вагона при движении по неровности. Будем рассматривать только колебания подпрыгивания (в общем случае масса имеет шесть степеней свободы). Составим и преобразуем расчетную схему согласно рисунка 12.
Рисунок 12 – Исходная и приведенные расчетные
схемы движения вагона
Последовательность составления уравнений Даламбера.
Лист
Изм. Лист
№ докум.
Подпись Дата
1. Выбрать положительное направление всех координат и их производных.
2. Выбрать знак положительной деформации (сжатие со знаком плюс).
3. Мысленно разрезать связи и
направить реакции в соответствии с
пунктом 2.
4. Приложить инерционные силы
(направить
их
противоположно
направлению координат).
. Составить уравнения по Даламберу, а именно сумма сил действующих на
массу (все силы выражены через положительную деформацию):
mz  R  P(t )
(29)
Приведенное уравнение записано в неявном виде, так как не ясно, что такое
R. В данном случае реакция связи R представляют собой упругую (пружина) и неупругую (гаситель колебаний) составляющие: R  2  C  z  2    z . Здесь С – жесткость пружин рессорного комплекта,   параметр сопротивления гасителя колебаний.
Тогда уравнение (29) примет вид:
mz  2z  2Cz  P(t )
(30)
Лист
Изм. Лист
№ докум.
Подпись Дата
Уравнение (30) это дифференциальное уравнение колебаний механической
системы в явном виде.
1.2 Уравнение Лагранжа второго рода. Составим и преобразуем расчетную
схему согласно рисунка 1.
Известно, что уравнение Лагранжа второго рода имеет вид:
d T Ф П


0,
dt q q qi
(32)
где Т – кинетическая энергия рассматриваемой механической системы;
qi , q  обобщенные координаты и обобщенные скорости (в данном случае
система обладает одной степенью свободы, то есть q1  z, q1  z );
П – потенциальная энергия системы;
Ф – функция рассеивания, равная мощности развиваемой силами неупругого сопротивления.
1. Кинетическая энергия системы равна:
m( z ) 2
Т
2
(33)
2. Потенциальная энергия системы равна:
K
П  2
где
Сz 2
  P(t )dz ,
2
H
(34)
Сz 2
 энергия сжатия рессорного комплекта;
2
K
 P(t )dz  работа силы
P (t ) на перемещении z.
H
3. Функция рассеивания Ф представляет мощность, развиваемую силами
неупругого сопротивления:
Ф  2
z 2
2
.
(35)
Согласно выражения (33), продифференцируем функции энергии:
Лист
Изм. Лист
№ докум.
Подпись Дата
d T d

dt z dt
Ф

z
 (2 
(
mz 2
)
2  d ( 1  m  2  z )  d (m  z )  m  d ( z )  mz
z
dt 2
dt
dt
z
)
2  2  ( 1    2  z)  2z
z
2
П 
Сz 2
1
K
 (2 
  P(t )dz  2  (  C  2  z )  P(t ) H  2Cz  [ P(t 2 )  P(t1 )] 
z z
2 H
2
K
 {H (начало) t1  0; К (конец ) t 2  t}  2Cz  P(t )
Подставив в (34), получим:
mz  2z  2Cz  P(t )
(36)
Выражение (35) аналогично уравнению (34) и также является дифференциальным уравнением колебаний механической системы.
Выбор способа составления уравнений движения механической системы
остается за исследователем.
2. Рассмотрим вынужденные колебания, возникающие при движении груженого вагона по геометрической неровности вида:
  h  cos t ,
(37)
где h  (5 – 10) мм амплитуда геометрической неровности (рисунок 2);
  круговая частота внешнего возмущения.

2
V ,
LН
LH – длина неровности (принимаем равной длине рельса – 25 м);
V – скорость движения вагона – 33 м/с.

2  3,14
1
 33  8,29
25
с
Принимаем следующие допущения:
1. Кузов рассматривается как одноосная система. Деформация пути не учитывается.
2. Вагон считается симметричным, т.е. l1 = l2.
3. Кузов с грузом принимаются абсолютно жесткими.
Лист
Изм. Лист
№ докум.
Подпись Дата
4. Перемещения кузова вдоль оси Х отсутствуют в виду сопротивления в
поглощающих аппаратах.
Рисунок 13 – Расчетная схема
Выполним действия согласно последовательности составления уравнений
Даламбера.
Составим сумму сил, действующих на кузов:
mz  R1T  R2T  0
(38)
Выясним, что представляют собой реакции связей R1T и R2T. Рассмотрим
связь кузова вагона и тележки (рис 14).
Рисунок 14 – Схема связей кузова вагона и тележки
Согласно рисунка 14 реакция первой тележки на кузов вагона может быть
вычислена как:
R1T  2  C( z 1T )  2   ( z 1T ) .
(39)
Лист
Изм. Лист
№ докум.
Подпись Дата
Средняя величина перемещений (деформаций рессорных комплектов) тележек от
неровностей пути:
1Т 
1   2
2
 2Т 
3   4
2
(40)
Аналогично реакция второй тележки на кузов вагона равна:
R2T  2  C( z 2T )  2   ( z T ) .
(41)
В таком случае, дифференциальное уравнение вынужденных колебаний вагона будет иметь вид:
mz  2  C( z 1T )  2   ( z 1T )  2  C( z 2T )  2  ( z 2T )  0
Раскроем скобки и приведем подобные (на практических занятиях выполнить), получим:
mz  4  z  4  Cz  С (1  2  3  4 )   (1  2  3  4 )
(42)
Далее будем рассматривать консервативную систему, то есть систему, в которой отсутствует рассеивание энергии (нет гасителей колебаний). Уравнение
(42) примет вид:
mz  4  Cz  С (1  2  3  4 )
(43)
Текущие значения неровностей под каждым колесом вычисляются по зависимостям:
1  h cos(t  1) ; 2  h cos(t  2 ) ; 3  h cos(t  3 ) ; 4  h cos(t  4 ) (44)
где  i 
xi
 2 - сдвиг фазы.
LH
Вычислим сдвиг фазы для каждого колеса вагона (рис 15):
Рисунок 15 – К вычислению сдвига фаз
При базе тележки 2lT  1,85 м и базе вагона 2l  11,23 м, имеем:
Лист
Изм. Лист
№ докум.
Подпись Дата
1  0;
3  161,712;
2  26,640;
4  294,9.
Согласно зависимости (45) сложение неровностей под каждым колесом
произведем графически. Для чего построим единичную окружность радиусом 1 =
R = 30 мм, что соответствует амплитуде неровности h= 5 мм (0,005 м). На окружности отметим единичные вектора соответственно углам сдвига фаз. Произведем
попарно сложение векторов. В результате получим суммарный вектор, который в
а1С 
l1C
 раз больше исходного h = 0,005 м (рисунок 16).
R
ас
а3
а4
а2
а1
Рисунок 16 – Векторное сложение текущих значений амплитуд неровностей
Из диаграммы  l1с =57 мм,
а1с 
62
 1,9
30
В таком случае уравнение (43) будет иметь вид:
mz  4  Cz  С  а1С  h cos(t  C )  R1C  cos(t  1C ) ,
(45)
где R1C  C  a1C  h  амплитуда возмущающей силы, действующей на вагон в
направлении оси Z. При С = 429,6 тс/м  R1C= 429,61,90,005=4,146 тс. Таким
образом все коэффициенты уравнения (44) известны.
Лист
Изм. Лист
№ докум.
Подпись Дата
Возмущающая сила
R1C  cos(t  1C ) имеет вид гармонической функции
сходной с функцией возмущения (45).
Решение уравнения (45) будем искать в виде: z  zC  zВ , состоящее из решения собственных колебаний: zC  A1  cos(t   ) и решения вынужденных колебаний: zB  B1  cos(t   ) , где  - частота собственных колебаний;  - частота вынужденных колебаний. Исходя из условия плавности хода, рассмотрению подлежат
резонансные колебания, т.е.  = .
Константы А1 и В1;  и  решения
z  A1  cos(t   )  B1  cos(t   )
(46)
находим из начальных условий, то есть при t  0 : z  0 и z  0 (в начальный момент
времени перемещение и скорость равны нулю). Скорость определяется первой
производной от перемещения, то есть
z   A1    sin( t   )  B1    sin( t   ) .
При t  0 :
A1  cos( )  B1  cos( )  0
 A1    sin(  )  B1    sin(  )  0
(47)
(48)
Уравнение (48) разделим на , помня о том, что  = :
A1  cos( )  B1  cos( )
 A1  sin(  )  B1  sin(  )
(49)
(50)
Разделим уравнение (50) на уравнение (49), получим:
- tg(-) = - tg(-), то есть  = , следовательно А1 = - В1.
Подставив в (46) получим:
z   В1  cos(t   )  B1  cos(t   )  B1cos(t   )  cos(t   )   (в квадратных
скобках разность косинусов двух углов) 
(t    t   )
(t    t   ) 

 В1 2  sin
 sin

2
2


Лист
Изм. Лист
№ докум.
Подпись Дата

 


 В1 2  sin(
 t   )  sin(
 t )  В1  2sin( t   )  sin t )  (так как
2
2


  ,
тогда       очень маленькая величина, то sin(t)  t)   В1  2  t  sin( t   ) .
Получили решение уравнения (45) в виде:
z  В1  2  t  sin( t   )
(51)
В решении (51) неизвестна постоянная В1. Для ее нахождения необходимо в
уравнение (49) подставить выражения для z и z (на практическом занятии сделать
необходимые вычисления). После подстановки и приведения подобных получим:
B1 
R1C
m 2  2
.(52)
Подставим в (51) получим
z
R1C
 2  t  sin( t   )
m 2  2
(53)
или
z
R1C  t
 sin( t   )
2 m 
(54)
есть решение уравнения (49) в явном виде.
Проанализируем данное решение, а именно при t  0 и z  0 , с увеличением
времени t увеличивается и амплитуда колебаний z (рисунок 17).
Рисунок 17 – График колебаний
Приращение амплитуды колебаний за один период t  T 
A  z 
R1C
2 R1C  


2 m  
m 2
A  Z 
2

составит
(55)
4,146  3,14
 0,0025 м
74,48  8,29 2
Лист
Изм. Лист
№ докум.
Подпись Дата
где: m – масса обрессоренных частей вагона:

m  P  T  8Pкп  8 Рбр

(56)
m  70  22  8 1,54  8  0,65  74,48т
Чтобы обеспечить устойчивое равновесное движение системы при резонансе необходимо, чтобы за один период колебаний приращение потенциальной
энергии П было равно работе сил сопротивления гасителя за тот же промежуток
времени: П  W .
Приращение потенциальной энергии происходит за счет дополнительного
сжатия пружин одного рессорного комплекта, будет равно:
П  П2  П1
где П1 
(57)
С  z0
С  ( z0  z )2
; П2 
. Выполнив преобразования и пренебрегая вели2
2
2
С  (z )2
чиной
 ввиду ее малости, получим:
2
П  С  z 0  z
(58)
где z 0  амплитуда колебаний.
Фрикционный гаситель колебаний. Работа сил трения гасителя за один период определяется площадью параллелограмма (рисунок 18):
W  ( FН  FР )  2  z0
.(59)
Тогда
С  z0  z  ( FН  FР )  2  z0
(60)
отсюда
( FН  FР ) 
С  z
2
(61)
Известно, что коэффициент относительного трения есть отношения сил
трения развиваемых гасителем к упругой реакции рессорного комплекта, т.е.

( FН  FР ) С  z
С  R1C  


,
PУП
2  РУП 2  РУП  m   2
(62)
Лист
Изм. Лист
№ докум.
Подпись Дата
где    
4C
.
m
Рисунок 18 – Силовая характеристика гасителя колебаний
Пример вычисления частоты. При C  429,6  10 4 H / м и m  74,48  10 3 H  с 2 / m
имеем
угловую
частоту
собственных
колебаний
равной:
4  429,6  10 4
1
 230,71  15,189
3
с
74,48  10

Линейная частота (количество колебаний в одну секунду) будет равна:
* 

15,189

 2,41 Гц
2 2  3,14
Подставим и сократим выражение (52)


С  R1C  
С  C  h  a1C    m h  a1C  


2
2  РУП  m  
2  С  fСТ  m  4  C
8  fCT
(63)
h  a1C   0,005  1,9  3,14

 0,07575
8  f CT
8  0,05
Гидравлический гаситель колебаний. Работа сил гидравлического сопротивления за один период определяется (рисунок 19):
АВ         02 , где  0  0,015 м  амплитуда колебаний.
Лист
Изм. Лист
№ докум.
Подпись Дата
Рисунок 19 – Диаграмма работы гидравлического гасителя колебаний
Тогда
С  z 0  z         02
(64)
отсюда

С  z 0  z
С  z 0  R1C  

2
     02  m   2
  0
(65)
По условию    . Тогда

С  z 0  R1C  
Cz R
 2 0 13C
2
2
   0  m  
0  m  
(66).
В качестве примера, определим потребную величину параметра сопротивления гидравлического гасителя колебаний:

429,6  10 4  0,05  4,146  10 4
Н с
кГ  с
.
 151924
 151,9
2
3
3
м
см
0,015  74,48  10  15,18
Лист
Изм. Лист
№ докум.
Подпись Дата
8
ПРОЕКТИРОВАНИЕ
ГАСИТЕЛЯ
КОЛЕБАНИЙ
ИСХОДЯ
ИЗ
ТРЕБУЕМОГО ЗНАЧЕНИЯ КОЭФФИЦИЕНТА ОТНОСИТЕЛЬНОГО ТРЕНИЯ
Спроектировать гаситель колебаний это значит необходимо установить зависимости между силовыми параметрами, геометрическими размерами и материалом деталей гасителя.
Для центрального рессорного подвешивания будем проектировать клиновой
гаситель колебаний, аналогичный тележки мод. 18-100 (рисунок 20).
1 – подклиновая пружина; 2 – надрессорная балка;
3 – фрикционный клин; 4 – фрикционная планка.
Рисунок 20 – Клиновой гаситель колебаний в рессорном комплекте
тележки модели 18 – 100
Принимаем, что фрикционная планка изготовлена из материала Сталь 45, а
фрикционные клинья из чугуна СЧ 28-48. Коэффициент трения   1  0,15 .
Лист
Изм. Лист
№ докум.
Подпись Дата
Угол наклона рабочей поверхности клина и надрессорной балки принимаем равным  1 450 , а поверхности клина и фрикционной планки равным  2  2 0 .
Известно, что коэффициент относительного трения это отношение суммы
сил трения развиваемых устройством в рессорном комплекте к реакции рессорного комплекта на действие внешней нагрузки:

F
P
(67)
Проектируемый гаситель колебания развивает различные по величине силы
трения при нисходящем и восходящем движении:
FН   Н  C  z КЛ ;
FВ   В  C  z КЛ
(68)
Под действием внешней нагрузки Р детали гасителя колебаний совершают
относительные перемещения: клин перемещается относительно фрикционной
планки на величину  , а надрессорная балка относительно клина на величину 1
(рис 21).
Рисунок 21 – Схема нагружения деталей гасителя колебаний
В таком случае прогиб подклиновой пружины будет равен:
Лист
Изм. Лист
№ докум.
Подпись Дата
z КЛ 
z КЛ 
z
(69)
1  tg1  tg 2
50
50

 48,31 мм (0,04831 м)
1  tg 45 0  tg 2 0 1  1  0,035
А) Нисходящее движение деталей гасителя колебаний
FН    N Н    C  z КЛ 
sin 1  1 cos1
;
Н
(70)
cos 2   sin  2
Н
(71)
F1Н  1  N1Н  1  C  z КЛ 
 Н  (1    1) cos(1   2 )  ( 1   ) sin(1   2 ) 
 (1  0,15  0,15) cos(450  20 )  (0,15  0,15) sin( 450  20 )  1,00225  0,731  0,7326
Вычислим силы трения на рабочих поверхностях:
FН  0,15  53,63  0,04831 
sin 450  0,15  cos 450
 0,32 тс  (3,5 кН )
0,7326
cos 20  0,15  sin 20
F1Н  0,15  53,63  0,04831  
 0,53 тс  (5,8 кН )
0,7326
Суммарные силы трения, создаваемые гасителем колебаний при нисходящем движении будут равны:
 FН  2( FН  F1Н )  2  (0,32  0,53)  1,7 тс  (17 кН ) . (72)
Вычислим реакцию рессорного подвешивания на действие внешней нагрузки Р при движении вниз (рисунок 22):
РН  2  С  z КЛ  5  C  z  2  FН
(73)
2  53,63  0,04831  5  53,63  0,04831  2  0,32  18,78 тс (187,8 кН )
где по формуле (67) имеем:
Н 
1,7
FН

 0,09
PН
18,78
Лист
Изм. Лист
№ докум.
Подпись Дата
Рисунок 22 – Равновесие деталей гасителя колебаний
при нисходящем движении
Б) Восходящее движение деталей гасителя колебаний
FВ    N В    C  z КЛ 
sin 1  1 cos1
В
F1В  1  N1В  1  C  z КЛ 
cos 2   sin  2
В
(74)
(75)
где
 В  (1    1) cos(1   2 )  ( 1   ) sin(1   2 ) 
 (1  0,15  0,15) cos(450  20 )  (0,15  0,15) sin( 450  20 )  1,00225  0,731  0,7326
Вычислим силы трения на рабочих поверхностях:
sin 450  0,15  cos 450
FВ  0,15  53,63  0,04831 
 0,43 тс  (4,3 кН )
0,7326
cos 20  0,15  sin 20
F1В  0,15  53,63  0,04831 
 0,53 тс  (5,8 кН )
0,7326
Суммарные силы трения, создаваемые гасителем колебаний при восходящем движении будут равны:
F
В
F
В
 2( FВ  F1В )
.(76)
 2  (0,43  0,53)  1,92 тс  (19,2кН ) .
Лист
Изм. Лист
№ докум.
Подпись Дата
Вычислим реакцию рессорного подвешивания на действие внешней нагрузки Р при движении вверх (рисунок 23):
РВ  2  С  z КЛ  5  C  z  2  FВ
РВ  2  53,63  0,04831  5  53,63  0,04831  2  0,94  16,26 тс (162,6 кН )
Тогда по формуле (67) имеем:
В 
 F В 1,92

 0,11
PВ
16,28
Рисунок 23 – Равновесие деталей гасителя колебаний
при восходящем движении
Среднее значение коэффициента относительного трения гасителя колебаний
будет равно:
   В 0,09  0,11
СР  Н

 0,10
2
2
Вывод: Спроектированный фрикционный гаситель колебаний с фрикционными клиньями из чугуна имеет коэффициент относительного трения равный потребному.
Лист
Изм. Лист
№ докум.
Подпись Дата
9 Определение усилий, действующих на колесную пару в кривой пути и проверка запаса устойчивости колесной пары
Передние колеса тележек вагонов при движении по кривым, а часто и на
прямых участках пути набегают гребнями на боковые грани головок рельсов.
Угол набегания может доходить до 0,01 рад и даже несколько больше (в крутых
кривых). Место контакта гребня с головкой рельса находится впереди от вертикального радиуса колеса, что вызывает предварительное касание (рисунок 24).
Рисунок 24 – Положение колесной пары при набегании на рельс
Устойчивость колесной пары против схода с рельс проверяется для наиболее опасных случаев сочетания боковой поперечной силы взаимодействия набегающего колеса с рельсом и малой вертикальной нагрузки на это колесо. При одновременном в течение некоторого времени действие такого сочетания указанных
сил возможно вкатывание («вползание») гребня набегающего колеса на головку
рельса и последующий сход вагона с рельсов.
Критическое сочетание действующих на колесную пару сил может возникать в следующих двух случаях.
 При ударном входе вагона в кривую, при проходе стрелок на боковой путь,
при интенсивном вилянии тележки при движении с максимальной скоЛист
Изм. Лист
№ докум.
Подпись Дата
ростью по прямому участку пути, при интенсивных боковых колебаниях кузова и сопутствующих невыгодных обстоятельствах взаимодействия колесной пары и пути.
 При экстренном торможении тяжеловесного поезда на малой скорости с головного локомотива при, прохождении составом кривого участка пути, когда возникающие значительные квазистатические усилия сжатия состава
могут привести к перекосу (сдвигу) вагона в колее и появление больших
поперечных сил взаимодействия колес с рельсами, а в экстренных условиях
и к «выжиманию» легковесного (например, порожнего) вагона.
Коэффициент устойчивости колесной пары против схода с рельса (по условию вкатывания) определяется по формуле:
КУС 
P
tg  
 В  КУС 
1    tg РБ
(77)
где  – угол наклона образующей конусообразной поверхности гребня колеса с
горизонталью;
 – коэффициент трения поверхностей колес и рельсов;
РВ – вертикальная нагрузка от набегающего колеса на рельс;
РБ – боковое усилие взаимодействия гребня набегающего колеса и головки
рельса (рисунок 24);
КУС  – допускаемое значение коэффициента запас устойчивости.
Допускаемое значение коэффициента запаса устойчивости для данного расчетного случая принимается равным: для грузовых вагонов КУС  =1,4.
Лист
Изм. Лист
№ докум.
Подпись Дата
Рисунок 25 – Схема сил действующих в точке контакта
К ус 
tg 65  0,15 18,12

 5,12
1  0,15  tg 65 5,34
1. Вертикальная нагрузка от набегающего колеса на рельс вычисляется по
формуле:
b  a2
b
r
 b  a2

РВ  2  QСТ 
(1  k ДВ1 )  k ДБК   Н Р  q
l
l
l
 l

(78)
где QСТ  сила тяжести обрессоренных частей вагона, действующая на шейку оси
колесной пары;
QСТ 
70  22  2  2  0,6
 22,4 ,
22
где Т и Р – тара и грузоподъемность вагона;
Лист
Изм. Лист
№ докум.
Подпись Дата
q – сила тяжести необрессоренных частей, приходящихся на колесную пару;
n – число осей в тележке.
kДВ1 – расчетное значение коэффициента вертикальной динамики экипажа,
приближенно принимается kДВ1 = 0,75 kДВ, kДВ,=0,750,17=0,12 где
k ДВ  a  3.6  10 4  b 
k ДВ  0,05  0,00036  1 
v  15
f СТ
(79)
33,3  15
 0,16 ,
0,09215
где а – коэффициент, равный для элементов кузова а = 0,05, для обрессоренных
частей тележки а = 0,10, для необрессоренных частей тележки а = 0,15;
b
n2
– коэффициент, учитывающий влияние числа осей в тележке или
2 n
группе тележек под одним концом вагона;
v – расчетная скорость движения, м/с;
fСТ– статический прогиб рессорного подвешивания, м.
kДБК – расчетное значение коэффициента динамики боковой качки приближенно принимается kДБК1 = 0,25 kДВ;
Н Р  р0  b   (5  v) – расчетное среднее значение рамной силы,
где р0 – расчетная статическая осевая нагрузка;
 – коэффициент, учитывающий тип ходовых частей вагона. Для грузовых
вагонов на безлюлечных тележках с большой горизонтальной жесткостью подвешивания  = 0,003, для пассажирских на безлюлечных тележках с пневмоподвешиванием  = 0,0018, для пассажирских и изотермических на тележках с люлькой
 = 0,0015 и  = 0,002.
2b – расстояние между серединами шеек осей, для стандартных колесных
пар 2b = 2,036 м;
Лист
Изм. Лист
№ докум.
Подпись Дата
l – среднее расстояние между точками контакта колес с рельсами, принимается l =1,58 м;
а1 = 0,250 м и а2 = 0,220 м – расчетные расстояния от точек контакта до середине шеек;
r = 0,45 м – радиус средневзвешенного колеса.
Приведенные параметра показаны на рисунке 3.
Рисунок 26 – Схема расчета устойчивости колес против схода с рельсов
2. Боковое усилие взаимодействия гребня набегающего колеса и головки
рельса (рисунок 26) вычисляется по формуле:
PБ  H Р    P2
(80)
b  a1
b  a1
b
r

(1  k ДВ1 )  k ДБК   Н Р  q
– вертикальная нагрузка от втоl
l
l
 l

где Р2  2  QСТ 
рого колеса на рельс;
Лист
Изм. Лист
№ докум.
Подпись Дата
Экспериментальная проверка устойчивости от схода колеса с рельса производится по результатам ходовых динамических испытаний опытных образцов новых вагонов по РД 24.050.37.
Лист
Изм. Лист
№ докум.
Подпись Дата
10 Расчет на прочность рамы вагона на продольные нагрузки 3
режим
Препроцессорная обработка
1. Выбираем тип конечного элемента
2.Задаём характеристики материала
3. Строим геометрию модели
4. Построение конечно-элементной модели
Процессорная обработка.
1 Закрепляем модель в переднем упоре автосцепки
2. Прикладываем сосредоточенную нагрузку
1
ELEMENTS
DEC 23 2006
00:49:28
U
F
Y
Z
X
Рисунок 27 –модель рамы вагона после процессорной обработки
Лист
Изм. Лист
№ докум.
Подпись Дата
Постпроцессорная обработка.
Получаем результат в графическом виде.
1
NODAL SOLUTION
DEC 23 2006
00:50:52
STEP=1
SUB =1
TIME=1
SEQV
(AVG)
DMX =.074328
SMN =26737
SMX =.774E+08
MX
Y
X
MN
Z
26737
.172E+08
.862E+07
.344E+08
.258E+08
.516E+08
.430E+08
.688E+08
.602E+08
.774E+08
1
NODAL SOLUTION
DEC 23 2006
00:53:16
STEP=1
SUB =1
TIME=1
SEQV
(AVG)
DMX =.074328
SMN =26737
SMX =.774E+08
MN
26737
.172E+08
.862E+07
X
Y
Z
.344E+08
.258E+08
.516E+08
.430E+08
.688E+08
.602E+08
.774E+08
Рисунок 28 – Поля распределений эквивалентных напряжений по раме
Лист
Изм. Лист
№ докум.
Подпись Дата
Список использованных источников
1. Вагоны. Л. А. Шадур. М.: Транспорт, 1973. – 440с.
2. Спиридонов Б. К., Пастухов И. Ф. Конструкция и расчет вагонов. – М.: Машиностроение, 1980.-248с.
3. Пастухов И. Ф., Лукин В. В., Жуков Н. И. Вагоны. – М.: Транспорт, 1988.-280с.
4. Смольянинов А. В. Вагоны и контейнеры. Методические указания по изучению тем программы, выполнению контрольных работ и курсового проекта.
Екатеринбург. УрГАПС, 1995.-36с.
5. С. В. Вершинский, В.Н. Данилов, В.Д. Хусидов, Динамика вагона. – М.:
Транспорт, 1991 – 360с.
Лист
Изм. Лист
№ докум.
Подпись Дата