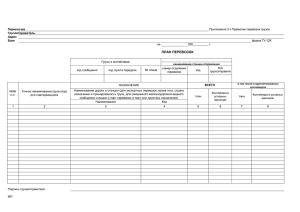
Министерство транспорта Российской Федерации «РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА (МИИТ)» Институт управления и информационных технологий Кафедра "Логистические транспортные системы и технологии" ОТЧЕТ по практической работе №2 номер варианта 5 «Классическая транспортная задача» по учебной дисциплине «Транспортная логистика» Выполнил:студент группы ПТП-313 ____________________И. А. Башев дата, подпись Руководитель:проф. кафедры ЛТСТ ___________________ Н.Н.Пашков дата, подпись Москва 2019 1. Задача «Оптимальный план перевозки грузов» Условия задачи. У поставщиков А1, А2 и А3 сосредоточены запасы однородного груза 𝑄А1 , 𝑄А2 , 𝑄А3 , который необходимо доставить потребителям В1, В2, В3 и В4 в соответствии с их потребностями𝑄В1 , 𝑄В2 , 𝑄В3 , 𝑄В4 . Известна стоимость перевозки𝐶𝑖𝑗 одной тонны груза от поставщикаi до потребителяj. Требуетсясоставить такой план перевозок, чтобы суммарные затраты на перевозку груза были минимальными. Исходные данные задачи № 2 представлены в таблицах 1 и 2. Таблица 1 потребитель В1 В2 В3 В4 Запасы поставщик 1 n 3 4 А1 𝑄А1 =60 4 m 2 3 А2 𝑄А2 =80+а 2 4 k 1 А3 𝑄А3 =100+b Потребность 𝑄В1 =40+b 𝑄В2 =60 𝑄В3 =80+а 𝑄В4 =50 № варианта 5 a 20 b 40 m 1 n 3 Таблица 2 k 1 Чтобы определить численные значения исходных данных задачи для заданного варианта, перенесем таблицы 1 и 2 в Excel, скопируем таблицу 1 и вставим её ниже таблицы 2. Заполним переменные ячейки таблицы 3 в соответствии с рисунком 1. Рис. 1. – Подготовка исходных данных задачи для решения в Excel 1 Таким образом, получим таблицу 3 с заданными численными значениями исходных данных задачи. Таблица 3. Исходные данные задачи ПР 2, вариант № 5 потребитель поставщик В1 В3 В4 Запасы 300 А1 А2 А3 Потребность В2 1 4 2 80 1 3 4 60 3 2 1 100 4 3 1 50 60 100 140 290 Задача поиска оптимального плана перевозки грузовможет быть сформулирована в формеклассической транспортной задачи. Особенность решения классической транспортной задачи состоит в том, что число уравнений относительно неизвестных переменных задачи может быть больше, меньше или равно числу переменных задачи. Для решения такого типа задач применяются методы исследования операций [1, 2]. 2. Математическая модель задачи Для формализованной постановки задачи введем следующие обозначения: 𝑥𝑖𝑗 – искомые неизвестные объемы перевозки груза от поставщика i до потребителя j; 𝐶𝑖𝑗 – стоимость перевозки единицы груза от поставщикаiдо потребителяj; 𝐹 - целевая функция; 𝐵𝑗 = 𝑄В𝑗 – потребность потребителя j; 𝐴𝑖 = 𝑄А𝑖 – предложение поставщика i. В принятых обозначениях формальная постановка задачи следующая. Найти минимальное значение целевой функции 𝐹: 𝑚,𝑛 𝐹 = min ∑ 𝐶𝑖𝑗 𝑥𝑖𝑗. 𝑥𝑖𝑗 𝑖=1,𝑗=1 С учетом ограниченной потребности𝐵𝑗 : 𝑚 ≥ ∑ 𝑥𝑖𝑗 =𝐵𝑗 , ≤ 𝑖=1 𝑗 = ̅̅̅̅̅ 1, 𝑛. И ограниченного предложения 𝐴𝑖 : 2 𝑛 ≥ ∑ 𝑥𝑖𝑗 =𝐴𝑖 , ≤ 𝑗=1 𝑖 = ̅̅̅̅̅̅ 1, 𝑚. Решение. 1. Решим задачу методом северо-западного угла. Результат решения представлен в таблице 4. Стоимость перевозок, найденная методом северо-западного угла равна 490 р. Таблица 4 Решение задачи № 2 методом северо-западного угла потребитель поставщик В1 А1 А2 А3 Потребность 60 20 80 В2 60 60 В3 20 80 100 В4 Запасы 300 60 100 140 50 50 300 2. Решим задачу методом наименьшей тарифной стоимости. Результат решения представлен в таблице 5. Стоимость перевозок, найденная этим методом равна 460 р. Таблица 5 Решение задачи № 2 методом потенциалов потребитель поставщик В1 А1 А2 А3 Потребность 60 20 80 В2 60 60 В3 30 70 100 В4 50 50 Запасы 300 60 100 140 290 1. Решим задачу симплекс-методом. Для решения задачи симплекс-методом с помощью сервиса Excel «Поиск решения» определим область изменяемых ячеек D17:G19. Выбираем целевую ячейку С15. В нее вводим формулу: =СУММПРОИЗВ(С4:F6; C10:F12). В ячейки G10, G11 и G12 вводим формулы суммы по строкам: =СУММ(C10:F10), =СУММ(C11:F11), =СУММ(C12:F12). В ячейку C9, D9, E9иF9 вводим формулы суммы по столбцам: 3 =СУММ(C10:C12), =СУММ(D10:D12), =СУММ(E10:E12), =СУММ(F10:F12). Для настройки Поиска решения также нужно ввести ограничения (рисунок 2): Рис. 2 – Настройка Поиска решения В настройке Параметры выбран симплекс-метод. Вычислим в Поиске решения минимальную стоимость перевозок. Получим следующий результат (рисунок 3). Рис. 3 – План перевозок, полученный симплекс-методом. Вывод: Стоимость перевозок, вычисленная симплекс-методом равна 699 р. Наименьшая из трех вычисленных разными методами суммарная стоимость перевозок 460 р. получена методом наименьшей тарифной стоимости. Оптимальный план 4 перевозок с минимальными транспортными затратами представлен в таблице 5, у поставщика А2 осталось 10 тонн нереализованных запасов. Литература 1. Нестеров Е.П. Транспортные задачи линейного программирования.– М.: Транспорт, 1971. – 216 с. 2. Карманов В.Г. Математическое программирование: Учеб.пособие./5-е изд., стереотип. – М.: ФИЗМАТЛИТ, 2004. – 264 5