Проект синхронного и асинхронного конвейеризованных

Проект синхронного и асинхронного конвейеризованных
умножителей с переменной задержкой
(Design of synchronous and asynchronous variable-latency pipelined multipliers)
Mauro Olivieri
Dept. of Electronic Engineering
University of Rome “La Sapienza”, Italy
Email: olivieri@die.ing.uniroma1.it
Перевод, техническое и литературное редактирование Гринфельд Ф.И., ИПИ РАН
Резюме: Эта статья представляет новую архитектуру умножителя с переменной
задержкой, подходящую для реализации в качестве самосинхронного ядра умножителя
или полностью синхронного ядра многоциклового умножителя. Архитектура
комбинирует алгоритм Booth 2-ого порядка с конвейеризованной организацией
матрицы сохранения расщепленного переноса, включая многократный пропуск строки
и оконечный сумматор с предсказанием завершения, выбранного переносом. В статье
изложены архитектурный и логический проект, проектирование схем CMOS и оценка
производительности. В технике CMOS 0,35 мкм ожидаемое устойчивое время цикла для
32-разрядной синхронной реализации – 2,25 нс. Моделирование командного уровня дает
оценку 54 % одноцикловых и 46 % двухцикловых операций в выполнении SPEC95.
Используя ту же технологию CMOS, 32-разрядная асинхронная реализация в SPEC95
выполнении, как ожидается, достигнет средней производительности 1,76 нс и задержки
3,48 нс.
I. Введение
Быстрые целочисленные умножители – ключевая тема в VLSI-проектах
быстродействующих микропроцессоров. Последние результаты показали, что в тщательно
выполненном полностью заказном проекте CMOS возможно 54x54-разрядное умножение
меньше чем за 3 нс [21]. Однако с обычно доступными CMOS-технологиями коммерчески
доступны микроархитектуры со временем цикла 2 нс [28]. В результате из-за установки
регистров и удержания времени даже быстрое 32-разрядное умножение не может уместиться
в отдельном цикле, и для того, чтобы вся микроархитектура не была ограничена
относительно медленным умножителем, обычно выбирается проект конвейеризованных
многоцикловых умножителей.
Зависимость данных всегда вносит ограничение в производительность
конвейеризованных арифметических устройств [22] из-за неактивных циклов между
последовательными зависимыми операциями. Чтобы преодолеть это, недавно в
промышленном проекте DSP были предложены синхронные конвейеризованные устройства
сложения с переменной задержкой [30]. Устройство с переменной задержкой работает как
нормальное конвейеризованное устройство, но для большинства операндов оно может
завершать свою операцию в отдельном цикле, избегая, таким образом, вставки холостых
циклов и улучшая среднюю производительность. Синхронный сигнал отмечает, в каком
цикле операция была завершена. Асинхронному проекту с самосинхронными устройствами,
способными к более быстрой средней реакции, чем в худшем случае, присуща более
2
агрессивная реализация этой идеи [6] [9] [14] [25] [29] [39] [52]. В самосинхронном
арифметическом устройстве асинхронный сигнал полного завершения сообщает, в какой
момент операция завершилась. Практическая проблема такого полностью асинхронного
устройства – интерфейс с синхронной архитектурой микропроцессора; проблема вызывается
эффектами метастабильности синхронизации сигналов [2]. Это дало импульс разработке
полностью асинхронных микроархитектур, где были достигнуты важные результаты [16] [17]
[43] [44] [47] [48], несмотря на то, что концептуально подобные синхронные устройства с
переменной задержкой и самосинхронные устройства существенно различаются по своей
архитектуре и VLSI-разработке 1.
Хотя алгоритмы умножения с переменной задержкой исторически известны
(например, сдвиг из-за нулей после кодирования Booth [22] [4]), современные
быстродействующие синхронные реализации VLSI обращались к умножителям с
фиксированным временем [19] [21], поскольку они наилучшим образом приближаются к
концептуальному проекту синхронной архитектуры системы команд с фиксированной
задержкой
[22].
Фактически
переменная
задержка
имеется
в
некоторых
неконвейеризованных многоцикловых устройствах умножения для дешевых центральных
процессоров, основанных на итерационном последовательном алгоритме [35]. Другой пример
этого подхода – 8-разрядный умножитель, недавно представленный в [45]. Синхронная
переменная задержка была также предложена для сложения [32] и выполнена в
быстродействующем конвейеризованном сумматоре VLSI [30]. Никаких специфических
обращений к синхронным умножителям с переменной задержкой, имеющим целью высокую
скорость, не было.
С другой стороны, отдельные научно-исследовательские работы обращались к
асинхронным VLSI-умножителям. Ранний пример концепции переменной задержки с
асинхронной реализацией имеется в [36]. Некоторые исследования обращаются к
последовательным асинхронным низкоскоростным умножителям [13] [46], в то время как
несколько исследований адресуется к асинхронному (т.е. несинхронизированному) проекту,
но не с переменной задержкой [1] [33] [7] [11] [38] (с целью сокращения потребляемой
мощности, ухода от распределения синхросигналов и т.д.), или частично выполняют
переменную задержку, обычно в оконечном сумматоре с распространением переноса для
умножителя матриц [31] [37] [10]. Некоторые работы обращаются, прежде всего, к
переменной задержке [40] [20] [26]: в [40] и [20] цель – не абсолютная скорость, а, скорее,
выбор между площадью, мощностью и скоростью. В [26] Kearney и Bergmann представляют
разработку, концептуально подобную этой работе, т.е. матрицу с переменной задержкой и
сохранением переноса и оконечный сумматор с переменной задержкой.
Эта статья представляет архитектуру целочисленного (с дополнительным негативным
кодированием по основанию 2) конвейеризованного умножителя, которая объединяет
несколько методов алгоритмизации и проектирования, чтобы позволить VLSI-реализацию в
качестве самосинхронного ядра умножителя или полностью синхронного ядра умножителя с
переменной задержкой. Синхронная версия – по существу, новая разработка, в то время как
асинхронная версия – реальное развитие [26] в архитектуре (использование кодирования
Booth, особая матрица, зависимая от данных, с сохранением переноса, особый оконечный
сумматор) с дополнительными различиями в реализации (особая микроконвейерная схема,
заказное ядро вместо конструкции ИС на библиотечных элементах). Цель предлагаемых
Для простоты в этой статье используется термин "задержка" и для синхронных, и для асинхронных
устройств, означающий время получения готового результата (измеряемое в циклах или в нс). Это не вызывает
неоднозначности в контексте этой статьи.
1
3
проектов – скорость худшего случая, сравнимая с самыми быстрыми существующими
умножителями, и существенно лучшая средняя производительность. В статье дается
всесторонний анализ (на командном уровне) статистической эффективности переменной
задержки, а также моделирование (на схемном уровне), показывающее ожидаемую
эффективность проекта.
II. Предпосылки архитектуры параллельного умножителя
Основной алгоритм умножения с суммированием сдвига двух n-битных целых чисел А
и B выражается следующим псевдокодом:
for j = 0 .. n-1 loop
product <= product + A AND bj ;
A <= 2*A ;
end loop ;
где bj – j-тый бит B, а обозначение A AND bj указывает разрядный вектор, следующий из
AND каждого бита А с битом bj .
Умножитель матрицы может пользоваться преимуществом CSA (Carry Save Adders –
сумматоров с сохранением переноса), чтобы избежать распространения переноса на каждом
шаге цикла суммирования сдвига [22]. На рис. 1 показан эскиз структуры умножителя матриц
CSA; каждая строка матрицы составлена из полных сумматоров (для первой строки –
полусумматоров) без горизонтального распространения переноса, а последняя внизу строка–
сумматор с распространением переноса (CPA – Сarry Propagation Adder), который выполняет
распространение переноса для получения окончательной суммы. На рис. 1 операции сдвига
среди последовательных строк CSA – неявные для сохранения простоты картины. Матрица
CSA, имеющая задержку O(n), может быть преобразована в структуру дерева по основанию 3
с задержкой O(log n) без нарушения корректности конечного результата (дерева Wallace,
[22]). Нерегулярная структура такого дерева может быть исправлена вводом компрессоров 4:2
[49], т.е. сумматоров с 4 входами и 2 выходами, которые делают более регулярным дерево по
основанию 2. Другая возможность состоит в том, чтобы разбить матрицу CSA на пару
матриц, действующих в параллель [22], и, таким образом, получить регулярную
прямоугольную структуру, обычно используя простые полные сумматоры, но только
сокращая задержку CSA до O(n/2).
Независимо от структуры CSA число частичных продуктов, которые нужно
суммировать, может быть сокращено применением кодирования Booth 2-ого порядка к
операнду умножителя [22] [4]. Кодирование Booth 2-ого порядка использует наличие единиц
или нулей в операнде умножителя, чтобы объединить два сложения в одной операции, как
определено в таблице 1. Кодирование в таблице 1 применяется для j = 0, 2, 4, …, n-2,
сокращая, таким образом, число рассматриваемых частичных продуктов до n/2. Таблица 1
показывает специальную реализацию битов кодирования – кодирование Booth с выбором
знака [19]. По существу, биты pj и mj указывают, должна ли выполняться операция "плюс"
или "минус", а sj и dj указывают, используется ли "одиночное" или "удвоенное" значение А в
качестве частичного продукта. Следуя этой реализации, алгоритм умножения псевдокода с
суммированием сдвига становится:
for j = 0 .. n-2 step 2 loop
product <= product + (A AND pj – A AND mj) AND sj
+(2*A AND pj – 2*A AND mj) AND dj ;
A <= 4*A ;
4
end loop ;
Таблица 1
bj +1
0
0
0
0
1
1
1
1
bj bj –1
0
0
0
1
1
0
1
1
0
0
0
1
1
0
1
1
Операция
операции нет
+А
+А
+2A
-2A
-А
-А
операции нет
sj
0
1
1
0
0
1
1
0
dj
1
0
0
1
1
0
0
1
pj
0
1
1
1
0
0
0
0
mj
0
0
0
0
1
1
1
0
В реализации матрицы CSA вышеупомянутого алгоритма отдельный набор
кодирования битов pj, mj, sj и dj управляет операцией строки CSA, за исключением первой
строки матрицы, которой нужны два набора кодируемых битов, потому что она
непосредственно обрабатывает два частичных продукта.
Наконец, для улучшения производительности регистры конвейера могут быть
вставлены в информационный канал умножителя.
III. Архитектура и логический проект предлагаемых умножителей
Предлагаемая архитектура базируется на выборе знака кодирования Booth 2-го
порядка и разбиении матрицы CSA. Для n-битных операндов в каждой из двух матриц CSA
имеется n/2 частичных продуктов, т.е. (n/2)(1/2)-2 строк полных сумматоров (рис. 2).
Компрессор 4:2 используется для объединения результатов разбиения матрицы CSA с
просмотром разрешения регулярного размещения, хотя эта работа не сосредотачивается на
разработке размещения. Каждая строка полных сумматоров условно пронумерована
индексом j битов кодирования Booth, управляющих этой строкой, таким образом,
начинающихся с j = 4 для матрицы слева и j = n/2+4 для матрицы справа. Такое обозначение
нумеруемых строк упрощает логические уравнения в следующем.
Непосредственная реализация с фиксированной задержкой схемы на рис. 2 имеет
следующие компоненты задержки: Delay = DBooth-enc+DBooth-sel+Dha+(n/4–2)Dfa+D4:2+Dcpa, где
составляющие задержки: DBooth-enc – логика кодирования Booth, производящая биты
кодирования pj, mj, sj, dj; DBooth-sel – логика, которая выбирает операцию каждой строки CSA
согласно битам кодирования; Dha – полусумматор (строка CSA); Dfa – полный сумматор
(строка CSA), D4:2 – компрессор 4:2; Dcpa – конечный CPA. Предназначение последнего –
сумматор с фиксированной задержкой.
Чтобы предписывать переменную (и кратчайшую) задержку в операции CSA над
матрицей, предлагаемая архитектура содержит ряд сигналов пропуска (skip). Что касается
одной из двух матриц CSA, каждый сигнал skiphk указывает, что все последовательные строки
CSA, нумерованные h, h+2, h+4, … k, не должны выполнять никакой операции. Сигналы
skiphk выражают возможность обхода не только отдельной строки CSA в случае, если
операции нет, но также и кратных последовательных строк CSA.
5
Рис. 3 иллюстрирует подробности операции пропуска в строках CSA. Селектор Booth
выбирает среди возможных операций ту, которая должна выполняться, в то время как
сигналы skiphk заставляют данные обходить строки CSA, которые не выполняют никакой
эффективной операции (т.е. должны прибавлять нуль). Операция обхода происходит за одну
задержку мультиплексора даже для многократного обхода строк, благодаря многократным
сигналам skiphk, покрывающим все последовательные комбинации обхода строк.
Kearney и Bergmann в [26] показали, что обход строки CSA в умножителе матрицы
подразумевает стоимость пересылки к конечному CPA нерешенной пары битов
«перенос+сумма» для младшего бита строки, вместо одиночного бита конечного продукта. В
архитектуре кодирования не Booth это увеличивает конечный размер CPA до 2n битов вместо
n битов, требующихся для стандартной матрицы CSA [26]. Однако в архитектуре Boothкодирования необходим, во всяком случае, конечный CPA размером в 2n битов, чтобы
управлять дополнительными переносами, произведенными вычитанием Booth дополнения до
2 [21], так что представление переменной задержки не увеличивает размер конечного CPA.
Рис. 3 детализирует механизм, используемый для эксплуатации этого свойства и отличающий
предлагаемую архитектуру от предыдущего "пропуска строк" матриц CSA: непропущенная
строка может пересылать младший перенос, вызванный вычитанием дополнения до 2;
пропущенная строка пересылает младший перенос, исходящий из предшествующей строки.
Логическая разработка генерации сигнала skiphk – особый аспект предлагаемой
архитектуры и заслуживает специального внимания. Из таблицы 1, выражение сигналов
skiphk, h  k:
skiphk = (~ph ~mh) (~ph+2 ~mh+2) …. (~pk ~mk),
где символ ~ указывает логическую инверсию.
Чтобы операция была эффективной, необходимо генерировать сигналы skiphk скорее
параллельно, чем многократно (например, skiphk = skiph,k-1 ~pk ~mk). Кроме того, чтобы
генерировать сигналы максимально быстро и избежать увеличения разветвления кодеров
Booth, хорошо получать сигналы skiphk непосредственно из битов операнда B, а не с выхода
кодеров Booth ph и mh. Логическое выражение обобщенного сигнала skiphk получается (из
таблицы 1):
skiphk =
(~bh+1 ~bh ~bh-1 + bh+1 bh bh-1)
(~bh+3 ~bh+2 ~bh+1 + bh+3 bh+2 bh+1)
(~bk+1 ~bk ~bk-1 + bk+1 bk bk-1);
преобразованиями De Morgan оно может быть сокращено до
~ skiphk =
(~bh+1 bh + ~bh+1 bh-1 + bh+1 ~bh + ~bh bh-1 + bh+1 ~bh-1 + bh ~bh-1) +
...
(~bk+1 bk + ~bk+1 bk-1 + bk+1 ~bk + ~bk bk-1 + bk+1 ~bk-1 + bk ~bk-1).
Это выражение NOR-AND не позволяет производить биты skiphk одновременно с
битами кодирования Booth mh и ph. С другой стороны, оно вводит избыточную логику.
При некоторых алгебраических проходах мы можем наблюдать, что число сигналов
skiphk для обнаружения всех комбинаций последовательных строк среди x строк – x(x+1)/2.
Для некоторых размеров матрицы CSA было бы непрактично генерировать полный набор
сигналов skiphk из-за сложности межсоединений (см. рис. 3). В 32  32-разрядной реализации
архитектура с полным обходом нуждалась бы в 26 сигналах skiphk и 8-входовых
6
мультиплексорах на последней строке CSA. Такая сложность кажется бесполезной, потому
что первая строка CSA состоит из относительно быстрых полусумматоров, и потому что
полный пропуск обеих матриц CSA предположительно очень редок (вероятность от 0,25 14 до
4.10-9 при однородном распространении операндов). Одна возможность состоит в том, чтобы
разбить матрицу CSA на блоки ограниченного размера, которые представляют максимальное
количество одновременно пропускаемых строк CSA. В предлагаемой 32  32-разрядной
реализации обе 7-строчные матрицы разделяются на два блока, по 3 пропускаемые строки
каждый, плюс непропускаемая строка полусумматоров (первая строка). Фактически эти
пределы выбора 6 skiphk говорят о сложности каждого пропускаемого блока; в качестве
альтернативы, три 2-строчных блока уничтожили бы большую часть возможности
многократного пропуска строк, в то время как 4-строчный блок, сопровождаемый 2строчным блоком, приведет к очень несбалансированной сложности блоков.
Для конечного сумматора CPA предлагаемая архитектура использует схему CS (Carry
Select – выбор переноса) [5], время завершения которой, зависимое от данных, было
исследовано и доказано в предыдущих работах [15] [29] [30]. В частности, размер групп CS в
конечном 64-разрядном CPA следует схеме 8, 8, 8, 8, 8, 6, 6, 5, 4, 3 битов, если рассматривать
наибольший значащий разряд слева. С этим выбором установления размеров, после
задержки, эквивалентной 7 полным сумматорам, выходные переносы из 3-, 4-, 5- и 6-битных
групп несомненно достоверны, в то время как выходной сигнал переноса 8-разрядных групп
может быть достоверен (ускоренный перенос [15]). В этом случае происходит раннее
завершение CPA. В худшем случае для завершения цепочки выбора переноса необходима
дополнительная задержка в 5 мультиплексоров. Выбор размеров CPA имеет целью
возможность изменения подобной задержки (в наносекундах) в CPA и в матрице CSA.
Результирующая задержка умножителя – групповое выражение формы
Delay = DBooth-enc + DBooth-sel + Dha + N(B) (Dfa + Dmux) + b Dmux + D4:2 + Dcpa(A, B),
где Dmux – задержка мультиплексора, b – число пропускаемых блоков строк в матрице CSA,
N(B) – фактическое число частичных продуктов, складываемых/вычитаемых двумя
матрицами CSA (фактически максимум между двух). Обозначения N(B), Dcpa(A, B) указывают
зависимость от значений операнда. В частности, формула предполагает перекрывающееся
вычисление сигнала skiphk, т.е. Dskiplogic < DBooth-enc + DBooth-sel + Dha, где Dskiplogic – время
генерации сигналов skiphk.
Функциональные возможности предлагаемой архитектурной схемы были
подтверждены алгоритмической моделью, выполнимой на уровне битов [24].
IV. Проект VLSI синхронной реализации с переменной задержкой
На рис. 4 показана принципиальная схема реализации синхронной 32-разрядной
архитектуры с переменной задержкой. Каждая из двух матриц CSA содержит два
пропускаемых 3-строчных блока. На каждом из них действует 6 сигналов skiphk.
Умножитель конвейеризован регистром на выходе разбиения матрицы CSA. Если
рассматривать задержки худшего случая, приблизительные критические пути двух ступеней:
Delay_1st|worst = DBooth-enc + DBooth-sel + Dha + 6 Dfa + 6 Dmux ,
Delay_2nd|worst = Dmux + D4:2 + Dcpa  Dmux + D4:2 + 7 Dfa + 5 Dmux ,
где распространение переноса и генерация суммы в полном сумматоре для простоты
индицируются как Dfa. Операция умножителя может завершаться за один или два цикла
часов, в зависимости от фактических значений операндов. Чтобы завершить операцию за
7
один цикл, мультиплексор разрешает частичным результатам матрицы CSA отменять
конвейерный регистр, если есть возможность пройти весь логический путь умножителя за
отдельный цикл.
Чтобы выполнить предсказание выполнения за один/два цикла, мы должны
установить ряд условий, ведущих к полной задержке, приблизительно эквивалентной
половине полной задержки худшего случая, а затем подбирать величину времени цикла VLSI
по такой сокращенной задержке. В предлагаемой реализации условия готовности результата
за один цикл – то, что каждая из матриц CSA создает максимум два частичных продукта, и
что вторая ступень конвейера не занята (обработкой предыдущего 2-циклового умножения), и
что все 8-битные группы CS в конечном CPA ожидают своих нереносов. Если все эти условия
выполнены, фактический критический путь обеих ступеней – номинально
Delay_singlecycle = DBooth-enc + DBooth-sel + Dha + 2(Dfa + Dmux) + 2Dmux + Dmux + D4:2 + 7Dfa + Dmux.
Условия определяются целью их относительно простого логического детектирования; VLSIреализация умножителя должна заботиться, чтобы задержка одноцикловой операции была
приблизительно сравнима с задержками худшего случая двух отдельных ступеней конвейера
(Delay_1st|worst и Delay_2nd|worst). Время цикла VLSI устанавливается соответственно, как будет
показано позже.
Функционально сигнал busy показывает, что вторая ступень конвейера занята, сигналы
unresolved-carryi – что CPA не может предвидеть свои внутренние переносы, сигналы no-skipi
показывают строки CSA, которые не могут быть пропущены, а сигналы onecycle отмечают,
что операция заканчивается в текущем цикле. Блоки ">2" отмечают, что в каждой матрице
CSA обрабатывается больше двух частичных продуктов, в то время как блок ">0" (оператор
OR) показывает, что имеется, по крайней мере, одна 8-битная группа CS в конечном
сумматоре с неразрешенным переносом.
Если предположить, что на входах умножителя операнды обеспечены на падающем
фронте i-того синхроимпульса, то в случае, если результат готов в одном цикле, сигнал
onecycle высокий на падающем фронте (i+1)-ого синхримпульса; иначе сигнал onecycle
низкий, и результат готов на растущем фронте (i+2)-ого синхроимпульса. Важно, что сигнал
onecycle – синхронный с часами, т.е. стабильный внутри текущего цикла часов, и активный
только в случае раннего завершения умножения.
На рис. 5 показана заказная VLSI-разработка "логики пропуска" для 3-строчного
блока. Все 3-строчные блоки на рис. 4 и соответствующая "логика пропуска" идентичны
этому. Рис. 6 показывает VLSI-разработку конечной логики, производящей сигнал onecycle.
Рис. 7 детализирует VLSI-проект блока выбора переноса в опознавании переноса завершения
CPA. Вся логика в умножителе разработана в CMOS-стиле динамического "домино", с
инверторами между каскадированными логическими блоками [50]. Задание размеров
транзисторов выполняется согласно методологии оптимизации "логической работы" [42],
хотя и с упрощением предположений относительно ветвления схемы. В соответствии с
методом логической работы число ступеней CMOS на критическом пути блоков главной
схемы должно быть оптимизировано. В частности, в схеме "логики пропуска" (рис. 5)
имеется 2 статических буфера инвертирования на каждом входном бите (не показаны), и
функция NOR-AND разбита на 2 ступени домино. На рис. 5 критический путь – от входных
битов b3 … b9 до выходного сигнала skip48. На рис. 6 критические входы логической схемы –
биты unresolvedj, потому что они приходят из блоков выбора переноса в конечном CPA и,
следовательно, появляются позже, чем сигналы no-skiph, приходящие непосредственно из
логики пропуска (рис. 4). Критическое условие задержки для сигнала onecycle появляется,
только когда активны два no-skiph (т.е. матрица CSA обрабатывает 2 частичных продукта), но
8
имеются некоторые активные unresolvedj. Результирующая критическая задержка всей
логики, производящей сигнал onecycle – приблизительно Donecycle = DBooth-enc + DBooth-sel + Dha +
2(Dfa + Dmux) + 2Dmux + Dmux + D4:2 + 7Dfa + Ddetect, где Ddetect – задержка схемы рис. 6 от битов
unresolvedj до onecycle выходного сигнала.
Сигналы в схемах предзаряжаются до высокого уровня в течение низкого полупериода
часов, кроме сигнала busy, который готов немедленно после падающего фронта
синхроимпульса, потому что вырабатывается регистром, запускаемым падающим фронтом.
Следующие параметры синхронизации, дополненные регистром и накладными
расходами предзаряда, определяют время цикла, приемлемое для умножителя: для худшего
случая Delay_1st|worst и Delay_2nd|worst; задержка в случае одноцикловой операции
Delay_singlecycle; прогнозируемая задержка Donecycle.
V. VLSI-проект самосинхронной реализации с переменной задержкой
Схема асинхронного умножителя с переменной задержкой базируется на
микроконвейерной парадигме [41]. Умножитель разработан как двухступенчатый
микроконвейер, связанный с внешней средой через пару двухфазных сигналов
запроса/подтверждения на входе и другую пару на выходе умножителя. Схема использует
элементы памяти, переключаемые двумя фронтами и реализованные в соответствии с [51],
что сокращает микроконвейерные межсоединения и активность переключений.
На рис. 8 показана микроконвейерная реализация. Существенная особенность проекта
в том, что задержка каждой из двух микроконвейерных ступеней зависима от данных
благодаря сигналам skiphk в CSA и опознаванию завершения CPA. Специализированные с
этой целью схемы ответственны за выработку сигналов завершения матриц CSA и CPA. Для
матрицы CSA фиктивный логический путь, управляемый сигналами skiphk, воспроизводит
логические уровни двух матриц CSA, зависимые от данных. Сигналы Z1 и Z2 переключаются
номинально, как только готов соответствующий выход матрицы CSA. Это время зависит от
фактических значений данных посредством сигналов skiphk. Для конечного CPA сигнал
завершения генерируется спекулятивной методикой завершения [52], т.е. выбором одной из
двух задержек для сигнала завершения: чем короче задержка в случае, если никакой сигнал
unresolvedi не активен, тем длиннее задержка в противоположном случае. Дублированные
ждущие элементы, переключаемые фронтом сигнала, обеспечивают сигнал предзаряда для
динамических логических вентилей умножителя. В обе ступени конвейера вставляется
программируемый элемент задержки, компенсирующий время предзаряда и корректирующий
возможное ухудшение параметров в задержке сигналов управления, как было показано в [14]
и [10].
В микроконвейеризованной реализации не необходимо ни обеспечивать логику для
отмены конвейерного регистра, ни проверять, занята ли вторая ступень, когда готов результат
первой ступени, потому что сигнал управления регистра определяется зависимым от данных
квитированием двух ступеней конвейера. Таким образом, гибкое поведение микроконвейера
автоматически реализует переменное время срабатывания умножителя.
Все компоненты информационного канала имеют такую же реализацию схем, как в
синхронной версии, кроме конвейерного регистра, переключаемого двумя фронтами.
Средние задержки двух ступеней с переменной задержкой:
Delay_1st|avg = DBooth-enc + DBooth-sel + Dha + app·(Dfa + Dmux) + 2Dmux,
Delay_2nd|avg = D4:2 + E{Dcpa}  D4:2 + 7Dfa + pncp·Dmux + (1 - pncp)·5Dmux ,
9
где app – среднее число ненулевых частичных продуктов, которые нужно прибавить/вычесть
при разбиении матрицы CSA; pncp – вероятность, что конечный CPA не нуждается в
распространении переноса, т.к. все 8-битные группы CS опережают свой выходной перенос.
Параметры синхронизации, определяющие производительность микроконвейерной
реализации умножителя – худшая и лучшая задержка ступеней и их среднее значение
Delay_1st|avg и Delay_2nd|avg для получения производительности и задержки умножителя.
VI. Статистическая релевантность уровня команд переменной задержки
Проект устройства с переменной задержкой должен быть поддержан свидетельством,
что его средняя задержка операции в реальном приложении короче задержки худшего случая.
Поскольку кодирование Booth воздействует на распространение нулей и единиц в операндах,
нам нужен прямой анализ поведения на разрядном уровне специальной архитектуры,
выполняющей реальные операции. Здесь представлено изучение, основанное на
моделировании
MIPS-подобной
архитектуры
системы
команд
посредством
инструментальной версии набора средств Simplescalar [8]; рассматриваются две команды
умножения: MULT (32-разрядное целочисленное умножение) и MULTU (32-разрядное
целочисленное умножение без знака). Команда MULTU менее значительна, поскольку
происходит редко или вообще никогда. Трассировка операндов извлекается и используется
на модели C-языка разрядного уровня архитектуры с переменной задержкой [24], получая
статистические параметры из таблиц 2 и 3. Таблица 2 отсылает к последовательности
умножения с теоретическим стандартным распространением операндов. Таблица 3 отсылает
к выполнению эталонного комплекта программ SPEC95 с входными файлами ссылок [23]. В
таблицах 2 и 3 даны параметры app, pncp и параметр 1cyc, т.е. вероятность совпадения
условий для одноцикловой операции в синхронной реализации.
Таблица 2
Команда 
Параметр 
Однородные операнды
Операнды Гаусса
Операнды Пуассона
app
4,51
2,90
3,89
MULT
1cyc
0,01
0,02
0,02
pncp
0,40
0,03
0,09
MULTU
app
1cyc
4,50
0,01
2,99
0,01
3,90
0,02
pncp
0,39
0,03
0,09
Таблица 3
Команда 
Параметр 
applu
compress
gcc
go
ijpeg
li
m88ksim
mgrid
swim
tomcatv
turb3d
app
1,65
0,06
1,48
0,07
3,79
0,09
0,03
1,11
0,32
0,20
1,20
MULT
1cyc
0,17
0,95
0,45
0,97
0,00
0,92
0,97
0,00
0,88
0,80
0,00
pncp
0,17
0,95
0,79
0,97
0,00
0,92
0,96
0,00
0,88
0,80
0,00
app
1,81
6,00
1,86
1,95
2,67
MULTU
1cyc
0,05
0,00
0,23
0,14
0,24
pncp
0,06
0,00
0,35
0,17
0,40
10
vortex
wave5
СРЕДНЕЕ
1,55
0,78
1,01
0,30
0,65
0,54
0,30
0,65
0,57
5,99
0,38
0,00
0,11
0,35
0,22
VII. Результаты производительности
На рис. 9 показана выборка моделирования HSpice уровня 49 синхронного
умножителя, относящегося к процессу 0,35 мкм CMOS, при типичных условиях
эксплуатации. Размещение маски схем не было полностью разработано; однако паразитные
емкости длинной металлической линии были закодированы вручную в списки соединений
Spice на основании гипотетического размещения схем. Во всех схемах не было серьезных
требований к задачам совместного использования, возможно, потому, что емкость
внутренних вершин, которые могут вызывать эффект перераспределения требований,
фактически мала сравнительно с емкостью загрузки и паразитной емкостью выходных
вершин. На рис. 9, слева направо, показаны сначала случай двухциклового умножения, а
затем одноцикловый случай. Значения данных выбираются регистрами на падающем фронте
синхросигналов. Задержка регистра перекрывается со следующей фазой предзаряда
динамических комбинационных схем.
В таблице 4 показана характеристика задержки, полученная для релевантных
устройств схемы умножителя; в асинхронной версии предзаряд начинается после того, как
сигнал управления предзарядом проходит соответствующее буферное дерево, чтобы
управлять всеми динамическими схемами ступени конвейера; в синхронной версии задержка
буферизации часов перекрывается операцией схемы, и предзаряд начинается точно на
падающем фронте синхросигнала. По этой причине в самосинхронной реализации
фактическое время, занимаемое предзарядом, больше.
Таблица 4
Синхронный [нс]
Delay1st|worst
1,65
nd
Delay2 |worst
1,23
pipe register
0,29
precharge hold time 0,40
Dskiplogic
0,55
DBooth_enc
0,34
DBooth_sel
0,19
st
Dha in 1 CSA row
0,08
Delay_singlecycle
1,83
Donecycle
1,84
Самосинхронный [нс]
Delay1st|worst
1,65
nd
Delay2 |worst
1,20
pipe register
0,32
задержка precharge
0,78
Dskiplogic
0,55
DBooth_enc
0,34
DBooth_sel
0,19
st
Dha in 1 CSA row
0,08
Delay1st|best
0,76
nd
Delay2 |best
0,81
Dfa in CSA row
0,11
Dmux in CPA
0,08
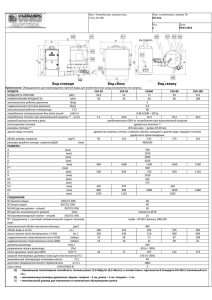
Таблица 5 (n.a. = неприменимый; N.A. = недоступный)
Тип
SA PPC PIII NEC M·CORE M·CORE Эта работа Эта работа
(лучшая
(худшая
(лучшая (худшая
задержка) задержка) задержка) задержка)
Статистика с переменной n.a. n.a. n.a. n.a.
N.A.
N.A.
54 %
46 %
задержкой (умножение
SPEC95)
Задержка [циклы]
2
3
4
1
2
18
1
2
11
Задержка [нс]
9,60 6,44 6,67 2,73
60,00
540,00
2,25
4,50
Производительность [нс] 4,80 2,14 1,67 2,73
60,00
540,00
2,25
2,25
Размер элемента [мкм]
0,35 0,22 0,18 0,25
0,36
0,35
Таблица 6 (источник для производительности сравниваемых проектов: [27])
Печать
Размер слова [битов]
Задержка [нс]
Производительность [нс]
Питающее напряжение [В]
Размер элемента [мкм]
BFB
16  16
25,00
5,51
5,00
1,20
SK
16  16
64,0
6,40
5,00
1,00
KB
16  16
15,00
10,80
5,00
0,60
Эта работа
32  32]
3,48
1,76
3,30
0,35
Рассеяние мощности не было полностью исследовано; как в любом параллельном
умножителе, активность переключений строго зависит от последовательности входных
операндов. Приблизительная оценка на базе накладных расходов в транзисторах может
показать издержки рассеяния мощности меньше 20 % по отношению к архитектуре
умножителя матриц с фиксированной задержкой.
A. Синхронная реализация
Предел временного цикла для синхронной реализации, предсказанный по задержке
выполнения Donecycle – 1,84 нс. Если рассматривать время задержки для сигнала предзаряда, то
ожидаемое время цикла, приемлемое для умножителя – номинально 2,25 нс (с
асимметричной формой синхроимпульса). Область издержек может быть оценена в терминах
числа транзисторов относительно реализации той же синхронной архитектуры умножителя с
фиксированной задержкой: полное число транзисторов в предлагаемой реализации – 22609, а
число транзисторов всей логики, специализированной для переменной задержки – 3329.
Накладные расходы составляют приблизительно 17 %. Дополнительная задержка из-за
управления переменной задержкой существенна из-за мультиплексоров, вставленных в
матрицы CSA. Что касается рис. 4, схемотехническое моделирование показывает, что сумма
задержек мультиплексоров проходных транзисторов вызывает издержки в 0,32 нс в первой (и
самой медленной) ступени конвейера. Таким образом, реализация предлагаемой архитектуры
с фиксированной задержкой, как ожидается, будет поддерживать время цикла 1,75 нс и
фиксированную задержку 3,50 нс.
На рис. 10 показано сравнение с существующим современным состоянием
синхронных 32-разрядных умножителей. Метки "M·CORE", "PIII", "SA" и "PPC" относятся к
M·CORE MMC2001 33 MГц (включая умножитель с переменной задержкой), PentiumIII 600
МГц, StrongARM 1110 206 МГц и PowerPC 750 466 МГц, соответственно. Метка "NEC"
отсылает к сверхбыстродействующей архитектуре умножителя 2,7 нс фирмы NEC [21], здесь
представленной для 32-разрядного проекта вместо 54-разрядного. Первоначальные доли
задержки, сообщенные в [21]: 0,53 нс – кодеры/селекторы Booth, 0,95 нс – дерево
компрессора 4:2, 1,22 нс – 108-разрядный CarryLookahead CPA. Масштабирование дерева
компрессора и конечного CPA для 32-разрядных операндов умножителя приводит к оценке
полной задержки в 2,33 нс и времени цикла в 2,73 нс, включая время предзаряда.
Если считать, что 54 % – статистическая вероятность операций с одиночным циклом
при выполнении SPEC95 (таблица 3), средняя ожидаемая задержка предлагаемого
умножителя остается немного больше, чем в проекте фирмы NEC, из-за улучшенной
12
оптимизации схемы и технологии. В целом ожидаемые показатели производительности
синхронного проекта с переменной задержкой, несомненно, замечательны.
B. Самосинхронная реализация
Из таблицы 4 видно, что задержки худшего и лучшего случая при самосинхронной
реализации – 4,41 нс и 3,13 нс, соответственно, в то время как средние задержки двух
микроконвейерных ступеней при выполнении SPEC95:
Delay_1st|avg = 0,76 нс + 1,01(Dfa + Dmux) = 0.94 нс,
Delay_2nd|avg = 0,76 нс + 0,57Dmux + 0,43 5Dmux = 0,98 нс.
Результирующая приблизительная средняя задержка целого микроконвейера: 0,78 +
0,94 + 0,78 + 0,98 = 3,48 нс; средняя производительность продиктована задержкой второй
ступени: 0,98 + 0,78 = 1,76 нс. Архитектура организована так, чтобы фаза предзаряда второй
ступени накладывалась на задержку распространения через микроконвейерный регистр.
Сложность издержек на переменную задержку в самосинхронной реализации – такая
же, как в синхронном случае, поскольку основные логические блоки – те же самые.
Рис. 11 показывает сравнение с объявленной производительностью асинхронных
умножителей. Все сравниваемые проекты –16-разрядные умножители. Метки "BFB" и "SK"
соответственно относятся к самосинхронным проектам с фиксированной задержкой,
опубликованным в [7] и [38], а метка "KB" относится к проекту с переменной задержкой,
опубликованному в [26]. Технологические параметры для всех проектов объявлены.
VIII. Заключение
Предлагаемая архитектура и VLSI-проект показывают, что умножитель с переменной
задержкой
в
синхронной
или
асинхронной
реализации
может
преодолеть
производительность, предлагаемую быстрыми умножителями с фиксированной задержкой.
Представленный проект предполагает использование регистров, запускаемых фронтом
сигнала, чтобы уменьшить сложность основных регистров логического проекта в синхронной
реализации и маршрутизации межсоединений в самосинхронной реализации. Исследование
влияния использования защелок на производительность может быть областью дальнейшей
работы. Дальнейшая работа может быть обращена также на компромиссы между
производительностью
и
числом
ступеней
конвейера
в
самосинхронной
микроконвейеризованной реализации.
IX. Благодарность
Автор благодарен профессору David Kearney за его ценные предложения и профессору
Alessandro De Gloria за его поддержку.
X. Ссылки
[1] Acosta A. J., Jimenez R., Barriga A., Bellido M. J., Valencia M., and Huertas J. L.,
Design and characterisation of a CMOS VLSI self timed multiplier architecture based on a bit level
pipelined array structure. IEE Proceedings, Circuits, Devices and Systems, 145(4):247 253, August
1998.
[2] Afgahi M. and Svensson C., "Performance of Synchronous and Asynchronous Design
Scheme for VLSI Systems", IEEE Trans. on Computers, 41(7):838 872, July 1992.
13
[3] Alvarez J., Barkin E., Chai Chin Chao., Johnson B., D'Addeo M., Lassandro F., Nicoletta
G., Patel P., Reed P., Reid D., Sanchez H., Siegel J., Snyder M., Sullivan S., Taylor S. and Minh Vo,
450 MHz PowerPCTM microprocessor with enhanced instruction set and copper interconnect ,
IEEE International Solid State Circuits Conference, Piscataway, NJ, USA., 1999., p.96 7.
[4] Baer J. L., Computer systems architecture, Computer Science Press, Rockville, Maryland,
1980, pp. 100 106.
[5] Bedrij, O.J., "Carry Select Adder", IRE Trans. on Electronic Comp., 11:340 346, 1962.
[6] Briley, B. "Some new results on average worst case carry", IEEE Trans. on Computers,C
22:459 463, 1973.
[7] Burford R. G., Fan X., and Bergmann N. W., An 180 MHz 16 bit multiplier using
asynchronous logic design techniques. In Proc. IEEE Custom Integrated Circuits Conference, pages
215 218, 1994.
[8] Burger, D. and Austin, T. M. , The Simplescalar Tool Set, Version 2.0, Tech. Rep.
#1342, Univ. of Wisconsin Madison, June 1997. Available at http://www.
cs.wisc.edu/~mscalar/simplescalar.html
[9] Burks, A.W. and Goldstine, H. and Von Neumann, J. , "Preliminary discussion on the
logical design of an electronic computing instrument", Tech. Report, The Institute of Advanced
Study", Princeton, NJ, 1947.
[10] Chandramouli V., Brunvand E., Smith KF, Self timed design in GaAs case study of a
high speed, parallel multiplier, IEEE Transactions on VLSI Systems.vol.4, no.1., March 1996., p.146
9.
[11] Chiang Jen Shiun and Liao Jun Yao. A novel asynchronous control unit and the
application to a pipelined multiplier. In Proc. International Symposium on Circuits and Systems,
volume 2, pages 169 172, June 1998.
[12] Christensen K. T., Jensen P., Korger P., and Sparso J., The design of an asynchronous
Tiny RISC TR4101 microprocessor core. In Proc. International Symposium on Advanced Research
in Asynchronous Circuits and Systems, pages 108 119, 1998.
[13] De Angel E., Swartzlander E. Jr. and Abraham J., A new asynchronous multiplier using
enable/disable CMOS differential logic. In Proc. International Conf. Computer Design (ICCD).
IEEE Computer Society Press, October 1994.
[14] De Gloria A. and Olivieri M., "Statistical Carry Lookahead Adders", IEEE Trans. on
Comp., 45(3):340 347, Mar. 1996.
[15] De Gloria A. and Olivieri M., "Completion-detecting Carry Select Addition", IEE Proc.
- Comput. and Dig. Techn. , 147(2):93-100, Mar. 2000.
[16] Furber S.B., Garside J. D., and Gilbert D.A., AMULET3: A high performance self
timed ARM microprocessor. In Proc. International Conf. Computer Design (ICCD), October 1998.
[17] Furber S.B., Garside J.D., Riocreux P., Temple S., Day P., Liu J., Paver N.C.,
AMULET2e: An asynchronous embedded controller. Proc. of the IEEE, 87(2):243 256, Feb. 99.
[18] Goodman R. M. and McAuley A. J., An efficient asynchronous multiplier. In K.
Bromley, S. Y. Kung, and E. Swartzlander, editors, Proceedings of the Second International
Conference on Systolic Arrays, pages 593 599. IEEE Computer Society Press, May 1988.
[19] Goto g., Inoue A., Kashiwakura S., Mitarai S, Tsuru T. and Izawa T., A 4.1 ns 54x54 b
Multiplier utilizing sign select Booth Encoders, IEEE Jour. of Solid State Circuits, 32(11):1676
1681, Nov. 1997.
[20] Haans J., van Berkel K., Peeters A., Schalij F, Asynchronous multipliers as
combinational handshake circuits IFIP Transactions A (Computer Science and Technology).vol.A
28., 1993., p.149 63.
14
[21] Hagihara Y., Inui S., Yoshikawa A., Nakazato S., Iriki S., Ikeda R., Shibue Y., Inaba T.,
Kagamihara M., Yamashina M, A 2.7 ns 0.25 mu m CMOS 54*54 b multiplier, IEEE International
Solid State Circuits Conference. IEEE, New York, NY, USA., 1998., p.296-7
[22] Hennessy, J.L., Patterson, D.A., Computer Architecture: A Quantitative Approach,
Morgan Kaufmann, Palo Alto, CA, 1990.
[23] Official SPEC web site: http://www.spec.org
[24] Model source code at ftp://ss1.ing.uniroma1.it/pub/reports/mul*.c
[25] Johnson, D. and Akella, V., Design and Analysis of Asynchronous Adders, IEE
Proceedings Comp. and Dig. Tech., 145(1), 1998.
[26] Kearney D., Bergmann NW, Bundled data asynchronous multipliers with data
dependent computation times, Intern. Symp. on Advanced Research in Asynchronous Circuits and
Systems. IEEE Comput. Soc. Press, Los Alamitos, CA, USA., 1997., p.186 97.
[27] Kearney, K. and Bergmann, N., 1997. "VLSI Design of an Asynchronous Multiplier
with Data Dependent Processing Times". Proc. 14th Australian Microelectonics Conference. IEEE.
pp. 282-287.
[28] Kessler R. E., The Alpha 21264 Microprocessor, IEEE Micro, 19(2), pp. 24 36, March
/Apr 1999.
[29] Kinnement, D. J. , An Evaluation of Asynchronous Addition, IEEE Trans. on VLSI
Systems, 4(1):137 140, Mar 1996.
[30] Kondo, Y. , Ikumi N., Ueno K., Mori J. and Hirano M., An Early Completion Detecting
ALU for a 1GHz 64b Datapath, IEEE Intern. Solid State Circuits Conference. IEEE, New York, NY,
USA., 1997.
[31] Lau CH., Renshaw D., Mavor J, A self timed wavefront array multiplier, IEEE
International Symposium on Circuits and Systems. IEEE, New York, NY, USA., 1989., p.138 41
vol.1.
[32] Lee J. and Asada K., "A synchronous completion prediction adder", IEICE Transactions
on Fundamentals of Electronics, Comm. and Comp. Sci., vol. E80-A, no. 3, pp. 606-609, March
1997.
[33] Marc R., El Hassan Bachar, A low power, 100 MHz 12*18+30 b multiplier accumulator
operating in asynchronous and synchronous modes, ESSCIRC '94.Twentieth European Solid State
Circuits Conference. Editions Frontieres, Gif sur Yvette, France., 1994.
[34] Martin A. J., Lines A., Manohar R., Nystroem M., Penzes P., Southworth R., and
Cummings U., The design of an asynchronous MIPS R3000 microprocessor. In Advanced Research
in VLSI, pages 164 181, Sept. 1997.
[35] Motorola Inc., M•CORE™ MMC2001 reference Manual, 1998., available at
http://www.motorola.com
[36] Noaks DR., Burton DP, A high speed, asynchronous, digital multiplier, Radio and
Electronic Engineer, vol.36, no.6., Dec. 1968., p.357 66.
[37] Rao VM., Nowrouzian B, Design and implementation of asynchronous parallel multiply
accumulate arithmetic architectures, 38th Midwest Symposium on Circuits and Systems. IEEE, New
York, NY, USA., 1996., p.761 4 vol.2.
[38] Salomon O., Klar H, Self timed fully pipelined multipliers, IFIP Transactions A
(Computer Science and Technology), vol.A 28., 1993., p.45 55.
[39] Seitz C.L., "System Timing", in C.Mead and L. Conway, Introduction to VLSI Systems
Design, pp. 218 262. Addison Wesley, 1980.
15
[40] Sparso J., Nielsen C. D., Nielsen L. S., and Staunstrup J., Design of self timed
multipliers: A comparison. In S. Furber and M. Edwards, editors, Asynchronous Design
Methodologies, volume A 28, IFIP Trans., pages 165-179. Elsevier Science Publishers, 1993.
[41] Sutherland I.E., Micropipelines. Communications of the ACM, 32(6):720 738, June
1989.
[42] Sutherland, I., Sproull, B., Harris, D., Logical Effort: Designing fast CMOS circuits,
Morgan Kaufmann, San Francisco, CA, 1999.
[43] Takamura A., Kuwako M., Imai M., Fujii T., Ozawa M., Fukasaku I., Ueno Y., and
Nanya T., TITAC 2: An asynchronous 32 bit microprocessor based on scalable delay insensitive
model. Intern. Conference on Computer Design (ICCD), pp. 288-294, Oct. 1997.
[44] Terada H., Miyata S., and Iwata M., DDMP's: Self timed super pipelined data driven
multimedia processors. Proceedings of the IEEE, 87(2):282 296, Feb. 1999.
[45] Tang, T.Y., Choy, C.S., Siu, P.L., and Chan, C.F., "Design of Self-timed Asynchronous
Booth's multiplier", Proc. of Asia & South Pacific Design Automation Conference, Jan. 2000, pp.
15-16.
[46] Tosic M. B., Stojcev M. K., Maksimovic D. M., and Djordjevic G. L., The
asynchronous counterflow pipeline bit serial multiplier, Journal of Systems Architecture, 44(12):985
1004, Dec. 1998.
[47] Van Berkel K., Burgess R., Kessels J., Peeters A., Roncken M., and Schalij F., A fully
asynchronous low power error corrector for the DCC player. IEEE Journal of Solid State Circuits,
29(12):1429 1439, December 1994.
[48] Van Gageldonk H., Baumann D., Van Berkel K., Gloor D., Peeters A., and Stegmann
G., An asynchronous low power 80c51 microcontroller. International Symposium on Advanced
Research in Asynchronous Circuits and Systems, pages 96 107, 1998.
[49] Weinberger A., 4-2 carry-save adder module, IBM-Technical-Disclosure-Bulletin,
vol.23, no.8; Jan. 1981; p. 3811-14.
[50] Weste, N.H. and Eshraghian, K., Principles of CMOS VLSI Design, Addison Wesley,
1993.
[51] Yun K. Y., Beerel P. A., and Arceo J., High-Performance Two-Phase Micropipeline
Building Blocks: Double Edge-Triggered Latches and Burst-Mode Select and Toggle Circuits , IEE
Proceedings Circuits, Devices and Systems. pp 282-288. Vol. 143, No. 5, October 1996.
[52] Yun Y. K., Nowick S.M, Beerel P. A., Dooply A. E., Speculative Completion for the
Design of High Performance Asynchronous Dynamic Adders, Proceedings of ASYNC 97,
Eindhoven, The Netherlands, 1997.
16
Рис. 1. Основная схема умножителя матриц. ha – полусумматоры, fa – полные сумматоры
Рис. 2. Схема архитектуры умножителя расщепленных матриц с кодированием Booth.
Bsel = селектор Booth, HA – полусумматоры, FA – полные сумматоры
17
Рис. 3. Деталь архитектуры обхода строки. Каждая строка мультиплексоров
управляется отдельным набором сигналов пропуска. Символ * указывает генератор битов
частичного продукта. Выделенная часть внизу детализирована на рис. 5 на транзисторном
уровне.
18
Рис. 4. 32-разрядная синхронная реализация умножителя с переменной задержкой
19
Рис. 5. Заказной VLSI проект "логики пропуска" для 3-строчного блока в матрице CSA
20
Рис. 6. VLSI проект логики, производящей сигнал "onecycle". Сверху справа
детализирована подсхема «> 0»; внизу справа части, детализирована подсхема «> 2»
21
Рис. 7. Заказной VLSI-проект блокировки выбора переноса в конечном сумматоре со
схемой детектирования неразрешенного переноса
22
Рис. 8. 32-разрядная самосинхронная реализация умножителя с переменной задержкой.
δ – элемент программируемой задержки
23
Рис. 9. Моделирование Spice синхронного умножителя с переменной задержкой CMOSреализации. Границы цикла синхронизации выделены
–