Документ 609678

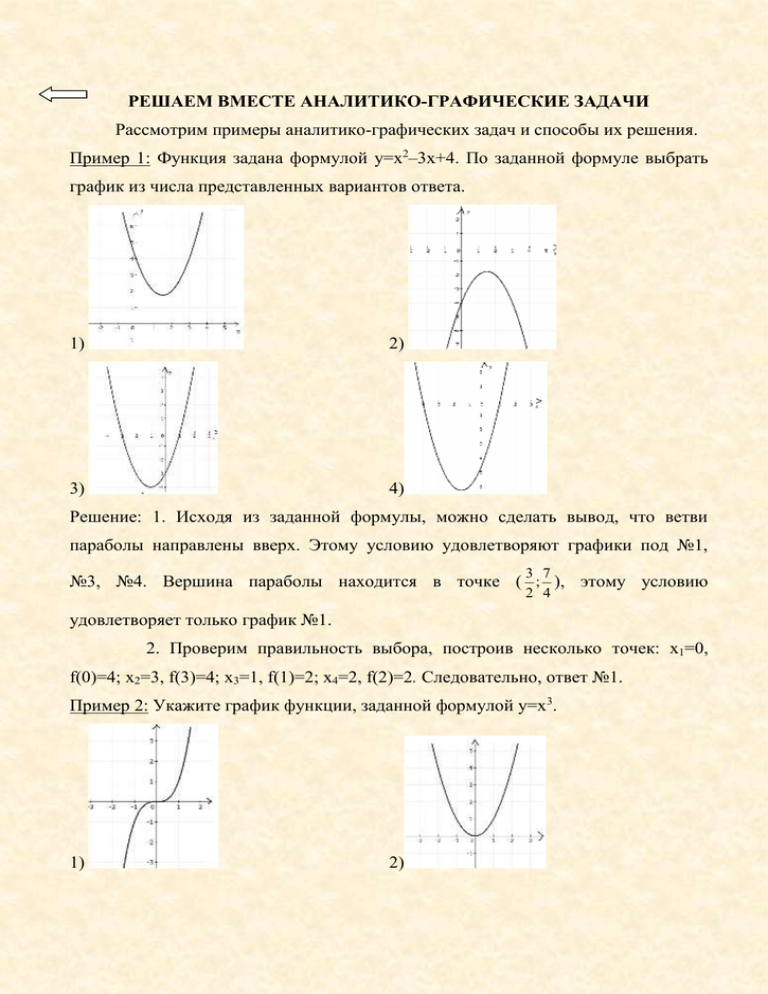
РЕШАЕМ ВМЕСТЕ АНАЛИТИКО-ГРАФИЧЕСКИЕ ЗАДАЧИ
Рассмотрим примеры аналитико-графических задач и способы их решения.
Пример 1: Функция задана формулой у=х2–3х+4. По заданной формуле выбрать
график из числа представленных вариантов ответа.
1)
2)
3)
4)
Решение: 1. Исходя из заданной формулы, можно сделать вывод, что ветви
параболы направлены вверх. Этому условию удовлетворяют графики под №1,
3 7
2 4
№3, №4. Вершина параболы находится в точке ( ; ), этому условию
удовлетворяет только график №1.
2. Проверим правильность выбора, построив несколько точек: x1=0,
f(0)=4; x2=3, f(3)=4; x3=1, f(1)=2; x4=2, f(2)=2. Следовательно, ответ №1.
Пример 2: Укажите график функции, заданной формулой у=х3.
1)
2)
3)
Решение:
4)
1) Проанализировав заданную формулу, можно сказать, что это
кубическая парабола, которая во всей области определения возрастает. А этому
условию удовлетворяет график №1.
2)Проверим правильность выбора вычислением контрольных точек: при х=1,
получаем у=1, при х=-1, получаем у=-1.
3)Делаем вывод: ответ №1.
Пример 3: Укажите график функции, заданной формулой у= х  1 .
1)
2)
3)
4)
Решение: 1) Исходя из формулы, можно сказать, что график данной функции
возрастает. Данному условию удовлетворяют графики №1, 2, 4.
2) Найдем контрольные точки для заданной функции: при х=1,
получаем у=0, при х=2, получаем у=1.
3) Делаем вывод, ответ №2.
Пример 4: Укажите график функции у=|x|-1 из числа заданных вариантов ответов.
1)
2)
3)
4)
Решение: 1) Анализируя формулу, можно сделать вывод, что график зависимости,
содержащий неизвестную под знаком модуля, сдвинут вдоль оси Оу на 1 единицу
вниз. Данному условию удовлетворяет график №2.
2) Проверим правильность выбора, вычислив контрольные точки
(1;0) и (-1;0).
3) Записываем ответ: №2.
1
, х  1;
Пример 5: Укажите график функции, заданной формулами у=  х
 х 2 , х  1.

1)
2)
3)
4)
Решение: 1) Анализируя формулу можно сделать вывод, что ответом может быть
график, состоящий из графиков двух функций, одна из которых гипербола на
промежутке х  1, другая – парабола на промежутке х<1. Данным требованиям
удовлетворяет график №4.
2) Проверим правильность выбора контрольными точками (1;1) и
(0;0).
3) Записываем ответ: №4.
 1
 х  3, х  4
Пример 6: Постройте график функции, заданной формулами f(x)=  2
 x  3, x  4
Решение: 1) Анализируя формулу, делаем вывод – функция кусочно-заданная.
График искомой функции – график, состоящий из графиков двух линейных
1
2
функций, причем функция у   х  3 задана на промежутке х<4, другая у=х – 3
на промежутке х  4.
1
2
2) При х<4 график функции у   х  3 убывает, ему принадлежат
точки (0;3) и (2;2). При х  4 график функции у=х – 3 возрастает, причем графику
принадлежат точки (0;-3) и (3;0). Тогда график функции выглядит следующим
образом:
Пример 7: Для каждой функции, заданной формулой, укажите ее график.
1) у=-х+1;
2) у=х-1;
3) у=х2-1
а)
b)
c)
Решение: 1) Проанализировав содержание задачи, можно сделать вывод о том,
что эта задача на соотнесение, т.е. для каждой формулы должен быть найден
соответствующий график;
2) Анализируя формулы, можно сделать вывод, графиками формул №1
и №2 должны быть прямые, этому требованию удовлетворяют графики а) и b),
следовательно, формуле №3 соответствует график с). Поскольку в формуле №1
коэффициент при х равен -1, то график функции должен убывать. Этому
требованию
удовлетворяет только график №2, следовательно, формуле №2
соответствует график а).
3) Запишем ответ: №1b, №2a, №3c.
Пример 8: Для каждой функции, заданной графиком, укажите ее график.
1
х
1
х
1) у= ;
а)
2) у=  ;
b)
3) у=х2-1.
c)
Решение: 1) Проанализировав содержание задачи, можно сделать вывод о том,
что эта задача на соотнесение, т.е. для каждой формулы должен быть найден
соответствующий график;
2)Воспользуемся промежутками знакопостоянства функций: функция,
заданная формулой №1 принимает положительные значения при x>0, а
отрицательные – при x<0, следовательно, ей соответствует график b.
Функция,
заданная
отрицательные
при
формулой
x>0,
№2
является
следовательно,
ей
Следовательно, формуле №3 соответствует (а)
3) Запишем ответ: №1b, №2с, №3а.
назад
положительной
соответствует
при
график
x<0,
с.