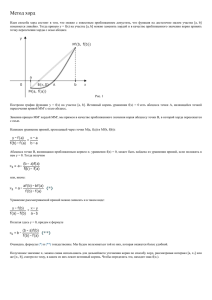
Приближенное решения уравнения методом хорд и касательных
реклама

Расчетная работа РЕШЕНИЕ УРАВНЕНИЙ 1. Приближенное решение уравнения методом хорд и касательных Методом хорд и касательных найти наименьший положительный корень уравнения x 2 sin x 0 . а) Выполнить графическое отделение корней; б) сузить отрезок изоляции корня методом проб до 0,05; в) уточнить корень комбинированным методом хорд и касательных (один шаг); г) записать приближенное значение корня и указать погрешность этого значения. Решение. 1. Графическое отделение корней уравнения. Запишем заданное уравнение в виде ( x) ( x) . В данном случае: x 2 sin x . Построим графики функций y x 2 и sin x . На отрезке [0,5; 1] содержится один корень x0 заданного уравнения. Это искомый наименьший положительный корень. 2. Сужение отрезка изоляции корня методом проб. Функция f ( x ) x 2 sin x непрерывна на , значит она непрерывна и на [0,5; 1] . Вычислим значения f (0,5) 0,75 0 , f (1) 1 0 . f (0,5) f (1) 0 . Следовательно, на [0,5;1] действительно содержится корень заданного уравнения. Выберем точку, принадлежащую интервалу (0,5; 1) , например, x 0,8 и вычислим f (0,8) 0,0522 0 . При этом f (0,5) f ( 0,8) 0 . Значит, x0 [0,5; 0,8] . Продолжим вычисления методом проб до тех пор, пока длина отрезка изоляции корня не достигнет величины 0,05 : f (0,7) 0,319 0 , x0 [0,7; 0,8] ; f (0,75) 0,1446 0 , x0 [0,75; 0,8] . 3. Уточним значение корня комбинированным методом хорд и касательных. Убедимся, что знаки производных f '( x ) и f ''( x) не изменяются на отрезке [0,75; 0,8] : f '( x ) 2 x cos x 0 x [0,75; 0,8] ; f "( x ) 2 2 sin x 0 x [0,75; 0,8] . Так как f (0,8) f "(0,8) 0 , то формулу касательных следует применить в точке b 0,8 и использовать формулы ba f ( b) . f (a ) , b1 b f ( b) f ( a ) f '(b) В данном случае: a1 a a 0,75 , b 0,8 , f (a) f (0,75) 0,1446 , f (b) f (0,8) 0,0522 ; f '(0,8) 2 0,8 cos( 0,8) 4,1416 , 0,8 0,75 ( 0,1446) 0,7867 , 0,0522 ( 0,1446) 0.0522 b1 0,8 0,7874 . 4,1416 a1 0,75 4. Приближенное значение корня x0 b1 a1 0,7867 0,7874 0,78705 . 2 2 Абсолютная погрешность корня b1 a1 0,7874 0,7867 0,00035 0,001 . 2 2 Так как 0,0001 0,001, то необходимо округлить значение корня до 0,001 : x0 0,787 . Замечание. Если f (a) f ''(a) 0 , то следует применить формулы f (a ) ba , b1 b a1 a f ( b) . f '(a ) f (b) f (a ) 2. Вычисление комплексных корней уравнения Решить уравнение (3z 2)(6 4iz )( z 2 7 z 49) 0. Записать корни в алгебраической, тригонометрической и показательной формах. Построить корни на комплексной плоскости. Решение. 1. Заданное уравнение равносильно совокупности уравнений 3z 2 0, 6 4iz 0, z 2 7 z 49 0. Решим эти уравнения: 2 . 3 3 3 2) 6 4iz 0 ; z2 i . 2i 2 2 3) z 7 z 49 0 ; 1) 3z 2 0 ; z1 7 72 4 49 7 3 49 7 7 3 1 . 2 2 2 7 7 3 i 7 7 3 7 7 3 , z3 z3,4 i , z4 i. 2 2 2 2 2 z Заданное уравнение имеет 4 корня. Их алгебраическая форма: z1 2 3 7 7 3 7 7 3 , z2 i , z3 i , z4 i. 3 2 2 2 2 2 2. Построим эти корни. 3. Запишем корни в тригонометрической и показательной формах. 3 2 2 ; z1 , arg z1 1 0 . 3 3 Тригонометрическая форма: 2 z1 (cos0 i sin 0) . 3 2 Показательная форма: z1 e0i . 3 1) z1 2 4 2 3 3 3 2) z2 i , z2 02 , 2 2 2 arg z2 2 . 2 Тригонометрическая форма: 3 z2 cos i sin . 2 2 2 3 i Показательная форма: z2 e 2 . 2 2 2 2 7 7 3 7 7 3 7 3) z3 i , z3 4 7 ; arg z3 3 . 2 2 2 2 2 7 3 7 2 . tg3 : 3 ; arctg 3 ; 3 3 2 2 3 3 2 2 i sin Тригонометрическая форма: z3 7 cos . 3 3 Показательная форма: z3 2 i 7e 3 . 2 2 2 7 7 3 7 7 3 7 4) z4 i , z4 4 7 ; arg z4 4 . 2 2 2 2 2 7 3 7 2 . tg4 : 3 ; arctg 3 ; 4 3 3 3 2 2 2 2 Тригонометрическая форма: z4 7 cos i sin . 3 3 Показательная форма: z4 7e 2 i 3 .