Анализ результатов индивидуального тура по математике 14

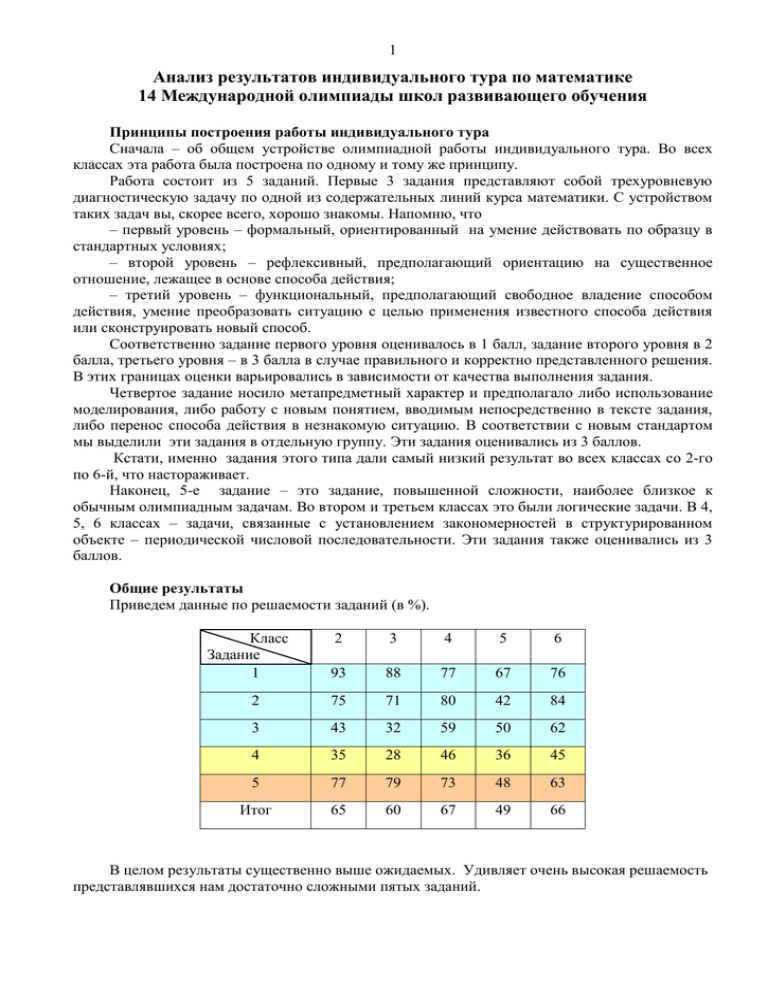
1
Анализ результатов индивидуального тура по математике
14 Международной олимпиады школ развивающего обучения
Принципы построения работы индивидуального тура
Сначала – об общем устройстве олимпиадной работы индивидуального тура. Во всех
классах эта работа была построена по одному и тому же принципу.
Работа состоит из 5 заданий. Первые 3 задания представляют собой трехуровневую
диагностическую задачу по одной из содержательных линий курса математики. С устройством
таких задач вы, скорее всего, хорошо знакомы. Напомню, что
– первый уровень – формальный, ориентированный на умение действовать по образцу в
стандартных условиях;
– второй уровень – рефлексивный, предполагающий ориентацию на существенное
отношение, лежащее в основе способа действия;
– третий уровень – функциональный, предполагающий свободное владение способом
действия, умение преобразовать ситуацию с целью применения известного способа действия
или сконструировать новый способ.
Соответственно задание первого уровня оценивалось в 1 балл, задание второго уровня в 2
балла, третьего уровня – в 3 балла в случае правильного и корректно представленного решения.
В этих границах оценки варьировались в зависимости от качества выполнения задания.
Четвертое задание носило метапредметный характер и предполагало либо использование
моделирования, либо работу с новым понятием, вводимым непосредственно в тексте задания,
либо перенос способа действия в незнакомую ситуацию. В соответствии с новым стандартом
мы выделили эти задания в отдельную группу. Эти задания оценивались из 3 баллов.
Кстати, именно задания этого типа дали самый низкий результат во всех классах со 2-го
по 6-й, что настораживает.
Наконец, 5-е задание – это задание, повышенной сложности, наиболее близкое к
обычным олимпиадным задачам. Во втором и третьем классах это были логические задачи. В 4,
5, 6 классах – задачи, связанные с установлением закономерностей в структурированном
объекте – периодической числовой последовательности. Эти задания также оценивались из 3
баллов.
Общие результаты
Приведем данные по решаемости заданий (в %).
Класс
Задание
1
2
3
4
5
6
93
88
77
67
76
2
75
71
80
42
84
3
43
32
59
50
62
4
35
28
46
36
45
5
77
79
73
48
63
Итог
65
60
67
49
66
В целом результаты существенно выше ожидаемых. Удивляет очень высокая решаемость
представлявшихся нам достаточно сложными пятых заданий.
2
У нас была возможность сопоставить результаты олимпиады с результатами ряда
мониторинговых исследований. Естественно, для этого были выбраны задания, по которым
такое сопоставление корректно. Олимпиадные результаты оказались существенно выше, иногда
в разы. Возможно, это связано с тем, что уровень участников олимпиады превосходит уровень
детей, принимавших участие в мониторинге. Но, к сожалению, есть и другая гипотеза,
связывающая данный факт с заочным характером олимпиады.
Общие замечания
Участникам предлагалось для каждого задания привести краткое описание решения и
ответ. В решении хотелось бы, прежде всего, видеть логику рассуждений, приводящих к
результату. Вместо этого в большинстве работ приводятся цепочки вычислений, из которых не
всегда можно понять, что из чего вытекает. Последовательность действий зачастую носит
случайный характер. Уделяется излишнее внимание второстепенным моментам, например,
подробно объясняется, как дроби приводятся к общему знаменателю, а о том, откуда взялись
эти дроби – ни слова. Если вводится х для обозначения неизвестного, то на каждом шаге
решения этим х-ом без всяких пояснений обозначаются совершенно разные вещи. Кстати,
удивляет и настораживает страсть к уравнениям у многих второклассников и третьеклассников.
Еще один момент – неумение видеть рациональное решение, блуждание по лабиринту
ненужных действий, когда результат может быть достигнут за один шаг. Проиллюстрирую это
на примере задания первого уровня для шестого класса. Вот это задание.
3
В начале учебного года в 6 А классе было 28 учеников,
от которых составляли
7
мальчики. В течение учебного года в этот класс пришли еще один мальчик и одна девочка.
Какую часть от всех учащихся класса составляют мальчики в конце учебного года?
3
от 28 человек, т.е. 12. В
7
13
конце года мальчиков стало 13, а всего учеников 30. Мальчики стали составлять
. Вместо
30
этого в ряде работ определяется не только количество мальчиков но и количество девочек в
начале и в конце года, количество учащихся определяется как сумма тех и других… В
результате количество шагов решения увеличивается в несколько раз. А ведь каждый
бессмысленный шаг – это не только потеря рациональности и красоты решения, это еще и
дополнительная возможность допустить ошибку.
Еще одна типичная ошибка – запись цепочки действий через знак равенства:
2 + 5 = 7 – 3 = 4  3 = 12 и т.д.
Знак равенства теряет свой смысл и используется в качестве разделителя – вроде точки с
запятой.
Решение элементарно. В начале года в классе мальчиков было
Далее, обращают на себя внимание неточные формулировки ответа, его несоответствие
поставленному вопросу. Например, вопрос в задаче формулируется так: Кто приехал раньше,
мотоциклист или велосипедист? А ответ дается в виде «велосипедист приехал позже». Мелочь?
Но мелочь, на которую тоже следует обращать внимание.
Все перечисленные недочеты носят общий характер, повторяются от задания к заданию.
Общий вывод. Необходимо уделить большее внимание представлению учащимися
результатов своей работы, логичности и последовательности описания решений, поиску
рациональных способов решения задач.
3
Разбор отдельных заданий
2 класс
Задание 1 – элементарное задание на разностное отношение.
Задание 2 – способ действия, рассмотренный в задании 1, необходимо применить дважды
(для определения массы ящика и массы ядра), а затем объединить результаты.
Задание 3 – здесь, в отличие от первых двух заданий, в разностном отношении выступает
изначально не известная величина – масса ядра. Удаляя по одному ядру с каждой чашки весов,
в первом случае находим массу пустого ящика, во втором – массу двух ядер, что позволяет
сразу найти массу четырех ядер, не вычисляя массу одного ядра. Однако таким, наиболее
рациональным способом практически никто не действовал – вычисляли сначала массу одного
ядра, затем массу четырех ядер.
Задание 4 предполагало активную работу с математической моделью – числовой прямой.
При этом необходимо понимать число не только как точку на числовой прямой, но и как длину
отрезка, выраженную в количестве единичных шагов, независимо от положения этого отрезка
на числовой прямой (именно на этом основан способ присчитывания). Важно, что концы
отрезков, представляющих числа а и b, не совпадают с целочисленными точками числовой
прямой, что требует работу именно с «отрезочной», а не «точечной» формой представления
чисел.
Типичные ошибки при выполнении этого задания:
– игнорируется указанный единичный шаг, вместо этого делается попытка использовать
стандартную единицу 1 см,
– концы отрезков «подгоняются» под целочисленные точки. Тот факт, что при этом
единичные отрезки получаются разными, игнорируется.
В результате в ряде работ получен правильный ответ при неправильном определении
чисел a и b.
Задание 5. Логическая задача, не вызвавшая затруднений у большинства учащихся.
Встречались курьезные решения: «Колина собака – Колли, потому что имена похожие».
3 класс
Задания 1 – 3 несколько усложненная версия аналогичных заданий для второго класса.
Удивляет, что в некоторых работах при решении третьего задания в качестве исходного
факта принимается, что масса ядра равна3 г, а далее подробно описываются очевидные
действия. Хотя определение массы ядра – это самое нетривиальное действие во всем решении,
требующее сопоставления рисунков 1 и 2.
Задание 4 предполагало перенос известного способа действия – построения таблицы
умножения – в новую ситуацию, применительно к недесятичной системе счисления. С этой
частью задания учащиеся справились хорошо. После этого требовалось с помощью этой
таблицы выполнить умножение многозначных чисел. К сожалению, при разработке заданий не
было учтено, что умножение многозначных чисел рассматривается не во всех программах 3-го
класса. Это учитывалось при оценке работ.
Задание 5. Логическая задача, требующая анализа ряда гипотез на непротиворечивость.
Типичный недостаток – обнаружив одну непротиворечивую гипотезу, учащиеся не
проводят дальнейшего анализа (является ли данная гипотеза единственно возможной).
В ряде работ условие «Если Коля скажет правду, то Миша тут же соврет; если Коля
соврет, то Миша скажет правду» истолковывалось как то, что Коля сначала обязательно
4
говорит правду. Такое толкование свидетельствует о недостаточном понимании текста. Это
тоже приводило к неполной проверке гипотез.
4 класс
Задания 1– 3 – на понятия площади и периметра. 1-е и 2-е задания не вызвали серьезных
затруднений. Ошибки связаны, прежде всего, с перепутыванием размерностей: площадь
измеряется в сантиметрах.
В задании 3 нужно было заметить, что фигура, площадь которой требуется найти, состоит
из частей, дополняющих круг до квадрата. Следовательно, ее площадь равна a см2. Никакие
дальнейшие действия не требуются.
Подавляющее большинство учащихся не ограничивались этим, а пытались найти
конкретные числовые значения площади (используя палетку, формулу площади круга и т.п.).
Результаты такого подсчета – от близких к реальным до абсурдных.
Задание 4 – текстовая задача, включающая целый ряд отношений между входящими в
условие величинами. Анализ этих отношений наиболее естественно проводить с помощью
графической модели (описание такой модели при ограничениях, накладываемых форматом
описания решения в ПК КОД – довольно сложная задача, но ряд учащихся с нею справился.
Достаточно было дать хотя бы ссылку на использование чертежа и привести вытекающий из
него способ дальнейших действий). Например, признавалось вполне корректным такое
описание решения: «С помощью чертежа я установил, что стоимость всей покупки в 4 раза
больше суммы, взятой из правого кармана, а 80 рублей – в 2 раза больше этой суммы. Значит,
из правого кармана взяли 80:2 =40 (руб.), а вся покупка стоит 404 =160 (руб.)». Вместо этого
типичным являлось такое решение: «3:2, 80:2 = 40, 403 = 120, 40 + 120 = 160. Ответ: 160 руб.»
Во многих работах задача решалась с помощью уравнений, причем четвероклассники
демонстрировали весьма уверенное владение формальным аппаратом их решения – переносом
слагаемых из одной части в другую, приведением подобных членов…
В ряде работ учащиеся просто произвольным образом вводили дополнительную величину
и решали задачу для такого частного случая. Естественно, никакой попытки обосновать
независимость конечного результата от значения этой величины не делалось. В некоторых
работах была ссылка на метод подбора. Причем подбор почему-то сводился к двум попыткам:
«150 – не подошло, 160 – подходит».
Задание 5. Задача на поиск и анализ закономерностей в числовой последовательности.
Необходимо выделить полное число повторяющихся фрагментов и проанализировать остаток.
Типичные ошибки и недостатки:
– игнорирование остатка,
– выполнение ряда ненужных действий: вместо того чтобы подсчитывать сразу
количество троек в последовательности, сначала подсчитывают количество единиц и двоек, что
ничуть не легче,
– решение «в лоб» – выписываются все 100 элементов последовательности. А если бы в
условии было задано не 100, а 1000 элементов?! (При рациональном подходе это практически
не осложняет решения).
Кроме того, несколько удивляет в ряде работ владение четвероклассниками такой
терминологией, как «период последовательности», «неполный период». То же самое можно
сказать о 5 и 6 классах.
5
5 класс
Задания 1 – 3 – задачи на движение.
Задание 1 – стандартная задача. Результат несколько ниже, чем можно было ожидать.
Наибольшее
число ошибок связано с преобразованием единиц: часов в минуты и,
соответственно, км/ч в км/мин.
Кроме того, как уже отмечалось, в ряде работ дается недостаточно четкий ответ на
поставленный вопрос: спрашивается, кто приедет раньше, ответ «велосипедист приедет позже».
Аналогичное замечание можно отнести и к другим заданиям.
Задание 2. Ключ к решению в том, чтобы увидеть, что криволинейный участок первой
трассы имеет ту же длину, что и вся вторая трасса. Вместо этого в ряде работ учащиеся
пытаются найти длину каждой трассы (например, с помощью нитки), и только после этого – их
разность. Вообще, это довольно распространенный стереотип – представление о том, что для
нахождения разности величин всегда необходимо знать каждую из них по отдельности.
Задание 3. Перенос задачи на встречное движение на случай криволинейного движения. В
отличие от стандартных задач, кроме того, вместо соотношения скоростей дано соотношение
времен.
Неожиданно по этому заданию получен очень высокий результат.
Задание 4 – рассчитано на работу с новым понятием.
Наиболее рациональное решение состоит в представлении x в виде дроби и последующем
ее сокращении
К замеченным недостаткам можно отнести следующее:
– уравнение приводится к виду 99!101! = 100!х98!, после чего дальнейшие
преобразования становятся гораздо менее очевидными;
– в отдельных работах, как и ожидалось, производится «сокращение» дробей на знак
факториала.
Задание 5 – полностью справедлив комментарий к аналогичному заданию для 4 класса.
6 класс
Задания 1 – 3 – текстовые задачи на дроби.
Задание 1 уже было проанализировано, задание 2 не вызвало серьезных затруднений.
В задании 3 ищутся числа из заданного промежутка, делящиеся на 8, на 12, на 24, и
выбирается удовлетворяющее всем трем условиям, хотя достаточно найти число, делящееся на
24 – оно наверняка будет делиться и на 8, и на 12.
Задание 4. Решение требует моделирования описанной ситуации. Фактически – это
сопоставление двух координатных прямых с разными направлениями, началами отсчета и
единичными шагами. Требуется произвести перевод некоторого числа (значения температуры)
из одной системы координат в другую. Основная ошибка при решении этой задачи –
игнорировалась разнонаправленность температурных шкал: положительному значению 16 по
шкале Цельсия соответствует отрицательное значение –32 по Вовиной шкале. Видимо, было
трудно преодолеть стереотип: когда тепло – температура положительная.
Задание 5. Задание на анализ периодической числовой последовательности. Справедливы
все замечания к аналогичному заданию для 4 класса.
Если у вас возникнут какие-либо вопросы, постараюсь ответить на них. Мой электронный
адрес zaslavsky@inbox.ru
С уважением, В. Заславский