Документ 605488

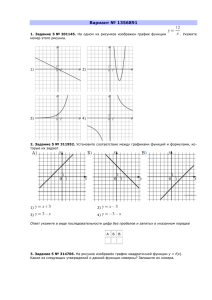
Контрольная работа № 1. Неравенства. Системы неравенств.
Вариант 1.
1. Решите неравенство 6x  1  1 . В ответе укажите его наименьшее целое решение.
Ответ. ________
7 y  35,
2. Решите систему неравенств 
18  6 y  0.
а) y  5
б) y  3
в) 3  y  5
г) решений нет
3. Укажите геометрическую модель, соответствующую решению неравенства
x 2  251  x   0 .
+
+
+
x
x
1
5
1
5
а)
б)
+
+
+
+
x
-5
1
5
-5
1
5
в)
г)
4. Решите неравенство 2 x 2  7 x  4  0 . В ответе укажите длину промежутка,
соответствующую решению неравенства.
Ответ. _________
2x  6
 0.
5. Решите неравенство
x 1
а)  1  x  3 б)  1  x  3
в)  1  x  3
г) x  3, x  1
x
6. Решите неравенство 2 x  5  3 .
а) x  4
б)  4  x  4
в) x  1
г) 1  x  4
3  x  3x  5,
7. Сколько целых чисел является решением системы неравенств  2
 x  x  12  0 ?
Ответ. _________
8. Сопоставьте заданное множество с соответствующим ему числовым промежутком:
 1

 0
1) x 3x  1  2
2)  x
3) x x 2  1
 x 1 
а)  ;  1
б)  ; 1
в)  1;  
г)  1; 1
Ответ.
1) 2) 3)


_______________________________________________________
6x  x 2
.
3x  15
10. Виктор спешил к проходящему поезду, чтобы повидаться с другом. Когда он вышел из
дома, до отправления поезда оставалось 1 ч 30 м. 8 км от дома до шоссе Виктор дошел
пешком, а затем до станции еще 8 км ехал на маршрутном такси, которое двигалось со
скоростью на 42 км/ч большей, чем он шел пешком. В результате Виктор прибыл на
станцию раньше, чем прибыл поезд. С какой скоростью мог идти Виктор пешком?
2
 x  2 x  3  0,
11. При каких значениях параметра p система неравенств 
имеет два
 x  12  x  p   0
целочисленных решения?
9. Найдите область определения выражения
Контрольная работа № 1. Неравенства. Системы неравенств.
Вариант 2.
1. Решите неравенство 2  3x  2 . В ответе укажите его наибольшее целое решение.
Ответ. _________
8 y  56  0,
2. Решите систему неравенств 
 3 y  12.
а) y  4
б) y  7
в)  7  y  4
г) y  7
3. Укажите геометрическую модель, соответствующую решению неравенства
x 2  163  x   0 .
+
+
+
x
x
3
4
3
4
а)
б)
+
+
+
+
x
-4
3
4
-4
3
4
в)
г)
4. Решите неравенство 2 x 2  9 x  4  0 . В ответе укажите длину промежутка,
соответствующую решению неравенства.
Ответ. _________
3x  6
 0.
5. Решите неравенство
x
а) x  2, x  0
б) x  0, x  2
в) x  0, x  2 г) 0  x  2
6. Решите неравенство 4 x  3  11 .
x
в)  3,5  x  2
г) x  3,5
 4  x  2 x  5,
7. Сколько целых чисел является решением системы неравенств  2
 x  x  12  0 ?
Ответ. _________
8. Сопоставьте заданное множество с соответствующим ему числовым промежутком:
 2

 0
1) x 4 x  1  3
2)  x
3) x x 2  1
 x 1 
а)  ; 1
б) 1;  
в)  ;  1  1;  
г)  1;  
Ответ.
1) 2) 3)
а) x  2
б)  2  x  2


____________________________________________________________________
x 2  8x
9. Найдите область определения выражения
.
4 x  28
10. Павел опаздывал на автобус, который отправлялся через 1 ч 20 м. 6 км от деревни до шоссе
он шел по лесной дороге, а затем еще 6 км ехал на попутной машине, скорость которой
была на 40 км/ч больше, чем его скорость пешком. В результате Павел прибыл на
автостанцию немного раньше отправления автобуса. С какой скоростью мог идти пешком
Павел?
 x 2  3x  4  0,
11. При каких значениях параметра p система неравенств 
имеет два
 x  2 2  x  p   0
целочисленных решения?
Контрольная работа № 2. Системы уравнений.
Вариант 1
 y  x  4  0,
1. Укажите пару чисел, которая является решением системы уравнений 
 y  2 x  1  0.
а) (3; 1)
б) ( 2;  3)
в) (3;  1)
г) (1; 3)
2. Найдите координаты центра окружности ( x  2) 2  ( y  1) 2  16 .
а) (2; 1)
б) ( 2;  1)
в) (1;  2)
г) (1; 2)
3. Укажите уравнение, которое задает окружность, изображенную на рисунке.
y
1
0
-1
x
а) x 2  ( y  1) 2  2
б) x 2  ( y  1) 2  4 в) x 2  ( y  1) 2  4 г) ( x  1)2  y 2  2
 x 2  y 2  9,
4. Сколько решений имеет система уравнений 
3  xy  0 ?
Ответ. _________
5. Укажите систему уравнений, которая является математической моделью ситуации,
описанной в задаче: «Диагональ прямоугольника со сторонами x и y равна 26, а его
периметр равен 68».
 x 2  y 2  676,
 x 2  y 2  676,
 x 2  y 2  676,
 x  y  26,
а) 
б) 
в) 
г) 
 xy  68
 x  y  34
 x  y  68
 xy  68
6. Каждой системе уравнений поставьте в соответствие ее решение:
 x 2  5 y 2  56,
 x  y  5,
 xy  12,
1)  2
2) 
3)  2
2
2
x  y  1
 x  y  15
 x  5 y  16
а) 4; 1
б) 6; 2
в) 4;  3,  3; 4
г) 6; 2, 6;  2,  6; 2,  6;  2
7. Найдите радиус окружности с центром в точке A( 10;  19) , касающейся оси абсцисс.
Ответ. _________
 x 2  y 2  49,
8. При каком значении параметра p система уравнений 
имеет одно решение?
2
y

x

p

Ответ. _________
____________________________________________________________________
24
9. При каких значениях переменных выражение
достигает
2
2 x  y  14  ( x  3 y  11) 2  6
своего наибольшего значения?
10. Один сплав содержит 10 % олова, а другой – 40 %. Масса первого сплава на 8 кг меньше
массы второго сплава. Из этих двух сплавов получили третий сплав, содержащий 30 %
олова. Найдите массу третьего сплава.
11. При каких значениях параметров a и b решением системы уравнений
(a  b) x  y (a  b) 2  2,
является пара чисел (3; 2)?

ay  (2 x  1)b  5
Контрольная работа № 2. Системы уравнений.
Вариант 2
 y  x  3  0,
1. Укажите пару чисел, которая является решением системы уравнений 
 y  2 x  3  0.
а) (1;  2)
б) (1;  1)
в) ( 2;  1)
г) ( 2; 1)
2. Найдите координаты центра окружности ( x  4) 2  ( y  3) 2  9 .
а) (3; 4)
б) ( 3;  4) в) (4; 3)
г) ( 4;  3)
3. Укажите уравнение, которое задает окружность, изображенную на рисунке.
y
-3
а) ( x  3) 2  y 2  16
0
1 x
б) ( x  3) 2  y 2  4 в) ( x  3) 2  y 2  16 г) x 2  ( y  3) 2  4
 x 2  y  3,
4. Сколько решений имеет система уравнений 
 x  2  y  1 ?
Ответ. _________
5. Укажите систему уравнений, которая является математической моделью ситуации,
описанной в задаче: «Диагональ прямоугольника со сторонами x и y равна 15, а его
периметр равен 42».
 x 2  y 2  225,
 x 2  y 2  225,
 x 2  y 2  225,
 x  y  15,
а) 
б) 
в) 
г) 
 xy  42
 x  y  42
 x  y  21
 xy  21
6. Каждой системе уравнений поставьте в соответствие ее решение:
 x 2  2 y 2  81,
 x  y  6,
 xy  15,
1)  2
2)
3)

 2
2
2
 x  y  8
 x  y  24
 x  y  17
а) (7; 4) б)  5;  3 ,  3;  5
в) 7; 4, 7;  4,  7; 4,  7;  4
г) 5;  1
7. Найдите радиус окружности с центром в точке A( 14;  17) , касающейся оси ординат.
Ответ. _________
 x 2  y 2  36,
8. При каком значении параметра p система уравнений 
имеет три решения?
2
y  x  p
Ответ. _________
____________________________________________________________________
48
9. При каких значениях переменных выражение 2
достигает
y  xy  12  (  x  3 y  10) 2  8
своего наибольшего значения?
10. Один сплав содержит 30 % меди, а другой – 60 %. Масса первого сплава на 12 кг меньше
массы второго сплава. Из этих двух сплавов получили третий сплав, содержащий 45 %
меди. Найдите массу третьего сплава.
11. При каких значениях параметров a и b решением системы уравнений
2 x(a  b) 2  (2 y  1)( a  b)  15,
является пара чисел (2; 3)?

(2 y  1)a  bx  1
Контрольная работа № 3. Числовые функции
Вариант 1
1. На рисунке изображен график функции y  f (x ) . Найдите:
y
0
-3
7
-1
x
1) D ( f ) 2) E ( f )
3) промежуток убывания функции
а)  1; 4
б)  2; 0
в)  1; 1
г)  3; 7
Ответ.
1) 2) 3)
2. Укажите рисунок, на котором задан график некоторой функции y  f (x ) .
y
y
0
x
0
а)
x
б)
y
y
0
0
x
в)
г)
3. Найдите область определения функции y  x  4 x  3 .
а) x  4
б) x  3
в) x  3, x  4
г)  3  x  4
4. Найдите наименьшее значение функции y  x 2  18 x  3 .
Ответ. _________
5. Укажите функцию, которая является ограниченной снизу:
а) y  2 x  4
б) y  4  x 2
в) y  x  1
г) y 
2
1
x
x
6. Функция задана формулой y  2 x 2
Укажите высказывание, которое НЕ является верным для данной функции:
а) D( f )  ( ; 0)  (0;  ) ;
б) E ( f )  (0;  ) ;
в) функция четная;
г) функция возрастает на всей области определения.
7. На рисунке изображена часть графика нечетной функции.
y
0
x
f ( 2)  f ( 1)
.
f (0)
Ответ. _________
8. Решите графически уравнение ( x  1) 3  3  x .
Ответ. _________
____________________________________________________________________
1
 ab

3

ab

3 b.
9. Преобразуйте выражение  3


3
3
3
 a b
 a b
4
10. Дана функция y  f (x ) , где f ( x )  x  1 . Найдите, при каких значениях x выполняется
Найдите
равенство f 2 ( x )  83 f ( x )  82  0 .
11. Исследуйте функцию y  3 x  1 на четность и постройте ее график.
Контрольная работа № 3. Числовые функции
Вариант 2
1. На рисунке изображен график функции y  f (x ) . Найдите:
y
-4
0
6
x
-5
1) D ( f ) 2) E ( f )
3) промежуток возрастания функции
а)  3;  1
б)  4; 6
в)  2; 0
г)  4;1
Ответ.
1) 2) 3)
2. Укажите рисунок, на котором задан график некоторой функции y  f (x ) .
y
0
y
2
x
а)
0
2 x
б)
y
0
y
2
x
0
2 x
в)
г)
3. Найдите область определения функции y  ( x  4)( x  3) .
а) x  4
б) x  3
в) x  3, x  4
г)  3  x  4
4. Найдите наибольшее значение функции y   x 2  16 x  5 .
Ответ. _________
5. Укажите функцию, которая является ограниченной сверху:
а) y  3x  5
б) y  7  x 2
в) y  x  1
г) y  x  3
6. Функция задана формулой y  x 4  3 . Укажите высказывание, которое НЕ является верным
для данной функции:
а) D( f )  0;   ;
б) функция четная;
в) наименьшее значение функции равно  3 ;
г) функция выпукла вниз.
7. На рисунке изображена часть графика четной функции.
y
0
x
f ( 3)  f ( 4)
.
f (0)
Ответ. _________
8. Решите графически уравнение 3 x  2  4  x .
Ответ. _________
____________________________________________________________________
1
 ab

 3 ab   3
3 a .
9. Преобразуйте выражение  3
3
3
a

b
a

b


4
10. Дана функция y  f (x ) , где f ( x )  x  3 . Найдите, при каких значениях x выполняется
Найдите
равенство f 2 ( x)  11 f ( x )  26  0 .
11. Исследуйте функцию y 
0,5 x 5
x2
на четность и постройте ее график.
Контрольная работа № 4. Прогрессии
Вариант 1
1. Последовательность задана формулой x n  n 3  3 . Найдите четвертый член
последовательности.
Ответ. ________
2. Укажите последовательность, которая является арифметической прогрессией.
1 1
а) 1; 4; 9; …
б) 2; 5; 8; … в) 2; 4; 8; … г) 1; ; ; ...
2 3
3. Арифметическая прогрессия задана формулой a n  3n  10 . Укажите число, которое НЕ
является членом прогрессии.
а) 7
б)  5
в) 13
г) 4
4. Дана арифметическая прогрессия a n  . Вычислите a 7 , если a1  3, d  4 .
Ответ. ________
5. Дана арифметическая прогрессия a n  , где a 3  5, a 7  11 . Найдите:
1) a 1
2) d
а) 45,5 б) 8 в) 1,5 г) 2
Ответ.
1) 2) 3)
3) S n , если n  7
д) 10,5
6. Какая из приведенных ниже последовательностей является геометрической прогрессией?
2
2
а) y n   2 n б) y n  n 2
в) y n  2n  4
г) y n 
3
n
1 1
7. Дана геометрическая прогрессия bn  : ; ; ... . Найдите:
8 4
1) q
2) b7
3) S 7
а) 0,5 б) 8 в) 15,75
г) 2 д) 16
Ответ.
1) 2) 3)
8. Между числами 180 и 80 вставьте положительное число так, чтобы получились три члена
геометрической прогрессии.
Ответ. ________
____________________________________________________________________
9. Дана геометрическая прогрессия bn  . Известно, что число B  bn  . Найдите номер числа B,
2
если bn   3 2 n  3 , B  162 .
3
10. Вкладчик положил в банк на 3 года 30000 р под 9 % годовых. Какую сумму получит
вкладчик по истечении срока вклада, если снимать деньги и пополнять счет он не будет?
11. Найдите сумму пяти членов арифметической прогрессии, если сумма второго и восьмого
членов прогрессии равна 19, а произведение седьмого и третьего – равно 48.
Вариант 2
1. Последовательность задана формулой x n  n 2  2 . Найдите девятый член
последовательности.
Ответ. ________
2. Укажите последовательность, которая является арифметической прогрессией.
1 1
а) 16; 8; 0; …
б) 1; 3; 4; 7; …
в) 16; 8; 4; … г) 1; ; ; ...
4 9
3. Арифметическая прогрессия задана формулой a n  0,5n  7,5 . Укажите число, которое НЕ
является членом прогрессии.
а)  7,5
б)  6,5
в)  5,5
г)  4,5
4. Дана арифметическая прогрессия a n  . Вычислите a 6 , если a1  2, d  5 .
Ответ. ________
5. Дана арифметическая прогрессия a n  , где a 4  10, a 8  2 . Найдите:
1) a 1
2) d
3) S n , если n  8
а) 6
б) 72
в) 16
г)  2
Ответ.
1) 2) 3)
д) 104
6. Какая из приведенных ниже последовательностей является геометрической прогрессией?
3
3
а) y n  3n 3
б) y n  3n  1 в) y n   3 n
г) y n 
4
4n
1
1
7. Дана геометрическая прогрессия bn  : ;  ; ... . Найдите:
9
3
1) q
2) b6
3) S 6
2
1
а)  27
б)  3
в)  20
г)  д) 81
9
3
Ответ.
1) 2) 3)
8. Между числами 50 и 450 вставьте отрицательное число так, чтобы получились три члена
геометрической прогрессии.
Ответ. ________
____________________________________________________________________
9. Дана геометрическая прогрессия bn  . Известно, что число B  bn  . Найдите номер числа B,
3
если bn    2 3n 5 , B  768 .
4
10. Вкладчик положил в банк на 3 года 40000 р под 5 % годовых. Какую сумму получит
вкладчик по истечении срока вклада, если снимать деньги и пополнять счет он не будет?
11. Найдите сумму пяти членов арифметической прогрессии, если сумма третьего и седьмого
членов прогрессии равна 13, а произведение четвертого и шестого – равно 42.
Итоговая контрольная работа.
Вариант 1
1. Соотнесите графическое задание функции с его аналитической записью.
y
y
-2
1
0
0
x
y
2
0
8
x
-8
-8
1)
2)
а) y  x
Ответ.
3
б) y  x
3
3)
в) y  x
3
г) y   x
3
1) 2) 3)
2.
3.
4.
5.
6.
7.
Даны три множества A, B и C такие, что A  2; 4; 6; ... 60, B  3; 6; 9; ... 60,
C  6; 12; 18; ... 60. Укажите высказывание, верное для данных множеств.
а) C  A  B б) C  A  B в) A  C
г) B  C
4
Функция задана формулой y  5  x . Найдите наибольшее значение функции на отрезке
1
 3
  2 ;  2  .
Ответ. ________
2x  4
Сколько целых чисел содержит область определения функции y 
?
3 x
Ответ. ________
4 x 2  4 xy  y 2  36,
Решите систему уравнений 
 x  y  3.
а) (3; 0) б) (-1; 4)
в) (0; 3), (4; -1)
г) (3; 0), (-1; 4)
Найдите длину хорды, концы которой являются точками пересечения окружности
( x  2) 2  ( y  1) 2  25 и прямой y  2 .
Ответ. ________
Арифметическая прогрессия задана формулой a n  5n  11 . Начиная, с какого номера,
выполняется условие a n  172 ?
Ответ. ________
8. Дан график распределения среднемесячной температуры воздуха в 1956 году. Укажите:
1) размах
2) моду
3) медиану
а)
б)
в)
г)
Ответ.
x
1) 2) 3)
____________________________________________________________________
9. Найдите знаменатель геометрической прогрессии bn  , если b5  7, b8  448 .
10. Первый и второй насосы заполняют бассейн за 3 ч, второй и третий – за 6 ч, а первый и
третий – за 4 ч. За какое время наполнят бассейн все три насоса, работая одновременно?
2 x, если x  2,

11. Дана функция y  f (x ) , где f ( x )  4, если 2  x  4,
2 x  4, если x  4.

Найдите, при каких значениях k уравнение f ( x )  kx имеет три корня.
Итоговая контрольная работа.
Вариант 2
1. Соотнесите графическое задание функции с его аналитической записью.
y
16
y
y
0
x
1
0
1)
а) y   x
Ответ.
1 2
x
б) y  x
0
4
2)
в) y   3 x
x
3)
г) y  x 2
1) 2) 3)
Даны три множества A, B и C такие, что A  2; 4; 6; ... 60, B  10; 20; ... 60,
C  5; 10; 15; ... 60. Укажите высказывание, верное для данных множеств.
а) B  A  C б) A  B
в) B  C
г) A  B  C
3
3. Функция задана формулой y  ( x  2) . Найдите наименьшее значение функции на отрезке
1 3
 2 ; 2  .
Ответ. ________
5 x
4. Сколько целых чисел содержит область определения функции y 
?
3x  6
Ответ. ________
2.
 x 2  6 xy  9 y 2  25,
5. Решите систему уравнений 
 x  y  3.
а) (-1; 2) б) (2; -1)
в) (-1; 2), (-3,5; -0,5) г) (-2; 1), (0,5; 3,5)
6. Найдите длину хорды, концы которой являются точками пересечения окружности
( x  1) 2  ( y  2) 2  25 и прямой x  2 .
Ответ. ________
7. Арифметическая прогрессия задана формулой a n  4n  15 . Начиная, с какого номера,
выполняется условие a n  240 ?
Ответ. ________
8. Дан график распределения среднемесячной температуры воздуха в 1956 году. Укажите:
1) размах
2) моду
3) медиану
а)
б)
в)
г)
Ответ.
1) 2) 3)
____________________________________________________________________
9. Найдите знаменатель геометрической прогрессии bn  , если b5  7, b8  448 .
10. Первый и второй насосы заполняют бассейн за 9 ч, второй и третий – за 15 ч, а первый и
третий – за 10 ч. За какое время наполнят бассейн все три насоса, работая одновременно?
2 x, если x  1,

11. Дана функция y  f (x ) , где f ( x )  2, если 1  x  4, .
2 x  6, если x  4.

Найдите, при каких значениях k уравнение f ( x )  kx имеет три корня.
ПРИЛОЖЕНИЕ