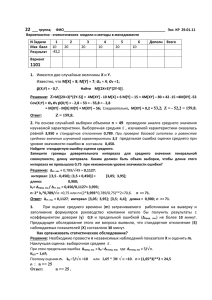
Методичка по статистике!

Печатается
по
решению
редакционно-издательского
совета
Нижегородского
института развития образования
Статистические методы в психологических исследованиях: учебное пособие
/С.А.Гапонова, А.В.Поршнев. – Н.Новгород:
2010. – 93 с.
Учебное пособие представляет собой практическое руководство для психологов,
студентов
психологических
факультетов,
магистров
и
аспирантов
психологических
специальностей, поставивших цель статистически обосновать свои научные и практические
выводы. Принцип отбора методов, представленных в рекомендациях – ясность и простота.
Все они могут быть использованы для быстрой и качественной обработки количественных и
качественных данных, полученных в исследовании.
Методы рассматриваются на реальных примерах и сопровождаются алгоритмами
расчета статистических критериев.
Настоящее учебное пособие является вторым, исправленным и дополненным
изданием. Первое издание вышло в 2006 году в Нижегородском гуманитарном центре под
названием «Методы статистической обработки в психологических исследованиях».
Составители: Гапонова С.А., докт. психол. наук, профессор, зав. кафедрой
социальной психологии НГПУ.
Поршнев А.В., канд. психол. наук, доцент кафедры социально-гуманитарных наук
НФ ГУ-ВШЭ.
Рецензенты:
Сорокина Т.М.., доктор психол. наук, профессор, зав.каф. социальной педагогики,
психологии и предметных методик начального образования
Шляхтин Г.С.,
канд. психол. наук, доцент, зав. каф. общей и социальной психологии
ННГУ
Ответственный за выпуск:
СОДЕРЖАНИЕ
ВВЕДЕНИЕ .................................................................................................................. 5
Некоторые основные понятия ................................................................................ 7
Условные обозначения ............................................................................................ 9
ПРИМЕНЕНИЕ НЕПАРАМЕТРИЧЕСКИХ КРИТЕРИЕВ СТАТИСТИКИ В
ПСИХОЛОГИЧЕСКИХ ИССЛЕДОВАНИЯХ....................................................... 10
1. Случай связанных выборок. Критерий знаков «G». ...................................... 10
2. Случай независимых измерений. Критерий Вилкоксона – Манна–
Уитни «U».............................................................................................................. 16
3. Метод ранговой корреляции. Коэффициент корреляции
рангов Спирмена «ρ» ............................................................................................. 21
4. Оценка связи между качественными признаками. Метод χ² ("хи-квадрат")29
5. Сравнение двух выборок по качественно и количественно определенному
признаку. Критерий Фишера - «φ» ...................................................................... 34
ПРИМЕНЕНИЕ ПАРАМЕТРИЧЕСКИХ КРИТЕРИЕВ СТАТИСТИКИ В
ПСИХОЛОГИЧЕСКИХ ИССЛЕДОВАНИЯХ....................................................... 39
1. Проверка нормальности распределения эмпирических данных .................. 40
1.1 Двойной составной критерий ...................................................................... 40
1.2 Критерий χ² (модификация Фишера) ......................................................... 46
2. Меры связи ......................................................................................................... 54
2.1 Коэффициент корреляции Пирсона «r» ..................................................... 54
3. Оценка различий между сравниваемыми группами наблюдений ................ 60
3.1 F критерий Фишера ...................................................................................... 60
3.2 t-критерий Стьюдента .................................................................................. 62
3.3 t-критерий Стьюдента для связанных выборок ........................................ 63
3.4 t-критерий Стьюдента для несвязанных выборок .................................... 65
3.5 Применение t-критерия Стьюдента для определения значимости
различий в вероятностях появления событий ................................................. 66
ЛИТЕРАТУРА ........................................................................................................... 69
ПРИЛОЖЕНИЕ ......................................................................................................... 70
3
Таблица I. Критические значения критерия знаков G для уровней
статистической значимости р<0,05 и р<0,01 (по Оуэну Д., 1966) .................... 70
Таблица II. Критические значения критерия U Манна-Уитни для уровней
статистической значимости р<0,05 и р<0,01 (по Гублеру Е.В., Генкину А.А.
1973) ........................................................................................................................ 71
Таблица III. ............................................................................................................. 75
Таблице IV. Квантили χ²-распределения для уровней значимости p<0,05 и
p<0,01 (по Суходольскому Г.В., 1998) ................................................................ 76
Таблица V. Диапазоны двойного составного критерия (по К.Д.Зароченцеву и
А.И.Худякову 2005) ............................................................................................... 77
Таблица VI. Значения двойного составного критерия (по К.Д.Зароченцеву и
А.И.Худякову 2005) ............................................................................................... 77
Таблица VII. Таблица интегральной функции нормального распределения (по
Суходольскому Г.В., 1998) ................................................................................... 78
Таблица VIII. Нормальная корреляция (по Гублеру Е.В., Генкину А.А. 1973)79
Таблица IХ. F-распределение для уровня значимости р<0,05 и р<0,01 (по
Суходольскому Г.В., 1998) ................................................................................... 80
Таблица Х. Квантили t-распределения Стьюдента для уровней значимости
p<0,05, p<0,01 и p<0,001 (по Суходольскому Г.В., 1998) ................................. 84
Таблица XI Величины угла (в радианах) для разных процентных долей (по
Ермолаеву ) ............................................................................................................. 85
Таблица XII Уровни статистической значимости разных значений критерия
φ Фишера ................................................................................................................ 89
4
ВВЕДЕНИЕ
Главным ориентиром в деятельности высших учебных заведений,
готовящих психологов, работающих в различных сферах профессиональной
деятельности, на современном этапе является принятие в качестве важнейшей
цели обучения и воспитания установки на развитие творческого потенциала
студента и создания для этой цели благоприятных условий. Социальные и
профессиональные функции психологов расширяются и усложняются и, кроме
знания предмета, он должен быть для своих учеников носителем культурного
содержания. О необходимости формирования у студентов самостоятельной
творческой деятельности говорится и в Законе «О высшем и послевузовском
образовании», одной из задач которого является «развитие наук посредством
научных исследование и творческой деятельности научно-педагогических
работников и обучающихся, использование полученных результатов в
образовательном
процессе».
И
овладение
навыками
исследовательской
деятельности является не только требованием времени, но и важнейшим
атрибутом цивилизованного отношения к будущей профессии.
Самостоятельная
научно-исследовательская
работа
студентов
необходима для более полного, глубокого и осознанного усвоения учебного
материала,
приобретения
навыков
исследовательской
работы
и
опыта
творческой деятельности. Традиционными формами такой работы в вузе
следует отнести подготовку курсовых, квалификационных и дипломных
проектов, в которую с каждым годом включается всё больше студентов.
Написание научной работы – сложный вид учебной деятельности
студента, к которой он должен быть соответственно подготовлен: уметь
работать со специальной литературой, писать рефераты, проводить научное
исследование,
с
применением
исследовательских
методов
и
уметь
анализировать результаты, то есть обнаруживать определенные закономерности
5
и
правильно
их
интерпретировать.
Для
этого
необходимо
научиться
планировать исследование и критично оценивать полученные данные с точки
зрения их достоверности - статистической значимости.
Термин «статистика» часто ассоциируется со словом «математика», что
пугает студентов-гуманитариев, связывающих это понятие со сложными
формулами и вычислениями. В то же время, по меткому выражению МакКоннелла, «статистика – это, прежде всего, способ мышления и для её
применения нужно лишь иметь немного здравого смысла и знать основы
математики». Такие виды деятельности, как планирование семейного бюджета,
расчет времени, необходимого для проведения какого-то мероприятия, анализ
влияния того или иного события на наше будущее, заставляют нас постоянно
отбирать, классифицировать и систематизировать информацию, связывать
вновь поступившую информацию с уже имеющейся для того, чтобы сделать
выводы и принять верное решение.
Те же мыслительные операции лежат и в основе научного исследования:
анализ и синтез данных, полученных в эксперименте на различных объектах и
группах объектов, их систематизация и сравнение, с целью выявления сходства
или
различия
подтверждающих
между
или
ними
и,
наконец,
опровергающих
формулировка
гипотезы
выводов,
исследования.
Цель
статистической обработки данных как раз и заключается в том, чтобы иметь
солидную основу для интерпретации полученных в исследовании результатов.
Результаты, или данные в статистике - это основные элементы,
подлежащие анализу. Данные могут быть трех типов:
1. Количественные данные, получаемые при измерениях (например,
данные о времени, результатах тестирования, объеме памяти, внимания и т.д.);
6
2. Порядковые данные, соответствующие
местам (рангам)
этих
признаков в последовательности, полученной при их расположении в
возрастающем порядке (например, иерархии мотивов или ценностей в методике
Р.Рокича, последовательность предпочтение в выборе каких-то качеств и т.д.);
3. Качественные данные, представляющие собой какие-то свойства,
которые нельзя измерить и их оценкой служит частота встречаемости (больше
нормы – меньше нормы, есть изменения – нет изменений, хуже – лучше и т.д.).
Для статистической обработки количественных данных используются,
так называемые, параметрические методы, основанные на таких показателях,
как средняя арифметическая, стандартное отклонение, ошибка средней и т.д.
Например, для определения достоверности различий средних арифметических
двух выборок применяют метод Стьюдента (t – критерий).
Если же мы имеем дело с качественными или порядковыми данными или
выборки слишком малы более эффективны непараметрические методы
обработки результатов исследования: критерий знаков, критерий Вилкоксона –
Манна – Уитни, ранговая корреляция Спирмена для порядковых данных и т.д.
Некоторые основные понятия
Признаки и переменные – это измеряемые психологические явления:
время решения задач, количество допущенных ошибок, уровень тревожности,
показатель интеллекта, социометрический статус и т.п. Понятия признака и
7
переменной могут использоваться как взаимозаменяемые, иногда вместо них
используются понятия «показатель» или «уровень».
Популяция – в статистике совокупность всех элементов реальной или
теоретической группы лиц, предметов и т.п.
Выборка
–
группа
испытуемых,
представляющая
определенную
популяцию, отобранная для экспериментального исследования (студенческая
или
ученическая
группа,
сообщество
подростков,
профессиональное
объединение и др.):
1. Зависимые измерения – результаты исследования одних и тех же
испытуемых;
2. Независимые измерения – результаты исследования различных
испытуемых.
Гипотеза – предположение, которое выдвигается как временное на
основе имеющихся наблюдений и уточняемое в последующем эксперименте.
Статистическая гипотеза – гипотеза, которая может быть проверена
методами статистики. При рассмотрении статистических гипотез выделяются
два вида:
1. Нулевая гипотеза – это гипотеза о случайности различий или сходства
(Но);
2. Конкурирующая гипотеза (Н1) – это гипотеза о значимости различий
или сходства. то, что мы хотим доказать в своем исследовании, поэтому иногда
её называют экспериментальной гипотезой..
Статистический
критерий
–
статистический
показатель,
позволяющий принять или опровергнуть ту или иную гипотезу в зависимости
от вероятности того, что различия обусловлены чистой случайностью.
Уровень статистической значимости – это вероятность того, что мы
сочли различия существенными.
8
Когда мы указываем, что различия достоверны в 95% случаев (или на 5%
уровне значимости, или при p < 0,05), то мы имеем в виду, что вероятность
того, что они все-таки недостоверны (или вероятность ошибки), составляет 5%.
Когда мы указываем, что различия достоверны в 99% случаев (или на 1%
уровне значимости, или при p < 0,01), то мы имеем в виду, что вероятность того,
что они все-таки недостоверны (или вероятность ошибки), составляет 1%.
Условные обозначения
n  число наблюдений (измерений )
N  общее число наблюдений в двух и более выборках
r  нормальный коэффициент корреляции ( Пирсона )
  ранговый коэффициент корреляции (Спирмена )
G  критерий знаков
F  критерий Фишера
t  критерий Стьюдента
 2  критерий " хи квадрат "
U  критерий Вилкоксона  Манна  Уитни
х , M , Мх, Му  среднее значение (по выборке )
SD  стандартное отклонение (по выборке )
D  дисперсия (по выборке )
df  размерность системы
d  разность рангов
х  середина интервала
Ф  интегральная функция функции нормального распределения
p  уровень статистической значимости , то же, что и 
  выроятность ошибки 1 рода (отклонения H 0 в время когда она верна )
v  число измерений попавших в один класс, интервал
P  верояность того, что событие произойдет
i, k  индексы
с  количество групп, классов, интервалов
9
ПРИМЕНЕНИЕ НЕПАРАМЕТРИЧЕСКИХ КРИТЕРИЕВ
СТАТИСТИКИ В ПСИХОЛОГИЧЕСКИХ ИССЛЕДОВАНИЯХ
В последнее время непараметрические методы оценки различий двух
групп
наблюдений,
оценки
связи
(корреляции)
между
двумя
рядами
наблюдений и отнесения наблюдений к одному из двух классов получили
широкое распространение в статистике.
Непараметрические
статистические
критерии
значительно
менее
трудоемки, чем параметрические. Нами рассматриваются 5 различных
критериев в типичных случаях их применения. Это позволит при наиболее
частых вариантах обработки экспериментальных данных выбрать наиболее
подходящий критерий для проверки достоверности вывода о различиях между
сравниваемыми группами наблюдений.
1. Случай связанных выборок. Критерий знаков «G».
При сравнении двух связанных (парных) измерений очень удобен
критерий знаков [1, 2, 3]. Напомним, что связанными называют такие
измерения, которые соответствуют одному и тому же параметру одного и того
же испытуемого. Иногда это – измеряемая величина у испытуемых контрольной
группы; иногда это связь, обусловленная временем: контрольный эксперимент
проводит, в то же время, когда и основной и т.д.
Критерий знаков основан на подсчете числа однонаправленных сдвигов
в парных сравнениях и при большом числе пар достаточно эффективен, хотя
учитывает не степень различий в каждой паре, а лишь их направленность –
знак. Он позволяет установить, изменяются ли показатели в сторону улучшения,
повышения, усиления или, наоборот, в в сторону ухудшения, понижения,
ослабления.
10
Таблица I приложения позволяет применять критерий знаков при
численности сравниваемых выборок до 300.
Пример. 12 участников комплексной программы тренинга партнерского общения,
продолжавшегося 7 дней, дважды оценивали у себя уровень владения тремя важнейшими
коммуникативными навыками. Первое измерение проводилось в первый день тренинга,
второе – в последний. Все изменения оценивались по 10-балльной шкале. Данные
представлены в таблице 1.
Вопрос: Ощущаются ли участниками достоверные сдвиги в уровне владения каждым
из трех навыков после тренинга?
Таблица 1
Изменение психологических показателей в начале и конце тренинга
Показатели
1 измерение
2 измерение
Активное
Снижение
Аргумента-
Активное
Снижение
Аргумента-
слушание
эмоциональ-
ция
слушание
эмоциональ-
ция
ФИО
ного напря-
ного напря-
жения
жения
1. И.В.Л.
6
5
5
7
6
7
2. Я.Е.А.
3
1
4
5
4
5
3. К.С.И.
4
4
5
8
7
6
4. Р.М.Н.
4
4
5
6
5
5
5. Н.М.Т.
6
4
4
4
5
5
6. Е.Л.П.
6
5
3
8
7
6
7. Л.К.С.
3
5
2
7
8
5
8. Т.А.П.
6
5
3
5
8
5
9. Б.В.В.
6
5
5
7
6
5
10.С.М.А.
5
6
5
7
7
6
11.В.П.Р.
6
6
3
5
4
3
12.Ч.Н.Г.
6
3
4
7
6
5
11
Преобразуя таблицу 1, составим таблицу сдвигов, для чего из значения,
полученного во 2-м замере, вычтем значение, полученное данным испытуемым
по соответствующей шкале в 1-м замере (табл. 2).
Из таблицы 2 мы видим, что положительных сдвигов по всем шкалам
больше.
Таблица 2
Сдвиги в значениях психологических показателей в начале и конце тренинга
Сдвиги
ФИО
Активное
Слушание
1. И.В.Л.
1
Снижение
эмоционального
напряжения
1
2. Я.Е.А.
2
3
1
3. К.С.И.
4
3
1
4. Р.М.Н.
2
1
0
5. Н.М.Т.
-2
1
1
6. Е.Л.П.
2
2
3
7. Л.К.С.
4
3
3
8. Т.А.П.
-1
2
2
9. Б.В.В.
1
1
0
10.С.М.А.
2
1
1
11.В.П.Р.
-1
-2
0
12.Ч.Н.Г.
1
3
1
Количество
нетипичных
сдвигов (Gэмп)
Всего
сдвигов
3
1
0
12
12
9
Аргументация
2
Сформулируем гипотезы:
Но – преобладание типичного (положительного) сдвига в самооценках
уровня владения коммуникативными навыками является случайным;
12
Н1 - преобладание типичного (положительного) сдвига в самооценках
уровня владения коммуникативными навыками не является случайным.
Проверим гипотезы, определив критические значения критерия знаков
(Gкр.) по таблице I приложения.
1) Для шкалы «Активное слушание», n = 12:
2 (p < 0,05)
Gкр. =
1 (p < 0,01)
Gэмп. = 3, следовательно, Gэмп. > Gкр.
Ответ: Но принимается. Преобладание положительного сдвига по
уровню
владения
навыком
активного
слушания
является
случайным,
достоверного улучшения показателей не отмечается.
2) Для шкалы «Снижение эмоционального напряжения», n = 12:
2 (p < 0,05)
Gкр. =
1 (p < 0,01)
Gэмп. = 1, следовательно, Gэмп. < Gкр.
Ответ: Но отвергается. Принимается Н1. Преобладание положительного
сдвига по уровню владения навыком снижения эмоционального напряжения не
13
является случайным. Отмечается достоверные положительные сдвиги по
данному показателю.
3) Для шкалы «Аргументация», n = 9.
1 (p < 0,05)
Gкр. =
0 (p < 0,01)
Gэмп. = 0, следовательно, Gэмп. < Gкр.
Ответ: Но отвергается. Принимается Н1. Преобладание положительного
сдвига по уровню владения навыком аргументации не являются случайным.
Отмечаются достоверные положительные сдвиги по данному показателю.
14
АЛГОРИТМ РАСЧЕТА КРИТЕРИЯ ЗНАКОВ «G»
1. Составить таблицу сдвигов
2. Подсчитать количество нулевых реакций и исключить их из
рассмотрения.
В результате n уменьшится на количество нулевых реакций.
3. Определить преобладающее направление изменений. Считать
сдвиги в преобладающем направлении «типичными».
4.Определить количество «нетипичных» сдвигов. Считать это
число эмпирическим значением G (Gэмп.).
5. По таблице Приложения 1 определить критические значения
G (Gкр.) для данного n.
6. Сопоставить Gэмп. с Gкр. Если Gэмп. меньше Gкр. или по
крайней мере равен ему (Gэмп. < Gкр.), то сдвиг в типичную сторону
может считаться достоверным.
15
2. Случай независимых измерений.
Критерий Вилкоксона – Манна– Уитни «U»
Критерий U применяют при независимых измерениях [1]. Он особенно
удобен, когда число наблюдений невелико. Таблица 2 приложения позволяет
применять критерий U при числе наблюдений – до 60.
Пример. Пусть в контрольной группе и в группе после формирующего
эксперимента обнаружены следующие показатели какого-то психологического параметра:
в контрольной группе (7 испытуемых) – 39, 38, 44, 6, 25, 25, 30;
в экспериментальной группе (9 испытуемых) – 46, 8, 68, 45, 41, 41, 30, 100.
Вопрос:
Имеются
ли
различия
по
этому
параметру
в
контрольной
и
экспериментальной группах?
Сформулируем гипотезы:
Но – после формирующего эксперимента в экспериментальной группе не
произошло изменений исследуемого параметра;
Н1 – в результате проведения формирующего эксперимента в
экспериментальной
группе
произошли
достоверные
сдвиги
в
уровне
исследуемого психологического параметра
Необходимо упорядочить (расположить в порядке возрастания) первый
и второй ряды в виде одного, так называемого общего упорядоченного ряда
(табл.
). Для того, чтобы можно было различить
числа, относящиеся к
основной и контрольной сериям, контрольные опыты располагаются левее, а
основные – правее некоторой вертикальной черты (если общий упорядоченный
ряд расположен вертикально).
16
Таблица 3
Изменение психологических показателей в контрольной и экспериментальной
группах
Исследуемый показатель
Х
У
(контрольная группа)
(экспериментальная
Число инверсий
группа)
6
0
8
25
1
25
1
30
1
30
32
38
3
39
3
41
41
44
5
45
46
68
100
Всего
14
В первом и втором рядах примера есть пара неразличающихся
наблюдений (30 и 30). Их может быть и больше. Вопрос о порядке их
расположения в упорядоченном ряду можно решить с помощью следующего
приема. Если неразличающихся чисел всего два, их расположение в общем
упорядоченном ряду должно быть случайным. Поэтому, какое из них
располагать раньше, можно определить подбрасыванием монеты. Если есть два
17
других неразличающихся числа в левой и правой части упорядоченного ряда, их
надо расположить в обратном порядке. Если неразличающихся чисел 3, их
располагают так:
30
30
или
30
30
30
30
Если четыре:
30
30
30
или
30
30
30
30
30
И так далее. Принцип расположения заключается в том, чтобы по возможности
не давать приоритета ни левой, ни правой половинам общего упорядоченного
ряда. Одинаковые числа левого и правого рядов должны быть, как можно более
равномерно перемешаны.
Иногда рекомендуют исключать пары неразличающихся наблюдений,
соответственно уменьшая число членов выборок. Однако это может привести к
искажениям: к завышению существенности различий. Все сказанное не
относится к одинаковым наблюдениям в пределах одного ряда. Порядок их
расположения естественно не имеет значения.
В таблице 3 результаты расположены в порядке их возрастания, причем
на каждой строке помещен только один результат, полученный либо в контроле,
либо в опыте. Для критерия U существенны не сами значения результатов
наблюдения, а порядок их расположения. Обозначим результаты первой группы
наблюдений через Х, а второй группы – через У. Тогда наш упорядоченный ряд
18
можно изобразить так: ХУХХХУУХХУУХУУУУ. Будем считать идеальным
такое расположения чисел, когда после упорядочения располагаются сначала
все числа первого ряда (в таблице 3 - первого столбца), а потом второго:
ХХХХХХХУУУУУУУУУ.
Дальнейший анализ заключается в подсчете нарушений расположения
чисел по сравнению с их идеальным расположением. Одним нарушением инверсией – считают такое расположение, когда перед некоторым числом
первого столбца стоят два числа второго столбца, это считают за две инверсии и
т.д. Число инверсий обозначают через U.
Подсчитаем число инверсий в нашем примере. Числа 25, 25 и 30 первого
столбца имеют перед собой по одному числу второго столбца – 8, то есть
имеют по одной инверсии. Числа 38 и 39 первого столбца имеют перед собой по
3 числа второго столбца – 8, 30 и 32, то есть имеют по 3 инверсии. Последнее
число первого столбца 44 имеет перед собой 5 чисел второго столбца. Общее
число инверсий, таким образом, составляет:
Uэмп. = 1 + 1 + 1 + 3 + 3 + 5 = 14
Примечание. В любом общем упорядоченном ряду инверсии можно
подсчитывать двумя способами – относительно группы Х и относительно
группы У. Следует выбрать тот способ, который дает наименьшую сумму
инверсий.
Обращаемся к таблице II приложения, где для числа наблюдений (у нас –
число испытуемых) 7 и 9 находим максимальное значение Uэмп., при котором
можно делать вывод о существенном различии выборок – Uкр.
19
15 (р < 0,05)
Uкр. =
9 (р < 0, 01)
Uэмп. < Uкр. (р < 0,05).
Следовательно, при 14 инверсиях в этом случае можно утверждать, что
различия между двумя взятыми рядами чисел существенны.
Ответ: Но не принимается. В результате формирующего эксперимента
произошли достоверные изменения в уровне исследуемого психологического
параметра.
Критерий U в некоторых случаях целесообразно применять при
связанных выборках, рассматривая их при этом как независимые. Дело в том,
что связи между парами «опыт – контроль» могут оказаться слабыми, а
различия между ними – сильными. Тогда, рассматривая выборки как
независимые, мы можем обнаружить различия, не выявляемые критериями для
связанных выборок. Это особенно важно для очень малых выборок, так как
критерий знаков можно применять при выборках, включающих не менее 5 пар
наблюдений, а критерий U применим уже при 3 парах.
20
АЛГОРИТМ РАСЧЕТА КРИТЕТРИЯ
ВИЛКОКСОНА – МАННА – УИТНИ «U»
1.
Упорядочить – расположить в порядке возрастания первый
и второй ряды в виде общего упорядоченного ряда.
2.
Числа, относящиеся к первой группе, располагаются в
левый, а числа, относящиеся ко второй группе – в правый столбик с
учетом «принципа расположения» одинаковых значений.
3.
Подсчитываем число инверсий - нарушений расположения
чисел, по сравнению с их «идеальным» расположением.
4.
По таблице
Приложения 2 определяем критические
значения U. Если Uэмп. > Uкр., принимается нулевая гипотеза (Но).
Если Uэмп. < Uкр., Но отвергается. Чем меньше значение U, тем
достоверность различий выше.
3. Метод ранговой корреляции.
Коэффициент корреляции рангов Спирмена «ρ»
Возможность измерять корреляцию не между самими значениями, а
между их относительными оценками – рангами, позволяет оценивать связь и
между качественными признаками, когда точное количественное измерение
признака по тем или иным причинам оказывается невозможным, а также когда
кривые распределения слишком асимметричны и не позволяют использовать
21
такие параметрические критерии, как коэффициент корреляции Пирсона r: в
этих случаях бывает необходимо превратить количественные данные в
порядковые – проранжировать их. Как правило, меньшему значению признака
присуждается меньший ранг, хотя для процедуры подсчета это несущественно главное, чтобы в обоих рядах ранжирование было однонаправленным.
Если два признака связаны положительно, то испытуемые, имеющие
низкие ранги по одному из них, будут иметь низкие ранги и по другому, а
испытуемые, имеющие высокие ранги по одному из признаков, будут иметь по
другому признаку также высокие ранги.
Для подсчета «ρ» необходимо определить разности между рангами (d),
полученными данным испытуемым по обоим признакам. Затем эти показатели
возводятся в квадрат (d²) и подсчитывается сумма квадратов. Данные
проставляются в формулу:
n
  1
6 di2
i 1
2
n(n  1)
где ρ – коэффициент ранговой корреляции Спирмена
Σ
(d²) – сумма квадратов разности между рангами по двум
переменным для каждого испытуемого;
n – количество ранжируемых значений.
Чем меньше разности между рангами, тем больше будет «ρ» - тем ближе
он будет к (+1).
Если корреляция отсутствует, то все ранги будут перемешены и между
ними не будет никакого соответствия. В этом случае «ρ» окажется близким к
нулю.
В случае отрицательной корреляции низким рангам испытуемых по
одному признаку будут соответствовать высокие ранги по другому признаку, и
22
наоборот. Чем больше несовпадение между рангами испытуемых , тем ближе
«ρ» к (–1).
Коэффициент корреляции рангов может быть значимым лишь при
достаточном числе пар данных, взятых в анализ – не менее 5 пар. Критические
значения определяется по таблице критических значений (см. Приложение,
таблица III).
Пример
1.
Корреляция
между
индивидуальными
профилями.
В
исследовании, посвященном проблеме ценностных ориентаций, выявлялись иерархии
терминальных ценностей по методике М. Рокича у родителей и их взрослых детей (Е.В.
Сидоренко). Ранги терминальныхценностей, полученные при обследовании пары мать – дочь
представлены в таблице.
Вопрос: Как эти ценностные иерархии коррелируют друг с другом.
Сформулируем гипотезы:
Но – корреляция между иерархиями терминальных ценностей матери и
дочери статистически не значима;
Н1 – корреляция между иерархиями терминальных ценностей матери и
дочери статистически значима.
Поскольку ранжирование ценностей предполагается самой процедурой
исследования, нам остается лишь подсчитать разности между рангами 18
ценностей в двух иерархиях.
Начиная с верхней строки, из оценки, стоящей в графе «ранг ценностей в
иерархии матери», вычитаем оценку, стоящую в графе «ранг ценностей в
иерархии дочери», результат записываем в графе d, возводим его в квадрат и
этот результат записываем в графе d².
23
Таблица 4
Расчет терминальных ценностей по списку М. Рокича в индивидуальных иерархиях
матери и дочери
Ранг
ценностей
в иерархии
матери
15
Ранг
ценностей
в иерархии
дочери
15
d
(разность
рангов)
D²
0
0
2. Жизненная мудрость
1
3
-2
4
3. Здоровье
7
14
-7
49
4. Интересная работа
8
12
-4
16
17
-1
1
Терминальные ценности
1. Активная деятельная жизнь
5. Красота природы и искусство
6. Любовь
11
10
1
1
7. Материально обеспеченная
12
13
-1
1
9
11
12
4
9.Общественное признание
17
5
12
144
10.Познание
5
1
4
16
11.Продуктивная жизнь
2
2
0
0
12.Развитие
6
8
-2
4
13.Развлечения
18
18
0
0
14.Свобода
4
6
-2
4
15.Счастливая семейная жизнь
13
4
9
81
16.Счастье других
14
16
-2
4
17.Творчество
10
9
1
1
18.Уверенность в себе
3
7
-4
16
171
171
0
346
жизнь
8. Наличие хороших и верных
друзей
Суммы( Σ )
Определяем эмпирическое значение «ρ»:
24
ρ = 1
6  346
2076
= 0,643
 1
2
18  (18  1)
5814
По таблице 3 Приложения определяем критические значения:
0,47 (р < 0,05)
ρ кр. =
0,60 (р < 0, 01)
ρ эмп. > ρ кр. (р < 0, 01)
Ответ: Но отвергается. Принимается Н1. Корреляция между иерархиями
терминальных ценностей матери и дочери статистически значима (р < 0, 01) и
является положительной. Из таблицы
видно, что основные расхождения
приходятся на ценности «Счастливая семейная жизнь», «Общественное
признание» и «Здоровье», ранги остальных ценностей достаточно близки.
Пример 2. Корреляция между двумя признаками.
В исследовании, моделирующем деятельность авиадиспетчера, группа испытуемых,
студентов физического факультета ЛГУ проходила подготовку перед началом работы на
тренажере. Испытуемые должны были решать задачи по выбору оптимального типа взлетнопосадочной полосы для заданного типа самолета.
Вопрос:
Связано
ли
количество
ошибок,
допущенных
испытуемыми
в
тренировочной сессии, с показателями вербального интеллекта, измеренными по методике Д.
Векслера?
Сформулируем гипотезы:
25
Но
–
корреляция
между
показателем
количества
ошибок
в
тренировочной сессии и уровнем вербального интеллекта статистически не
значима;
Н1
–
корреляция
между
показателем
количества
ошибок
в
тренировочной сессии и уровнем вербального интеллекта статистически
значима.
Далее, в отличие от первого примера, нам необходимо вначале
проранжировать оба показателя, приписывая меньшему значению меньший
ранг, а затем подсчитать разности между этими рангами, возвести их в квадрат
и суммировать. В индивидуальных значениях переменной Б (вербального
интеллекта) имеются одинаковые показатели, поэтому их ранги представляют
собой среднюю арифметическую. Данные представлены в таблице 6
Таблица 6.
Расчет коэффициента корреляции рангов (Спирмена) при сопоставлении показателей
количества ошибок и вербального интеллекта у студентов-физиков (n = 10)
Испытуемые
Переменная А:
Переменная Б:
количество ошибок
вербальный интеллект
d
d²
Инд.значе
Ранги
Инд.
Ранги
(разность
ния по А
по А
значения по Б
по Б
рангов)
1. Т.А.
29
9
131
4
5
25
2. П.А.
54
10
132
5,5
4,5
20,25
3. Ч.И.
13
4
121
1
3
9
4. Ц.Е.
8
2
127
3
-1
1
5. С.Н.
14
5
136
9
-4
16
6. К.Ю.
26
8
124
2
6
36
26
7. Л.П.
9
3
134
7
-4
16
8. Б.Н.
20
7
136
9
-2
4
9. И.К.
2
1
132
5,5
-4,5
20,25
10.Ф.Д.
17
6
136
9
-3
9
Суммы ( Σ )
55
55
156,5
Определяем эмпирическое значение «ρ»:
ρ = 1
6  156,5
939
= 0,052
 1
2
10  (10  1)
990
По таблице III Приложения определяем критические значения:
0,64 (р < 0,05)
ρ кр. =
0,79 (р < 0, 01)
ρ эмп. < ρ кр. (р < 0, 01)
Ответ: Но принимается. Корреляция между показателем количества
ошибок
в
тренировочной
сессии
и
уровнем
вербального
интеллекта
статистически не значима.
27
АЛГОРИТМ РАСЧЕТА КОЭФФИЦИЕНТА РАНГОВОЙ
КОРРЕЛЯЦИИ СПИРМЕНА – «ρ»
1.
Определить, какие два признака или две иерархии
признаков будут участвовать в сопоставлении как переменные А и Б.
2.
Если
это
два
признака,
проранжировать
значения
переменной А, присуждая ранг 1 наименьшему значению. Занести
ранги в соответствующий столбец таблицы по порядку номеров
испытуемых или признаков.
3.
Проранжировать значения переменной Б, в соответствии с
теми же правилами. Занести ранги в соответствующий столбец
таблицы по порядку номеров испытуемых или признаков.
4.
При наличии одинаковых показателей присвоить им ранг,
представляющий среднюю арифметическую совпадающих рангов.
5.
Подсчитать разности d между рангами А и Б по каждой
строке таблицы и занести и занести их в соответствующий столбец.
6.
Возвести каждую разность рангов в квадрат d² и занести в
соответствующий столбец.
7.
Подсчитать сумму квадратов рангов Σd².
28
8.
Рассчитать коэффициент ранговой корреляции по формуле:
n
  1
6 di2
i 1
n(n 2  1)
ρ , где ρ – коэффициент ранговой корреляции
Спирмена, Σ(d²) – сумма квадратов разности между рангами по двум
измерениям для каждого испытуемого, n – количество ранжируемых
значений
9. Определить по таблице Приложения 3 критические значения
ρ для данного количества пар (df). Если ρ превышает критическое
значение или, по крайней мере равен ему, корреляция статистически
значима.
4. Оценка связи между качественными признаками. Метод χ² ("хиквадрат")
Иногда в процессе проведения эксперимента возникает необходимость
сравнения не абсолютных средних значений величин, а частотных, например
процентных, распределений результатов для того, чтобы выяснить, связаны они
друг с другом или, наоборот, независимы.
Так бывает необходимо проверить:
-
существуют ли достоверные различия между числом людей,
справляющихся (или нет) с заданиями какого-то интеллектуального теста, и
числом этих же людей, получающими при обучении высокие или низкие
оценки;
29
-
между возрастом людей и их успехом или неудачей в выполнении
заданий на запоминание и т.д.
В подобных случаях может помочь метод χ²-критерий (хи-квадрат).
Пример. Для экспериментального исследования была взята выборка из 100
учащихся и с ними проведен формирующий эксперимент. До эксперимента 30 человек
успевали на «удовлетворительно», 30 – на «хорошо», а остальные 40 – на «отлично». После
эксперимента ситуация изменилась: теперь на «удовлетворительно» успевают только 10
учащихся, на «хорошо» – 45 учащихся и на «отлично» – 45 учащихся.
Вопрос: Можно ли, опираясь на эти данные, утверждать, что формирующий
эксперимент, направленный на улучшение успеваемости, удался?
Для ответа на данный вопрос подсчитаем χ² - критерий по следующей
формуле:
c
2  
i 1
(Vi  Pi )2
Pi
где Pi -частоты результатов наблюдения до эксперимента;
Vi -частоты результатов наблюдений, сделанных после эксперимента;
с - общее число групп, на которые разделились результаты
наблюдений.
Воспользуемся приведенным примером, чтобы продемонстрировать, как
работает χ²-критерий.
Сформулируем гипотезы:
Но
–
Распределения
учащихся
по
группам
успевающих
на
«удовлетворительно», «хорошо» и «отлично» до и после формирующего
эксперимента не отличаются между собой.
30
Н1
–
Распределения
учащихся
по
группам
успевающих
на
«удовлетворительно», «хорошо» и «отлично» до и после формирующего
эксперимента отличаются между собой.
В нашем примере P переменная принимает следующие значения: 30%,
30%. 40%, а переменная V – такие значения: 10%. 45%, 45%. Составим таблицу
7.
Таблица 7.
Промежуточные расчеты для критерия χ²
Группы
Pk
( Vk – Pk)
Vk
(Vk – Pk)²
Испытуемых
1. Успевающие на
30
10
20
400
30
45
-15
225
40
45
-5
25
«удовлетворительно
»
2. Успевающие на
«хорошо»
3. Успевающие на
«отлично»
Подставим полученные значения в формулу для χ² и определим его
эмпирическую величину.
χ²эмп. =
400 225 25


 = 21,5
30
30 40
Теперь воспользуемся таблицей IV Приложения, где для заданного числа
степеней свободы df= (с – 1) можно выяснить степень значимости полученных
различий в распределении оценок до и после формирующего эксперимента. В
нашем
случае
было
3
группы
испытуемых:
успевающие
на
31
«удовлетворительно», «хорошо» и «отлично», следовательно, число степеней
свободы df будет равно 2 (3 – 1 = 2).
По таблице IV Приложения определяем критические значения χ²:
3,84 (р < 0,05)
χ² кр. =
10,86 (р < 0,001)
χ² эмп. < χ² кр. (р < 0,001)
Можно видеть, что полученное нами значение χ² = 21,5 больше
соответствующего табличного значения df (c – 1 = 2) степеней свободы,
составляющего 13,82 при вероятности допустимой ошибки р < 0, 001.
Ответ: Но отвергается. Принимается Н1. Предположения о значимых
изменениях, которые произошли в оценках учащихся в результате введения
новой методики обучения (формирующего эксперимента) подтвердились:
успеваемость учащихся достоверно улучшилась (р < 0,001).
АЛГОРИТМ РАСЧЕТА КРИТЕРИЯ «χ²»
1.
Занести в таблицу частоты результатов наблюдений,
сделанных до эксперимента - Pk (первый столбец).
2.
Занести в таблицу частоты результатов наблюдений,
сделанных после эксперимента - Vk (второй столбец).
3.
Подсчитать разности между этими значениями по каждой
строке таблицы (Vk – Pk), возвести их в квадрат (Vk – Pk)² и каждое
разделить на Pk
4. Просуммировать результаты. Полученную сумму обозначить
32
как χ².
5. Определить число степеней свободы по формуле: df = с – 1,
где c - количество разрядов признака (число групп, число наблюдений
и т.д.).
6. Определить по таблице IV приложения критические значения
для данного числа степеней свободы df.
Если χ² эмп. меньше критического значения, расхождения между
распределениями статистически недостоверны.
Если χ² эмп. равно критическому значению или превышает его,
расхождения между распределениями статистически достоверны.
33
5. Сравнение двух выборок по качественно и количественно
определенному признаку. Критерий Фишера - «φ»
Критерий Фишера предназначен для сопоставления двух рядов
выборочных значений по частоте встречаемости какого-либо признака. Его
можно применять для оценки различий, как в зависимых, так и в независимых
выборках, а также сравнивать показатели одной и той же выборки, измеренные
в разных условиях.
Пример 1. Сравнение двух выборок по качественно определенному
признаку.
Психолог провел эксперимент, в котором выяснилось, что из 23 учащихся
математической школы 15 справились с заданием. А из 28 учащихся обычной школы с тем
же заданием справились 11 человек.
Вопрос: Можно ли считать различия в успешности выполнения заданий между
учащимися математической и обычной школами достоверными? (О.Ю.Ермолаев).
Сформулируем гипотезы:
Но – различия в выполнении задания учащимися математической и
обычной школой отсутствуют.
Н1 – существуют достоверные различия в успешности выполнения
задания учащимися математической и обычной школами.
Для решения этой задачи показатели успешности выполнения задания по
каждой школе необходимо перевести в проценты, что составит:
15 · 100 = 65,2 % для математической школы;
23
11 · 100 = 39,3 % для обычной школы.
28
По таблице Приложения XI находим величины φ1 и φ2 - соответствующие
процентным долям в каждой группе. Так для 65,2 % согласно таблице
соответствующая величина φ1 = 1,880, а для 39,3 % величина φ2 = 1,355.
Эмпирическое значение φэмп. = (1  2 ) 
n1  n2
n1  n2
34
где
φ1 – величина, взятая из таблицы Приложения XI, соответствующая
большей процентной доле;
φ2 - величина, взятая из таблицы Приложения XI, соответствующая
меньшей процентной доле;
n1 - количество наблюдений в выборке 1;
n2 - количество наблюдений в выборке 2.
В нашем случае φэмп. = (1,880  1,355) 
23  28
= 1,86
23  28
По таблице Приложения XII определяем, какому уровню значимости
соответствует φэмп. = 1,86.
С таблицей Приложения XII работаем следующим образом: находим
внутри её число, равное вычисленному φэмп., и смотрим, между какими
уровнями значимости (с учетом тысячной доли) оно находится. Первый левый
столбец таблицы соответствует уровням значимости от 0,00 (самое верхнее
значение) до 010 (самое нижнее значение). Верхняя строчка таблицы –
соответствует тысячной доле уровня значимости. Итак, находим наше число,
равное 1,86 внутри таблицы, оно находится на пересечении строчки,
соответствующей уровню значимости 0,03 и столбца, обозначенного цифрой 1.
Следовательно, уровень значимости φэмп. равен 0,03 +0,001 = 0,031.
Необходимо подчеркнуть, что поскольку критические значения для 5% и
1% уровней значимости имеют фиксированную величину и составляют,
соответственно, для 5% φкр. = 1,64, а для 1% φкр. = 2,28, то данная таблица
Приложения 6 практически не нужна, так как этими величинами критических
уровней можно пользоваться всегда.
35
Итак,
5,99 (р < 0,05)
φкр.
=
9,21 (р < 0,001)
φэмп.
<
φкр.(р
< 0,001) >
φкр.(
р < 0,05), поэтому мы можем принять
гипотезу Н1 на 5% уровне значимости и отклонить её на 1% уровне значимости.
Ответ: Но отвергается, принимается Н1:
на 5% уровне значимости
можно считать различия в успешности выполнения заданий между учащимися
математической и обычной школами достоверными.
Критерий Фишера с успехом может быть применен и при сравнении
распределений количественных признаков.
Пример 2. Сравнение двух выборок по количественно определенному
признаку.
Психолог проводил анализ выраженности уровня тревожности в группе сирот и в
группе детей из полных семей при помощи опросника Тейлора. 40 баллов и выше
рассматривались как показатель очень высокого уровня тревожности. В группе сирот из 10
человек очень высокий уровень тревожности наблюдался у 7 испытуемых (70%). В группе
детей из полных семей из 13 человек такой уровень наблюдался у 3 испытуемых (23,1%).
Вопрос: Будет ли уровень тревожности у подростков-сирот более высоким, чем у их
сверстников из полных семей? (О.Ю.Ермолаев).
Сформулируем гипотезы:
Но – статистические различия в уровне тревожности у детей-сирот и
детей из полных семей отсутствуют;
Н1 – существуют статистические различия в уровне тревожности у детейсирот и детей из полных семей.
36
По
таблице
Приложения
5
определяем
величины
φ1
и
φ2,
соответствующие процентным долям в каждой группе:
φ1 = 1,982 для 70% и φ2 =1,003 для 23,1%.
Подсчитываем φэмп. по формуле:
Φэмп. = (1,982-1,003) ·
10  13
= 2,32
10  13
Напомним, что критические величины для этого критерия таковы:
5,99 (р < 0,05)
φкр.
=
9,21 (р < 0,001)
φэмп.
>
φкр.(
р < 0,001), следовательно, различия между группами
значимы на уровне 1%, то есть, в группе сирот измеряемый признак выражен в
существенно большей степени, чем в группе детей из полных семей.
Ответ: Но отвергается, принимается Н1: подростки-сироты более
тревожны, чем дети из полных семей.
Следует обратить внимание на тот факт, что для получения подобного
вывода понадобилась очень малая выборка испытуемых.
37
АЛГОРИТМ РАСЧЕТА КРИТЕРИЯ ФИШЕРА - «φ»
1.
Перевести
абсолютные
значения
анализируемых
показателей в проценты.
2. По таблице Приложения XI найти величины φ1 и φ2,
соответствующие процентным долям в каждой группе.
3. Подсчитать эмпирическое значение φэмп. по формуле
φэмп. = (1  2 ) 
n1  n2
n1  n2
где φ1 – величина, взятая из таблицы Приложения XI,
соответствующая большей процентной доле;
φ2 - величина, взятая из таблицы Приложения XI,
соответствующая меньшей процентной доле;
n1 - количество наблюдений в выборке 1;
n2 - количество наблюдений в выборке 2.
4. По таблице приложения XII определить, какому уровню
значимости соответствует φэмп.
Если φэмп. меньше критического значения, различия между
выборками статистически недостоверны.
Если φэмп. равно критическому значению или превышает его,
различия между выборками статистически достоверны.
38
ПРИМЕНЕНИЕ ПАРАМЕТРИЧЕСКИХ КРИТЕРИЕВ СТАТИСТИКИ В
ПСИХОЛОГИЧЕСКИХ ИССЛЕДОВАНИЯХ
Параметрические критерии - это критерии, использующие то, что нам
известно распределение случайной величины, т.е. ее функция распределения
однозначно
задается
некоторым
числом
параметров.
Например,
для
нормального распределения этих параметров два – математическое ожидание и
дисперсия. Нормальное распределение случайной величины часто встречается в
природе
при
большом
количестве
измерений.
Хотя
есть
и
другие
распределения: Гамма-распределение, χ2, биномиальное, и др., но нас будут
интересовать критерии, основанные на предположении, что распределение
нормальное.
Для того чтобы можно было с уверенно применять критерии, основанные
на предположении, что распределение нормальное необходимо проверить
действительно ли это так. Это можно сделать по графику или по специальным
критериям проверки нормальности распределения.
Таким образом, перед использованием критерия корреляции Пирсона или
t-критерия Стьюдента, необходимо проверить соответствует ли распределение
эмпирических данных нормальному.
Несмотря на кажущуюся сложность применения, параметрические
критерии имеют большую мощность, нежели параметрические. Мощность
критерия – это характеристика области, в которой критерий может определять
различия, если они есть. Так, например, мощность t-критерия Стьюдента
приблизительно в 1,5 раза больше чем G-критерия знаков. Это значит, что из
трех случаев, в которых существуют значимые различия и будет выполняться tкритерий, G-критерий будет выполняться только в двух.
39
Итак, непараметрические критерии имеют большую область определения
(могут применяться для любых распределений), но меньшую различительную
способность – мощность, а параметрические более мощные, но могут
применяться только на распределениях определенного вида.
Нами
рассматриваются
2
критерия
для
оценки
нормальности
распределения и 2 различных критерия в типичных случаях их применения.
Рассказывается о мощном и самом часто употребляемом t-критерии Стьюдента
в трех его вариантах (для зависимых измерений, для независимых измерений и
процентильный) и критерий корреляции Пирсона.
1. Проверка нормальности распределения эмпирических данных
По ГОСТ 8.207-76 "Прямые измерения с многократными наблюдениями.
Методы обработки результатов наблюдений" рекомендуется следующие
способы проверки гипотезы о нормальности распределения эмпирических
данных (Худяков, Зароченцев). Если объем выборки менее 16, то не
рекомендуется использовать параметрические критерии. Если количество
измерений больше 15 но менее 50, то следует применять "Двойной составной
критерий". Для выборок объемом более 50 рекомендован критерий χ².
1.1 Двойной составной критерий
Двойной
распределений
распределение
составной
критерий
эмпирического
удовлетворяет
и
направлен
на
нормального.
двойному
сопоставление
Если
составному
двух
эмпирическое
критерию,
то
с
вероятностью 0,98 можно считать, что к полученным данным применима
нормальная модель распределения.
Таблица V приложения позволяет применять Двойной составной
критерий при численности сравниваемых выборок от 16 до 50.
40
Пример 2.1. Участники тренинга уверенное поведение, продолжавшегося 1 день,
оценили у себя уровень личностной тревожности. Первое измерение проводилось в первый
день тренинга, на следующий после тренинга день. Все изменения оценивались по 10балльной шкале. Данные представлены в таблице 8.
Вопрос: Можно ли утверждать, что полученные эмпирические данные подчиняются
закону нормального распределения?
Таблица 8
Личностная тревожность
ФИО
До
После
1. И.В.Л.
5
5
2. Я.Е.А.
4
1
3. К.С.И.
4
4
4. Р.М.Н.
4
4
5. Н.М.Т.
5
4
6. Е.Л.П.
6
5
7. Л.К.С.
3
5
8. Т.А.П.
6
5
9. Б.В.В.
6
5
10.С.М.А.
5
6
11.В.П.Р.
6
6
12.Ч.Н.Г.
6
3
13.А.С.П
3
1
14.В.С.К.
4
3
15.В.П.П.
4
3
16.Л.Г.Т
4
4
17.Т.И.Ч
4
4
4,65
4
M
41
D
1,12
2,12
SD
1,06
1,46
ДСК состоит из двух проверок. В первой проверяется, попадает ли расчетный
коэффициент dэмп в заданную для нормального распределения область. Если нет, то с
вероятностью 0.98 можно считать, что распределение эмпирических данных не соответствует
нормальному закону Н0 принимается. Если расчетный коэффициент dэмп попадает в заданную
для нормального распределения область, то переходят ко второй проверке.
Во втором сравнении необходимо найти из таблицы VI приложения коэффициент z
соответствующий объему выборки. Далее необходимо рассчитать дисперсию D и найти
стандартное отклонение SD, после чего необходимо найти расчетное отклонение s=SD*z.
Потом следует сосчитать количество mэмп, случаев когда |хi – Мх| оказался больше s.
По таблице VI приложения необходимо найти mкр и если mэмп меньше mкр, то можно
считать распределение эмпирических данных нормальным, в противном случае нельзя.
Проведем расчеты для данных участников, полученных до проведения тренинга.
Сформулируем гипотезы:
Но – распределение эмпирической случайной величины данных измеренных до
проведения тренинга отличается от нормального закона распределения.
Н1 – распределение эмпирической случайной величины подчиняется нормальном
закону распределения.
Первое условие.
Проведем первое сравнение, для чего будет необходимо рассчитать dэмп
dэмп =
Для того чтобы рассчитать dэмп, найдем x
x =4,65
Заполним 1 столбец таблицы 9.
Просуммируем содержание столбца 1.
Σ|x- x |=15,65
Далее найдем D и SD
Для этого возведем разность xдо-..до в квадрат и запишем в столбец 2
42
Подсчитаем сумму Σ(x- x ) 2 = 18 и поделим на n-1=17-1=16
D = 1,12
Возьмем квадратный корень из D, SD= D
SD = 1,057
Пользуясь формулой рассчитаем dэмп
dэмп=0,9
Далее пользуясь таблицей 9 определим d1 и d2, соответствующие объему выборки, если
dэмп>d2 dэмп<d1, то можно переходить к второму сравнению.
d2=0,6829 d1=0,9137
0,9>0,6829 и 0,9<0,9137
Значит dэмп удовлетворяет первому условию.
Таблица 9
Фамилия
|xдо- x до|
(xдо- x до)2
|xпосле- x после|
(xпосле- x после)2
SDдо=1,92
SDпосле=3,76
1. И.В.Л.
0,35
0,12
1,00
1,00
0
0
2. Я.Е.А.
0,65
0,42
3,00
9,00
0
0
3. К.С.И.
0,65
0,42
0,00
0,00
0
0
4. Р.М.Н.
0,65
0,42
0,00
0,00
0
0
5. Н.М.Т.
0,35
0,12
0,00
0,00
0
0
6. Е.Л.П.
1,35
1,83
1,00
1,00
0
0
7. Л.К.С.
1,65
2,71
1,00
1,00
0
0
8. Т.А.П.
1,35
1,83
1,00
1,00
0
0
9. Б.В.В.
1,35
1,83
1,00
1,00
0
0
10.С.М.А.
0,35
0,12
2,00
4,00
0
0
11.В.П.Р.
1,35
1,83
2,00
4,00
0
0
12.Ч.Н.Г.
1,35
1,83
1,00
1,00
0
0
13.А.С.П
1,65
2,71
3,00
9,00
0
0
14.В.С.К.
0,65
0,42
1,00
1,00
0
0
15.В.П.П.
0,65
0,42
1,00
1,00
0
0
16.Л.Г.Т
0,65
0,42
0,00
0,00
0
0
17.Т.И.Ч
0,65
0,42
0,00
0,00
0
0
Сумма
15,65
17,88
18
34,00
0
0
43
Второе условие.
Найдем z из таблицы VI приложения для объема выборки n=17.
z=2,58
Рассчитаем
вспомогательное
значение
s,
воспользовавшись
рассчитанным
стандартным отклонением SD, s=SD*z
s=1,057*2,58=1,92
Заполним 3 столбец таблицы 9. Если значение в столбце 1 будет больше
рассчитанного s=1,92, то пишем 1, если нет то 0.
Считаем сумму mэмп ячеек столбца 3.
mэмп=0
По таблице VI приложения находим mкр
mкр=1
Сравниваем mкр и mэмп
mкр>mэмп
Значит условие два выполняется, а следовательно принимается гипотеза Н1.
Ответ: Принимается гипотеза Н1. Данные учащихся до исследования можно считать
распределенными по нормальному закону.
2) Проведем расчеты данных для результатов после исследования, n = 17:
Сформулируем гипотезы:
Но – распределение данных, измеренных после проведения тренинга, отличается от
нормального закона распределения.
Н1 – распределение данных, измеренных после проведения тренинга, подчиняется
нормальном закону распределения.
x =4
Σ|х- x |=18
Σ(х- x )2=34
D=34/(17-1)=2,12
SD=1,46
d=0,75
d2=0,6829 d1=0,9137
44
0,75>0,6829 и 0,75<0,9137
Условие 1. выполняется
z=2,58
s=2,58*1,46=3,76
mэмп=0
mкр=1
mкр>mэмп, 1>0
Условие 2 выполняется
Ответ: Принимается гипотеза Н1. Данные учащихся до исследования можно считать
распределенными по нормальному закону.
АЛГОРИТМ РАСЧЕТА ДВОЙНОГО СОСТАВНОГО КРИТЕРИЯ
1. Найти среднее значение результатов измерения.
2. Найти сумму модулей разности между значениями, полученными в
ходе измерения и средним значением
3. Найти стандартное отклонение результатов измерения.
4. Найти коэффициент dэмп по формуле
5. Сравнить полученный dэмп с данными в таблице V d1 и d2
6. Сделать вывод о выполнении первого условия. Если условие
выполняется, то продолжаем. Иначе выполняется Н0, расчеты окончены.
7. Найти по таблице VI и данному объему выборки z. Рассчитать
коэффициент s
8. Найти mэмп, сколько результатов отличаются от среднего на величину
большую по модулю чем s.
9. Сравнить mэмп и mкр найденное по таблице VI. Если mэмп < mкр, то
второе условие выполнятся, а следовательно принимается гипотеза Н1.
Иначе выполняется Н0
45
1.2 Критерий χ² (модификация Фишера)
Критерий χ² уже применялся нами для определения связи между
качественными признаками. Также его можно применять для определения
сходства эмпирических распределений или для проверки гипотезы о совпадении
эмпирического распределение с предсказанным теоретическим. С помощью
критерия χ² можно определить вероятность совпадения эмпирического
распределения с нормальным. Обычно χ² используется, когда количество
измерений больше или равно 50.
Критерий χ² в модификации Фишера предназначен для проверки сложных1
гипотез
и
является
модификацией
критерия
хи-квадрат
Пирсона,
предназначенного для проверки простых гипотез. Вычисление статистики
критерия хи-квадрат Фишера производится по фор  2 
1 с (ni  npi )2
муле
 p
n i 1
i
где c – количество классов (карманов), на которые можно разделить наши
измерения, pi - теоретические вероятности найденные по таблице или с
помощью функции НОРМРАСП() программы Excel, а n – общее число
наблюдений.
Для определения количества классов (карманов) можно использовать
следующее правило:
Если количество измерений:
 от 40 до 100 то рекомендуется выбрать от 7 до 9 классов
 от 100 до 500, то рекомендуется выбрать от 8 до 12 классов
 от 500 до 1000, то рекомендуется выбрать от 10 до 16 классов
Простой гипотеза будет в том случае, если теоретическое распределение задано всеми своими параметрами.
Сложной гипотеза будет, если все или некоторые параметры теоретического распределения оцениваются по
выборке. В нашем случае по выборке могут оцениваться среднее значение и дисперсия. В данном случае имеет
место сложная гипотеза, в которой по выборке оцениваются и среднее значение, и дисперсия.
1
46
 1000 – 10000, то рекомендуется выбрать от 12 до 22 классов
Нужно отметить, что если есть интервалы с частотами менее 5, то для
применения критерия χ², их необходимо объединить с соседними интервалами.
Величины интервалов классов при этом подлежат пересчету, переопределяются
границы классов от xi до xi+1 .
Параметры
нормального
распределения
для
расчета
теоретических
вероятностей вычисляются по эмпирическим частотам, т.к. мы не знаем
истинных параметров генеральной совокупности. Используются формулы для
среднего значения x и дисперсии Dx, соответственно, в следующей форме:
Mx   x i pi* , где x i середина i  го интервала x i 
( xi  xi 1 )
,
2
pi*  вероятность попадания в i  ый интервал pi* 
ni
n
с
i 1
с
Dx   ( xi  Mx ) 2 pi* , SDx  Dx
i 1
Пример 2.2. Проводилось экспериментальное исследование по изучению
влияния развлекательной телепередачи на молодежь. Испытуемые пожелавшие
принять участие в исследовании случайным образом были разделены на две
группы экспериментальную и контрольную. Одним из параметров оценки
влияния телепередачи служил показатель личностной тревожности. Результаты
испытуемых контрольной и экспериментальной группы даны в таблице 10.
Вопрос: Можно ли утверждать, что полученные эмпирические данные подчиняются
закону нормального распределения?
Таблица 10.
Контрольная группа
Количество
2
3
4
5
6
7
8
9
10
47
баллов
vi
2
4
10
20
38
20
15
5
5
Экспериментальная группа
Количество
2
3
4
5
6
7
8
9
10
7
7
15
30
23
17
12
5
5
баллов
vi
vi - Число испытуемых набравших данное количество баллов
Проверим, действительно ли можно считать данные, полученные в контрольной
группах, распределенными по нормальному закону.
Сформулируем гипотезы:
Но – данные, полученные в контрольной группе, не соответствуют нормальному
закону;
Н1 – данные, полученные в контрольной группе, соответствуют нормальному закону;
Разобьем данные на классы, частота которых себя не менее пяти измерений, для этого
нам придется объединить испытуемых набравших 2 и 3 балла в один класс. Перепишем
таблицу указав интервалы классов. Так в интервал от 2 (включая 2) до 4 (не включая 4) у нас
попадает 2+4=6 испытуемых. В интервал от 4 (включая 4) до 5 (не включая 5) попадает 10
испытуемых. И т.д. Проблемы возникают только с последним интервалом, а значит
необходимо добавить интервал от 10 до 11 (не включая). На частоту попадания испытуемых в
этот интервал это никак не скажется.
Начнем заполнять таблицу 11.
Таблица 11
Количество
[22,4)3
[4,5)
[5,6)
[6,7)
[7,8)
[8,9)
[9,10)
[10,11)
6
10
20
38
20
15
5
5
баллов
vi
2
3
Скобка "]" - означает, что значение границы интервала включено в интервал.
Скобка ")" - означает, что значение границы интервала в интервал не включаются.
48
pi*
xi
xi  pi*
xi  Mx
( xi  Mx ) 2
( xi  Mx ) 2 pi*
pi
(ni  npi )
( ni  npi ) 2
(ni  npi )2
pi
Сосчитаем общее число наблюдений , n=5+10+20+38+20+15+5+=118
Теперь необходимо рассчитать вероятность попадания в i-ый интервал pi*, pi* 
p1*=
ni
,
n
5
10
 0,042 , p1*=
 0,085 и т.д. занесем полученные данные в таблицу 11.
118
118
pi*
0,042
Найдем
0,085
0,169
теперь
0,127
0,042
0,42
каждого
интервала
( xi  xi 1 )
2
24
45
 3, х1 
 4.5, и т.д. . Занесем результаты в таблицу 11:
2
2
3
xi
0,169
середину
x i середина i  го интервала x i 
х1 
0,322
4,5
5,5
6,5
7,5
8,5
9,5
10,5
Теперь рассчитаем xi  pi* , x1  p1*  3* 0,042  0,148 , и т.д. Занесем результаты в
таблицу 11:
xi  pi*
0,127
0,381
0,932
2,093
1,271
1,08
0,402
0,444
49
k
По полученному столбцу сосчитаем сумму Mx   x i pi* ,
i 1
Мх=0,148+0,381+…+0,444=6,733
Продолжим
заполнение
таблицы
11.
-0,233
0,767
Найдем
xi  Mx .
разность
x1  Mx  3  6,75  3,733 и т.д.
xi  Mx
-3,733
-2,233
-1,233
1,767
2,767
3,767
Возведем полученные разности в квадрат ( xi  Mx ) 2 . ( x1  Mx )2  ( 3,733) 2  13,936
( xi  Mx ) 2
13,936
4,987
1,520
0,054
0,588
3,122
7,656
14.190
Умножим на вероятность попадания в интервал, чтобы получить ( xi  Mx ) 2 pi* .
( xi  Mx ) 2 pi*
0,59
0,422
0,257
0,017
0,099
0,396
0,324
0,601
k
Теперь мы можем рассчитать Dx= Dx   ( xi  Mx ) 2 pi* , Dx=0,59+0,422+..+0,601=2,71,
i 1
а стандартное отклонение SDx  Dx , SDx=1,64
Теперь необходимо найти теоретические вероятности попадания в i-ый интервал pi
для функции нормального распределения найденными параметрами Мх и SDx. Для этого
придется воспользоваться таблицей VII приложения.
Итак найдем вероятность попадания в i-ый интервал pi=Ф(
xi  Mx
x  Mx
)-Ф( i 1
),
SDx
SDx
составим вспомогательную таблицу 13.
Таблица 13
Границы
2
4
5
6
7
8
9
10
11
интервалов
xi  Mx
SDx
Ф(
xi  Mx
SDx
)
50
xi  Mx
x  Mx 2  6,733
, для левой границы 1

 2,874 , и т.д.
SDx
SDx
1,64
Рассчитаем
xi  Mx
SDx
-2,874
-1,66
-1,05
-,445
0,162
0,769
По таблице найдем приближенные значения Ф(
1,376
1,984
2,591
xi  Mx 4
) , т.к. функция Ф –
SDx
симметрична, то обычно приводятся значения только для положительных аргументов,
значения для отрицательных вычисляются по формуле Ф(-t)=1-Ф(t)
Ф(-2,874)=1-0,9979=0,0021
Ф(
xi  Mx
SDx
0,002
0,048
0,146
1
5
9
0,33
0,564
0,776
0,914
0,976
6
4
7
1
0,995
2
)
Рассчитаем значения pi=Ф(
xi 1  Mx
x  Mx
)-Ф( i
), занесем их в таблицу 11.
SDx
SDx
p1=0,0485-0,0021=0,0464
pi
0,0464
0,0984
0,1831
0,2346
0,2118
0,1383
0,0614
0,0191
82,100
394,8
(ni  npi )2 (5  118* 0,0464)2

 4,866 и т.д.
Рассчитаем
pi
0,0464
(ni  npi )2
pi
4,8
26,3
14,
453,7
117,6
12,5
Сосчитаем сумму и поделим на n, это и будет искомое значение χ²
χ²=1106/118=9,37
Теперь по таблице IV приложения необходимо найти x2 критическое, для этого
определим какую размерность имеет наша задача. m=k-3, где k – количество классов. m=83=5
χ² а=0,05 = 11,1, χ² а=0,01 = 15,1
Сравниваем χ²эмп≤ χ² а=0,05, значит принимается гипотеза о сходстве.
Ответ: Принимается гипотеза Н1. Данные учащихся до исследования можно считать
распределенными по нормальному закону.
Для вычисления удобней использовать программу Excel из пакета Microsoft Office, в данной программе есть
функция возвращающая значение интегральной функции нормального распределения, для этого необходимо
указать следующие параметры =НОРМРАСП(x, Mx,SDx, ИСТИНА), где х – граница интервала, а Mx и SDx это
рассчитанные ранее по выборке мат.ожидание и стандартное отклонение соответственно.
4
51
Проверим, действительно ли можно считать данные, полученные в контрольной
группах, распределенными по нормальному закону используя программу Excel.
Сформулируем гипотезы:
Но – данные, полученные в контрольной группе, не соответствуют нормальному
закону;
Н1 – данные, полученные в контрольной группе, соответствуют нормальному закону;
Рисунок 1.
Ячейка D2 =B2/C2 (копируем для всех D)
Ячейка E2 =(A2+A3)*D2/2 (копируем для всех E), Ячейка E12 = =СУММ(E2:E11)
Ячейка F =E11 (все строки F одинаковые)
Ячейка G2 =(F2)^2*D2 (копируем для всех G), G12= =СУММ(G3:G11), G13
=КОРЕНЬ(G12)
Ячейка H = G12 (все строки H одинаковые)
52
Ячейка I =НОРМ.РАСП(A3;$E$11;H2;ИСТИНА)НОРМ.РАСП(A2;$E$11;H2;ИСТИНА) (копируем для всех I, ссылка $E$11 – неизменяемая во
всех формулах)
Ячейка J = =(B2-C2*I2)^2/I2 (копируем для всех J)
Ячейка J11 = =СУММ(J2:J10)/B11
Итак, получаем χ²эмп = 9,422 , размерность системы m=k-3=9-3. Заметьте, что в случае
с экспериментальной группой нам не пришлось увеличивать интервалы как их было 9 так и
осталось, ведь частоты встречаемости каждого интервала больше или равна 5.
Сравниваем χ²эмп≤ χ² а=0,05, значит принимается гипотеза о сходстве.
Ответ: Принимается гипотеза Н1. Данные учащихся до исследования можно считать
распределенными по нормальному закону.
АЛГОРИТМ РАСЧЕТА КРИТЕТРИЯ χ²
1. Определяем интервалы, если в какой-то интервал приходится
менее 5 значений, то укрупняем интервалы.
2. Находим расчетные значения Mx, SDx
3. По таблице VII приложения определяем теоретические
вероятности pi
4. По формуле рассчитываем эмпирическое значение χ²эмп
5. По таблице IV приложения определяем критические значения χ².
Если χ²эмп≤ χ² а=0,05, значит принимается гипотеза о сходстве. Если
χ²эмп> χ² а=0,01, значит гипотеза о сходстве отвергается.
53
2. Меры связи
2.1 Коэффициент корреляции Пирсона «r»
Установление существования связи между двумя переменными важная и
интересная
задача,
постоянно
встречающаяся
в
психологических
исследованиях. Выше говорилось о возможности изучения связи между двумя
переменными, измеренными в шкале порядка или распределение которых не
соответствует нормальному закону. В этих случаях применяется коэффициент
ранговой корреляции Спирмена. Однако более мощным критерием корреляции
является критерий Пирсона «r». Он применяется, если данные измерены по
шкале интервалов и их распределение нормально. Наряду с коэффициентом
корреляции Пирсона существует коэффициент корреляции Кендалла «τ»,
который применяется реже.
Удобство любого коэффициента корреляции (Пирсона, Кендалла или
Спирмена), в том, что он нормированный. Т.е. вне зависимости от значений
данных коэффициент корреляции принимает значение от -1 до 1 включительно.
Модуль коэффициента корреляции свидетельствует о силе связи. Так r=1
означает, что существует линейная зависимость y=ax+b
Знак говорит о направленности связи "+" с увеличением одной
переменной возрастает и другая, "-" с увеличением одной другая уменьшается.
Для подсчета «r» необходимо убедиться, что распределение данных
нормально, после чего можно переходить к расчетам.
Допустим у нас есть две характеристики х и у одного процесса, на
необходимо выяснить связаны ли они.
n
r
 ( x  x )( y
i 1
i
i
 y)
(n  1)  SDx  SDy
, где r – коэффициент корреляции Пирсона, х –
значения первой переменной, у – значения второй переменной, n – количество
измерений, SDx – стандартное отклонение первой переменной, SDу –
54
стандартное отклонение второй переменной,
x
– среднее для первой
переменной и y –среднее для второй переменной. Напомним формулы расчета
n
среднего и стандартного отклонения: х 
Для
определения
значимости
n
1
 xi , SDx 
n i 1
(x  x)
i 1
коэффициента
2
i
n 1
.
корреляции
можно
воспользоваться таблицей VIII приложения.
Расчет 2.3 Продолжим рассмотрение примера 2.1. Для которого нами
было проверено соответствие распределения данных нормальному.
Участники тренинга уверенное поведение, продолжавшегося 1 день, оценили у себя
уровень личностной тревожности. Первое измерение проводилось в первый день тренинга, на
следующий после тренинга день. Все изменения оценивались по 10-балльной шкале. Данные
представлены в таблице 9.
Вопрос: Можно ли утверждать, что уровень личностной тревожности после
проведения тренинга зависит от исходного уровня личностной тревожности до тренинга?
Сформулируем гипотезы:
Но – корреляция между уровнем личностной тревожности до и после тренинга не отличается
от нуля;
Н1 – корреляция между уровнем личностной тревожности до и после тренинга значимо
отличается от нуля;
Поскольку алгоритм расчета коэффициента корреляции Пирсона есть практически в любой
статистической программе дадим два алгоритма расчета в ручную и с помощью программа из
пакета Microsoft Office, Microsoft Excel.
Занести данные в столбцы А, В и С (см. рис. 2)
55
Рисунок 2.
Заполнение первичных данными
В любой пустой ячейке набрать следующую формулу = КОРРЕЛ( Далее указателем мыши
выделить область расчета – "В1:B17", набрать ";" Далее снова указателем мыши выбрать
область – "С1:С17", набрать ")" и нажать "Enter". Подробнее на рисунке Р1.
56
Рисунок 3.
Выбор диапазона
Тогда результат вычисленный коэффициент корреляции окажется в ячейке С20 rэмп=0,52
Аналогичные вычисления можно было проделать вручную, этого составим таблицу 16
В столбцы 1,2,3 скопируем данные задачи.
Таблица 14
Участник
y- у
(x- x )*(y- у )
(y- у )2
Y
y
1
2
3
4
5
6
7
8
1. И.В.Л.
5,00
5,00
0,35
1,00
0,35
0,12
1,00
2. Я.Е.А.
4,00
1,00
-0,65
-3,00
1,94
0,42
9,00
3. К.С.И.
4,00
4,00
-0,65
0,00
0,00
0,42
0,00
4. Р.М.Н.
4,00
4,00
-0,65
0,00
0,00
0,42
0,00
x- x
(x- x )2
57
5. Н.М.Т.
5,00
4,00
0,35
0,00
0,00
0,12
0,00
6. Е.Л.П.
6,00
5,00
1,35
1,00
1,35
1,83
1,00
7. Л.К.С.
3,00
5,00
-1,65
1,00
-1,65
2,71
1,00
8. Т.А.П.
6,00
5,00
1,35
1,00
1,35
1,83
1,00
9. Б.В.В.
6,00
5,00
1,35
1,00
1,35
1,83
1,00
10.С.М.А.
5,00
6,00
0,35
2,00
0,71
0,12
4,00
11.В.П.Р.
6,00
6,00
1,35
2,00
2,71
1,83
4,00
12.Ч.Н.Г.
6,00
3,00
1,35
-1,00
-1,35
1,83
1,00
13.А.С.П
3,00
1,00
-1,65
-3,00
4,94
2,71
9,00
14.В.С.К.
4,00
3,00
-0,65
-1,00
0,65
0,42
1,00
15.В.П.П.
4,00
3,00
-0,65
-1,00
0,65
0,42
1,00
16.Л.Г.Т
4,00
4,00
-0,65
0,00
0,00
0,42
0,00
17.Т.И.Ч
4,00
4,00
-0,65
0,00
0,00
0,42
0,00
Вспом.
4,65
4,00
13,00
17,88
34,00
x - среднее по столбцу 2, x =4,65
у – среднее по столбцу 3, у =4
Заполним столбцы 4 и 5
Рассчитаем произведение (x- x )*(y- у ) и заполним столбец 6
Рассчитаем произведение (x- x ) 2 и заполним столбец 7
Рассчитаем произведение (y- у ) 2 и заполним столбец 8
Найдем сумму ячеек столбца 6 S1=13
Найдем сумму ячеек столбца 7 S2=17,88
Найдем сумму ячеек столбца 8 S3=34
Рассчитаем SDx=КОРЕНЬ (S2/(n-1)) SDx=1,057
Рассчитаем SDy=КОРЕНЬ (S2/(n-1)) SDy=1,46
Найдем коэффициент корреляции
r=S1/((n-1)*SDx*SDy) = 13/((17-1)*1,057*1,46)=0,52
Теперь по таблице VIII необходимо определить значима ли связь.
rа=0,05=0,482, rэмп>rа=0,05, значит выполняется Н1.
58
Ответ: Но отвергается. Принимается Н1. Корреляция между значениями личностной
тревожности до тренинга и после тренинга статистически значима (р < 0,05) и является
положительной. Из таблицы видно, что только у одного участника С.М.А. в результате
тренинга значение личностной тревожности возросло.
АЛГОРИТМ РАСЧЕТА КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ
ПИРСОНА– «r»
1. Определить, какие два признака или две иерархии признаков
будут участвовать в сопоставлении как переменные X и Y.
2. Определить
удовлетворяют
ли
распределения
переменных
нормальному распределению.
3. Найти среднее значение x по переменной X и My по переменной
Y
4. Найти суммы (x- x )*(y- у ), (x- x )2, (y- у )2
5. Найти SDx и SDу
6. По формуле найти коэффициент ранговой корреляции
7. Определить по таблице VIII приложения критические значения
r
для данного n. Если r превышает критическое значение или, по
крайней мере равен ему, корреляция достоверно отличается от
нуля.
59
3. Оценка различий между сравниваемыми группами наблюдений
3.1 F критерий Фишера
F-критерий Фишера направлен на определение равенства дисперсий двух выборок.
Данный критерий может служить первичным способом выявления различий в показателях
двух выборок. Данный критерий применяется для получения предварительного ответа на
вопрос: принадлежат ли обе выборки к одной генеральной совокупности. Этот критерий
проверяет равенство в двух выборках одного параметра нормального распределения –
дисперсии. Второй параметр проверяет t-критерий Стьюдента.
Если критерий Фишера указывает на то, что дисперсии двух выборок различаются, это
основание полагать, что различия между выборками значимы.
Сравнение двух выборочных дисперсий осуществляется следующим образом. Вычисляется
эмпирическое дисперсионное отношение (Fэмп)
Fэмп
D1

, при n1  n2

D2


, где D1 и D2 всегда выбираются таким образом, чтобы D1>D2, n1
D
(
n

1)
 1 2
, при n1  n2
 D2 ( n1  1)
это объем выборки с D1 и n2 это объем выборки с D2 . Далее по таблице IХ приложения
определяется для v1=n1-1 и v2=n2-1 Fа v1 v2 и проверяется условие Fэмп< F0.05 v1 v2 – то дисперсии
различаются лишь случайным образом (гипотеза о равенстве дисперсий подтверждается),
если Fэмп> F0.01
v1 v2
различия не случайны (гипотеза о значимой разнице дисперсий
подтверждается)
Расчет 4.1 Продолжим рассмотрение примера 2.1.
Вопрос: Значимо ли различие дисперсии данных у участников до и после тренинга.
Сформулируем гипотезы:
Но – дисперсии значимо не различаются (различия в дисперсиях выборок случайны);
Н1 – различие дисперсий значимо (различия в дисперсиях выборок неслучайны);
60
Мы уже рассматривали этот пример выше в пункте 2.1 и с помощью двойного составного
критерия определили, что распределение показателей может считаться нормальным. Также
нами были вычислены дисперсии результатов до и после тренинга. Dдо=1.12, Dпосле=2,12 (см.
пункт 2.1). В нашем примере n1=n2=17, т.к. Dпосле>Dдо, то D1= Dпосле, D2= Dдо
Fэмп=
2,12
=1,89
1.12
В таблицеIX приложения находим значение F0.05 16 16=2,33
Fэмп< F0.05
v1 v2
, значит гипотеза о том, что различия в дисперсиях незначительны
подтверждается.
Ответ: Принимается Н0. Различия в дисперсиях выборок случайны
Рассмотрим еще один пример
Расчет 4.2. Продолжим рассмотрение примера 2.2
Вопрос: Значимо ли различие дисперсий показателей личностной тревожности у испытуемых
в контрольной и экспериментальной группах.
Сформулируем гипотезы:
Но – дисперсии значимо не различаются (различия в дисперсиях выборок случайны);
Н1 – различие дисперсий значимо (различия в дисперсиях выборок неслучайны);
Мы уже рассматривали этот пример выше в пункте 2.2 и с помощью критерия χ² определили,
что распределение показателей может считаться нормальным 2.2(а,б). Также нами были
вычислены дисперсии результатов в экспериментальной и контрольной группах. Dэксп=3,48,
Dконтр=2,71 (см. пункт 2.1). т.к. Dэксп>Dконтр, то D1= Dэксп, D2= Dконтр
Тогла В нашем примере n1=nэкп=121, n2=nконтр=118 nэксп≠nконтр,
Fэмп=
3, 48(118  1)
=1,15
2,71(121  1)
61
В таблице IХ приложения нет значения F0.05
120 117
поэтому находим ближайшее значение
F0.05 100 беск=1,28
Fэмп< F0.05
v1 v2
, значит гипотеза о том, что различия в дисперсиях незначительны
подтверждается.
Ответ: Принимается Н0. Различия в дисперсиях выборок случайны
3.2 t-критерий Стьюдента
t-Критерий Сьюдента является одним из самых мощных и часто
используется при анализе результатов исследования. Данный критерий
t-Критерий Стьюдента был разработан английским химиком У.Госсетом,
когда он работал на пивоваренном заводе Гиннеса и по условиям контракта не
имел права открытой
публикации своих
исследований. Поэтому при
публикации своих статей по t-критерию У.Госсет сделал в 1908г. под
псевдонимом "Student", что в переводе означает "Студент". В отечественной же
литературе принято писать "Стьюдент".
Коварная простота вычисления t-критерия Стьюдента, а также его наличие
в большинстве статистических пакетов и программ привели к широкому
использованию этого критерия даже в тех условиях, когда применять его
нельзя. Для t –критерия этих условий три: шкала измерения должна быть не
ниже интервальной, данные должны иметь нормальное распределение и
дисперсия выборок должна быть одинаковой.
Рассмотрим все три требования.
1.
Требование
шкалы
интервалов.
Данные
можно
не
только
проранжировать в соответствии с выделенным признаком, но существует
определенная
метрика
шкалы,
выполняется
требование
равномерности
интервалов. В психологических исследованиях шкала интервалов встречается
при использовании стандартизированных тестов, для которых указан способ
62
перехода от сырых (порядковых оценок) к интервальным (стенам, станайнам и
т.д.). Информация о шкале измерения обычно указывается в инструкции к
тесту5.
2. Данные должны иметь нормальное распределение. Для того чтобы
проверить
это
необходимо
воспользоваться
либо
двойным
составным
критерием, либо критерием χ², которые рассматривались выше.
3. Дисперсия выборок должна быть одинаковой. Это условие проверяется
при помощи F-критерия Фишера, который рассматривался выше.
t-критерий Стьюдента существует в нескольких модификациях для связной
выборки, для несвязной выборки и для определения значимости различия
вероятностей появления событий. Рассмотрим все три модификации.
3.3 t-критерий Стьюдента для связанных выборок
t- критерий для связанных выборок или иначе говоря для зависимых
измерений используется для определения вероятности того, что наблюдаемое
различие между двумя условиями для одних и тех же6 участников обусловлено
случаем.
Расчет 2.6. Продолжим анализ примера 2.1. Как было выяснено в ходе
расчетов 2.1.и
2.4 полученные в примере 2.1 данные имеют нормальное
распределение
и
выборочные
дисперсии
значимо
не
отличаются.
Следовательно, попытаемся найти различия в средних используя t-критерий
Стьюдента. Попытаемся ответить на вопрос есть ли различия в показателях
участников до и после проведения тренинга, если уже известно, что
Подробнее о стандартизации и переходе к интервальной шкале можно узнать в книге А. А.Анастази, С.Урбина
"Психологическое тестирование" или М.Б.Челышковой "Теория и практика конструирования педагогических
тестов".
6
Д.Мартин предлагает использовать t-критерий Стьюдента для зависимых измерений при оценке различий в
попарно уравненных группах. Т.е. возможно сравнение показателей не только одного и того же испытуемого, но
и испытуемых с одинаковыми характеристиками.
5
63
распределение данных и до и после одинаково (является нормальным) и
дисперсии выборок не отличаются?
Вопрос: Различаются ли средние показатели участников до и после
тренинга?
Сформулируем гипотезы:
Н0 – Средние двух выборок различаются незначимо (различия в средних выборок случайны);
Н1 – Средние двух выборок различаются значимо (различия в средних выборок неслучайны);
Для наглядности скопируем таблицу 9 добавив к ней 2 столбца для
проведения расчетов
Таблица 16
ФИО
ХДо
ХПосле
δ
δ2
1. И.В.Л.
5
5
0
0
2. Я.Е.А.
4
1
3
9
3. К.С.И.
4
4
0
0
4. Р.М.Н.
4
4
0
0
5. Н.М.Т.
5
4
1
1
6. Е.Л.П.
6
5
1
1
7. Л.К.С.
3
5
-2
4
8. Т.А.П.
6
5
1
1
9. Б.В.В.
6
5
1
1
10.С.М.А.
5
6
-1
1
11.В.П.Р.
6
6
0
0
12.Ч.Н.Г.
6
3
3
3
13.А.С.П
3
1
2
2
14.В.С.К.
4
3
1
1
15.В.П.П.
4
3
1
1
16.Л.Г.Т
4
4
0
0
17.Т.И.Ч
4
4
0
0
S1=11
S2=33
Сумма
64
Сосчитаем разницу между Xдо и Xпосле запишем в таблицу 16 (δ =(Xдо-Xпосле)) и
найдем сумму Σδ.
Возведем δ в квадрат запишем в таблицу 16 и найдем сумму Σδ2.
Теперь найдем среднюю разницу  
S1 11

 0,64 ,
n 17
Далее найдем стандартное отклонение SDδ=
Рассчитаем tэмп=

2
( n  1)

33
 1, 43
16
 n 0,64

17  1,85 , определим размерность системы df=nSD 1, 43
1=16
Найдем по таблице Х приложения t0,05
16=2,12.
Гипотеза о сходстве
принимается если tэмп≤t0.05, таким образом т.к. 1,85<2,12, то отвергается
гипотеза о различии.
Ответ: Принимается Н0. Средние значения отличаются незначимо. Значимых различий
между выборками найдено не было.
На основании анализа 2.4, 2.6 можно заключить, что результаты участников тренинга
относятся к одной генеральной совокупности, а значит влияния тренинга на изменение
личностной тревожности незначительное.
3.4 t-критерий Стьюдента для несвязанных выборок
t-критерий используется для определения является ли различие в
распределении значений между двумя группами случайным или статистически
значимым. Для вычисления t-критерия Стьюдента используется следующая
формула:
t=
| M1  M 2 |
m m
2
1
2
2
, где М – среднее значение по выборке, m 
SDx
, а SDx –
(n  1)
стандартное отклонение
65
Расчет 2.7. Продолжим анализ примера 2.2.
Вопрос: Значимо ли различие средних показателей выборок личностной тревожности у
испытуемых в контрольной и экспериментальной группах.
Сформулируем гипотезы:
Н0 – Средние значения полученные в экспериментальной и контрольной группах различаются
незначимо;
Н1 – Средние значения полученные в экспериментальной и контрольной группах
различаются значимо;
Воспользуемся уже рассчитанными в пункте 2.2. значениями M, SD и n
рассчитанными для экспериментальной и контрольной группы.
Mэксп = 6,25 SDэксп= 1,86
Mконтр = 6,73 SDконтр = 1,64
mэксп= 0,169 (mэксп)2=0,028
mконтр=0,1509 (mконтр)2=0,022
t=
| M1  M 2 |
m m
2
1
2
2

определим
| 6, 25  6,73 |
0, 48

 2,18
0,028  0,022 0, 22
теперь
размерность
системы
df=nэксп-1+nконтр-1=121-1+118-
1=220+117=337
По таблице Х приложения найдем t0.05 = 1,968, сравним tэмп > t0.05 следовательно
гипотеза о значимости принимается.
Ответ: Принимается Н1. Средние значения отличаются значимо (p<0.05). Различия в
выборках неслучайны.
3.5 Применение t-критерия Стьюдента для определения значимости
различий в вероятностях появления событий
Для того чтобы иметь возможность сравнивать вероятности событий
необходимо
проанализировать
природу
процесса.
При
сопоставлении
66
вероятностей t-критерий Стьюдента основывается на предположении, что при
большом числе наблюдений вероятность события стремиться к вполне
определенной величине, т.е. существует предел вероятности при стремящемся к
бесконечности числе наблюдений. Таким образом данную модификацию можно
применять только к определенного рода последовательностям измерений.
Формула расчета данной модификации t-критерия проста:
t
| p1  p2 |
m m
2
1
2
2
, где p – вероятность одного события, а m 2 
p (1  p )
, где n –
n 1
количество наблюдений.
Рассмотрим пример.
Пример 3. Необходимо определить значимо ли различаются вероятности
записывания цифр "7" и "1" испытуемым, если число наблюдений 1300, а
частотность p("7")=0,108 p("1")=0,15.
Вопрос: действительно ли испытуемый предпочитает число предпочитает цифру "1"
цифре "7".
Сформулируем гипотезы:
Н0 – Вероятности написания цифр различаются незначимо (различия в средних выборок
случайны);
Н1 – Вероятности написания цифр различаются значимо (различия в средних выборок
неслучайны);
Найдем m12 
p1 (1  p1 )
0,108(1  0,108)
(
)  0,0001 ,
n 1
1300
Найдем m22 
p2 (1  p2 )
0,15(1  0,15)
(
)  0,0001 ,
n 1
1300
Тогда t 
| p1  p2 |
m12  m22

| 0,108  0,15 |
0,042

 2,99
0,0001  0,0001 0,014
Определим размерность df=n-1
67
По таблице Х приложения найдем t0.05
1300=
1,96 , т.к. tэмп> t0.05, то гипотеза о
существовании достоверных различий принимается.
Ответ: Принимается Н1. Вероятности событий значения отличаются значимо (p<0.05).
Различия неслучайны. Испытуемый значимо чаще пишет цифру "1" чем цифру "7".
68
ЛИТЕРАТУРА
1. Артемьева Е.Ю., Мартынов Е.М. Вероятностные методы в психологии. М.:
МГУ, 1975.
2. Гласс Д., Стенли Д. Статистические методы в педагогике и психологии. М.:
Прогресс, 1976.
3. Грабарь М.И., Краснянская К.А. Применение математической статистики в
педагогических исследованиях: Непараметрические методы. М.: Педагогика,
1977
4. Гублер Б.В., Генкин А.А. Применение непараметрических критериев
статистики в медико-биологических исследованиях.– Л. : Медицина, 1973
5. Зароченцев К.Д., Худяков А.И. Экспериментальная психология.М.: ТК
Велби, 2005.
6. Ительсон Л.Б. Математические и кибернетические методы в педагогике. М.:
Просвещение, 1964..
7. Крамер Г. Математические методы статистики. М.: Мир, 1975
8. Орлов А.И. Эконометрика. М.: Экзамен, 2003.
9. Паповян С.С. Математические методы в социальной психологии. М.: Наука
10.Сидоренко Е.В. Методы математической обработки в психологии. СПб.:
Речь, 2000.
11.Суходольский Г.В. Основы математической статистики для психологов. Л.:
ЛГУ, 1972
12.Тюрин Ю.Н., Литвак Б.Г., Орлов А.И., Сатаров Г.А., Шмерлинг Д.С. Анализ
нечисловой информации. М.: Научный совет АН СССР по комплексной
проблеме "Кибернетика", 1981
13.http://teorver-online.narod.ru/oknige.html
14.http://www.sevin.ru/fundecology/about.html
15.http://www.statsoft.ru/home/textbook
69
ПРИЛОЖЕНИЕ
Таблица I. Критические значения критерия знаков G для уровней
статистической значимости р<0,05 и р<0,01 (по Оуэну Д., 1966)
Преобладание "типичного" сдвига является достоверным, если Gэмп ниже
или равен G0,05 и тем более достоверным, если Gэмп ниже или равен G0,01 .
p
n
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
2021
22
25
24
25
26
0,05
0
0
0
1
1
1
2
2
3
3
3
4
4
5
5
5
6
6
7
7
7
8
n
0,01
0
0
0
0
1
1
1
2
2
2
3
3
4
4
4
5
5
5
6
6
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
p
0,05
8
8
9
10
10
10
11
11
12
12
13
13
13
14
14
15
15
16
16
16
17
17
p
n
0,01
77
7
8
8
8
9
9
10
10
10
11
11
12
12
13
13
13
14
14
15
15
49
50
52
54
56
58
60
62
64
66
68
70
72
74
76
78
80
82
84
86
88
90
0,05
18
18
19
20
21
22
23
24
24
25
26
27
28
29
30
31
32
33
33
34'
35
36
p
n
0,01
15
16
17
18
18
19
20
21
22'
23
23
24
25
26
27
28
29
30
30
31
32
33
92
94
96
98
100
110
120
130
140
150
160
170
180
190
200
220
240
260
280
300
0,05
37
38
39
40
41
45
50
55
59
64
69
73
78
83
87
97
106
116
125
135
0,01
34
35
36
37
37
42
46
51
55
60
64
69
73
78
83
92
101
110
120
129
70
Таблица II. Критические значения критерия U Манна-Уитни для уровней
статистической значимости р<0,05 и р<0,01 (по Гублеру Е.В., Генкину А.А.
1973)
Различия между двумя выборками можно считать значимыми (р<0,05), если
Uэмп ниже или равен U0,05. и тем более достоверными (р<0,01), если Uэмп ниже
или равен U0,01.
n1
n2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2
3
4
5
6
7
8
9
10
0
0
0
1
1
1
1
2
2
3
3
3
3
4
4
4
0
0
1
2
2
3
4
4
5
5
6
7
7
8
9
9
10
11
1
2
3
4
5
6
7
8
9
10
11
12
14
15
16
17
18
4
5
6
8
9
11
12
13
15
16
18
19
20
22
23
25
7
8
10
12
14
16
17
19
21
23
25
26
28
30
32
11
13
15
17
19
21
24
26
28
30
33
35
37
39
15
18
20
23
26
28
31
33
36
39
41
44
47
21
24
27
30
33
36
39
42
45
48
51
54
27
31
34
37
41
44
48
51
55
58
62
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
-
0
0
1
1
1
2
2
2
3
3
4
4
4
5
0
1
1
2
3
3
4
5
5
6
7
7
8
9
9
10
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3
4
6
7
8
9
11
12
13
15
16
18
19
20
22
6
7
9
11
12
14
16
17
19
21
23
24
26
28
9
11
13
15
17
20
22
24
26
28
30
32
34
14
16
18
21
23
26
28
31
33
36
38
40
19
22
24
27
30
33
36
38
41
44
47
,
0
0
0
0
0
0
1
1
11 12
p<0,05
34
38 42
42 47
46 51
50 55
54 60
57 64
61 68
65 72
69 77
p<0,01
25
28
31
34
37
41
44
47
50
53
31
35
38
42
46
49
53
56
60
13
14
15
16
17
51
56
61
65
70
75
80
84
61
66 72
71 77
77 83
82 88
87 94
92 100
83
89
95
101
107
96
102 109
109 116 123
115 123 130 138
39
43
47
51
55
59
63
67
47
51
56
60
65
69
73
66
71
76
82
87
77
82 88
88 94 101
93 100 107 114
56
61
66
70
75
80
18
19
20
71
Таблица II (продолжение)
n1
n2
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
4
5
6
7
8
9
10
19
20
21
22
23.
24
25
26
27
28
29
30
31
32
33
35
36
37
38
39
26
28
29
31
32
33
35
36
38
39
41
42
43
45
46
48
49
51
52
53
34
36
37
39
41
43
45
47
48
50
52
54
56
58
59
61
63
65
67
69
41
44
46
48
50
53
55
57
59
62
64
66
68
71
73
75
77
79
82
84
49
52
55
57
60
62
65
68
70
73
76
78
81
84
86
89
92
94
97
100
57
60
63
66
69
72
75
79
82
85
88
91
94
97
100
103
106
109
112
115
65
69
72
75
79
82
86
89
93
96
100
103
107
110
114
117
121
124
128
131
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
10
10
11
12
12
13
14
14
15
15
16
17
17
18
19
19
20
21
21
22
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
22
23
25
26
27
29
30
32
33
34
36
37
38
40
41
42
44
45
46
48
29
30
32
34
35
37
39
41
42
44
46
47
49
51
53
54
56
58
59
61
35
37
39
42
44
46
48
50
52
54
56
58
60
62
64
67
69
71
73
75
42 49
45 52
47 55
49 57
52 60
54 63
57 66
59 69
62 72
64 75
67 77
69 80
72 83
74 86
77 89
79 92
81 95
.84 97
86 100
89 103
11
12 13
p=0,05
73 81 89
77 85 94
81 90 99
85 94 103
89 98 108
93 103 113
96 107 118
100 111 122
104 116 127
108 120 132
112 124 137
116 129 141
120 133 146
124 137 151
128 142 156
132 146 160
135 150 165
139 155 170
143 159 175
147 163 179
p<0.01
56 63 70
59 66 74
62 70 78
66 74 82
69 77 86
72 81 90
75 85 94
78 88 98
82 92 102
85 95 106
88 99 110
91 103 114
95 106 118
98 110 122
101 114 126
104 117 130
108 121 134
111 125 138
114 128 142
117 132 146
14
15
16
17
18
19
20
21
97
102
107
113
118
123
128
193
139
144
149
154
159
164
170
175
180
185
190
196
105
111
116
122
128
133
139
144
150
156
161
167
173
178
184
189
195
201
206
212
113
119
125
131
137
143
150
156
162
168
174
180
186
192
198
204
210
216
222
228
121
128
134
141
147
154
160
167
173
180
186
193
199
206
212
219
225
232
238
245
130
136
143
150
157
164
171
178
185
192
199
206
213
.219
226
233
240
247
254
261
138
145
152
160
167
174
182
189
196
204
211
219
226
233
241
248
255
263
270
278
146
154
161
169
177
185
193
200
208
216
224
232
239
247
255
263
271
278
286
294
154
162
170
179
187
195
203
212
220
228
236
245
253
261
269
278
286
294
302
311
77
81
86
90
95
9У
103
108
112
117
121
126
130
134
13У
143
148
152
157
-161
84
89
94
98
103
108
113
118
123
127
132
137
142
147
152
156
161
166
171
176
91
96
102
107
112
117
122
128
133
138
143
149
154
159
164
170
175
180
185
191
98
104
109
115
121
126
132
138
143
149
155
160
166
172
177
1ЙЗ
189
1У4
200
206
105
111
117
123
130
136
142
148
154
160
166
172
178
184
19О
196
202
208
214
221
113
119
125
132
13В
145
151
15В
164
1/1
177
184
190
197
203
210
216
223
229
236
120
127
133
140
147
154
161
168
175
182
188
1У5
202
209
216
223
23U
237
244
251
127
134
141
149
156
163
171
178
185
192
200
207
214
222
229
236
244
251
258
266
72
Таблица II (продолжение)
n1
n2
41
42
43
44
45
46
47
48
49
50
51
52
55
54
55
56
57
58
59
60
22
23
24
25
26
27
28
29
336
345
353
362
371
380
388
397
406
414
423
432
441
449
458
467
476
484
493
502
353
362
371
380
390
399
408
417
426
435
445
454
463
472
481
491
500
509
518
527
370
380
389
399
408
418
428
437
447
457
466
476
485
495
505
514
524
534
543
553
387
397
407
417
427
437
447
458
468
478
488
408
508
518
528
538
548
558
568
578
404
415
425
436
446
457
467
478
488
499
509
520
530
541
551
562
572
583
594
604
421
432
443
454
465
476
4B7
498
509
520
531
542
553
564
575
586
597
608
619
630
438
450
461
473
484
495
507
518
530
541
553
564
575
587
598
610
621
633
644
655
456
467
479
491
503
515
527
539
550
562
574
586
598
610
622
634
645
657
669
681
41
42
43
44
45
46
47
48
49
50
51
52
55
54
55
56
57
58
59
60
289
296
304
312
320
328
335
343
351
359
366
374
382
390
398
405
413
421
429
437
304
312
321
329
337
345
353
362
370
378
386
395
403
411
419
427
436
444
452
460
320
328
337
346
354
363
372
380
389
398
406
415
423
432
441
449
458
467
475
484
336
345
354
363
372
381
390
399
408
417
526
435
444
453
462
471
581
490
499
508
351
361
370
380
389
399
408
418
427
437
446
456
465
475
484
494
503
513
522
532
367
377
387
397
407
416
426
436
446
456
466
476
486
496
506
516
526
536
545
555
383
393
403
414
424
434
445
455
465
476
486
496
507
517
527
538
548
559
569
579
398
409
420
431
441
452
463
474
484
495
506
517
528
538
549
560
571
582
592
603
30
31 32
p<0,05
473 490 507
485 503 520
497 515 533
510 528 547
522 541 560
534 554 573
547 566 586
559 579 600
571 592 613
583 605 626
596 618 639
608 630 652
620 643 666
633 656 679
645 й69 692
657 681 705
670 694 719
682 707 732
694 720 745
707 733 758
р<0,01
414 430 446
425 442 458
437 453 470
448 465 482
459 476 494
470 488 506
481 500 518
492 511 530
504 523 542
515 535 554
526 546 566
537 558 578
549 570 591
560 581 603
571 593 615
582 605 627
593 616 639
605 628 651
616 640 663
627 651 675
33
34
35
36
37
38
39
40
524
538
552
565
579
593
606
620
634
647
661
675
688
702
716
729
743
757
770
784
541
556
570
584
598
612
626
640
654
669
683
697
711
725
739
753
768
782
796
810
559
573
588
602
617
631
646
661
675
690
704
719
734
748
763
777
792
807
821
836
576
591
606
621
636
651
666
681
696
711
726
741
756
771
786
801
816
832
847
862
593
609
624
640
655
670
686
701
717
732
74Я
763
779
794
810
825
841
856
872
888
610
626
642
658
674
690
706
722
738
754
770
786
802
81B
834
850
865
881
897
913
628
644
660
677
693
709
726
742
759
775
791
808
824
841
857
874
890
906
923
939
645
662
679
695
712
729
746
763
780
796
813
830
S47
864
881
898
915
931
948
965
462
474
487
499
511
524
536
549
561
574
587
599
612
624
637
649
662
674
687
699
477
490
503
516
529
542
555
568
581
594
607
620
633
646
659
671
684
697
710
723
493
507
520
533
547
560
573
587
600
613
627
640
654
667
680
694
707
721
734
747
509
523
537
550
564
578
592
606
619
633
647
661
675
689
702
716
730
744
758
772
525
539
553
568
582
596
610
625
639
653
667
682
696
710
724
738
753
767
781
796
541
556
570
585
599
614
629
643
658
673
688
702
717
732
746
761
776
790
805
820
557
572
587
602
617
632
647
662
678
693
708
723
738
753
768
784
799
814
829
844
573
588
604
619
635
650
666
681
697
713
728
744
759
775
790
806
822
837
853
868
73
Таблица II (окончание).
n1
n2
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
611
43
44
45
46
47
48
49
662
679 697
697 715
714 733
731 750
749 768
766 786
783 804
800 821
818 839
835 857
852 875
870 893
887 910
904 928
922 946
939 964
956 981
974 999
991 1017
733
751
769
788
806
824
842
861
879
897
915
934
952
970
988
1007
1025
1043
770
789
807
826
845
863
882
901
919
938
957
975
994
1013
1032
1050
1069
808
827
846
865
884
903
922
942
961
980
999
1018
1037
1057
1076
109;
846
866
886
905
925
944
964
934
1003
1026
1046
1062
1082
1101
1121
886
906
926
946
966
986
100(
1026
104(
1067
1087
1107
1127
1147
927
947
968
988
100'
1029
105t
107(
1091
1111
1132
1152
1173
968
989
1010
1031
1052
1073
1094
1115
1136
1157
1178
1199
589
605
621
636
652
668
684
700
716
732
748
764
780
796
812
828
844
861
877
893
654
671
688
705
722
736
755
772
789
806
823
840
857
873
890
907
924
941
688
706 723
723 741 759
740 759 777 796
757 776 7У5 814
775 794 814 833
792 812 832 852
809 830 850 870
827 847 868 889
844 865 886 908
861 883 905 926
879 901 923 945
896 919 941 964
913 936 959 982
931 954' 978 100
948 972 996 1021
965 990 1014 1038
834
853
872
891
910
929
948
967
986
1005
1024
1044
1063
872
892
911
931
950
970
989
1009
1028
1048
1068
1087
41
42
621
637
654
670
687
703
719
736
752
769
785
802
818
834
851
867
884
900
917
50
51
p<0,05
1010
1032 1054
1053 1076
1075 109i
1096 1119
1113 1141
1139 1163
1161 1185
1182 1207
1204 1229
1225 1251
p<0,01
912
932
951
971
991
101
103
1051
1071
109
111
952
972
993
1013
1034
1054
1074
1095
1115
1136
52
53
54
55
56
57
58
59
60
1098
1120
1143
1165
1187
1210
123;
1255
1277
1143
1166
1189
1212
1235
1257
128(
1303
1189
1213
1236
1259
128:
1306
1329
1236
1260
1284
130f
1331
1355
1284
1309
1333
1357
1381
1333
1358 138:
1383 1408 1434
1407 1433 1460 1486
99J
1014
1035
1056
1077
1098
1118
1139
1161
1035
1057
1078
1099
1121
1142
1163
1185
1078
1100
1122
1141
1165
1187
1209
1122
1145
1167
1189
1211
1234
1167
1190
1213
1235
1258
1213
1236 1260
1259 1283 1307
1282 1307 1331 1356
74
Таблица III.
Критические значения коэффициента корреляции рангов Спирмена
n
5
6
7
8
9
10
11
12
13
14
15
16
0,05
0,91
0,85
0,78
0,72
0,68
0,64
0,61
0,58
0,56
0,54
0,52
0,50
P
0,01
0,94
0,88
0,83
0,79
0,76
0,73
0,70
0,68
0,66
0,64
P
n
17
18
19
20
21
22
23
24
25
26
27
28
0,05
0,48
0,47
0,46
0,45
0,44
0,43
0,42
0,41
0,49
0,39
0,38
0,38
0,01
0,62
0,60
0,58
0,57
0,56
0,54
0,53
0,52
0,51
0,50
0,49
0,48
n
29
30
31
32
33
34
35
36
37
38
39
40
0,05
0,37
0,36
0,36
0,36
0,34
0,34
0,33
0,33
0,33
0,32
0,32
0,31
P
0,01
0,48
0,47
0,46
0,45
0,45
0,44
0,43
0,43
0,43
0,41
0,41
0,40
75
Таблице IV. Квантили χ²-распределения для уровней значимости p<0,05 и
p<0,01 (по Суходольскому Г.В., 1998)
Различия можно считать значимыми на указанном в таблице уровне
значимости если χ²эмп достигает соответствующего критического значения или
превышает его.
df
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
P
0,05
3,84
5,99
7,82
9,49
11,1
12,6
14,1
15,5
16,9
18,3
19,7
21,0
22,4
23,7
25,0
26,3
27,6
28,9
30,1
31,4
32,7
33,9
35,2
36,4
37,6
38,9
40,1
41,3
42,6
43,8
0,01
6,64
9,21
11,3
13,3
15,1
16,8
18,5
20,1
21,7
23,2
24,7
26,2
27,7
29,1
30,6
32,0
33,4
34,8
36,2
37,6
38,9
40,3
41,6
43,0
44,3
45,6
47,0
48,3
49,6
50,9
df
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
52
54
56
58
60
62
64
66
68
70
p
0,05
45,0
46,2
47,4
48,6
49,8
51,0
52,2
53,4
54,6
55,8
56,9
58,1
59,3
60,5
61,7
62,8
64,0
65,2
66,3
67,5
69,8
72,2
74,5
76,8
79,1
81,4
83,7
86,0
88,2
90,5
0,01
52,2
53,5
54,8
56,1
57,3
58,6
59,9
61,2
62,4
63,7
65,0
66,2
67,5
68,7
70,0
71,2
72,4
73,7
74,9
76,2
78,6
81,1
83,5
86,0
88,4
90,8
93,2
95,6
98,0
100
df
72
74
76
78
80
82
84
86
88
90
92
94
96
98
100
110
120
130
140
150
200
250
300
400
500
600
700
800
900
1000
p
0,05
92,8
95,1
97,4
99,6
102
104
106
109
111
113
115
118
120
122
124
135
147
158
169
180
234
288
341
448
553
658
763
867
971
1075
0,01
103
105
108
110
112
115
117
119
122
124
126
129
131
133
136
147
159
170
182
193
249
305
360
469
576
683
790
896
1002
1107
76
Таблица V. Диапазоны двойного составного критерия (по К.Д.Зароченцеву
и А.И.Худякову 2005)
df
16
21
26
31
36
41
46
51
d1
0,9137
0,9001
0,8901
0,8826
0,8769
0,8722
0,8682
0,8648
d2
0,6829
0,6950
0,7360
0,7110
0,7167
0,7216
0,7256
0,7291
Таблица VI. Значения двойного составного критерия (по К.Д.Зароченцеву и
А.И.Худякову 2005)
df
11-14
15-20
21-22
23-35
36-50
m
1
1
2
2
2
z
2,33
2,58
2,17
2,33
2,58
77
Таблица VII. Таблица интегральной функции нормального распределения
(по Суходольскому Г.В., 1998)
Пример использования:
Для того чтобы найти Ф(1,15) найдем в первом столбце 1,1 (строка 13) и
найдем в каком столбце задано 0,05 (столбец 7) на пересечении строки 13
столбца 7 находим значение .8749, значит Ф(1,15)= 0.8749, если бы хотели
найти Ф(-1.15) необходимо найти Ф(1,15) и по формуле Ф(-t)=1-Ф(t), найти Ф(1,15)=1-Ф(1,15)=1-0.8749=0,1251.
T
0.
.1
.2
.3
.4
.5
.6
.7
.8
.9
1.0
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2.0
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
3.0
3.1
.00
.5000
.5398
.5793
.6179
.6554
.6915
.7257
.7580
.7881
.8159
.8413
.8643
.8849
.9032
.9192
.9332
.9452
.9554
.9641
.9713
.9772
.9821
.9861
.9893
.9918
.9938
.9953
.9965
.9974
.9981
.9987
.9990
.01
.5040
.5438
.5832
.6217
.6591
.6950
.7291
.7611
.7910
.8186
.8438
.8665
.8869
.9049
.9207
.9345
.9463
.9564
.9649
.9719
.9778
.9826
.9864
.9896
.9920
.9940
.9955
.9966
.9975
.9982
.9987
.9991
.02
.5080
.5478
.5871
.6255
.6628
.6985
.7324
.7642
.7939
.8212
.8461
.8686
.8888
.9066
.9222
.9357
.9474
.9573
.9656
.9726
.9783
.9830
.9868
.9898
.9922
.9941
.9956
.9967
.9976
.9982
.9987
.9991
.03
.5120
.5517
.5910
.6293
.6664
.7019
.7357
.7673
.7967
.8238
.8485
.8708
.8907
.9082
.9236
.9370
.9484
.9582
.9664
.9732
.9788
.9834
.9871
.9901
.9925
.9943
.9957
.9968
.9977
.9983
.9988
.9991
.04
.5160
.5557
.5948
.6331
.6700
.7054
.7389
.7704
.7995
.8264
.8508
.8729
.8925
.9099
.9251
.9382
.9495
.9591
.9671
.9738
.9793
.9838
.9875
.9904
.9927
.9945
.9959
.9969
.9977
.9984
.9988
.9992
.05
.5199
.5596
.5987
.6368
.6736
.7088
.7422
.7734
.8023
.8289
.8531
.8749
.8944
.9115
.9265
.9394
.9505
.9599
.9678
.9744
.9798
.9842
.9878
.9906
.9929
.9946
.9960
.9970
.9978
.9984
.9989
.9992
.06
.5239
.5636
.6026
.6406
.6772
.7123
.7454
.7764
.8051
.8315
.8554
.8770
.8962
.9131
.9279
.9406
.9515
.9608
.9686
.9750
.9803
.9846
.9881
.9909
.9931
.9948
.9961
.9971
.9979
.9985
.9989
.9992
.07
.5279
.5675
.6064
.6443
.6808
.7157
.7486
.7794
.8078
.8340
.8577
.8790
.8980
.9147
.9292
.9418
.9525
.9616
.9693
.9756
.9808
.9850
.9884
.9911
.9932
.9949
.9962
.9972
.9979
.9985
.9989
.9992
.08
.5319
.5714
.6103
.6480
.6844
.7190
.7517
.7823
.8106
.8365
.8599
.8810
.8997
.9162
.9306
.9429
.9535
.9625
.9699
.9761
.9812
.9854
.9887
.9913
.9934
.9951
.9963
.9973
.9980
.9986
.9990
.9993
.09
.5359
.5753
.6141
.6517
.6879
.7224
.7549
.7852
.8133
.8389
.8621
.8830
.9015
.9177
.9319
.9441
.9545
.9633
.9706
.9767
.9817
.9857
.9890
.9916
.9936
.9952
.9964
.9974
.9981
.9986
.9990
.9993
78
3.2
3.3
3.4
.9993
.9995
.9997
.9993
.9995
.9997
.9994
.9995
.9997
.9994
.9996
.9997
.9994
.9996
.9997
.9994
.9996
.9997
.9994
.9996
.9997
.9995
.9996
.9997
.9995
.9996
.9997
.9995
.9997
.9998
Таблица VIII. Нормальная корреляция (по Гублеру Е.В., Генкину А.А.
1973)
Минимальные значения коэффициентов нормальной корреляции, при
которых связь между двумя рядами наблюдений можно считать значимой с
уровнем надежности p, а п— число пар сравниваемых наблюдений
p
N
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
35
40
45
50
60
70
80
90
100
0,05
0,729
0,669
0,621
0,582
0,549
0,521
0,497
0,476
0,457
0,441
0,426
0,412
0,400
0,389
0,378
0,369
0,360
0,323
0,296
0,275
0,257
0,243
0,231
0,211
0,195
0,183
0,173
0,164
0,025
0,811
0,754
0,707
0,666
0,632
0,602
0,576
0,553
0,532
0,514
0,497
0,482
0,468
0,456
0,444
0,433
0,423
0,381
0,349
0,325
0,304
0,288
0,273
0,250
0,232
0,217
0,205
0,195
0,01
0,882
0:833
0,789
0,750
0,715
0,685
0,658
0,634
0,612
0,592
0,574
0,558
0,543
0,529
0,516
0,503
0,492
0,445
0,409
0,381
0,358
0,338
0,322
0,295
0,274
0,257
0,242
0,230
0,005
0,917
0,875
0,834
0,798
0,765
0,735
0,708
0,684
0,661
0,641
0,623
0,606
0,590
0,575
0,561
0,549
0,537
0,487
0,449
0,418
0,393
0,372
0,354
0,325
0,302
0,283
0,267
0,254
0,0025
0,941
0,905
0,870
0,836
0,805
0,776
0,750
0,726
0,703
0,683
0,664
0,647
0,631
0,616
0,602
0,589
0,576
0,524
0,484
0,452
0,425
0,403
0,384
0,352
0;327
0,307
0,290
0,276
0,0005
0,974
0,950
0,924
0,898
0,872
0,847
0,823
0,801
0,780
0,760
0,742
0,725
0,708
0,693
0,679
0,665
0,652
0,597
0,554
0,519
0,490
0,465
0,443
0,408
0,380
0,357
0,338
0,321
79
Таблица IХ. F-распределение для уровня значимости р<0,05 и р<0,01 (по
Суходольскому Г.В., 1998)
Различия можно считать значимыми на указанном в таблице уровне
значимости, если Fэмп достигает соответствующего критического значения или
превышает его.
Таблица IХа (начало). Уровень значимости р<0,05.
n2\n1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
∞
1
161,44
18,513
10,128
7,709
6,608
5,987
5,591
5,318
5,117
4,965
4,844
4,747
4,667
4,600
4,543
4,494
4,451
4,414
4,381
4,351
4,325
4,301
4,279
4,260
4,242
4,225
4,210
4,196
4,183
4,171
4,085
4,001
3,920
3,842
2
199,50
19,000
9,552
6,944
5,786
5,143
4,737
4,459
4,257
4,103
3,982
3,885
3,806
3,739
3,682
3,634
3,592
3,555
3,522
3,493
3,467
3,443
3,422
3,403
3,385
3,369
3,354
3,340
3,328
3,316
3,232
3,150
3,072
2,996
3
215,70
19,164
9,277
6,591
5,410
4,757
4,347
4,066
3,863
3,708
3,587
3,490
3,411
3,344
3,287
3,239
3,197
3,160
3,127
3,098
3,073
3,049
3,028
3,009
2,991
2,975
2,960
2,947
2,934
2,922
2,839
2,758
2,680
2,605
4
224,58
19,247
9,117
6,388
5,192
4,534
4,120
3,838
3,633
3,478
3,357
3,259
3,179
3,112
3,056
3,007
2,965
2,928
2,895
2,866
2,840
2,817
2,796
2,776
2,759
2,743
2,728
2,714
2,701
2,690
2,606
2,525
2,447
2,372
5
230,16
19,296
9,014
6,256
5,050
4,387
3,972
3,688
3,482
3,326
3,204
3,106
3,025
2,958
2,901
2,852
2,810
2,773
2,740
2,711
2,685
2,661
2,640
2,621
2,603
2,587
2,572
2,558
2,545
2,534
2,450
2,368
2,290
2,214
6
233,98
19,330
8,941
6,163
4,950
4,284
3,866
3,581
3,374
3,217
3,095
2,996
2,915
2,848
2,791
2,741
2,699
2,661
2,628
2,599
2,573
2,549
2,528
2,508
2,490
2,474
2,459
2,445
2,432
2,421
2,336
2,254
2,175
2,099
7
236,76
19,353
8,887
6,094
4,876
4,207
3,787
3,501
3,293
3,136
3,012
2,913
2,832
2,764
2,707
2,657
2,614
2,577
2,544
2,514
2,488
2,464
2,442
2,423
2,405
2,388
2,373
2,359
2,346
2,334
2,249
2,167
2,087
2,010
8
238,88
19,371
8,845
6,041
4,818
4,147
3,726
3,438
3,230
3,072
2,948
2,849
2,767
2,699
2,641
2,591
2,548
2,510
2,477
2,447
2,421
2,397
2,375
2,355
2,337
2,321
2,305
2,291
2,278
2,266
2,180
2,097
2,016
1,938
9
240,54
19,385
8,812
5,999
4,773
4,099
3,677
3,388
3,179
3,020
2,896
2,796
2,714
2,646
2,588
2,538
2,494
2,456
2,423
2,393
2,366
2,342
2,320
2,300
2,282
2,266
2,250
2,236
2,223
2,211
2,124
2,040
1,959
1,880
10
241,88
19,396
8,786
5,964
4,735
4,060
3,637
3,347
3,137
2,978
2,854
2,753
2,671
2,602
2,544
2,494
2,450
2,412
2,378
2,348
2,321
2,297
2,275
2,255
2,237
2,220
2,204
2,190
2,177
2,165
2,077
1,993
1,911
1,831
80
Таблица IХа (окончание).Уровень значимости р<0,05.
n2\n1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
∞
12
243,90
19,413
8,745
5,912
4,678
4,000
3,575
3,284
3,073
2,913
2,788
2,687
2,604
2,534
2,475
2,425
2,381
2,342
2,308
2,278
2,250
2,226
2,204
2,183
2,165
2,148
2,132
2,118
2,105
2,092
2,004
1,917
1,834
1,752
15
245,95
19,429
8,703
5,858
4,619
3,938
3,511
3,218
3,006
2,845
2,719
2,617
2,533
2,463
2,403
2,352
2,308
2,269
2,234
2,203
2,176
2,151
2,128
2,108
2,089
2,072
2,056
2,041
2,028
2,015
1,925
1,836
1,751
1,666
20
248,01
19,446
8,660
5,803
4,558
3,874
3,445
3,150
2,937
2,774
2,646
2,544
2,459
2,388
2,328
2,276
2,230
2,191
2,156
2,124
2,096
2,071
2,048
2,027
2,008
1,990
1,974
1,959
1,945
1,932
1,839
1,748
1,659
1,571
24
249,05
19,454
8,639
5,774
4,527
3,842
3,411
3,115
2,901
2,737
2,609
2,506
2,420
2,349
2,288
2,235
2,190
2,150
2,114
2,083
2,054
2,028
2,005
1,984
1,964
1,946
1,930
1,915
1,901
1,887
1,793
1,700
1,608
1,517
30
250,09
19,462
8,617
5,746
4,496
3,808
3,376
3,079
2,864
2,700
2,571
2,466
2,380
2,308
2,247
2,194
2,148
2,107
2,071
2,039
2,010
1,984
1,961
1,939
1,919
1,901
1,884
1,869
1,854
1,841
1,744
1,649
1,554
1,459
40
251,14
19,471
8,594
5,717
4,464
3,774
3,340
3,043
2,826
2,661
2,531
2,426
2,339
2,266
2,204
2,151
2,104
2,063
2,026
1,994
1,965
1,938
1,914
1,892
1,872
1,853
1,836
1,820
1,806
1,792
1,693
1,594
1,495
1,394
60
252,19
19,479
8,572
5,688
4,431
3,740
3,304
3,005
2,787
2,621
2,490
2,384
2,297
2,223
2,160
2,106
2,058
2,017
1,980
1,946
1,917
1,889
1,865
1,842
1,822
1,803
1,785
1,769
1,754
1,740
1,637
1,534
1,429
1,318
120
253,25
19,487
8,549
5,658
4,399
3,705
3,267
2,967
2,748
2,580
2,448
2,341
2,252
2,178
2,114
2,059
2,011
1,968
1,930
1,896
1,866
1,838
1,813
1,790
1,768
1,749
1,731
1,714
1,698
1,684
1,577
1,467
1,352
1,221
∞
254,31
19,496
8,526
5,628
4,365
3,669
3,230
2,928
2,707
2,538
2,405
2,296
2,206
2,131
2,066
2,010
1,960
1,917
1,878
1,843
1,812
1,783
1,757
1,733
1,711
1,691
1,672
1,654
1,638
1,622
1,509
1,389
1,254
1,000
81
Таблица IХб (начало). Уровень значимости р<0,01.
n2\n1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
inf
1
4052,1
98,503
34,116
21,198
16,258
13,745
12,246
11,259
10,561
10,044
9,646
9,330
9,074
8,862
8,683
8,531
8,400
8,285
8,185
8,096
8,017
7,945
7,881
7,823
7,770
7,721
7,677
7,636
7,598
7,562
7,314
7,077
6,851
6,635
2
4999,5
99,000
30,817
18,000
13,274
10,925
9,547
8,649
8,022
7,559
7,206
6,927
6,701
6,515
6,359
6,226
6,112
6,013
5,926
5,849
5,780
5,719
5,664
5,614
5,568
5,526
5,488
5,453
5,420
5,390
5,179
4,977
4,787
4,605
3
5403,3
99,166
29,457
16,694
12,060
9,780
8,451
7,591
6,992
6,552
6,217
5,953
5,739
5,564
5,417
5,292
5,185
5,092
5,010
4,938
4,874
4,817
4,765
4,718
4,675
4,637
4,601
4,568
4,538
4,510
4,313
4,126
3,949
3,782
4
5624,5
99,249
28,710
15,977
11,392
9,148
7,847
7,006
6,422
5,994
5,668
5,412
5,205
5,035
4,893
4,773
4,669
4,579
4,500
4,431
4,369
4,313
4,264
4,218
4,177
4,140
4,106
4,074
4,045
4,018
3,828
3,649
3,480
3,319
5
5763,6
99,299
28,237
15,522
10,967
8,746
7,460
6,632
6,057
5,636
5,316
5,064
4,862
4,695
4,556
4,437
4,336
4,248
4,171
4,103
4,042
3,988
3,939
3,895
3,855
3,818
3,785
3,754
3,725
3,699
3,514
3,339
3,174
3,017
6
5858,9
99,333
27,911
15,207
10,672
8,466
7,191
6,371
5,802
5,386
5,069
4,821
4,620
4,456
4,318
4,202
4,102
4,015
3,939
3,871
3,812
3,758
3,710
3,667
3,627
3,591
3,558
3,528
3,499
3,473
3,291
3,119
2,956
2,802
7
5928,3
99,356
27,672
14,976
10,456
8,260
6,993
6,178
5,613
5,200
4,886
4,640
4,441
4,278
4,142
4,026
3,927
3,841
3,765
3,699
3,640
3,587
3,539
3,496
3,457
3,421
3,388
3,358
3,330
3,304
3,124
2,953
2,792
2,639
8
5981,0
99,374
27,489
14,799
10,289
8,102
6,840
6,029
5,467
5,057
4,744
4,499
4,302
4,140
4,004
3,890
3,791
3,705
3,631
3,564
3,506
3,453
3,406
3,363
3,324
3,288
3,256
3,226
3,198
3,173
2,993
2,823
2,663
2,511
9
6022,4
99,388
27,345
14,659
10,158
7,976
6,719
5,911
5,351
4,942
4,632
4,388
4,191
4,030
3,895
3,780
3,682
3,597
3,523
3,457
3,398
3,346
3,299
3,256
3,217
3,182
3,149
3,120
3,092
3,067
2,888
2,718
2,559
2,407
10
6055,8
99,399
27,229
14,546
10,051
7,874
6,620
5,814
5,257
4,849
4,539
4,296
4,100
3,939
3,805
3,691
3,593
3,508
3,434
3,368
3,310
3,258
3,211
3,168
3,129
3,094
3,062
3,032
3,005
2,979
2,801
2,632
2,472
2,321
82
Таблица IХб (окончание).Уровень значимости р<0,01.
n2\n1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
∞
12
15
20
24
30
40
60
120
∞
6106.32
99.416
27.052
14.374
9.888
7.718
6.469
5.667
5.111
4.706
4.397
4.155
3.960
3.800
3.666
3.553
3.455
3.371
3.297
3.231
3.173
3.121
3.074
3.032
2.993
2.958
2.926
2.896
2.868
2.843
2.665
2.496
2.336
2.185
6157.28
99.433
26.872
14.198
9.722
7.559
6.314
5.515
4.962
4.558
4.251
4.010
3.815
3.656
3.522
3.409
3.312
3.227
3.153
3.088
3.030
2.978
2.931
2.889
2.850
2.815
2.783
2.753
2.726
2.700
2.522
2.352
2.192
2.039
6208.73
99.449
26.690
14.020
9.553
7.396
6.155
5.359
4.808
4.405
4.099
3.858
3.665
3.505
3.372
3.259
3.162
3.077
3.003
2.938
2.880
2.827
2.781
2.738
2.699
2.664
2.632
2.602
2.574
2.549
2.369
2.198
2.035
1.878
6234.63
99.458
26.598
13.929
9.466
7.313
6.074
5.279
4.729
4.327
4.021
3.780
3.587
3.427
3.294
3.181
3.084
2.999
2.925
2.859
2.801
2.749
2.702
2.659
2.620
2.585
2.552
2.522
2.495
2.469
2.288
2.115
1.950
1.791
6260.64
99.466
26.505
13.838
9.379
7.229
5.992
5.198
4.649
4.247
3.941
3.701
3.507
3.348
3.214
3.101
3.003
2.919
2.844
2.778
2.720
2.667
2.620
2.577
2.538
2.503
2.470
2.440
2.412
2.386
2.203
2.028
1.860
1.696
6286.78
99.474
26.411
13.745
9.291
7.143
5.908
5.116
4.567
4.165
3.860
3.619
3.425
3.266
3.132
3.018
2.920
2.835
2.761
2.695
2.636
2.583
2.535
2.492
2.453
2.417
2.384
2.354
2.325
2.299
2.114
1.936
1.763
1.592
6313.03
99.482
26.316
13.652
9.202
7.057
5.824
5.032
4.483
4.082
3.776
3.535
3.341
3.181
3.047
2.933
2.835
2.749
2.674
2.608
2.548
2.495
2.447
2.403
2.364
2.327
2.294
2.263
2.234
2.208
2.019
1.836
1.656
1.473
6339.39
99.491
26.221
13.558
9.112
6.969
5.737
4.946
4.398
3.996
3.690
3.449
3.255
3.094
2.959
2.845
2.746
2.660
2.584
2.517
2.457
2.403
2.354
2.310
2.270
2.233
2.198
2.167
2.138
2.111
1.917
1.726
1.533
1.325
6365.86
99.499
26.125
13.463
9.020
6.880
5.650
4.859
4.311
3.909
3.602
3.361
3.165
3.004
2.868
2.753
2.653
2.566
2.489
2.421
2.360
2.305
2.256
2.211
2.169
2.131
2.097
2.064
2.034
2.006
1.805
1.601
1.381
1.000
83
Таблица Х. Квантили t-распределения Стьюдента для уровней значимости
p<0,05, p<0,01 и p<0,001 (по Суходольскому Г.В., 1998)
Различия можно считать значимыми на указанном в таблице уровне
значимости если tэмп достигает соответствующего критического значения
или превышает его
df
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
0,05
12,706
4,303
3,182
2,776
2,571
2,447
2,365
2,306
2,262
2,228
2,201
2,179
2,160
2,145
2,131
2,120
2,110
2,101
2,093
2,086
2,080
2,074
2,069
2,064
2,060
2,056
2,052
2,048
2,045
2,042
p
0,01
63,657
9,925
5,841
4,604
4,032
3,707
3,450
3,355
3,250
3,169
3,106
3,054
3,012
2,977
2,947
2,921
2,898
2,878
2,861
2,845
2,831
2,819
2,807
2,797
2,787
2,779
2,771
2,763
2,756
2,750
df
0,001
636,619
31,599
12,924
8,610
6,869
5,959
5,408
5,041
4,781
4,587
4,437
4,318
4,221
4,140
4,073
4,015
3,965
3,922
3,883
3,850
3,819
3,792
3,768
3,745
3,725
3,707
3,690
3,674
3,659
3,646
35
40
45
50
55
60
65
70
75
80
85
90
95
100
105
110
120
130
140
150
200
300
400
500
600
700
800
900
1000
∞
0,05
2,030
2,021
2,014
2,009
2,004
2,000
1,997
1,994
1,992
1,990
1,988
1,987
1,985
1,984
1,983
1,982
1,980
1,978
1,977
1,976
1,972
1,968
1,966
1,965
1,964
1,9634
1,9629
1,9626
1,9623
1,9600
p
0,01
2,724
2,704
2,690
2,678
2,668
2,660
2,654
2,648
2,643
2,639
2,635
2,632
2,629
2,626
2,623
2,621
2,617
2,614
2,611
2,609
2,601
2, 592
2,588
2,586
2,584
2,5829
2,5820
2,5813
2,5808
2,5758
0,001
3,591
3,551
3,520
3,496
3,476
3,460
3,447
3,435
3,426
3,416
3,412
3,402
3,396
3,390
3,386
3,382
3,374
3,366
3,361
3,357
3,340
3,323
3,315
3,310
3,306
3,304
3,302
3,301
3,300
3,291
84
Таблица XI Величины угла (в радианах) для разных процентных долей
(по Ермолаеву )
%, последний десятичный знак
%
доля
0
1
2
3
4
5
6
7
8
9
Значения φ=2arcsin√P
0,0 0,000 0,020 0,028 0,035 0,040 0,045 0,049 0,053
0,057 0,060
0,1 0,063 0,066 0,069 0,072 0,075 0,077 0,080 0,082
0,085
0,087
0,2 0,089 0,092 0,094 0,096 0,098 0,100 0,102 0,104
0,106
0,108
0,3 0,110 0,111 0,113 0,115 0,117 0,118 0,120 0,122
0,123
0,125
0,4 0,127 0,128 0,130 0,131 0,133 0,134 0,136 0,137
0,139
0,140
0,5 0,142 0,143 0,144 0,146 0,147 0,148 0,150 0,151
0,153
0,154
0,6 0,155 0,156 0,158 0,159 0,160 0,161 0,163 0,164
0,165
0,166
0,7 0,168 0,169 0,170 0,171
0,172 0,173 0,175 0,176
0,177
0,178
0,179 0,180 0,182 0,183 0,184 0,185 0,186 0,187
0,188
0,189
0,9 0,190 0,191 0,192 0,193 0,194 0,195 0,196 0,197
0,198
0,199
0,8
1
0,200 0,210 0,220 0,229 0,237 0,246 0,254 0,262
0,269
0,277
2
0,284 0,291 0,298 0,304 0,311 0,318 0,324 0,330
0,336
0,342
3
0,348 0,354 0,360 0,365 0,371 0,376 0,382 0,387
0,392
0,398
4
0,403 0,408 0,413 0,418 0,423 0,428 0,432 0,437
0,442
0,446
5
0,451
0,456 0,460 0,465 0,469 0,473 0,478 0,482
0,486
0,491
6
0,495 0,499 0,503 0,507 0,512 0,516 0,520 0,524
0,528
0,532
7
0,536 0,539 0,543 0,547 0,551 0,555 0,559 0,562
0,566
0,570
8
0,574 0,577 0,581 0,584 0,588 0,592 0,595 0,599
0,602
0,606
9
0,609 0,613 0,616 0,620 0,623 0,627 0,630 0,633
0,637
0,640
10
0,644 0,647 0,650 0,653 0,657 0,660 0,663 0,666
0,670
0,673
11
0,676 0,679 0,682 0,686 0,689 0,692 0,695 0,698
0,701
0,704
12
0,707 0,711 0,714 0,717 0,720 0,723 0,726 0,729
0,732
0,735
13
0,738 0,741 0,744 0,747 0,750 0,752 0,755 0,758
0,761
0,764
14
0,767 0,770 0,773 0,776 0,778 0,781 0,784
0,787
0,790
0,793
15
0,795 0,798 0,801 0,804 0,807 0,809 0,812 0,815
0,818
0,820
16
0,823 0,826 0,828 0,831 0,834 0,837 0,839 0,842
0,845
0,847
17
0,850 0,853 0,855 0,858 0,861 0,863 0,866
0,871
0,874
0,868
85
Продолжение таблицы XIa.
%, последний десятичный знак
%
доля
0
1
2
3
4
5
6
7
8
9
Значения φ=2arcsin√P
18
0,876 0,879 0,881 0,884 0,887 0,889 0,892 0,894
0,897
0,900
19
0,902 0,905 0,907 0,910 0,912 0,915 0,917 0,920
0,922
0,925
20
0,927 0,930 0,932 0,935 0,937 0,940 0,942 0,945
0,947
0,950
21
0,952 0,955 0,957 0,959 0,962 0,964 0,967 0,969
0,972
0,974
22
0,976 0,979 0,981 0,984 0,986 0,988 0,991
0,993
0,996
0,998
23
1,000 1,003 1,005 1,007 1,010 1,012 1,015
1,017
1,019
1,022
24
1,024 1,026 1,029 1,031
1,033 1,036 1,038
1,040
1,043
1,045
25
1,047 1,050 1,052 1,054 1,056 1,059 1,061
1,063
1,066
1,068
26
1,070 1,072 1,075 1,077 1,079 1,082 1,084
1,086
1,088
1,091
27
1,093 1,095 1,097 1,100 1,102 1,104 1,106
1,109
1,111
1,113
28
1,115 1,117 1,120 1,122 1,124 1,126 1,129
1,131
1,133
1,135
29
1,137 1,140 1,142 1,144 1,146 1,148 1,151
1,153
1,155
1,157
30
1,159 1,161
1,164 1,166 1,168 1,170 1,172
1,174
1,177
1,179
31
1,182 1,183 1,185 1,187 1,190 1,192 1,194
1,196
1,198
1,200
32
1,203 1,205 1,207 1,209 1,211 1,213 1,215
1,217
1,220
1,222
33
1,224 1,226 1,228 1,230 1,232 1,234 1,237
1,239
1,241
1,243
34
1,245 1,247 1,249 1,251 1,254 1,256 1,258 1,260
1,262
1,264
35
1,266 1,268 1,270 1,272 1,274 1,277 1,279 1,281
1,283
1,285
36
1,287 1,289 1,291 1,293 1,295 1,297 1,299
1,302
1,304
1,306
37
1,308 1,310 1,312 1,314 1,316 1,318 1,320 1,322
1,324
1,326
38
1,328 1,330 1,333 1,335 1,337 1,339 1,341 1,343
1,345
1,347
39
1,349 1,351
1,353 1,355 1,357 1,359 1,361
1,363
1,365
1,367
40
1,369 1,371
1,374 1,376 1,378 1,380 1,382
1,384
1,386
1,388
41
1,390 1,392 1,394 1,396 1,398 1,400 1,402
1,404
1,406
1,408
42
1,410 1,412 1,414 1,416 1,418 1,420 1,422
1,424
1,426
1,428
43
1,430 1,432 1,434 1,436 1,438 1,440 1,442
1,444
1,446
1,448
44
1,451
1,453 1,455 1,457 1,459 1,461 1,463
1,465
1,467
1,469
45
1,471
1,473 1,475 1,477 1,479 1,481 1,483
1,485
1,487
1,489
46
1,491
1,493 1,495 1,497 1,499 1,501 1,503
1,505
1,507
1,509
86
Продолжение таблицы XIб.
%, последний десятичный знак (продолжение)
%
доля
0
1
2
3
4
5
6
7
8
9
Значения φ=2arcsin√P
47
1,511 1,513 1,515 1,517 1,519 1,521 1,523
1,525
1,527
1,529
48
1,531
1,533 1,535 1,537 1,539 1,541 1,543
1,545
1,547
1,549
49
1,551 1,553 1,555 1,557 1,559 1,561 1,563
1,565
1,567
1,569
50
1,571 1,573 1,575 1,577 1,579 1,581 1,583
1,585
1,587
1,589
51
1,591 1,593 1,595 1,597 1,599 1,601 1,603
1,605
1,607
1,609
52
1,611 1,613 1,615 1,617 1,619 1,621 1,623
1,625
1,627
1,629
53
1,631 1,633 1,635 1,637 1,639 1,641 1,643
1,645
1,647
1,649
54
1,651 1,653 1,655 1,657 1,659 1,661 1,663
1,665
1,667
1,669
55
1,671 1,673 1,675 1,677 1,679 1,681 1,683
1,685
1,687
1,689
56
1,691
1,693 1,695 1,697 1,699 1,701 1,703
1,705
1,707
1,709
57
1,711
1,713 1,715 1,717 1,719 1,721 1,723
1,725
1,727
1,729
58
1,731
1,734 1,736 1,738 1,740 1,742 1,744 1,746
1,748
1,750
59
1,752 1,754 1,756 1,758 1,760 1,762 1,764 1,766
1,768
1,770
60
1,772 1,774 1,776 1,778 1,780 1,782 1,784 1,786
1,789
1,791
61
1,793 1,795 1,797 1,799 1,801 1,803 1,805 1,807
1,809
1,811
62
1,813 1,815 1,817 1,819 1,821 1,823 1,826
1,828
1,830
1,832
63
1,834 1,836 1,838 1,840 1,842 1,844 1,846 1,848
1,850
1,853
64
1,855 1,857 1,859 1,861 1,863 1,865 1,867
1,869
1,871
1,873
65
1,875 1,878 1,880 1,882 1,884 1,886 1,888
1,890
1,892
1,894
66
1,897 1,899 1,901 1,903 1,905 1,907 1,909
1,911
1,913
1,916
67
1,918 1,920 1,922 1,924 1,926 1,928 1,930
1,933
1,935
1,937
68
1,939 1,941 1,943 1,946 1,948 1,950 1,952
1,954
1,956
1,958
69
1,961
1,963 1,965 1,967 1,969 1,971 1,974
1,976
1,978
1,980
70
1,982 1,984 1,987 1,989 1,991 1,993 1,995
1,998
2,000
2,002
71
2,004 2,006 2,009 2,011 2,013 2,015 2,018 2,020
2,022
2,024
72
2,026 2,029 2,031 2,033 2,035 2,038 2,040 2,042
2,044
2,047
73
2,049 2,051 2,053 2,056 2,058 2,060 2,062 2,065
2,067
2,069
74
2,071 2,074 2,076 2,078 2,081 2,083 2,085 2,087
2,090
2,092
75
2,094 2,097 2,099 2,101 2,104 2,106 2,108 2,111
2,113
2,115
87
Продолжение таблицы XIс.
%, последний десятичный знак (окончание)
%
доля
0
1
2
3
4
5
6
7
8
9
Значения φ=2arcsin√P
76
2,118 2,120 2,122 2,125 2,127 2,129 2,132 2,134
2,136
2,139
77
2,141 2,144 2,146 2,148 2,151 2,153 2,156 2,158
2,160
2,163
78
2,165 2,168 2,170 2,172 2,175 2,177 2,180 2,182
2,185
2,187
79
2,190 2,192 2,194 2,197 2,199 2,202 2,204 2,207
2,209
2,212
80
2,214 2,217 2,219 2,222 2,224 2,227 2,229 2,231
2,234
2,237
91
2,532 2,536 2,539 2,543 2,546 2,550 2,554 2357
2,561
2,564
92
2,568 2,572 2,575 2,579 2,583 2,587 2,591 2,594
2,598
2,602
93
2,606 2,610 2,614 2,618 2,622 2,626 2,630 2,634
2,638
2,642
94
2,647 2,651 2,655 2,659 2,664 2,668 2,673 2,677
2,681
2,686
95
2,691
2,295 2,700 2,705 2,709 2,714 2,719 2,724
2,729
2,734
96
2,739 2,744 2,749 2,754 2,760 2,765 2,771 2,776
2,782
2,788
97
2,793 2,799 2,805 2,811 2,818 2,824 2,830 2,837
2,844
2,851
98
2,858 2,865 2,872 2,880 2,888 2,896 2,904 2,913
2,922
2,931
99,0
2,941
2,942 2,943 2,944 2,945 2,946 2,948 2,949
2,950
2,951
99,1
2,952 2,953 2,954 2,955 2,956 2,957 2,958 2,959
2,960
2,961
99,2
2,963 2,964 2,965 2,966 2,967 2,968 2,969 2,971
2,972
2,973
99,3
2,974 2,975 2,976 2,978 2,979 2,980 2,981 2,983
2,984
2,985
99,4
2,987 2,988 2,989 2,990 2,992 2,993 2,995 2,996
2,997
2,999
99,5
3,000 3,002 3,003 3,004 3,006 3,007 3,009 3,010
3,012
3,013
99,6
3,015 3,017 3,018 3,020 3,022 3,023 3,025 3,027
3,028
3,030
99,7
3,032 3,034 3,036 3,038 3,040 3,041 3,044 3,046
3,048
3,050
99,8
3,052 3,054 3,057 3,059 3,062 3,064 3,067 3,069
3,072
3,075
99,9
3,078 3,082 3,085 3,089 3,093 3,097 3,101 3,107
3,113
3,122
100
3,142
88
Таблица XII Уровни статистической значимости разных значений
критерия φ Фишера
Р равно или
меньше
р равно или меньше (последний десятичный знак)
0
1
2
3
4
5
6
7
8
9
0,00
2,91
2,81
2,70 2,62
2,55
2,49 2,44 2,39
2,35
0,01
2,31
2,28
2,25 2,22
2,19
2,16 2,14 2,11
2,09
2,07
0,02
2,05
2,03
2,01
1,99
1,97
1,96 1,94
1,92
1,91
1,89
0,03
1,88
1,86
1,85 1,84
1,82
1,81 1,80 1,79
1,77
1,76
0,04
1,75
1,74
1,73 1,72
1,71
1,70 1,68
1,67
1,66
1,65
0,05
1,64
1,64
1,63 1,62
1,61
1,60 1,59
1,58
1,57
1,56
0,06
1,56
1,55
1,54 1,53
1,52
1,52 1,51
1,50
1,49
1,48
0,07
1,48
1,47
1,46 1,46
1,45
1,44 1,43
1,43
1,42
1,41
0,08
1,41
1,40
1,39 1,39
1,38
1,37 1,37
1,36
1,36
1,35
0,09
1,34
1,34
1,33 1,32
1,32
1,31 1,31 1,30
1,30
1,29
0,10
1,29
89