Таблица 14
реклама
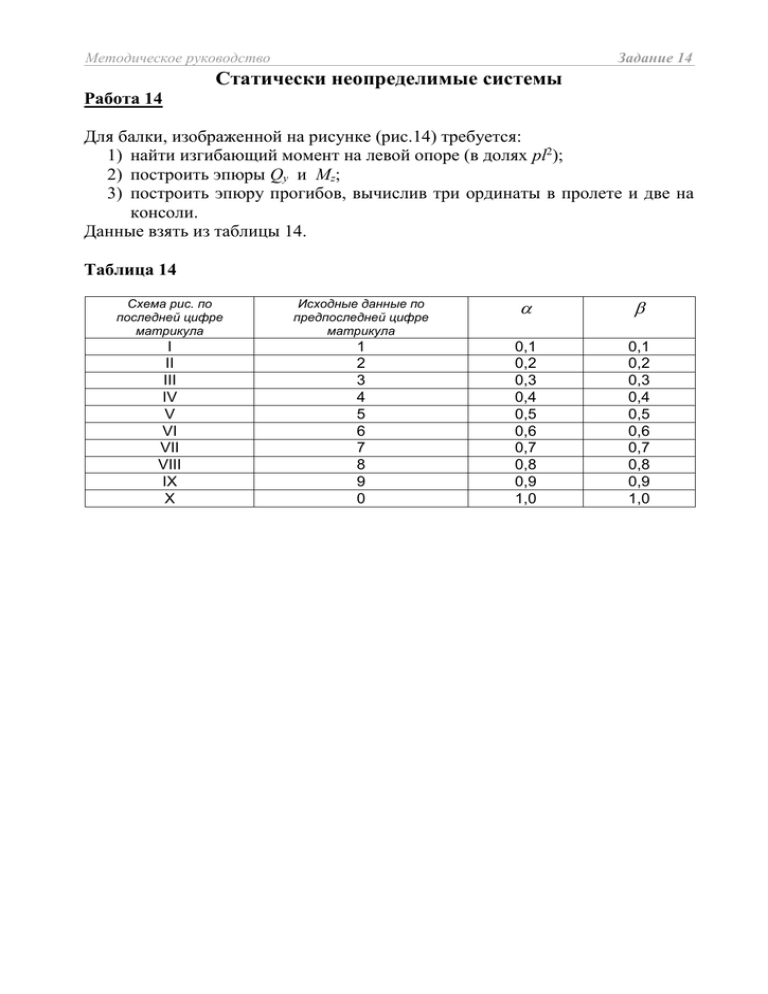
Методическое руководство Задание 14 Статически неопределимые системы Работа 14 Для балки, изображенной на рисунке (рис.14) требуется: 1) найти изгибающий момент на левой опоре (в долях pl2); 2) построить эпюры Qy и Mz; 3) построить эпюру прогибов, вычислив три ординаты в пролете и две на консоли. Данные взять из таблицы 14. Таблица 14 Схема рис. по последней цифре матрикула Исходные данные по предпоследней цифре матрикула I II III IV V VI VII VIII IX X 1 2 3 4 5 6 7 8 9 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 Методическое руководство Задание 14 I II F=pl F=pl p l l p l/2 III l/2 l IV F=pl F=pl p l/2 l/2 F=pl p l l/2 l/2 l F=pl V VI F=pl p p l/2 l/2 l l l VII F=pl VIII p p l/2 l/2 l l/2 l/2 l F=pl F=pl F=pl IX X p p l/2 l/2 F=pl l F=pl l/2 l/2 F=pl Рис.14 l Методическое руководство Задание 14 Пример решения: M=pl2 p C A D F=pl l E B l l l Определение степени статической неопределимости системы FAY н MA A FB M=pl2 FAX =0 C =0н D p E B F=pl l l l Имеем четыре неизвестные реакции опор (три в жесткой заделке А и одну в шарнирно-подвижной опоре). В данном случае силы расположены в одной плоскости, для которой можно составить только три уравнения равновесия (уравнения статики). Поэтому система является один раз статически неопределимой. 1. Составление “основной системы” метода сил 1.1 Первый вариант “основной системы” Выбираем основную систему путем замены жесткой заделки на опоре А шарнирно-неподвижной опорой и неизвестным моментом X1. Уравнение совместимости деформаций (уравнение метода сил) имеет вид 11 X 1 1 p 0 , которое физически выражает условие, что суммарный угол поворота на левой опоре от заданной нагрузки и от опорного момента X1 равен нулю. Где 11 - единичное перемещение в точке приложения неизвестного момента X1; 1 p - перемещение в той же точке А от заданной нагрузки. Определение перемещений можно выполнить или по формуле Мора или с помощью универсального уравнения изогнутой оси балки (уравнение метода начальных параметров). Статически эквивалентная “Основная система” заданной системе у M=pl2 X1 A p х C D F=pl l l E B l l Методическое руководство Задание 14 1.1.1 Определение неизвестного опорного момента X 1 Из уравнения совместности деформаций X1 1.1. 11 Определение перемещений по формуле Мора 11 где 1 p l mm 1 1 dx , 0 EI z l m1M p 0 EI z 1 p dx , m1 – единичная эпюра от единого момента, приложенного в точке А; Мр – грузовая эпюра от заданной нагрузки. Единичная эпюра m1 Реакции опор F и FB0 образуют пару сил, момент которой равен единичному 0 A моменту X 1 =1. Откуда X1 1 . 3l 3l F A0 = FB0 = у FB0 1 3l X1=1 A C х D E B l l FA0 1 3l l l m1 1/3 2/3 1 Грузовая эпюра M p FBp 2 pl M=pl2 A p C D FAp pl l F=pl l E B l l pl pl Qp ,кН pl pl2 pl2/2 Mp , кН м Методическое руководство Реакции опор FAp и FBp находим из уравнений равновесия Задание 14 6 pl 2 2 pl , pl l pl 3l p 2l 3l 0 3l 2 pl 2 pl 2 p p 2 pl . FA 3l pl 2l pl 0 FA 3l M A 0 FBp 2 MB 0 FBp Значения изгибающих моментов M p точка А Mp 0 точка С M p pl l pl 2 точка D– M p pl 2l pl l pl 2 M p pl 2 pl 2 0 D+ pl 2 pl 2 M p pl 3l pl 2l pl точка В . 2 2 Проверка в точке Е , где M p 0 (свободный конец балки) 2 M p pl 4l pl 3l pl 2 p2l 2 2 pl l 4 pl 2 3 pl 2 pl 2 2 pl 2 2 pl 2 0 . 2 Решение интегралов Мора можно выполнить способом Симпсона, для этого надо знать значения моментов на каждом участке интегрирования: в начале, в середине и в конце. Значения в серединах участков интегрирования для грузовой эпюры M p участок АС участок СD участок DB pl 2 2 pl 2 const 1 pl l pl 2 . 2 2 2 8 Значение момента M p в середине участка DB можно вычислить через 1 pl l pl 2 , ) 2 2 2 8 площадь эпюры Qp: а именно M p ( DB/2) = MD + ( Qp) =0+ ( где MD - начальное значение момента на участке DB, а ( Qp) площадь эпюры Qp на участке от точки D до середины участка. Для удобства "перемножения эпюр" по Симпсону приводятся совмещенные одна под другой эпюры m1 и M p . pl2 pl2/2 2 pl /2 pl2/8 A D C l l Mp , кН м B l E l m1 1 5/6 2/3 1/2 1/3 1/6 Методическое руководство Задание 14 "Перемножая эпюры", имеем l 11 6 EI z 2 2 5 1 4 6 2 l 2 3 6 EI 2 2 2 1 4 2 3 1 3 2 l 0 6 EI 2 1 2 1 4 0 3 6 100 4 1 1 1 4 l 1 4 36 9 4 4 9 9 36 6 36 EI 36 100 16 16 36 4 4 4 z 216 l l 6 36EI z EI z 1 p l 6 EI z l 6 EI z pl 2 5 pl 2 1 2 2 2 2 2 1 2 1 pl pl 4 pl pl 0 4 0 0 4 2 6 3 3 2 3 8 6 pl 3 5 2 2 1 1 pl 3 65 pl 3 20 8 8 24 4 1 2 6 EI z 3 3 3 3 12 6 12 EI z 6 12 EI z Отсюда X 1 1 p 11 65 pl 3 EI z 65 pl 2 6 12 EI z l 72 Методическое руководство Задание 14 1.2 Второй вариант” основной системы” Основную систему получаем, отбрасывая (заменяя) шарнирно-подвижную опору В неизвестной реакцией X1. M=pl2 p C A D F=pl l l E B X1 l l Уравнение совместимости деформаций (уравнение метода сил) имеет вид 11 X 1 1 p 0 , которое физически выражает условие, что перемещение на правой опоре от заданной нагрузки и реакции X1 равно нулю. Для определения перемещений методом Мора строим соответственно единичную и грузовую эпюры. A D C B E X1=1 l l l l m1 l 2l 3l M=pl2 p C A D F=pl l 6pl2 E B l l l 4pl2 2pl2 pl2/2 Mp΄, кН м pl2 pl2 Mp“ , кН м Mp’’’ , кН м pl2 Методическое руководство Задание 14 Где M 'p , M "p , M 'p' ' - соответственно от распределенной нагрузки p (NB! квадратичная парабола и прямая линия стыкуются на эпюре M 'p без 2 перелома), сосредоточенного момента M pl и сосредоточенной силы F pl . Перемножая эпюры, имеем 2 l 54l 3 m1m1 l 3l 11 dx 3l 3l 4 0 EI 6 EI 2 z z 0 6 EI z , при вычислении 1 p учитываем, что M P = M 'p + M "p + M 'p'' 5 pl 2 2 2 2 2 2 2 2 1 p 3 l 6 pl pl pl 4 l 5 pl pl 2 l 4 pl pl 0 2 2 l 3 2 2 2 l 4 pl pl 0 4 l 3 pl 2 pl 2 0 l 2 pl 2 pl 2 0 6 EI z 2 l 6 EI z l 6 EI z l 9 2 497 pl 4 2 l 2 pl 0 0 4 pl 0 0 0 . 2 8 24 EI z Значения в серединах участков интегрирования для грузовой эпюры M p участок АС M 'p = 5 pl 2 , M "p = pl 2 , M 'p'' = pl 2 / 2 участок СD M 'p = 3 pl 2 , M "p = pl 2 , M 'p'' =0 участок DB M 'p = 9 pl 2 / 8 , M "p =0, M 'p'' =0. Откуда X 1 1 p 11 497 pl 4 EI z 24 54l 3 EI z 497 pl . 216 Методическое руководство Задание 14 2. Второй способ раскрытия статической неопределимости Этот способ основан на универсальном уравнении M x a EI z yx y0 0 x 2 положительными приняты: М – по часовой стрелке, 2! F x b 3 3! F– вверх, px c 4 4! p – вверх и ось y вверх. y FBp 2 pl pl2 MА A C x D pl FА p l l E B l FB l Составим два уравнения, одно из которых уравнение равновесия, а другое выражает условие равенства нулю прогиба на опоре В. FA 3l M A pl 2l pl 2 0 , MB 0 при x = 3l M a 3l 02 Fa 3l 03 pl 3l l 3 pl 2 3l 2l 2 p3l 2l 4 EI z y 3l 0 0 0 2 6 6 2 24 FA 3l M A 3 pl 2 0 3 2 l 9l 2 27l 3 43 pl 4 2 FA 0 M A 2 26 24 9 9 43 pl 4 3 M A l 2 l 2 pl 4 0 2 2 24 2 MA 65 pl 4 65 pl 2 . 72 243l 2 Из составленного ранее уравнения равновесия M B 0 определяем FA 65 pl 2 3 pl 2 0 72 2 pl 65 281pl 281pl FA . 3 3l 72 72 3 216 FA 3l M A 3 pl 2 0 Из уравнения равновесия F ky FA 3l 0 находим реакцию FВ FA pl 2 pl FB 0 , откуда FB pl FA pl 281pl 497 pl . 216 216 Получили такой же результат, что в предыдущем случае при решении методом сил и с использованием формулы Мора. Проверка: M A pl l pl 2 p 2l 3l FB 3l 0 , M A 0 65 pl 2 497 pl 2 3 2 2 2 pl pl 6 pl 0. 72 216 Уравнение равновесия обращается в тождества. Методическое руководство Задание 14 3. Построение эпюр Qy и Мz 3.1 Первый вариант основной системы у M=pl2 X1 A p х C D F=pl l l E B l l Построение можно сделать двумя способами. 3.1.1Первый способ Это классический способ построения эпюр методом сечений. Реакции X 1 M A 281pl 497 pl 65 pl 2 , FA и FB найдены. 72 216 216 Теперь строим обычным путем эпюры Qy и Мz . pl2 X1=MА=65pl2/72 A C E D l FА=281pl/216 pl l B FB=497pl/216 l l 281pl/216 65pl/216 281pl/216 Qy , кН 151pl2/216 86pl2/216 pl2 pl pl2/2 Mp , кН м 65pl2/72 65pl2/216 NB! Вычисление значений изгибающих моментов производится с помощью интегральных зависимостей между Mz и Qу, т.е. значение момента в конце рассматриваемого участка равно алгебраической сумме значений моментов в начале участка и площади эпюры Qу на этом участке. При вычислении слева: 65 pl 2 MA 72 MC M A Q yAC 65 pl 2 281pl l 86 pl 2 72 216 216 Методическое руководство Задание 14 86 pl 65 pl l 151pl 216 216 216 2 2 151pl 65 pl M D pl 2 216 216 65 pl 2 1 65 281 2 108 pl 2 1 M B M D Q yDB pl pl 2 . 216 2 216 216 2 2 M D M C Q yCD Для проверки вычисляем значение MB 2 МВ, идя справа 1 1 pl l pl 2 . 2 2 Как видно результаты вычисления МВ справа и слева совпадают. 3.1.2 Второй способ Это способ основан на сложении грузовой и уточненной (исправленной) эпюр. Общие реакции опор 1 65 pl 2 281pl FA MA pl 3l 72 216 2 1 65 pl 497 pl FB FB M A FBp 2 pl , 3l 72 216 FA FAp где FA0 и FB0 единичные реакции от единичного момента МА=1, а FA0 M A и FB0 M A уточненные (исправленные) реакции опор. Тогда окончательно эпюра поперечных сил Qу будет pl pl pl Qр , кН pl 65pl/216 65pl/216 Q(МА), кН 281pl/216 65pl/216 281pl/216 Qy = Qр+ Q(МА), кН Аналогично получается эпюра изгибающих моментов Методическое руководство Задание 14 pl2 pl2/2 Mp , кН м M1= m1МА , кН м 65pl2/72 13pl2/216 65pl2/216 151pl2/216 86pl2/216 pl2 pl2/2 Mz=Mp+M1, кН м 65pl2/72 65pl2/216 Методическое руководство Задание 14 3.2 Второй вариант основной системы M=pl2 l C A D F=pl l l E B X1 l l Складывая грузовые эпюры M 'p , M "p , M 'p' ' и уточненную эпюру M 1 m1 X 1 , получим окончательную эпюру M z . Эпюра поперечных сил Q y строится как для консоли со свободного правого конца. M=pl2 p C A l D F=pl l B l E X1=497pl/216 l M1=m1X1, кНм 2 497pl /72 994pl/216 6pl2 497pl2/216 4pl2 2pl2 pl2/2 Mp΄, кН м pl2 pl2 Mp“ , кН м Mp’’’ , кН м pl2 281pl/216 65pl/216 281pl/216 Qy , кН 2 151pl /216 86pl2/216 pl2 pl pl2/2 Mp , кН м 65pl2/72 65pl2/216 Методическое руководство Задание 14 4. Контроль результатов решения 4.1 Статическая проверка pl2 X1=MА=65pl2/72 A FА=281pl/216 C l pl E D p l B FB=497pl/216 l l Подставив найденные значения реакций в уравнения равновесия, получим тождества. 281 pl 65 pl 2 2 3l pl 2l pl 2 M B 0 FA 3l M A pl 2l pl 0 216 72 281 65 2 72 72 281 281 pl 2 pl 2 0 ! 72 72 65 pl 2 2 pl l pl 2 M A 0 M A pl l pl p 2l 3l FB 3l 0 72 497 pl 65 72 72 72 6 497 432 432 p 2l 3l 3l pl 2 pl 2 0! 216 72 72 281 pl 497 pl pl 2 pl 216 216 281 216 216 2 497 497 497 pl pl 0! 216 216 Fky 0 FA pl 2 pl FB 0 4.2 Кинематическая проверка Кинематическая проверка заключается в нахождении перемещения на одной из опор, которое должно равняться нулю (угол поворота в жесткой заделке А или вертикальное перемещение в точке В). Например, вертикальное перемещение на опоре В по методу Мора находится путем перемножения единичной эпюры m1 от единичной силы, приложенной в точке В и окончательной эпюры изгибающих моментов M z . m1M z l 65 pl 2 5l 109 pl 2 86 pl 2 3l B dx 4 2l EI 6 EI 72 2 432 216 0 z z l l 86 pl 2 3l 237 pl 2 151 pl 2 l 65 pl 2 l 11 pl 2 2 l 4 l l 4 0 6 EI z 216 2 432 216 6 EI z 216 2 432 l 3832 pl 2 l 4136 pl 2 l 304 pl 2 0! 6 EI z 2 432 6 EI z 2 432 6 EI z 2 432 Методическое руководство Задание 14 l l l l m1 l 3l 2l 65pl/216 281pl/216 281pl/216 Qy , кН 2 151pl /216 86pl2/216 pl2 pl pl2/2 Mp , кН м 65pl2/72 65pl2/216 Значения в серединах участков интегрирования для эпюры M z 1 65 pl 2 86 pl 2 109 2 M z pl участок АС 2 72 216 432 участок СD участок DB 1 86 pl 2 151 pl 2 237 2 M z pl 2 216 216 432 65 pl 2 1 65 pl 173 pl l 11 pl 2 , Mz MD 216 2 216 432 2 где Q yDB / 2 - площадь эпюры Q y на участке DB/2, учитывая, что значение QyDB / 2 1 65 pl 281 pl 173 pl поперечной силы в середине этого участка Q y . 2 216 216 Методическое руководство Задание 14 5. Определение перемещений Здесь целесообразнее использовать уравнение метода начальных параметров, учитывая, что y0 0 и 0 0 . M A l 02 FA l 03 65 pl 2 l 2 281pl l 3 pl 4 304 0,234 pl 4 2 6 72 2 216 6 1296 2 3 3 2 2 M A 2l 0 FA 2l 0 pl 2l l 65 pl 4l 281pl 8l 3 pl 4 EI z y 2l 2 6 6 72 2 216 6 6 EI z y l 308 pl 4 0,238 pl 4 1296 Найдем на участке АС эпюры Мz координату х, при которой Мz=0 195 x 65 pl 2 216 x 86 l x 72 86 pl 2 l x 195l 195x 86x x 195l 0,694l . 195 86 Тогда перемещение в этой точке (в точке перегиба) M A 0,694l 02 FA 0,694l 03 65 pl 2 0,6942 l 2 EIy 0,694l 2 6 72 2 281pl 0,6943 l 3 0,145 pl 4 216 6 M 4l 02 FA 4l 03 pl 4l l 3 pl 2 4l 2l 2 p4l 2l 4 EIy 4l A 2 6 6 2 24 FB 4l 3l 3 65 pl 2 16l 2 281pl 64l 3 pl 27l 3 pl 2 4l 2 p 16l 4 6 72 2 216 6 6 2 24 497 pl l 3 0,43 pl 4 216 6 При построении эпюры прогибов надо учесть, что упругая линия обращена выпуклостью вниз там, где изгибающий момент положительный, а выпуклостью вверх там, где он отрицательный. Нулевым точкам эпюра М соответствует точки перегиба упругой линии в точке х = 0,694l перегиб упругой линии прогибов оси балки. Значения на эпюре прогибов надо pl 4 умножить на . EI z y 0,234 0,238 0,145 B A x 0,694 l l 0,431 2l 3l 4l Методическое руководство Задание 14 6. Общая картина всех эпюр, используемых при решении 6.1 Первый вариант основной системы у M=pl2 X1 A p х C D F=pl l l l l FB0 X1=1 A E B C 1 3l х D E B l l FA0 1 3l l l m1 1/3 2/3 M=pl 1 A FBp 2 pl 2 p C D FAp pl F=pl l E B l l l pl pl Qp ,кН pl 2 pl pl2/2 Mp , кН м 65pl/216 65pl/216 Q(МА), кН M1= m1МА , кН м 65pl2/72 13pl2/216 65pl2/216 281pl/216 65pl/216 281pl/216 Qy = Qр+ Q(МА), кН pl 2 86pl2/216 pl2 151pl /216 pl2/2 Mz=Mp+M1, кН м 65pl2/72 65pl2/216 2 Методическое руководство Задание 14 6.2 Второй вариант основной системы M=pl2 p C A l E B X1=497pl/216 D F=pl l l l m1 l 2l 3l M1=m1X1, кНм 2 497pl /72 497pl2/216 994pl/216 6pl2 4pl2 2pl2 pl2/2 Mp΄, кН м pl2 pl2 Mp“ , кН м Mp’’’ , кН м pl2 281pl/216 65pl/216 281pl/216 Qy , кН 2 151pl /216 86pl2/216 pl2 pl pl2/2 Mp , кН м 65pl2/72 65pl2/216